buck电路 小信号模型传递函数
BuckBoost传递涵数

九、在稳定状态下 d (t ) 0 ,即瞬态过后,电感电流、电容电压、输入电流均达到各自的稳定值,则:
Vo Vin * IL
D 1 D
(9-1) (9-2)
Io 1 V Vo * o 1 D 1 D R 1 D R I in I L D
(9-3)
十、把式(9-1)代入式(8-2)得:
图 4 Q 截止等效电路
I sw :开关管电流平均值, iC (t ) :电容电流瞬时值,
d (t ) :开关管导通占空比瞬时值,
D :开关管导通占空比,
1 x (t ) Ts Ts
t Ts
x( )d :代表 x(t ) 在一个周期里的低频分量平均值。
t
五、Q 导通时,如图 3:
(10-1)
L
把式(9-1)代入(9-2)得
IL
把式(10-2)代入(8-4)得
D D 1 Vin *Vin * 1 D R 1 D 1 D 2 R
(10-2)
^ ^ d v (t ) 1 ^ D C o vo (t ) Vin d (t ) 1 D iL (t ) 2 dt R 1 D R
1 Vin d ( s ) 1 D vo ( s ) 1 D
1 1 D iL ( s ) Vin d ( s ) vo ( s ) sL1 D sL
把式(12-2)代入(11-3)得
(12-2)
sCvo ( s )
D 1 1 1 D vo ( s ) V d s D V d s v s ( ) 1 ( ) ( ) in in o sL1 D R sL 1 D 2 R
15、buck变换器DCM小信号建模
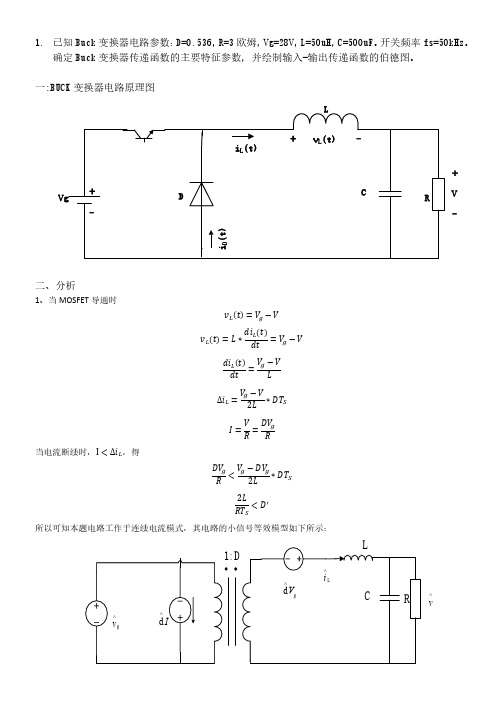
一:BUCK 变换器电路原理图 L
+ Vg
-
iL(t)
+ vL(t) -
D
C
+
带入参数得:
0.536 ∗ 3 ������ (������) =
7.5 ∗ 10 ∗ ������ + 5 ∗ 10 ∗ ������ + 3
② 、控制扰动与输出扰动的传递函数: 忽略输入扰动的作用,其小信号模型等效电路图为:
L
iL
d Vg
C
R
v
������
∗
1 ������������
������(������) ������ ������(������)
MATLAB 程序如下: >>num=[0.536*3]; >>den=[7.5*10^(-8),5*10^(-5),3]; >>figure(1);bode(num,den);grid; Bode 图如下:
RV -
iD(t)
二、分析
1、当 MOSFET 导通时
������ (������) = ������ − ������
������������ (������)
������ (������) = ������ ∗
= ������ − ������
������������
������������ (������) ������ − ������
应用三端开关器件模型法推导开关变换器的传递函数

VI = I c × R L + Vcp + Vout VI 1 ( ) Vout = RL 1 D 1+ R(1 D) 2
Boost变换器的推导
交流小信号分析:稳态直流分量为零(输入电压为零) 原边电压环路方程: 副边电压环路方程:
∧ ∧ ∧ i c × ( Ls + R L ) + v cp v ap = 0 ∧ ∧ ∧ v cp = D v ap + d V ap V ap = Vout ∧ ∧ v = v out cp ∧ ∧ ∧ 1 (i c i a )( + Rc ) // R = v out cs
d× I c
VI
+
ia
D
1: D
ic
Buck变换器的推导
稳态直流分析:令 d (t ) = 0 ,电路中电感短路,电容开路
∧
D × VI = I c × ( R L + R )
Vout = I c × R
∧ ∧
Vout × ( R L + R ) VI = R× D
交流小信号分析:稳态直流分量为零(输入电压为零)
应用三端开关器件模型法推导开 关变换器的传递函数
Buck变换器的推导
c
Gate drive C R
ia
VI
a
L
RL
ic
RC
Vout
p
Buck变换器的推导
在一个开关周期内:
i c (t ) i a (t ) = 0
v ap (t ) v cp (t ) = 0
0 ≤ t ≤ dT dT ≤ t ≤ T
Vcp + vcp = ( D × d (t )) × (Vap + vap ) = D × Vap + D × vap + d (t )× Vap + vap × d (t ) = D × Vap + D × vap + d (t )× Vap
Buck电路小信号分析

1. Buck 电路小信号线性化交流模型为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-=+-=)(~)(~)(~)(~)(~)(~)(~)(~)(~)(~o o o t d I t i D t i R t u t i dt t u d C t d V t u t u D dt t i d L L L in L in in L (1-1)2. Buck 电路小信号交流模型等效电路图2-1Buck 电路小信号交流模型等效电路3. 传递函数 ()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++=++===112020s R L LCs V s d s v s R L LCs D s v s v g s v o s d g o g (3-1) 谐振频率Hz LC f 3.503210==π--------徐德鸿.电力电子系统建模及控制.机械工业出版社,2005.4. 主电路参数设计(1)输入直流电压in V :100V(2)输出电压o V :50V , 纹波系数:00001≤δ(3)占空比:5.0o ==inV V D (4)负载:Ω=10R(5)功率:W R V P 2502o ==(6)开关频率:kHz f s 10=(7)开关管由于是小功率DC-DC 变换器,所以选用功率MOSFET 作为开关器件,MOSFET 的型号选择IRF250(V U DS 200=,A I D 30=,()Ω=085.0on DS R )。
(8)电感电感的大小决定了开关电源主回路处于CCM 还是DCM 模式,由Buck 电路工作于电感电流连续状态下的条件:21D RT L S -≥ (4-1)得: S RT D L 21-≥(4-2) 所以mH L 25.0≥,取mH L 1=(9)电容电容的作用是保持恒定的输出电压,可根据允许的输出电压纹波值来选择电容的大小: 所以F C μ5.62=,取F C μ100=--------[1] 裴云庆,杨旭,王兆安.开关稳压电源的设计和应用[M].机械工业出版社,2010.[2] 英飞凌公司.IRF250 数据手册.[3] 巩鲁洪, 曹文思. 基于BUCK 变换器的建模与设计[J]. 科学之友,2008.5. 扰动信号占空比扰动:)2sin()(~t f d t d sd π=其中: 005.05.01001=⨯≤d kHz kHz f sd 110101=⨯≤ 输入电压扰动:)2sin()(~t f u t u su in π= 其中: V V u 5.0501001=⨯≤kHz kHz f sd 110101=⨯≤ 负载扰动:)2sin()(~t f i t i si o π=其中: A A I 05.051001=⨯≤kHz kHz f sd 110101=⨯≤ 6. 仿真因素电路与小信号模型对比输入电压小扰动)(~t u in占空比小扰动)(~t d → 输出电压)(~o t u 纹波等稳态性能负载小扰动7. 仿真结果分析电路与小信号模型对比,模型是否精确?加各种扰动,对输出电压的影响?。
DCDC降压BUCK变换的基本介绍
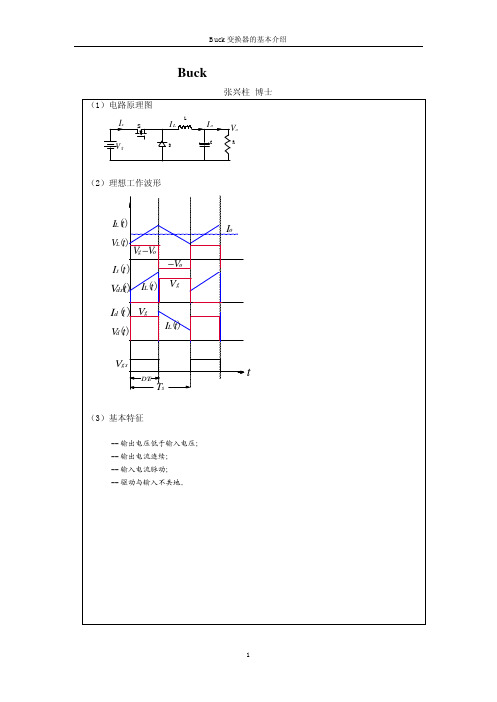
G ′ig ( s ) ≈
其中: G ′vc 0 =
ωp =
F1 1 1 π 1 ,ωzc = ,Qp = ,ωn = ,ωzp = RC RC C π [ mcD′ − 0.5] Ts RC
F1 = 1+
RT s L
( mcD ′ − 0.5) , F 2 = D[ mcD ′ − (1 −
D )] 2
Buck 变换器在峰值电流控制下的 CCM 小信号传递函数
张兴柱 博士 (1)峰值电流型控制的传递函数框图(电压开环)
ˆ vo( s)
iˆ( s) L
ˆ vg ( s)
ˆ vo( s) = Gvd × d (s) + Gvg × vg (s) − Z out × ˆ(s) ˆ ˆ io
ˆ i o(s )
Buck 变换器的 CCM 稳态关系
张兴柱 博士 (1)电路原理图
Is
Vg
L
s
IL
D
Io
C
Vo
R
(2)CCM 稳态关系
= DVg 输入/输出电流关系: Ig = DI o 其它关系: IL = I o R Rg = 2 D
输入/输出电压关系: Vo
1
Buck 变换器的 DCM 稳态关系
Buck 变换器的 DCM 稳态关系
Gig ( s ) =
Gii( s ) =
其中: ω 0 =
1 1 , Q= ω 0[ L R + ( RL + RC ) C] LC
RL 1 1 , ωzc = , ωzp = L RC C RC
ωzL =
1
Buck 变换器的 DCM 小信号传递函数
Buck 变换器的 DCM 小信号传递函数
20170715-Buckboost变换器在电阻负载下的小信号传递函数
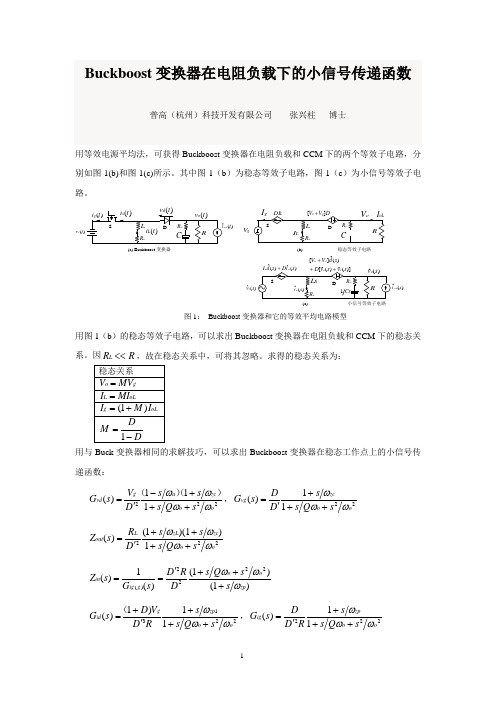
Buckboost 变换器在电阻负载下的小信号传递函数普高(杭州)科技开发有限公司 张兴柱 博士用等效电源平均法,可获得Buckboost 变换器在电阻负载和CCM 下的两个等效子电路,分别如图1(b)和图1(c)所示。
其中图1(b )为稳态等效子电路,图1(c )为小信号等效子电路。
)(t v g )(tgV(ˆs vg )(ˆ][s dV V g o +)(ˆs oL图1: Buckboost 变换器和它的等效平均电路模型用图1(b )的稳态等效子电路,可以求出Buckboost 变换器在电阻负载和CCM 下的稳态关系。
因R R L <<,故在稳态关系中,可将其忽略。
求得的稳态关系为:Buckboost 变换器在稳态工作点上的小信号传递函数:222111)(o o zc a g vd s Q s s s D V s G ωωωω+++−′=)()(,2211)(o o zc vg s Q s s D Ds Gωωω+++′= 2221)1)(1()(oo zc zL L out s Q s s s D R s Z ωωωω++++′=)1()1()(1)(2222)(zp o o g ig in s s Q s D R D s G s Z ωωω+++′== 221311)1)(o o zp g id s Q s s R D V D s G ωωω+++′+=(,22211)(oo zpig s Q s s R D D s G ωωω+++′=22111)(o o zcii s Q s s D s G ωωω+++′=其中:D D −=′1,LC D o ′=ω,])([122C D R R R D L Q L c o ′++′=ω,DL R D a 2′=ω L R L zL =ω,C R C zc 1=ω,RC zp 1=ω,RCD zp +=11ω有两个小信号传递函数,即)()(s G g id ,)()(s G g ii 没有给出,有兴趣的读者,可以作为作业自己去推导。
Buck电路的小信号频域模型

在已知环路其他部分的传递函数表达式后,即可设计电压误差放大器了。
由于KLC提供了一个零点和两个谐振极点,因此,一般将E/A设计成PI调节器即可,KEA=KP(1+ωz/s)。
其中ωz用于消除稳态误差,一般取为KLC零极点的1/10以下;KP用于使剪切频率处的开环增益以-20dB/十倍频穿越0dB线,相角裕量略小于90°。
2 电压模式控制(VMC)电压模式控制方法仅采用单电压环进行校正,比较简单,容易实现,可以满足大多数情况下的性能要求,如图2所示。
图2中,当电压误差放大器(E/A)增益较低、带宽很窄时,Vc波形近似直流电平,并有D=Vc/Vs (15)d=Vc'/Vs (16)式(16)为式(15)的小信号波动方程。
整个电路的环路结构如图3所示。
图3没有考虑输入电压的变化,即假设Uin=0。
图3中,(一般为0)及分别为电压给定与电压输出的小信号波动;KFB=UREF/Uo,为反馈系数;误差e为输出采样值偏离稳态点的波动值,经电压误差放大器KEA放大后,得;KMOD为脉冲宽度调制器增益,KMOD=d/=1/Vs;KPWR为主电路增益,KPWR=/d=Uin;KLC为输出滤波器传递函数,KLC=(1+sCRe)/[S2LC+s(ReC+L/Ro)+1]。
在已知环路其他部分的传递函数表达式后,即可设计电压误差放大器了。
由于KLC提供了一个零点和两个谐振极点,因此,一般将E/A设计成PI调节器即可,KEA=KP(1+ωz/s)。
其中ωz用于消除稳态误差,一般取为KLC零极点的1/10以下;KP用于使剪切频率处的开环增益以-20dB/十倍频穿越0dB线,相角裕量略小于90°。
VMC方法有以下缺点:1)没有可预测输入电压影响的电压前馈机制,对瞬变的输入电压响应较慢,需要很高的环路增益;2)对由L和C产生的二阶极点(产生180°的相移)没有构成补偿,动态响应较慢。
VMC的缺点可用下面将要介绍的CMC方法克服。
buck电路 小信号模型传递函数

buck电路小信号模型传递函数Buck电路是一种常用的DC-DC转换电路,其特点在于输入电压高于输出电压,并且可以通过调节占空比来控制输出电压。
在设计和分析Buck电路时,需要推导出其小信号模型和传递函数。
下面将分步骤阐述如何进行这些推导。
1. Buck电路的基本原理Buck电路由开关管、输出电容和负载组成。
当开关管导通时,电感存储了电流,然后当开关管关断时,电感的电流通过输出电容和负载产生输出电压。
通过调节开关管的导通时间占空比,可以控制输出电压的大小。
2. 推导Buck电路的小信号模型为了推导Buck电路的小信号模型,需要采用线性化的方法,将非线性元件进行虚拟短路或虚拟开路。
以Buck电路为例,假设开关管T的导通时间为DT,开关管关断时间为(1-D)T。
因此,开关管T的小信号模型可以表示为:I = gm(Vgs-Vth)Vds = VdVgs = Vin – Vout其中,I为T管的源电流,gm为T管的跨导,Vgs为T管的栅极-源极电压,Vth为T管的阈值电压,Vds为T管的漏极-源极电压,Vin 为输入电压,Vout为输出电压。
3. 推导Buck电路的传递函数Buck电路的传递函数为输出电压与输入电压之比。
在推导传递函数时,可以采用控制电压法或控制电流法。
以控制电压法为例,假设输入电压为Vin,输出电压为Vout,输出电容为C,开关管导通时间为DT,电感为L,电阻为R。
则可以得到以下方程:Vin = Vout + L(di/dt) + Vrdi/dt = (Vout – Vc)/L其中,Vr为开关管的二极管反向电压,di/dt为电感电流的变化速率,Vc为电容器的电压。
带入传递函数公式:Vout/Vin = 1/(1-D)可以得到Buck电路的传递函数为1/(1-D),这意味着通过调节开关管的占空比,可以控制输出电压的大小。
总结:Buck电路的小信号模型和传递函数的推导可以帮助我们更好地理解Buck电路的工作原理,并在电路设计和分析中应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
buck电路小信号模型传递函数
Buck电路是一种常见的降压型DC-DC转换器,其小信号模型传递函数是指在小信号条件下,输入电压和输出电压之间的传递函数关系。
在实际应用中,了解Buck电路的小信号模型传递函数对于设计和优化电路具有重要意义。
Buck电路的小信号模型传递函数可以通过对电路进行线性化处理得到。
在小信号条件下,电路中的元件可以被视为线性元件,因此可以使用线性电路分析方法来求解电路的传递函数。
具体来说,可以将Buck电路分为两个部分:输入端和输出端。
输入端包括输入电压源和输入电感,输出端包括输出电感、输出电容和负载电阻。
在小信号条件下,可以将输入电压和输出电压表示为其平均值加上一个小信号分量,即:
Vin = Vavg + δVin
Vout = Vavg + δVout
其中,δVin和δVout表示输入电压和输出电压的小信号分量。
根据线性电路分析方法,可以得到Buck电路的小信号模型传递函数为:
H(s) = δVout / δVin = -D / (1-D) * 1 / (sLout + Rload + 1 / (sCout))其中,D表示开关管的导通比,Lout表示输出电感的电感值,Cout 表示输出电容的电容值,Rload表示负载电阻的阻值,s表示复频域
变量。
从上式可以看出,Buck电路的小信号模型传递函数与电路中的元件参数密切相关。
例如,当输出电感的电感值增大时,传递函数的分母会增大,从而导致传递函数的幅频特性发生变化。
同样地,当负载电阻的阻值增大时,传递函数的分母也会增大,从而导致传递函数的幅频特性发生变化。
在实际应用中,了解Buck电路的小信号模型传递函数可以帮助工程师更好地设计和优化电路。
例如,可以通过调整电路中的元件参数来改变传递函数的幅频特性,从而实现更好的电路性能。
此外,还可以通过仿真和实验验证传递函数的准确性,从而进一步优化电路设计。
Buck电路的小信号模型传递函数是电路设计和优化中的重要概念。
了解传递函数的特性可以帮助工程师更好地设计和优化电路,从而实现更好的电路性能。
