《中级计量经济学》非选择题 参考答案.
计量经济学(数字教材版)课后习题参考答案

课后习题参考答案第二章教材习题与解析1、 判断下列表达式是否正确:y i =β0+β1x i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i ,i =1,2,⋯nE(y i |x i )=β0+β1x i +u i ,i =1,2,⋯n E(y i |x i )=β0+β1x i ,i =1,2,⋯nE(y i |x i )=β̂0+β̂1x i ,i =1,2,⋯ny i =β0+β1x i +u i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n y ̂i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n答案:对于计量经济学模型有两种类型,一是总体回归模型,另一是样本回归模型。
两类回归模型都具有确定形式与随机形式两种表达方式:总体回归模型的确定形式:X X Y E 10)|(ββ+= 总体回归模型的随机形式:μββ++=X Y 10样本回归模型的确定形式:X Y 10ˆˆˆββ+= 样本回归模型的随机形式:e X Y ++=10ˆˆββ 除此之外,其他的表达形式均是错误的2、给定一元线性回归模型:y =β0+β1x +u (1)叙述模型的基本假定;(2)写出参数β0和β1的最小二乘估计公式;(3)说明满足基本假定的最小二乘估计量的统计性质; (4)写出随机扰动项方差的无偏估计公式。
答案:(1)线性回归模型的基本假设有两大类,一类是关于随机误差项的,包括零均值、同方差、不序列相关、满足正态分布等假设;另一类是关于解释变量的,主要是解释变量是非随机的,如果是随机变量,则与随机误差项不相关。
(2)12ˆi iix yxβ=∑∑,01ˆˆY X ββ=- (3)考察总体的估计量,可从如下几个方面考察其优劣性:1)线性性,即它是否是另一个随机变量的线性函数; 2)无偏性,即它的均值或期望是否等于总体的真实值;3)有效值,即它是否在所有线性无偏估计量中具有最小方差;4)渐进无偏性,即样本容量趋于无穷大时,它的均值序列是否趋于总体真值; 5)一致性,即样本容量趋于无穷大时,它是否依概率收敛于总体的真值;6)渐进有效性,即样本容量趋于无穷大时,它在所有的一致估计量中是否具有最小的渐进方差。
计量经济学题库(超完整版)及答案.详解

计量经济学题库(超完整版)及答案.详解计量经济学题库计算与分析题(每⼩题10分)1X:年均汇率(⽇元/美元) Y:汽车出⼝数量(万辆)问题:(1)画出X 与Y 关系的散点图。
(2)计算X 与Y 的相关系数。
其中X 129.3=,Y 554.2=,2X X 4432.1∑(-)=,2Y Y 68113.6∑(-)=,()()X X Y Y ∑--=16195.4 (3)采⽤直线回归⽅程拟和出的模型为 ?81.72 3.65YX =+ t 值 1.2427 7.2797 R 2=0.8688 F=52.99解释参数的经济意义。
2.已知⼀模型的最⼩⼆乘的回归结果如下:i i ?Y =101.4-4.78X 标准差(45.2)(1.53) n=30 R 2=0.31 其中,Y :政府债券价格(百美元),X :利率(%)。
回答以下问题:(1)系数的符号是否正确,并说明理由;(2)为什么左边是iY ⽽不是i Y ;(3)在此模型中是否漏了误差项i u ;(4)该模型参数的经济意义是什么。
3.估计消费函数模型i i i C =Y u αβ++得i i ?C =150.81Y + t 值(13.1)(18.7) n=19 R 2=0.81 其中,C :消费(元) Y :收⼊(元)已知0.025(19) 2.0930t =,0.05(19) 1.729t =,0.025(17) 2.1098t =,0.05(17) 1.7396t =。
问:(1)利⽤t 值检验参数β的显著性(α=0.05);(2)确定参数β的标准差;(3)判断⼀下该模型的拟合情况。
4.已知估计回归模型得i i ?Y =81.7230 3.6541X + 且2X X 4432.1∑(-)=,2Y Y 68113.6∑(-)=,求判定系数和相关系数。
5.有如下表数据(1拟合什么样的模型⽐较合适?(2)根据以上数据,分别拟合了以下两个模型:模型⼀:16.3219.14P U=-+ 模型⼆:8.64 2.87P U =-分别求两个模型的样本决定系数。
计量经济学课后题答案
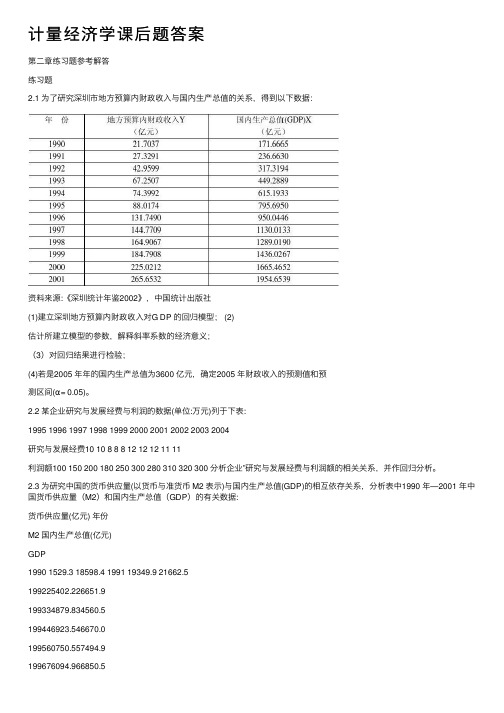
计量经济学课后题答案第⼆章练习题参考解答练习题2.1 为了研究深圳市地⽅预算内财政收⼊与国内⽣产总值的关系,得到以下数据:资料来源:《深圳统计年鉴2002》,中国统计出版社(1)建⽴深圳地⽅预算内财政收⼊对G DP 的回归模型; (2)估计所建⽴模型的参数,解释斜率系数的经济意义;(3)对回归结果进⾏检验;(4)若是2005 年年的国内⽣产总值为3600 亿元,确定2005 年财政收⼊的预测值和预测区间(α= 0.05)。
2.2 某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费10 10 8 8 8 12 12 12 11 11利润额100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系,并作回归分析。
2.3 为研究中国的货币供应量(以货币与准货币 M2 表⽰)与国内⽣产总值(GDP)的相互依存关系,分析表中1990 年—2001 年中国货币供应量(M2)和国内⽣产总值(GDP)的有关数据:货币供应量(亿元) 年份M2 国内⽣产总值(亿元)GDP1990 1529.3 18598.4 1991 19349.9 21662.5199225402.226651.9199334879.834560.5199446923.546670.0199560750.557494.9199676094.966850.5199790995.373142.71998104498.576967.21999119897.980579.42000134610.388228.12001158301.994346.4资料来源:《中国统计年鉴2002》,第51 页、第662 页,中国统计出版社对货币供应量与国内⽣产总值作相关分析,并说明分析结果的经济意义。
计量经济学试题答案

计量经济学试题一答案一、判断题(20分)1.线性回归模型中,解释变量是原因,被解释变量是结果。
(F)2.多元回归模型统计显著是指模型中每个变量都是统计显著的。
(F)3.在存在异方差情况下,常用的OLS法总是高估了估计量的标准差。
(F)4.总体回归线是当解释变量取给定值时因变量的条件均值的轨迹。
(Y)5.线性回归是指解释变量和被解释变量之间呈现线性关系。
(F)6.判定系数2R的大小不受回归模型中所包含的解释变量个数的影响。
( F )7.多重共线性是一种随机误差现象。
(F)8.当存在自相关时,OLS估计量是有偏的并且也是无效的。
(F )9.在异方差的情况下,OLS估计量误差放大的原因是从属回归的2R变大。
(F )10.任何两个计量经济模型的2R都是可以比较的。
(F )二.简答题(10)1.计量经济模型分析经济问题的基本步骤。
(4分)答:1)经济理论或假说的陈述2) 收集数据3)建立数理经济学模型4)建立经济计量模型5)模型系数估计和假设检验6)模型的选择7)理论假说的选择8)经济学应用2.举例说明如何引进加法模式和乘法模式建立虚拟变量模型。
(6分)答案:设Y为个人消费支出;X表示可支配收入,定义210t D ⎧=⎨⎩2季度其他31t D ⎧=⎨⎩3季度其他 140D t ⎧=⎨⎩4季度其他如果设定模型为12233445t t t t t t Y B B D B D B D B X u =+++++此时模型仅影响截距项,差异表现为截距项的和,因此也称为加法模型。
如果设定模型为()()()12233445627384t t t t tt t t t t t tY B B D B D B D B X B D X B D X B D X u =++++++++此时模型不仅影响截距项,而且还影响斜率项。
差异表现为截距和斜率的双重变化,因此也称为乘法模型。
三.下面是我国1990-2003年GDP 对M1之间回归的结果。
中级计量课后习题参考答案(第九章)

中级计量课后习题参考答案(第九章)第九章参考答案1、表⾯不相关回归的含义是,所涉及的各个回归似乎不相关,但实际上相关。
各个回归⽅程分别写出,这使得它们似乎不相关,但是它们有共同点。
在本章的例⼦中,四个回归中的每⼀个关系到⼀个不同的制造产业,但它们都会受到宏观经济条件变动(如衰退)的影响。
⼀般来说,影响⼀个回归结果的事件也很可能影响其他回归的结果,这个事实表明,表⾯不相关回归中的各回归之间存在相关。
这种相关在数学上表现为扰动项跨⽅程相关。
表⾯不相关回归的步骤是:(1)⽤ols法分别估计每个⽅程,计算和保存回归中得到的残差;(2)⽤这些残差来估计扰动项⽅差和不同回归⽅程扰动项之间的协⽅差;(3)上⼀步估计的扰动项⽅差和协⽅差被⽤于执⾏⼴义最⼩⼆乘法,得到各⽅程系数的估计值。
2、在不同的横截⾯种类的截距之间的差异被认为是固定的⽽不是随机的情况下,应采⽤固定效应模型。
如果横截⾯个体是随机地被选择出来代表⼀个较⼤的总体,则采⽤随机效应模型⽐较合适。
随机效应模型与固定效应模型⼀样,允许不同横截⾯种类的截距不同,但这种不同被认为是随机的,⽽不是固定的。
3、随机影响模型的扰动项不再满⾜普通最⼩⼆乘法各期扰动项相互独⽴的假设,扰动项的⼀个分量在各期都相同。
4、并不总是。
尽管将数据合在⼀起将增加⾃由度,但有时采⽤混合数据也是不合适的。
如果不同横截⾯种类的斜率系数不同的话,则最好是分别回归。
如果试图通过使⽤斜率虚拟变量来解决不同横截⾯种类不同斜率系数的问题,需要假定扰动项⽅差为常数。
⽽采⽤分别回归,每个回归的扰动项⽅差可以不同,也就是每个产业或每个横截⾯种类的扰动项⽅差不同。
5、随机系数模型即每个横截⾯个体的解释变量对被解释变量的影响在横截⾯个体之间的差异的变动时随机的。
有滞后因变量做⾃变量的动态模型就是动态⾯板数据模型。
6、(1)对钢铁产业⽤OLS法估计的结果如下:Dependent Variable: Y1Method: Least SquaresDate: 12/02/10 Time: 10:39Sample: 1980 2000Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C 3919.180 1702.691 2.301756 0.0335EMP1 31.99998 5.305756 6.031181 0.0000OTM1 722.7758 348.2873 2.075229 0.0526R-squared 0.674135 Mean dependent var 10339.75Adjusted R-squared 0.637928 S.D. dependent var 1653.825S.E. of regression 995.1473 Akaike info criterion 16.77522Sum squared resid 17825726 Schwarz criterion 16.92444Log likelihood -173.1398 Hannan-Quinn criter. 16.80761F-statistic 18.61879 Durbin-Watson stat 0.436339Prob(F-statistic) 0.000041橡胶和塑料产业:Dependent Variable: Y2Method: Least SquaresDate: 12/02/10 Time: 10:40Sample: 1980 2000Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -49122.54 3331.606 -14.74440 0.0000EMP2 135.4948 6.703255 20.21328 0.0000OTM2 2646.557 1087.284 2.434099 0.0256R-squared 0.989264 Mean dependent var 80662.43Adjusted R-squared 0.988071 S.D. dependent var 13744.48S.E. of regression 1501.188 Akaike info criterion 17.59746Sum squared resid 40564183 Schwarz criterion 17.74668Log likelihood -181.7734 Hannan-Quinn criter. 17.62985F-statistic 829.2748 Durbin-Watson stat 1.590448Prob(F-statistic) 0.000000SUR的估计:在主菜单选择Object->New Object,在弹出的对话框中选择System,点击OK。
(完整word版)计量经济学中级教程(潘省初 清华大学出版社)课后习题答案

计量经济学中级教程习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据(4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3 时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YYn==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 经典线性回归模型2.1 判断题(说明对错;如果错误,则予以更正) (1)对 (2)对 (3)错只要线性回归模型满足假设条件(1)~(4),OLS 估计量就是BLUE 。
(4)错R 2 =ESS/TSS 。
(5)错。
我们可以说的是,手头的数据不允许我们拒绝原假设。
(6)错。
因为∑=22)ˆ(tx Var σβ,只有当∑2t x 保持恒定时,上述说法才正确。
2.2 应采用(1),因为由(2)和(3)的回归结果可知,除X 1外,其余解释变量的系数均不显著。
《中级计量经济学》非选择题参考答案

《中级计量经济学》非选择题参考答案第3章多元线性回归模型3.4.3 简答题、分析与计算题1.给定二元回归模型:yt=b0+b1x1t+b2x2t+ut (t=1,2,…n)(1) 叙述模型的古典假定;(2)写出总体回归方程、样本回归方程与样本回归模型;(3)写出回归模型的矩阵表示;(4)写出回归系数及随机误差项方差的最小二乘估计量,并叙述参数估计量的性质;(5)试述总离差平方和、回归平方和、残差平方和之间的关系及其自由度之间的关系。
2.在多元线性回归分析中,为什么用修正的决定系数衡量估计模型对样本观测值的拟合优度?3.决定系数R与总体线性关系显著性F检验之间的关系;在多元线性回归分析中,F检验与t检验有何不同?在一元线性回归分析中二者是否有等价的作用?4.为什么说对模型施加约束条件后,其回归的残差平方和一定不比未施加约束的残差平方和小?在什么样的条件下,受约束回归与无约束回归的结果相同?5.观察下列方程并判断其变量是否呈线性,系数是否呈线性,或都是或都不是。
(1)yt=b0+b1xt3+ut (2)yt=b0+b1logxt+ut (3)logyt=b0+b1logxt+ut (4)yt=b0+b1(b2 xt)+ut(5)yt=b0/(b1xt)+ut (6)yt=1+b0(1 xt1)+ut (7)yt=b0+b1x1t+b2x2t/10+ut 6.常见的非线性回归模型有几种情况?7.指出下列模型中所要求的待估参数的经济意义:(1)食品类需求函数:lnY=α0+α1lnI+α2lnP1+α3lnP2+u中的α1,α2,α3(其中Yb2为人均食品支出额,I为人均收入,P。
1为食品类价格,P2为其他替代商品类价格)(2)消费函数:Ct=β0+β1Yt+β2Yt 1+ut中的β1和β2(其中C为人均消费额,Y为人均收入)。
8.设货币需求方程式的总体模型为ln(Mt/Pt)=b0+b1ln(rt)+b3ln(RGDPt)+ut其中M为名义货币需求量,P为物价水平,r为利率,RGDP 为实际国内生产总值。
计量经济学-参考答案3-4

第三章 多元线性回归模型一、名词解释1、多元线性回归模型:在现实经济活动中往往存在一个变量受到其他多个变量影响的现象,表现在线性回归模型中有多个解释变量,这样的模型被称做多元线性回归模型,多元是指多个解释变量2、调整的可决系数2R :又叫调整的决定系数,是一个用于描述多个解释变量对被解释变量的联合影响程度的统计量,克服了2R 随解释变量的增加而增大的缺陷,与2R 的关系为2211(1)1n R R n k -=----。
3、偏回归系数:在多元回归模型中,每一个解释变量前的参数即为偏回归系数,它测度了当其他解释变量保持不变时,该变量增加1单位对被解释变量带来的平均影响程度。
4、正规方程组:采用OLS 方法估计线性回归模型时,对残差平方和关于各参数求偏导,并令偏导数为0后得到的方程组,其矩阵形式为ˆX X X Y β''=。
5、方程显著性检验:是针对所有解释变量对被解释变量的联合影响是否显著所作的检验,旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出判断。
二、单项选择题 1、C 2、A3、B4、A5、C6、C7、A8、D 9、B 10、D三、多项选择题1、ACDE2、BD3、BCD4、BC5、AD四、判断题、 1、√2、√3、×4、×5、√五、简答题 1、 答:多元线性回归模型与一元线性回归模型的区别表现在如下几个方面:一是解释变量的个数不同;二是模型的经典假设不同,多元线性回归模型比一元线性回归模型多了个“解释变量之间不存在线性相关关系”的假定;三是多元线性回归模型的参数估计式的表达更为复杂。
2、 答:在满足经典假设的条件下,参数的最小二乘估计量具有线性性、无偏性以及最小性方差,所以被称为最优线性无偏估计量(BLUE )对于多元线性回归最小二乘估计的正规方程组,能解出唯一的参数估计量的条件是(X X ')-1存在,或者说各解释变量间不完全线性相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 多元线性回归模型3.4.3 简答题、分析与计算题1.给定二元回归模型:t t t t u x b x b b y +++=22110 (t=1,2,…n)(1) 叙述模型的古典假定;(2)写出总体回归方程、样本回归方程与样本回归模型;(3)写出回归模型的矩阵表示;(4)写出回归系数及随机误差项方差的最小二乘估计量,并叙述参数估计量的性质;(5)试述总离差平方和、回归平方和、残差平方和之间的关系及其自由度之间的关系。
2.在多元线性回归分析中,为什么用修正的决定系数衡量估计模型对样本观测值的拟合优度?3.决定系数2R 与总体线性关系显著性F 检验之间的关系;在多元线性回归分析中,F 检验与t 检验有何不同?在一元线性回归分析中二者是否有等价的作用?4.为什么说对模型施加约束条件后,其回归的残差平方和一定不比未施加约束的残差平方和小?在什么样的条件下,受约束回归与无约束回归的结果相同?5.观察下列方程并判断其变量是否呈线性,系数是否呈线性,或都是或都不是。
(1) t t t u x b b y ++=310(2) t t t u x b b y ++=log 10(3)t t t u x b b y ++=log log 10 (4) t t t u x b b b y +⋅+=)(210(5) t t t u x b b y +=)/(10(6) t bt t u x b y +−+=)1(110(7)t t t t u x b x b b y +++=10/22110 6.常见的非线性回归模型有几种情况?7.指出下列模型中所要求的待估参数的经济意义:(1)食品类需求函数:u P P I Y ++++=231210ln ln ln ln αααα中的321,,ααα(其中Y为人均食品支出额,I 为人均收入,为食品类价格,为其他替代商品类价格)。
1P 2P (2)消费函数:t t t t u Y Y C +++=−1210βββ中的1β和2β(其中C 为人均消费额,Y 为人均收入)。
8.设货币需求方程式的总体模型为)/ln(t t P M =t t t u RGDP b r b b +++)ln()ln(310其中M 为名义货币需求量,P 为物价水平,r 为利率,RGDP 为实际国内生产总值。
假定根据容量为n=19的样本,用最小二乘法估计出如下样本回归模型:)/ln(t t P M =t t t e RGDP r ++−)ln(54.0)ln(26.003.0t = (13) (3)9.02=R 1.0=DW其中括号内的数值为系数估计的t 统计值,为残差。
t e (1)从经济意义上考察估计模型的合理性;(2)在5%显著性水平上,分别检验参数的显著性; 21,b b (3)在5%显著性水平上,检验模型的整体显著性。
9.一项关于Waikiki 1965-1973年洒店投资的研究估计出以下生产函数:u e K AL R βα=其中:A=常数;L=土地投入(单位面积:平方尺);K=资本投入(建设成本:千美元);R=酒店的年净收入(千美元);u =满足古典假定的随机误差项。
请回答以下问题:(1)你认为α和β的总体值一般应为正值还是负值?在理论上如何解释? (2)为本方程建立具体的零假设和备择假设。
(3)如果显著性水平为5%,自由度为26,问(2)中的两个假设应如何作出具体的决定? (4)在以下回归方程基础上计算出适当的统计量t 值(括号内为参数估计值的标准差),并进行t 检检验。
−=R ln 0.9175十0.273 ln L 十0.733 ln K(0.135) (0.125)你是拒绝还是接受零假设?(5)如果你打算建造一所Waikiki 理想酒店,你是否还想知道一些额外的信息?10.David 将教师工资作为其“生产力”的函数,估计出具有如下系数的回归方程:ii i i i i Y D E A B S 1894891201823011155ˆ+++++= 其中:=1969-1970年每年第i 个教授按美元计的工资;=该教授一生中出版书的数量;=该教授—生中发表文章的数量;=该教授一生中发表的“优秀”文章的数量;=该教授自1964年指导的论文数量;=该教授的教龄。
请回答以下问题:i S i B i A i E i D i Y (1)系数的符号符合你的预期吗? (2)系数的相对值合理吗?(3)假设一个教授在授课之余所剩时间仅够用来或者写一本书,或者写两篇优秀文章,或者指导三篇论文,你将建议哪一个,为什么?(4)你会重新考虑(2)的答案吗?哪个系数是不协调的?对该结果你如何解释?此方程在一定意义上是否是有效的,给出判断并解释原因。
11.以企业研发支出(R&D )占销售额的比重为被解释变量Y ,以企业销售额与利润占销售额的比重为解释变量,一个容量为32的样本企业的估计结果如下:1X 2X 2105.0log 32.0472.0X X Y ++=s = (1.37) (0.22) (0.046)099.02=R其中括号内数字为系数估计值的标准差。
(1)解释的系数。
如果增加10%,估计Y 会变化多少个百分点?这在经济上是一个很大的影响吗?1log X 1X (2)针对R&D 强度随销售额的增加而提高这一备择假设,检验它不随而变化的假设。
分别在5%和10%的显著性水平上进行这个检验。
1X (3)利润占销售额的比重对R&D 强度是否在统计上有显著的影响?2X Y 12.表3-6给出某地区职工平均消费水平,职工平均收入和生活费用价格指数,试根据模型:t y t x 1t x 2t t t t u x b x b b y +++=22110作回归分析。
表3-6 某地区职工收入、消费和生活费用价格指数年份t y t x 1tx 2年份t yt x 1tx 21985 20.10 30.00 1.00199142.1065.20 0.901986 22.30 35.00 1.02199248.8070.00 0.951987 30.50 41.20 1.20199350.5080.00 1.101988 28.20 51.30 1.20199460.1092.10 0.951989 32.00 55.20 1.50199570.00102.00 1.021990 40.10 61.401.05199675.00120.301.0513.设有模型t t t t u x b x b b y +++=22110,试在下列条件下: (1),(2),分别求出和的最小二乘估计量。
121=+b b 21b b =1b 2b 14.某地区统计了机电行业的销售额y (万元)和汽车产量x 1(万辆)以及建筑业产值x 2(千万元)的数据如表3-7所示。
试按照下面要求建立该地区机电行业的销售额和汽车产量以及建筑业产值之间的回归方程,并进行检验(显著性水平05.0=α)。
表3-7 某地区机电行业的销售额、汽车产量与建筑业产值数据 年份 销售额y 汽车 产量x 1建筑业产值x 2年份销售额y 汽车 产量x 1建筑业 产值x 2 1981 280.0 3.9099.43 1990620.8 6.11332.17 1982 281.5 5.11910.361991513.6 4.25835.09 1983 337.4 6.66614.501992606.9 5.59136.42 1984 404.2 5.33815.751993629.0 6.67536.58 1985 402.1 4.32116.781994602.7 5.54337.14 1986 452.0 6.11717.441995656.7 6.93341.30 1987 431.7 5.55919.771996998.5 7.63845.62 1988 582.3 7.92023.761997877.6 7.75247.38 1989596.65.81631.61(1)根据上面的数据建立对数模型:t t t t u x b x b b y +++=22110ln ln ln (1)(2)所估计的回归系数是否显著?用p 值回答这个问题。
(3)解释回归系数的意义。
(4)根据上面的数据建立线性回归模型:t t t t u x b x b b y +++=22110 (2)(5)比较模型(1)、(2)的2R 值。
(6)如果模型(1)、(2)的结论不同,你将选择哪一个回归模型?为什么? 15.对下列模型进行适当变换化为标准线性模型:(1)u xb x b b y +⋅+⋅+=221011 (2) ue K AL Q βα=(3)ux b b e y ++=10(4))(1011u x b b ey ++−+=16.表3-8给出了一个钢厂在不同年度的钢产量。
找出表示产量和年度之间关系的方程:,并预测2002年的产量。
bx ae y =表3-8 某钢厂1991-2001年钢产量(单位:千吨)年度 19911992 1993 1994199519961997199819992000 2001 千吨 12.212.0 13.9 15.917.920.122.726.029.032.5 36.117.某产品的产量与科技投入之间呈二次函数模型:u x b x b b y +++=2210其统计资料如表3-9所示,试对模型进行回归分析。
表3-9 某产品产量与科技投入数据年份1991 1992 1993199419951996199719981999 2000 产量y 30 40 48 60 80 100 120 150 200 300 投入x 2.02.83.03.54.05.05.57.08.010.018.表3-10给出了德国1971-1980年间消费者价格指数y (1980=100)及货币供给x (亿德国马克)的数据。
表3-10 德国1971-1980年消费者价格指数与货币供给数据年份yx 年份y x 1971 64.1110.021980100.0237.971972 67.7125.021981106.3240.771973 72.4132.271982111.9249.251974 77.5137.171983115.6275.081975 82.0159.511984118.4283.891976 85.6176.161985121.0296.051977 88.7190.801986120.7325.751978 91.1216.201987121.1354.931979 94.9232.41(1)根据上表数据进行以下回归:①y 对x ;②lny 对lnx ;③lny 对x ;④ y 对lnx 。
