一阶系统的冲激响应.ppt
合集下载
《电工技术》教学课件 第四章 暂态分析 知识点： 一阶RC电路的冲激响应-教学文稿
2C
t
e RC (t )
1 (t) R
1 R2C
t
e RC (t )
四、归纳总结
1．求一阶RC电路的冲激响应的两种方法之一是按零输入响应计算，此法的关 键是确定在冲激函数作用的瞬间电容电压的初值。 2.求一阶RC电路的冲激响应的另外一种方法是将电路中的冲激激励函数 (t)换 为阶跃激励函数ε(t)，求其阶跃响应，然后再将阶跃响应对时间求一阶导数得到 冲激响应。
一种是按零输入响应计算，此法的关键是确定在冲激函数作用的瞬间电容 电压的初值。由于电路处于零状态，在t = 0 时电容视为短路，求出在0到0+ 时间内电容电流的冲激函数，然后根据电容元件电压电流关系的积分形式求得 电容电压的初值。
另一种方法是将电路中的冲激激励函数 (t)换为阶跃激励函数ε(t)，求其 阶跃响应，然后再将阶跃响应对时间求一阶导数得到冲激响应。
1 R2C
t
e RC (t )
三、知识深化
解法二：
电路的阶跃响应为
t
uC (t) (1 e RC ) (t)
电路的冲激响应为
i(t)
1
t
e RC
(t )
R
uC
(t)
d
t
[(1 e RC
dt
) (t)]
1 RC
t
e RC (t )
i
(t)
d dt
[1 R
t
e RC
(t)]
1
t
e RC
高等职业教育数字化学习中心
电单工电击子此技处术 编辑母版标题样式
主 讲：张 强
单击此处编辑母版标题样式
讲授内容
项目一： 电路分析基本定律与分析方法
t
e RC (t )
1 (t) R
1 R2C
t
e RC (t )
四、归纳总结
1．求一阶RC电路的冲激响应的两种方法之一是按零输入响应计算，此法的关 键是确定在冲激函数作用的瞬间电容电压的初值。 2.求一阶RC电路的冲激响应的另外一种方法是将电路中的冲激激励函数 (t)换 为阶跃激励函数ε(t)，求其阶跃响应，然后再将阶跃响应对时间求一阶导数得到 冲激响应。
一种是按零输入响应计算，此法的关键是确定在冲激函数作用的瞬间电容 电压的初值。由于电路处于零状态，在t = 0 时电容视为短路，求出在0到0+ 时间内电容电流的冲激函数，然后根据电容元件电压电流关系的积分形式求得 电容电压的初值。
另一种方法是将电路中的冲激激励函数 (t)换为阶跃激励函数ε(t)，求其 阶跃响应，然后再将阶跃响应对时间求一阶导数得到冲激响应。
1 R2C
t
e RC (t )
三、知识深化
解法二：
电路的阶跃响应为
t
uC (t) (1 e RC ) (t)
电路的冲激响应为
i(t)
1
t
e RC
(t )
R
uC
(t)
d
t
[(1 e RC
dt
) (t)]
1 RC
t
e RC (t )
i
(t)
d dt
[1 R
t
e RC
(t)]
1
t
e RC
高等职业教育数字化学习中心
电单工电击子此技处术 编辑母版标题样式
主 讲：张 强
单击此处编辑母版标题样式
讲授内容
项目一： 电路分析基本定律与分析方法
一阶电路(电路原理)阶跃函数和冲激函数
一阶电路阶跃函数和冲激函数
目录
• 引言 • 一阶电路基础知识 • 阶跃函数在一阶电路中应用 • 冲激函数在一阶电路中应用 • 一阶电路与阶跃函数、冲激函数关系探讨 • 实际应用与案例分析数和冲激 函数的作用和影响。
背景
在电路分析中，一阶电路是最基 本的电路模型之一，而阶跃函数 和冲激函数是描述电路动态特性 的重要工具。
等效变换法
等效变换法是通过将复杂电路中的元 件进行等效变换，从而简化电路的分 析过程。
03 阶跃函数在一阶电路中应 用
阶跃函数定义及性质
阶跃函数定义
阶跃函数是一种特殊的连续时间函数，表示在某一时刻瞬间发生的跃变。
阶跃函数性质
在跃变时刻之前，函数值为0；跃变时刻之后，函数值为1（或其他常数）。
阶跃响应概念及求解方法
THANKS FOR WATCHING
感谢您的观看
电力电子器件开关过程分析
电力电子器件在开关过程中会产生阶跃或冲激电流和电压，分析这些电流和电压对器件性能和系统稳定性的 影响，有助于提高电力电子系统的可靠性。
系统故障分析与保护
在电力系统中发生故障时，故障电流和电压往往具有阶跃或冲激特性，利用这些特性可以实现对故障的快速 检测和准确定位，为系统保护提供重要依据。
05 一阶电路与阶跃函数、冲 激函数关系探讨
阶跃函数与冲激函数关系
1
阶跃函数和冲激函数都是描述信号突变特性的函 数。
2
阶跃函数表示信号在某一时刻发生跃变，而冲激 函数则表示信号在某一时刻发生瞬时变化。
3
两者之间的关系可以通过微分和积分相互转换， 即冲激函数是阶跃函数的导数，阶跃函数是冲激 函数的积分。
案例分析
滤波器类型与性 能要求
目录
• 引言 • 一阶电路基础知识 • 阶跃函数在一阶电路中应用 • 冲激函数在一阶电路中应用 • 一阶电路与阶跃函数、冲激函数关系探讨 • 实际应用与案例分析数和冲激 函数的作用和影响。
背景
在电路分析中，一阶电路是最基 本的电路模型之一，而阶跃函数 和冲激函数是描述电路动态特性 的重要工具。
等效变换法
等效变换法是通过将复杂电路中的元 件进行等效变换，从而简化电路的分 析过程。
03 阶跃函数在一阶电路中应 用
阶跃函数定义及性质
阶跃函数定义
阶跃函数是一种特殊的连续时间函数，表示在某一时刻瞬间发生的跃变。
阶跃函数性质
在跃变时刻之前，函数值为0；跃变时刻之后，函数值为1（或其他常数）。
阶跃响应概念及求解方法
THANKS FOR WATCHING
感谢您的观看
电力电子器件开关过程分析
电力电子器件在开关过程中会产生阶跃或冲激电流和电压，分析这些电流和电压对器件性能和系统稳定性的 影响，有助于提高电力电子系统的可靠性。
系统故障分析与保护
在电力系统中发生故障时，故障电流和电压往往具有阶跃或冲激特性，利用这些特性可以实现对故障的快速 检测和准确定位，为系统保护提供重要依据。
05 一阶电路与阶跃函数、冲 激函数关系探讨
阶跃函数与冲激函数关系
1
阶跃函数和冲激函数都是描述信号突变特性的函 数。
2
阶跃函数表示信号在某一时刻发生跃变，而冲激 函数则表示信号在某一时刻发生瞬时变化。
3
两者之间的关系可以通过微分和积分相互转换， 即冲激函数是阶跃函数的导数，阶跃函数是冲激 函数的积分。
案例分析
滤波器类型与性 能要求
阶跃响应与冲激响应1
duC uC C + = δ (t) dt R
图 6.30
duC uC C + = δ (t) dt R
对方程积分并应用冲击函数的性质得：
图 6.30
∫
0+
0
duC uC +∫ = ∫ δ (t ) = 1 C 0 dt R 0
0+
0+
因为 uc不是冲激函数，否则电路的 KVL 方程中将出现冲击函 数的导数项使方程不成立，因此上式第一项积分为零，得：
L[iL (0 ) iL (0 )] = 1,
+
1 iL (0 ) = ≠ iL (0 ) L
+
说明电感上的冲激电压使电感电流发生跃变。
2） t＞0+ 后冲击电源为零，电路为一阶 RL 零输入响应问题， 如图 6.34 所示， 因此
iL = iL (0 + )e
t
τ
1 τt = e , t ≥ 0+ L
duC 1 2t iC = C = e ε (t ) mA dt 5
由齐次性和叠加性得实际响应为：
1 2t 1 2 ( t 0. 5 ) iC = 5[ e ε ( t ) e ε ( t 0.5)] 5 5
= e ε (t ) e
2 t
2 ( t 0. 5 )
ε ( t 0.5) mA
1
1
(1) u ( t )ε ( t )
( 2 ) u ( t 1)ε ( t )
0
2 t 1
－1
0
1
t
( 3 ) u ( t 1)ε ( t 1) 1
( 4 ) u ( t 2 )ε ( t 1 )
冲激响应和阶跃响应
1
R2C
电容器的电流在 t =0 时有一冲激，这就是电容电压突变的原因
3．n 阶系统的冲激响应
(1)冲激响应的数学模型 对于线性时不变系统,可以用一高阶微分方程表示
C0
dn r(t) dtn
C1
dn1 r(t) d t n1
Cn1
d r(t ) dt
Cnr(t)
E0
dm d
e(t ) tm
E1
dm1 e(t) d t m1
R
iC (t)
(t)
C
vC (t)
解答
列系统微分方程：
RC
d
vC (t dt
)
vC
(t
)
(t
)
t 0, t 0
RC
d
vC (t) dt
vC
(t)
0
冲激 t在 t 时0 转为系统的储能（由
体vC现(0）， )
t >0 时，在非零初始条件下齐次方程的解，即为原系统
的冲激响应。
求解 特征方程
RC 1 0
2．阶跃响应与冲激响应的关系 线性时不变系统满足微、积分特性
t
t
u(t) (t)d t g(t) h(t) d t
阶跃响应是冲激响应的积分，注意积分限：
t , 对因果系统：t
－
0
三．齐次解法求冲激响应（补充） 令方程左端系数为 1，右端只有一项 (t)时，冲激响应为
dn d
hˆ(t tn
将h(t), h(t), h(t)代入原方程
A1 A2 (t) 3A1 A2 (t) 0u(t) (t) 2 (t)
根据系数平衡，得
h(t) 1 et e3t u(t) 2
信号与系统冲激响应和阶跃响应
r t
t2
t
t
a t a t
b
bu
t t
c
u
t
rt aut
h 0 1 ,h '0 2
代入h(t),得
hh'00A A113AA2212
h(t)1ete3t u(t)
A A121212
2
X
12
第
用奇异函数项相平衡法求待定系数 页
h ( t ) A 1 e t A 2 e 3 tu ( t )
RC (t)A (t)
1 RCA1 A
RC
X
波形
htvC(t)R 1C eR 1C tu(t)
vC (t) h(t) 1 RC
iC(t)
CdvC(t) dt
O
注意！
iC (t)
R12CeR1Ctu(t)
1 (t)
R
1
O R
电容器的电流在
t =0时有一冲激， 这就是电容电压突
1 R 2C
变的原因 。
•当nm时 ， ht中 应 包 t含 ；
•当nm时 ， ht应 包含 t及 其 各 阶 导 数 。 X
10
第
例2-5-2 页
求系统 d d 2r t(2 t)4d d r(tt)3 r(t)的 冲d d e 激(tt响) 应2 e 。(t) 解：
将e(t)→(t)， r(t)→h(t)
d 2 d h t( 2 t) 4d d h (tt)3 h (t)d d ( tt)2 (t)
CtR1CeR1Ctut
X
6
方法2：奇异函数项相平衡原理
第 页
已知方程 冲激响应 求导 代入原方程
RC dvdCt(t)vC(t)(t) t vC(t)Ae RCu(t)
电路原理课件-冲激响应
R t L
t
ε( t )
电感电压曲线
R uLδ ( t ) δ( t ) Riδ ( t ) δ( t ) e L
ε( t )
di δ ( t ) 求出。 电感电压也可由 uLδ ( t ) L dt
小结：
一阶电路的冲激响应实质上是在冲激电压（或电 流）作用下使电路获得非零初始状态，在t > 0时的响 应是仅由这个初始状态产生的零输入响应。 求一阶电路冲激响应的关键是确定在冲激函数作 用的瞬间电容电压（或电感电流）的初值。在t = 0 时 电容视为短路，电感视为开路，求出在0到0+时间内电 容电流（或电感电压）的冲激函数后根据电容（或电 感）元件电压电流关系的积分形式求得电容电压（或 电感电流）的初值。
t RC ( t )
t RC ( t )]
e
t RC ( t )
1 (t ) e RC
t RC ( t )
二、一阶RL电路的冲激响应
分析: 1.i(0-)=0
电感相当于 断路元件
2.从0-到0+时间内uL=δ(t) 冲激电压施加在电感两端 t = 0+ 时
例2
求图示电路的冲激响应iL(t) 与uL(t)。
1.i 解： L(0-)=0 2.t 从0-到0+时刻uL=2δ(t)V
1 0 i L (0 ) 2δ( t )dt 2 A L 0 3.求时间常数τ L 1 s R 2 2 t 4.电感中的冲激响应电流为 i L (t ) 2e ε(t ) A
2.从0-到0+时间内iC =δ(t) 冲激电流流过电容 t = 0+ 时
1 uCδ (0 ) C
t
ε( t )
电感电压曲线
R uLδ ( t ) δ( t ) Riδ ( t ) δ( t ) e L
ε( t )
di δ ( t ) 求出。 电感电压也可由 uLδ ( t ) L dt
小结：
一阶电路的冲激响应实质上是在冲激电压（或电 流）作用下使电路获得非零初始状态，在t > 0时的响 应是仅由这个初始状态产生的零输入响应。 求一阶电路冲激响应的关键是确定在冲激函数作 用的瞬间电容电压（或电感电流）的初值。在t = 0 时 电容视为短路，电感视为开路，求出在0到0+时间内电 容电流（或电感电压）的冲激函数后根据电容（或电 感）元件电压电流关系的积分形式求得电容电压（或 电感电流）的初值。
t RC ( t )
t RC ( t )]
e
t RC ( t )
1 (t ) e RC
t RC ( t )
二、一阶RL电路的冲激响应
分析: 1.i(0-)=0
电感相当于 断路元件
2.从0-到0+时间内uL=δ(t) 冲激电压施加在电感两端 t = 0+ 时
例2
求图示电路的冲激响应iL(t) 与uL(t)。
1.i 解： L(0-)=0 2.t 从0-到0+时刻uL=2δ(t)V
1 0 i L (0 ) 2δ( t )dt 2 A L 0 3.求时间常数τ L 1 s R 2 2 t 4.电感中的冲激响应电流为 i L (t ) 2e ε(t ) A
2.从0-到0+时间内iC =δ(t) 冲激电流流过电容 t = 0+ 时
1 uCδ (0 ) C
2019年最新-7.一阶电路的阶跃和冲激、状态方程-精选文档
－2 02t 1来自1(1)u(t)(t)
(2)u(t1)(t) 0
2 t －1 0 1
t
(3 )u(t 1 )(t 1 )1
1
(4 )u(t 2 )(t 1 )
01
t0 1 2
t
返回 上页 下页
2. 一阶电路的阶跃响应
阶跃响应
激励为单位阶跃函数时，电路 中产生的零状态响应。
t
uC(t)(1eR
(t0.5)]
e 2 t (t) e 2 (t 0 .5 ) (t 0 .5 ) mA
100F 100F
+ 5k
5 (t)
ic
-
+
5k ic
- 5(t0.5)
返回 上页 下页
分段表示为：
iC e 2 t ( t) e 2 (t 0 .5 ) ( t 0 .5 )
iCe2t[(t)(t0.5)] 0.63e22(t0.5)(t0.5)
e2t mA (0 t0.5s) 分段表示为： iC(t) -0.6e-2 3t(-05 2 .)mA (t0.s5)
1 iC(mA)
波形 0.368
0 0.5
t(s)
-0.632
返回 上页 下页
9.5 一阶电路的阶跃响应
1. 单位阶跃函数
定义
(t) 10
(t 0) (t 0)
(t)
1
0
t
单位阶跃函数的延迟
(t-t0)
1
0 t0
t
(t
0 t0)1
(t t0) (t t0)
返回 上页 下页
单位阶跃函数的作用
①在电路中模拟开关的动作 t = 0 合闸 u(t) = E (t)
(2)u(t1)(t) 0
2 t －1 0 1
t
(3 )u(t 1 )(t 1 )1
1
(4 )u(t 2 )(t 1 )
01
t0 1 2
t
返回 上页 下页
2. 一阶电路的阶跃响应
阶跃响应
激励为单位阶跃函数时，电路 中产生的零状态响应。
t
uC(t)(1eR
(t0.5)]
e 2 t (t) e 2 (t 0 .5 ) (t 0 .5 ) mA
100F 100F
+ 5k
5 (t)
ic
-
+
5k ic
- 5(t0.5)
返回 上页 下页
分段表示为：
iC e 2 t ( t) e 2 (t 0 .5 ) ( t 0 .5 )
iCe2t[(t)(t0.5)] 0.63e22(t0.5)(t0.5)
e2t mA (0 t0.5s) 分段表示为： iC(t) -0.6e-2 3t(-05 2 .)mA (t0.s5)
1 iC(mA)
波形 0.368
0 0.5
t(s)
-0.632
返回 上页 下页
9.5 一阶电路的阶跃响应
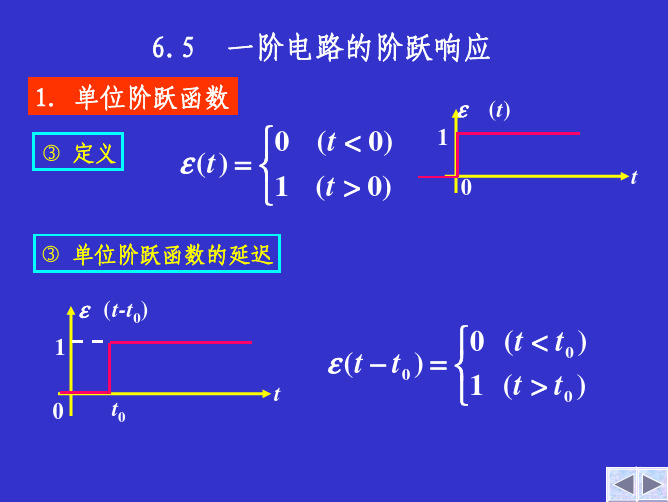
1. 单位阶跃函数
定义
(t) 10
(t 0) (t 0)
(t)
1
0
t
单位阶跃函数的延迟
(t-t0)
1
0 t0
t
(t
0 t0)1
(t t0) (t t0)
返回 上页 下页
单位阶跃函数的作用
①在电路中模拟开关的动作 t = 0 合闸 u(t) = E (t)
6-6一阶电路(冲击响应)
§6-6 一阶电路的冲激响应 一、单位冲激函数的定义：⎪⎪⎭⎪⎪⎬⎫=-≤+≥=⎰∞∞-1)(0)(dt t o t o t t δδ或 ⎩⎨⎧=∞≠=o t0)(o t t δ⎰∞∞-=1)(dt t δ单位冲激函数又称δ函数或狄拉克函数。
)(t δ可以用来描述某些物理现象，如冲击力、闪电等一些作用时间短，强度大，能达到一定作用结果的情况。
用一条短路线对电容器放电，放电电流因O R →而非常大，时间很短，其情形也比较近似)(t δ函数。
)(t δ函数可以看作单位脉冲函数的一种极限情况，（数学意义单位脉冲函数∆P (t )⎰∞∞-∆=1)(dt t P⎪⎪⎩⎪⎪⎨⎧∆≥∆<<∆≤=++--∆t o t o o t o t P 1)( 当0→∆时∞→∆1而+→+∆o即得⎪⎪⎩⎪⎪⎨⎧+≥∞→∆-≤=∆→∆o t o o t o t p o 1 )(lim⎰∞∞-∆=1)(dt t P上述表达的极限就是)(t δ)(t δ是一种理想化的或者说理论上的脉冲波型 单位冲激函数的波形：如果冲激函数脉冲发生的时间不是o t=而是o t t =，而且强度不是1而是k （波形面积为k ），则可表示为)(o t t k -δ，其中)(o t t -δ称为延时（延迟）冲激函数。
对于单位冲激函数)(t δ 当o t ≠时，0)(=t δ对o t =时连续的)(t f 有 )()()()(t o f t t f δδ=∴⎰⎰∞∞-∞∞-==)()()()()(o f dt t o f dt t t f δδt)(t δ1tk )(t δ ktf(t)t 0k )(o t t -δ同理，对于在任意时刻τ=t 处连续的函数)(t f 有)()()(ττδf dt t t f =-⎰∞∞-这个式子说明了δ函数有将某函数在某时刻的值“筛”出来的本领。
这一性质称为δ函数的抽样特性或“筛”选特性。
单位冲激函数)(t δ与单位阶跃函数)(t ε的数学关系：)(o t 10)()(t o t d tεξξδ=⎩⎨⎧+≥-≤=⎰∞- 可见单位阶跃函数)(t ε可以看作单位冲击函数)(t δ的积分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
O R
t
电容器的电流在
t =0时有一冲激， 这就是电容电压突
1
R2C
变的原因 。
方法1：求 vC 0
据方程可设
dυ
C
t
a
t
but
dt
υ C t aut
代入方程得 RCa t RCbut aut t
得出
RCa 1 即 a 1 RC
所以
υC
0
υ C 0
1 RC
1 RC
t >0时，在非零初始条件下齐次方程的解，即为原系统
的冲激响应。
求解
特征方程 RC 1 0
特征根 1
RC
t
vC (t) Ae RC u(t)
t 0时的解
下面的问题是确定系数A,求A有两种方法：
方法1：冲激函数匹配法求出 vC (0， )定系数A。
方法2：奇异函数项相平衡法，定系数A。
例2-5-1 一阶系统的冲激响应
求下图RC电路的冲激响应。（条件：vC 0 0）
R
iC (t)
列系统微分方程：
(t)
RC
d
vC (t dt
)
vC
(t
)
(t
)
C
vC (t)
t 0, t 0
RC
d
vC (t dt
)
vC
(t
)
0
齐次方程
冲激 t在 t时转0 为系统0 代入C t
Ae
1 RC
t
得A
1 RC
C t
1 RC
1 t
e RC u t
方法2：奇异函数项相平衡原理
已知方程 冲激响应
RC
d
vC (t dt
)
vC
(t
t
)
(t
)
vC (t ) Ae RC u(t )
求导
d vC (t) A (t)
A
1t
e RC u(t )
dt
RC
代入原方程
注意！
RC
1
Ae
t RC
u(t
)
RCA
(t
)
Ae
t RC
u(t
)
(t
)
RC
整理，方程左右奇异函数项系数相平衡
RCA (t) (t)
RCA 1 A 1 RC
A 1
RC
vC (t)
1 RC
1t
e RC u(t )
波形
即:
h(t)
1
1t
e RC u(t )
RC
波形
ht
vC (t)
1 RC
1t
e RC u(t )
vC (t ) h(t ) 1 RC
iC
(t)
C
d
vC (t) dt
O
注意！
iC (t)
t
1 R2C
1t
e RC u(t )
1 R
(t)