龙贝格算法-数值分析-实验报告
数值分析积分实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析的方法,研究几种常见的数值积分方法,包括梯形法、辛普森法、复化梯形法和龙贝格法,并比较它们在计算精度和效率上的差异。
通过实验,加深对数值积分理论和方法的理解,提高编程能力和实际问题解决能力。
二、实验内容1. 梯形法梯形法是一种基本的数值积分方法,通过将积分区间分割成若干个梯形,计算梯形面积之和来近似积分值。
实验中,我们选取了几个不同的函数,对积分区间进行划分,计算积分近似值,并与实际积分值进行比较。
2. 辛普森法辛普森法是另一种常见的数值积分方法,它通过将积分区间分割成若干个等距的区间,在每个区间上使用二次多项式进行插值,然后计算多项式与x轴围成的面积之和来近似积分值。
实验中,我们对比了辛普森法和梯形法的计算结果,分析了它们的精度差异。
3. 复化梯形法复化梯形法是对梯形法的一种改进,通过将积分区间分割成多个小区间,在每个小区间上使用梯形法进行积分,然后计算所有小区间积分值的和来近似积分值。
实验中,我们对比了复化梯形法和辛普森法的计算结果,分析了它们的精度和效率。
4. 龙贝格法龙贝格法是一种通过外推加速提高计算精度的数值积分方法。
它通过比较使用不同点数(n和2n)的积分结果,得到更高精度的积分结果。
实验中,我们使用龙贝格法对几个函数进行积分,并与其他方法进行了比较。
三、实验步骤1. 编写程序实现梯形法、辛普森法、复化梯形法和龙贝格法。
2. 选取几个不同的函数,对积分区间进行划分。
3. 使用不同方法计算积分近似值,并与实际积分值进行比较。
4. 分析不同方法的精度和效率。
四、实验结果与分析1. 梯形法梯形法在计算精度上相对较低,但当积分区间划分足够细时,其计算结果可以接近实际积分值。
2. 辛普森法辛普森法在计算精度上优于梯形法,但当积分区间划分较细时,计算量较大。
3. 复化梯形法复化梯形法在计算精度上与辛普森法相当,但计算量较小。
4. 龙贝格法龙贝格法在计算精度上优于复化梯形法,且计算量相对较小。
Romberg算法的实验报告
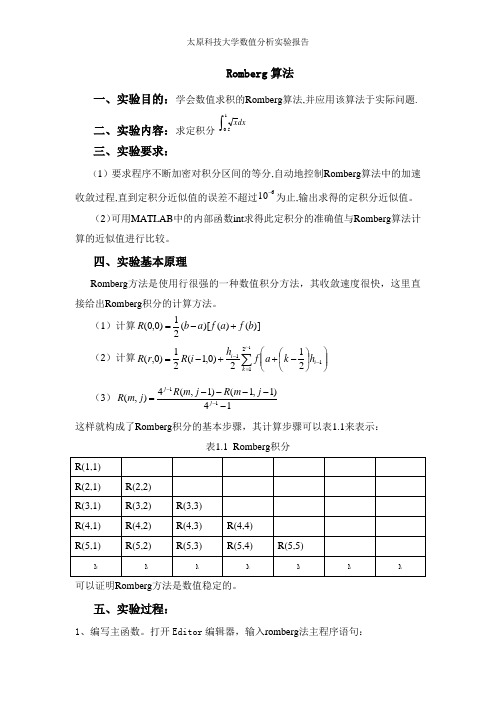
Romberg 算法一、实验目的:学会数值求积的Romberg 算法,并应用该算法于实际问题.二、实验内容:求定积分 ⎰15.0dxx三、实验要求:(1)要求程序不断加密对积分区间的等分,自动地控制Romberg 算法中的加速收敛过程,直到定积分近似值的误差不超过610-为止,输出求得的定积分近似值。
(2)可用MATLAB 中的内部函数int 求得此定积分的准确值与Romberg 算法计算的近似值进行比较。
四、实验基本原理Romberg 方法是使用行很强的一种数值积分方法,其收敛速度很快,这里直接给出Romberg 积分的计算方法。
(1)计算)]()()[(21)0,0(b f a f a b R +-=(2)计算∑-=--⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-++-=12111212)0,1(21)0,(i k i i h k a f h i R r R (3)14)1,1()1,(4),(11-----=--j j j m R j m R j m R这样就构成了Romberg 积分的基本步骤,其计算步骤可以表1.1来表示:表1.1 Romberg 积分R(1,1)R(2,1) R(2,2)R(3,1) R(3,2) R(3,3)R(4,1) R(4,2) R(4,3) R(4,4)R(5,1) R(5,2) R(5,3) R(5,4) R(5,5)可以证明Romberg 方法是数值稳定的。
五、实验过程:1、编写主函数。
打开Editor编辑器,输入romberg法主程序语句:function [R,wugu,h]=romberg(fun,a,b, wucha,m)n=1;h=b-a; wugu=1; x=a;k=0; RT=zeros(4,4);RT(1,1)=h*(feval(fun,a)+feval(fun,b))/2;while((wugu>wucha)&(k<m)|(k<4))k=k+1; h=h/2; s=0;for j=1:nx=a+h*(2*j-1); s=s+feval(fun,x);endRT(k+1,1)= RT(k,1)/2+h*s; n=2*n;for i=1:kRT(k+1,i+1)=((4^i)*RT(k+1,i)-RT(k,i))/(4^i-1);endwugu=abs(RT(k+1,k)-RT(k+1,k+1));endR=RT(k+1,k+1);以文件名romberg.m保存。
数值分析实验报告

数值分析实验报告⼀.实验⽬的1.通过实际计算体会各种积分⽅法的精确度;会编写⽤龙贝格算法求定积分的程序。
2.熟悉求解线性⽅程组的有关理论和⽅法;并会编制列主元消去法、LU 分解法。
⼆.实验环境及要求MATLAB 软件等。
三.实验学时2学时四.实验内容1.数值积分实验:复化积分、龙贝格积分;2.线性代数⽅程组的直接解法:列主元消去法、LU 分解法。
五.实验题及结果1. ⽤复化⾟欧森公式计算积分I=dx x ?+10211。
int_com_simp.m ⽂件:function s=int_comp_simp(f,a,b,n)format long ;h=(b-a)/(2*n);s1=0;s2=0;for k=1:nx=a+h*(2*k-1);s1=s1+f(x);endfor k=1:(n-1)x=a+h*2*k;s2=s2+f(x);ends=h*(f(a)+f(b)+4*s1+2*s2)/3;函数f1.m ⽂件:function y=f1(x)y=1/(1+x*x);对函数调⽤的f11.m ⽂件:for i=1:4n=2^i;s=int_comp_simp(@f1,0,1,n);display(n);display(s); end结果及其分析:结果:>> f11n =2s =0.785392156862745n =4s =0.785398125614677n =8s =0.785398162806206n =16s =0.785398163388209 结果分析:当n=8时结果已经达到6位有效数字;2. ⽤龙贝格⽅法计算积分I=dx x ?+10211 。
龙贝格⽅法的函数⽂件:function [T,quad,err,h]=int_romberg(f,a,b,n,tol) format longM=1;h=b-a;err=1;k=0;T=zeros(4,4);T(1,1)=h*(f(a)+f(b))/2;while ((err>tol)&&(kk=k+1;h=h/2;s=0;for p=1:Mx=a+h*(2*p-1);s=s+f(x);endT(k+1,1)=T(k,1)/2+h*s;M=2*M;for kk=1:kT(k+1,kk+1)=T(k+1,kk)+(T(k+1,kk)-T(k,kk))/(4^kk-1);enderr=abs(T(k,k)-T(k+1,kk+1));endquad=T(k+1,k+1);所求函数的⽂件:function y=f1(x)y=1/(1+x*x);结果及其分析:>> [T,quad,err,h]=int_romberg(@f1,0,1,4,1e-6)T =Columns 1 through 40.750000000000000 0 0 0 0.775000000000000 0.783333333333333 0 00.782794117647059 0.785392156862745 0.785529411764706 00.784747123622772 0.785398125614677 0.785398523531472 0.785396445940468 0.785235403010347 0.785398162806206 0.785398165285641 0.785398159599199 Column 50.785398166319429quad =0.785398166319429err =1.720378960845537e-06h =0.062500000000000结果分析:最后结果是0.785398166319429,误差为1.720378960845537e-06;3.⽤列主元消去法解⽅程组0.101x1+2.304x2+3.555x3=1.183-1.347x1+3.712x2+4.623x3=2.137-2.835x1+1.072x2+5.643x3=3.035⾼斯主元消去法的m⽂件:function solution=Gauss_main(gauss,precision)if nargin==2trydigits(precision);catchdisp('您输⼊的精度有误,这⾥按照缺省的精度(10位有效数字)计算');digits(10);endA=vpa(gauss);row=size(A,1);col=size(A,2);if ndims(A)~=2|col-row~=1disp('矩阵的⼤⼩有误,不能使⽤Gauss主元素消去法')returnendif det(gauss(:,1:row))disp('该⽅程的系数矩阵⾏列式为零,⽆解或有⽆穷多解,不能使⽤Gauss主元素消去法') returnendfor i=1:rowMax=0.0;for j=i:rowif double(abs(A(j,i))-Max)>0Max=abs(A(j,i));max_row=j;endendtemp=A(i,:);A(i,:)=A(max_row,:);A(max_row,:)=temp;for k=i+1:rowA(k,:)=vpa(A(k,:)-A(i,:)*A(k,i)/A(i,i));endendfor i=row:-1:1temp=A(i,col);for k=i+1:rowtemp=vpa(temp-soulution(k)*A(i,k));endsolution(i)=vpa(temp/A(i,i));end结果:>> solution=Gauss_main(A,4)solution =[ -0.3982, 0.0138, 0.3351]结果分析:x(1)=-0.3982,x(2)=0.0138,x(3)=0.3351;4.LU直接分解法求⽅程组0.101x1+2.304x2+3.555x3=1.183-1.347x1+3.712x2+4.623x3=2.137-2.835x1+1.072x2+5.643x3=3.035LU的m⽂件:function solution=Mlu(M,precision)if nargin==2trydigits(precision);catchdisp('你输⼊的精度有误,这⾥按照缺省的精度(10位有效数字)计算'); digits(10);endelsedigits(10);endA=vpa(M);row=size(A,1);col=size(A,2);if ~ismatrix(A)||col-row~=1disp('矩阵的⼤⼩有误,不能使⽤LU分解')returnendif det(M(:,1:row))==0disp('该⽅程的系数矩阵⾏列式为零,⽆解或有穷多解,不能使⽤LU分解') returnend[L,U,P]=lu(double(A));for i=row:-1:1temp=U(i,col);for k=i+1:rowtemp=vpa(temp-t_solution(k)*U(i,k));endt_solution(i)=vpa(temp/U(i,i));endfor i=1:rowtemp=t_solution(i);for k=1:i-1temp=vpa(temp-t_solution(k)*U(i,k));endsolution(i)=temp;end结果及分析:结果:>> solution=Mlu(A,4)solution =[ -0.3982, 0.0138, 0.3351]结果分析:x(1)=-0.3982,x(2)=0.0138,x(3)=0.3351;。
数值积分龙贝格matlab

《数值分析》课程实验报告一、实验目的1、进一步熟悉向量矩阵的运算;2、掌握龙贝格(Romberg )算法,并能用高级程序语言MATLAB 编写实现此算法的程序;3、进而加深对龙贝格(Romberg )算法的理解。
二、实验内容1. 使用Romberg 积分,对于计算下列⎰+4802)cos (1dx x 各近似值a.确定1,51,41,31,21,1,,,,R R R R Rb.确定5,54,43,32,2,,,R R R Rc.6,65,64,63,62,61,6,,,,,R R R R R Rd.确定10,109,98,87,7,,,R R R R三、实验步骤1. 编写程序龙贝格积分方法如下:n=5;a=0;b=48;h(1,1)=b-a;fa=sqrt(1+(cos(a))^2);fb=sqrt(1+(cos(b))^2);r(1,1)=h(1,1)/2*(fa+fb);disp('R11,R21,R31,R41,R51分别为');disp(r(1,1));for i=2:nh(i,1)=(b-a)/(2^(i-1));sum=0;for k=1:2^(i-2)x=a+(2*k-1)*h(i,1);sum=sum+sqrt(1+(cos(x)).^2);endr(i,1)=0.5*(r(i-1,1)+h(i-1,1)*sum);disp(r(i,1));enddisp('R22,R33,R44,R55分别为');for k=2:nfor j=2:kr(k,j)=r(k,j-1)+(r(k,j-1)-r(k-1,j-1))/(4^(j-1)-1);enddisp(r(k,k));enddisp('R61,R62,R63,R64,R65,R66分别为');n=6;for i=2:nh(i,1)=(b-a)/(2^(i-1));sum=0;for k=1:2^(i-2)x=a+(2*k-1)*h(i,1);sum=sum+sqrt(1+(cos(x)).^2);endr(i,1)=0.5*(r(i-1,1)+h(i-1,1)*sum);endfor k=2:nfor j=2:kr(k,j)=r(k,j-1)+(r(k,j-1)-r(k-1,j-1))/(4^(j-1)-1);endendfor i=1:ndisp(r(6,i));enddisp('R77,R88,R99,R10,10分别为');n=10;for i=2:nh(i,1)=(b-a)/(2^(i-1));sum=0;for k=1:2^(i-2)x=a+(2*k-1)*h(i,1);sum=sum+sqrt(1+(cos(x)).^2);endr(i,1)=0.5*(r(i-1,1)+h(i-1,1)*sum);endfor k=2:nfor j=2:kr(k,j)=r(k,j-1)+(r(k,j-1)-r(k-1,j-1))/(4^(j-1)-1);endendfor i=7:10disp(r(i,i));end运行结果如下:R11,R21,R31,R41,R51分别为62.437457.288656.443856.263156.2188R22,R33,R44,R55分别为55.572356.201556.205656.2041R61,R62,R63,R64,R65,R66分别为58.362759.077359.268959.317559.329759.3328R77,R88,R99,R10,10分别为58.422158.470758.470558.4705四、实验小结在这次编程中我学到了很多东西,把程序写进软件中也出现了很多错误,细节问题使我们必须注意的,自己有了很多的收获,自己进一步理解和学习了Matlab软件。
河北工业大学数值分析实验三实验四实验报告

数值分析实验报告指导老师:宛艳萍姓名:班级:学号:实验三 复化辛卜生法,龙贝格法1.实验名称:复化辛卜生法,龙贝格法2.实验目的1)通过实际计算体会各种方法的精确度。
2)会编写用复化辛卜生、龙贝格算法求定积分的程序。
3.算法描述1)用复化辛卜生法计算积分 dxx I ⎰+=12)1/(1算法:复化辛卜生公式为S n =h/6∑∑+-=+++)]()2/(4)([11k k kn k x f h x f xf ,计算过程为:1.令,/)(n a b h -= ),2/(1h a f s +=;02=s2.对1,,2,1-=n k计算),2/(11h kh a f s s +++=)(22kh a f s s ++=3.))(24)((6/21b f s s a f h s +++= 。
2)龙贝格算法计算dxxI ⎰+=102)1/(156e ε=-算法)((12/12∑-=++=n k k n n n x f h T T ;/)(n a b h n -= n k h k x )2/1(2/1+=+)(3/122n n n n T T T S -+= )_(15/122n n n n S S S C +=)(63/122n n n n C C C R -+=用事后估计法控制精度2|5e -6n n R R -< 。
4.源程序:1)/* 用复化辛卜生公式求积分 */ #include "stdio.h" float fx(float x){double f;f=1.0/(1.0+x*x); return f; } double fs(int n){double a=0.0,b=1.0,h,s,s1,s2=0; int i;h=(b-a)/n; s1=fx(a+h/2); for(i=1;i<n;i++){s1=s1+fx(a+i*h+h/2); s2=s2+fx(a+i*h);}s=(h/6.0)*(fx(a)+fx(b)+4*s1+2*s2);return s;}void main(){printf("实验三复化辛卜生法计算机112 耿向飞学号:112434\n");printf("s(2)=%lf\ns(4)=%lf\ns(8)= %lf",fs(2),fs(4),fs(8));}2)/* 龙贝格法 */#include "stdio.h"#include "math.h"#define E 2.71828182//被积函数f(x)double fx(double x){double f;f=1/(1+x*x);return f;}//梯形公式求tndouble tx(int n){double s3=0.0,h,t,b=1.0,a=0.0;int i;h=(b-a)/n;for(i=1;i<n;i++)s3=s3+fx(i*h);t=(h/2)*(fx(a)+fx(b)+2*s3);return t;} double s(int n){double s;s=tx(2*n)+(1.0/3.0)*(tx(2*n)-tx(n ));return s;}double c(int n){double c;c=s(2*n)+(1.0/15.0)*(s(2*n)-s(n)) ;return c;}double r(int n){double r;r=c(2*n)+(1.0/63.0)*(c(2*n)-c(n)) ;return r;}void main(){double rr,pp;int n=1;rr=r(n);pp=r(2*n)-r(n);printf("实验三龙贝格法计算机112 耿向飞学号:112434\n");printf("结果为:%.15lf 误差小于等于: %.15lf",rr,pp);}5.运行结果1)复化辛卜生公式2)龙贝格算法6.对算法的理解与分析:复化辛卜生公式和龙贝格算法适用于求数值积分,而且都能提高计算积分的精度龙贝格算法其实是在复化辛卜生公式递推的基础之上生成的一种精度高,而且收敛速度也较快的一种算法。
龙贝格算法报告

龙贝格算法报告 中国地质大学姓名:马立华 班号:121112 学号:20111000536 (一)、龙贝格算法的推导工程的形成。
()()baI f f x dx =⎰n 等份,分点1、梯形公式是将区间[,a b ⎤⎦ 有为kx =a+kh ,h=b a n- ,k=0,1,2,3....在每个小区间上采用梯形公式为110[()()]2n i i i h T f x f x -+==+∑.通过计算复合梯形公式的余项为. (梯形公式是把大区间分成一些小区间,通过梯形面积近似曲边提醒的体积)2、梯形公式的递推法,复合梯形公式在区间[,a b ⎤⎦ 上,共有n 等份,则共有n+1个分点,将求积区间在二分一次,则分点增加至2n+1个,由梯形公式()()()⎥⎦⎤⎢⎣⎡+-=∑-=1122n k k n b f x f a f h T 得式()∑-=++=121222n k k n nx f h T T 求出n T 2;(梯形公式是通过增加区间每一次都是将上一次区间加倍)3,外推技巧:由1,2,可以看出梯形公式收敛地速度较慢,并且精确地阶数较低由余项得 h=b a n -,。
(外推技巧是通过将梯形公式的递推法得到的公式进行加减乘除法提高其精确度。
) 定理四 设](),f x c a b ∞⎡∈⎣,则有2462123()........l l T h I h h h h αααα=++++++ (1)其中2"()12n b a R h f η-=-]2''(),,12n b a I T h f a b ηη-⎡-=-∈⎣3201x x dx+⎰系数l α(l=1,2,3....)与h 无关。
通过定理四 则有24212().......() (24162)l l h h h h T I ααα=+++++。
(2),通过(1)(2)得46124(/2)()() (3)T h T h S h I h h ββ-==+++发现我们只是通过简单地加减法,就将误差的阶数提高了两阶。
龙贝格积分算法实验

实验题目2 Romberg 积分法摘要考虑积分()()b aI f f x dx =⎰欲求其近似值,可以采用如下公式: (复化)梯形公式 11[()()]2n ii i hT f x f x-+==+∑2()12b a E h f η-''=-[,]a b η∈ (复化)辛卜生公式 11102[()4()()]6n i i i i hS f x f x f x -++==++∑4(4)()1802b a h E f η-⎛⎫=- ⎪⎝⎭ [,]a b η∈(复化)柯特斯公式 111042[7()32()12()90n i i i i hC f x f x f x -++==+++∑31432()7()]i i f xf x +++6(6)2()()9454b a h E f η-⎛⎫=- ⎪⎝⎭[,]a b η∈这里,梯形公式显得算法简单,具有如下递推关系121021()22n n n i i h T T f x -+==+∑因此,很容易实现从低阶的计算结果推算出高阶的近似值,而只需要花费较少的附加函数计算。
但是,由于梯形公式收敛阶较低,收敛速度缓慢。
所以,如何提高收敛速度,自然是人们极为关心的课题。
为此,记0,k T 为将区间[,]a b 进行2k等份的复化梯形积分结果,1,k T 为将区间[,]a b 进行2k等份的复化辛卜生积分结果,2,k T 为将区间[,]a b 进行2k等份的复化柯特斯积分结果。
根据李查逊(Richardson )外推加速方法,可得到1,11,,0,1,2,40,1,2,41m m k m km k m k T T T m -+-=-⎛⎫=⎪=-⎝⎭可以证明,如果()f x 充分光滑,则有,lim ()m k k T I f →∞= (m 固定),0lim ()m m T I f →∞=这是一个收敛速度更快的一个数值求积公式,我们称为龙贝格积分法。
该方法的计算可按下表进行0,0T 0,1T 0,2T … 0,m T 1,0T 1,1T … 1,1m T - 2,0T … 2,2m T - … … ,0m T很明显,龙贝格计算过程在计算机上实现时,只需开辟一个一维数组,即每次计算的结果,m k T ,可存放在0,k T 位置上,其最终结果,0m T 是存放在0,0T 位置上。
Romberg龙贝格算法实验报告

Romberg龙贝格算法实验报告课程实验报告课程名称:专业班级: CS1306班学号: Uxx14967 姓名:段沛云指导教师:报告日期:计算机科学与技术学院目录1 实验目的 ........................................................12 实验原理 ........................................................13 算法设计与流程框图 (2)4 源程序 ........................................................ .. 45 程序运行 ........................................................76 结果分析 ........................................................77 实验体会 ........................................................71 实验目的掌握Romberg公式的用法,适用范围及精度,熟悉Romberg算法的流程,并能够设计算法计算积分31得到结果并输出。
1x2 实验原理2.1 取k=0,h=b-a,求T0=数)。
2.2 求梯形值T0(b-a),即按递推公式(4.1)计算T0。
k2h[f(a)+f(b)],令1→k,(k记区间[a,b]的二分次22.3 求加速值,按公式(4.12)逐个求出T表的第k行其余各元素Tj(k-j)(j=1,2,….k)。
2.4 若|Tk+1-Tk|n-111T2n=[Tn+hn∑f(xi+)]22i=01Sn=T2n+(T2n-Tn)31Cn=S2n+(S2n-Sn)151Rn=C2n+(C2n-Cn)633 算法设计与流程框图算法设计:(先假定所求积分二分最大次数次数为20) 3.1 先求T[k][0] 3.2 再由公式T(k)m4m(k+1)1)=mTm-1-mTm(k-1(k=1,2,) 求T[i][j] 4-14-13.3 在求出的同时比较T[k][k]与T[k-1][k-1]的大小,如果二者之差的绝对值小于1e-5,就停止求T[k][k];此时的k就是所求的二分次数,而此时的T[k][k]就是最终的结果 3.4 打印出所有的T[i][j];程序流程图4 源程序#include #include #include #include int main(void) {float f(float(x)) {float y; y=1/x; return y; }floata,b,e,h,s,k,x,T1=0,T2=0,S1=0,S2=0,C1=0,C2=0,R1=0,R2=0; inti=0;printf("请输入积分下限 : "); scanf("%f",&a);printf("\n请输入积分上限 :"); scanf("%f",&b);printf("\n请输入允许误差 :"); scanf("%f",&e); k大学网=1; h=b-a;T1=h*(f(a)+f(b))/2;printf("____________________________________________\n"); printf("计算结果如下 : \n");printf("\nk T2 S2 C2 R2\n");printf("%d %10.7f %10.7f %10.7f %10.7f\n",i,T1,S1,C1,R1); do {x=a+h/2; s=0; while(x{ s=s+f(x); x=x+h; }T2=(T1+s*h)/2; S2=T2+(T2-T1)/3; if(k==1) {T1=T2; S1=S2; h=h/2; k=k+1; }else if(k==2) {C2=S2+(S2-S1)/15; C1=C2; T1=T2; S1=S2; h=h/2; k=k+1; }else if(k==3) {R2=C2+(C2-C1)/63; C2=S2+(S2-S1)/15; C1=C2; T1=T2; S1=S2; h=h/2; k=k+1; } else {C2=S2+(S2-S1)/15;R2=C2+(C2-C1)/63; if(fabs(R2-R1)printf("%d %10.7f %10.7f %10.7f %10.7f\n",i+1,T2,S2,C2,R2); break;} else { R1=R2; C1=C2; T1=T2; S1=S2; h=h/2; k=k+1; } } i++; printf("%d %10.7f %10.7f %10.7f %10.7f\n",i,T2,S2,C2,R2); } while(1); system("pause"); return 0; }5 程序运行6 结果分析如上所示的结果与课本中求得的结果完全一样,表明程序编写正确,且符合要求,事实上,只要再将所求值的精度设置得更小,则所求的结果将更加准确,最终将无限接近于标准值,由上表也可以看出用龙贝格积分法求函数的积分值在精度比较低的情况下就能求到很准确的值!7 实验体会本次实验较为简单,主要时间是耗费在循环判断上面,因为书上已经给了流程图,都是基本的C语言,难度不大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 / 13
一、任务综述于分析
1.1 任务
1、 根据所掌握龙贝格算法,独立编写程序,实现具体问题的求解等; 2、 自己设计一个多项式,根据设定的代数多项式进行测试,调式程序; 3、 对所设计的程序解决实际问题并分析,撰写分析报告
1.2 分析
1、 首先先明确什么是龙贝格算法,了解他的基本原理,画出流程图,编写程序代码。 2、 自己设计一个多项式,对他利用龙贝格算法求出他的积分。并与真实值比较,检测程序是否有错误。 并进一步修改完善程序。可以多试几个多项式,来判断程序的正确性。 3、 任务三实际上是求平面曲线长的问题。利用弧长微分公式可求得结果。
四、测试 ................................................................................................................................................. 8
主要参考资料
《数值分析简明教程》 《数值分析课程设计》
王能超 陈越、童若锋
高等教育出版社 浙江大学出版社
教研室签字: 年 月 日
院签字: 年 月 日
2 / 13
目录
目录 ......................................................................................................................................................... 3 一、任务综述于分析 ............................................................................................................................. 4
二、算法分析与设计 ............................................................................................................................. 4 三、程序实现 ......................................................................................................................................... 6
六、总结 ............................................................................................................................................... 13
二、算法分析与设计
根据梯形法的误差公式,积分值 的截断误差项整理,知 ( 由此可见,只要二分前后两个积分值 ) (1) 的误差 的一种补
与 相当接近,就可以保证计算结果 ),如果用这个误差值作为
很小。按式(2),积分值得误差大致等于 ( 偿,可以期望,所得到的 ̅ 应当是更好的结果。 (
5 / 13
三、程序实现
3.1 龙贝格算法的流程图如下:
输入 a , b ,
h=b-a;
( ( )
( ))
;k=1;
S=0;
x=a+h/2;
S=S+f(x);
x=x+h;
< x<b ?
(
)
(
)
k=1 No (
?
Yes
K=k+1;h=h/2;
)
k=2 No (
?
Yes
) Yes
k=3 No | Yes NO |
《数值分析)》课程设计任务书
指导教师姓名 课程设计题目 设计目的、任务和要求 (一) 目的 要求学生运用龙贝格算法解决实际问题(塑料雨篷曲线满足函数 y(x)=lsin(tx),则给定雨篷的长度后, 求所需要平板材料的长度)。 (二)任务 1. 根据所掌握龙贝格算法,独立编写程序,实现具体问题的求解等; 2. 自己设计一个多项式,根据设定的代数多项式进行测试,调式程序; 3. 对所设计的程序解决实际问题并分析,撰写分析报告。 (三)要求 学生 1 个人组成一个小组,要求根据上述任务,通过查找资料,完成程序设计,并撰写分析报告,报告 要体现工作过程、测试结果、分析等内容。 王恒友 龙贝格算法的应用 教研室 人数 1 学时 信计 5天
3.1 龙贝格算法的流程图如下: ....................................................................................................... 6 3.2 龙贝格算法的代码实现: ........................................................................................................... 7
)
(2)
4 / 13
直接验证易知 (3) 这就是说,用梯形法二分前后两个积分值 法的积分值 。 与 按式(3)做线性组合,结果得到辛普生
再考察辛普生法。按 ,其截断误差与 成正比。因此,若将步长折半,则误差相应的减 至 1/16,即有
由此得
不难验证, 上式右端的值其实等于
, 就是说, 用辛普生法二分前后的两个积分值 ,即有
1.1 任务 ............................................................................................................................................... 4 1.2 分析 ............................................................................................................................................... 4
?
?
No
输出
6 / 13
3.2 龙贝格算法的代码实现:
void { double h,T1,T2,S,S1,S2,C1,C2,R1,R2,z[100][4]; int k=1; h=b-a; while(1) { S=0; for(double x=a+h/2;x<b;x+=h) S+=f(x); T2=(T1+h*S)/2; z[k][0]=T2; S2=T2+(T2-T1)/3; z[k][1]=S2; if(k==1); else { C2=S2+(S2-S1)/15; z[k][2]=C2; if(k==2); else { R2=C2+(C2-C1)/63; z[k][3]=R2; if(k==3); else { if(fabs(R2-R1)<e) break; } R1=R2; } C1=C2; } k++;h/=2;T1=T2;S1=S2; } T1=(f(a)+f(b))*h/2; z[0][0]=T1; Romberg(double a,double b)
设计的方法和步骤 查阅资料,展开充分理论分析,在掌握算法原理后进行软件设计,完成下列任务: 1、 熟悉此次设计的目标,查阅相关资料; 2、 对算法理论进行剖析,论证算法实现的可行性; 3、 根据可行的算法设计,进行软件程序实现,并最终解决实际问题。
1 / 13
设计工作计划 本案例时间为 5 天,具体安排如下 熟悉课设目标,查阅相关资料:1 天 算法理论进行剖析,论证算法实现的可行性:1 天 根据可行的算法设计,进行软件程序实现:2 天 对所设计的程序解决实际问题并分析,撰写分析报告:1 天
4.1 测试函数(1):............................................................................................................................... 8 4.2 测试函数(2):.................................................................................................................................. 9 4.3 测试曲线(3):............................................................................................................................. 10
7 / 13
printf("%3c %6c %12c %12c %12c\n",'k','T','S','C','R'); for(int i=0;i<k;i++) { printf("%3d",i); if(i<3) { for(int j=0;j<=i;j++) printf("%12.7f ",z[i][j]); printf("\n"); } else { for(int j=0;j<4;j++) printf("%12.7f ",z[i][j]); printf("\n"); } } }
