结构化学(第七章)(1)概述
物质结构(结构化学)

荧光屏 亮度 曲线
•衍射条件: △=sin(a) × d/2=λ/2, sin(a) = λ/d, Δx = d, ΔPx = sin(a)×P= λ/d× h/ λ= h/d
不确定关系式(测不准关系式): Δ结x论Δp:x≥h
具有波粒二象性的微观粒子 (r~h),没有经典轨道。
•根源:微观粒子的波粒二象性
二.力学量算符方程 1. 薛定谔方程-------能量方程
2 2(r) V (r)(r) E(r) 2m Hˆ 2 2 V (r) 2m
Hˆ(r) E(r)
2 算符方程
A f x gx,
A f x af x
后者为算符 Aˆ 的本征方程;
当控制电子一个一个地射出 与电子束一次射出衍射图形一样。
(Born统计解释) 大量电子: (1)衍射强度大的地方出现的电子多 (2)衍射强度小的地方出现的电子少 单个电子: (1)衍射强度大的地方电子出现的机会多 (2)衍射强度小的地方电子出现的机会少
物质波是几率波。
五 不确定关系
1927年,海森堡提出:微观粒子在某 一时刻同一方向的坐标和动量不能同时确 定。
结构化学
主讲: 潘 秀 梅
东北师范大学化学学院
参考书:
结构化学(面向21世纪教材),高教社 2003 潘道皑等 “ 物质结构 ” 高教社 1987 江元生 “ 物质结构 ” 高教社 1999 周公度 等 “结构学习基础” 北大出版社
1995
倪行等 “物质结构学习指导 ”科学出版 社 1999
绪
论
f(x) -- 算符 Aˆ 的本征函数(本征态);
a-- 算符 Aˆ 的本征函数f(x)的本征值。
3力学量的本征值和平均值
结构化学知识点归纳

2. 光谱项: 2S+1 L ,光谱支项: 2S+1 LJ 。
L:
0
1
2
3
4
5
符号:
S
P
D
F
G
H
3. 谱项能级的高低:Hund 规则:
(1)原子在同一组态时,S 值越大其能量越低;
(2)S 值相同时,L 值越大其能量越低;
(3)S,L 都相同时,电子少于半充满,J 值小能量低;电子多于半充满时,J
值大能量低。
− =2 d2ψ = Eψ 2m dx2
其解为:ψ n (x) =
2 l
sin( nπ l
x),
En
=
n2h2 8ml 2
解的特点:(1)粒子可以存在多种运动状态;(2)能量是量子化的;(3)存 在零点能;(4)没有经典运动轨道,只有概率分布;(5)存在节点,节点越多, 能量越高。以上这些特点是所以量子力学体系都有的特点。
∫ ∫ 自厄算符:满足
ψ
* 2
(
Aˆψ
1
)dτ
=
ψ 2 ( Aˆψ1)*dτ 的算符。
自厄算符的性质:(1)本证值都是实数;(2)不同本证值的本证函数相互正 交。
3. 假设 3:若某一物理量 A 的算符 Aˆ 作用于某一状态函数ψ ,等于某一常数 a 乘
以ψ ,即: Aˆψ = aψ ,那么对ψ 所描述的这个微观体系的状态,物理量 A 具有确
(2)外层电子对内层无屏蔽作用,σ = 0 ;
(3)同一组电子σ = 0.35 (1s 组内电子间的σ = 0.30 );
(4)对于 s,p 电子,相邻内一组的电子对它的屏蔽常数是 0.85;对于 d,f 电
子,相邻内一组的电子对它的屏蔽常数是 1.00;
第七章晶体的点阵结构和晶体的性质

第七章晶体的点阵结构和晶体的性质第七章晶体的点阵结构和晶体的性质⼀、概念及问答题1、由于晶体内部原⼦或分⼦按周期性规律排列,使晶体具有哪些共同的性质?答:a. 均匀性,⼀块晶体内部各个部分的宏观性质是相同的。
b. 各向异性,在晶体中不同的⽅向上具有不同的物理性质。
c. ⾃发地形成多⾯体外形,晶体在⽣长过程中⾃发地形成晶⾯,晶⾯相交成为晶棱,晶棱会聚成项点,从⽽出现具有多⾯体外形的特点。
2、点阵答:点阵是⼀组⽆限的点,连结其中任意两点可得⼀向量,将各个点按此向量平移能使它复原,凡满⾜这条件的⼀组点称为点阵。
点阵中的每个点具有完全相同的周围环境。
3、晶体的结构基元点阵结构中每个点阵点所代表的具体内容,包括原⼦或分⼦的种类和数量及其在空间按⼀定⽅式排列的结构,称为晶体的结构基元。
结构基元与点阵点是⼀⼀对应的。
4、晶体结构在晶体点阵中各点阵点的位置上,按同⼀种⽅式安置结构基元,就得整个晶体的结构,所以地晶体结构⽰意表⽰为:晶体结构=点阵+结构基元5、直线点阵根据晶体结构的周期性,将沿着晶棱⽅向周期地重复排列的结构基元,抽象出⼀组分布在同⼀直线上等距离的点列,称为直线点阵。
6、晶胞按照晶体内部结构的周期性,划分出⼀个个⼤⼩和形状完全⼀样的平⾏六⾯体,以代表晶体结构的基本重复单位,叫晶胞。
晶胞的形状⼀定是平⾏六⾯体。
晶胞是构成晶体结构的基础,其化学成分即晶胞内各个原⼦的个数⽐与晶体的化学式⼀样,⼀个晶胞中包含⼀个结构基元,为素晶胞,包今两个或两个以上结构基元为复晶胞,分别与点阵中素单位与复单位相对应。
7、晶体中⼀般分哪⼏个晶系?根据晶体的对称性,可将晶体分为7个晶系,每个晶系有它⾃⼰的特征对称元素,按特征对称元素的有⽆为标准划分晶系。
⼀般分为7个晶系,有⽴⽅晶系、六⽅晶系、四⽅晶系、三⽅晶系、正交晶系、单斜晶系和三斜晶系。
8、CsCl 是体⼼⽴⽅点阵还是简单⽴⽅点阵?是简单⽴⽅点阵。
在CsCl 晶体中,结构基元是由⼀个Cs +和⼀个Cl -构成,点阵点可以选Cs +的位置,也可以选Cl -的位置,还可以选在其他任意位置,但不能同时将Cs +和Cl -作为点阵点,因为这样选取不符合点阵的定义,同时也不能将晶体CsCl误认为是体⼼⽴⽅点阵,因为每个点阵点代表⼀个Cs +和⼀个Cl -。
《结构化学》课件

contents
目录
• 结构化学简介 • 原子结构与性质 • 分子的电子结构与性质 • 晶体结构与性质 • 结构化学实验结构化学的定义
总结词
结构化学是一门研究物质结构与 性质之间关系的科学。
详细描述
结构化学主要研究原子的排列方 式、电子分布和分子间的相互作 用,以揭示物质的基本性质和行 为。
晶体的电导率、热导率等性质取决于其内 部结构,不同晶体在这些方面表现出不同 的特性。
晶体的力学性质
晶体材料的应用
晶体的硬度、韧性等力学性质与其内部原 子排列密切相关,这些性质决定了晶体在 不同工程领域的应用价值。
晶体材料广泛应用于电子、光学、激光、 半导体等领域,如单晶硅、宝石等。了解 晶体的性质是实现这些应用的关键。
分子的选择性
分子的选择性是指分子在化学反应中对反应物的选择性和对产物的选择性。选择性强的分 子可以在特定条件下优先与某些反应物发生反应,产生特定的产物。
04
晶体结构与性质
晶体结构的基础知识
晶体定义与分类
晶体是由原子、分子或离子在空 间按一定规律重复排列形成的固 体物质。根据晶体内部原子、分 子或离子的排列方式,晶体可分 为七大晶系和14种空间点阵。
电子显微镜技术
• 总结词:分辨率和应用 • 电子显微镜技术是一种利用电子显微镜来观察样品的技术。相比光学显微镜,
电子显微镜具有更高的分辨率和更大的放大倍数,因此可以观察更细微的结构 和组分。 • 电子显微镜技术的分辨率一般在0.1~0.2nm左右,远高于光学显微镜的分辨 率(约200nm)。因此,电子显微镜可以观察到更小的晶体结构、病毒、蛋 白质等细微结构。 • 电子显微镜技术的应用范围很广,例如在生物学领域中,可以用于观察细胞、 病毒、蛋白质等生物样品的结构和形态;在环境科学领域中,可以用于观察污 染物的分布和形态;在材料科学领域中,可以用于观察金属、陶瓷、高分子等 材料的表面和断口形貌等。
第七章 群论基础 - ===欢迎访问结构化学精品课程网站===

⎡ −1 ⎢ 2 ⎢ 2 ˆ C3 = ⎢ − 3 2 ⎢ ⎢ 0 ⎢ ⎣ 3 2 2 0⎤ ⎥ ⎥ ˆ (240) 0⎥ = C 3 ⎥ 1⎥ ⎥ ⎦
ˆ φ = 1200 C 3,
n
y ' = x sin φ + y cos φ
(x, y)
φ
α
z' = z
⎡ x' ⎤ ⎡ x ⎤ ⎡cos φ ⎢ '⎥ ˆ ⎢ ⎥ ⎢ ⎢ y ⎥ = C (φ ) ⎢ y ⎥ = ⎢ sin φ ⎢ z' ⎥ ⎢ ⎣z⎥ ⎦ ⎢ ⎣ 0 ⎣ ⎦ − sin φ cos φ 0 0⎤ ⎡ x ⎤ ⎢ y⎥ 0⎥ ⎥⎢ ⎥ 1⎥ ⎦⎢ ⎣z⎥ ⎦
理论与计算化学实验室
第七章 群论基础
量子化学与群论
Ĉ3
Ĉ
Ĉ3
3
3
Ĉ
3=
Ĉ
3
2
Ĉ3
=Ê
Ĉ3
旋转轴次 n =
2π
α
; α 为基转角 (规定为逆时针旋转)
理论与计算化学实验室
第七章 群论基础
量子化学与群论
7.2.2 分子点群
分子中或多或少地存在一些对称元素, 这些对称元 素对应的对称操作的组合满足群的定义, 构成群, 称为对 称操作群. 因为分子中的对称元素至少通过一点公共点, 故称为点群. 对称操作构成群的命题可以用通过乘法表示验证:
量子化学与群论
对称操作的表示矩阵为:
⎡ a11 ⎢a ⎢ 21 ⎢ ⎣ a31
a12 a22 a32
a13 ⎤ ⎥ a23 ⎥ a33 ⎥ ⎦
7结构化学
J值的大小表示了偶合作用的强弱;
偶合常数与化学键性质有关,与外加磁场强度无关;
相互偶合的两组质子,彼此间作用相同,其偶合常数相同;
ab
CH3CH2Br
J ab = J ba
一般间隔四个单键以上,J值趋于零;
O
CH3CH2CCH3 ab c
Ha与Hc, Hb与Hc 均不发生偶合
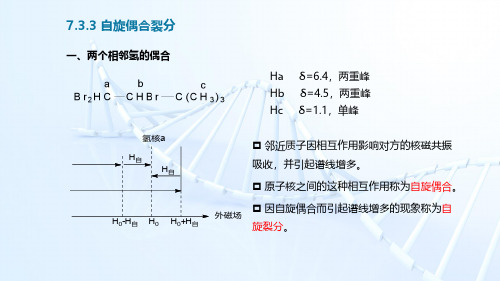
7.3.3 自旋偶合裂分
7.3.3 自旋偶合裂分
四、自旋偶合的条件
2、化学不等价的质子才会发生自旋偶合。 (1)化学等价和化学位移等价 分子中两个相同的原子处于相同的化学环境称为化学等价。 分子中两个原子具有严格相同的化学位移值,称它们是化 学位移等价。 化学等价的质子具有相同的化学位移。 具有相同化学位移的质子不一定是化学等价的。
通过镜面对称操作能互换的质子叫对映异位质子。 (对映异位质子在手性环境中是非化学等价的,在非 手性环境中是化学等价的。)
Ha C
Hb
Cl
Br Cl
CH3
不能通过对称操作进行互换的质子叫做非对映异位质子。 (非对映异位质子在任何环境中都是化学不等价的。)
CH3 Ha
CH2CH3
Hb
7.3.3 自旋偶合裂分
7.3.3 自旋偶合裂分
四、自旋偶合的条件 2、化学不等价的质子才会发生自旋偶合。 (2)怎样判别两个质子是否化学等价?
通过对称轴旋转而能互换的质子叫等位质子。(等位质子在任何环境中都是化 学等价的。)
7.3.3 自旋偶合裂分
四、自旋偶合的条件 2、化学不等价的质子才会发生自旋偶合。 (2)怎样判别两个质子是否化学等价?
常温下十二个氢表现为一组峰, 极低温下十二个氢表现为两组峰。 只有化学不等价的质子才能显示出自旋耦合。
结构化学 课件 第七章

OP矢量r=ua+vb+wc=3a+2b+3c, 所以,P点阵点指标为323
直线点阵指标 [uvw]
OQ矢量 r =ua+vb+wc=1a+2b+1c, 直线点阵MN与OQ平行或重合,所以,MN直线点阵指标为[121]
平面点阵指标(h*k*l* )
(h*k*l*)=(010)
(111)晶面
相互平行的一族平面点阵, 其(h*k*l*)相同:
矩形框中内容为一个结构基元,可抽象为一个点阵点.安 放点阵点的位置是任意的,但必须保持一致,这就得到点阵:
三维周期性结构与空间点阵
下列晶体结构如何抽象成点阵?
Mn
(简单立方)
Li Na K Cr Mo W…
(体心立方)
以上每一个原子都是一个结构基元,都可以抽象成一个点阵点.
例:Ni Pd Pt Cu Ag Au ……
净含一个点阵点的平面格子是素格子,多于一个点 阵点者是复格子;平面素格子、复格子的取法都有 无限多种. 所以需要规定一种 “正当平面格子”标准.
正当平面格子的标准
1. 平行四边形 2. 对称性尽可能高 3. 含点阵点尽可能少 平面格子净含点阵点数:顶点为1/4;棱心为 1/2;格内为1. 正当平面格子有4种形状,5种型式(其中矩 形有带心与不带心两种型式):
面心立方是一种常见 的金属晶体结构,其 中每个原子都是一个 结构基元,都可被抽 象成一个点阵点.
CsCl型晶体结构
CsCl型晶体中A、B是不同的原子,不能都被抽象为点阵 点. 否则,将得到错误的体心立方点阵!这是一种常见的错误:
体心立方虽不违反点阵定义,却不是CsCl型晶体的点阵! 试将此所谓的“点阵”放回晶体,按“点阵”上所示的矢量,对 晶体中的原子平移,原子A与B将互换,晶体不能复原!
结构化学课件

结构化学课件结构化学课件结构化学简介结构化学是在原子- 分子水平上研究物质分子构型与组成的相互关系以及结构和各种运动的相互影响的化学分支学科。
它又是阐述物质的微观结构与其宏观性能的相互关系的基础学科。
结构化学不但与其他化学学科联系密切,而且与生物科学、地质科学、材料科学和医药学等各学科的研究相互关联、相互配合、相互促进。
由于许多与物质结构有关的化学数据库的建立,结构化学也愈来愈被农学家和化工工程师所重视。
结构化学详细介绍结构化学首先是一门直接应用多种近代实验手段测定分子静态、动态结构和静态、动态性能的实验科学。
结构化学它要从各种已知的化学物质的分子构型和运动特征中归纳出物质结构的规律性,还要从理论上说明为什么原子会结合成为分子,为什么原子按一定的量的关系结合成为数目众多的形形色色的分子,以及在分子中原子相互结合的各种作用力方式和分子中原子相对位置的立体化学特征。
结构化学还说明某种元素的原子或某种基团在不同的微观化学环境中的价态、电子组态、配位特点等结构特征。
另一方面,从结构化学的角度还能阐明物质的各种宏观化学性能(包括化学反应性能)和各种宏观非化学性能(包括各种物理性质和许多新技术应用中的技术性能等)与微观结构之间的关系及其规律性。
在这个基础上就有可能不断地运用已知的规律性,设法合成出具有更新颖、结构特点更不寻常的新物质,在化学键理论和实验化学相结合的过程中创立新的结构化学理论。
与此同时,还要不断地努力建立新的阐明物质微观结构的物理的'和化学的实验方法。
与其他的化学分支一样,结构化学一般从宏观到微观、从静态到动态、从定性到定量按各种不同层次来认识客观的化学物质。
演绎和归纳仍是结构化学研究的基本思维方法。
早期的有关物质化学结构的知识可以说是来自对于物质的元素组成和化学性质的研究。
当时人们对化学物质(包括各种单质和为数不多的几种化合物),只能从对物质组成的规律性认识,诸如定比定律、倍比定律等加以概括。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
2、各向异性 表现:晶体中不同方向具有不同的物理性
质。如在不同的方向上具有不同的电导率、热 膨胀系数、折光率以及机械强度等。
原因:周期性结构中,不同方向原子或分 子排列情况各不相同。
6
晶
体
的
云 母
异
片
向
性
产地:甘肃省肃北县
玻 蜡滴 璃
a:晶轴不一定相互垂直。
c
b:分数坐标与选取的晶胞原点有关。
c:分数坐标的个数 = 晶胞内的原子个数。
β Oα γ
b
a
d:分数坐标尽量小。
c
P
zc
O yb
xa
b
a
OP=xa+yb+zc
P点坐标为(x,y,z)
40
NaCl型晶体
原子的分数坐标: A: 0 0 0
0 1/2 1/2 1/2 0 1/2 1/2 1/2 0 B: 1/2 0 0
3
晶体多有漂亮对称的外形
4
一、晶体结构的特征(P250) 晶体是由原子或分子在空间按一定的规律周期
性的重复排列构成的物质,周期性规律是晶体结构 的最突出的特征。
内部原子或分子按周期性规律的排列,使晶体 具有如下共同性质: 1、均匀性
表现:同种晶体内部各部分的宏观性质,如密 度、化学性质是相同的。
阵点,即可得到空间点阵。
36
37
四、晶胞 1.定义 平行六面体, 代表晶体结构的重复单位; 能体现晶体化学组成之比。 2.分类 素晶胞 — 结构基元 复晶胞 正当晶胞:在照顾对称性的前提下,选取体积最 小的晶胞。
3.晶胞两个基本要素
晶胞的大小和形状 :晶胞参数(a、b、c、α、β、γ) 晶胞中原子的位置 :用分数坐标(x、y、z)表示。
结 构 化 学 课 程 内 容
(48学时)
量子力学基础 (第 1 章) 单电子原子结构
原子结构
(第 2 章)
分子结构
(第 3-5章)
晶体结构
(第 7-9 章)
多电子原子结构
原子光谱
双原子分子结构 (第 3 章)
多原子分子结构 (第 5 章)
分子对称性
(第 4 章)
分子光谱和光电子能谱(第 3 章)
概述
二、点阵和点阵结构 1、有关定义
(1)点阵:点阵是一组无限的点,连接其中任 意两点可得一向量,将各点沿向量平移能使其复原, 凡是满足以上条件的一组点称为点阵。
(2)点阵点:点阵结构中构成点阵的点叫做点 阵点,每个点阵点应具有相同的周围环境。
14
2、点阵的分类 (1)直线点阵
一组分布在同一直线上等距离的无穷点列,称 为直线点阵。
(第 7 章)
金属晶体和离子晶体结构
(第 8-9 章)
第七章 晶 体 结 构
气体
聚集 物质 状态
液排列) 晶体结构的对称性
固体 非晶体
晶体结构的测定
准晶体
2
§7.1 晶体结构的周期性和点阵
教学重点: 1、晶体的特性 2、点阵与点阵结构 3、点阵与晶体结构之间的关系 4、晶胞 5、晶面和晶面指标的计算
片
云母薄片上的热导率有异向性
蓝晶石两个方向上的硬度差异显著,有“二硬石”之称; 古代的宝石工匠早就知道钻石的八面体面(111)特别难以 抛光…… 1669年巴尔托林发现了光束通过冰洲石的双折射现象:
❖ 石墨在平行于层的方向上电导率高且为半金属性导电;
垂直于层的方向上电导率低且为半导体性导电.
图 中 红 、 蓝 球 均 为 C 原 子
17
分类: 素单位(素格子):每个单位包含一个点阵点。
复单位(复格子):每个单位包含一个以上 点阵点。
处于格子顶点点阵点贡献1/4
边线点阵点贡献1/2
内部点阵点贡献1
18
正当单位(正当格子)标准:
1. 平行四边形 2. 对称性尽可能高 3. 含点阵点尽可能少
19
(3) 空间点阵 一组分布三维方向上的点列,称为空间点阵。
式或叫做14种布拉威格子。
22
(R心六方)
23
24
25
26
27
28
29
30
三、晶体结构与点阵之间的关系
晶体具有空间点阵结构。
晶体结构
-周-期结性构重基复元的部分
点阵
+ 结构基元
Na (立方体心)
1、晶体的结构基元
把晶体结构抽象为点阵的过程中,每个点阵点
所代表的具体内容。
包括原子、分子的种类、数量及其在空间一定
按同一方式排列,所以当温度升高,热振动均 加剧,开始融化时,各部分需要的温度是一样 的,因而具有一定熔点。
11
5、晶体对X射线衍射 晶体的周期性结构使它成为天然的三维光栅,
周期与X光波长相当,能够对X光产生衍射。
12
6、晶体的对称性 晶体的理想外形(宏观)和内部结构(微观)
具有特定的对称性。
13
20
空间点阵单位(格子) 定义:空间点阵中,以一组不平行的向量a,b,c(右
手定则)为边画出的平行六面体叫做空间点阵的单位。 空间点阵单位参数:矢量长度a=|a|、b=|b|、 c=|c|
及其相互间的夹角α、β、γ。 分类:
素单位:每个单位包含一个点阵点。
复单位:每个单位包含一个以上点阵点。
21
正当单位的标准: 1、 平行六面体 2、 对称性尽可能高 3、 含点阵点尽可能少 正当空间单位有7种形状,14种空间点阵形
定义:连接两个点阵点的矢量a
直线点阵单位 参数:矢量长度a=|a|
分类:素单位和复单位
(2) 平面点阵 一组分布在同一平面上的二维点列,称为平面
点阵。
16
平面点阵单位(格子) 定义:在平面点阵中选择
一组不平行的向量a、b,以平 移向量为边画出的平行四边形 叫做平面点阵的单位。
平面点阵单位参数:矢 量长度a=|a|、 b=|b|及其夹 角γ。
3、自发形成多面体外形(自范性) 表现:晶体在生长过程中能自发地形成晶面、晶
面相交形成晶棱、晶棱汇聚形成顶点,构成多面体的 外形,呈现出一定的对称性。
理想晶体的晶面(F)和晶棱(E)及顶点(V) 之间的关系:
F+V=E+2
立方体: 6个面(F=6) 12条棱(E=12) 8个顶点(V=8)
10
4、晶体有确定的熔点 原因:晶体具有周期性结构,各个部分都
的排列方式。
2、晶体中点阵的获得
数学抽象
具体内容
点阵点 直线点阵 平面点阵 空间点阵 空间点阵单位
结构基元 晶棱 晶面 晶体 晶胞
晶体结构的基本重复单位
结构基元与点阵点
(1) 一维周期性结构与直线点阵
(2)晶面和平面点阵 将晶面上周期性重复排列的结构基元抽象
为点阵点,即可得到平面点阵。
35
(3)晶体和空间点阵 将晶体上周期性重复排列的结构基元抽象为点
