交流电路的频率特性(精)
第七章交流电路的频率特性

( j )| 式中, | H 是 的实函数,表征了电路响应与激励的幅值比 (振幅比 改有效值比)随变化的特性,称为电路的幅频特性; 也是 ( ) 的实函数,表征了电路响应与激励的相位差(相移)随 变化的特性, 称为电路的相频特性。幅频特性和相频特性总称电路的频率特性。习 (j )| 变化的情况用曲线来表示,分别称为幅频特 ( ) 惯上常把 和|H 随 性曲线和相频特性曲线。 纯电阻网络的网络函数是与频率无关的,这类网络的频率特性是 不需要研究的。研究含有动态元件的网络频率特性才是有意义的。 由RC元件按各种分式组成的电路能起到选频或滤波的作用,从 而在实际中有着广泛的应用。下面讨论简单的RC低通、高通、带通、 带阻及全通网络的频率特性。
7-1-1 RC低通网络
当 c
1 1 时,网络函数的幅值为最大幅值的 ,即 RC 2
开阔你的视野
• 共振现象(续)
这该是一本科幻或者荒诞小说吧?否则,一件大不过拳头、重不过几斤的小 东西,真的就有那么厉害,能把一座巍然耸立的大楼甚至是一座巨无霸似的 大桥震垮?它是一件什么物品呢? 原来,它是一件共振器,它的威力主要在于它能发出各种频率的波,这些 不同频率的波作用于不同的物体,就能够相应地产生出一种共振波,当这种 共振波达到一定程度时,就能使物体被摧毁。 共振是物理学上的一个运用频率非常高的专业术语。共振的定义是两个振动 频率相同的物体,当一个发生振动时,引起另一个物体振动的现象。共振在 声学中亦称“共鸣”,它指的是物体因共振而发声的现象,如两个频率相同 的音叉靠近,其中一个振动发声时,另一个也会发声。而在电学中,振荡电 路的共振现象称为“谐振”。
7-1 RC电路的频率特性
上海交通大学---电路元件交流阻抗频率特性

SHANGHAIJIAOTONG UNIVERSITY电路元件交流阻抗频率特性一、实验目的(1)加深了解R 、L 、C 元件的频率与阻抗的关系。
(2)加深理解R 、L 、C 元件端电压与电流间的相位关系。
(3)熟悉低频信号发生器等常用电子仪器的使用方法。
二、实验内容正弦交流可用三角函数表示,即由最大值(U m 或I m );频率f(或角频率ω=2πf)和初相位三要素来决定。
在正弦稳态电路的分析中,由于电路中各处电压、电流都是同频率的交流电,所以电流、电压可用相量表示。
在频率较低的情况下,电阻元件通常略去其电感及分布电容而看成是纯电阻。
此时其电压与电流可用复数欧姆定律来描述:U ∙=R I ∙式中R 为线性电阻元件。
U ∙与I ∙之间无相角差。
电阻中吸收的功率为P=UI=I 2R因为略去附加电感和分布电容,所以电阻元件的阻值与频率无关。
即R-f 关系如图1.11-1。
电容元件在低频也可略去其附加电感及电容极板间介质的功率损耗,因而可认为只具有电容C 。
在正弦电压作用下流过电容的电流之间也可用复数欧姆定律来表示:U ∙=X C I ∙式中X C 是电容的容抗,其值为X C =1/j ωc 所以有U ∙=1/j ωc ·I ∙= I ωc ∠-90°电压U 滞后电流I 的相角为90°,电容所吸收的功率平均为零。
电容的容抗与频率的关系X C -f 曲线如图1.11-2。
电感元件因其由导线绕成,导线有电阻,在低频时如略去其分布电容则它仅由电阻R L 与电感L 组成。
在正弦电流的情况下其复阻抗为Z=R L + j ωL=Z∠Φ式中R L 为线圈导线电阻。
阻抗角Φ可由R L 及L 参数来决定:..。
SHANGHAIJIAOTONG UNIVERSITYΦ=arctg ωL/R电感线圈的电压与流过的电流间关系为U ∙==(R L + j ωL )I ∙= Z · I ∙=∠Φ如果R L =0,电压超前电流90°电感线圈所吸收的平均功率为P=UIcos ψ=I 2R L 感抗与频率的关系如图1.11-3。
电路实验

图14-1实验十四交流电路频率特性的测定一.实验目的1.研究电阻、感抗、容抗与频率的关系,测定它们随频率变化的特性曲线; 2.了解滤波器的原理和基本电路; 3.学习使用信号源、交流毫伏表。
二.原理说明1.单个元件阻抗与频率的关系对于电阻元件,根据︒∠=0RR R I U ,其中R I U=R R ,电阻R 与频率无关;对于电感元件,根据LL Lj X I U = ,其中fL X I U π2L L L ==,感抗X L 与频率成正比; 对于电容元件,根据CCC j X I U -= ,其中fC X I U π21C C C ==,容抗X C 与频率成反比。
测量元件阻抗频率特性的电路如图14—1所示,图中的r 是提供测量回路电流用的标准电阻,流过被测元件的电流(I R 、I L 、I C )则可由r 两端的电压U r除以r 阻值所得,又根据上述三个公式,用被测元件的电流除对应的元件电压,便可得到R 、X L 和X C 的数值。
2.交流电路的频率特性由于交流电路中感抗X L 和容抗X C 均与频率有关,因而,输入电压(或称激励信号)在大小不变的情况下,改变频率大小,电路电流和各元件电压(或称响应信号)也会发生变化。
这种电路响应随激励频率变化的特性称为频率特性。
若电路的激励信号为Ex(jω),响应信号为R e(jω),则频率特性函数为)()()j ()j ()j (x e ωϕωωωω∠==A E R N式中,A (ω)为响应信号与激励信号的大小之比,是ω的函数,称为幅频特性;ϕ(ω)为响应信号与激励信号的相位差角,也是ω的函数,称为相频特性。
A A fffa)(b)(c)(图21-2C C C1C2图14-2在本实验中,研究几个典型电路的幅频特性,如图14-2所示,其中,图(a)在高频时有响应(即有输出),称为高通滤波器,图(b)在低频时有响应(即有输出),称为为低通滤波器,图中对应A=0.707的频率fC称为截止频率,在本实验中用RC网络组成的高通滤波器和低通滤波器,它们的截止频率fC均为1/2πRC。
交流电路频率特性的测定

u-+Ri Li Ci R u Lu Cu ru RL X CX S r图21-1交流电路频率特性的测定一.实验目的1.研究电阻,感抗、容抗与频率的关系,测定它们随频率变化的特性曲线; 2.学会测定交流电路频率特性的方法; 3.了解滤波器的原理和基本电路; 4.学习使用信号源、频率计和交流毫伏表。
二.原理说明1.单个元件阻抗与频率的关系对于电阻元件,根据︒∠=0R RR I U ,其中R I U =R R ,电阻R 与频率无关; 对于电感元件,根据LL Lj X I U = ,其中fL X I U π2L L L ==,感抗X L 与频率成正比; 对于电容元件,根据CC Cj X I U -= ,其中fC X I U π21C C C ==,容抗X C与频率成反比。
测量元件阻抗频率特性的电路如图21—1所示,图中的r 是提供测量回路电流用的标准电阻,流过 被测元件的电流(I R 、I L 、I C )则可由r 两端的电压U r除以r 阻值所得,又根据上述三个公式,用被测元件的电流除对应的元件电压,便可得到R 、X L 和X C 的数值。
2.交流电路的频率特性由于交流电路中感抗X L 和容抗X C 均与频率有关,因而,输入电压(或称激励信号)在大小不变的情况下,改变频率大小,电路电流和各元件电压(或称响应信号)也会发生变化。
这种电路响应随激励频率变化的特性称为频率特性。
若电路的激励信号为Ex(jω),响应信号为R e(jω),则频率特性函数为)()()j ()j ()j (x e ωϕωωωω∠==A E R N式中,A (ω)为响应信号与激励信号的大小之比,是ω的函数,称为幅频特性; ϕ(ω)为响应信号与激励信号的相位差角,也是ω的函数,称为相频特性。
在本实验中,研究几个典型电路的幅频特性,如图21-2所示,其中,图(a)在高频时有响应(即有输出),称为高通滤波器,图(b)在低频时有响应(即有输出),称为为低通滤波器,图中对应A=0.707的频率fC称为截止频率,在本实验中用RC网络组成的高通滤波器和低通滤波器,它们的截止频率fC均为1/2πRC。
幅频特性和相频特性

电路分析实验报告幅频特性和相频特性一、实验摘要电容元件在交流电路中的阻抗会随电源频率的改变而变化。
本实验用电容搭建一个电路,用示波器观察加上一个正弦波之后,该电路幅值和相位随频率变化的规律曲线。
二、实验环境示波器函数信号发生器 0.1μF电容电阻面包板导线三、实验原理电阻作为响应时,可用作高通滤波器电容作为响应时,可用作低通滤波器RC串并联(文氏电桥)电路四、实验步骤在面包板上搭建电路加上4vpp,频率从100赫兹到用示波器观察波形的幅值和位相差,记录相20千赫兹的正弦波应电压是输入电压0.707倍时的波形图将电容作响应加上4vpp,频率从100赫兹到20千赫兹的正弦波,用示波器观察波形的幅值和位相差,记录响应电压是输入电压0.707倍时的相关数据搭建文氏电桥加上4vpp,频率从100赫兹到20千赫兹的正弦波,用示波器观察波形的幅值和位相差,记录响应电压最高时的相关数据五、实验数据1.电阻作响应(高通滤波器)输入信号峰峰值的测量值为3.9v100 200 600 1000 1400 1500 5000 10000 15000 20000 输入频率/HzVpp/v 0.297 0.320 1.61 2.33 2.77 2.85 3.74 3.9 3.9 3.9相位差-85 -79 -66 -55 -48 -45 -19 -10 -8 -6 /°2.由李萨如图形计算得相位差= -49°,直接测量的相移为-48°,误差0.02当频率增大时,响应电压增大,体现出高通当频率增大时,位相差减小2.电容作响应(低通滤波器)100 500 1000 1500 16002000 3000 5000 8000 10000 输入频率/HzVpp/v 4.14 3.94 3.38 2.89 2.81 2.49 1.89 1.29 0.880 0.7204 18 32 43 4651 61 71 77 80相位差/°当频率增大时,响应电压减小,体现出低通当频率增大时,位相差增大3.文氏电桥100 500 1000 1500 2000 4000 5000 10000 15000 20000 输入频率/HzVpp/v 0.273 1.03 1.31 1.35 1.33 1.09 0.98 0.580 0.420 0.340 -80 -41 -15 -1 11 33 43 62 75 80相位差/°在某一频率,响应电压最大随频率增加,位相差先减小再增大六、实验总结在本次实验中了解到了RC串联电路和文氏电桥的幅频特性和相频特性。
正弦交流电路中的R、L、C特性

P UI
1
T
UI(1 cos2 t)dt UI
T0
3-4.2 电感元件的交流电路
基本关系式: u L di dt
i uL
设 i 2 I sin t
则 u L di 2 I L cost
dt
2 I L sin(t 90 )
2 U sin(t 90 )
电感电路中电流、电压的关系
复数形式的欧姆定律
U IR U I( j X L) U I( j XC )
电阻电路
电感电路
电容电路
3.简单正弦交流电路的关系(以R-L电路为例)
* 电压、电流瞬时值的关系符合欧姆定律、克氏
定律。
i
u
R
uR
u uR uL iR L di
L uL
dt
* 电流、电压相量符合相量形式的欧姆定律、克氏
T0
3. 无功功率 Q
瞬时功率达到的最大值(吞吐规模)
p UI sin 2t
Q UI
(电容性无功取负值)
例 求电容电路中的电流
i
u
C
已知: C =1μF
u 70.7 2sin(314 t )
求:I 、i
6
解:X C
1
C
1 314106
3180
电流有效值 I U 70.7 22 . 2 mA X C 3180
p i u 2UI sin t cost UI sin 2t
i uL
p i u UI sin 2t
u
i
t
i
i
i
i
u uuu
p
可逆的 能量转换
过程
+
P <0
电路实验_电路频率特性的研究
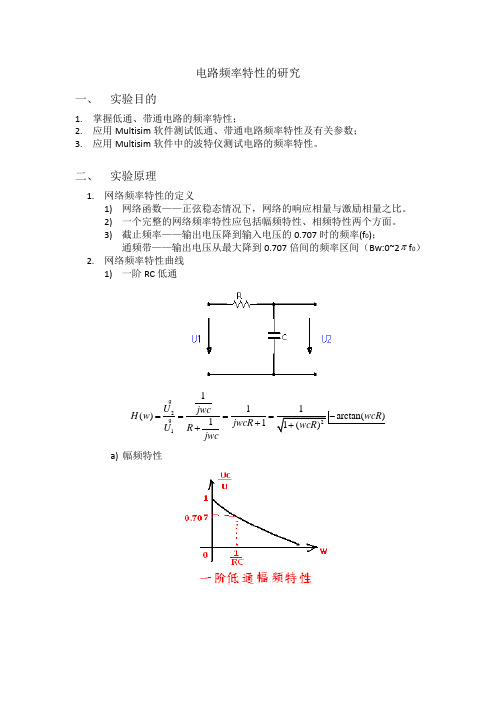
电路频率特性的研究一、 实验目的1. 掌握低通、带通电路的频率特性;2. 应用Multisim 软件测试低通、带通电路频率特性及有关参数;3. 应用Multisim 软件中的波特仪测试电路的频率特性。
二、 实验原理1. 网络频率特性的定义1) 网络函数——正弦稳态情况下,网络的响应相量与激励相量之比。
2) 一个完整的网络频率特性应包括幅频特性、相频特性两个方面。
3) 截止频率——输出电压降到输入电压的0.707时的频率(f 0);通频带——输出电压从最大降到0.707倍间的频率区间(Bw:0~2πf 0)2. 网络频率特性曲线1) 一阶RC 低通2111()11U jwcH w jwcR U R jwc====++a) 幅频特性2121221()0,;,0;1,0.707U H w U w U U w U w U U CR ===→∞→===||=则有由图像看出,频率越低,信号越容易通过——低通。
b) 相频特性()a r c t a n ()10,0;,45;,90w w c Rw w w CRϕϕϕϕ=-====-→∞=-。
c) 截止频率:012f RCπ= 2) 二阶RLC 带通a)谐振频率0f =(0w =,此时有电路如下图特性:b)品质因数001w L Q R w RC ===(L 、C 一定时,改变R 值就能影响电路的选频特性,R 越小,Q 越大,选频特性越好);c) 幅频特性和相频特性00000,,U w f I I R w f U IU I η======另则有故=,如下图d) 由上图得,通频带"'0022()w f Bw f f Q Qππ=-== 3) 二阶RLC 低通a)谐振频率0f =b) 幅频特性和相频特性0201()(,)1(1)|()|c U w L jQ w jwCH w Q U jQ R w R jwL jwC H w ηηη∙-=====+-++==则有122|()|(|()|)0,00;2m c H w d H w w w w d w f U ηηπ=======令解得即对应的U 极大值为如下图所示:c)m f =3. 测量方法对特征频率点极其上下百倍频程范围内选取频率点进行测量,包括对()H w 及ϕ的测量,并根据测得的数据作出幅频特性曲线及相频特性曲线。
RLC交流电路的分析(电路的串并联谐振)

在电力系统中,串联谐振可以用于无功补偿和滤波,提高电力系统的 稳定性和可靠性。
03
RLC交流电路的并联谐振
并联谐振的定义
• 并联谐振是指RLC交流电路在特定频率下,电路的阻抗呈现 最小值,即达到最小电阻状态。此时,电流在电路中最大, 电压则呈现最小值。
并联谐振的条件
• 并联谐振的条件是:XL=XC,其中XL是电感L的感抗,XC是 电容C的容抗。当感抗等于容抗时,电路发生并联谐振。
RLC电路的工作原理
01
02
03
当交流电源施加到RLC电 路时,电流和电压的相 位关系会发生变化,产
生不同的响应特性。
在串联谐振状态下,RLC 电路的总阻抗最小,电 流最大;在并联谐振状 态下,RLC电路的总导纳
最大,电流最小。
通过分析RLC电路在不同 频率下的响应特性,可 以了解其工作原理和特
性。
串并联谐振在实际电路中的应用
滤波器设计
利用串联或并联谐振电路的频率选择性,可以设计出不同频段的 滤波器,用于信号的筛选和处理。
信号放大
利用串联或并联谐振电路的增益特性,可以对特定频率的信号进行 放大,用于信号的增强和处理。
测量技术
利用串联或并联谐振电路的测量技术,可以测量电感、电容等元件 的参数,以及电路的频率特性等。
04
05
1. 搭建RLC交流 电路
2. 设定电源和信 号源
3. 测量并记录数 4. 观察和调整 据
5. 分析数据
根据实验箱提供的组件, 搭建RLC交流电路,包括电 阻、电感和电容。
将电源供应器设定为适当 的电压和频率,使用信号 发生器产生正弦波信号输 入到RLC交流电路中。
使用测量工具测量RLC交流 电路的电流、电压等参数 ,记录数据。
