三角形倒角模型
翻折倒角的结论

翻折倒角的结论一、倒角的数学原理与一般方法【数学原理】倒角的数学原理,本质上只有一条,即为三角形的内角和定理及其推论——三角形外角的性质。
由于三角形的外角性质是加和的形式,会使得运算更简洁。
【计算方法】倒角的计算方法,其实就只有一条:利用内角和或外角性质找等量关系,列方程!不过,列方程也是有讲究的,总体思路是宁可多设几个字母,也要尽可能地使方程简洁,进而降低角度计算过程的复杂度。
二、倒角的四个重要模型倒角的模型主要有四个:①平行线与拐点模型②字与飞镖模型③双角平分线模型④折角模型前两个模型已经在上一篇文章中说明,继续介绍后两个模型,重点介绍“双角平分线模型”。
(一)平行线与拐点模型(三)字与飞镖模型(三)双角平分线模型1、模型条件&结论2、应用场景在应对与多条角平分线相关的角度问题时,“双角平分线模型”非常好用,所求夹角∠BPC的大小只有∠A有关!3、证明思路或方法(以双内角平分线图形为例)模型的证明依然是朴素的,即为最基本的方法:“根据三角形的内角和定理或外角性质列方程”。
其它两个图形对应的结论也可类似证明。
整个证明过程,只有朴素的数学原理,没有太多需要动脑筋的地方,便可轻松地把问题解决。
这也是我一贯的解题方法,我希望我的学生是更富有逻辑思考能力的,而不是记住一堆华丽的技巧,正所谓“大道至简”。
4、经典例题(四)折角模型1、模型条件&结论2、应用场景在三角形的翻折问题求解角度时使用。
以上两个图形的唯一区别仅在于翻折后的点A'是落在△ABC的内部还是外部。
如果点A'是落在△ABC的内部,则为左边的模型;如果点A'是落在△ABC的外部,则为右边的模型。
3、证明思路或方法(以右边图形为例)4、经典例题(五)其它常见模型1、四边形的双角平分线模型区别:唯一之处就在于所求角是四边形的相邻两角的平分线所构成角(适用于左边模型)还是相对两角的角平分线所构成的角(适用于右边模型)。
初中数学三角形中的倒角模型-平行线-拐点模型及参考答案

三角形中的倒角模型-平行线+拐点模型近年来各地中考中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
平行线+拐点模型在初中数学几何模块中属于基础工具类问题,也是学生必须掌握的一块内容,熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题就平行线+拐点模型(猪蹄模型(M型)、铅笔头模型、牛角模型、羊角模型、“5”字模型)进行梳理及对应试题分析,方便掌握。
拐点(平行线)模型的核心是一组平行线与一个点,然后把点与两条线分别连起来,就构成了拐点模型,这个点叫做拐点,两条线的夹角叫做拐角。
通用解法:见拐点作平行线;基本思路:和差拆分与等角转化。
模型1:猪蹄模型(M型)【模型解读】图1图2图3如图1,①已知:AM∥BN,结论:∠APB=∠A+∠B;②已知:∠APB=∠A+∠B,结论:AM∥BN.如图2,已知:AM∥BN,结论:∠P1+∠P3=∠A+∠B+∠P2.如图3,已知:AM∥BN,结论:∠P1+∠P3+...+∠P2n+1=∠A+∠B+∠P2+...+∠P2n.1(2022·河南洛阳·统考二模)如图,AB∥CD,∠ABM=30°,∠CDM=45°,则∠BMD的度数为()A.105°B.90°C.75°D.70°2(2023春·安徽蚌埠·九年级校联考期中)太阳灶、卫星信号接收锅、探照灯及其他很多灯具都与抛物线有关.如图,从点O照射到抛物线上的光线OB,OC反射后沿着与PO平行的方向射出,已知图中∠ABO =46°,∠OCD=88°,则∠BOC的度数为()A.116°B.124°C.134°D.135°3(2023春·四川泸州·七年级校考期末)如图所示,若AB∥EF,用含α、β、γ的式子表示x,应为()A.α+β+γB.β+γ-αC.180°-α-γ+βD.180°+α+β-γ4(2023·广东深圳·校联考模拟预测)北京冬奥会掀起了滑雪的热潮,谷爱凌的励志故事也激励着我们青少年,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,如果不想体验人仰马翻的感觉,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB ∥CD ,当人脚与地面的夹角∠CDE =60°时,求出此时上身AB 与水平线的夹角∠BAF 的度数为()A.60°B.45°C.50°D.55°5(2023春·河南驻马店·九年级专题练习)已知AB ∥CD ,∠EAF =13∠EAB ,∠ECF =13∠ECD ,若∠E =66°,则∠F 为()A.23°B.33°C.44°D.46°6(2022·浙江七年级期中)如图(1)所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”.(1)如图(2)所示,已知AB ⎳CD ,请问∠B ,∠D ,∠E 有何关系并说明理由;(2)如图(3)所示,已知AB ⎳CD ,请问∠B ,∠E ,∠D 又有何关系并说明理由;(3)如图(4)所示,已知AB ⎳CD ,请问∠E +∠G 与∠B +∠F +∠D 有何关系并说明理由.模型2:铅笔头模型图1图2图3如图1,①已知:AM∥BN,结论:∠1+∠2+∠3=360°;②已知:∠1+∠2+∠3=360°,结论:AM∥BN.如图2,已知:AM∥BN,结论:∠1+∠2+∠3+∠4=540°如图3,已知:AM∥BN,结论:∠1+∠2+⋯+∠n=(n-1)180°.7(2023·广东·统考二模)如图所示,已知AB∥EF,那么∠BAC+∠ACE+∠CEF=()A.180°B.270°C.360°D.540°8(2023·山西吕梁·校联考模拟预测)如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=32°,∠2=62°,则∠3的度数为()A.118°B.148°C.150°D.162°9(2023·河南三门峡·校联考一模)如图,图1是某小区车库门口的“曲臂直杆道闸”,可抽象为图2所示的数学图形.已知CD垂直地面上的直线DF于点D,当车牌被自动识别后,曲臂直杆道闸的BC段将绕点C 缓慢向上抬高,AB段则一直保持水平状态上升(即AB始终平行于DF).在该运动过程中,当∠ABC=112°时,∠BCD的度数是()A.112°B.138°C.158°D.128°10(2023春·新疆·七年级校考阶段练习)如图,如果AB∥CD,那么∠B+∠F+∠E+∠D=°.11(2022春·河北保定·七年级校考期中)如图,已知A1B∥A n C,则∠A1+∠A2+∠A3=,则∠A1+∠A2 +⋅⋅⋅+∠A n等于(用含n的式子表示).模型3:牛角模型图1图2如图1,已知:AB∥DE,结论:α=β-γ.如图2,已知:AB∥DE,结论:α=β+γ-180°.12(2023·安徽滁州·校联考二模)如图,若AB∥CD,则()A.∠1=∠2+∠3B.∠1+∠3=∠2C.∠1+∠2+∠3=180°D.∠1-∠2+∠3=180°13(2023·江苏·七年级假期作业)如图,若AB ⎳CD ,则∠1+∠3-∠2的度数为14(2022·湖北洪山·七年级期中)如图,已知AB ∥CD ,P 为直线AB ,CD 外一点,BF 平分∠ABP ,DE 平分∠CDP ,BF 的反向延长线交DE 于点E ,若∠FED =a ,试用a 表示∠P 为.15(2023春·广东深圳·九年级校校考期中)已知直线AB ∥CD ,点P 为直线AB ,CD 所确定的平面内的一点,(1)问题提出:如图1,∠A =120°,∠C =130°.求∠APC 的度数:(2)问题迁移:如图2,写出∠APC ,∠A ,∠C 之间的数量关系,并说明理由:(3)问题应用:如图3,∠EAH :∠HAB =1:3,∠ECH =20°,∠DCH =60°,求∠H ∠E的值.16(2023·余干县八年级期末)已知直线AB ∥CD ,(1)如图1,直接写出∠BME 、∠E 、∠END 的数量关系为;(2)如图2,∠BME 与∠CNE 的角平分线所在的直线相交于点P ,试探究∠P 与∠E 之间的数量关系,并证明你的结论;(3)如图3,∠ABM =1n ∠MBE ,∠CDN =1n∠NDE ,直线MB 、ND 交于点F ,则∠F=.∠E模型4:羊角模型图1图2如图1,已知:AB∥DE,结论:α=γ-β.如图2,已知:AB∥DE,结论:α+β+γ=180°.17(2023春·上海·七年级专题练习)如图所示,AB∥CD,∠E=37°,∠C=20°,则∠EAB的度数为.18(2022·江苏七年级期中)如图所示,已知AB∥CD,∠A=50°,∠C=∠E.则∠C等于()A.20°B.25°C.30°D.40°19(2023春·浙江·七年级专题练习)已知AB⎳CD,求证:∠B=∠E+∠D20(2023·河南·统考三模)如图,已知AB∥DE,∠ABC=150°,∠CDE=75°,则∠BCD的度数为()A.55°B.60°C.45°D.50°21(2023·河北沧州·校考模拟预测)如图,∠A=58°,∠D=122°,∠1=3∠2,∠2=25°,点P是BC上一点.(1)∠DFE的度数为;(2)若∠BFP=50°.则CE与PF(填“平行”或“不平行”).模型5:蛇形模型(“5”字模型)基本模型:如图,AB∥CD,结论:∠1+∠3-∠2=180°.图1图2如图1,已知:AB∥DE,结论:α=β+180°-γ.如图2,已知:AB∥DE,结论:α=γ+180°-β.22(2023·四川广元·统考三模)珠江流域某江段江水流向经过B、C、D三点,拐弯后与原来方向相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE等于()A.50°B.40°C.30°D.20°23(2023·湖南长沙·九年级校联考期中)如图,若AB∥CD,∠α=65°,∠γ=25°,则∠β的度数是()A.115°B.130°C.140°D.150°24(2023·河南周口·校联考三模)如图,AB∥EF,∠B=100°,∠CDE=25°,则∠BCD的度数是()A.125°B.75°C.95°D.105°25(2023·陕西西安·校考模拟预测)如图,AB∥CD,CD∥EF,CE平分∠BCD,若∠ABC=58°,则∠CEF 的度数为()A.131°B.141°C.151°D.161°26(2023·江西·九年级校考阶段练习)如图∠BAC=10°,∠ACD=125°,CD⊥EF于点D,将AB绕点A 逆时针旋转α,使AB∥EF,则α的最小值为.课后专项训练1(2023·山东临沂·统考二模)如图,a∥b,∠1=45°,则∠2的度数为()A.105°B.125°C.135°D.145°2(2023春·安徽·九年级专题练习)如图,已知:AB∥EF,∠B=∠E,求证:BC∥DE.在证明该结论时,需添加辅助线,则以下关于辅助线的作法不正确的是()A.延长BC交FE的延长线于点GB.连接BEC.分别作∠BCD,∠CDE的平分线CG,DHD.过点C作CG∥AB(点G在点C左侧),过点D作DH∥EF(点H在点D左侧)3(2023·浙江台州·统考一模)如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若∠1= 30°,∠2=50°,则∠3的度数为( ).A.130°B.140°C.150°D.160°4(2023·江苏·八年级假期作业)如图,两直线AB、CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=( ).A.630°B.720°C.800°D.900°5(2023·辽宁抚顺·统考三模)如图,若AB∥CD∥EF,∠1=15°,∠2=60°,那么∠BCE=()A.120°B.125°C.130°D.135°6(2022·安徽芜湖·七年级期中)如图,AB ∥CD ,BF ,DF 分别平分∠ABE 和∠CDE ,BF ∥DE ,∠F 与∠ABE 互补,则∠F 的度数为A.30°B.35°C.36°D.45°7(2023·内蒙古呼伦贝尔·统考三模)如图是一款手推车的平面示意图,其中AB ∥CD ,∠1=24°,∠3=148°,则∠2的度数为()A.56B.66C.98D.1048(2023春·重庆江津·七年级校联考期中)如图,AB ⎳CD ,∠ABE =12∠EBF ,∠DCE =13∠ECF ,设∠ABE =α,∠E =β,∠F =γ,则α,β,γ的数量关系是()A.4β-α+γ=360°B.3β-α+γ=360°C.4β-α-γ=360°D.3β-2α-γ=360°9(2022·江苏七年级期末)如图,AB ∥CD ,则∠1+∠3-∠2的度数等于.10(2023·湖南长沙·校联考二模)如图所示,AB∥DE,∠1=130°,∠2=36°,则∠3=度.11(2022·四川成都·七年级期末)已知直线AB∥DE,射线BF、DG分别平分∠ABC,∠EDC,两射线反向延长线交于点H,请写出∠H,∠C之间的数量关系:.12(2022·黑龙江·七年级月考)如图,AB⎳CD,E是CD上的点,过点E作EF⎳DP,若∠PEF=∠PEH,EG平分∠DEH,∠B=152°,∠PEG=65°,则∠BPD=.13(2023·浙江·九年级专题练习)如图,已知AB∥DE,∠BCD=30°,∠CDE=138°,求∠ABC的度数.14(2023春·重庆南岸·九年级校考期中)在数学课上老师提出了如下问题:如图,∠B=160°,当∠A与∠D满足什么关系时,BC∥DE?小明认为∠D-∠A=20°时BC∥DE,他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:15(2023春·河北廊坊·七年级校考阶段练习)(1)如图(1)AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.(2)观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.(3)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.16(2023秋·广东江门·八年级校考阶段练习)(1)如图①,如果AB∥CD,求证:∠APC=∠A+∠C.(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C=.(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m=(用x、y、z表示).17(2023春·山东淄博·九年级校考期中)如图,AB∥CD,点E为两直线之间的一点.(1)如图1,若∠BAE=30°,∠DCE=20°,则∠AEC=;如图1,若∠BAE=α,∠DCE=β,则∠AEC=;(2)如图2,试说明,∠BAE+∠AEC+∠ECD=360°;(3)如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC的数量关系,并说明理由.18(2022·湖南株洲市八年级期末)已知直线a∥b,直线EF分别与直线a,b相交于点E,F,点A,B分别在直线a,b上,且在直线EF的左侧,点P是直线EF上一动点(不与点E,F重合),设∠PAE=∠1,∠APB=∠2,∠PBF=∠3.(1)如图1,当点P在线段EF上运动时,试说明∠1+∠3=∠2;(提示:过点P作PM∥a)(2)当点P在线段EF外运动时有两种情况,①如图2写出∠1,∠2,∠3之间的关系并给出证明.②如图3所示,猜想∠1,∠2,∠3之间的关系(不要求证明).19(2023·内蒙古鄂尔多斯·七年级校考期中)问题探究:如下面四个图形中,AB∥CD.(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.(2)请你从中任选一个加以说明理由.解决问题:(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=°.20(2023春·湖北黄冈·七年级校考期中)如图,已知:点A、C、B不在同一条直线,AD∥BE(1)求证:∠B+∠C-∠A=180°:(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)如图③,在(2)的前提下,且有AC∥QB,直线AQ、BC交于点P,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE=.21(2023春·广东·七年级专题练习)(1)如图1,AB∥CD,∠ABE=45°,∠CDE=21°,直接写出∠BED 的度数.(2)如图2,AB∥CD,点E为直线AB,CD间的一点,BF平分∠ABE,DF平分∠CDE,写出∠BED与∠F之间的关系并说明理由.(3)如图3,AB与CD相交于点G,点E为∠BGD内一点,BF平分∠ABE,DF平分∠CDE,若∠BGD=60°,∠BFD=95°,直接写出∠BED的度数.22(2023春·福建三明·七年级校考期中)探索:小明在研究数学问题:已知AB⎳CD,AB和CD都不经过点P,探索∠P与∠A、∠C的数量关系.发现:在图1中,∠APC=∠A+∠C;如图5小明是这样证明的:过点Р作PQ⎳AB∴∠APQ=∠A∵PQ⎳AB,AB⎳CD.∴PQ⎳CD∴∠CPQ=∠C∴∠APQ+∠CPQ=∠A+∠C即∠APC=∠A+∠C(1)为小明的证明填上推理的依据;(2)理解:①在图2中,∠P与∠A、∠C的数量关系为;②在图3中,若∠A=30°,∠C=70°,则∠P的度数为;(3)拓展:在图4中,探究∠P与∠A、∠C的数量关系,并说明理由.23(2023春·山东·七年级专题练习)如图1,直线AB⎳CD,点P在两平行线之间,点E在AB上,点F 在CD上,连接PE,PF.(1)若∠PEB=60°,∠PFD=50°,请求出∠EPF.(请写出必要的步骤,并说明理由)(2)如图2,若点P,Q在直线AB与CD之间时,∠1=30°,∠2=40°,∠3=70°,请求出∠4=.(不需说明理由,请直接写出答案)(3)如图3,在图1的基础上,作P1E平分∠PEB,P1F平分∠PFD,若设∠PEB=x°,∠PFD=y°,则∠P1= (用含x,y的式子表示).若P2E平分∠P1EB,P2F平分∠P1FD,可得∠P2;P3E平分∠P2EB,P3F平分∠P2 FD,可得∠P3⋯,依次平分下去,则∠Pn=.(用含x,y的式子表示)三角形中的倒角模型-平行线+拐点模型近年来各地中考中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
第4讲 倒角模型(教师版)
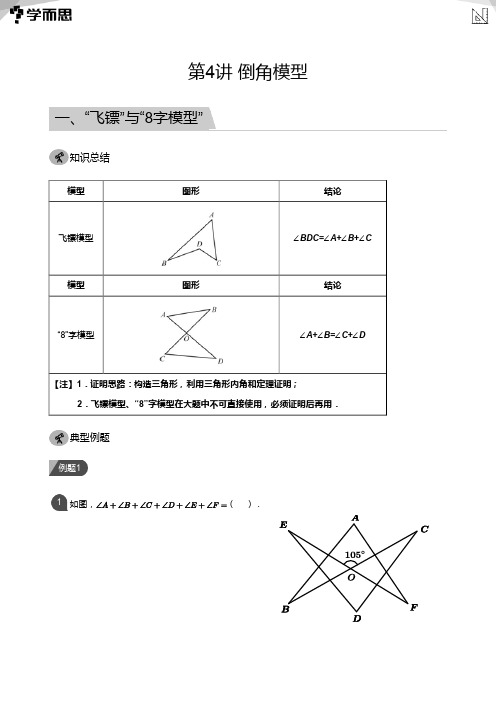
知识总结典型例题1如图,2如图,3如图1如下图,已知2如图1如图,在凹四边形2如图,3如图,知识总结典型例题题型:三角形-外角角分线如图所示,1如图,点两个外角平分线的交点,如果23如图,在D.如图,已知射线41如图,2如图,,三、数学万花筒帕斯卡12岁证明任意三角形内角和180度帕斯卡12岁证明任意三角形内角和180度。
任意两个相同直角三角形一定能拼成长方形,每一个长方形的内角和是360(四个直角)恰好包含了直角三角形的6个内角,所以一个直角三角形的内角和是360÷2=180。
任意两个相同的直角三角形一定能拼成长方形在此基础上证明任意锐角三角形内角和是180°. 在三角形内作一条高,会分割出两个不同的直角三角形。
因为直角三角形的内角和是180°,所以除直角外的两个锐角和为180°-90°=90°.两个直角三角形中共有4各锐角,恰好组成了原来大锐角三角形的三个内角,即可得出任意锐角三角形内角和为90°+90°=180°.同理可证,任意钝角三角形内角和也是180°,因为只有一条高在其内部,所以作高是没有选择余地了。
任意锐角三角形内作高任意钝角三角形内作高既然任意直角三角形、锐角三角形钝角三角形的内角和都是180°,小帕斯卡才会非常肯定地说:任意三角形的内角和是都是180°。
这里有个误区,有的教师以为学生在三种类型的三角形中各选择一个分别测量,就是代表了全部的三角形,实际上具体的锐角三角形不能代表所有的锐角三角形,这与帕斯卡证明方法中的任意三角形有本质的不同。
四、巩固加油站三角形>三角形及多边形>多边形>题型:不规则图形的多角求和题型:三角形内角的应用两个外角平分线的交点,如果D.。
三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型(解析版)

三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型近年来各地中考中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题“8”字模型、“A”字模型与三角板模型进行梳理及对应试题分析,方便掌握。
模型1、“8”字模型图1图28字模型(基础型)条件:如图1,AD、BC相交于点O,连接AB、CD;结论:①∠A+∠B=∠C+∠D;②AB+CD<AD+BC。
8字模型(加角平分线)条件:如图2,线段AP平分∠BAD,线段CP平分∠BCD;结论:2∠P=∠B+∠D1(2021·河北·统考中考真题)下图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E 保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应(填“增加”或“减少”)度.【答案】减少10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系,进行计算即可判断.【详解】解:∵∠A+∠B=50°+60°=110°,∴∠ACB=180°-110°=70°,∴∠DCE=70°,如图,连接CF并延长,∴∠DFM=∠D+∠DCF=20°+∠DCF,∠EFM=∠E+∠ECF=30°+∠ECF,∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD=110°,则∠EFD减少了10°,若只调整∠D的大小,由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠D+100°,因此应将∠D减少10度;故答案为:①减少;②10.【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.2(2023·浙江·八年级假期作业)如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数.【答案】540°【分析】如图所示,由三角形外角的性质可知:∠A+∠B=∠IJL,∠C+∠D=∠MLJ,∠H+∠K=∠GIJ,∠E+∠F=∠GML,然后由多边形的内角和公式可求得答案.【详解】解:如图所示:由三角形的外角的性质可知:∠A+∠B=∠IJL,∠C+∠D=∠MLJ,∠H+∠K=∠GIJ,∠E+∠F=∠GML,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=∠IJL+∠MLJ+∠GML+∠G+∠GIJ=(5-2)×180°=3×180°=540°.【点睛】本题主要考查的是三角形外角的性质和多边形的内角和公式的应用,利用三角形外角和的性质将所求各角的和转化为五边形的内角和是解题的关键3(2023·山东德州·八年级校考阶段练习)如图1,已知线段AB,CD相交于点O,连接AC,BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+∠D;(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD,AB分别相交于点M、N.①若∠B=100°,∠C=120°,求∠P的度数;②若角平分线中角的关系改为“∠CAP=13∠CAB,∠CDP=13∠CDB”,试探究∠P与∠B,∠C之间的数量关系.【答案】(1)见解析(2)①110°;②∠P=13∠B+2∠C【分析】(1)利用三角形内角和定理和对顶角相等即可证明;(2)①根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据“8字形”得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C-∠P=∠P-∠B,即∠P=1 2∠B+∠C,即可求解.②根据∠CAP=13∠CAB,∠CDP=13∠CDB,可得∠BAP=23∠BAC,∠BDP=23∠BDC,再由三角形内角和定理和对顶角相等,可得2∠C-∠P=∠P-∠B,即可求解.【详解】(1)证明:在△AOC中,∠A+∠C=180°-∠AOC,在△BOD中,∠B+∠D=180°-∠BOD,∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;(2)解:①∵∠CAB和∠BDC的平分线AP和DP相交于点P,∴∠CAP=∠BAP,∠BDP=∠CDP,∵∠CAP+∠C=∠CDP+∠P①,∠BAP+∠P=∠BDP+∠B②,由①-②,得:∠C-∠P=∠P-∠B,即∠P=12∠C+∠B,∵∠B=100°,∠C=120°,∴∠P=12100°+120°=110°;②∵∠CAP=13∠CAB,∠CDP=13∠CDB,∴∠BAP=23∠BAC,∠BDP=23∠BDC,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C-∠P=13∠BDC-13∠BAC=13∠BDC-∠BAC,∠P-∠B=23∠BDC-23∠BAC=2 3∠BDC-∠BAC,∴2∠C-∠P=∠P-∠B,∴∠P=13∠B+2∠C,故答案为:∠P=13∠B+2∠C.【点睛】本题考查了三角形内角和、有关角平分线的计算,解题的关键是灵活运用“8字形”求解.4(2023春·广东深圳·七年级统考期末)定理:三角形任意两边之和大于第三边.(1)如图1,线段AD ,BC 交于点E ,连接AB ,CD ,判断AD +BC 与AB +CD 的大小关系,并说明理由;(2)如图2,OC 平分∠AOB ,P 为OC 上任意一点,在OA ,OB 上截取OE =OF ,连接PE ,PF .求证:PE =PF ;(3)如图3,在△ABC 中,AB >AC ,P 为角平分线AD 上异于端点的一动点,求证:PB -PC >BD -CD .【答案】(1)AD +BC >AB +CD ;理由见详解(2)证明见详解(3)证明见详解【分析】(1)根据三角形任意两边之和大于第三边知,AE +BE >AB ,CE +ED >CD ,两式相加即可得出结论;(2)根据SAS 证△OEP ≌△OFP 即可得出结论;(3)在AB 上取一点E ,使AE =AC ,连接DE 交BP 于点F ,证△APE ≌△APC ,即PC =PE ,同理证CD =DE ,然后同理(1)得PB +CD >PC +BD ,变形不等式即可得出结论.【详解】(1)解:AD +BC >AB +CD ,理由如下:∵AE +BE >AB ,CE +ED >CD ,∴AE +BE +CE +ED >AB +CD ,即AD +BC >AB +CD ;(2)证明:∵OC 平分∠AOB ,∴∠EOP =∠FOP ,在△OEP 和△OFP 中,OE =OF∠EOP =∠FOP OP =OP,∴△OEP ≌△OFP SAS ,∴PE =PF ;(3)证明:在AB 上取一点E ,使AE =AC ,连接DE 交BP 于点F,∵AD 是∠BAC 的角平分线,∴∠EAP =∠CAP ,在△APE 和△APC 中,AE =AC∠EAP =∠CAP AP =AP,∴△APE ≌△APC SAS ,∴PE =PC ,同理可证DE =DC ,∵EF +PF >EP ,BF +FD >BD ,∴EF +PF +BF +FD >EP +BD ,即PB +DE >EP +BD ,∴PB +CD >PC +BD ,∴PB -PC >BD -CD .【点睛】本题主要考查三角形的综合题,熟练掌握三角形的三边关系和全等三角形的判定和性质等知识是解题的关键.5(2023春·江苏苏州·七年级校联考期中)阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论∠A +∠B =∠C +∠D .我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论∠AOC =∠A +∠C +∠P .(1)直接利用上述基本图形中的任意一种,解决问题:如图2,AP 、CP 分别平分∠BAD 、∠BCD ,说明:∠P =12∠B +∠D .(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:①如图3,直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,若∠B =30°,∠D =20°,求∠P 的度数.②在图4中,AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系(直接写出结果,无需说明理由).③在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系(直接写出结果,无需说明理由).【答案】(1)见解析(2)①25°;②∠P =180°-12∠B +∠D ;③∠P =90°+12∠B +∠D 【分析】(1)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据题干的结论列出∠P +∠3=∠2+∠ABC ,∠P +∠1=∠4+∠ADC ,相加得到2∠P +∠2+∠3=∠1+∠4+∠ABC +∠ADC ,继而得到2∠P =∠ABC +∠ADC ,即可证明结论;(2)①如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,根据(1)的结论得到∠H =12∠B +∠D =25°,再由角平分线的定义和平角的定义证明∠PCH =90°,∠PAH =90°,再根据题干的结论可推出∠P =∠H =25°;②如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,由(1)的结论可知∠H =12∠B +∠D ,,同理可得∠PCH =90°,∠PAH =90°,则由四边形内角和定理可得∠P =180°-12∠B +∠D ;③由题干的结论可得∠P =∠B +∠BAP +∠BCP ,由角平分线的定义得到∠BAP =12∠BAO ,∠BCP =12∠BCE ,再求出∠BCP =90°-12∠BCD ,由题干的结论可知∠B +∠BAO =∠D +∠BCD ,由此可得∠P =∠B +∠BAP +∠BCP =90°+12∠B +∠D .【详解】(1)解:∵AP 、CP 分别平分∠BAD 、∠BCD ,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠1+∠4,由题干的结论得:∠P +∠3=∠2+∠ABC ,∠P +∠1=∠4+∠ADC ,∴2∠P +∠1+∠3=∠2+∠4+∠ABC +∠ADC ,∴2∠P =∠ABC +∠ADC ,∴∠P =12∠ABC +∠ADC ,即∠P =12∠B +∠D ;(2)解:①如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,由(1)的结论可知∠H =12∠B +∠D =25°,∵PC ,HC 分别平分∠BCE ,∠BCD ,∴∠BCP =12∠BCE ,∠BCH =12∠BCD ,∵∠BCD +∠BCE =180°∴∠BCP +∠BCH =12∠BCD +12∠BCE =90°,∴∠PCH =90°,同理可得∠PAH =90°,由题干的结论可得∠P +∠PAH =∠H +∠PCH ,∴∠P =∠H =25°;②如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,由(1)的结论可知∠H =12∠B +∠D ,,同理可得∠PCH =90°,∠PAH =90°,∴∠P =360°-∠PAH -∠PCH -∠H =180°-12∠B +∠D ;③由题干的结论可得∠P =∠B +∠BAP +∠BCP ,∵AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,∴∠BAP =12∠BAO ,∠BCP =12∠BCE ,∵∠BCE =180°-∠BCD ,∴∠BCP =90°-12∠BCD ,由题干的结论可知∠B +∠BAO =∠D +∠BCD ,∴∠BAO =∠D +∠BCD -∠B ,∴∠P=∠B+∠BAP+∠BCP=∠B+12∠BAO+90°-12∠BCD=∠B+12∠D+12∠BCD-12∠B+90°-12∠BCD=90°+12∠B+∠D.【点睛】本题考查了三角形的内角和定理,角平分线的定义,多边形内角和定理,准确识图并运用好“8”字形的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.模型2、“A”字模型结论:①∠3+∠4=∠D+∠E;②∠1+∠2=∠A+180°。
三角形倒角8个基本型

三角形倒角8个基本型
三角形倒角8个基本型
一、直角三角形型
指三角形的三条边均为直线,作工时采ユ直角三角形的两个外角倒角。
该型可分为正直角三角形和倒直角三角形两种型型。
二、锐角三角形型
指三角形的三条边均为直线,作工时采ユ锐角三角形的两个外角倒角。
该型可分为正锐角三角形和倒锐角三角形两种型型。
三、圆角三角形型
指三角形的三条边均为弧线,作工时采ユ圆角三角形的两个外角倒角。
该型可分为正圆角三角形和倒圆角三角形两种型型。
四、菱形型
指四条边均为直线的多边形,作工时采ユ菱形的两个外角倒角。
该型可分为正菱形和倒菱形两种型型。
五、六边形型
指六条边均为直线的多边形,作工时采ユ六边形的四个外角倒角。
该型可分为正六边形和倒六边形两种型型。
六、椭圆型
指四条边均为椭圆的多边形,作工时采ユ椭圆的两个外角倒角。
该型可分为正椭圆和倒椭圆两种型型。
七、不规则四边形型
指由不同正方形、长方形或多边形组成的不规则四边形,作工时
采ユ不规则四边形的四个外角倒角。
该型可分为正不规则四边形和倒不规则四边形两种型型。
八、五角形型
指五条边均为直线的多边形,作工时采ユ五角形的五个外角倒角。
该型可分为正五角形和倒五角形两种型型。
最新三角形的倒角模型(答案)
喜欢□一般□不喜欢□
大学生购买力有限,即决定了要求商品能价廉物美,但更注重的还是在购买过程中对精神文化爱好的追求,满足心理需求。
标题:手工制作坊2004年3月18日
三角形的倒角模型:
培养动手能力□学一门手艺□打发时间□兴趣爱好□
据调查,大学生对此类消费的态度是:手工艺制品消费比“负债”消费更得人心。
(3)年龄优势
十“漂亮女生”饰品店的分析
众上所述,我们认为:我们的创意小屋计划或许虽然会有很多的挑战和困难,但我们会吸取和借鉴“漂亮女生”和“碧芝”的成功经验,在产品的质量和创意上多下工夫,使自己的产品能领导潮流,领导时尚。在它们还没有打入学校这个市场时,我们要巩固我们的学生市场,制作一些吸引学生,又有使学生能接受的价格,勇敢的面对它们的挑战,使自己立于不败之地。
三角形倒角模型2024

引言:在三维建模中,倒角模型是一种常用的技术,用于给几何体的尖锐边缘添加平滑的圆角效果。
在本文中,我们将继续探讨三角形倒角模型的相关内容。
首先我们会简要回顾前文介绍的方法,然后深入讨论另外五个方面的内容,包括:双曲线倒角、坡度倒角、螺旋倒角、圆柱倒角和体积倒角。
通过详细的阐述,我们希望读者能够更好地理解和应用这些倒角模型技术。
概述:三角形的倒角模型是指给三角形的边缘或角度添加圆角效果。
倒角模型可以使模型更显真实,同时也能够消除尖锐边缘的刺眼感。
在之前的文章中,我们介绍了一种基本的三角形倒角模型方法,即通过增加额外的顶点来切割原始三角形,然后连接这些顶点以形成圆角效果。
在本文中,我们将深入讨论更多的三角形倒角模型技术。
正文内容:1.双曲线倒角1.1定义双曲线倒角1.2双曲线倒角的计算方法1.3双曲线倒角的应用实例1.4双曲线倒角的优缺点1.5双曲线倒角与其他倒角方法的比较2.坡度倒角2.1坡度倒角的原理2.2坡度倒角的计算方法2.3坡度倒角的应用实例2.4坡度倒角的优缺点2.5坡度倒角与其他倒角方法的比较3.螺旋倒角3.1螺旋倒角的原理3.2螺旋倒角的计算方法3.3螺旋倒角的应用实例3.4螺旋倒角的优缺点3.5螺旋倒角与其他倒角方法的比较4.圆柱倒角4.1圆柱倒角的定义4.2圆柱倒角的计算方法4.3圆柱倒角的应用实例4.4圆柱倒角的优缺点4.5圆柱倒角与其他倒角方法的比较5.体积倒角5.1体积倒角的概念5.2体积倒角的计算方法5.3体积倒角的应用实例5.4体积倒角的优缺点5.5体积倒角与其他倒角方法的比较总结:通过本文的讨论,我们详细了解了五种不同的三角形倒角模型技术。
双曲线倒角、坡度倒角、螺旋倒角、圆柱倒角和体积倒角都是常用的倒角方法。
它们各自具有不同的原理、计算方法、应用实例和优缺点。
通过比较不同的倒角方法,我们可以根据具体需求选择最适合的方法来创建高质量的倒角模型。
文末400字,请将前文正文段落补足至1300字。
第4讲 倒角模型(学生版)
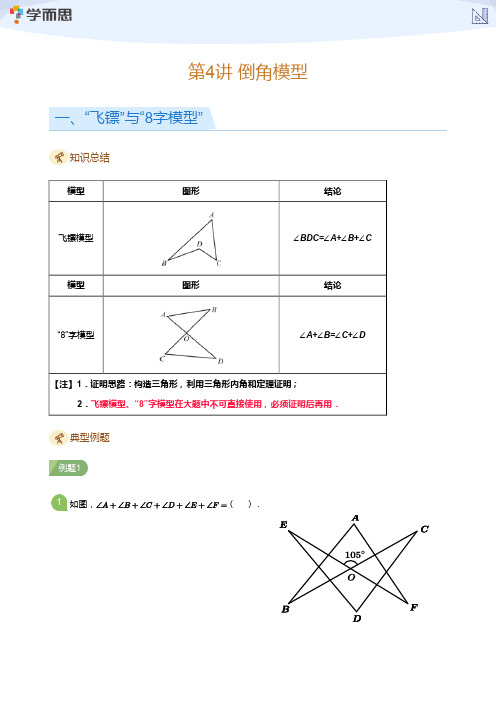
巩固1
如图,
,
,
,则
.
巩固2
如下图,
,
,
,则 的度数为
度.
巩固3 如图,
度.
巩固4
如图,点 和点 分在
的边 和 的延长线上, , 分别平分
和
,若
,
,则 的大小是
.
巩固5
如图,点 是
两个内角平分线的交点,点 是
,则
的度数为( )
两个外角平分线的交点,如果
A.
B.
C.
D.
巩固6
如图,在
中,
交于点 ,依次类推,
,
与
的角平分线交于 ,
与
的角平分线交于点 ,则
与
的角平分线
的度数是
度.
巩固7
如图⑴, 、 是任意
的 、 的角平分线.
(1) 探求
与 的数量关系.
(2)
能等于 吗?说明理由.
(3) 当 为多少度时,
?
(4) 把图⑴中的
变成图⑵中的四边形
, 、 仍然是 , 的平分线,猜想
与 、 有何数量关系?(只写出猜想结果,不写过程)
首先得到:当 时,如图 ,
,
当 时,如图 ,
,
如图 ,猜想
.
A
B
C
图
图
图
三、数学万花筒
帕斯卡12岁证明任意三角形内角和180度 帕斯卡12岁证明任意三角形内角和180度。 任意两个相同直角三角形一定能拼成长方形,每一个长方形的内角和是360(四个直角)恰好包含了直 角三角形的6个内角,所以一个直角三角形的内角和是360÷2=180。
;
的平
