第2讲:三角形的角及倒角模型
多边形内角和中常用倒角模型

第二讲三角形的倒角模型黑逗小可爱【要点梳理】知识点一、多边形内角和定理n边形的内角和为(n-2)·180°(n≥3).要点诠释:(1)内角和定理的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数;(2)正多边形的每个内角都相等,都等于(2)180nn°;(1(((证明过程:结论:∠1+∠2=180°+∠C(2)飞镖模型证明过程:结论:∠BOC=∠A+∠B+∠C(3)八字模型证明过程:结论:∠A+∠B=∠D+∠C精讲精练1.如图,四边形ABCD中,∠B=40°,沿直线MN剪去∠B,则所得五边形AEFCD中,∠1+∠2=2.如图,∠1+∠2+∠3+∠4+∠5=320°,则∠6=.3.如图,∠B+∠C+∠D+∠E﹣∠A等于()A.360°B.300°C.180°D.240°4.如图,求∠A+∠B+∠C+∠D+∠E的大小.5.如图所示,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2的度数为()A.135°B.240°C.270°D.300°6.7.如图,∠1=∠2,∠A=60°,则∠ADC=度.模块二、三角形折叠问题解题关键:折叠前后对应角相等精讲精练1.如图把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间的数量关系保持不变,请找一找这个规律,你发现的规律是()A、∠A=∠1+∠2B、2∠A=∠1+∠2C、2∠A=2∠1+∠2D、3∠A=2(∠1+∠2)2.如图,把∠ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是()A.2∠A=∠1-∠2B.3∠A=2(∠1-∠2)C.3∠A=2∠1-∠2D.∠A=∠1-∠23.如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置.通过计算我们知道:2∠A=∠1+∠2.请你继续探索:(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A′的位置,如图②所示.此时∠A与∠1、∠2之间存在什么样的关系?并说明理由。
三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型(解析版)

三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型近年来各地中考中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题“8”字模型、“A”字模型与三角板模型进行梳理及对应试题分析,方便掌握。
模型1、“8”字模型图1图28字模型(基础型)条件:如图1,AD、BC相交于点O,连接AB、CD;结论:①∠A+∠B=∠C+∠D;②AB+CD<AD+BC。
8字模型(加角平分线)条件:如图2,线段AP平分∠BAD,线段CP平分∠BCD;结论:2∠P=∠B+∠D1(2021·河北·统考中考真题)下图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E 保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应(填“增加”或“减少”)度.【答案】减少10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系,进行计算即可判断.【详解】解:∵∠A+∠B=50°+60°=110°,∴∠ACB=180°-110°=70°,∴∠DCE=70°,如图,连接CF并延长,∴∠DFM=∠D+∠DCF=20°+∠DCF,∠EFM=∠E+∠ECF=30°+∠ECF,∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD=110°,则∠EFD减少了10°,若只调整∠D的大小,由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠D+100°,因此应将∠D减少10度;故答案为:①减少;②10.【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.2(2023·浙江·八年级假期作业)如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数.【答案】540°【分析】如图所示,由三角形外角的性质可知:∠A+∠B=∠IJL,∠C+∠D=∠MLJ,∠H+∠K=∠GIJ,∠E+∠F=∠GML,然后由多边形的内角和公式可求得答案.【详解】解:如图所示:由三角形的外角的性质可知:∠A+∠B=∠IJL,∠C+∠D=∠MLJ,∠H+∠K=∠GIJ,∠E+∠F=∠GML,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=∠IJL+∠MLJ+∠GML+∠G+∠GIJ=(5-2)×180°=3×180°=540°.【点睛】本题主要考查的是三角形外角的性质和多边形的内角和公式的应用,利用三角形外角和的性质将所求各角的和转化为五边形的内角和是解题的关键3(2023·山东德州·八年级校考阶段练习)如图1,已知线段AB,CD相交于点O,连接AC,BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+∠D;(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD,AB分别相交于点M、N.①若∠B=100°,∠C=120°,求∠P的度数;②若角平分线中角的关系改为“∠CAP=13∠CAB,∠CDP=13∠CDB”,试探究∠P与∠B,∠C之间的数量关系.【答案】(1)见解析(2)①110°;②∠P=13∠B+2∠C【分析】(1)利用三角形内角和定理和对顶角相等即可证明;(2)①根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据“8字形”得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C-∠P=∠P-∠B,即∠P=1 2∠B+∠C,即可求解.②根据∠CAP=13∠CAB,∠CDP=13∠CDB,可得∠BAP=23∠BAC,∠BDP=23∠BDC,再由三角形内角和定理和对顶角相等,可得2∠C-∠P=∠P-∠B,即可求解.【详解】(1)证明:在△AOC中,∠A+∠C=180°-∠AOC,在△BOD中,∠B+∠D=180°-∠BOD,∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;(2)解:①∵∠CAB和∠BDC的平分线AP和DP相交于点P,∴∠CAP=∠BAP,∠BDP=∠CDP,∵∠CAP+∠C=∠CDP+∠P①,∠BAP+∠P=∠BDP+∠B②,由①-②,得:∠C-∠P=∠P-∠B,即∠P=12∠C+∠B,∵∠B=100°,∠C=120°,∴∠P=12100°+120°=110°;②∵∠CAP=13∠CAB,∠CDP=13∠CDB,∴∠BAP=23∠BAC,∠BDP=23∠BDC,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C-∠P=13∠BDC-13∠BAC=13∠BDC-∠BAC,∠P-∠B=23∠BDC-23∠BAC=2 3∠BDC-∠BAC,∴2∠C-∠P=∠P-∠B,∴∠P=13∠B+2∠C,故答案为:∠P=13∠B+2∠C.【点睛】本题考查了三角形内角和、有关角平分线的计算,解题的关键是灵活运用“8字形”求解.4(2023春·广东深圳·七年级统考期末)定理:三角形任意两边之和大于第三边.(1)如图1,线段AD ,BC 交于点E ,连接AB ,CD ,判断AD +BC 与AB +CD 的大小关系,并说明理由;(2)如图2,OC 平分∠AOB ,P 为OC 上任意一点,在OA ,OB 上截取OE =OF ,连接PE ,PF .求证:PE =PF ;(3)如图3,在△ABC 中,AB >AC ,P 为角平分线AD 上异于端点的一动点,求证:PB -PC >BD -CD .【答案】(1)AD +BC >AB +CD ;理由见详解(2)证明见详解(3)证明见详解【分析】(1)根据三角形任意两边之和大于第三边知,AE +BE >AB ,CE +ED >CD ,两式相加即可得出结论;(2)根据SAS 证△OEP ≌△OFP 即可得出结论;(3)在AB 上取一点E ,使AE =AC ,连接DE 交BP 于点F ,证△APE ≌△APC ,即PC =PE ,同理证CD =DE ,然后同理(1)得PB +CD >PC +BD ,变形不等式即可得出结论.【详解】(1)解:AD +BC >AB +CD ,理由如下:∵AE +BE >AB ,CE +ED >CD ,∴AE +BE +CE +ED >AB +CD ,即AD +BC >AB +CD ;(2)证明:∵OC 平分∠AOB ,∴∠EOP =∠FOP ,在△OEP 和△OFP 中,OE =OF∠EOP =∠FOP OP =OP,∴△OEP ≌△OFP SAS ,∴PE =PF ;(3)证明:在AB 上取一点E ,使AE =AC ,连接DE 交BP 于点F,∵AD 是∠BAC 的角平分线,∴∠EAP =∠CAP ,在△APE 和△APC 中,AE =AC∠EAP =∠CAP AP =AP,∴△APE ≌△APC SAS ,∴PE =PC ,同理可证DE =DC ,∵EF +PF >EP ,BF +FD >BD ,∴EF +PF +BF +FD >EP +BD ,即PB +DE >EP +BD ,∴PB +CD >PC +BD ,∴PB -PC >BD -CD .【点睛】本题主要考查三角形的综合题,熟练掌握三角形的三边关系和全等三角形的判定和性质等知识是解题的关键.5(2023春·江苏苏州·七年级校联考期中)阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论∠A +∠B =∠C +∠D .我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论∠AOC =∠A +∠C +∠P .(1)直接利用上述基本图形中的任意一种,解决问题:如图2,AP 、CP 分别平分∠BAD 、∠BCD ,说明:∠P =12∠B +∠D .(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:①如图3,直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,若∠B =30°,∠D =20°,求∠P 的度数.②在图4中,AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系(直接写出结果,无需说明理由).③在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系(直接写出结果,无需说明理由).【答案】(1)见解析(2)①25°;②∠P =180°-12∠B +∠D ;③∠P =90°+12∠B +∠D 【分析】(1)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据题干的结论列出∠P +∠3=∠2+∠ABC ,∠P +∠1=∠4+∠ADC ,相加得到2∠P +∠2+∠3=∠1+∠4+∠ABC +∠ADC ,继而得到2∠P =∠ABC +∠ADC ,即可证明结论;(2)①如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,根据(1)的结论得到∠H =12∠B +∠D =25°,再由角平分线的定义和平角的定义证明∠PCH =90°,∠PAH =90°,再根据题干的结论可推出∠P =∠H =25°;②如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,由(1)的结论可知∠H =12∠B +∠D ,,同理可得∠PCH =90°,∠PAH =90°,则由四边形内角和定理可得∠P =180°-12∠B +∠D ;③由题干的结论可得∠P =∠B +∠BAP +∠BCP ,由角平分线的定义得到∠BAP =12∠BAO ,∠BCP =12∠BCE ,再求出∠BCP =90°-12∠BCD ,由题干的结论可知∠B +∠BAO =∠D +∠BCD ,由此可得∠P =∠B +∠BAP +∠BCP =90°+12∠B +∠D .【详解】(1)解:∵AP 、CP 分别平分∠BAD 、∠BCD ,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠1+∠4,由题干的结论得:∠P +∠3=∠2+∠ABC ,∠P +∠1=∠4+∠ADC ,∴2∠P +∠1+∠3=∠2+∠4+∠ABC +∠ADC ,∴2∠P =∠ABC +∠ADC ,∴∠P =12∠ABC +∠ADC ,即∠P =12∠B +∠D ;(2)解:①如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,由(1)的结论可知∠H =12∠B +∠D =25°,∵PC ,HC 分别平分∠BCE ,∠BCD ,∴∠BCP =12∠BCE ,∠BCH =12∠BCD ,∵∠BCD +∠BCE =180°∴∠BCP +∠BCH =12∠BCD +12∠BCE =90°,∴∠PCH =90°,同理可得∠PAH =90°,由题干的结论可得∠P +∠PAH =∠H +∠PCH ,∴∠P =∠H =25°;②如图所示,分作∠BAD ,∠BCD 的角平分线交于H ,由(1)的结论可知∠H =12∠B +∠D ,,同理可得∠PCH =90°,∠PAH =90°,∴∠P =360°-∠PAH -∠PCH -∠H =180°-12∠B +∠D ;③由题干的结论可得∠P =∠B +∠BAP +∠BCP ,∵AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,∴∠BAP =12∠BAO ,∠BCP =12∠BCE ,∵∠BCE =180°-∠BCD ,∴∠BCP =90°-12∠BCD ,由题干的结论可知∠B +∠BAO =∠D +∠BCD ,∴∠BAO =∠D +∠BCD -∠B ,∴∠P=∠B+∠BAP+∠BCP=∠B+12∠BAO+90°-12∠BCD=∠B+12∠D+12∠BCD-12∠B+90°-12∠BCD=90°+12∠B+∠D.【点睛】本题考查了三角形的内角和定理,角平分线的定义,多边形内角和定理,准确识图并运用好“8”字形的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.模型2、“A”字模型结论:①∠3+∠4=∠D+∠E;②∠1+∠2=∠A+180°。
2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型近年来各地考试中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题高分线模型、双垂直模型、子母型双垂直模型(射影定理模型)进行梳理及对应试题分析,方便掌握。
模型1:高分线模型条件:AD 是高,AE 是角平分线结论:∠DAE=2B C∠∠-例1.(2023秋·浙江·八年级专题练习)如图,在ABC 中,30A ∠=︒,50B ∠=︒,CD 为ACB ∠的平分线,CE AB ⊥于点E ,则ECD ∠度数为()A .5︒B .8︒C .10︒D .12︒【答案】C 【分析】依据直角三角形,即可得到40BCE ∠=︒,再根据30A ∠=︒,CD 平分ACB ∠,即可得到BCD ∠的度数,再根据DCE BCD BCE ∠=∠-∠进行计算即可.【详解】解:50,B CE AB ∠=︒⊥ ,40BCE ∴∠=︒,又30A ∠=︒ ,CD 平分ACB ∠,1118050305022()BCD BCA ∴∠=∠=⨯︒-︒-︒=︒,504010DCE BCD BCE ∴∠=∠-∠=︒-︒=︒,故选:C .【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180︒是解答此题的关键.例2.(2023春·河南南阳·七年级统考期末)如图,在△ABC 中,∠1=∠2,G 为AD 的中点,BG 的延长线交AC 于点E ,F 为AB 上的一点,CF 与AD 垂直,交AD 于点H ,则下面判断正确的有()①AD 是△ABE 的角平分线;②BE 是△ABD 的边AD 上的中线;③CH 是△ACD 的边AD 上的高;④AH 是△ACF 的角平分线和高A .1个B .2个C .3个D .4个【答案】B【详解】解:①根据三角形的角平分线的概念,知AG 是△ABE 的角平分线,故此说法错误;②根据三角形的中线的概念,知BG 是△ABD 的边AD 上的中线,故此说法错误;③根据三角形的高的概念,知CH 为△ACD 的边AD 上的高,故此说法正确;④根据三角形的角平分线和高的概念,知AH 是△ACF 的角平分线和高线,故此说法正确.故选:B .【点睛】本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.例3.(2023·安徽合肥·七年级统考期末)如图,已知AD 、AE 分别是Rt △ABC 的高和中线,AB =9cm ,AC =12cm ,BC =15cm ,试求:(1)AD 的长度;(2)△ACE 和△ABE 的周长的差.【答案】(1)AD 的长度为365cm ;(2)△ACE 和△ABE 的周长的差是3cm .【分析】(1)利用直角三角形的面积法来求线段AD 的长度;(2)由于AE 是中线,那么BE =CE ,再表示△ACE 的周长和△ABE 的周长,化简可得△ACE 的周长﹣△ABE 的周长=AC ﹣AB 即可.【详解】解:(1)∵∠BAC =90°,AD 是边BC 上的高,∴S △ACB =12AB•AC =12BC•AD ,∵AB =9cm ,AC =12cm ,BC =15cm ,∴AD =AB AC CB ⋅=91215⨯=365(cm ),即AD 的长度为365cm ;(2)∵AE 为BC 边上的中线,∴BE =CE ,∴△ACE 的周长﹣△ABE 的周长=AC+AE+CE ﹣(AB+BE+AE )=AC ﹣AB =12﹣9=3(cm ),即△ACE 和△ABE 的周长的差是3cm .【点睛】此题主要考查了三角形的面积,关键是掌握直角三角形的面积求法.例4.(2023·广东东莞·八年级校考阶段练习)如图,在ABC 中,AD ,AE 分别是ABC 的高和角平分线,若30B ∠=︒,50C ∠=︒.(1)求DAE ∠的度数.(2)试写出DAE ∠与C B ∠-∠关系式,并证明.(3)如图,F 为AE 的延长线上的一点,FD BC ⊥于D ,这时AFD ∠与C B ∠-∠的关系式是否变化,说明理由.【答案】(1)10︒(2)()12DAE C B ∠=∠-∠(3)不变,理由见解析【分析】(1)根据三角形内角和求出BAC ∠,根据角平分线的定义得到50BAE ∠=︒,根据高线的性质得到90ADE ∠=︒,从而求出60BAD ∠=︒,继而根据角的和差得到结果;(2)根据角平分线的定义得到12BAE BAC ∠=∠,根据三角形内角和求出119022EAC B C ∠=︒-∠-∠,根据角的和差得到结果;(3)过A 作AG BC ⊥于G ,结合(2)知1()2EAG C B ∠=∠-∠,证明FD AG ∥,得到AFD EAG ∠=∠,即可证明.【详解】(1)解:∵30B ∠=︒,50C ∠=︒,∴1805030100BAC ∠=︒-︒-︒=︒,∵AE 平分BAC ∠,∴1502BAE CAE BAC ∠=∠=∠=︒,∵AD 是高,∴90ADE ∠=︒,∵30B ∠=︒,∴60BAD ∠=︒,∴10DAE BAD BAE ∠=∠-∠=︒;(2)()12DAE C B ∠=∠-∠,证明如下:∵AE 平分BAC ∠,∴12EAC BAC ∠=∠,∵180BAC B C ∠=︒-∠-∠,∴()11101902822B C B C EAC ︒-∠-∠-∠︒-==∠∠,∴EAD EAC DAC ∠=∠-∠()11090922B C C =︒∠---∠︒-∠()12C B =∠-∠;(3)不变,理由是:如图,过A 作AG BC ⊥于G ,由(2)可知:1()2EAG C B ∠=∠-∠,AG BC ⊥ ,90AGB ∠=︒,FD BC ⊥ ,90FDC ∴∠=︒,AGD FDC ∴∠=∠,FD AG ∴∥,AFD EAG ∴∠=∠,1()2AFD C B ∴∠=∠-∠.【点睛】本题主要考查三角形的内角和定理、角平分线的性质、直角三角形的性质和平行线的判定与性质,熟练掌握三角形的内角和定理和角平分线的性质是解题的关键.模型2:双垂直模型结论:①∠A =∠C ;②∠B =∠AFD =∠CFE ;③AB CD AE BC ⋅=⋅。
三角形中的倒角模型——飞镖模型、风筝模型以及翻角模型 学生版
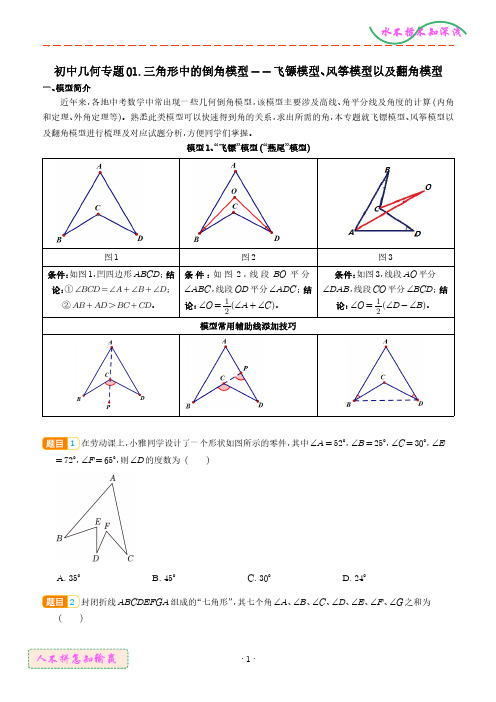
初中几何专题01.三角形中的倒角模型--飞镖模型、风筝模型以及翻角模型一、模型简介近年来,各地中考数学中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉此类模型可以快速得到角的关系,求出所需的角,本专题就飞镖模型、风筝模型以及翻角模型进行梳理及对应试题分析,方便同学们掌握。
模型1、“飞镖”模型(“燕尾”模型)图1图2图3条件:如图1,凹四边形ABCD;结论:①∠BCD=∠A+∠B+∠D;②AB+AD>BC+CD。
条件:如图2,线段BO平分∠ABC,线段OD平分∠ADC;结论:∠O=12(∠A+∠C)。
条件:如图3,线段AO平分∠DAB,线段CO平分∠BCD;结论:∠O=12(∠D-∠B)。
模型常用辅助线添加技巧1在劳动课上,小雅同学设计了一个形状如图所示的零件,其中∠A=52°,∠B=25°,∠C=30°,∠E =72°,∠F=65°,则∠D的度数为()A.35°B.45°C.30°D.24°2封闭折线ABCDEFGA组成的“七角形”,其七个角∠A、∠B、∠C、∠D、∠E、∠F、∠G之和为()A.180°B.270°C.360°D.720°3请阅读下列材料,并完成相应的任务:有趣的“飞镖图”如图,这种形似飞镖的四边形,可以形象地称它为“飞镖图”.当我们仔细观察后发现,它实际上就是凹四边形.那么它具有哪些性质呢?又将怎样应用呢?下面我们进行认识与探究:凹四边形通俗地说,就是一个角“凹”进去的四边形,其性质有:凹四边形中最大内角外面的角等于其余三个内角之和.(即如图1.∠ADB=∠A+∠B+∠C)理由如下:方法一:如图2,连结AB,则在△ABC中,∠C+∠CAB+∠CBA=180°,即∠1+∠2+∠3+∠4+∠C=180°,又∵在△ABD中,∠1+∠2+∠ADB=180°,∴∠ADB=∠3+∠4+∠C,即∠ADB=∠CAD+∠CBD+∠C.方法二:如图3,连结CD并延长至F,∵∠1和∠3分别是△ACD和△BCD的一个外角,⋯大家在探究的过程中,还发现有很多方法可以证明这一结论.任务:(1)填空:“方法一”主要依据的一个数学定理是;(2)探索及应用:根据“方法二”中辅助线的添加方式,写出该证明过程的剩余部分.2、风筝模型(鹰爪模型)或角内翻模型图1图21)风筝(鹰爪)模型:结论:∠A+∠O=∠1+∠2;2)风筝(鹰爪)模型(变形):结论:∠A+∠O=∠2-∠1。
三角形倒角模型结论和证明

三角形倒角模型结论和证明1. 引言好啦,今天咱们聊聊三角形倒角模型!这个名字听起来挺高大上的,但其实说白了就是把一个三角形的角给“修整”一下,让它看起来更柔和,更圆润。
就像我们在生活中总是希望把事情搞得圆滑一点,避免那些尖锐的冲突一样,倒角模型的主要目的是为了优化、提高效率,简直是“顺其自然”的典范嘛。
接下来,我会跟大家细说这个模型的结论和证明,保证你听完后,不仅会觉得有趣,还能带点干货回家。
2. 三角形倒角模型的基本概念2.1 什么是倒角?首先,咱得弄明白啥叫“倒角”。
通俗点说,就是把三角形的角切掉,留下一个小平面。
你可以想象一下,如果你有一个三角形的饼干,把那尖尖的角削平,这样就不会刮到嘴巴,吃起来也更爽口了。
倒角的目的是为了降低尖锐的边界,给人一种更加温和、亲切的感觉。
这就像我们在社交场合中,总是希望用更柔和的方式与人交流,不让人觉得不适。
2.2 倒角的应用在很多地方,倒角都是一个关键的设计元素。
比如说,在工业设计中,很多产品的边角都是经过倒角处理的,这样既好看,又能提高安全性。
想象一下,家里的家具如果都有尖角,那可真是个安全隐患。
小孩玩耍时不小心撞到,家长可就要心疼得直叫唤了!而且,倒角还可以让产品在生产时更容易加工,减少磨损,简直是一举两得,聪明得不得了。
3. 三角形倒角模型的结论3.1 模型的结论通过对三角形倒角模型的分析,我们得出一个结论:倒角处理可以有效提升结构的稳定性,同时降低受力集中现象。
这听起来可能有点抽象,简单来说,就是给三角形的角“减负”,让它在受到外力时不容易崩溃。
就像一个团队,大家都团结一致,才能更好地面对外部挑战,毕竟“团结就是力量”嘛!3.2 生活中的反思再说说这个模型在生活中的启示吧。
我们每个人都是一座小小的三角形,在生活中不可避免地会遇到各种冲突和挑战。
如果我们能够像倒角那样,适度地“软化”自己的态度,处理问题时就会更有智慧,减少不必要的摩擦。
比如说,当朋友之间有误会时,咱不妨先放下架子,真诚沟通,总比剑拔弩张要强得多。
三角形中角度计算相关的模型(飞镖模型、8字模型、角分线模型)

三角形中与角度计算相关的模型两个定理:一、平面内,三角形的三个内角和为180°。
二、平面内,三角形的一个外角等于其不相邻的两个外角和。
由上述两个定理可导出本文如下说要讲述的相关模型:8字模型、飞镖模型、两内角角平分线模型、两外角角平分线模型、内外角角平分线模型、共顶点的角平分线与高线夹角模型。
下面一一推导证明。
条件:AD、BC相交于点O。
结论:∠A+∠B=∠C+∠D。
(上面两角之和等于下面两角之和)证明:在∠ABO中,由内角和定理:∠A+∠B+∠BOA=180°在∠CDO中,∠C+∠D+∠COD=180°,∠∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,由对顶角相等:∠BOA=∠COD故有∠A+∠B=∠C+∠D应用:如下左图所示,五角星中,∠A+∠B+∠C+∠D+∠E=180°条件:四边形ABDC如上左图所示。
结论:∠D=∠A+∠B+∠C。
(凹四边形凹外角等于三个内角和)证明:如上右图,连接AD并延长到E,则:∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C。
本质为两个三角形外角和定理证明。
应用:如下左图,则∠A+∠B+∠C+∠D+∠E+∠F=260°(下右图中两个飞镖)。
条件:△ABC 中,BI 、CI 分别是∠ABC 和∠ACB 的角平分线,且相交于点I 。
结论:A I ∠+︒=∠2190 证明: ∵BI 是∠ABC 平分线,∴ABC ∠=∠212 ∵CI 是∠ACB 平分线,∴ACB ∠=∠213由A →B →I →C →A 的飞镖模型可知: ∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190. 应用:如上图,BI 、CI 分别是∠ABC 和∠ACB 的角平分线,且相交于点I 。
(1) 若∠A =60° ,则∠I =120° (2) 若∠I =110°,则∠A =40° (3) 若∠A =α,则∠I =α2190+︒。
初中数学——三角形的内外角和倒角模型

飞镖模型
A
12
D
B
34
C
结论:∠BDC=∠A+∠B+∠C
A
D B
连接BC
∵三角形内角和180°
∴∠A+∠ABC+ ∠ACB =180°
∠DBC+∠D+ ∠DCB=180°
C
∴∠A+∠ABC+ ∠ACB= ∠DBC+∠D+ ∠DCB 又∵ ∠ABC= ∠ABD+ ∠DBC
∠ACB= ∠ACD+ ∠DCB
∠A+∠B+∠F=∠BOF
在飞镖模型EDCO中
∠D+∠E+∠C=∠EOC
∠BOF=∠EOC=105 °(对顶角相等)
O
∴ ∠A+∠B+∠C +∠D+∠E+∠F=210°
“8”字模型
∵三角形内角和180°
∴∠A+∠B+ ∠1 =180° ∠C+∠D+ ∠2=180°
∠A+∠B+ ∠1 =∠C+∠D+ ∠2
∴∠A+∠ABC+∠ACB=∠BDC
飞镖模型
A
D
B
C
实现角的数量转换
飞镖模型
连接BD 在飞镖模型ABDN中 ∠A+∠ABD+∠NDB=∠AND=100 ° 在飞镖模型BDCM中 ∠C+∠BDA+∠DBM=∠CMB=130 ° ∴ ∠A+∠ABM+∠C+∠NDC=230 °
M N
在飞镖模型ABOF中
∵∠1=∠2(对顶角相等)
∴∠A+∠B=∠C+∠D
三角形倒角模型2024

引言:在三维建模中,倒角模型是一种常用的技术,用于给几何体的尖锐边缘添加平滑的圆角效果。
在本文中,我们将继续探讨三角形倒角模型的相关内容。
首先我们会简要回顾前文介绍的方法,然后深入讨论另外五个方面的内容,包括:双曲线倒角、坡度倒角、螺旋倒角、圆柱倒角和体积倒角。
通过详细的阐述,我们希望读者能够更好地理解和应用这些倒角模型技术。
概述:三角形的倒角模型是指给三角形的边缘或角度添加圆角效果。
倒角模型可以使模型更显真实,同时也能够消除尖锐边缘的刺眼感。
在之前的文章中,我们介绍了一种基本的三角形倒角模型方法,即通过增加额外的顶点来切割原始三角形,然后连接这些顶点以形成圆角效果。
在本文中,我们将深入讨论更多的三角形倒角模型技术。
正文内容:1.双曲线倒角1.1定义双曲线倒角1.2双曲线倒角的计算方法1.3双曲线倒角的应用实例1.4双曲线倒角的优缺点1.5双曲线倒角与其他倒角方法的比较2.坡度倒角2.1坡度倒角的原理2.2坡度倒角的计算方法2.3坡度倒角的应用实例2.4坡度倒角的优缺点2.5坡度倒角与其他倒角方法的比较3.螺旋倒角3.1螺旋倒角的原理3.2螺旋倒角的计算方法3.3螺旋倒角的应用实例3.4螺旋倒角的优缺点3.5螺旋倒角与其他倒角方法的比较4.圆柱倒角4.1圆柱倒角的定义4.2圆柱倒角的计算方法4.3圆柱倒角的应用实例4.4圆柱倒角的优缺点4.5圆柱倒角与其他倒角方法的比较5.体积倒角5.1体积倒角的概念5.2体积倒角的计算方法5.3体积倒角的应用实例5.4体积倒角的优缺点5.5体积倒角与其他倒角方法的比较总结:通过本文的讨论,我们详细了解了五种不同的三角形倒角模型技术。
双曲线倒角、坡度倒角、螺旋倒角、圆柱倒角和体积倒角都是常用的倒角方法。
它们各自具有不同的原理、计算方法、应用实例和优缺点。
通过比较不同的倒角方法,我们可以根据具体需求选择最适合的方法来创建高质量的倒角模型。
文末400字,请将前文正文段落补足至1300字。
