有限元分析入门
《ABAQUS有限元分析从入门到精通 第3版 》读书笔记思维导图PPT模板下载

《ABAQUS有限元 分析从入门到精通
第3版 》
思维导图PPT模板
本书关键字分析思维导图
结构
材料
文件
网格
过程
模块
信息
分析
小结
属性 第章
求解
问题
描述
设置
用户
实例
功能
模拟
01 内容简介
目录
02 第一部分 基础知识
03
第二部分 应用实例分 析
04
附录A 错误信息和警 告信息总汇
A.2.4 接触的过 盈量太大
A.2.5 过多次迭 代尝试
A.2.6 局部塑性 变形过大
A.2.7 时间增量 步达到下限
A.2.8 环境参数 standard_m...
A.3.2 ABAQUS本 身的缺陷
A.3.1 用户子程 序出现错误
A.3.3 环境参数 pre_memory...
A.4.1 不能 为非独立实 体设置网格
告信息
A.3 log文件中 的错误信息
A.4 ABAQUS/CAE 中的错误信息...
01
A.1.1 文件中有 空行
02
A.1.2 未注明实 体名称
03
A.1.3 关键词拼 写错误
04
A.1.4 关键词前 没有星号
06
A.1.6 关键词的 参数错误
05
A.1.5 关键词的 数据错误 与警告
A.1.7 标点符号 错误
内容简介
第一部分 基础知识
第1章
1
ABAQUS概述
2
第2章 前处 理模块
3 第3章 相互
作用定义
4 第4章 划分
Proe Mechanica有限元分析入门
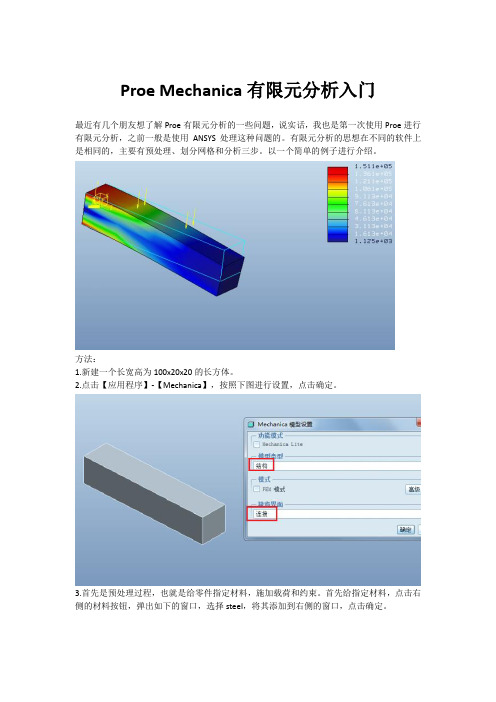
Proe Mechanica有限元分析入门
最近有几个朋友想了解Proe有限元分析的一些问题,说实话,我也是第一次使用Proe进行有限元分析,之前一般是使用ANSYS处理这种问题的。
有限元分析的思想在不同的软件上是相同的,主要有预处理、划分网格和分析三步。
以一个简单的例子进行介绍。
方法:
1.新建一个长宽高为100x20x20的长方体。
2.点击【应用程序】-【Mechanica】,按照下图进行设置,点击确定。
3.首先是预处理过程,也就是给零件指定材料,施加载荷和约束。
首先给指定材料,点击右侧的材料按钮,弹出如下的窗口,选择steel,将其添加到右侧的窗口,点击确定。
点击右侧的指定材料按钮,按照下图进行设置。
指定完成后,出现如下的符号图标。
有限元分析基础知识

2000,4
ANSYS单元分类
1. 杆单元,包括二维杆单元和三维杆单元,线性调节 元,主要包括: LINK1,LINK8,LINK10,LINK11,LINK180等。 2. 弹簧阻尼单元,包括COMBIN系列: COMBIN7,COMBIN14,COMBIN37,COMBIN40等。 3. 质量元,MASS21。
ANSYS/Structural求解功能
ANSYS/Structural求解功能
Static -- 结构静力问题(包括线性和非线性问题) Modal -- 模态振动特性计算分析(结构固有频率和振型) Harmonic -- 谐波分析 Transient -- 瞬态分析 Spectrum -- 谱分析 Eigen Buckling -- 特征值屈曲分析(线性) Substructural -- 子结构分析 。。。。。。
2000,4
有限元分析步骤(续)
• 集合所有单元的平衡方程,集合依据的是所有相邻 单元在公共节点 处的位移相等;建立总体的有限元方程组。 • 引入边界条件 • 求解有限元方程组,得到未知节点位移 • 计算单元应力,对不同的单元,对应力的处理还有不同的方法
2000,4
ANSYS文件结构
二进制文件 Jobname.db (数据库文件) Jobname.dbb (备份文件) Jobname.rst (结构分析结果文件) Jobname.rth (热分析结果文件) Jobname.rmg (电磁场分析结果文件) Jobname.rfl (流体分析结果文件) Jobname.tri (三角化刚度矩阵文件) Jobname.emat (单元矩阵文件) Jobname.esav (单元保存文件)
2000,4
简例(续)
UG有限元分析教程

UG有限元分析教程有限元分析(Finite Element Analysis,简称FEA)是一种工程设计和数值计算的方法,通过将复杂结构分割为许多简单的有限元单元,然后通过建立有限元模型,进行数值计算,最终得到结构的力学响应。
本文将向大家介绍UG有限元分析教程。
UG是一种集成的CAD/CAM/CAE软件,具有功能强大且广泛应用的特点。
UG有限元分析是UG软件中的一个功能模块,它可用于进行各种结构的有限元分析,例如静态分析、动态分析、热传导分析等。
2.有限元网格划分:将结构几何模型划分为许多有限元单元,每个单元由节点和单元单元构成。
UG提供了自动网格划分工具,用户可以选择合适的网格密度和单元类型。
3.材料属性定义:为结构的各个部分定义材料属性,包括杨氏模量、泊松比、密度等。
用户可以根据实际情况选择合适的材料模型。
4.边界条件和加载:为结构的边界和加载部分定义边界条件和加载,包括支撑约束、力、压力等。
用户可以根据实际情况选择合适的加载方式。
5.求解:通过对有限元模型进行离散化和求解,得到结构的力学响应。
UG提供了高效的求解器和迭代算法,可以快速求解大规模的有限元模型。
6.结果后处理:对求解结果进行后处理,包括位移、应力、应变等的分析和可视化。
UG提供了丰富的后处理工具,用户可以生成各种工程报表和图形。
UG有限元分析教程提供了详细的步骤和示例,帮助用户快速学习和掌握UG有限元分析的基本方法和技巧。
课程内容包括UG软件的基本操作、几何建模、有限元网格划分、材料属性定义、边界条件和加载的设定、求解器和后处理工具的使用等。
学习UG有限元分析需要一定的工程基础和计算机技巧,但是通过系统的学习和实践,任何人都可以掌握这一方法,并在工程设计和研究中应用它。
总之,UG有限元分析教程提供了全面的学习资料和实例,帮助用户了解和掌握UG有限元分析的基本理论和应用方法,为工程设计和研究提供了有力的工具和支持。
有限元方法基础教程

有限元方法是一种用于计算复杂物理问题的数值分析方法。
它可以用来解决各种工程、物理和化学问题,如流体力学、固体力学、传热学和电场分析。
本文将介绍有限元方法的基本原理,并且通过几个例子来说明如何使用它来解决实际问题。
1. 什么是有限元方法?
有限元方法是一种数值分析技术,可以帮助我们快速准确地解决复杂的物理问题。
它将复杂的物理场中的所有量都表述为一些小而独立的“单元”(finite elements) ,然后对这些单元应用相应的数学表达式得到想要得到的信息。
例如:当我们想要解决一个固体力学问题时,我们可能会需要考虑不同部位上不同大小、形态和弹性应力之间相互作用承受不同大小、形态和弹性应力之间相互作用承受不同大小、形态和弹性应力之间相互作用承受不同大小、形态。
有限元分析经典课件

有限元分析经典课件1. 简介有限元分析(Finite Element Analysis, FEA)是一种以数值模拟方法为基础,通过离散化处理求解结构力学问题的工程方法。
本课件将介绍有限元分析的基本原理和常用的应用领域。
2. 有限元分析的基本原理2.1 有限元方法概述有限元方法(Finite Element Method, FEM)是有限元分析的基础理论和计算方法。
本部分将介绍有限元方法的基本概念、基本步骤、离散化处理等内容。
2.2 有限元网格划分有限元网格划分是有限元分析的关键步骤,它将结构离散化为有限个小单元。
本部分将介绍有限元网格划分的方法、常用网格类型以及网格质量评价的方法。
2.3 有限元方程与加载有限元方程是描述结构力学问题的关键方程。
本部分将介绍有限元方程的推导过程,以及加载条件的处理方法。
2.4 有限元解与后处理有限元解是通过有限元分析得到的结构响应结果。
本部分将介绍有限元解的计算方法以及后处理方法,包括位移、应力、应变等结果的计算和可视化展示。
3. 有限元分析的应用案例3.1 结构力学分析结构力学分析是有限元分析的主要应用之一。
本部分将通过实例演示有限元分析在结构力学分析中的具体应用,包括静力学分析、动力学分析等。
3.2 热力学分析热力学分析是有限元分析的另一个重要应用领域。
本部分将通过实例演示有限元分析在热力学分析中的具体应用,包括热传导、热稳定性等问题的分析。
3.3 流体力学分析流体力学分析是有限元分析的扩展应用领域之一。
本部分将通过实例演示有限元分析在流体力学分析中的具体应用,包括流体流动、压力分布等问题的分析。
4. 有限元分析软件的介绍有限元分析软件是进行有限元分析的工具,市场上有多种成熟的有限元分析软件可供选择。
本部分将介绍一些常用的有限元分析软件,包括Ansys、Abacus等。
5. 总结有限元分析作为一种重要的数值模拟方法,已广泛应用于不同领域的工程问题。
本课件从理论原理到实际应用都进行了全面的介绍,相信对有限元分析的学习和应用都有很大帮助。
第二章有限元分析基础

第二章有限元分析基础有限元分析是一种常用的工程计算方法,在工程学科中被广泛应用。
本章将介绍有限元分析的基本概念和基础知识。
有限元分析是一种数值分析方法,用于求解复杂的物理问题。
它的基本思想是将一个连续的物体或结构离散化为有限数量的基本单元,通过在每个单元上进行计算,最终得到整个物体或结构的行为。
这些基本单元通过节点连接在一起,形成了一个有限元网格。
通过在每个节点上求解方程,可以得到整个物体或结构的应力、变形等相关信息。
在有限元分析中,有三个重要的步骤:建模、离散和求解。
建模是指将实际物体或结构转化为数学模型的过程。
在建模过程中,需要确定物体或结构的几何形状、边界条件和力学性质等。
离散是指将物体或结构划分为有限数量的基本单元。
常用的基本单元有三角形、四边形和六面体等。
离散过程中需要确定每个基本单元的几何属性和材料性质等。
求解是指在离散的基础上,通过求解节点上的方程,得到物体或结构的应力、变形等结果。
求解过程中,需要确定节点的位移和应变等参数。
有限元分析的基本假设是在每个基本单元内,应力和应变满足线性关系。
这意味着在小变形和小位移的情况下,有限元分析是有效的。
此外,为了提高计算精度,通常会增加更多的基本单元。
但是,增加基本单元数量会增加计算复杂度和计算时间。
因此,在实际应用中,需要根据问题的复杂程度和计算资源的限制进行权衡。
有限元分析广泛应用于各个领域,例如结构力学、热传导、电磁场、流体力学等。
在结构力学中,有限元分析可以用于求解静力学和动力学问题。
在热传导中,有限元分析可以用于求解温度分布和热流问题。
在电磁场中,有限元分析可以用于求解电荷和电场分布等。
在流体力学中,有限元分析可以用于求解流速和压力分布等。
总之,有限元分析是一种重要的工程计算方法,可以用于求解各种物理问题。
通过建模、离散和求解等步骤,可以得到物体或结构的应力、变形等结果。
有限元分析在工程学科中有着广泛的应用前景,对于工程设计和优化起着重要作用。
ansys workbench 2022有限元分析入门与提高

ansys workbench 2022有限元分析入门与提高ANSYSWorkbench2022是一款很受欢迎的有限元分析软件,它能够帮助工程师快速解决各种类型的结构力学问题和复杂材料性质的分析问题。
本文将针对有限元分析的基础知识介绍ANSYS Workbench 2022,并以实际的例子探讨ANSYS Workbench 2022如何帮助工程师解决结构有限元分析中的问题。
1. ANSYS Workbench 2022有限元分析:软件简介ANSYS Workbench 2022是一款建立在ANSYS有限元解决器之上的强大的软件工具,可以帮助工程师解决许多结构力学问题和复杂材料性质的问题,比如振动和强度分析。
有限元分析是一种分析技术,它可以帮助研究工程师计算并分析各种不同类型的材料在不同环境下的行为。
ANSYS Workbench 2022包含了大量的有限元分析功能,使工程师能够对实际的物理系统进行有效的分析。
2. ANSYS Workbench 2022有限元分析:功能概述ANSYS Workbench 2022能够结合了有限元分析的众多功能,此外还提供了高度的可扩展性和易用性,使用户能够快速解决各种复杂的结构力学问题,具体功能如下:(1)多种结构力学分析:ANSYS Workbench 2022提供了多种不同类型的结构力学分析,比如强度分析、温度分析、振动分析、时域分析等,可以帮助研究工程师精确的计算物体的特性。
(2)网格划分:ANSYS Workbench 2022可以帮助研究者快速地对实际物体进行网格划分,并以其为基础进行数值模拟计算。
(3)对结果进行可视化:ANSYS Workbench 2022可以帮助研究者清楚地看到模拟结果,以便客观地理解结果。
3. ANSYS Workbench 2022有限元分析:实际案例下面以空气盒子为实际例子,介绍如何利用ANSYS Workbench 2022使用有限元分析来解决实际模型的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试求:杆的位移分布,杆 的应变和应力。
自重作用下等截面直杆的材料力学解答
N(x) q(L x)
x
E x
q (L A
x)
x
du dx
q (L EA
x)
du(x )
N(x )dx EA
商业有限元软件
ANSYS(通用) SDRC/I-DEAS(复杂模型) PATRAN/NASTRAN(通用) ABAQUS(非线性/复杂) Dyna-3D(碰撞)
1.4有限单元法的进展与应用
1.4.1 主要研究领域与有限元软件
从二十世纪60年代中期以来,进行了大量的理论 研究,不但拓展了有限单元法的应用领域,还开 发了许多通用或专用的有限元分析软件。 主要的研究领域有:
T.H.H. Pian(卞学磺)等许多人的工作, 认识到有限单元法就是变分原理中Ritz 近似法的一种变形,发展了用各种不同 变分原理导出的有限元计算公式。
有限单元法的数学基础(2)
1965 年 O.C.Zienkiewicz 和 Y.K.Cheung (张佑启)发现只要能写成变分形式的 所有场问题,都可以用与固体力学有限 单元法的相同步骤求解。
结构力学
有限元理论
有限元软件
什么是有限元方法?
思想:将一个复杂问题分解为许多可以求解的小 问题
例:房子和砖,圆的面积求解
1.将圆划分为小三角形单元
单元i i
R
2.求每个三角形面积=
1 2
R
2
sin(i )
3.圆的面积=
S N
N
Si
i 1
1 R 2N
2
sin(2 N
)
N
R
2
数学概念
有限元方法是为偏微分方程或者积分方程寻 求近似解的一种数值方法
平面桁架结构,由6个承受 轴向力的“杆单元”组成。
1889年建成的Effiel塔,由 18036个部件组成
大型编钟“中华和钟”的振动分析及优化设计。
第二类问题,通常可以建立它们应遵循的 基本方程,即微分方程和相应的边界条件。 例如弹性力学问题,热传导问题,电磁场 问题等。
热传导问题的控制方程与换热边界条件如 下:
2)用单元节点位移表示单元内 部位移
第i个单元中的位移用所包含的
结点位移来表示。
u(x)
ui
ui1 ui Li
(x
xi )
ui 第i结点的位移
xi 第i结点的坐标
第i个单元的应变
i
du dx
ui1 ui Li
应力 内力
i
E i
E(ui1 ui ) Li
Ni
A i
EA(ui1 Li
ui )
SYSWELD
/products/sysweld/
飞箭公司的有限元程序自动生成系统FEPG
/
1.4.2应用实例
有限单元法已经成功地应用在以下一些领 域:
固体力学 包括强度、稳定性、震动和瞬态问题的分析;
1.3.1网格划分
通常把三维实体划分成四面体(Tetrahedron)或 六面体(Hexahedron)单元的网格
四面体4结点单元
六面体8结点单元
1.3.1网格划分
三维实体的四面体 单元划分
三维实体的六面体 单元划分
1.3.1网格划分
通常把平面问题划分成三角形(triangular)或四边 形(quadrilateral)单元的网格
iui2
q 2EA
(1
1
i
)L2i
4)建立结点的力平衡方程
对于第i+1结点,由力的平衡方程可得:
Ni
Ni1
q(Li
2
Li 1 )
EA(ui1 Li
ui )
EA(ui2 ui1 ) Li1
q 2 (Li
Li1 )
令
i
Li Li1
ui
(1
i )ui1
iui2
q 2EA
(1
1
i
)L2i
(tensor)来表示
Fe K e e
1.3.3整体分析
对由各个单元组成的整体进行分析,建立节点 外载荷与结点位移的关系,以解出结点位移, 这个过程为整体分析。
在边界结点i上受到集中力 作用。结点i是三个单元的 结合点,因此要把这三个单 元在同一结点上的结点力汇 集在一起建立平衡方程。
1.3.3整体分析
淬火3.06 min 时的温度、组织分布
课程目标
理解有限元的基本概念 掌握课程中提到的不同类型单
元的性质及用途 能够为具体问题建立合适的有
限元模型 能解释分析结果并预测结果的
准确性(理解物理过程) 明白有限元方法的局限性(数
值计算方法)
为什么用有限元方法?
有限元方法的意义
设计分析:手算,实验和计算机模拟 有限元分析是计算机模拟中应用最广泛
三角形3节点单元
四边形4节点单元
1.3.1网格划分
平面问题的三角形单元划分
平面问题的四边形单元划分
1.3.2单元分析 单元的所有结点位移、结点力,可以表示
为结点位移、结点力向量(vector)
ui
vi
e
u v
j j
um
vm
Ui
Vi
Fe
U
V
j j
U
m
Vm
单元的结点位移和结点力之间的关系用张量
传热学 电磁场 流体力学
转向机构支架的强度分析(刘道勇,东风汽车 工程研究院动,用MSC/Nastran完成)
金属体积成形过程的分析(用Deform软 件完成)
型材挤压成形模拟
T形锻件的成形模拟
焊接残余应力分析(用Sysweld完成)
结构与焊缝布置
焊接过程的温度分布 与轴向残余应力
复杂形状工件的组织转变预测(用 NSHT3D完成)
x
T x
y
T y
z
T z
Q
c
T t
λ
T n
h Tf
T
300MW汽轮机低压转子淬火
有限单元法的数学基础(1)
数学家们则发展了微分方程的近似解法, 包括有限差分方法,变分原理和加权余 量法。
在1963年前后,经过J. F. Besseling,
R.J. Melosh, R.E. Jones, R.H. Gallaher,
20世纪60年代初期,冯康等人在大型水坝应力计算的基 础上,独立于西方创造了有限元方法并最早奠定其理论 基础。--《数学辞海》第四卷
1.2 有限单元法的基本思路
将连续系统分割成有限个分区或单元 用标准方法对每个单元提出一个近似
解 将所有单元按标准方法组合成一个与
原有系统近似的系统。
自重作用下等截面直杆的解
i结点的结点力:
U (1) i
U
(2) i
U
(3) i
U
(e) i
e
V (1) i
Vi(2)
V (3) i
Vi ( e )
e
i结点的平衡方程:
U
(e) i
e
Vi ( e )
e
Pxi Pyi
有限元与计算机
计算机模拟步骤
前处理(建模,加载荷和边界条件) 求解(建立并求解方程组) 后处理(归纳并显示结果)
非线性分析软件
通用结构分析软件
非线性分析软件
非线性分析软件
一些专用的有限元软件如下表所列
软件名称 Deform Autoform
DYNAFORM
SysWeld
简介 金属体积成形分析 金属板料成形分析 金属板料成形分析 焊接与热处理分析
MSC中国
/
3)把外载荷集中到节点上
把第i单元和第i+1单 元重量的一半,集中 到第i+1结点上
4)建立结点的力平衡方程
对于第i+1结点,由力的平衡方程可得:
Ni
Ni1
q(Li
2
Li 1 )
EA(ui1 Li
ui )
EA(ui2 ui1 ) Li1
q 2 (Li
Li1 )
令
i
Li Li1
ui
(1
i )ui1
P1: u"(x) f (x) in (0,1)
u(0) u(1) 0
P
2
:
u {
x
x
(
x,
y)
u
yyf (x, y) in
u0
on
误差 u(x)
1.1有限单元法的形成
两类典型的工程问题
第一类问题,可以归结为有限个已知单元 体的组合。 例如,材料力学中的连续梁、建筑结构框 架和桁架结构。
描述每一单元的物理特性
将所有单元通过节点连接 起来,得到求解整体结构 的近似方程组
解方程组求得每一节点的 未知量(如位移)
求解指定单元的其他未知 量(如应力,应变)
整体分析
1.3.1网格划分
对弹性体进行必要的简化,再将弹性体划 分为有限个单元组成的离散体。 单元之间通过单元节点相连接。 由单元、结点、结点连线构成的集合称为 网格。
有限元分析入门
Introduction to Finite Element Analysis
课程内容
有限元的思想 有限元的方法
杆件结构的有限元法 平面结构的有限元法 有限元软件 ANSYS软件建模和分析的方法
考试安排
笔考 (理论) 机考(实践操作)
第一章 绪论
结构力学,有限元理论与有限元软件
