04第四章 图论方法建模2
图论模型的构建

【方形柱体堆砌问题分析】
对符合要求的方形柱体来讲,交换任意两个正 方体的上下位置,得到的方形柱体仍是符合要求的, 即它的4个侧面都有4种颜色。它的每一对对面由4 个正方体各一个对面组成,因此问题的要素是4个正 方体各3个对面的颜色的构成,于是从每个对面的着 色考虑。用字母b,g,r,y分别表示蓝、绿、红、黄4种 颜色,并作为图的4个 顶点,4个正方体的各三个对 面依各对面的颜色连以边,并分别标以e1、e2、e3、 e4,比如第一个正方体有一对面着蓝、黄两色,则 从顶点b到y引一条边标以e1,另两对面为红对红、红 对绿,故联结r,e和r,g,均标以 e1。同样地根据第二、 三、四正方体的各对面着色分别连以边并分别标以 e2 、e3、e4。则得图G,如图1—3所示。
si<si+p
(0≤i≤n-p)
si+q<si
(0≤i≤n-q)
【奇怪的数列分析】
下面,我们把每个si抽象成一个点,则根据上述两个不 等式可以建立一个有向图,图中共有n+1个顶点,分别 为s0,s1,……,sn。若si>sj(0≤i,j≤n),则从si往sj 引出一条有向边。例如对于n=6,p=5,q=3的情况, 我们可以建立图4
begin
if i+p<=n then begin
g[i+p,i]=1;
d[i]=d[i]+1;
end;
if i+q<=n then begin
g[i,i+q]=1;
d[i+q]=d[i+q]+1;
end;
end;
【奇怪的数列分析】
显然,按照上面的定义,如果建立的图可以拓扑排序,其 顶点的拓扑序列可以对应满足条件的整数数列;反之,不 存在这样的整数数列。 算法框架为:
图论方法

算法的基本思想
直接在图的带权邻接矩阵中用插入顶点的方法 依次构造出 个矩阵 D(1)、 D(2)、… 、D( ),使最 后得到的矩阵 D( )成为图的距离矩阵,同时也求出 插入点矩阵以便得到两点间的最短路径.
返回
算法原理—— 求距离矩阵的方法
( 把带权邻接矩阵 W 作为距离矩阵的初值,即 D(0)= (d ij0) ) =W
G 的图解如图
V={v1 ,v2 , v3 , v4}, E={e1, e2 , e3, e4, e5},
定义2在图 G 中, V 中的有序偶(vi, vj)对应的边 e , 与 称为图的有向边
(或弧) 而与 V 中顶点的无序偶 vivj 相对应的边 e , , 称为图的无 向边.每一条边都是无向边的图,叫无向图;每一条边都是有向 边的图,称为有向图;既有无向边又有有向边的图称为混合图.
数学建模的图论方法
图论的基本概念
一、 图 的 概 念 1.图的定义 2.顶点的次数
3.子图
二、 图 的 矩 阵 表 示
1. 关联矩阵
2. 邻接矩阵
返回
图的定义
定义1 有序三元组G=(V,E, )称为一个图,如果: [1] V= {v1 , v2 ,, vn } 是有限非空集,V 称为顶点集,
其中的元素叫图 G 的顶点. [2] E 称为边集,其中的元素叫图 G 的边. [3] 是从边集 E 到顶点集 V 中的有序或无序的元素 偶对构成集合的映射,称为关联函数. 例1 设 G=(V,E, ),其中
(e1 ) v1v2 , (e2 ) v1v3 , (e3 ) v1v4 , (e4 ) v1v4 , (e5 ) v4v4 .
定义3 若将图 G 的每一条边 e 都对应一个实数 w ( e ),则称 w ( e )为边的
[高等教育]图论方法建模
![[高等教育]图论方法建模](https://img.taocdn.com/s3/m/6af62872e45c3b3567ec8bd7.png)
四、匹配问题
例1 求二部图G中的最大匹配。
X1
X2
X3
X4
Y1
Y2
2019/5/13
Y3
Y4
四、匹配问题
M
xS
B
{x2y2,x3y3} x1 {x1}
{x1,x2} {y2}
{x1y2,x2,y x4 {x4}
1,x3y3}
{x4,x1} {y2}
N(s) y N(S) B yu M P
2019/5/13
五、旅行商问题
Euler图和Hamilton图
定义 经过G 的每条边的迹叫做G 的 Euler 迹;闭的 Euler 迹叫做 Euler 回路或 E 回路;含 Euler 回路的图叫做 Euler 图。
定义 包含G 的每个顶点的轨叫做 Hamilton(哈密顿)轨;
闭的 Hamilton 轨叫做 Hamilton 圈或 H 圈;含 Hamilton 圈的图
{y2} y2饱和 y2x2 点
{y1,y2,y y1非饱
4}
和点
x1y2x 2y1
{y2,y3} y2饱和 y2x1
{y2,y3} y3饱和 y3x3
{x4,x1, {y2,y {y2,y3} N(s)=B 结束
x3}
3}
2019/5/13
四、匹配问题 • 最大匹配就是:
X1
X2
X3
X4
Y1
Y2
<<a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40; a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;a(4,7)=42; a(5,6)=70; <<leasttree_2(a)
数学建模中的图论方法

出最 少 。
使用不 同时间设备所需 的维修费分别为 56 , , 。 ,, 1 1 8 18 建立最短路模型 1 2: b表示设备在第 f 图 , ) 图 设 年年 初的购买费 , 表示设 备使用 年后 的维修 费, ={ % c
作者简介 : 艾素梅( 5 一 , 河北沧州人 , 州师范学院数学 系主任 、 。  ̄ 8 )女, 9 沧 教授
9 ・ 8
・
从 上 图 中 容 易 得 到 l 到 6只 有 两 条 路 : / 6和 J3 )
V” , 146而这两条路都是 l 到 6 的最短路。
2 网络流 问题
对 1 ≤m,ol 必为 G中从 。 ≤k … 到 的最短路 : 最短路
是一条路 , 且最短路 的任一段 也是最短路 。
1 例 题 . 2
例 1 ( 设备更新问题 ) 某企业使用一台设备 , 每年年初 ,
图2
收 稿 日期 : 1—1—2 20 0 5 0
基金项 目: 河北省教育厅 2O 年度科研计划项 目“ 3 9 高职 高专数学建模教学和实践 的探 索”。
,
G中 任 一边 野 有 流量 ,称集 合 厂=
一
}为 网络 G上 的
个流。
定义 4 满足下述条件的流 厂 称为可行 流 : 1( )容量限制条件) 对每一边 甜, 0 ≤ ; 有 ≤
2( )平衡条件) 于中间点 有 对 的输入量 :输出量。 如果 ,是可行 流, 则对收、 发点 、 有 2f = , = , = , 即中间点
第 2 卷第 4 I 5 期
l年 l 0 2月
图论算法总结及图论建模

else if (v in S)
// 如果节点v还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u])
// 如果节点u是强连通分量的根
repeat
v = S.pop
// 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}
算法演示
边的分类
一条边(u, v)可以按如下规则分类
• 树边(Tree Edges, T): v通过边(u, v)发现 • 后向边(Back Edges, B): u是v的后代 • 前向边(Forward Edges, F): v是u的后代 • 交叉边(Cross Edges, C): 其他边,可以连接同一个DFS树中没
1. 2. procedure tarjan(u:longint); var p:node; v:longint; begin f[u]:=false;inc(top);stack[top]:=u; instack[u]:=true;p:=head[u]; inc(time);dfn[u]:=time;low[u]:=time; while p^.key<>u do begin v:=p^.key; if f[v] then begin tarjan(v); low[u]:=min(low[u],low[v]);
tarjan(j); if (LOW[j]<LOW[i])
LOW[i]=LOW[j]; } else if (instack[j] && DFN[j]<LOW[i])
LOW[i]=DFN[j]; }
if (DFN[i]==LOW[i]){ Bcnt++; do { j=Stap[Stop--]; instack[j]=false; Belong[j]=Bcnt; } while (j!=i);
数学模型课件图论方法建模2
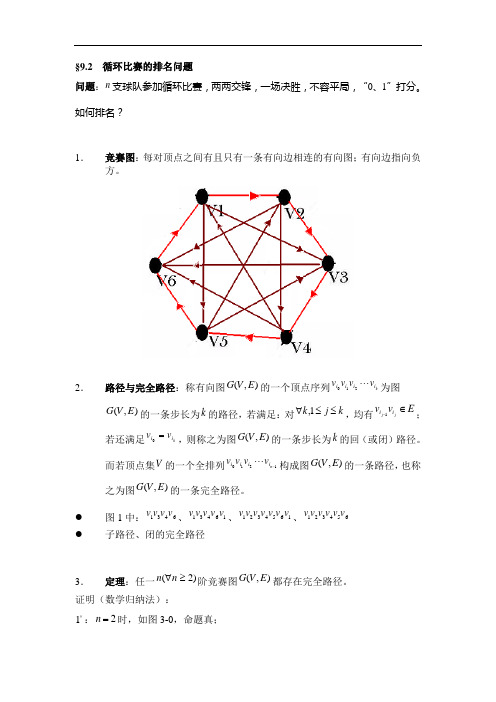
§9.2 循环比赛的排名问题问题:n 支球队参加循环比赛,两两交锋,一场决胜,不容平局,“0、1”打分。
如何排名?1.竞赛图:每对顶点之间有且只有一条有向边相连的有向图;有向边指向负方。
2.路径与完全路径:称有向图),(E V G 的一个顶点序列ki i i i v v v v 210为图),(E V G 的一条步长为k 的路径,若满足:对k j k ≤≤∀1,,均有E v v j j i i ∈-1;若还满足ki i v v =0,则称之为图),(E V G 的一条步长为k 的回(或闭)路径。
而若顶点集V 的一个全排列1210-n i i i i v v v v 构成图),(E V G 的一条路径,也称之为图),(E V G 的一条完全路径。
● 图1中:6431v v v v 、16431v v v v v 、1654321v v v v v v v 、654321v v v v v v ●子路径、闭的完全路径3.定理:任一)2(≥∀n n 阶竞赛图),(E V G 都存在完全路径。
证明(数学归纳法):1:2=n 时,如图3-0,命题真;2:设k n =时命题真;3:当1+=k n 时,设{}121,,,+=k k v v v v V 为顶点集,记{}k v v v V ,,21~=,~G 为图),(E V G 关于{}k v v v V ,,21~=的生成子图;由归纳假设2,在~G 中存在完全路径,不失一般性,设k k v v v v 121...-为~G 中的一条完全路径,考虑顶点1+k v 与{}k v v v V ,,21~=的邻接关系,有如下三种情形:图3-1:k k k v v v v v 1211...-+为G 中的一条完全路径;图3-2:1121...+-k k k v v v v v 为G 中的一条完全路径图3-3:k k i k i v v v v v v v 11121......-+-为G 中的一条完全路径。
数学建模中图论方法

第15页/共39页
数学建模中的图论方法----综合例题
3.综合例题 例1 证明任意六个人的集会上,总会有三人互相认识或 者不认识. 证明 这是1947年匈牙利数学竞赛出的一道试题,因为它 很有趣且很重要,后来曾收录到《美国数学月刊》及其它 数学刊物上。这类问题可以转化为图论中的完全图染色问 题.
最低。 数学模型:在一个连通加权图上求权最小的连通生成
子图,显然,即求权最小的生成树,称最小生成树。
Kruskal算法(避圈法)1956年
设G为由n个顶点、m条边构成的加权连通图。先将G中
所有的边按权的大小次序进行排列,不妨
设e1 e2 em ,
ⅰ k 1, A ;
ⅱ 若Ae 导出的子图不含回路,则A Ae;
从它们所在的结点出发,走过图中的所有边最后到达结
点e处。如果他们的速度相同,问谁先到达目的地?
第12页/共39页
数学建模中的图论方法----图论的基础知识
哈密尔顿回路,起源于一个名叫“周游世界”的游戏, 它是由英国数学家哈密尔顿(Hamilton)于1859年提出的。 他用一个正十二面体的20个顶点代表20个大城市(图 (a)),这个正十二面体同构于一个平面图(图(b))。要
a
b
f
a
b
e
c
e
d
c
d
(1)
第11页/共39页
(2)
数学建模中的图论方法----图论的基础知识 a
D
E
b
e
C
F
G
A
B
c
d
数学建模方法之图论模型

定理 d (v) 2.
vV
推论 任何图中奇点 的个数为偶数. d (v1) 4
d (u3) 1
d (u3) 2
一个顶点记为 ui1,置 Si1 Si {ui1}.
3) 若 i 1,则停Hale Waihona Puke ;若 i 1,则用 i+1 代
替i,并转2).
S0 {u0},l(u j ) , j 1,2,...,7.
u1 S0 l(u1) min{,0 1}
Dijkstra算法: 求G中从顶点u0到其余顶点的最短路.
G[{v1,v2,v3}] G[{e3,e4,e5,e6}]
3) 若 V V,且 V ,以 V 为顶点集,以两端点 均在V 中的边的全体为边集的图 G 的子图,称 为G的由V 导出的子图,记为 G[V ] .
4) 若E E,且 E ,以 E为边集,以 E 的端点 集为顶点集的图 G 的子图,称为 G 的由E 导出的
第二讲 图论模型
1. 问题引入与分析
2. 图论的基本概念
3. 最短路问题及算法
4. 最小生成树及算法
回
5. 旅行售货员问题
停
6. 模型建立与求解 下
1. 问题引入与分析
1) 98年全国大学生数学建模竞赛B题“最佳灾 情巡视路线”中的前两个问题是这样的:
今年(1998年)夏天某县遭受水灾. 为考察灾情、 组织自救,县领导决定,带领有关部门负责人到 全县各乡(镇)、村巡视. 巡视路线指从县政府 所在地出发,走遍各乡(镇)、村,又回到县政 府所在地的路线.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 图论方法建模20 第四章 图论方法建模图论是离散数学的重要分支,是研究离散问题的重要手段,已经建立起来了一些重要的理论和算法,虽然这些理论还不系统、不完备,但是能解决许多的实际问题。
不系统就没有太强的连贯性,这就使得学习起来较为方便,可以随意挑选适宜的内容去学习。
如果将要解决的实际问题归结为图论中的某些概念或某些算法,就可以利用图论中已有的理论,这样就可以较快的解决问题。
在国内外的大学生数学建模竞赛中,利用图论知识去建立数学模型的机会还是很多的。
限于时间与篇幅,我们在本章先学习一些图论知识,愿意深入学习的可以参阅有关的资料。
然后学习一个较为完整的数学建模例子。
§4.1 有关的图论知识——图、算法与矩阵一.图的定义例1.城市之间的运输通路问题A 城与B 城间有通路,为2公里,B 城与C 城间有通路,为1公里,C 城与D 城间有通路,为5公里,D 城与F 城间有通路,为3公里,F 城与A 城间有通路,为7公里,B 城与F 城间有通路,为6公里。
问A 城到D 城的最短路程为多少?用这么长的一段话来表述,听起来太累,想起来也不清楚。
若换一种方式,用下面的图4.1来描述该问题,看起来就清楚多了。
C图4.1由此我们引进图的定义。
定义1:称}),(),({G G E G V G ψ=为一个图,其中φ≠)(G V 叫做顶点集合,E(G)第四章 图论方法建模 21叫做边集合,φ=)()(G E G V I ,而G ψ是关联函数,使G的每条边对应于G的无序顶点对。
若,而,使得)(G E e ∈)(,G V v u ∈uv e G =)(ψ,则称与u 、相关联。
顶点和称为的端点,此时也称和相邻。
e v u v e u v 一个图常常简记为G=(V,E )或G (V,E ),这是因为边集E 中的任一 元素总是和某二顶点相连接的,所以V 、E 确定了,就可以了。
上述例子的图即为:G(V,E),其中V={A,B,C,D,F },E={e 1,e 2,e 3,e 4,e 5,e 6},e 1=AB, e 2=BC, e 3=CD, e 4=DF, e 5=FA, e 6=BF 。
说明:①这里用图表述城市间的运输通路问题很清楚,说明对这类问题,用图来表述是恰当的,“图”是一个强有力的表述工具。
②数学里有“图论”这门学科,一个问题用图表达后,可用图论的知识、算法等来解决此问题。
关于图论方面的知识可参阅有关的书籍、资料。
③若A为一集合,其元素个数记为:|A|。
如上例中的顶点集合和边集的元素个数分别为:|V|=5,|E|=6。
例2.哥尼斯堡(königsberg )七桥问题1736年以前,哥尼斯堡市民热中于一有趣的游戏,在如下图4.2所示的该市桥河图中,从A,B,C,D四块陆地某一处出发,通过每座桥恰好一次,再回到出发地,是否可能?1736年,欧拉(Euler )发表了图论的第一篇论文,证明了七桥问题无解.欧拉就是把A,B,C,D四陆地抽象成为四个点,桥用连接两点的线段表示,于是就得到一个图G(V,E)。
, },,,{D C B A V =},,,,,,{7654321e e e e e e e E =, 这里,e 1=AD, e 2=BD, e 3=CD, e 4=BC, e5=BC, e 6=AB, e 7=AB 。
定义2:图G(V , E)中顶点的度数是指顶点所连的边数。
图G 的度数为图G 中各顶点度数中的最大者。
记为或V v ∈)(v d v Δ)(G Δ。
说明:①七桥问题可归结为一笔画问题。
②关于一笔画问题有如下的结论:若图中每个顶点的度数都为偶数,则可从某点画完每条边,且回到起点。
第四章 图论方法建模22 若图中顶点的度数为奇数的顶点仅仅有两个,则可从此二点中的一个起始,画完每条边到达另一顶点(即不能回到起始点)。
③七桥问题的图中4个顶点的度数为奇数,由上面的结论知,不可能从出发点走完每条边恰好一次,又回到出发点。
定义3:一个图中任意两顶点之间至多有一边,则称之为简单图。
定义4:若图G(V ,E)中边有头尾之分,即E uv ∈vu uv ≠,则称之为有向图。
以后说“图”皆指无向图,要指有向图应特别说明。
并且若无特别说明,我们所说的图皆指简单图。
每对顶点都相邻的图称为完全图。
定理:对于简单图,有:),(E V G ∑∈=)(||2)(G V v E v d 。
二.最短路问题及其算法定义5:在G 中, 其中,...2110k k e v e v e v w =)(G E e i ∈,k i ≤≤1;)(G V v i ∈,;与、关联,称是从到的一条途径,也记为或。
若途径中的边,,……,互不相同,称为迹。
若的顶点,,…,也互不相同,则称为路。
k i ≤≤0i e 1−i v i v w 0v k v ),(0k v v w ),(0k v v 1e 2e k e w w 0v 1v k v w 上述例1中问题的一般提法为:给定连接若干城市的铁路网,寻找两个指定城市间的最短路。
这个问题用图论的语言来描述就是:已知图及每条边的权,对于任意指定的二点、,寻找路,使得),(E V G )(e w 0v )(0G V u ∈),(00u v P )}({)),((min 00P w u v P w P Ω∈=其中是从到的所有路的集合,是路Ω0v 0u )(P w P 上的各边权之和。
解决这一问题可用下面的Dijkstra 算法:(1):令;,;0)(0=v l ∞=)(v l 0v v ≠}{00v S =;0=i ;(2):对每个,用i S v ∉)}()(),(min{v v w v l v l i i +代替,计算)(v l )}({min v l iS v ∉,并把达到这个最小值的一个顶点记为,置1+i v }{11++=i i i v S S U 。
(3):若1−=V i ,则停止。
若1−<V i ,则用1+i 代替,并转入第二步。
i 说明:①当算法结束时,从到的距离(最短路的长度)由标号的终值给出。
即算法求出了至其它所有顶点的最短路的长度。
0v v )(v l 0v ②Dijkstra 算法仅确定了从到所有其它顶点的距离,而并未给出实际最短路。
实际最短路可以很容易确定。
0v ③若只是想计算某指定两点、的最短路(或最短距离)也较为容易求出。
0v 0u第四章 图论方法建模 23三.对集和二部图例3.人员分派问题:工作人员x 1,x 2,……,x n 去做n 项工作y 1,y 2,……,y n ,每人适合做其中一项或几项工作,问能否每人都能被分派一项适合的工作?如果不能,最多几人可以有适合的工作?作为一个简单的例子,我们设n=4,将4个人用4个点表示,将4项工作也用4个点表示,若有某人x i适合作某项工作y j ,则用边连接起来。
这样可以得到一个图如下:定义5:二部图(偶图)是指一个图G(V ,E),V=X ∪Y ,X ∩Y=∅,,X 中无相邻顶点,Y 中亦无相邻顶点。
0||||≠•Y X 定义6:若,)(G E M ⊆M e e j i ∈∀,,与无公共顶点(i e j e j i ≠),则称M 为图G 的对集(或称为匹配)。
M 中的一条边的两个端点叫做在对集中相配;M 中的边的端点叫做被M 许配;若图G 中每个端点皆被M 许配时,M 称为完备对集。
若G 中无使的对集M’,则称M 为最大对集。
|||'|M M >说明:①人员分派问题的图是二部图。
②若人员分派问题的图有完备对集,则可以为每人分派一项适合的工作。
③最多有几个人可以有适合的工作,就是人员分派图中最大对集M 的边数,即|M |。
四.求最大对集的算法定义7:若G 中有一条路,其边交替地在对集M 内外出现,则称此路为M 的交错路,交错路之起止顶点都未被M 许配时,此交错路称为可增广路。
注:若把可增广路上在M 外的边纳入对集,把M 内的边从对集中删除,则被许配的顶点数增加2,对集中的边增加一个。
关于一般图求最大对集的算法,Edmonds 在1965年提出了一种算法。
关于偶图求最大对集的算法有多种。
这里介绍一种偶图求完备对集的算法――匈牙利算法。
设G 为二分图,,求此图的完备对集的匈牙利算法如下:(0):从G 中任意取定一个初始对集M 。
(1):若M 把X 中的顶点都许配,止。
M 即为完备对集;否则取X 中未被M 许配的一顶点u ,记S={u},T=∅。
第四章 图论方法建模24 (2):若N(S)=T ,止。
无完备对集;否则取y ∈N(S)-T 。
(3):若y 是被M 许配的,设yz ∈M ,S ←S ∪{z},T ←T ∪{y},转(2)。
否则,取可增广路P(u,y),令M ←M ΔE(P),转(1)。
说明:①算法的要点是把已有的对集通过可增广路逐次增广以至得到完备对集。
②N(S)={y | y 与S 中的某点相邻}③M ΔE(P)是将可增广路P 中的在M 外的边纳入对集,把M 内的边从对集中删除,该运算结果仍为对集。
五.独立数与色数例4.化学制品的存放问题一家公司制造n 种化学制品,C 1,C 2,……,C n ,其中某些制品是互不相容的,如果它们互相接触则会引起爆炸。
作为一种预防措施,该公司希望把它的仓库分成若干隔间,以便使不相容的药品存放在不同的隔间里。
试问,这个仓库至少应分成几个隔间?为了方便,设n=6,这6种化学制品C 1,C 2,……,C 6分别用6个点代表,它们之间互不相容的制品用一条边连接起来,这样就得到一个图如下所示:定义8:若,I 中任意二顶点不相邻,则称I 为图G 的一个独立集。
,不是独立集,则称I 为极大独立集。
顶点数最多的独立集叫做最大独立集,其顶点数记成)(G V I ⊆I G V u −∈∀)(}{u I ∪)(G α,称为图G 的独立数。
定义9:把图G 的顶点都染上颜色,且使相邻顶点异色,又使所用的颜色数最少,称这个颜色数为G 的顶点色数,记成)(G χ。
定理:1)(+Δ≤G χ,(其中为图G 的度数)。
Δ说明:①每个隔间里存放的化学制品集合即为独立集。
②极大独立集和最大独立集是不同的。
③仓库至少应分成几个隔间就化为求一个图的顶点色数)(G χ,而)(G χ的求法是较为困难的。
虽然也有些算法可求,但都不是十分有效。
六.关联矩阵与邻接矩阵一个图存放在计算机里的方式很多,但一般是以矩阵的方式来存储的。
第四章 图论方法建模 25定义10:设图G(V, E),,},...,,{21γv v v V =},......,,{21εe e e E =,称矩阵()γγ×=ij a G A )(为图G 的邻接矩阵,其中)(G V =γ, ⎪⎩⎪⎨⎧∉∈=).(,0);(,1G E v v G E v v a j i j i ij 称矩阵()εγ×=ij b G B )(为图G 的关联矩阵,其中)(G V =γ,|)(|G E =ε,。
