九年级数学二次函数与一元二次方程2(1)
二次函数与一元二次方程_课件

=0
没有交点
没有实根
<0
有交点
有实根
≥0
归纳
△<0 △=0
△>0
求抛物线与坐标轴的交点 如何求抛物线与坐标轴的交点? 如何确定抛物线与x轴的交点个数?
例题 答案:
例题
答案:有(2.5,0),(-1,0) 归纳:一元二次方程
,则抛物线
例题 不与x轴相交的抛物线是( D )
练习——求交点 (0,-5)
例题
可以通过不断缩小根所在的范围,来估计一元二次方程的根 第二步:取平均数 取2和3的平均数2.5, 当x=2.5,y=-0.75<0. 那根是在2与2.5之间, 还是2.5与3之间呢?
例题
可以通过不断缩小根所在的范围,来估计一元二次方程的根 第三步:取异号缩小范围 一定得让相应的y值异号, 这样才能保证抛物线穿过x轴, 即根在该范围之间. 当x=2.5时,y<0, 当x=2时,y<0, 当x=3时,y>0, 所以根是在2.5与3之间
解:(3)当h = 20.5时,
因为
,所以方程无实根.
球的飞行高度达不到 20.5m .
思考 (4)球从飞出到落地要用多少时间? 解:(4)落地即h = 0,
当球飞行 0s 和 4s 时,它的高度为 0m , 即0s时,球从地面飞出,4s 时球落回地面.
讨论
通过刚才的例子可以发现,
二次函数
何时为一元二次方程?
例题
可以通过不断缩小根所在的范围,来估计一元二次方程的根 第四步:再取平均数 取2.5和3的平均数2.75, 当x=2.75,y=0.0625 > 0. 第五步:再取异号 所以根是在2.5与2.75之间
所以该抛物线与 x 轴有两个交点.
人教版九年级上册数学课件:二次函数与一元二次方程

x
人教版九年级上册数学课件:二次函 数与一 元二次 方程
人教版九年级上册数学课件:二次函 数与一 元二次 方程
归纳:
当二次函y数 a x2 bxc,当给定y的值时,则二次函数
可转化为一元二次. 方程
如:二次函数 y x24x的值为 3,求自变量 x的值, 可以解一元二次方x程 2 4x 3(即x2 4x30). 反过来,解方程x2 4x30又可以看作已知二次 函数y x24x3的值为 0,球自变量 x的值.
如果h=20,那50-20t2= 20 ,
如果h=0,那50-20t2= 0 。 如果要想求t的值,那么我们可以求 方程
人教版九年级上册数学课件:二次函 数与一 元二次 方程
的解。
人教版九年级上册数学课件:二次函 数与一 元二次 方程
问题:王明手里抛出的篮球的飞行路线是一条抛物线,如果
不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t
人教版九年级上册数学课件:二次函 数与一 元二次 方程
呢?
∴当球飞行2s时,它的高度为4m。 (3)解方程4.1=4t-t2 即: t2-4t+4.1=0
因为(-4)2-4×4.1<0,所以方程无解,
从上面我们看出, 对于二次函数 高为个度什时为么间3在球mh其 二两的=?实 次4就 方(t –是程4t)∴2把的t中球1解=函解的,0方,t飞数。程已2=行0值4知=高4hht换度-的t2达成值不常,即到数:求4.,1t时2m-求4间。t=一t0,元
人教版九年级上册数学课件:二次函 数与一 元二次 方程
拓展升华
二次函数 yax2 bxc(a0)的图像如图,
根据图像解答下列问题:
(1)写出方程 ax2bxc0的两个根;
九年级数学下册30、5二次函数与一元二次方程的关系第2课时用二次函数的图像解一元二次方程授课课件新版

知1-讲
例1 求方程x2-2x-6=0的近似值.(结果精确到0.1)
解:如图 ,画出二次函数 y=x2-2x-6的图像. 观察画出的抛物线,设它与 x轴的交点的横坐标为x1和x2, 不妨设 x1<x2. 现在来求x1的近似值.
知1-讲
(1) 容易看出:当 x=-2 时,y>0; 当x=-1时,y<0,且在-2<x<-1范围内, y随x的增大二减小,所以-2<x1<-1
知1-练
4 【中考·兰州】下表是一组二次函数y=x2+3x-5的 自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4 y -1 -0.49 0.04 0.59 1.16
那么方程x2+3x-5=0的一个近似根是( C )
A.1
B.1.1
C.1.2
D.1.3
知1-练
5 【中考·包头】已知一次函数y1=4x,二次函数y2= 2x2+2,在实数范围内,对于x的同一个值,这两个
况,如有公共点,则公共点的横坐标即为ax2+bx+ c=0的根.
知1-练
1 求例题中x2精确到0.1的近似值.
解:如图 ,画出二次函数 y=x2-2x-6的图像. 观察画出的抛物线,现在求x2 的近似值. (1)容易看出:当x=3时,y<0,当x=4时,y>0,且 在3<x<4范围内,y随x的增大而增大,∴3<x2<4.
知1-讲
例2 利用函数的图像,求方程x2+2x-3=0的根.
解:先把方程化成x2=-2x+3. 如图,在同一直角坐标系中 分别画出函数y=x2和 y=-2x+3的图像,得到它 们的交点为(-3,9)和(1,1), 则方程x2+2x-3=0的解为x=-3或x=1.
总结
知1-讲
利用图像交点法求一元二次方程的根的步骤: (1)将ax2+bx+c=0化为ax2=-bx-c的形式; (2)在同一坐标系中画出y=ax2与y=-bx-c的图像; (3)观察图像:两图像的公共点情况即为方程的根的情
人教版九年级上册数学第22章 二次函数 二次函数与一元二次方程之间的关系

22.2二次函数与一元二次方程
第1课时二次函数与一元二 次方程之间的关系
1 课堂讲解 二次函数
一元二次方程 实数根的个数
2 课时流程
逐点 导讲练
课堂 小结
课后 作业
以前我们从一次函数的角度看一元一次方程, 认识了一次函数与一元一次方程的联系.本节 我们从二次函数的角度看一元二次方程,认识 二次函数与一元二次方程的联系.先来看下面 的问题.
3 A.x1<-1<2<x2B.-1<x1<2<x2 4 C.-1<x1<x2<2D.x1<-1<x2<2
知2-导
知识点 2 二次函数与其图象与x轴的交点个数之间的关系
二次函数y=x2+x-2,y=x2-6x+9,y=x2–x+1的图象如图所示.
(1)每个图象与x轴有几个交点? (2)一元二次方程x2+x-2=0,x2-6x+9=0有几个根? 验证一下一元二次方程x2–x+1=0有根吗? (3)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一 元 二次方程ax2+bx+c=0的根有什么关系?
由“数” 到“形”
由“形” 到“数”
图象
与x轴交点情况
完成教材中习题
解:无实根
知2-导
二次函数
与x轴交点坐 标
相应方程的根
y=x2+x-2 (-2,0),(3,0)
x1=x2=3
y=x2-x+1 无交点 无实根
归纳
知2-讲
通过二次函数y=ax2+bx+c(a≠0)的图象可知, (1)如果抛物线y=ax2+bx+c(a≠0)与x轴有公 共点,公共点的横坐标是x0,那么当x=x0时, 函数的值为0,因此x=x0就是方程ax2+bx+ c=0的一个根.
二次函数与一元二次方程教学设计人教版九年级数学上册

探究新知问题:如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。
如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系。
考虑以下问题:(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?(2)小球的飞行高度能否达到20m?如果能,需要多少飞行时间?(3)小球的飞行高度能否达到20.5m?为什么?(4)小球从飞出到落地需要多少时间?归纳:从上面的问题可以看出,二次函数与一元二次方程有如下关系第(1)问师生共同分析,先用代数的方法解答,然后引导学生用图象法对此问进行解释和分析.第(2)问由学生分析并展示过程,同时让学生用图象演示为什只有一个时间小球的飞行高度达到20m?接着老师引导学生从二次函数的性质(即二次函数的最大值)来说明为什么只有一个时间?剩下的学生独立完成,学生代表分析并展示过程.根据刚才例题的讲解,类比一次函数与一元一次方程的联系,现在以小组为单位对二次函数与一元二次方程的关系进行讨论,并请代表展示结果.利用快传采集学生结果采用笔记通过探究问题体现数学来源于生活,其次也以解决实际问题的形式为后续体验一元二次方程与二次函数的联系作铺垫.让学生用数与形这两种不同的方法解决实际问题.培养学生自主思考的习惯,增强学生的归纳概括能力和表达能力,并激发好奇心和求知欲.探究新知问题:观察下图抛物线与x轴的交点情况,回答下列问题.(1)二次函数y=x2+x−2的图象与x轴有个交点,分别为则一元二次方程方程的解为,根的判别式Δ0。
(2)二次函数y=x2−6x+9的图像与x轴有个交点,分别为则一元二次方程方程的解为,根的判别式Δ0。
(3)二次函数y=x2−x+1的图象与x轴公共点,则一元二次方程方程,根的判别式Δ0。
第(1)问师生共同分析,先引导学生观察图象对此问进行解释和分析.再用代数的方法解答验证。
剩下的学生独立完成,学生代表分析并展示过程.利用快传采集学生结果通过学生讨论、观察,得出判别式和二次函数与x轴交点个数的情况的关系.并让学生掌握特殊到一般的学习方法.归纳:二次函数的图象与x轴交点横坐标与一元二次方程根的关系:.二次函数y=ax2+bx+c(a≠0)的图象和x轴交点的情况一元二次方ax2+bx+c=0(a≠0)的根的情况一元二次方程ax2+bx+c=0(a≠0)根的判别式Δ=b24ac的情况有两个相等的实数根分别为:x1=x2=x0Δ=b2 – 4ac < 0通过以上环节的探究,教师指导学生思考归纳,并展示结果。
部编数学九年级上册专题22.4二次函数与一元二次方程【六大题型】(人教版)(解析版)含答案
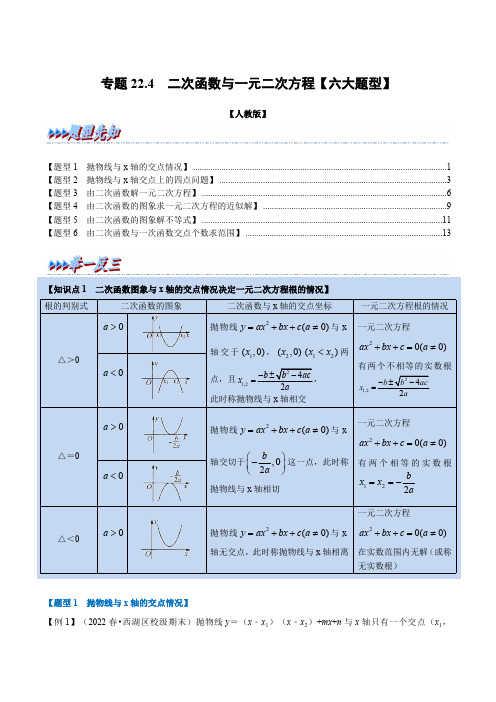
专题22.4 二次函数与一元二次方程【六大题型】【人教版】【题型1 抛物线与x 轴的交点情况】....................................................................................................................1【题型2 抛物线与x 轴交点上的四点问题】........................................................................................................3【题型3 由二次函数解一元二次方程】................................................................................................................6【题型4 由二次函数的图象求一元二次方程的近似解】....................................................................................9【题型5 由二次函数的图象解不等式】..............................................................................................................11【题型6 由二次函数与一次函数交点个数求范围】 (13)【题型1 抛物线与x 轴的交点情况】【例1】(2022春•西湖区校级期末)抛物线y =(x ﹣x 1)(x ﹣x 2)+mx +n 与x 轴只有一个交点(x 1,0).下列式子中正确的是( )A.x1﹣x2=m B.x2﹣x1=m C.m(x1﹣x2)=n D.m(x1+x2)=n【分析】由抛物线与x轴只有一个交点(x1,0)可得抛物线顶点式,从而可得x1,x2与m的关系.【解答】解:∵抛物线经过(x1,0),且抛物线与x轴只有一个交点,∴抛物线顶点坐标为(x1,0),y=(x﹣x1)2,∴x2﹣2x1x+x21=(x﹣x1)(x﹣x2)+mx+n=x2﹣(x1+x2﹣m)x+x1x2+n,∴x1+x2﹣m=2x1,即x2﹣x1=m,故选:B.【变式1-1】(2022春•澧县校级月考)抛物线y=x2+2x﹣3与坐标轴的交点个数有( )A.0个B.1个C.2个D.3个【分析】由b2﹣4ac的大小可判断抛物线与x轴交点个数,由c的大小可判断抛物线与y轴的交点,进而求解.【解答】解:∵y=x2+2x﹣3,∴a=1,b=2,c=﹣3,∴b2﹣4ac=22+12=16>0,∴抛物线与x轴有2个交点,∵c=﹣3,∴抛物线与y轴交点为(0.﹣3),∴抛物线与坐标轴有3个交点,故选:D.【变式1-2】(2022•广阳区一模)已知抛物线y=﹣3x2+bx+c与x轴只有一个交点,且过点A(m﹣2,n),B(m+4,n),则n的值为( )A.﹣9B.﹣16C.﹣18D.﹣27【分析】根据点A、B的坐标易求该抛物线的对称轴是直线x=m+1.故设抛物线解析式为y=﹣3(x﹣m ﹣1)2,直接将A(m﹣2,n)代入,通过解方程来求n的值.【解答】解:∵抛物线y=﹣3x2+bx+c过点A(m﹣2,n)、B(m+4,n),∴对称轴是直线x=m+1,又∵抛物线y=x2+bx+c与x轴只有一个交点,∴顶点为(m+1,0),∴设抛物线解析式为y=﹣3(x﹣m﹣1)2,把A(m﹣2,n)代入,得:n=﹣3(m﹣2﹣m﹣1)2=﹣27,即n=﹣27.故选:D.【变式1-3】(2022春•汉滨区期中)已知抛物线y=x2+bx+c与x轴的两个交点之间的距离为6,对称轴为x =3,则抛物线的顶点P关于x轴对称的点P'的坐标是( )A.(3,9)B.(3,﹣9)C.(﹣3,9)D.(﹣3,﹣9)【分析】根据抛物线y=x2+bx+c与x轴两个交点间的距离为6.对称轴为直线x=3,可以得到b、c的值,然后即可得到该抛物线的解析式,再将函数解析式化为顶点式,即可得到点P的坐标,然后根据关于x 轴对称的点的特点横坐标不变,纵坐标互为相反数,即可得到点P关于x轴的对称点的坐标.【解答】解:设抛物线y=x2+bx+c与x轴两个交点坐标为(x1,0),(x2,0),∵抛物线y=x2+bx+c与x轴两个交点间的距离为6,对称轴为直线x=3,=3,∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=36,−b2×1∴(﹣b)2﹣4×c=36,b=﹣6,解得:c=0,∴抛物线的解析式为y=x2﹣6x=(x﹣3)2﹣9,∴顶点P的坐标为(3,﹣9),∴点P关于x轴的对称点的坐标是(3,9),故选:A.【题型2 抛物线与x轴交点上的四点问题】【例2】(2022•武汉模拟)二次函数与一元二次方程有着紧密的联系,一元二次方程问题有时可以转化为二次函数问题.请你根据这句话所提供的思想方法解决如下问题:若s,t(s<t)是关于x的方程1+(x﹣m)(x﹣n)=0的两根,且m<n,则m,n,s,t的大小关系是( )A.s<m<n<t B.m<s<n<t C.m<s<t<n D.s<m<t<n【分析】由y=(x﹣m)(x﹣n)可得抛物线与x轴交点坐标为(m,0),(n,0),开口向上,则抛物线y=(x﹣m)(x﹣n)与直线y=﹣1的交点坐标为(s,﹣1),(t,﹣1),从而可得m,n,s,t 的大小关系.【解答】解:由1+(x﹣m)(x﹣n)=0可得(x﹣m)(x﹣n)=﹣1,由y=(x﹣m)(x﹣n)可得抛物线y=(x﹣m)(x﹣n)与x轴交点坐标为(m,0),(n,0),抛物线开口向上,则抛物线y=(x﹣m)(x﹣n)与直线y=﹣1的交点在x轴下方,坐标为(s,﹣1),(t,﹣1),∴m<s<t<n.故选:C.【变式2-1】(2022•定远县模拟)二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则下列结论正确的是( )A.x1<﹣1<5<x2B.x1<﹣1<x2<5C.﹣1<x1<5<x2D.﹣1<x1<x2<5【分析】方程a(x+1)(x﹣5)=﹣3的两根即为抛物线y=a(x+1)(x﹣5)与直线y=﹣3交点的横坐标,据此可判断选项.【解答】解:令y=a(x+1)(x﹣5),则抛物线y=a(x+1)(x﹣5)与y=ax2+bx+c形状相同、开口方向相同,且与x轴的交点为(﹣1,0)、(5,0),函数图象如图所示,由函数图象可知方程a(x+1)(x﹣5)=﹣3的两根即为抛物线y=a(x+1)(x﹣5)与直线y=﹣3交点的横坐标,∴x1<﹣1<5<x2,故选:A.【变式2-2】(2022•张店区期末)已知二次函数y=(x﹣1)2﹣t2(t是常数,且t≠0),方程(x﹣1)2﹣t2﹣1=0的两根分别为m,n(m<n),方程(x﹣1)2﹣t2﹣3=0的两根分别为p,q(p<q),判断m,n,p,q的大小关系是( )A.p<q<m<n B.p<m<n<q C.m<p<q<n D.m<n<p<q【分析】在平面直角坐标系中画出二次函数y=(x﹣1)2﹣t2(t是常数,且t≠0)的图象,再作出直线y =1,y=3,它们与抛物线交于A,B和C,D,分别过交点作x轴的垂线,则垂足对应的数值为题干中方程的根,利用数形结合的方法即可得出结论.【解答】解:在平面直角坐标系中画出二次函数y=(x﹣1)2﹣t2(t是常数,且t≠0)的图象如下图:作直线y=1与抛物线y=(x﹣1)2﹣t2(t是常数,且t≠0)交于A,B,分别经过A,B作x轴的垂线,垂足对应的数值分别为m,n,∴m,n是方程(x﹣1)2﹣t2﹣1=0的两根;作直线y=3与抛物线y=(x﹣1)2﹣t2(t是常数,且t≠0)交于C,D,分别经过AC,D作x轴的垂线,垂足对应的数值分别为p,q,∴p,q是方程(x﹣1)2﹣t2﹣3=0的两根.由图象可知m,n,p,q的大小关系是:p<m<n<q.故选:B.【变式2-3】(2022•河东区期末)已知抛物线y=x2+bx+c的图象与x轴的两交点的横坐标分别α,β(α<β),而x2+bx+c﹣2=0的两根为M、N(M<N),则α、β、M、N的大小顺序为( )A.α<β<M<N B.M<α<β<N C.α<M<β<N D.M<α<N<β【分析】依题意画出函数y=(x﹣α)(x﹣β)和y=2的图象草图,根据二次函数的图象可直接求解.【解答】解:依题意,画出函y=(x﹣α)(x﹣β)的图象,如图所示.函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为α,β(α<β),方程x2+bx+c﹣2=0的两根是抛物线y=(x﹣α)(x﹣β)与直线y=2的两个交点.由M<N,可知对称轴左侧交点横坐标为M,右侧为N.由图象可知,M<α<β<N,故选:B.【题型3 由二次函数解一元二次方程】【例3】(2022•娄底一模)已知二次函数y=ax2+bx+c的图象经过(﹣1,0)与(3,0)两点,关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是5.则关于x的方程ax2+bx+c+n=0(0<n<m)有两个整数根,这两个整数根是( )A.﹣2或4B.﹣2或0C.0或4D.﹣2或5【分析】根据二次函数y=ax2+bx+c的图象经过(﹣1,0)与(3,0)两点求对称轴,后面两个方程二次项、一次项系数没变,所以两根的和也不变还是2.【解答】解:∵二次函数y=ax2+bx+c的图象经过(3,0)与(﹣1,0)两点,∴当y=0时,0=ax2+bx+c的两个根为3和﹣1,函数y=ax2+bx+c的对称轴是直线x=1,又∵关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是5.∴方程ax2+bx+c+m=0(m>0)的另一个根为﹣3,函数y=ax2+bx+c的图象开口向下,如图,∵0<n<m,∴﹣m>﹣m,∵关于x的方程ax2+bx+c+n=0 (0<n<m)有两个整数根,∴直线y=﹣n与y=ax2+bx+c的交点的横坐标为﹣2,4,∴这关于x的方程ax2+bx+c+n=0 (0<n<m)有两个整数根,是﹣2或4,故选:A.【变式3-1】(2022•潮南区模拟)已知二次函数y=ax2﹣2ax+c(a≠0)的图象与x轴的一个交点为(﹣1,0),则关于x的一元二次方程ax2﹣2ax+c=0的根是 x1=﹣1,x2=3 .【分析】利用二次函数y=ax2﹣2ax+c的解析式求得抛物线的顶点坐标,利用抛物线的对称性求得抛物线与x轴的另一个交点,再利用抛物线与x轴的交点的横坐标与一元二次方程的根的关系得出结论.【解答】解:∵y=ax2﹣2ax+c,=1.∴抛物线的对称轴为直线x=−−2a2a∵二次函数y=ax2﹣2ax+c(a≠0)的图象与x轴的一个交点为(﹣1,0),∴该抛物线与x轴的另一个交点为(3,0).∴关于x的一元二次方程ax2﹣2ax+c=0的根是:x1=﹣1,x2=3.故答案为:x1=﹣1,x2=3.【变式3-2】(2022•咸宁一模)已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的y与x的部分对应值如下表:x﹣5﹣4﹣202y60﹣6﹣46则关于x的一元二次方程ax2+bx+c=0的根是 x1=﹣4,x2=1 .【分析】由抛物线经过点(﹣5,6),(2,6)可得抛物线对称轴,根据抛物线对称性及抛物线经过(﹣4,0)求解.【解答】解:由抛物线经过点(﹣5,6),(2,6)可得抛物线抛物线对称轴为直线x=−522=−32,∵抛物线经过(﹣4,0),对称轴为直线x=−32,∴抛物线经过(1,0),∴一元二次方程ax2+bx+c=0的根是x1=﹣4,x2=1.故答案为:x1=﹣4,x2=1.【变式3-3】(2022•永嘉县校级模拟)已知二次函数y=﹣x2+bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )A.5B.7C.12D.﹣7【分析】先由二次函数y=﹣x2+bx+c的图象经过(﹣1,0)与(5,0)两点,求出b、c,再把b、c代入方程﹣x2+bx+c+d=0后,由方程的根是6求出d.【解答】解:∵二次函数y=﹣x2+bx+c的图象经过(﹣1,0)与(5,0)两点,∴−1−b+c=0−25+5b+c=0,解得:b=4 c=5,将b=4,c=5代入方程﹣x2+bx+c+d=0,可得:﹣x2+4x+5+d=0,又∵关于x的方程﹣x2+4x+5+d=0有两个根,其中一个根是6,∴把x=6代入方程﹣x2+4x+5+d=0,得:﹣36+4×6+5+d=0,解得:d=7,经验证d=7时,Δ>0,符合题意,∴d=7.故选:B.【题型4 由二次函数的图象求一元二次方程的近似解】【例4】(2022•平度市期末)如表给出了二次函数y=x2+2x﹣10中x,y的一些对应值,则可以估计一元二次方程x2+2x﹣10=0的一个近似解为( )x… 2.1 2.2 2.3 2.4 2.5…y…﹣1.39﹣0.76﹣0.110.56 1.25…A.2.2B.2.3C.2.4D.2.5【分析】根据函数值,可得一元二次方程的近似根.【解答】解:如图:x=2.3,y=﹣0.11,x=2.4,y=0.56,x2+2x﹣10=0的一个近似根是2.3.故选:B.【变式4-1】(2022•灌云县期末)已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解的范围是 6.18<x<6.19 .x 6.17 6.18 6.19 6.20y﹣0.03﹣0.010.020.04【分析】根据表格中自变量、函数的值的变化情况,得出当y=0时,相应的自变量的取值范围即可.【解答】解:由表格数据可得,当x=6.18时,y=﹣0.01,当x=6.19时,y=0.02,于是可得,当y=0时,相应的自变量x的取值范围为6.18<x<6.19,故答案为:6.18<x<6.19.【变式4-2】(2022•渠县一模)如图,是二次函数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是 x1=0.8,x2=3.2合理即可 .(精确到0.1)【分析】直接利用抛物线与x 轴交点的位置估算出两根的大小.【解答】解:由图象可知关于x 的一元二次方程ax 2+bx =c 的两个根可能是:x 1=0.8,x 2=3.2合理即可.故答案为:x 1=0.8,x 2=3.2合理即可.【变式4-3】(2022秋•萍乡期末)代数式ax 2+bx +c (a ≠0,a ,b ,c 是常数)中,x 与ax 2+bx +c 的对应值如下表: x ﹣1−12 0121 322 523ax 2+bx +c﹣2−141742741−14 ﹣2请判断一元二次方程ax 2+bx +c =0(a ≠0,a ,b ,c 是常数)的两个根x 1,x 2的取值范围是下列选项中的( )A .−12<x 1<0,32<x 2<2B .﹣1<x 1<−12,2<x 2<52C .−12<x 1<0,2<x 2<52D .﹣1<x 1<−12,32<x 2<2【分析】观察表格可知,在x <1时,随x 值的增大,代数式ax 2+bx +c 的值逐渐增大,x 的值在−12~0之间,代数式ax 2+bx +c 的值由负到正,故可判断ax 2+bx +c =0时,对应的x 的值在−12~0之间,在x >1时,随x 的值增大,代数式ax 2+bx +c 逐渐减小,x 的值在2~52之间,代数式ax 2+bx +c 的值由正到负,故可判断ax 2+bx +c =0时,对应的x 的值在2~52之间,【解答】解:根据表格可知,代数式ax 2+bx +c =0时,对应的x 的值在−12~0和2~52之间,即:一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是−12<x1<0,2<x2<52故选:C.【题型5 由二次函数的图象解不等式】【例5】(2022秋•垦利区期末)如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c<n的解集为( )A.x>﹣1B.x<3C.﹣1<x<3D.x<﹣3或x>1【分析】由抛物线与直线交点横坐标确定直线在抛物线上方时x的取值范围.【解答】解:∵A(﹣1,p),B(3,q),∴﹣1<x<3时,直线在抛物线上方,即﹣1<x<3时,ax2+c<mx+n,∴不等式ax2﹣mx+c<n的解集为﹣1<x<3.故选:C.【变式5-1】(2022•定远县二模)抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…请求出当y<0时x的取值范围 x<﹣2或x>3 .【分析】把点(0,6)代入求出c,把点(﹣1,4)和(1,6)代入抛物线的解析式列方程组,解出可得a、b,即可得抛物线的解析式,进而可列不等式求出y<0时x的取值范围.【解答】解:由表得,抛物线y=ax2+bx+c(a≠0)过点(0,6),∴c=6,∵抛物线y=ax2+bx+6过点(﹣1,4)和(1,6),∴a−b+6=4a+b+6=6,解得:a=−1 b=1,∴二次函数的表达式为:y=﹣x2+x+6,所以令﹣x2+x+6<0,解得:x<﹣2或x>3.故答案为:x<﹣2或x>3.【变式5-2】(2022•工业园区校级模拟)若二次函数y=ax2+bx+c(a、b、c为常数)的图象如图所示,则关于x的不等式a(x+2)2+b(x+2)+c<0的解集为 x<﹣1或x>1 .【分析】根据图象可得x<1或x>3时ax2+bx+c<0,则a(x+2)2+b(x+2)+c<0时x+2<1或x+2>3,进而求解.【解答】解:由图象可得x<1或x>3时ax2+bx+c<0,∴当a(x+2)2+b(x+2)+c<0时,x+2<1或x+2>3,解得x<﹣1或x>1,故答案为:x<﹣1或x>1.【变式5-3】(2022•驿城区校级期末)如图,二次函数y=x2﹣4x+m的图象与y轴交于点C,点B是点C 关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.则满足kx+b≥x2﹣4x+m的x的取值范围是( )A.x≤1或x≥4B.1≤x≤4C.x≤1或x≥5D.1≤x≤5【分析】由二次函数解析式可得抛物线对称轴为直线x=2,从而可得点B横坐标,进而求解.【解答】解:∵y=x2﹣4x+m,∴抛物线对称轴为直线x=2,∵点B和点C关于直线x=2对称,∴点B横坐标为4,∵点A横坐标为1,∴1≤x≤4时,kx+b≥x2﹣4x+m,故选:B.【题型6 由二次函数与一次函数交点个数求范围】【例6】(2022•虞城县三模)已知抛物线y=a(x﹣2)2+c(a>0).(1)若抛物线与直线y=mx+n交于(1,0),(5,8)两点.①求抛物线和直线的函数解析式;②直接写出当a(x﹣2)2+c>mx+n时自变量x的取值范围.(2)若a=c,线段AB的两个端点坐标分别为A(0,3),B(3,3),当抛物线与线段AB有唯一公共点时,直接写出a的取值范围.【分析】(1)①利用待定系数法求解析式即可,②抛物线开口向上,数形结合直接写出答案;(2)结合抛物线和线段AB,分情况讨论求a的取值范围.【解答】解:(1)①∵抛物线y=a(x﹣2)2+c与直线y=mx+n交于(1,0),(5,8)两点,∴a+c=09a+c=8,m+n=05m+n=8,解得a=1c=−1,m=2n=−2,∴抛物线和直线的函数解析式分别为y=(x﹣2)2﹣1,y=2x﹣2.②∵a>0,抛物线开口向上,抛物线与直线y=mx+n交于(1,0),(5,8)两点,∴当a(x﹣2)2+c>mx+n时自变量x的取值范围为x<1或x>5.(2)若a=c,则抛物线y=a(x﹣2)2+a(a>0),∴开口向上,对称轴为x=2,顶点坐标为(2,a),当抛物线顶点在线段AB上时有唯一公共点,此时a=3,当抛物线顶点在线段AB下方时,当经过B(3,3)时,a+a=3,解得a=32,当经过A(0,3)时,4a+a=3,解得a=35,∴当抛物线与线段AB有唯一公共点时,a的取值范围为35≤a<32或a=3.【变式6-1】(2022•余姚市一模)已知:一次函数y1=2x﹣2,二次函数y2=﹣x2+bx+c(b,c为常数),(1)如图,两函数图象交于点(3,m),(n,﹣6).求二次函数的表达式,并写出当y1<y2时x的取值范围.(2)请写出一组b,c的值,使两函数图象只有一个公共点,并说明理由.【分析】(1)将(3,m),(n,﹣6)代入直线解析式求出点坐标,然后通过待定系数法求解,根据图象可得y1<y2时x的取值范围.(2)﹣x2+bx+c=2x﹣2,由Δ=0求解.【解答】解:(1)将(3,m)代入y1=2x﹣2得m=6﹣2=4,将(n,﹣6)代入y1=2x﹣2得﹣6=2n﹣2,解得n=﹣2,∴抛物线经过点(3,4),(﹣2,﹣6),将(3,4),(﹣2,﹣6)代入y2=﹣x2+bx+c得4=−9+3b+c−6=−4−2b+c,解得b=3 c=4,∴y=﹣x2+3x+4,由图象可得﹣2<x<3时,抛物线在直线上方,∴y1<y2时x的取值范围是﹣2<x<3.(2)令﹣x2+bx+c=2x﹣2,整理得x2+(2﹣b)x﹣(2+c)=0,当Δ=(2﹣b)2+4(2+c)=0时,两函数图象只有一个公共点,∴b=2,c=﹣2,满足题意.【变式6-2】(2022•河南模拟)小新对函数y=a|x2+bx|+c(a≠0)的图象和性质进行了探究.已知当自变量x的值为0或4时,函数值都为﹣3;当自变量x的值为1或3时,函数值都为0.探究过程如下,请补充完整.(1)这个函数的表达式为 y=|x2﹣4x|﹣3 ;(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质: 函数关于直线x=2对称 ;(3)进一步探究函数图象并解决问题:①直线y=k与函数y=a|x2+bx|+c有三个交点,则k= 1 ;②已知函数y=x﹣3的图象如图所示,结合你所画的函数图象,写出不等式a|x2+bx|+c≤x﹣3的解集: x=0或3≤x≤5 .【分析】(1)将x=0,y=﹣3;x=4,y=﹣3;x=1,y=0代入y=a|x2+bx|+c(a≠0),得到:c=﹣3,b=﹣4,a=1,即可求解析式为y=|x2﹣4x|﹣3;(2)描点法画出函数图象,函数关于x=2对称;(3)①从图象可知:当x=2时,y=1,k=1时直线y=k与函数y=|x2﹣4x|﹣3有三个交点;②y=x﹣3与y=x2﹣4x﹣3的交点为x=0或x=5,结合图象,y=|x2﹣4x|﹣3≤x﹣3的解集为3≤x≤5.【解答】解:(1)将x=0,y=﹣3;x=4,y=﹣3;x=1,y=0代入y=a|x2+bx|+c(a≠0),得到:c=﹣3,b=﹣4,a=1,∴y=|x2﹣4x|﹣3,故答案为:y=|x2﹣4x|﹣3;(2)如图:函数关于直线x=2对称,故答案为:函数关于直线x=2对称;(3)①当x=2时,y=1,∴k=1时直线y=k与函数y=|x2﹣4x|﹣3有三个交点,故答案为1;②y=x﹣3与y=|x2﹣4x|﹣3的交点为x=0或x=3,结合图象,y=|x2﹣4x|﹣3≤x﹣3的解集为x=0或3≤x≤5,故答案为:x=0或3≤x≤5.x+t与函数y=【变式6-3】(2022•海珠区一模)令a、b、c三个数中最大数记作max{a,b,c},直线y=12 max{﹣x2+4,x﹣2,﹣x﹣2}的图象有且只有3个公共点,则t的值为 1或65 .16【分析】只需画出函数y=max{﹣x2+4,x﹣2,﹣x﹣2}的图象,然后结合图象并运用分类讨论的思想,就可解决问题.【解答】解:在直角坐标系中画出函数y=max{﹣x2+4,x﹣2,﹣x﹣2}的图象,如图所示.当直线y =12x +t 经过(﹣2,0)或与抛物线y =﹣x 2+4相切时,直线y =12x +t 与函数y =max {﹣x 2+4,x ﹣2,﹣x ﹣2}的图象有且只有3个公共点.①若直线y =12x +t 经过(﹣2,0),则有0=12×(﹣2)+t ,解得t =1;②若直线y =12x +t 与抛物线y =﹣x 2+4相切,则关于x 的方程12x +t =﹣x 2+4即x 2+12x +t ﹣4=0有两个相等的实数根,则△=(12)2﹣4×1×(t ﹣4)=0,解得t =6516.综上所述:t =1或6516.故答案为1或6516.。
人教版九年级数学上册《二次函数与一元二次方程》二次函数PPT优秀课件
函数
与一元二次方程
人教版九年级上册数学
回顾旧知
二次函数的一般式:
y ax2 bx c (a≠0)
___x___是自变量,__y__是__x__的函数。
当 y = 0 时, ax²+ bx + c = 0
ax²+ bx + c = 0
这是什么方程? 一元二次方程与二次函数 有什么关系?
上一章中我们学习了“一元二次方程”
当球飞行 0s 和 4s 时,它的高度为 0m ,即 0s时,球从地面飞出,4s 时球落回地面。
探究
下列二次函数的图象与 x 轴有交点吗? 若有,求出交点坐标.
(1) y = 2x2+x-3
y
(2) y = 4x2 -4x +1
(3) y = x2 – x+ 1
o
x
令 y= 0,解一元二次方程的根
实际问题
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的 飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题: (1)球的飞行高度能否达到 15 m? 若能,需要多少时间? (2)球的飞行高度能否达到 20 m? 若能,需要多少时间? (3)球的飞行高度能否达到 20.5 m?为什么? (4)球从飞出到落地要用多少时间?
探究
(1) y = 2x2+x-3 y
解:当 y = 0 时, 2x2+x-3 = 0
(2x+3)(x-1) = 0
3
o
x 1 =- ,x 2 = 1
x
2
所以与 x 轴有交点,有两个交点。
九年级数学二次函数与一元二次方程(含答案)
学生做题前请先回答以下问题问题1:二次函数与一元二次方程之间的关系:①一元二次方程的根是二次函数的图象与_____________;当时,二次函数图象与x轴有_____个交点;当时,二次函数图象与x轴有_____个交点;当时,二次函数图象与x轴_______交点.②方程的根是对应的________________,求两个函数交点的坐标就是求对应方程组的解.问题2:结合一次函数、反比例函数以及二次函数的性质,思考函数y值比大小,主要利用函数的________和数形结合;两函数值比大小,借助数形结合,_____________________.二次函数与一元二次方程一、单选题(共10道,每道10分)1.若关于x的二次函数的图象与x轴仅有一个公共点,则k的取值范围是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:二次函数图象与方程、不等式2.如图是二次函数(a,c为常数,)与一次函数(k,b为常数,)的图象,方程的解为_______;不等式的解集为_________.( )A.;B.;C.;D.;答案:A解题思路:试题难度:三颗星知识点:数形结合思想3.已知二次函数中,函数y与自变量x的部分对应值如下表:则当时,x的取值范围是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:二次函数的对称性4.若一元二次方程的两个实数根分别为,则实数的大小关系为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:二次函数图象上点的坐标特征5.已知二次函数的图象与x轴交于两点,且,则实数的大小关系为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:二次函数图象平移6.方程的根有( )个.A.0B.1C.2D.3答案:B解题思路:试题难度:三颗星知识点:数形结合思想7.方程的根的个数为( )个A.1B.2C.3D.4答案:C解题思路:试题难度:三颗星知识点:数形结合思想8.已知函数,当直线y=k与此图象有两个公共点时,k的取值范围是( )A. B.C. D.或k=-1答案:D解题思路:试题难度:三颗星知识点:数形结合思想9.关于x的一元二次方程的两个不相等的实数根都在-1和0之间(不包括-1和0),则a取值范围是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:数形结合的思想10.方程(k是实数)有两个实根,且,那么k的取值范围是( ) A. B. C. D.无解答案:C解题思路:试题难度:三颗星知识点:数形结合的思想第11页共11页。
沪科版数学九年级上册21.3二次函数与一元二次方程 课件(共24张PPT)
21.3 二次函数与一元二次方程
学习目标
学习重难点
重点
难点
1.理解二次函数与一元二次方程(不等式)的关系.2.能运用二次函数及其图象、性质确定方程的解.3.了解用图象法求一元二次方程的近似根的方法.
二次函数图象、性质确定方程的解.
二次函数与一元二次方程(不等式)的关系.
D
C
3.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.解:当k=3时,函数y=2x+1是一次函数.∵一次函数y=2x+1与x轴有一个交点,∴k=3;当k≠3时,y=(k-3)x2+2x+1是二次函数.∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,∴Δ=b2-4ac≥0.∵b2-4ac=22-4(k-3)=-4k+16,∴-4k+16≥0. ∴k≤4且k≠3.综上所述,k的取值范围是k≤4.
归纳小结
1.二次函数与一元二次方程的关系: 一般地,关于x的一元二次方程 的根,就是二次函数 的值为0时自变量x的值,也就是函数 的图像与x轴交点的横坐标.2.二次函数 与x轴交点个数的确定. 可有一元二次方程的根的判别式来表示判定二次函数图象与x轴的交点的情况,由根与系数的关系来解决相关问题.在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程.
思 考: 如何利用二次函数求一元二次方程的近似解.例:求一元二次方程x2+2x-1=0的根的近似值(精确到 0.1). 分析:一元二次方程x²+2x-1=0的根就是抛物线y=x²+2x-1与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
想一想:观察下列二次函数,图象与x轴有公共点吗? 如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?(1) y=x2+x-2.(2)y=x2-6x+9.(3)y=x2-x+1.
人教版数学九年级上册22.2 二次函数和一元二次方程课件(共55张PPT)
例如,已知二次函数 y = -x2+4x 的值为3,求自变量 x 的值, 可以解一元二次方程-x2+4x=3 ( 即x2-4x+3=0 ). 反过来,解方程 x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自 变量x的值,还可以看做y = -x2+4x 和y=3的交点
x
-1
-2
-3
-4 -5
当x1=x2=-3时,函数值为0.
二、利用一元二次方程讨论二次函数与x轴的交点
思考
问题1 不解方程,判断下列一元二次方程根的情况. (1)x2+x-2=0; ∵∆ = b2-4ac=9>0,∴方程有两个不相等的实数根. (2)x2-6x+9=0; ∵∆ = b2-4ac=0,∴方程有两个相等的实数根. (3)x2-x+1=0. ∵∆ = b2-4ac=-3<0,∴方程有没有实数根.
公共点的坐标.
(1)y=x2+x-2;
y
两个(-2,0),(1,0)
2 1
-2 -1 O 1 2 x
-1
-2
(2)y=x2-6x+9;
y 4
一个(3,0)
3
2
1
-1 O 1 2 3 4
x
(3)y=x2-x+1
y 4
没有公共点
3
2 1
-1 O 1 2
x
二次函数图象与x轴的公共点我们也可以通过平移来观察,发现最多有两 个公共点,最少没有公共点.
O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)利用图象或将t =7代入
h=-5t 2+40t 中都可以得到:当t =7 秒时,小球距地面的高度时35m。 (2)方程-5t2+40t=75的根的实际 意义是小球的高度为75m时所运动 的时间。
-----------------------------------
拓展提高
(3)何时小球离地面的高度是60m? 与同学进行交流。
探索研究
一元二次方程ax2+bx+c =0有两个不相等的实数根,你又能得 到什么呢? 可以知道:二次函数y=ax2+bx+c的图象与x轴有两个交点。 一元二次方程ax2+bx+c=0有两个相等的实数根,那么二次 函数y=ax2+bx+c的图象与x轴有一个交点。 一元二次方程ax2+bx+c没有实数根,那么二次函数y=ax2 +bx+c的图象与x轴没有交点。
例题
例 不画图象,判断下列函数的图象与x轴是否有公 共点,并说明理由。
(1) y 2x2 3x 4 2 (2) y 3x x 1
解: (1)由 2 x 2 3x 4 0得 b 4ac 3 4 2 4 41 0
2 2
(2)由 3 x 2 x 1 0得
问题情境
一个小球从地面以一定的速度竖直向上抛起,小球的高度h(m) 与运动时间t(s)之间的关系为二次函数 h=-5t 2+40t ,其函数 图象如下图所示. 请问小球经过多少秒后落地?与同学进行交流。 解:方法一:利用函数图象解决问题。
图象与x轴的交点坐标为(0,0) (8,0),可知小球经过8秒后落地。
方法二:利用一元二次方程解决问题。 由h=0可得方程: -5t 2+40t =0。解得:t1=0,t2=8,可知 小球经过8秒后落地。
第六章 二次函数
6.3 二次函数与一元二次方程
探索研究
二次函数与一元二次方程有怎样的关系?
y=x2-2x-3 (1)观察:二次函数y=x2-2x-3的图象 与x轴有几个交点?你能说出交点的 坐标吗?
∴此方程有两个不相等的实数根. ∴该抛物线与x轴有两个交点。
b 2 4ac 12 4 3 1 11 0
∴此方程没有实数根. ∴该抛物线与x轴没有公共点。
练一练
y =ax2+bx+c
1、根据图象提供的信息写 出一元二次方程 ax2+bx+c=0 x2 = 0 。 的根:x 1=-2, ━━━━━━━━━━━━。 2、二次函数 y =x2-5x+6的图象 两 个交点,交点坐标是 与x轴有━━━
探索研究
一般地二次函数y=ax2+bx+c的图象与一元二次方程
ax2+bx+c =0的根有什么关系呢?
二次函数y=ax2+bx+c 的图象与x轴有两个交点,那么一元 二次方程ax2+bx+c =0有两个不相等的实数根。 二次函数y=ax2+bx+c的图象与x轴有一个交点,那么一元二 次方程ax2+bx+c =0有两个相等的实数根。 二次函数y=ax2+bx+c的图象与x轴没有交点,那么一元二 次方程ax2+bx+c =0没有实数根。
h=-5t2+40t
-----------------------
方法一:从图象上看,就是图象 上纵坐标为60的点的横坐标。 因此当t=2秒或t=6秒时,小 球离地面的高度是60m。
-----------------------------
-----------------------------
(3)何时小球离地面的高度是60m?
交点的坐标是(-1,0),(3,0)。
(2)思考:利用交点的坐标你能 说出x取何值时,y=0吗? 当x=-1时,y=0;当x=3时,y=0。 (3)探究:你能说出一元二次方程 x 2 -2x -3=0的根吗? 一元二次方程 x2-2x - 3=0的根为x1=-1,x2=3。
探索研究
y=x2-6x+9 y=x2-2x+3
类似的,你能利用二次函数y=x2-6x+9的图象研究一元二 次方程x2-6x+9=0的根的情况吗?一元二次方程x2-2x+3=0呢? 二次函数y=x2-6x+9的图象与x轴有一个交点:(3,0), 一元二次方程x2-6x+9=0有两个相等的实数根:x1=x2=3。
二次函数y=x2-2x+3的图象与x轴没有交点, 一元二次方程x2-2;40t
方法二:解方程-5t2+40t=60. 得t1=2,t2=6. 所以,当小球被抛出2秒和6秒 时离地面的高度是60m.
回顾小结
通过这节课的学习: 我发现了…… 我学会了……
作业:P33 –P34 4 ,7
; / 除尘器布袋 骨架 脉冲阀uv光氧 除尘器厂家
━━━━━━━━━━━━━━。
( 2 , 0 ) , ( 3, 0)
3、课本P22 练习1,2.
拓展提高
在本节一开始的小球上抛问题中, 请问: (1)当t=7秒时,小球距地面的高度是多少? (2) 方程 -5t 2+40 t =75的根的实际意义是什么?
h=-5t 2+40t
----------------------------
uyd08vau
听。但她没有想到的是,乔氏听着听着,就忍不住咯咯咯地笑起来,她压地嗓音对女儿说:“好你一个死丫头啊,我当是什么 事情呢!你也真够小气的了,耿正他们知道什么啊。再说了,人家也没有说什么啊。大家的对话多好啊!”小青拽着乔氏的胳 膊撒娇,嗲声嗲气地说:“姆妈,人家都气死了,你还这样说话!”乔氏用右手的食指头点着小青的鼻子,小声儿发狠说: “记着啊,以后可不许这样了。再这样小家子气,看谁还会喜欢你!”小青怯怯地小声说:“我承认错了还不行吗?姆妈,我 答应你,以后再也不这样了。就是,我自己也感觉很不好呢,现在很后悔的。但就是不清楚,当时为什么要那样子说话呢。唉, 真是的,我都气死自己了!”乔氏又开始心痛女儿了,伸手爱抚地摸一摸这心肝儿宝贝好看的脸蛋儿,哄她说:“好啦,好啦, 知道错了就行了。今儿个罚你帮我做晚饭!”109第三十三回 亮家累垮耿老爹|(周密细致巧安排,亮家效果颇满意;只因程 序太紧张,生生累垮耿老爹。)午饭后,亮家程序正式开始了。这一程序首先需要做的,是必须将石灰泥搅拌好,这可是一个 一点儿也马虎不得的活计。耿老爹一边示范着一边给小青和耿正兄妹三人讲:“榆皮毛拉絮必须要事先泡透了。拉絮泡透了之 后,用手攥一攥,感觉很柔软;如果不够柔软,就必须继续泡,一直到泡透了为止。你们都来攥一攥,看看这些拉絮是不是足 够柔软了?”大家都用手攥一攥,感觉已经很柔软了。耿老爹:“记住了,必须泡到这么柔软才行!”大家都点点头说:“唔, 记住了!”耿老爹又说:“这样,把一大桶石灰膏全部铲到搅拌盆内。注意啊,一定要一边放石灰膏,一边往里边加这些泡透 了的榆皮毛拉絮。估计着,石灰膏全部放进搅拌盆里了,榆皮毛拉絮也差不多加完了,这样最好。还有,用小铲子把木桶里的 石灰膏全部刮干净了,不要浪费。然后,用小铲子和大木棍充分地翻动、搅拌,直到把石灰膏和榆皮毛拉絮充分搅拌均匀,并 且石灰泥柔软适度;如果石灰泥感觉僵硬,可以适当加入少量的清水,直到柔软适度为止。”耿老爹一边说着,一边用小铲子 上下翻动盆里的石灰膏,然后用力搅拌;再翻动,再搅拌;一直到一点儿也看不出来一点点的榆皮毛拉絮了。此时,加入了榆 皮毛拉絮的石灰膏变成了多半盆柔软适度的石灰泥。耿老爹这才说:“翻动搅拌到这个程度就可以了。”大家都试着翻动搅拌 几下。看着四个小家伙都翻动搅拌过了,耿老爹又说:“石灰泥不能一次搅拌太多,必须用完一桶,再搅拌一桶。因为搅拌好 的石灰泥如若不能够很快用完,就会变僵硬了。倘若变僵硬了,短时间内尚可以再次搅拌使其软化;如若时间长了,就只能弃 之不用了。”大家都说:“记住
