自然数的字母符号
数学中一些常用的数集及其记法

数学中一些常用的数集及其记法大家好!今天咱们来聊聊数学中那些数集的事儿。
听到“数集”这俩字,别以为它们是啥高深的数学术语,其实它们跟我们平常生活中见到的数字关系密切。
你瞧,数学可不是冷冰冰的,它也有它的“小伙伴”,咱们一起来看看吧!1. 自然数(N)1.1 什么是自然数?自然数就是咱们平时最常用的数,从1开始,1, 2, 3,一直到无穷大。
想想你小时候数数,一二三四五就是自然数。
这些数在数学里起着基础性的作用,仿佛是数的“开山祖师”。
1.2 自然数的记法通常用大写字母N来表示自然数。
看起来简单,却是数学的“基石”。
有时我们会用“ℕ”来表示,它和N基本一样,只不过多了点艺术感。
2. 整数(Z)2.1 整数的介绍整数包括了所有的自然数,还加上了它们的负数,比如1, 2, 3,还有0。
这些数就像咱们的生活一样,有起有落,有正有负。
整整齐齐的整数帮我们解决了很多问题,比如负债、温度的变化等。
2.2 整数的记法整数用大写字母Z表示,源于德语中的“Zahlen”,意为“数”。
看到这个字母,你就知道它代表了所有整整齐齐的数,不管是正的还是负的。
3. 有理数(Q)3.1 有理数的定义有理数就是可以表示成两个整数比值的数,比如1/2,3/4,甚至是5(它可以写作5/1)。
简单来说,就是那些可以用分数形式表达的数。
它们就像是数学里的“分割师”,把大数拆成小块,更容易操作。
3.2 有理数的记法有理数用大写字母Q表示,来自于“Rational”的首字母。
Q就像是数学里的万能钥匙,帮我们打开了数的世界。
4. 无理数(I)4.1 无理数的特点无理数是那些不能用简单的分数表示的数,比如π(圆周率)和√2(根号2)。
它们的十进制表示方式是无限不循环的,像是数学里的“小怪兽”。
这些数不易把握,却是数学世界中不可或缺的一部分。
4.2 无理数的记法无理数的记法就比较“神秘”了,通常没有单独的字母来表示,不过我们会用符号来代表它们。
例如π和√2就是直接用符号表达的。
集合数学知识点高一字母

集合数学知识点高一字母数学是一门广阔而深奥的学科,其中集合论是数学领域中的一块重要内容。
集合是数学中最基本的概念之一,它可以简单理解为具有共同特征的一组事物的总称。
在集合论中,字母常常被用来表示集合的名称,不同字母代表着不同的集合。
本文将通过讨论一些高一常见的字母表示的集合,来探讨集合数学的相关知识。
1. 自然数集N自然数是人类最早使用的一组数,表示为1、2、3、4……N。
自然数集合被标记为字母N,它包含了所有正整数。
自然数集合是一个无限集合,它的元素个数是无穷多个。
2. 整数集Z整数是由正整数、零和负整数组成的数集,用Z表示。
整数集合包括了所有整数,正负无穷。
整数集合是一个有序集合,它的元素包含了自然数集合中的所有元素,并且包括了负整数和零。
3. 有理数集Q有理数集合用Q表示,它是可以表示为两个整数的比值的数,其中除数不为0。
有理数集合包括了所有整数及所有分数,它是自然数集合和整数集合的超集。
有理数集合是一个有序集合,它可以用分数的形式来表示。
4. 实数集R实数集合用字母R表示,它由所有有理数和无理数组成。
实数集合包括了所有的小数和无限不循环小数,如π(圆周率)和√2等。
实数集合是数学中最常见的一个集合,它是自然数集合、整数集合和有理数集合的超集。
5. 复数集C复数集合用C表示,它由实数集合中的所有实数和虚数组成。
虚数是不能表示为实数形式的数,它的平方是一个负数。
复数集合是用实部和虚部组成的,例如a+bi,其中a和b分别是实数。
复数集合是数学中一个非常重要的集合,它在代数等领域有着广泛的应用。
除了上述几个常见的字母表示的集合外,数学中还有其他一些字母表示的集合,如集合论中常用的字母E表示全集,U表示并集,∩表示交集,∪表示非空集合的并集等。
这些字母和符号都有各自明确的数学定义和用法,用来描述集合的关系和运算。
集合数学是数学中的一个重要分支,它涉及到了多个学科领域,如代数、几何、概率论等。
通过了解和学习集合数学,我们能够更好地理解和应用数学知识,提高数学问题的解决能力。
数学集合字母

数学集合字母数学中有许多用于表示集合的字母,这些字母不仅仅是为了方便表示数学概念,更是为了使我们更好地理解和应用数学原理。
下面将介绍一些常见的集合字母及其含义,帮助我们更好地理解数学集合的概念和运用。
首先,让我们来介绍一些常见的集合符号。
大写字母N代表自然数集合,即{0, 1, 2, 3, ...},它包括了所有正整数和零。
大写字母Z代表整数集合,即{..., -3, -2, -1, 0, 1, 2, 3, ...},它包括了所有的正整数、零和负整数。
大写字母Q代表有理数集合,即可以表示为两个整数比的数,例如1/2、-3/4等。
大写字母R代表实数集合,它包括了所有的有理数和无理数,例如π、√2等。
而大写字母C代表复数集合,它包括了所有的形式为a+bi的数,其中a和b都是实数,而i是虚数单位。
除了常见的数集合字母外,数学中还有一些表示特殊集合的字母。
例如,大写字母U表示并集,表示合并两个或多个集合中的所有元素,例如A∪B表示A和B两个集合的并集。
大写字母∩表示交集,表示两个或多个集合中共有的元素,例如A∩B表示A和B两个集合的交集。
而大写字母∈表示属于,用来说明一个元素是否属于某一个集合,例如a∈A表示元素a属于集合A。
另外,大写字母∅表示空集,即不包含任何元素的集合。
对于集合中的元素,我们可以使用小写字母来表示。
例如,小写字母a、b、c等常用于表示集合中的具体元素。
而对于表示集合的字母,可以使用大写字母,例如A、B、C等。
我们可以使用数学符号来描述集合,例如用花括号{}来表示集合中的元素,用逗号分隔每个元素。
例如,集合A={1, 2, 3}表示A由元素1、2、3组成。
集合字母在数学中具有重要的指导意义。
通过使用集合字母,我们可以清晰地描述和表示数学概念,使其更加生动和具体。
例如,当我们学习数论时,使用自然数集合N可以方便地表示问题中涉及到的正整数和零;当我们研究解析几何问题时,使用实数集合R可以表示问题中的点的位置和距离。
数学中数的分类及符号

数学中数的分类及符号
数学里,常用一些特定的大写英文字母来表示某些常见数集。
高中数学里的常见数集及其字母表示(符号表示)分别如下:
中学数学常见数集的符号表示
(1)正整数集:所有正整数构成的集合。
正整数包括:1,2,3,4,5,……。
正整数集的集合符号为:N+(注:“+”为下标),也可记为N*(注:“*”为上标)。
(2)自然数集:不小于0的所有整数构成的数集,也称为“非负整数集”。
自然数(非负整数)包括:0,1,2,3,4,5,……。
自然数集的集合符号为:N。
(3)整数集:所有整数构成的集合。
整数包括:0,±1,±2,±3,±4,±5,……。
整数集的集合符号为:Z。
(4)有理数集:所有有理数构成的集合。
有理数包括:整数、分数、有限小数、无限循环小数等。
有理数集的集合符号为:Q。
(5)实数集:所有实数构成的集合。
实数包括:有理数、无理数。
实数集的集合符号为:R。
(6)复数集:所有复数构成的集合。
复数包括:实数、虚数。
复数集的集合符号为:C。
常见数集符号、含义及记忆法

Prime?number Odd?number? Even?number? Complex?number
因数只有两,自身以及 1
2k+1 k 是整数 乘方符号问题 2k k 是整数
有 i 存在即为复数
数集的扩张史: 数字刚刚诞生的时候,人们给他起了个好听的名字— 自然。 人们结绳计数,记录打了几只野鸡,摘了多少苹果,排列谁是老
无理数吸收后,他构成了一根横贯前后的数轴。就这样实数出现在了人们的面前。
7
质数
8
奇数
9
偶数
10 复数
一个大于 1的自然数,除了 1和它自身外,
P
不能整除其他自然数叫作质数,又称素数
否则称为合数。
O
又称单数, 整数 中,不能被 2整除的数是奇数,
E
又称双数,整数中,能被 2整除的数是偶数,
C
形如 z=a+bi (a,b均为实数)的数称为复数, 其中 a称为实部, b称为虚部, i 称为虚数单位
Rational number 这个词来源于古希腊,其英文词 根为 ratio,就是比率的意思。用 商的英文 Quotient表示。
整数的扩张,整数 +分数
常见的无理数有非完全平方数 π=3.141
的平方根、 π和e
e=2.718
6
实数
R
有理数 +无理数
Real number
实数和数轴上的点一一对应。
序号 名称 1 自然数 2 正整数
3
整数
符号
意义
N
1 、表示物体 个数和顺序 的数; 2 、0 + 正整数
N*或N+ 除去“ 0”的自然数
正整数 + 零 + 负整数 Z
常见数集符号、含义及记忆法
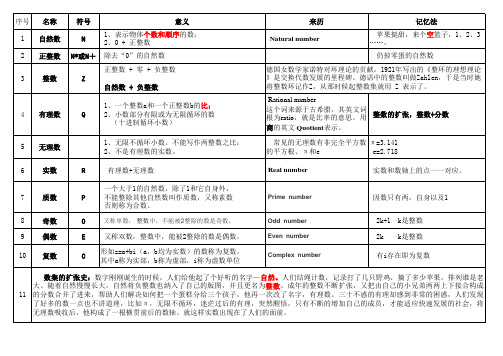
这个词来源于古希腊,其英文词 根为ratio,就是比率的意思。用
整数的扩张,整数+分数
商的英文 Quotient表示。
常见的无理数有非完全平方数 π=3.141
的平方根、π和e
e=2.718
6 实数
R
有理数+无理数
Real number
实数和数轴上的点一一对应。
7 质数
8 奇数 9 偶数 10 复数
序号 名称 1 自然数 2 正整数数和顺序的数; 2、0 + 正整数
N*或N+ 除去“0”的自然数
正整数 + 零 + 负整数 Z
自然数 + 负整数
4 有理数
1、一个整数a和一个正整数b的比;
Q
2、小数部分有限或为无限循环的数
(十进制循环小数)
5 无理数
1、无限不循环小数。不能写作两整数之比; 2、不是有理数的实数。
一个大于1的自然数,除了1和它自身外,
P
不能整除其他自然数叫作质数,又称素数
否则称为合数。
O
又称单数, 整数中,不能被2整除的数是奇数,
E
又称双数,整数中,能被2整除的数是偶数,
C
形如z=a+bi(a,b均为实数)的数称为复数, 其中a称为实部,b称为虚部,i称为虚数单位
Prime number
Odd number Even number Complex number
来历
记忆法
Natural number
苹果挺甜,来个空篮子,1、2、3 ……。
仍掉零蛋的自然数
德国女数学家诺特对环理论的贡献,1921年写出的《整环的理想理论 》是交换代数发展的里程碑。德语中的整数叫做Zahlen,于是当时她 将整数环记作Z,从那时候起整数集就用 Z 表示了。
自然数

自然数自然数:用以计量事物的件数或表示事物次序的数。
即用数码0,1,2,3,4,…所表示的数。
表示物体个数的数叫自然数,自然数由0开始(包括0),一个接一个,组成一个无穷的集体。
分类①按能否被2整除分②按因数数个数分关于0 ,2,3,5数学术语自然数集:常用大写字母N表示【英译】natural number自然数是一切等价有限集合共同特征的标记。
注:自然数就是我们常说的正整数和0。
整数包括自然数。
自然数集有加法和乘法运算,两个自然数相加或相乘的结果仍为自然数,也可以作减法或除法,但相减和自然数相除的结果未必都是自然数,所以减法和除法运算在自然数集中并不是总能成立的。
自然数是人们认识的所有数中最基本的一类,为了使数的系统有严密的逻辑基础,19世纪的数学家建立了自然数的两种等价的理论:自然数的序数理论和基数理论,使自然数的概念、运算和有关性质得到严格的论述。
自然数一定是整数。
用以计量事物的件数或表示事物次序的数。
即用数码0,1,2,3,4,……所表示的数。
表示物体个数的数叫自然数,自然数由0开始(包括0),一个接一个,组成一个无穷的集体。
序数理论是意大利数学家G.皮亚诺提出来的。
他总结了自然数的性质,用公理法给出自然数的如下定义。
自然数集N是指满足以下条件的集合:①N中有一个元素,记作1。
②N中每一个元素都能在N 中找到一个元素作为它的后继者。
③1不是任何元素的后继者。
④不同元素有不同的后继者。
⑤(归纳公理)N的任一子集M,如果1∈M,并且只要x在M中就能推出x的后继者也在N中,那么M=N。
基数理论则把自然数定义为有限集的基数,这种理论提出,两个可以在元素之间建立一一对应关系的有限集具有共同的数量特征,这一特征叫做基数。
这样,所有单元素集{x},{y},{a},{b}等具有同一基数,记作1 。
类似,凡能与两个手指头建立一一对应的集合,它们的基数相同,记作2,等等。
自然数的加法、乘法运算可以在序数或基数理论中给出定义,并且两种理论下的运算是一致的。
《用字母表示数》

用字母表示数引言在数学中,我们经常会使用数字来表示各种各样的数量。
数字是一种很方便的符号系统,可以帮助我们更好地理解和计算数学问题。
然而,除了数字以外,我们还可以使用字母来表示数。
在本文中,我们将介绍一些常用的字母符号表示数的方法。
自然数的表示首先,让我们从最基本的数开始,自然数。
自然数是从1开始的整数,用字母n来表示是一种常见的方式。
例如,我们可以用n表示1,n+1表示2,n+2表示3,以此类推。
这种表示方法可以帮助我们更直观地描述一般性质。
整数的表示在自然数的基础上,我们可以使用字母z来表示整数。
字母z一般用作整数的符号,表示一般的整数。
例如,可以用z表示0,z+1表示1,z-1表示-1,以此类推。
这种表示方法可以帮助我们更灵活地进行整数运算。
有理数的表示有理数是可以表示为两个整数的比值的数。
在有理数的表示中,我们可以使用字母q来表示有理数。
字母q一般用作有理数的符号,表示一般的有理数。
例如,可以用q表示0,q+1表示1,q-1表示-1,以此类推。
这种表示方法可以帮助我们更方便地解决有理数运算问题。
实数的表示在实数的表示中,我们可以使用字母r来表示实数。
字母r一般用作实数的符号,表示一般的实数。
例如,可以用r表示0,r+1表示1,r-1表示-1,以此类推。
这种表示方法可以帮助我们更深入地理解实数的性质和运算规律。
复数的表示在复数的表示中,我们可以使用字母a和b来表示复数的实部和虚部。
字母a 和b一般分别用作复数的实部和虚部的符号。
例如,可以用a+bi表示一个复数,其中a为实部,b为虚部。
复数的表示方法可以帮助我们更方便地进行复数运算和解决数学问题。
向量的表示在向量的表示中,我们可以使用字母v来表示向量。
字母v一般用作向量的符号,表示一般的向量。
例如,可以用v表示一个向量,其中包含多个分量。
向量的表示方法可以帮助我们更清晰地描述向量运算和解决向量相关的问题。
矩阵的表示在矩阵的表示中,我们可以使用字母M来表示矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自然数的字母符号
摘要:
I.自然数的定义和性质
A.自然数的定义
B.自然数的性质
II.自然数的字母符号表示
A.字母符号的起源
B.常见字母符号及其含义
C.字母符号在数学中的应用
III.自然数与其他数学概念的关系
A.整数与自然数
B.有理数与自然数
C.实数与自然数
IV.自然数的重要性和应用
A.自然数在数学中的基础地位
B.自然数在实际生活中的应用
C.自然数在计算机科学中的应用
正文:
自然数,也称为正整数,是指从1 开始的整数序列。
自然数具有许多基本性质,例如:每个自然数都有一个唯一的后继,0 是自然数的起点,自然数的集合是无限的等。
在数学中,自然数通常用字母"N"表示。
有时,为了表示自然数集合,我们也可以使用""这个符号。
在某些领域,如计算机科学和逻辑学,自然数也被称为“基数”(cardinal number)。
自然数在数学中具有基石的地位,许多其他数学概念都基于自然数进行扩展。
例如,整数集合包括自然数和它们的负数,有理数集合包括整数和分数,实数集合包括有理数和无理数。
此外,自然数还是皮亚诺公理(Peano axioms)的基础,该公理体系定义了自然数的性质和规律。
自然数在实际生活中有许多应用,例如:计数、测量、编码等。
在计算机科学中,自然数经常用于表示数据类型的大小、索引和计数器等。
此外,自然数还与质数、斐波那契数列、阶乘等著名数学概念密切相关。
总之,自然数作为数学中最基本的整数,具有重要的理论和应用价值。
