2020年武汉广雅发二中一模(武汉市第二初级中学)
湖北省武汉市第二初级中学武汉二中广雅中学2019-2020学年八年级下学期质量评估物理试题(二)

湖北省武汉市第二初级中学&武汉二中广雅中学2019-2020学年八年级下学期质量评估物理试题(二)学校:___________姓名:___________班级:___________考号:___________一、单选题1.2020年,新型冠状病毒在全球范围内传播防止病毒扩散,我校响应教育部号召开展线上教学,某同学在家极其不自觉,整天玩手机看电视,荒废学业,某天一阵暴风雨(暴打,应正确合理的教育孩子,切勿模仿)过后,妈妈心疼,爸爸手疼,某同学全身都疼,上述有关力学知识,描述最合理的是()A.力的作用效果只跟力的大小有关B.力的作用是相互的C.不接触的两物体间也能产生力D.力能改变物体的运动状态2.如图所示实例中,主要说明力改变物体运动状态的是()A.跳高时撑竿被压弯B.气球被压扁C.弹簧被拉长D.铅球沿曲线运动二、未知3.如图所示人驾驶平衡车在水平路面上匀速直线运动时,下列说法错误的是()A.平衡车轮胎上的花纹是为了增大摩擦B.平衡车轮胎做得较宽,可以减小车对地面的压强C.平衡车的重力与地面对平衡车的支持力是一对平衡力D.关闭电源后,平衡车仍继续前进是由于其具有惯性4.图中所示的装置为某同学设计的惯性实验仪,a为上表面光滑的阶梯形木块,b、c 为下表面光滑的象棋子,d为橡皮筋,用手把a、b、c一起水平向左拉出一小段距离后再松手,从松手到木块a被右侧的挡板挡住时,b、c的运动情形是()A.松手后,b、c都随a向右运动,当a被挡住时,b、c也停止运动B.松手后,b、c都随a向右运动,当a被挡住时,b、c向右飞出C.松手后,b会下落,c立即脱离a,向右飞出D.松手后,b会下落,当a被挡住时,c向右飞出三、单选题5.如图所示,将弹簧测力计A、B的挂钩挂在一起,然后用手水平左右拉弹簧测力计的圆环使其保持静止状态,当弹簧测力计A的示数为3N时,则弹簧测力计B的示数及右手对弹簧测力计B的拉力大小分别是()A.3N、3N B..3N、6N C..0N、6N D..6N、3N四、未知6.水平地面上的一物体受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体的速度v与时间t的关系如图所示,以下说法正确的是()A.0~2秒,物体没有推动,是因为推力小于摩擦力B.2~4秒,物体做匀速直线运动C.2~4秒,物体受到的摩擦力是2ND.4~6秒,物体受到的摩擦力是3N五、单选题7.如图所示的措施中,为了减小压强的是()A.破窗锤的锤头很尖B.滑雪板的面积较大C.切果器的刀片很薄D.图钉的尖很尖锐六、未知8.下列关于浮力的应用叙述不正确的是()A.用同一密度计测量不同液体的密度时,密度计露出体积大的液体密度大B.潜水艇是靠改变自身所受的重力来实现其浮沉的C.气球上升是因为气球里充的是密度小于空气的气体D.同一艘轮船从长江驶入大海,所受的浮力变大七、单选题9.如图所示不属于连通器的是()A.U形“反水弯”B.锅炉水位计C.地漏存水杯D.自制气压计八、未知10.如图(a)所示,底面积不同的圆柱形容器分别盛有甲、乙两种液体,甲乙密度分别为ρ甲和ρ乙。
2020年湖北武汉江岸区武汉二中广雅中学初三一模数学试卷

____________________ .
第14题
在
中,
在一条直线上时,则
,将
绕 点逆时针旋转,点 落在 边上的点 ,点 落在 ,当 、 、
__________ .
第15题
二次函数
的图象如图所示,给出下列结论:①
;②
;③若
,
则
;④
.
其中正确的结论是 __________ .
4/29
第16题
如图Rt ,
地的路程 (米)与所用时间 (分)的函数图象,其间在 地休息 分钟.已知乙比甲早 分钟出发,往返运动 了两趟,并且比甲每分钟多走 米.若乙在 、 两地均不停留,则两人在途中相遇的次数共有( )次.
A. B. C. D.
第9题
如图, 是半圆的直径, 为 的弦, 为 内一点, ,则 的长为( ).
,
,
,若
A. B. C. D.
第10题
设
,
数,则
A.
B. C. D.
第11题
, 的值是( ).
,,
3/29
,其中 为正整
计算
的结果是 __________ .
第12题 在防治新型冠状病毒知识问答中, 名参赛选手得分情况如下表:那么这 名选手所得分数的中位 数 __________ .
人数
分数
第13题 计算:
,请用无刻度的直尺画图
1 在图 中,画
的角平分线 交 于点 .
2 在图 中,过点 画直线. Nhomakorabea在图 中,过点 画点 到线段 的垂线段 .
3
第21题 如图,
是⊙ 的直径,
是⊙ 的切线,
于点 ,交⊙ 于点 ,连接 交 于点 .
2020年湖北省武汉二中、武汉二中广雅中学中考物理模拟试卷(二)(附答案详解)

2020年湖北省武汉二中、武汉二中广雅中学中考物理模拟试卷(二)1. 人体的密度跟水的密度差不多,据此小明同学估计估算出了下列跟自己身体或用具相关的一些数据,你认为其中最不合理的是( )A. 八下物理课本重量约3NB. 课桌的高度大约是0.8mC. 教室中空气重力大约2200ND. 人体的体积约为5000cm32. “神州八号”飞船与“天宫一号”成功对接后,携手绕地球飞行。
下列说法错误的是( )A. “神州八号”相对于地球是运动的B. “天宫一号”相对于“神州八号”是静止的C. “神州八号”受到的力是平衡力D. “天宫一号”运动状态会改变3. 如图记录了甲、乙两辆汽车在平直公路上同时自西向东行驶时的运动情况,下列说法不正确的是( )A. 在前2s内甲车运动的路程大于乙车运动的路程B. 在第4s内以乙车为参照物甲车在向东运动C. 甲车做匀速直线运动,速度小于16m/sD. 甲、乙两车在4s内的平均速度相同4. 在研究凸透镜成像实验中,当烛焰离凸透镜的距离小于焦距时,眼睛通过透镜观察到的虚像可能是如图中的( )A. B.C. D.5. 如图所示,早期照相馆里摄影师取景时看到的像是倒立的。
有几位同学对此现象展开了讨论:甲:将照相机再靠近两位照相的人,才可看到两位照相的人的全身像;乙:调整相机和两位照相人之间的距离,人像变大时,应增大相机镜头和胶片之间的距离;丙:要使人像更亮,必须在两位照相的人身后进行补光;丁:现在的相机利用光学成像电子技术、把倒立的像转变成正立的,便于观察。
这些说法正确的是( )A. 乙与丁B. 乙与丙C. 甲与乙D. 甲与丁6. 如图所示是近视眼和远视眼的成因示意图。
下列说法正确的是( )A. 甲是远视眼,应佩戴凹透镜矫正B. 甲是远视眼,晶状体折光能力较弱C. 乙是近视眼,应佩戴凸透镜矫正D. 乙是近视眼,晶状体折光能力较弱7. 如图所示,在探究凸透镜成像规律的实验中,当蜡烛、凸透镜和光屏之间的距离为如图时,在光屏上得到一个清晰缩小的实像。
武汉二中广雅中学2020年九年级(下)英语统一作业(一)AB答案

武汉市第二初级中学&武汉二中广雅中学九年级(下)英语统一作业(一)A部分2020年4月11日星期六命题人:李安袁希红审题人:邵晓梅听力部分(25分)(共三节)第一节(共4小题,每小题1分,满分4分)听下面4个问题。
每个问题后有三个答语,从题中所给的A、B、C三个选项中选出最佳选项。
听完每个问题后,你都有5秒钟的时间来作答和阅读下一小题,每个问题仅读一遍。
A 1. A. H-U-N-T. B. I’m a boy. C.Tom.C 2. A. Very cute. B. I like it. C. Some sand, I guess.B 3. A. Next week. B. My parents. C. By bike.C 4. A. A toy cat. B. Very nice. C. The red one.第二节(共8小题,每小题1分,满分8分)听下面7段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每个问题,你都有时间来作答和阅读下一小题。
每个问题仅读一遍。
A 5.How many days are they going to stay in Wuhan?A.5.B. 6.C. 7.C 6.Who will go out for a walk in the park soon?A.The manB.The womanC.Both of themA 7. What’s the woman planning to do?A.She is going to take a test.B.B. She will learn to use computers.C. She is planning to find a new job.W: Do I need to know how to use a computer?M: You do not need computer experience to take the test. The test instructions are easy to understand.A 8. How would the man like to go to work?A.By bus.B. By car.C. By subway.C 9. What does the woman mean?A. She wants to go with Tim.B. She will travel around the world.C. She can’t afford to go anywhere.C 10. What does the woman think of herself?A. She was thoughtful.B. She was serious.C. She was careless.M: You didn’t do well in today’s math test. What was the matter?W: I was in a hurry, and I didn’t check over my answers.B 11. What’s the woman’s advice for the man?A.He should hang out with his parents.B.He should talk with his parents properly.C.He should follow the family rules.A 12. What will the man do?A.Stop smoking at once.B.Go out to smoke.C.Put the cigarette into his pocket. W: Would you mind not smoking, sir? My baby is coughing now.M: Sorry, I’ll put out my cigarette 掐灭烟right away.第三节(共13小题,每小题1分,满分13分)听下面4段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟,听完后,各小题将给出5秒钟的作答时间,每段对话或独白读两遍。
2020届湖北省武汉二中广雅中学中考物理模拟试卷(一)(含解析)

2020届湖北省武汉二中广雅中学中考物理模拟试卷(一)一、单选题(本大题共10小题,共30.0分)1.如图所示人类从月球上拍摄因地球形成的“日食”照片。
下列对发生此现象的判断,正确的是()A. 此时月球正处在太阳和地球之间B. 此时太阳正处在月球和地球之间C. 此时在地球上的某一地区可能出现“日食”现象D. 此时在地球上的某一地区可能出现“月食”现象2.将闹钟放在玻璃钟罩内,抽出罩内空气,在抽气过程中()A. 听到闹钟走时声音越来越小B. 听到闹钟走时声音越来越大C. 听到闹钟走时声音大小不变D. 无法判断3.小红同学在厨房里劳动时,发现了许多与学过物理知识有关的现象,下列说法不正确的是()A. 瓷砖表面的吸盘式挂钩,是利用大气压将吸盘紧压在瓷砖表面B. 高压锅能很快煮熟食物,是由于锅内气压增大,水的沸点升高C. 抽油烟机能将油烟吸走,是因为空气流速越大的位置,压强越大D. 茶壶的壶身和壶嘴构成了连通器4.在观察凸透镜成像实验中,把物体从距凸透镜2倍焦距之外,逐渐向凸透镜靠拢的过程中,像的大小将()A. 变大B. 变小C. 先变大后变小D. 先变小后变大5.把体积为2dm3、重为12N的物体放入水中,若g取10N/kg,当它静止时所处的状态及受到的浮力大小分别是()A. 漂浮,20NB. 漂浮,12NC. 沉底,20ND. 沉底,12N6.如图所示,关于电磁现象,下列说法正确的是()A. 如图,把小磁针放在地理赤道附近,小磁针静止时磁针N极指向地理南极附近B. 如图,通电线圈在磁场作用下转动,机械能转化为电能C. 如图,利用“电生磁”将铁钉磁化,利用安培右手定则可判定铁钉上端为N极D. 如图,当用力让线圈发生转动时,电流表就有电流通过,工作原理是法拉第电磁感应现象7.能源、信息和材料是现代社会发展的三大支柱,下列说法中正确的是()A. 超导材料可用于制作电饭锅的发热体B. 太阳能、风能和核能都是可再生能源C. 手机贴膜能防止屏幕粘上灰尘,是因为这种材料有较好的防静电特性D. 电报、电话都是利用超声波传递信息的8.关于质量和密度,下列说法中正确的是()A. 把一杯水喝掉一半,杯内剩余水的密度是原来的一半B. 把一杯水喝掉一半,杯内剩余水的密度是原来的2倍C. 质量相同的物质,体积大的密度也大D. 体积相同的物质,质量大的密度也大9.某家庭电路的部分电路如图所示,其中甲、乙两处分别装用电器和开关。
武汉市二中广雅中学2020年九年级(下)英语统一作业(二)含答案

武汉市第二初级中学&武汉二中广雅中学九年级(下)英语统一作业(二)命题人:刘建翠吴晓霞审题人:邵晓梅一、听力测试(共三节)第一节(共4小题,每小题1分,满分4分)听下面5个问题。
每个问题后有三个答语,从题中所给的A、B、C三个选项中选出最佳选项。
听完每个问题后,你都有5秒钟的时间来作答和阅读下一小题。
每个问题仅读一遍。
1. A. H-U-N-T. B. I’m a boy. C. Tom.2. A. V ery cute. B. I like it. C. Some sand, I guess.3. A. Next week. B. My parents. C. By bike.4. A. A toy cat. B. V ery nice. C. The red one.第二节(共8小题,每小题1分,满分8分)听下面7段对话。
每段对话后有一个小题,从题中所给的A、B、c三个选项中选出最佳选项.听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
5.How many days are they going to stay in Wuhan?A. 5.B. 6.C. 7.6.Who will go out for a walk in the park soon?A.The manB.The womanC.Both of them7. What is the woman going to do this evening?A. Go to dinner.B. Visit her sister.C. Go to the airport.8. Who made the cake?A. The woman.B. The man.C. The man’s mother.9. Why is the woman moving to a new house?A. The present house is too expensive.B. There is too much noise from the neighbor.C. She wants to save money to buy a violin.10. Where are these two people probably?A. In a store.B. In a classroom.C. In a hotel.11. What can we learn from the conversation?A. The woman had a photo shop of her own.B. The woman developed her photos all by herself.C. The woman developed part of her own film.12. What time is it now?A. 7:30.B. 8:00.C. 6:30.第三节(共13小题,每小题1分,满分13分)听下面4段对话或独白。
2020年湖北省武汉二中广雅中学中考数学模拟试卷(二) 解析版
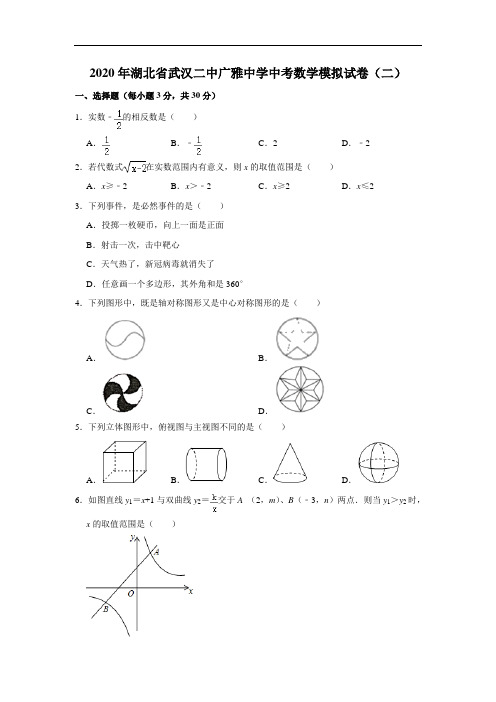
2020年湖北省武汉二中广雅中学中考数学模拟试卷(二)一、选择题(每小题3分,共30分)1.实数﹣的相反数是()A.B.﹣C.2D.﹣22.若代数式在实数范围内有意义,则x的取值范围是()A.x≥﹣2B.x>﹣2C.x≥2D.x≤23.下列事件,是必然事件的是()A.投掷一枚硬币,向上一面是正面B.射击一次,击中靶心C.天气热了,新冠病毒就消失了D.任意画一个多边形,其外角和是360°4.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.5.下列立体图形中,俯视图与主视图不同的是()A.B.C.D.6.如图直线y1=x+1与双曲线y2=交于A(2,m)、B(﹣3,n)两点.则当y1>y2时,x的取值范围是()A.x>﹣3或0<x<2B.﹣3<x<0或x>2C.x<﹣3或0<x<2D.﹣3<x<27.在两个不透明的口袋中分别装有两把不同的钥匙和三把锁,其中两把钥匙分别能打开两把锁,且不能打开第三把锁,随机取出一把钥匙和一把锁,能打开的概率是()A.B.C.D.8.星期天早晨,小广,小雅两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,小广到达B地后立即以另一速度按原路返回,如图是两人离A地的距离y(米)与小雅运动的时间x(分)之间的函数图象,则下列说错误的是()A.小广返回到A地时,小雅还需要8分钟到达A地B.整个运动过程中,他们遇见了2次C.A、B两地相距3000米D.小广去时的速度小于返回时的速度9.如图,以矩形ABCD对角线BD上一点O为圆心作⊙O过A点并与CD切于E点,若CD=3,BC=5,则⊙O的半径为()A.B.3C.D.10.有76个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是1,第二个数是﹣1,那么这76个数的积是()A.(﹣2)23B.(﹣2)24C.(﹣2)25D.(﹣2)26二、填空题(每小题3分,共18分)11.计算的结果是.12.下面是防“新冠”的医护人员对一辆过往班车的15名乘客测体温的数据:体温(℃)36.436.536.636.736.836.937.0人数(人)1132341这组数据的中位数是.13.计算的结果是.14.如图,将△ABC绕点B顺时针旋转得到△A'BC',使点A'落在AC上,已知∠C=40°,AC∥BC',则∠A=度.15.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与轴的交点分别(﹣3,0),(1,0),且函数与y轴交点在(0,﹣1)的下方,现给以下结论:①abc<0:②关于方程a(x2﹣1)+b(x﹣1)+c=0始终有两个不相等的实数解;③当﹣2≤x≤3时,y的取值范围是﹣≤y≤6b;则上述说法正确的是.(填序号)16.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为.三、解答愿(共8小题,共72分)17.(8分)计算:.18.(8分)如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.19.(8分)“微信运动“被越来越多的人关注和喜爱,某兴趣小组随机调查了某市50名教师某日微信运动中的步数情况并进行统计整理,绘制了如下的统计图表(不完整),请根据以上信息,解答下列问题:(1)写出a,b的值;(2)补全频数分布直方图;(3)若该市约有40000名教师,估计日行走步数超过1.2万步(包含1.2万步)的教师约有多少名?步数(万步)频数频率0≤x<0.48a0.4≤x<0.8150.300.8≤x<1.2120.241.2≤x<1.6100.201.6≤x<230.062≤x<2.4b0.0420.(8分)请仅用无刻度的直尺按照下列要求作图.(1)如图C、D是菱形网格中的格点,作出线段CD的一个三等分点E;(2)如图是翻折后的矩形ABCD,请作出△BOD中∠BOD的角平分线;(3)以等腰Rt△ABC中AB为直径作⊙O交斜边AB于D,请作出过点D的切线.21.(8分)如图,在△ABC中,∠A=45°,以AB为直径的⊙O经过AC的中点D,E为⊙O上的一点,连接DE、BE,DE交OA于点F.(1)求证:BC为⊙O的切线;(2)若OF=2AF,若BE=,求⊙O的半径.22.(10分)有一根直尺短边长4cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长为16cm,如图甲,将直尺的短边DE与直角三角形纸板的斜边AB重合,且点D与点A重合.将直尺沿射线AB方向平移,如图乙,设平移的长度为xcm,且满足0≤x≤12,直尺和三角形纸板重叠部分的面积为Scm2.(1)当x=0cm时,S=;当x=4cm时,S=;当x=12cm时,S=.(2)当4<x<8(如图丙),请用含x的代数式表示S.(3)是否存在一个位置,使重叠部分面积为28cm2?若存在求出此时x的值.23.(10分)如图,等腰Rt△ABC中,∠ACB=90°,D为BC边上一点,连接AD.(1)如图1,作BE⊥AD延长线于E,连接CE,求证:∠AEC=45°;(2)如图2,P为AD上一点,且∠BPD=45°,连接CP.①若AP=2,求△APC的面积;②若AP=2BP,直接写出sin∠ACP的值为.24.(12分)如图1,抛物线y=2ax2﹣5ax﹣3a与x交于A、B两点(A在B左侧),与y轴交于点C,且3OC=2OB.(1)求抛物线的解析式;(2)如图2,连接BC,在线段BC上有一动点P,过P作y轴的平行线l1,交抛物线于点N,交x轴于点M,若以C、P、N为顶点的三角形与△BPM相似时,求P点的横坐标;(3)如图3,T(t,0)为x轴上一动点,过T作y轴的平行线l2,Q为x轴上方抛物线上任意一点,直线AQ、BQ分别交l2于点E、F,则当t为何值时,TE+TF为定值,并求出该定值.2020年湖北省武汉二中广雅中学中考数学模拟试卷(二)参考答案与试题解析一、选择题(每小题3分,共30分)1.实数﹣的相反数是()A.B.﹣C.2D.﹣2【分析】根据只有符号不同的两数叫做互为相反数解答.【解答】解:实数﹣的相反数是,故选:A.2.若代数式在实数范围内有意义,则x的取值范围是()A.x≥﹣2B.x>﹣2C.x≥2D.x≤2【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.【解答】解:根据题意得:x﹣2≥0,解得x≥2.故选:C.3.下列事件,是必然事件的是()A.投掷一枚硬币,向上一面是正面B.射击一次,击中靶心C.天气热了,新冠病毒就消失了D.任意画一个多边形,其外角和是360°【分析】根据事件发生的可能性大小判断即可.【解答】解:A、投掷一枚硬币,向上一面是正面,是随机事件;B、射击一次,击中靶心,是随机事件;C、天气热了,新冠病毒就消失了,是不可能事件;D、任意画一个多边形,其外角和是360°,是必然事件;故选:D.4.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念判断即可.【解答】解:A、不是轴对称图形,是中心对称图形;B、是轴对称图形,但不是中心对称图形;C、既不是轴对称图形,也不是中心对称图形;D、既是轴对称图形,又是中心对称图形.故选:D.5.下列立体图形中,俯视图与主视图不同的是()A.B.C.D.【分析】从正面看所得到的图形是主视图,从左面看到的图形是左视图,从上面看到的图象是俯视图.据此作答.【解答】解:A.俯视图与主视图都是正方形,故选项A不合题意;B.俯视图与主视图都是长方形,故选项B不合题意;C.俯视图是圆(带圆心),主视图是等腰三角形;故选项C符合题意;D.俯视图与主视图都是圆,故选项D不合题意;故选:C.6.如图直线y1=x+1与双曲线y2=交于A(2,m)、B(﹣3,n)两点.则当y1>y2时,x的取值范围是()A.x>﹣3或0<x<2B.﹣3<x<0或x>2C.x<﹣3或0<x<2D.﹣3<x<2【分析】当y1>y2时,x的取值范围就是y1的图象落在y2图象的上方时对应的x的取值范围.【解答】解:根据图象可得当y1>y2时,x的取值范围是:﹣3<x<0或x>2.故选:B.7.在两个不透明的口袋中分别装有两把不同的钥匙和三把锁,其中两把钥匙分别能打开两把锁,且不能打开第三把锁,随机取出一把钥匙和一把锁,能打开的概率是()A.B.C.D.【分析】三把锁分别用A、B、C表示,A、B对应的钥匙分别用a、b表示,画树状图展示所有6种等可能的结果数,能打开的结果数为2,然后根据概率公式计算.【解答】解:三把锁分别用A、B、C表示,A、B对应的钥匙分别用a、b表示画树状图为:共有6种等可能的结果数,随机取出一把钥匙和一把锁,能打开的结果数为2,∴随机取出一把钥匙和一把锁,能打开的概率为=;故选:B.8.星期天早晨,小广,小雅两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,小广到达B地后立即以另一速度按原路返回,如图是两人离A地的距离y(米)与小雅运动的时间x(分)之间的函数图象,则下列说错误的是()A.小广返回到A地时,小雅还需要8分钟到达A地B.整个运动过程中,他们遇见了2次C.A、B两地相距3000米D.小广去时的速度小于返回时的速度【分析】根据题意可知A、B两地的距离为3000米,根据“路程,时间与速度的关系”可分别求出小广从A地到B地的速度、小雅的速度以及小广返回的速度,进而求出小广到达A地时,小雅到达A地还需要的时间.再根据函数图象对其他选项逐一判断即可.【解答】解:根据题意得,小广从A地到B地的速度为:3000÷30=100(米/分),小雅的速度为:(3000﹣100×20)÷20=50(米/分),小广返回的速度为:45×50÷(45﹣30)=150(米/分),小广到达A地时,小雅到达A地还需要的时间为:3000÷50﹣3000÷150﹣30=10(分钟).故选项A符合题意;由图象可知,整个运动过程中,他们遇见了2次,故选项B不合题意;由图象可知,A、B两地相距3000米,故选项C不合题意;由直线的陡与缓可知小广去时的速度小于返回时的速度,故选项D不合题意.故选:A.9.如图,以矩形ABCD对角线BD上一点O为圆心作⊙O过A点并与CD切于E点,若CD=3,BC=5,则⊙O的半径为()A.B.3C.D.【分析】作OF⊥AD于F,连接OE,如图,设⊙O的半径为r,利用切线的性质OE⊥CD,利用四边形ABCD为矩形得到OF=DE,DF=OE=r,再证明△DOE∽△DBC,利用相似比得到DE=r,然后在Rt△AOF中利用勾股定理得到(5﹣r)2+(r)2=r2,最后解方程即可.【解答】解:作OF⊥AD于F,连接OE,如图,设⊙O的半径为r,∵CD为切线,∴OE⊥CD,易得四边形ABCD为矩形,∴OF=DE,DF=OE=r,∵OE∥BC,∴△DOE∽△DBC,∴=,即=,解得DE=r,∴OF=r,在Rt△AOF中,OA=r,AF=5﹣r,∴(5﹣r)2+(r)2=r2,整理得9r2﹣250r+625=0,解得r1=25(舍去),r2=,即⊙O的半径为.故选:A.10.有76个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是1,第二个数是﹣1,那么这76个数的积是()A.(﹣2)23B.(﹣2)24C.(﹣2)25D.(﹣2)26【分析】首先根据题意写出前面一些数,观察分析归纳找出规律,然后根据规律求解.【解答】解:根据据题意写出前面一些数:1,﹣1,﹣2,﹣1,1,2,1,﹣1,经观察发现从左向右数每排列六个数后,从第七个数开始重复出现,即这76个数是由1,﹣1,﹣2,﹣1,1,2这6个数组成的数组重复排列而成,而1×(﹣1)×(﹣2)×(﹣1)×1×2=﹣4,又76=12×6+4,故这76个数的积是:(﹣4)12×(﹣2)=(﹣2)25.故选:C.二、填空题(每小题3分,共18分)11.计算的结果是4.【分析】根据二次根式的性质求出即可.【解答】解:=4,故答案为:4.12.下面是防“新冠”的医护人员对一辆过往班车的15名乘客测体温的数据:体温(℃)36.436.536.636.736.836.937.0人数(人)1132341这组数据的中位数是36.8.【分析】求中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.【解答】解:将这组数据从小到大的顺序排列后,处于中间位置的那个数是36.8,那么由中位数的定义可知,这组数据的中位数是36.8.故答案为:36.8.13.计算的结果是.【分析】根据分式的运算法则即可求出答案.【解答】解:原式=,=,=.故答案为:.14.如图,将△ABC绕点B顺时针旋转得到△A'BC',使点A'落在AC上,已知∠C=40°,AC∥BC',则∠A=70度.【分析】由平行线的性质知∠CBC′=∠ABA′=40°,根据旋转性质得出BA=BA′,从而知∠A=∠AA′B=70°,可得出答案.【解答】解:∵AC∥BC′,∠C=40°,∴∠CBC′=∠ABA′=40°,∵BA=BA′,∴∠A=∠AA′B=70°,故答案为:70.15.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与轴的交点分别(﹣3,0),(1,0),且函数与y轴交点在(0,﹣1)的下方,现给以下结论:①abc<0:②关于方程a(x2﹣1)+b(x﹣1)+c=0始终有两个不相等的实数解;③当﹣2≤x≤3时,y的取值范围是﹣≤y≤6b;则上述说法正确的是①②.(填序号)【分析】根据题意抛物线开口向上,对称轴在y轴的左侧,与y轴交于负半轴,得到a >0,b>0,c<0,即可判断①;方程变形为ax2+bx+c=﹣c,根据二次函数的性质得到二次函数y=ax2+bx+c(a≠0)的图象与直线y=﹣c一定有两个交点,即可判断②;③根据对称轴和开口方向,得出当﹣2≤x≤3时,x=﹣1时取最小值,x=3时取最大值,代入求得最小值和最大值即可判断③.【解答】解:∵二次函数y=ax2+bx+c(a≠0)的图象与轴的交点分别(﹣3,0),(1,0),且函数与y轴交点在(0,﹣1)的下方,∴开口向上,对称轴为直线x=﹣==﹣1,c<0,∴a>0,b=2a>0,∴abc<0,故①正确;把(1,0)代入y=ax2+bx+c得,a+b+c=0,∴a+b=﹣c>1,∴a(x2﹣1)+b(x﹣1)+c=0变形为ax2+bx+c=﹣c,∵二次函数y=ax2+bx+c(a≠0)的图象开口向上,与x轴有两个交点,∴二次函数y=ax2+bx+c(a≠0)的图象与直线y=﹣c一定有两个交点,∴关于方程a(x2﹣1)+b(x﹣1)+c=0始终有两个不相等的实数解,故②正确;∵二次函数的图象开口向上,对称轴为直线x=﹣==﹣1,∴抛物线的最小值为y=a﹣b+c,∴b=2a,∴最小值为y=﹣+c,当﹣2≤x≤3时,x=3时取最大值为y=9a+3b+c,即y=b+3b+c=b+c,∴当﹣2≤x≤3时,y的取值范围是﹣+c≤y≤b+c,故③错误;故答案为①②.16.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为.【分析】如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.由勾股定理得到ME+2AF =+2=+,欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′.【解答】解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.∵四边形ABCD是矩形,∴∠BAD=∠B=∠D=90°,∵MH⊥BC,∴∠MHB=90°,∴四边形ABHM是矩形,∴AM=DM=BH=1,AB=MH=1,∴EH=1﹣2x,∴ME+2AF=+2=+,欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,∵J′(0,﹣4),K(1,1),∴KJ′==,∴ME+2AF的最小值为,故答案为.三、解答愿(共8小题,共72分)17.(8分)计算:.【分析】利用积的乘方的性质、单项式除以单项式法则、单项式乘以单项式法则进行计算即可.【解答】解:原式=a6•(4a4﹣12a4)=a6•(﹣8a4)=﹣a10.18.(8分)如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.【分析】运用角平分线的定义,结合图形可知∠ABD=2∠1,∠BDC=2∠2,又已知∠1+∠2=90°,可得同旁内角∠ABD和∠BDC互补,从而证得AB∥CD.【解答】解:∵BE平分∠ABD,DE平分∠BDC(已知),∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),∵∠1+∠2=90°,∴∠ABD+∠BDC=2(∠1+∠2)=180°,∴AB∥CD(同旁内角互补,两直线平行).19.(8分)“微信运动“被越来越多的人关注和喜爱,某兴趣小组随机调查了某市50名教师某日微信运动中的步数情况并进行统计整理,绘制了如下的统计图表(不完整),请根据以上信息,解答下列问题:(1)写出a,b的值;(2)补全频数分布直方图;(3)若该市约有40000名教师,估计日行走步数超过1.2万步(包含1.2万步)的教师约有多少名?步数(万步)频数频率0≤x<0.48a0.4≤x<0.8150.300.8≤x<1.2120.241.2≤x<1.6100.201.6≤x<230.062≤x<2.4b0.04【分析】(1)根据频率=频数÷总数可得答案;(2)根据(1)求出b的值,即可补全统计图;(3)用样本中超过1.2万步(包含1.2万步)的频率之和乘以总人数可得答案.【解答】解:(1)a=8÷50=0.16,b=50×0.04=2;(2)根据(1)求出的频数,补全统计图如下:(3)根据题意得:40000×(0.20+0.06+0.04)=12000(名),答:估计日行走步数超过1.2万步(包含1.2万步)的教师约有12000名.20.(8分)请仅用无刻度的直尺按照下列要求作图.(1)如图C、D是菱形网格中的格点,作出线段CD的一个三等分点E;(2)如图是翻折后的矩形ABCD,请作出△BOD中∠BOD的角平分线;(3)以等腰Rt△ABC中AB为直径作⊙O交斜边AB于D,请作出过点D的切线.【分析】(1)利用平行线等分线段定理画出图形即可;(2)利用轴对称的性质画出图形即可;(3)利用圆周角定理画出图形即可.【解答】解:(1)如图所示:点E即为所求.(2)如图所示:OE即为所求.(3)如图所示:DF即为所求.21.(8分)如图,在△ABC中,∠A=45°,以AB为直径的⊙O经过AC的中点D,E为⊙O上的一点,连接DE、BE,DE交OA于点F.(1)求证:BC为⊙O的切线;(2)若OF=2AF,若BE=,求⊙O的半径.【分析】(1)连接OD,由三角形的中位线和切线的判定证明即可;(2)设AF=t,OF=2t,则⊙O的半径为3t,证明△AEF∽△DBF,由相似三角形的性质得出,求出AE,由勾股定理得出,解得t=.则可求出答案.【解答】证明:(1)连接OD,∵OA=OD,∠A=45°,∴∠ADO=∠A=45°,∴∠AOD=90°,∵D是AC的中点,∴AD=CD,∴OD∥BC,∴∠ABC=∠AOD=90°,∴BC是⊙O的切线;(2)解:设AF=t,OF=2t,则⊙O的半径为3t,∵AD=BD,∴=,∴∠AOD=∠BOD=×180°=90°,∴BD=OB=3t,∵FD===t,∵∠AFE=∠BFD,∠ABD=∠FEA,∴△AEF∽△DBF,∴,∴AE=t=t,在Rt△ABE中,∵AE2+BE2=AB2,∴,解得t=.∴⊙O的半径为3t=.22.(10分)有一根直尺短边长4cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长为16cm,如图甲,将直尺的短边DE与直角三角形纸板的斜边AB重合,且点D与点A重合.将直尺沿射线AB方向平移,如图乙,设平移的长度为xcm,且满足0≤x≤12,直尺和三角形纸板重叠部分的面积为Scm2.(1)当x=0cm时,S=8cm2;当x=4cm时,S=24cm2;当x=12cm时,S=8cm2.(2)当4<x<8(如图丙),请用含x的代数式表示S.(3)是否存在一个位置,使重叠部分面积为28cm2?若存在求出此时x的值.【分析】(1)当x=0cm时,直尺和三角形纸板重叠部分的面积是两直角边都为4厘米的三角形面积;当x=4cm时,直尺和三角形纸板重叠部分的面积=两直角边都为8厘米的三角形面积﹣两直角边都为4厘米的三角形面积;当x=12cm时,直尺和三角形纸板重叠部分的面积是两直角边都为4厘米的三角形面积;(2)过点C作CM⊥AB于点M.当4<x<6时,根据S=梯形GDMC的面积+梯形CMEF 的面积,列式计算即可求解;(3)根据阴影部分面积为28cm2,列出方程﹣x2+12x﹣8=28,解方程即可求解.【解答】解:(1)当x=0cm时,S=4×4÷2=8m2;当x=4cm时,S=8×8÷2﹣4×4÷2=24cm2;当x=12cm时,S=4×4÷2=8cm2.故答案为:8cm2;24cm2;8cm2.(2)如图所示:过点C作CM⊥AB于点M.当4<x<8时,梯形GDMC的面积=(GD+CM)×DM=(x+8)(8﹣x)=﹣x2+32,梯形CMEF的面积=(EF+CM)×ME=[16﹣(x+4)+8][(x+4)﹣8]=(20﹣x)(x﹣4)=﹣x2+12x﹣40,S=梯形GDMC的面积+梯形CMEF的面积=(﹣x2+32)+(﹣x2+12x﹣40)=﹣x2+12x﹣8.(3)当x=4时,S=24cm2,所以当S=28cm2时,x必然大于4,即﹣x2+12x﹣8=28,解得x1=x2=6,所以当x=6cm时,阴影部分面积为28cm2.23.(10分)如图,等腰Rt△ABC中,∠ACB=90°,D为BC边上一点,连接AD.(1)如图1,作BE⊥AD延长线于E,连接CE,求证:∠AEC=45°;(2)如图2,P为AD上一点,且∠BPD=45°,连接CP.①若AP=2,求△APC的面积;②若AP=2BP,直接写出sin∠ACP的值为.【分析】(1)由题意可证点A,点B,点E,点C四点共圆,可得∠AEC=∠ABC=45°;(2)①通过证明△APB∽△CEB,可求CE==,由等腰直角三角形的性质可求CF=1,即可求解;②过点B作BE⊥AD,交AD的延长线于点E,过点C作CF⊥AD于F,过点P作PH⊥AC于H,设AP=2a,则BP=a,可得CE==a,CF=EF=a,BE=PE=a,由勾股定理可求AC2,CP2,利用面积法可求PH2,即可求解.【解答】证明:(1)∵等腰Rt△ABC中,∠ACB=90°,∴AC=BC,∠ABC=∠CAB=45°,AB=BC,∵BE⊥AD,∴∠AEB=90°=∠ACB,∴点A,点B,点E,点C四点共圆,∴∠AEC=∠ABC=45°;(2)①如图2,过点B作BE⊥AD,交AD的延长线于点E,过点C作CF⊥AD于F,∵∠BPD=45°,BE⊥AD,∴∠PBE=45°=∠ABC,∴∠ABP=∠CBE,∵∠AEB=90°=∠ACB,∴点A,点B,点E,点C四点共圆,∴∠BAE=∠BCE,∠AEC=∠ABC=45°,∴△APB∽△CEB,∴,∴CE==,∵CF⊥AD,∠AEC=45°,∴∠FCE=∠CEF=45°,∴CF=EF=CE=1,∴△APC的面积=×AP×CF=1;②如图,过点B作BE⊥AD,交AD的延长线于点E,过点C作CF⊥AD于F,过点P 作PH⊥AC于H,设AP=2a,则BP=a,由①可知,CE==a,CF=EF=a,∵BP=a,∠BPE=45°,∠BEP=90°,∴BE=PE=a,∴AF=AE﹣EF=2a+a﹣a=a+a,PF=a﹣a,∴CP2=CF2+PF2=a2+(a﹣a)2=a2﹣a2,AC2=AF2+CF2=a2+(a+a)2=a2+a2,∵S△ACP=×AC×PH=×AP×CF,∴(AC•PH)2=(AP•CF)2,∴PH2=a2,∵(sin∠ACP)2===,∴sin∠ACP=,故答案为:.24.(12分)如图1,抛物线y=2ax2﹣5ax﹣3a与x交于A、B两点(A在B左侧),与y轴交于点C,且3OC=2OB.(1)求抛物线的解析式;(2)如图2,连接BC,在线段BC上有一动点P,过P作y轴的平行线l1,交抛物线于点N,交x轴于点M,若以C、P、N为顶点的三角形与△BPM相似时,求P点的横坐标;(3)如图3,T(t,0)为x轴上一动点,过T作y轴的平行线l2,Q为x轴上方抛物线上任意一点,直线AQ、BQ分别交l2于点E、F,则当t为何值时,TE+TF为定值,并求出该定值.【分析】(1)先求出点C(0,﹣3a),点A(﹣,0),点B(3,0),由3OC=2OB,可求a的值,即可求解;(2)由相似三角形的性质可得∠CNP=∠PMB=90°或∠NCP=∠PMB=90°,由平行线的性质和勾股定理可求解;(3)设点Q(m,﹣m2+m+2),分别求出直线AQ,BQ解析式,可求点E,点F 坐标,可得ET+FT=﹣mt+m+t+4=﹣m(4t﹣5)+,即可求解.【解答】解:(1)∵抛物线y=2ax2﹣5ax﹣3a与x交于A、B两点(A在B左侧),与y 轴交于点C,∴点C(0,﹣3a),点A(﹣,0),点B(3,0),∴OB=3,OA=,OC=﹣3a,∵3OC=2OB,∴﹣3a×3=6,∴a=﹣,∴抛物线解析式为:y=﹣x2+x+2;(2)∵以C、P、N为顶点的三角形与△BPM相似,∠BPM=∠CPN,∴∠CNP=∠PMB=90°或∠NCP=∠PMB=90°,若∠CNP=∠PMB=90°,∴CN∥BM,∴点N的纵坐标与点C的纵坐标相同,∴点N的纵坐标为2,∴2=﹣x2+x+2,∴x1=0(舍去),x2=,∴点N的横坐标为;若∠NCP=∠PMB=90°,∵点B(3,0),点C(0,2),∴直线BC解析式为:y=﹣x+2,设点M(c,0),则点N(c,﹣c2+c+2),点P(c,﹣c+2),∴NP2=(﹣c2+c+2+c﹣2)2=(﹣c2+4c)2,NC2=c2+(﹣c2+c)2,CP2=c2+(﹣c+2﹣2)2=c2,∵NP2=NC2+CP2,∴(﹣c2+4c)2=c2+(﹣c2+c)2+c2,∴c1=0(舍去),c2=,∴点N的横坐标为,综上所述:点N的横坐标为或;(3)设点Q(m,﹣m2+m+2),又∵点A(﹣,0),点B(3,0),∴直线AQ的解析式为y=﹣(m﹣3)(x+),直线BQ的解析式为y=﹣(2m+1)(x﹣3),当x=t时,点E[t,﹣(m﹣3)(t+)],点F[t,﹣(2m+1)(t﹣3)],∴ET=﹣(m﹣3)(t+),FT=﹣(2m+1)(t﹣3),∴ET+FT=﹣mt+m+t+4=﹣m(4t﹣5)+,∴当t=时,ET+FT有定值为.。
湖北省武汉二中广雅中学2020年中考模拟语文试卷三含答案

武汉市第二初级中学&武汉二中广雅中学九年级(下)语文模拟(三)一、(共9分,每小题3分)1.依次填入下面横线处的词语,恰当的一组是()过度被保护和溺爱的孩子失去的是独立与思考,他们只有满足的经验,却丧失了被要求负责的勇气,丧失了学会接受考验和失败的______,丧失了容纳失望的______。
一句话,他们在百般呵护下,_______了自我的成长性和控制力的发展。
他们的脑海深处永远藏着一个软骨的啼哭的婴孩,因为愤怒自己的无力,并把这种无能感储入内心,因而导致_______的忧郁。
A.胸怀能力损耗无以名状 B.能力胸怀损耗难以割舍C.胸怀能力阻碍难以割舍 D.能力胸怀阻碍无以名状2.下列各句中,有语病的一项是()A.能否在初三阶段始终保持一颗宁静的心,是在高手如云的中考中能否脱颖而出的关键。
B.为弘扬中华民族传统文化,增加学生的国学素养,我校将开展古诗文背诵活动,同学们都积极响应。
C.调查显示,高校毕业生到企业工作,最先关注的是发展空间,然后是薪酬和福利水平。
D.在抗击新冠肺炎的过程中,中医药发挥了重大作用。
这一现象引起了国际社会高度关注。
3.下列各句标点符号使用不规范的一项是()A.从事兼职的长期目标,通常是有一份全职工作保底,同时又能做一些新的实验和尝试,在这个过程中,人们可以重新定义财务自由。
B.日本青年女指挥家西本智实成功列举过三种必备要素:天赋、运气、意志力。
这三个要素中,西本特别强调了“意志力”,因为意志力最终主宰着我们的天赋。
C.离世之前,他几乎把所有的钱都捐了出去,没有留给子孙。
他认为,后代如果是能干的,总会找到自己的路;如果能力不行,这样反倒是害了他们。
D.来自美国、澳大利亚、新西兰、日本的华人华侨商会企业家朋友,还有准备回汉创业的海归,纷纷点赞武汉新政,很多人表示希望到武汉这片热土投资创业。
二、(共9分,每小题3分)艺术的欣赏讲究于“痴”①好的艺术创作往往是创作者个人执着的痴迷。
痴这个字,在中国艺术中常常被用到,用来形容艺术创作中最动人,最不可解,执着而又专注,一直浑然忘我的那种境界。
