直线与平面垂直的判定经典例题
直线与平面的垂直练习题
直线与平面的垂直练习题1.在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上。
证明：AP⊥BC。
证明：连接OP，由于PO⊥平面ABC，所以OP垂直于平面ABC，又因为D为BC的中点，所以AD⊥BC，所以AP 垂直于平面ABC，即AP⊥BC。
2.在直三棱柱ABC-A1B1C1中，AC⊥BC，点D是AB的中点，D1是A1B1中点。
1）证明：AC1 //平面CDB1.连接AC1，BD1，C1D1，由于AC⊥BC，所以AC⊥平面ABC，又因为ABCD为平行四边形，所以AD=BC，所以AD1=BC1，所以D1为B1C1的中点，所以BD1=CD1，所以BD1C1为等腰三角形，所以∠C1BD1=∠BD1C1，又因为AC⊥平面ABC，所以AC1⊥平面ABC，所以AC1与BD1C1平行，所以AC1//平面CDB1.2）证明：面AC1D//面B1CD。
连接A1D，C1B1，由于D为AB的中点，所以AD=C1B1，又因为AC⊥BC，所以AC⊥平面ABC，所以AC1⊥平面ABC，所以AC1与C1B1平行，所以AC1C1B1为平行四边形，所以AC1=CB1，所以AC1B1C1为菱形，所以∠C1A1D=∠C1B1D，又因为AC1⊥平面ABC，所以∠B1CD=∠C1BD，所以∠C1A1D=∠B1CD，所以面AC1D//面B1CD。
3）证明：AC⊥BC1.连接AC1，BC，由于AC⊥BC，所以AC垂直于平面BC1C，又因为AC1 //平面CDB1，所以AC1垂直于平面BC1C，所以AC与AC1均垂直于平面BC1C，所以AC⊥平面BC1C，即AC⊥BC1.3.四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，E 是SD的中点。
1）证明：XXX。
连接SE，AE，由于SD⊥平面ABCD，所以SD垂直于平面EAC，又因为E为SD的中点，所以SE垂直于平面EAC，所以SE与AE均垂直于平面EAC，所以SE//平面EAC，又因为SB与SE在平面EAC上，所以SB//平面EAC。
2.3.1直线与平面垂直的判定(经典)
如图,点Q是＿点＿P＿在＿平＿面＿内＿的＿射＿影＿ ＿线＿段＿PQ＿是点P到平面 的垂线段
（2）斜线
一条直线和一个平面相交，但不和
这个平面垂直，这条直线叫做这个平面
的斜线．
P
斜线和平面的交点
叫做斜足。
从平面外一点向平 面引斜线，这点与斜
R
足间的线段叫做这点
到这个平面的斜线段
思考：平面外一点到一个平面的垂线段有 几条？斜线段有几条？
A
B
O
D
α
C
这条直线垂直于梯形所在的平面。（√ ）
（4）若一条直线与一个平面不垂直,则这个平面内
没有与这条直线垂直的直线。(× )
定理应用
四：典型例题
例1 如图，已知 a//b,a，求证 b.
证明：在平面 内作两条相交
直线m，n．
a
b
m n
巩固练习
例2 如图，在三棱锥V—ABC中，VA=VC， AB=BC，求证：VB⊥AC。
如图，长方体ABCD—A1B1C1D1中，棱
AA1,BB1,CC1,DD1 所在直线与底面ABCD的 位置关系如何？它们彼此之间具有什么
位置关系？ C1
D1
B1
A1
C
D
B
A
一、线面垂直的性质定理
垂直于同一个平面的两条直线平行
已知:a⊥α, b⊥α, 求证:a // b
证明：
假设 a与b不平行.
记直线b和α的交点为o,
A
A
B
D
CB
C D
过 ABC 的顶点A翻折纸片，得到折痕AD，将翻
折后的纸片竖起放置在桌面上（BD，DC于桌面接
触）．
（1）折痕AD与桌面垂直吗？
线面垂直判定经典证明题
线面垂直判定经典证明题1.已知：在三角形ABC中，PA垂直于AB和AC。
证明PA垂直于平面ABC。
2.已知：在三角形ABC中，PA垂直于AB，BC垂直于平面PAC。
证明PA垂直于BC。
3.已知：在三棱锥V-ABC中，VA=VC，AB=BC。
证明VB垂直于AC。
4.已知：在正方体ABCD-EFGH中，O为底面ABCD的中心。
证明BD垂直于平面AEGC。
5.已知：在圆O中，AB是直径，PA垂直于AC和AB。
证明BC垂直于平面PAC。
6.已知：在三角形ABC中，AD垂直于BD和DC，AD=BD=CD，∠BAC=60°。
证明BD垂直于平面ADC。
7.已知：在矩形ABCD中，PA垂直于平面ABCD，M和N分别是AB和PC的中点。
1) 证明MN平行于平面PAD。
2) 证明XXX垂直于CD。
3) 若∠PDA=45°，证明MN垂直于平面PCD。
8.已知：在棱形ABCD所在平面外，P满足PA=PC。
证明AC垂直于平面PBD。
9.已知四面体ABCD中，AB=AC，BD=CD，平面ABC垂直于平面BCD，E是棱BC的中点。
1) 证明AE垂直于平面BCD。
2) 证明AD垂直于BC。
10.在三棱锥ABCD中，AB=1，BC=2，BD=AC=3，AD=2.证明AB垂直于平面BCD。
11.在四棱锥S-ABCD中，SD垂直于平面ABCD，底面ABCD是正方形。
证明AC垂直于平面SBD。
12.已知：正方形ABCD所在平面与三角形CDE所在平面相交于CD，AE垂直于平面CDE。
证明AB垂直于平面ADE。
13.在三棱锥P-ABC中，PA、PB、PC两两垂直，H是△XXX的垂心。
证明PH垂直于底面ABC。
14.在正方体ABCD-A1B1C1D1中，证明A1C垂直于平面BC1D1.15.在△ABC所在平面外一点S，SA垂直于平面ABC，平面SAB垂直于平面SBC。
证明AB垂直于BC。
16.在直三棱柱ABC-A1B1C1中，AC=BC=1，∠ACB=90°，AA1=2，D是A1B1的中点。
必修二线面垂直经典例题
又∵AB⊥AD 且 PA∩AD＝A， ∴AB⊥平面 PAD，而 PD⊂平面 PAD， ∴AB⊥PD.又∵AB∩AE＝A， ∴PD⊥平面 ABE.
解题小结:
破解此类问题的关键在于熟练把握空间垂直关系的判定与性质， 注意平面图形中的一些线线垂直关系的灵活利用，这是证明空间 垂直关系的基础．由于“线线垂直”、“线面垂直”、“面面垂 直”之间可以相互转化，因此整个证明过程围绕着线面垂直这个 核心而展开，这是化解空间垂直关系难点的技巧所在．
证明 (1)由四棱锥 P—ABCD 中， ∵PA⊥底面 ABCD，CD⊂平面 ABCD， ∴PA⊥CD.∵AC⊥CD，PA∩AC＝A， ∴CD⊥平面 PAC. 而 AE⊂平面 PAC，∴CD⊥AE. (2)由 PA＝AB＝BC，∠ABC＝60°， 可得 AC＝PA. ∵E 是 PC 的中点，∴AE⊥PC. 由(1)，知 AE⊥CD，且 PC∩CD＝C， ∴AE⊥平面 PCD.
（2）求证：VB ⊥AC
小结:
A
K
C
1、问题（1）的线线垂直是通过平面几何知识解决的。 B
体现了空间向平面的转化。
2.问题（2）的线线垂直是异面垂直，又转化为新的线面 垂直解决；
即：欲证线面垂直，需证线线垂直，
欲证线线垂直，又需证新的线面垂直。
体现了空间关系的相互转化。
变题一:
空间四边形ABCD中，AB=AD,CB=CD， 求证: AC⊥BD.
知识背景:
1、线面垂直的定义； 2、线面垂直的最基本性质 ； 3.线面垂直的判定定理。
例1.三棱锥V-ABC中，VA=VC,AB=BC,K是AC的中点。
（1）求证：AC ⊥平面VKB （2）求证：VB ⊥AC
直线与平面垂直的判定及其性质 测试题(答案)
直线与平面垂直的判定及其性质测试题(答案)直线与平面垂直的判定与性质一、选择题1．两异面直线在平面α内的射影（）A．相交直线 B．平行直线C．一条直线—个点 D．以上三种情况均有可能2．若两直线a与b异面，则过a且与b垂直的平面（）A．有且只有—个 B．可能存在也可能不存在C．有无数多个 D．—定不存在3．在空间，下列哪些命题是正确的（）①平行于同一条直线的两条直线互相平行；②垂直于同一条直线的两条直线互相平行；③平行于同一个平面的两条直线互相平行；④垂直于同—个平面的两条直线互相平行．A．仅②不正确 B．仅①、④正确 C．仅①正确 D．四个命题都正确4．若平面α的斜线l在α上的射影为l′，直线b∥α，且b⊥l′，则b与l（）A．必相交 B．必为异面直线 C．垂直 D．无法确定5．下列命题①平面的每条斜线都垂直于这个平面内的无数条直线；②若一条直线垂直于平面的斜线，则此直线必垂直于斜线在此平面内的射影；③若平面的两条斜线段相等，则它们在同一平面内的射影也相等；④若一条线段在平面外并且不垂直于这个平面，则它的射影长一定小于线段的长．其中，正确的命题有（）A．1个 B．2个 C．3个 n 4个6．在下列四个命题中，假命题为（）A．如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直B．垂直于三角形两边的直线必垂直于第三边C．过点A垂直于直线a的所有直线都在过点A垂直于a的平面内D．如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面7．已知P是四边形ABCD所在平面外一点且P在平面ABCD内的射影在四边形ABCD内，若P到这四边形各边的距离相等，那么这个四边形是（）A．圆内接四边形 B．矩形 C．圆外切四边形 D．平行四边形8．在△ABC中，AB＝AC＝5，BC＝6，PA⊥平面ABC，PA＝8，则P到BC 的距离等于（）A．5 B．25 C．35 D．45二、填空题9．AB是平面α的斜线段，其长为a，它在平面α内的射影A′B的长为b，则垂线A′A_________．10．如果直线l、m与平面α、β、γ满足：l＝β∩γ，l⊥α，α和m⊥γ，现给出以下四个结论：①α∥γ且l⊥m；②αγ且m∥β③αβ且l⊥m；④αγ且l⊥m；其中正确的为“________”．（写出序号即可）11．在空间四面体的四个面中，为直角三角形的最多有____________个．12．如图，正方形ABCD，P是正方形平面外的一点，且PA⊥平面ABCD 则在△PAB、△PBC、△PCD、△PAD、△PAC及△PBD中，为直角三角形有_________个．13．给出以下四个命题（1）两条平行直线在同一平面内的射影一定是平行直线；（2）两条相交直线在同一平面内的射影一定是相交直线；（3）两条异面直线在同一平面内的射影—定是两条相交直线；（4）一个锐角在平面内的射影一定是锐角．其中假命题的共有_________个．14．若一个直角在平面α内的射影是一个角，则该角最大为___________．三、解答题15．已知直线a∥平面α,直线b⊥平面α，求证：a⊥b．16．如图，在长方体AC1中，已知AB＝BC＝a，BB1＝b（b＞a），连结BC1，过Bl作B1⊥BC1交CC1于E，交BC1于Q，求证：AC⊥平面EBlD117．如图在△ABC中，已知∠ABC＝90°，SA⊥△ABC所在平面，又点A 在SC和SB上的射影分别是P、Q．求证：PQ⊥SC．18．已知在如图中，∠BAC在平面α内，点α，PE⊥AB，PF⊥AC，PO⊥α，垂足分别是E、F、O，PE＝PF，求证：∠BAO＝∠CAO，19．已知：点P与直线a，试证；过点P与a垂直的直线共面．20．四面体ABCD的棱AB⊥CD的充要条件是AC2＋BD2＝AD2＋BC2．四、思考题对于一个三角形，它的三条高线总相交于—点，而对于一个四面体，它的四条高线是否总相交于一点呢?若不总相交于一点，则怎样的四面体其四条高线才相交于一点呢?这是一个美丽而非凡的问题，请读者进行研究拓展．参考答案一、选择题1．D 2．B 3．B 4．C 5．A 6．A 7．C 8．D二、填空题9．a－b 10．③、④ 11．4 12．5 13．4 14．180°三、解答题 2215．证明：设β为过a的平面，且α∩β＝l．∵a∥α，∴a∥l．∵b⊥l，∴b⊥a．16．证明：∵AB⊥面B1C，BC1为AC1在平面B1C上的射影，且B1E⊥BC1，∴由三垂线定理知B1E⊥AC1．又∵AA1⊥面A1C1，AB＝BC，A1C1⊥B1D1，A1C1是AC1在面A1C1上的射影∴由三垂线定理得AC1⊥B1D1．又∵B1E∩B1D1＝B1，∴AC1⊥平面EB1D1．17．证明：∵SA⊥面ABC，面ABC，∴SA⊥BC．又∵AB⊥BC且SA∩AB＝A，∴BC⊥面SAB，面SAB．∴BC⊥AQ，又AQ⊥SB，BC∩SB＝B．∵AQ⊥面SBC．∴PQ是斜线AP在平面SBC上的射影，又∵AQ⊥SC，∴由三垂线定理的逆定理可得PQ⊥SC．18．证明：∵PO⊥α，PE＝PF，∴OE＝OF，又∵PE⊥AB、PF⊥AC，∴OE⊥AB、OF⊥AC．故Rt△AOE≌Rt△AOF，∴∠BAO＝∠CAO．19．证明：如图，在点P和直线a所在的平面β内，过点P作直线a 的垂线b，设垂足为A．设过点P与β垂直的直线为c，则必有c⊥a，再设由b、c确定的平面为α，则必有a⊥α．设l是过点P与a垂直的直线，下证：α．若α，设由l与c确定的平面为α′，则由a⊥l，a⊥c，l∩c＝P，∴a⊥α′，这样平面α与α′都是过点P与直线a垂直的平面．这是一个错误的结论，因此，假设不成立，故必有α，也就是说过点P与a垂直的直线均在平面α内，于是本题获证．20．证明：先证必要性：过B作CD的垂线，垂足E，连AE，∵CD⊥AB，∴CD⊥平面ABE，∴CD⊥AE．∴AC2＝AE2＋CE2、BD2＝BE2＋DE2；又有AD2＝AE2＋DE2、BC2＝BE2＋CE2．∴AC2＋BD2＝AE2＋BE2＋CE2＋DE2，而AD2＋BC2＝AE2＋BE2＋CE2＋DE2．∴AC2＋BD2＝AD2＋BC2．再证充分性：过A点作CD的垂线，垂足设为F，于是有：AD2＝AF2＋DF2、BC2＝BE2＋CE2；AC2＝AF2＋CF2、BD2＝BE2＋DE2；∵AD2＋BC2＝AC2＋BD2；∴AF2＋DF2＋BE2＋CE2＝AF2＋CF2＋BE2＋DE2∴DF2＋CE2＝CF2＋DE2，∴DF2―CF2＝DE2―CE2，∴（DF＋CF）（DF－CF）＝（DE＋CE）（DE－CE），∴DF－CF＝DE－CE．∴DF＋CE＝DE＋CF．∴E、F只能重合于一点，故有CD⊥平面ABE，∴CD⊥AB．四、思考题我们称：三对对棱分别互相垂直的四面体为对棱垂直的四面体．可以证明：对棱垂直的四面体的四条高线相交于一点，反过来，若一个四面体，若它的四条高线相交于一点，则该四面体一定是对棱垂直的四面体．。
人教课标版高中数学必修2典型例题：直线与平面垂直的判定
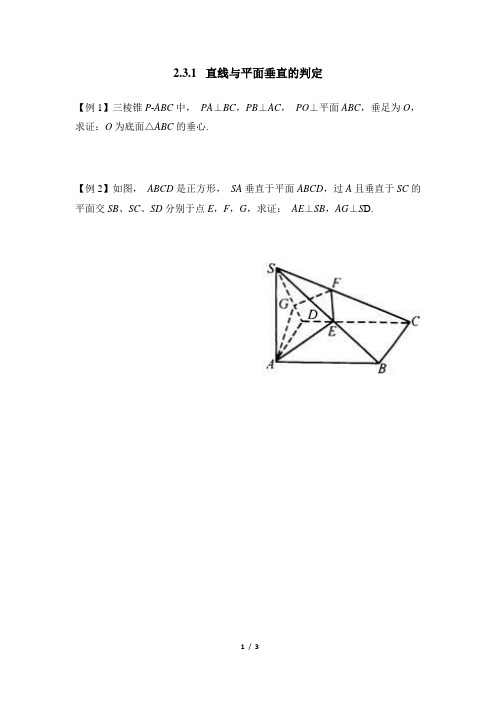
2.3.1 直线与平面垂直的判定
【例1】三棱锥P-ABC中，PA⊥BC，PB⊥AC，PO⊥平面ABC，垂足为O，求证：O为底面△ABC的垂心.
【例2】如图，ABCD是正方形，SA垂直于平面ABCD，过A且垂直于SC的平面交SB、SC、SD分别于点E，F，G，求证：AE⊥SB，AG⊥S D.
参考答案
例1
【分析】可证O为三角形ABC的两条高线的交点.
【证明】连接OA、OB、OC，∵PO⊥平面ABC，
∴.
又∵，
∴，得
,
∴O为底面△ABC的垂心.
【点拨】此例可以变式为“已知，求证”，其思路是接着利用射影是垂心的结论得到后进行证明. 三条侧棱两两垂直时，也可按同样的思路证出.
例2:
【分析】本题考查线面垂直的判定与性质定理，
以及线线垂直和线面垂直相互转化的思想．由于
图形的对称性，所以两个结论只需证一个即可．
欲证，可证平面，为此须
证，，进而转化证明平面，平面．
【证明】∵SA⊥平面ABCD，平面ABCD，
∴．
又∵ABCD为正方形，
∴．
∴平面．
∵平面，
∴．
又∵平面，
∴．
∴平面．
又∵平面，
∴，同理可证．
【点拨】(1)证明线线垂直，常用的方法有：同一平面内线线垂直、线面垂直的性质定理，三垂线定理与它的逆定理，以及与两条平行线中一条垂直就与另一条垂直．(2)本题的证明过程中反复交替使用“线线垂直”与“线面垂直”的相互联系，充分体现了数学化思想的优越性．。
线面垂直练习题及答案
线面垂直练习题及答案线面垂直是几何学中一个重要的概念，它涉及到直线和平面之间的关系。
在几何学中，我们经常需要判断线和平面是否垂直，以及如何确定它们的垂直关系。
为了帮助大家更好地理解和掌握线面垂直的概念，本文将介绍一些线面垂直的练习题及答案。
1. 练习题：判断线段和平面是否垂直题目：已知线段AB的两个端点分别为A(1, 2, 3)和B(4, 5, 6)，平面P的法向量为(2, -1, 3)，判断线段AB是否垂直于平面P。
解答：要判断线段AB是否垂直于平面P，只需判断线段AB的方向向量是否与平面P的法向量垂直。
线段AB的方向向量为AB = B - A = (4, 5, 6) - (1, 2, 3) = (3, 3, 3)。
两个向量的点积为3*2 + 3*(-1) + 3*3 = 9，不等于0。
因此，线段AB不垂直于平面P。
2. 练习题：确定两平面之间的垂直关系题目：已知平面P1的法向量为(1, 2, -1)，平面P2的法向量为(2, -1, 3)，判断平面P1和平面P2之间的垂直关系。
解答：两个平面垂直的条件是它们的法向量垂直，即两个法向量的点积为0。
计算两个法向量的点积为1*2 + 2*(-1) + (-1)*3 = 0，等于0。
因此，平面P1和平面P2垂直。
3. 练习题：求垂直平面上的直线题目：已知平面P的方程为2x + 3y - z = 6，求过点A(1, 2, 3)且垂直于平面P的直线的方程。
解答：垂直于平面P的直线的方向向量应该与平面P的法向量垂直。
由平面P的方程可知，平面P的法向量为(2, 3, -1)。
因此，过点A(1, 2, 3)且垂直于平面P 的直线的方向向量为(2, 3, -1)。
直线的方程可以表示为x = 1 + 2t，y = 2 + 3t，z = 3 - t，其中t为参数。
4. 练习题：判断直线和平面是否垂直题目：已知直线L的方程为x = 1 + 2t，y = 2 + 3t，z = 3 - t，平面P的方程为2x + 3y - z = 6，判断直线L是否垂直于平面P。
直线与平面的垂直判定和性质经典例题(教师)
典型例题一例1下列图形中，满足唯一性的是（ ）．A ．过直线外一点作与该直线垂直的直线B ．过直线外一点与该直线平行的平面C ．过平面外一点与平面平行的直线D ．过一点作已知平面的垂线分析：本题考查的是空间线线关系和线面关系，对定义的准确理解是解本题的关键．要注意空间垂直并非一定相关． 解：A ．过直线外一点作与这条直线垂直的直线，由于并没有强调相交，所以这样的垂线可以作无数条．事实上这无数条直线还在同一个平面内，这个平面为该直线的一个垂面．B ．过直线外一点可以作一条而且仅能作一条直线与该直线平行，但可以作无数个平面和该直线平行．C ．过此点作平面内任一直线的平行线，这条平行线都平行于平面．所以过平面外一点与平面平行的直线应有无数条．D ．过一点作已知平面的垂线是有且仅有一条．假设空间点A 、平面α，过点A 有两条直线AB 、AC 都垂直于α，由于AB 、AC 为相交直线，不妨设AB 、AC 所确定的平面为β，α与β的交线为l ，则必有l AB ⊥，l AC ⊥，又由于AB 、AC 、l 都在平面β内，这样在β内经过A 点就有两条直线和直线l 垂直，与平面几何中经过一点有县仅有一条直线与已知直线垂直相矛盾．故选D ．说明：有关“唯一性”结论的问题，常用反证法，或者借助于其它已证明过的唯一性命题来证明．在本书中，过一点作已知平面的垂线有且仅有一条，同时，过一点作已知直线的垂面也是有且仅有一个．它们都是“唯一性”命题，在空间作图题中常常用到．典型例题二例2 已知下列命题：（1）若一直线垂直于一个平面的一条斜线，则该直线必垂直于斜线在这个平面内的射影； （2）平面内与这个平面的一条斜线垂直的直线互相平行；（3）若平面外的两条直线，在这个平面上的射影互相垂直，则这两条直线互相垂直；（4）若两条直线互相垂直，且其中的一条平行一个平面，另一条是这个平面的斜线，则这两条直线在这个平面上的射影互相垂直．上述命题正确的是（ ）．A ．（1）、（2）B ．（2）、（3）C ．（3）、（4）D ．（2）、（4）分析：本题考查的三垂线定理及其逆定理的简单应用．应用这两个定理时要特别注意“平面内”这一条件，同时要注意各种不同位置的两定理的基本图形及其变式图形． 解：（1）已知直线不一定在平面内，所以不能用三垂线逆定理来判断垂直关系；（2）平面内与这个平面的一条斜线垂直的直线必定与斜线在平面内的射影垂直，所以它们之间也平行； （3）根据三垂线定理可证明直线与另一直线的射影垂直，但不能进一步说明直线和直线垂直； （4）根据三垂线定理的逆定理和空间两直线所成角的概念，不难证明此命题的正确性． 故选D ． 说明：（3）中若一直线与另一直线的射影垂直，则有另一直线必与这一直线的射影垂直．如在正方体1111D C B A ABCD -中，F E 、分别为棱1AA 和1BB 上的点，G 为棱BC 上的点，且1BB EF ⊥，EG FC ⊥1，求FG D 1∠．典型例题三例3 如图，在正方体1111D C B A ABCD -中，E 是1BB 的中点，O 是底面正方形ABCD 的中心，求证：⊥OE 平面1ACD ．分析：本题考查的是线面垂直的判定方法．根据线面垂直的判定方法，要证明⊥OE 平面1ACD ，只要在平面1ACD 内找两条相交直线与OE 垂直．证明：连结D B 1、D A 1、BD ，在△BD B 1中， ∵O E 、分别是B B 1和DB 的中点， ∴D B EO 1//． ∵⊥11A B 面D D AA 11，∴1DA 为1DB 在面D D AA 11内的射影．又∵D A AD 11⊥，∴11DB AD ⊥． 同理可证，C D D B 11⊥．又∵111D CD AD = ，1AD 、⊂C D 1面1ACD ，∴⊥D B 1平面1ACD ．∵EO D B //1，∴⊥EO 平面1ACD ．另证：连结CE AE 、，O D 1，设正方体1DB 的棱长为a ，易证CE AE =． 又∵OC AO =，∴AC OE ⊥． 在正方体1DB 中易求出：a a a DODD O D 2622222211=⎪⎪⎭⎫ ⎝⎛+=+=，a a a OBBEOE 232222222=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=+= ()a a aEB B D E D 232222212111=⎪⎭⎫⎝⎛+=+=．∵21221E D OEO D =+，∴OE O D ⊥1．∵O AC O D = 1，O D 1、⊂AC 平面1ACD ，∴⊥OE 平面1ACD ．说明：要证线面垂直可找线线垂直，这是立体几何证明线面垂直时常用的转化方法．在证明线线垂直时既要注意三垂线定理及其逆定理的应用，也要注意有时是从数量关系方面找垂直，即勾股定理或余弦定理的应用．典型例题四例4 如图，在△ABC 中， 90=∠B ，⊥SA 平面ABC ，点A 在SB 和SC 上的射影分别为N M 、，求证：SC MN ⊥．分析：本题考查的仍是线面垂直的判定和性质定理，以及线线垂直和线面垂直相互转化思想．欲证MN SC ⊥，可证⊥SC 面AMN ，为此须证AN SC ⊥，进而可转化为证明⊥AN 平面SBC ，而已知SB AN ⊥，所以只要证BC AN ⊥即可．由于图中线线垂直、线面垂直关系较多，所以本题也可以利用三垂线定理和逆定理来证线线垂直．证明：∵⊥SA 面ABC ，⊂BC 平面ABC ，∴BC SA ⊥．∵90=∠B ，即BC AB ⊥，A SA BA = ，∴⊥BC 平面SAB ． ∵⊂AN 平面SAB ．∴AN BC ⊥．又∵SB AN ⊥，B BC SB = ，∴⊥AN 平面SBC ． ∵⊂SC 平面SBC ，∴SC AN ⊥， 又∵SC AM ⊥，A AN AM = ，∴⊥SC 平面AMN ．∵⊂MN 平面AMN ．∴MN SC ⊥． 另证：由上面可证⊥AN 平面SBC ．∴MN 为AM 在平面SBC 内的射影．∵SC AM ⊥，∴SC MN ⊥．说明：在上面的证题过程中我们可以看出，证明线线垂直常转化为证明线面垂直，而证明线面垂直又转化为证明线线垂直．立体几何中的证明常常是在这种相互转化的过程中实现的．本题若改为下题，想想如何证：已知⊥SA ⊙O 所在平面，AB 为⊙O 的直径，C 为⊙O 上任意一点（C 与B A 、不重合）．过点A 作SB 的垂面交SB 、SC 于点N M 、，求证：SC AN ⊥．典型例题五例5 如图，AB 为平面α的斜线，B 为斜足，AH 垂直平面α于H 点，BC 为平面α内的直线，θ=∠ABH ，α=∠HBC ，β=∠ABC ，求证：θαβcos cos cos ⋅=．分析：本题考查的是线面角的定义和计算．要证明三个角余弦值之间关系，可考虑构造直角三角形，在直角三角形中求出三个角的余弦值，再代入验证证明，其中构造直角三角形则需要用三垂线定理或逆定理．证明：过H 点作HD 垂直BC 于D 点，连AD ． ∵α⊥AH ，∴AD 在平面α内射影为HD ．∵HD BC ⊥，α⊂BC ， ∴AD BC ⊥．在Rt △ABH 中有：BA BH =θcos ①在Rt △BHD 中有：BHBD =αcos ②在Rt △ABD 中有：BABD =βcos ③由①、②、③可得：αθβcos cos cos ⋅=．说明：由此题结论易知：斜线与平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角．若平面的斜线与平面所成角为θ，则斜线与平面内其它直线所成角β的范围为⎥⎦⎤⎢⎣⎡2πθ，典型例题六例6 如图，已知正方形ABCD 边长为4，⊥CG 平面ABCD ，2=CG ，F E 、分别是AD AB 、中点，求点B 到平面GEF 的距离． 分析：此题是1991年高考题，考查了直线与直线、直线与平面等位置关系以及逻辑推理和空间想像能力．本题是求平面外一点到平面的距离，可用转移法将该点到平面的距离转化为求另一点到该平面的距离．为此要寻找过点B 与平面GEF 平行的直线，因为与平面平行的直线上所有点到平面的距离相等． 证明：连结AC BD 、，EF 和BD 分别交AC 于O H 、，连GH ，作GH OK ⊥于K ． ∵ABCD 为正方形，F E 、分别为AD AB 、的中点，∴BD EF //，H 为AO 中点．∵EF BD //，⊄BD 平面GFE ，∴//BD 平面GFE ． ∴BD 与平面GFE 的距离就是O 点到平面EFG 的距离．∵AC BD ⊥，∴AC EF ⊥．∵⊥GC 面ABCD ，∴EF GC ⊥． ∵C AC GC = ，∴⊥EF 平面GCH ． ∵⊂OK 平面GCH ，∴OK EF ⊥．又∵GH OK ⊥，H EF GH = ，∴⊥OK 平面GEF ．即OK 长就是点B 到平面GEF 的距离． ∵正方形边长为4，2=CG ，∴24=AC ，2=HO ，23=HC ．在Rt △HCG 中，2222=+=CGHCHG ．在Rt △GCH 中，11112=⋅=HGGC HO OK ．说明：求点到平面的距离常用三种方法：一是直接法．由该点向平面引垂线，直接计算垂线段的长．用此法的关键在于准确找到垂足位置．如本题可用下列证法：延长CB 交FE 的延长线于M ，连结GM ，作ME BP ⊥于P ，作CG BN //交MG 于N ，连结PN ，再作PN BH ⊥于H ，可得⊥BH 平面GFE ，BH 长即为B 点到平面EFG 的距离．二是转移法．将该点到平面的距离转化为直线到平面的距离．三是体积法．已知棱锥的体积和底面的面积．求顶点到底面的距离，可逆用体积公式．典型例题七例7 如图所示，直角ABC ∆所在平面外一点S ，且SC SB SA ==．(1)求证：点S 与斜边AC 中点D 的连线SD ⊥面ABC ；(2)若直角边BC BA =，求证：BD ⊥面SAC ．分析：由等腰三角形底边上的中线得到线线垂直，从而得到线面垂直．证明：(1)在等腰SAC ∆中，D 为AC 中点，∴AC SD ⊥．取AB 中点E ，连DE 、SE ．∵BC ED //，AB BC ⊥，∴AB DE ⊥．又AB SE ⊥，∴AB ⊥面SED ，∴SD AB ⊥． ∴SD ⊥面ABC （AB 、AC 是面ABC 内两相交直线）．(2)∵BC BA =，∴AC BD ⊥．又∵SD ⊥面ABC ，∴BD SD ⊥．∵D AC SD = ，∴BD ⊥面SAC ．说明：证明线面垂直的关键在于寻找直线与平面内的两条相交直线垂直．寻找途径可由等腰三角形底边上的中线与底边垂直，可由勾股定理进行计算，可由线面垂直得线线垂直等．典型例题八例8 如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面． 已知：b a //，α⊥a ．求证：α⊥b ．分析：由线面垂直的判定定理知，只需在α内找到两条相交直线与b 垂直即可．证明：如图所示，在平面α内作两条相交直线m 、n ．∵α⊥a ，∴m a ⊥，n a ⊥． 又∵a b //，从而有m b ⊥，n b ⊥．由作图知m 、n 为α内两条相交直线．∴α⊥b ． 说明：本题的结论可以作为判定线面垂直的依据，即当要证的直线与平面的垂直关系不明确或不易证出时，可以考虑证明与已知直线平行的直线与平面垂直．典型例题九例9 如图所示，已知平面α 平面β=EF ，A 为α、β外一点，α⊥AB 于B ，β⊥AC 于C ，α⊥CD 于D ．证明：EF BD ⊥．分析：先证A 、B 、C 、D 四点共面，再证明EF ⊥平面ABCD ，从而得到EF BD ⊥． 证明：∵α⊥AB ，α⊥CD ，∴CD AB //．∴A 、B 、C 、D 四点共面． ∵α⊥AB ，β⊥AC ，EF =βα ，∴EF AB ⊥，EF AC ⊥．又A AC AB = ，∴EF ⊥平面ABCD ．∴BD EF ⊥． 说明：与线面平行和线线平行交替使用一样，线面垂直和线线垂直也常互为条件和结论．即要证线面垂直，先找线线垂直；要证线线垂直，先找线面垂直．本题证明“A 、B 、C 、D 四点共面”非常重要，仅由EF ⊥平面ABC ，就断定BD EF ⊥，则证明是无效的．典型例题十例10 平面α内有一半圆，直径AB ，过A 作SA ⊥平面α，在半圆上任取一点M ，连SM 、SB ，且N 、H 分别是A 在SM 、SB 上的射影．(1)求证：SB NH ⊥；(2)这个图形中有多少个线面垂直关系？(3)这个图形中有多少个直角三角形？(4)这个图形中有多少对相互垂直的直线？ 分析：注意利用直线与直线、直线与平面垂直的有关知识进行判断．(1)证明：连AM 、BM ．如上图所示，∵AB 为已知圆的直径，∴BM AM ⊥．∵SA ⊥平面α，α⊂BM ，∴MB SA ⊥．∵A SA AM = ，∴BM ⊥平面SAM ． ∵AN ⊂平面SAM ，∴AN BM ⊥．∵SM AN ⊥于N ，M SM BM = ，∴AN ⊥平面SMB ．∵SB AH ⊥于H ，且NH 是AH 在平面SMB 的射影，∴SB NH ⊥．解(2)：由(1)知，SA ⊥平面AMB ，BM ⊥平面SAM ，AN ⊥平面SMB ． ∵AH SB ⊥且HN SB ⊥，∴SB ⊥平面ANH ， ∴图中共有4个线面垂直关系．(3)∵SA ⊥平面AMB ，∴SAB ∆、SAM ∆均为直角三角形． ∵BM ⊥平面SAM ，∴BAM ∆、BMS ∆均为直角三角形．∵AN ⊥平面SMB ，∴ANS ∆、ANM ∆、ANH ∆均为直角三角形．∵SB ⊥平面ANH ，∴SHA ∆、BHA ∆、SHN ∆、BHN ∆均为直角三角形． 综上，图中共有11个直角三角形．(4)由SA ⊥平面AMB 知，AM SA ⊥，AB SA ⊥，BM SA ⊥． 由BM ⊥平面SAM 知，AM BM ⊥，SM BM ⊥，AN BM ⊥． 由AN ⊥平面SMB 知，SM AN ⊥，SB AN ⊥，NH AN ⊥． 由SB ⊥平面ANH 知，AH SB ⊥，HN SB ⊥． 综上，图中共有11对互相垂直的直线．说明：为了保证(2)(3)(4)答案不出错，首先应找准(2)的答案，由“线⊥面”可得到“线⊥面内线”，当“线⊥面内线”且相交时，可得到直角三角形；当“线⊥面内线”且不相交时，可得到异面且垂直的一对直线．典型例题十一例11 如图所示，︒=∠90BAC ．在平面α内，PA 是α的斜线，︒=∠=∠60PAC PAB ．求PA 与平面α所成的角．分析：求PA 与平面α所成角，关键是确定PA 在平面α上射影AO 的位置．由PAC PAB ∠=∠，可考虑通过构造直角三角形，通过全等三角形来确定AO 位置，构造直角三角形则需用三垂线定理． 解：如图所示，过P 作α⊥PO 于O ．连结AO ，则AO 为AP 在面α上的射影，PAO ∠为PA 与平面α所成的角．作AC OM ⊥，由三重线定理可得AC PM ⊥．作AB ON ⊥，同理可得AB PN ⊥．由PAC PAB ∠=∠，︒=∠=∠90PNA PMA ，PA PA =， 可得PMA ∆≌PNA ∆，∴PN PM =．∵OM 、ON 分别为PM 、PN 在α内射影，∴ON OM =．所以点O 在BAC ∠的平分线上． 设a PA =，又︒=∠60PAM ，∴a AM 21=，︒=∠45OAM ，∴a AM AO 222==．在POA ∆中，22cos ==∠PAAO PAO ，∴︒=∠45PAO ，即PA 与α所成角为︒45． 说明：(1)本题在得出PA 在面α上的射影为BAC ∠的平分线后，可由公式βαθcos cos cos ⋅=来计算PA 与平面α所成的角，此时︒==∠60θPAC ，α=∠PAO ，︒==∠45βCAO ．(2)由PA 与平面α上射影为BAC ∠平分线还可推出下面结论：四面体ABC P -中，若PAC PAB ∠=∠，PBC PBA ∠=∠，则点A 在面ABC 上的射影为ABC ∆的内心．典型例题十二例12 如图所示，在平面β内有ABC ∆，在平面β外有点S ，斜线AC SA ⊥，BC SB ⊥，且斜线SA 、SB 分别与平面β所成的角相等，设点S 与平面β的距离为cm 4，BC AC ⊥，且cm AB 6=．求点S 与直线AB 的距离．分析：由点S 向平面β引垂线，考查垂足D 的位置，连DB 、DA ，推得AC DA ⊥，BC DB ⊥，又︒=∠90ACB ，故A 、B 、C 、D 为矩形的四个顶点．解：作SD ⊥平面β，垂足为D ，连DA 、DB ．∵AC SA ⊥，BC DB ⊥，∴由三垂线定理的逆定理，有：AC DA ⊥，BC DB ⊥，又BC AC ⊥，∴ACBD 为矩形．又∵SB SA =，∴DB DA =，∴ACBD 为正方形， ∴AB 、CD 互相垂直平分．设O 为AB 、CD 的交点，连结SO ，根据三垂线定理，有AB SO ⊥，则SO 为S 到AB 的距离．在SOD Rt ∆中，cm SD 4=，cm AB DO 321==，∴cm SO 5=．因此，点S 到AB 的距离为cm 5．说明：由本例可得到点到直线距离的作法：(1)若点、直线在确定平面内，可直接由点向直线引垂线，这点和垂足的距离即为所求．(2)若点在直线所在平面外，可由三垂线定理确定：由这点向平面引垂线得垂足，由垂足引直线的垂线得斜足，则这点与斜足的距离为点到直线的距离．(3)处理距离问题的基本步骤是：作、证、算，即作出符合要求的辅助线，然后证明所作距离符合定义，再通过解直角三角形进行计算．典型例题十三例13 如图，ABCD 是正方形，SA 垂直于平面ABCD ，过A 且垂直于SC 的平面交SB 、SC 、SD 分别于点E 、F 、G ，求证：SB AE ⊥，SD AG ⊥．分析：本题考查线面垂直的判定与性质定理，以及线线垂直和线面垂直相互转化的思想．由于图形的对称性，所以两个结论只需证一个即可．欲证SB AE ⊥，可证⊥AE 平面SBC ，为此须证BC AE ⊥、SC AE ⊥，进而转化证明⊥BC 平面SAB 、⊥SC 平面AEFG ．证明：∵SA ⊥平面ABCD ，⊂BC 平面ABCD ，∴BC SA ⊥． 又∵ABCD 为正方形，∴AB BC ⊥．∴⊥BC 平面ASB ． ∵⊂AE 平面ASB ，∴AE BC ⊥． 又∵⊥SC 平面AEFG ，∴AE SC ⊥． ∴⊥AE 平面SBC ．又∵⊂SB 平面SBC ， ∴SB AE ⊥，同理可证SD AG ⊥．说明：(1)证明线线垂直，常用的方法有：同一平面内线线垂直、线面垂直的性质定理，三垂线定理与它的逆定理，以及与两条平行线中一条垂直就与另一条垂直．(2)本题的证明过程中反复交替使用“线线垂直”与“线面垂直”的相互联系，充分体现了数学化思想的优越性．典型例题十四例14 如图，求证：如果一个角所在平面外一点到角的两边距离相等，那么这一点在平面内的射影在这个角的平分线上．已知：BAC ∠在平面α内，点α∉P ，AB PE ⊥，AC PF ⊥，α⊥PO ，垂足分别是E 、F 、O ，PF PE =．求证：CAO BAO ∠=∠．证明：∵α⊥PO ，∴OE 为PE 在α内的射影．∵PE AB ⊥，α平面⊂AB ，∴OE AB ⊥． 同理可证：OF AC ⊥．又∵α⊥PO ，PF PE =，OF OE =， ∴CAO BAO ∠=∠．说明：本题是一个较为典型的题目，与此题类似的有下面命题：从一个角的顶点引这个角所在平面的斜射线，使斜射线和这个角两边的夹角相等，则斜射线在平面内的射影，是这个角的平分线所在的直线．由此结论和上一个例题很容易求解下面这道题：已知︒=∠90ACB ，S 为平面A C B 外一点，︒=∠=∠60SCB SCA ，求SC 与平面ACB 所成角．典型例题十五例15 判断题：正确的在括号内打“√”号，不正确的打“×”号． (1)一条直线和一个平面平行，它就和这个平面内的任何直线平行．（ ） (2)如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直．（ ） (3)垂直于三角形两边的直线必垂直于第三边．（ ）(4)过点A 垂直于直线a 的所有直线都在过点A 垂直于α的平面内．（ ）(5)如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面．（ ）解(1)直线与平面平行，则直线与平面内的直线的位置关系不外乎有两种①平行②异面，因此应打“×”号 (2)该命题的关键是这无数条直线具有怎样的位置关系．①若为平行，则该命题应打“×”号；若为相交，则该命题应打“√”，正是因为这两种情况可能同时具备，因此，不说明面内无这数条线的位置关系，则该命题应打“×”号．(3)垂直于三角形两边的直线必垂直于三角形所在的平面，由线面垂直定义的逆用，则该直线必垂直于三角形的第三边，∴该命题应打“√”．(4)前面介绍了两个命题，①过一点有且只有一个平面与已知直线垂直，②过一点有且只有一条直线与已知平面垂直，根据第一个命题知：过点A 垂直于直线a 的平面惟一，因此，过点A 且与直线a 垂直的直线都在过点A 且与直线a 垂直的平面内，∴该命题应打“√”号．(5)三条共点直线两两垂直，设为a ，b ，c 且a ，b ，c 共点于O ，∵b a ⊥，c a ⊥，0=c b ，且b ，c 确定一平面，设为α，则α⊥a ，同理可知b 垂直于由a ，c 确定的平面，c 垂直于由了确定的平面，∴该命题应打“√”号．说明：本题是利用直线和平面垂直的定义及判定定理等知识来解答的问题．解答此类问题必须作到：概念清楚、问题理解透彻、相关知识能灵活运用．典型例题十六例16 如图，已知空间四边形ABCD 的边AC BC =，BD AD =，引CD BE ⊥，E 为垂足，作BE AH ⊥于H ，求证：BCD AH 平面⊥．分析：若证BCD AH 平面⊥，只须利用直线和平面垂直的判定定理，证AH 垂直平面BCD 中两条相交直线即可．证明：取AB 中点F ，连CF 、DF ， ∵BC AC =，∴AB CF ⊥．又∵BD AD =，∴AB DF ⊥，∴CDF AB 平面⊥， 又CDF CD 平面⊂，∴AB CD ⊥又BE CD ⊥，∴ABE CD 平面⊥，AH CD ⊥， 又BE AH ⊥，∴BCD AH 平面⊥．典型例题十七例17 如果平面α与α外一条直线a 都垂直b ，那么α//a ． 已知：直线α⊄a ，b a 直线⊥，α⊥b ．求证：α//a ．分析：若证线面平行，只须设法在平面α内找到一条直线'a ，使得'//a a ，由线面平行判定定理得证． 证明：(1)如图，若a 与b 相交，则由a 、b 确定平面β，设'a =αβ ．αααβαα////,,'''''a a a a a ab a a b ab a b ⇒⎪⎭⎪⎬⎫⊄⊂⇒⎪⎭⎪⎬⎫⊂⊥⊥⇒⎭⎬⎫⊂⊥又∵． (2)如图，若a 与b 不相交，则在a 上任取一点A ，过A 作b b //'，a 、'b 确定平面β，设'a =αβ ．αααβααα////,,////'''''''''''a a a a a a ab a b a b b b a b a b b b b ⇒⎪⎭⎪⎬⎫⊄⊂⇒⎪⎪⎭⎪⎪⎬⎫⊂⊥⇒⎭⎬⎫⊥⊥⇒⎪⎭⎪⎬⎫⊂⊥⇒⎭⎬⎫⊥又又∵又∵． 典型例题十八例18 如图，已知在ABC ∆中，︒=∠60BAC ，线段ABC AD 平面⊥，DBC AH 平面⊥，H 为垂足．求证：H 不可能是DBC ∆的垂心．分析：根据本题所证结论，可采用反证法予以证明．证明：如图所示，假设H 是DBC ∆的垂心，则DC BH ⊥．∵DBC AH 平面⊥，∴AH DC ⊥， ∴ABH DC 平面⊥，∴DC AB ⊥．又∵ABC DA 平面⊥，∴DA AB ⊥， ∴DAC AB 平面⊥，∴AC AB ⊥，这与已知︒=∠60BAC 矛盾，∴假设不成立，故H 不可能是DBC ∆的垂心．说明：本题只要满足︒≠∠90BAC ，此题的结论总成立．不妨给予证明．典型例题十九例19 在空间，下列哪些命题是正确的（ ）．①平行于同一条直线的两条直线互相平行②垂直于同一条直线的两条直线互相平行 ③平行于同一个平面的两条直线互相平行④垂直于不一个平面的两条直线互相平行A ．仅②不正确B ．仅①、④正确C ．仅①正确D ．四个命题都正确分析：①该命题就是平行公理，即课本中的公理4，因此该命题是正确的；②如图，直线a ⊥平面α，α⊂b ，α⊂c ，且A c b = ，则b a ⊥，c a ⊥，即平面α内两条直交直线b ，c 都垂直于同一条直线a ，但b ，c 的位置关系并不是平行．另外，b ，c 的位置关系也可以是异面，如果把直线b 平移到平面α外，此时与a 的位置关系仍是垂直，但此时，b ，c 的位置关系是异面．③如图，在正方体1111D C B A ABCD -中，易知ABCD B A 平面//11，ABCD D A 平面//11，但11111A D A B A = ，因此该命题是错误的．④该命题是线面垂直的性质定理，因此是正确的． 综上可知①、④正确．∴应选B ．典型例题二十例20 设a ，b 为异面直线，AB 为它们的公垂线 (1)若a ，b 都平行于平面α，则α⊥AB ；(2)若a ，b 分别垂直于平面α、β，且c =βα ，则c AB //．分析：依据直线和平面垂直的判定定理证明α⊥AB ；证明线与线的平行，由于此时垂直的关系较多，因此可以考虑利用线面垂直的性质证明c AB //．图１ 图２证明：(1)如图1，在α内任取一点P ，设直线a 与点P 确定的平面与平面α的交线为'a ，设直线b 与点P 确定的平面与平面α的交线为'b∵α//a ，α//b ，∴'//a a ，'//b b 又∵a AB ⊥，b AB ⊥，∴'a AB ⊥，'b AB ⊥， ∴α⊥AB ．(2)如图2，过B 作α⊥'BB ，则a BB //'，则'BB AB ⊥又∵b AB ⊥，∴AB 垂直于由b 和'BB 确定的平面．∵β⊥b ，∴c b ⊥，α⊥'BB ，∴c BB ⊥'．∴c 也垂直于由'BB 和b 确定的平面．故AB c //．说明：由第(2)问的证明可以看出：利用线面垂直的性质证明线与线的平行，其关键是构造出平面，使所证线皆与该平面垂直．如题中，通过作出辅助线'BB ，构造出平面，即由相交直线b 与'BB 确定的平面．然后借助于题目中的其他垂直关系证得．典型例题二十一例21 如图，在正方体1111D C B A ABCD -中，EF 为异面直线D A 1与AC 的公垂线，求证：1//BD EF ．分析：证明1//BD EF ，构造与EF 、1BD 都垂直的平面是关键．由于EF 是AC 和D A 1的公垂线，这一条件对构造线面垂直十分有用．证明：连结11C A ，由于11//C A AC ，AC EF ⊥，∴11C A EF ⊥．又D A EF 1⊥，1111A C A D A = ，∴D C A EF 11平面⊥． ① ∵11111D C B A BB 平面⊥，111111D C B A C A 平面⊂， ∴111C A BB ⊥．∵四边形1111D C B A 为正方形，∴1111D B C A ⊥，1111B BB D B = ，∴D D BB C A 1111平面⊥， 而D D BB BD 111平面⊂，∴111BD C A ⊥．同理11BD DC ⊥，1111C C A DC = ，∴D C A BD 111平面⊥． ② 由①、②可知：1//BD EF ．典型例题二十二例22 如图，已知P 为ABC ∆外一点，PA 、PB 、PC 两两垂直，a PC PB PA ===，求P 点到平面ABC 的距离．分析：欲求点到平面的距离，可先过点作平面的垂线，进一步求出垂线段的长．解：过P 作ABC PO 平面⊥于O 点，连AO 、BO 、CO ，∴AO PO ⊥，BO PO ⊥，CO PO ⊥ ∵a PC PB PA ===，∴PAO ∆≌PBO ∆≌PCO ∆， ∴OC OB OA ==，∴O 为ABC ∆的外心． ∵PA 、PB 、PC 两两垂直， ∴a CA BC AB 2===，ABC ∆为正三角形，∴a AB AO 3633==，∴a AOPA PO 3322=-=．因此点P 到平面ABC 的距离a 33．说明：(1)求点到平面距离的基本程序是：首先找到或作出要求的距离；然后使所求距离在某一个三角形中；最后在三角形中根据三角形的边角关系求出距离．(2)求距离问题转化到解三角形有关问题后，在三角形中求距离常常用到勾股定理、正弦定理、余弦定理及有关三角函数知识．(3)点到平面距离是立体几何中一个重要内容，高考命题中出现较多，应充分注意，除了上面提到方法之外，还有其他一些方法，比如以后学习的等积法，希望同学们在学习过程不断总结．典型例题二十三例23 如图，已知在长方体1111D C B A ABCD -中，棱51=AA ，12=AB ，求直线11C B 和平面11BCD A的距离．分析：求线面距离，其基本方法是在线上选一点，作出点面距，距离然后根据求点面距的有关方法求解．解：如图，∵BC C B //11，且1111BCD A C B 平面⊄，11BCD A BC 平面⊂，∴1111//BCD A C B 平面．从而点1B 到平面11BCD A 的距离即为所求．过点1B 作B A E B 11⊥于E ，∵11ABB A BC 平面⊥，且B B AA E B 111平面⊂，∴E B BC 1⊥．又B B A BC =1 ，∴111BCD A E B 平面⊥．即线段E B 1的长即为所求，在B B A Rt 11∆中，13601251252211111=+⨯=⋅=B A BB B A E B ， ∴直线11C B 到平面11BCD A 的距离为1360．说明：本题考查长方体的性质，线面距离的概念等基础知识以及计算能力和转化的数学思想，解答本题的关键是把线面距离转化为点面距离，进而转化为点线距离，再通过解三角形求解，这种转化的思想非常重要，数学解题的过程就是将复杂转化为简单，将未知转化为已知，从而求解．典型例题二十四例24 AD 、BC 分别为两条异面直线上的两条线段，已知这两条异面直线所成的角为︒30，cm AD 8=，BC AB ⊥，BC DC ⊥．求线段BC 的长．分析：首先依据题意，画出图形，利用平移，将异面直线AD 、BC 所成的角、垂直关系转化到某一个或某几个平面内，应用平面几何有关知识计算出BC 之长．解：如图，在平面α内，过A 作BC AE //，过C 作AB CE //，两线交于E ．∵BC AE //，∴DAE ∠就是AD 、BC 所成的角，︒=∠30DAE ．∵BC AB ⊥，∴四边形ABCE 是矩形．连DE ，∵CD BC ⊥，CE BC ⊥，且C CE CD = ，∴CDE BC 平面⊥．∵BC AE //，∴CDE AE 平面⊥．∵CDE DE 平面⊂，∴DE AE ⊥．在AED Rt ∆中，得34=AE ，∴)(34cm AE BC ==．说明：解决空间问题，常常将空间关系转化一个或几个平面上来，只有将空间问题归化到平面上来，才能应用平面几何知识解题，而平移变换是转化的重要手段．。
线面垂直与面面垂直典型例题
线面垂直与面面垂直 基础要点1、假设直线a 与平面,αβ所成的角相等，则平面α与β的位置关系是〔 B 〕 A 、//αβB 、α不一定平行于βC 、α不平行于βD 、以上结论都不正确2、在斜三棱柱111ABC A B C -,90BAC ∠=,又1BC AC ⊥,过1C 作1C H ⊥底面ABC ，垂足为H ，则H 一定在〔 B 〕 A 、直线AC 上 B 、直线AB 上C 、直线BC 上D 、△ABC 的内部3、如图示，平面α⊥平面β，,,A B AB αβ∈∈与两平面,αβ所成的角分别为4π和6π，过A 、B 分别作两平面交线的垂线，垂足为,A B ''，则:AB A B ''=〔 A 〕 A 、2:1 B 、3:1 C 、3:2 D 、4:34、如图示，直三棱柱11ABB DCC -中，190,4ABB AB ∠==,12,1BC CC ==DC 上有一动点P ，则△1APC 周长的最小值是5.已知长方体1111D C B A ABCD -中，21==AB A A ,假设棱AB 上存在点P ，使得PC P D ⊥1,则棱AD 长的取值范围是 。
题型一：直线、平面垂直的应用1.〔2014，江苏卷〕如图，在三棱锥P-ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点. 已知,685PA AC PA BC DF ⊥===，，.求证：(1) PA DEF 平面；(2) BDE ABC ⊥平面平面 . 证明： (1) 因为D ，E 分别为棱PC ，AC 的中点，线面垂直线线垂直面面垂直B`A`BAαβBCD 1B 1C B 11D A D B A所以DE ∥PA.又因为PA ⊄ 平面DEF ，DE ⊂平面DEF ， 所以直线PA ∥平面DEF.(2) 因为D ，E ，F 分别为棱PC ，AC ，AB 的中点，PA ＝6，BC ＝8，所以DE ∥PA ，DE ＝12PA ＝3，EF ＝12BC ＝4. 又因 DF ＝5，故DF 2＝DE 2＋EF 2， 所以∠DEF ＝90°，即DE 丄EF.又PA ⊥AC ，DE ∥PA ，所以DE ⊥AC. 因为AC∩EF ＝E ，AC ⊂平面ABC ，EF ⊂平面ABC ，所以DE ⊥平面ABC. 又DE ⊂平面BDE ，所以平面BDE ⊥平面ABC.2. (2014,北京卷，文科)如图，在三棱柱111ABC A B C -中，侧棱垂直于底面，AB BC ⊥，12AA AC ==，E 、F 分别为11AC、BC 的中点. 〔1〕求证：平面ABE ⊥平面11B BCC ；〔2〕求证：1//C F 平面ABE . 证明：〔1〕在三棱柱111ABC A B C -中，11,,BB ABC BB AB ⊥∴⊥底面11,,AB BC AB B BCC ∴⊥∴⊥平面 ,AB ABE ⊂平面11ABE B BCC ∴⊥平面平面.(2)取AB 的中点G ，连接EG ，FGE 、F 分别为11AC 、BC 的中点, 1,2FG AC FG AC ∴=, 111111AC AC AC AC FG EC FG EC =∴=，，，,则四边形1FGEC 为平行四边形， 111,,,C F EG EG ABE C F ABE C F ABE ∴⊂⊄∴平面平面平面.3．如图，P 是ABC ∆所在平面外的一点，且⊥PA 平面ABC ，平面⊥PAC 平面PBC ．求证AC BC ⊥．分析：已知条件是线面垂直和面面垂直，要证明两条直线垂直，应将两条直线中的一条纳入一个平面中，使另一条直线与该平面垂直，即从线面垂直得到线线垂直．．证明：在平面PAC 内作PC AD ⊥，交PC 于D ．因为平面⊥PAC 平面PBC 于PC ，⊂AD 平面PAC ，且PC AD ⊥，所以PBC AD 平面⊥．又因为⊂BC 平面PBC ，于是有BC AD ⊥①．另外⊥PA 平面ABC ，⊂BC 平面ABC ，所以BC PA ⊥．由①②及A PA AD = ，可知⊥BC 平面PAC ．因为⊂AC 平面PAC ，所以AC BC ⊥．说明：在空间图形中，高一级的垂直关系中蕴含着低一级的垂直关系，通过此题可以看到，面面垂直⇒线面垂直⇒线线垂直．4. 过点S 引三条不共面的直线SA 、SB 、SC ，如图，︒=∠90BSC ，︒=∠=∠60ASB ASC ，假设截取a SC SB SA ===(1)求证：平面ABC ⊥平面BSC ； (2)求S 到平面ABC 的距离．分析：要证明平面ABC ⊥平面BSC ，根据面面垂直的判定定理，须在平面ABC 或平面BSC 内找到一条与另一个平面垂直的直线．(1)证明：∵a SC SB SA ===， 又︒=∠=∠60ASB ASC ，∴ASB ∆和ASC ∆都是等边三角形， ∴a AC AB ==，取BC 的中点H ，连结AH ，∴BC AH ⊥．在BSC Rt ∆中，a CS BS ==，∴BC SH ⊥，a BC 2=，∴2)22(222222a a a CH AC AH =-=-=，∴222a SH =． 在SHA ∆中，∴222a AH =，222a SH =，22a SA =，∴222HA SH SA +=，∴SH AH ⊥，∴⊥AH 平面SBC ．∵⊂AH 平面ABC ，∴平面ABC ⊥平面BSC ．或：∵AB AC SA ==，∴顶点A 在平面BSC 内的射影H 为BSC ∆的外心，又BSC ∆为∆Rt ，∴H 在斜边BC 上，又BSC ∆为等腰直角三角形，∴H 为BC 的中点，∴⊥AH 平面BSC ．∵⊂AH 平面ABC ，∴平面ABC ⊥平面BSC ． (2)解：由前所证：AH SH ⊥，BC SH ⊥，∴⊥SH 平面ABC ，∴SH 的长即为点S 到平面ABC 的距离，a BC SH 222==， ∴点S 到平面ABC 的距离为a 22．5、如图示，ABCD 为长方形，SA 垂直于ABCD 所在平面，过A 且垂直于SC 的平面分别交SB 、SC 、SD 于E 、F 、G ，求证：AE ⊥SB ,AG ⊥SD6.在四棱锥P-ABCD 中，侧面PCD 是正三角形，且与底面ABCD 垂直，已知底面是面积为32的菱形，︒=∠60ADC ，M 是PB 中点。
直线垂直平面典型例题
1．直线与平面垂直的定义(1)自然语言：如果直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直，记作l⊥α.直线l 叫做平面α的垂线，平面α叫做直线l的垂面．直线与平面垂直时，它们唯一的公共点P叫做垂足．(2)图形语言：如图．画直线l与平面α垂直时，通常把直线画成与表示平面的平行四边形的一边垂直．(3)符号语言：任意a⊂α，都有l⊥a⇒l⊥α.2．直线与平面垂直的判定定理(1)自然语言：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．(2)图形语言：如图所示．(3)符号语言：a⊂α，b⊂α，a∩b＝P，l⊥a，l⊥b⇒l⊥α.(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．如图，∠P AO就是斜线AP与平面α所成的角．(2)当直线AP与平面垂直时，它们所成的角是90°.(3)当直线与平面平行或在平面内时，它们所成的角是0°.(4)线面角θ的范围：0°≤θ≤90°.1列说法中正确的个数是()①如果直线l与平面α内的两条相交直线都垂直，则l⊥α；②如果直线l与平面α内的任意一条直线垂直，则l⊥α；③如果直线l不垂直于α，则α内没有与l垂直的直线；④如果直线l不垂直于α，则α内也可以有无数条直线与l垂直．A．0B．1 C．2 D．32．下列说法中，正确的是()A．若直线l与平面α内无数条直线垂直，则l⊥αB．若直线l垂直于平面α，则l与平面α内的直线可能相交，可能异面，也可能平行C．若a∥b，a⊂α，l⊥α，则l⊥b D．若a⊥b，b⊥α，则a∥α3如图所示，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB＝AC＝1，AA1＝2，∠B1A1C1＝90°，D为BB1的中点．求证：AD⊥平面A1DC1.4.如图，直角三角形ABC所在平面外有一点S，且SA＝SB＝SC，点D为斜边AC的中点．(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC.5．已知正三棱锥的侧棱长是底面边长的2倍，求侧棱与底面所成角的余弦值．如图，已知P A⊥圆O所在平面，AB为圆O的直径，C是圆周上的任意一点，过A作AE⊥PC于E.求证：AE⊥平面PBC.6.如图所示，若斜线段AB是它在平面α上的射影BO的2倍，则AB与平面α所成的角是()A．60° B．45°C．30° D．120°7．在△ABC中，AB＝AC＝5，BC＝6，P A⊥平面ABC，P A＝8，则P到BC的距离是()A. 5 B．25C．3 5 D．458．正方体ABCD－A1B1C1D1中，BB1与平面ACD1所成的角的余弦值为()A.23 B.33C.23 D.639.)正方体ABCD－A1B1C1D1中，面对角线A1B与对角面BB1D1D所成的角为________．10.如图，在直角三角形BMC中，∠BCM＝90°，∠MBC＝60°，BM＝5，MA＝3且MA⊥AC，AB ＝4，求MC与平面ABC所成角的正弦值．10.如图，AB是圆O的直径，P A垂直于圆O所在的平面，M是圆周上任意一点，AN⊥PM，垂足为点N.求证：AN⊥平面PBM.11如图，在正方体ABCD－A1B1C1D1中，(1)求A1B与平面AA1D1D所成的角；(2)求A1B与平面BB1D1D所成的角．12如图，在三棱锥A－SBC中，∠BSC＝90°，∠ASB＝∠ASC＝60°，SA＝SB＝SC，求直线AS与平面SBC所成的角．13．如图，在四棱锥P－ABCD中，底面ABCD是矩形，P A⊥平面ABCD，AP＝AB＝2，BC＝22，E，F分别是AD，PC的中点．证明：PC⊥平面BEF.14．如图所示，如果MC⊥菱形ABCD所在平面，那么MA与BD的位置关系是()A．平行B．垂直相交C．垂直但不相交D．相交但不垂直15．把正方形ABCD沿对角线AC折起，当以A，B，C，D四点为顶点棱锥体积最大时，直线BD和平面ABC所成的角的大小为()A．90° B．60°C．45° D．30°16．如图，正方体ABCD－A1B1C1D1的棱长为2.(1)求证：AC⊥B1D；(2)求三棱锥C－BDB1的体积．17.如图，P A⊥矩形ABCD所在的平面，M，N分别是AB，PC的中点．(1)求证：MN∥平面P AD；(2)若PD与平面ABCD所成的角为45°，求证：MN⊥平面PCD.18.如图所示，直角△ABC所在平面外一点S，且SA＝SB＝SC，点D为斜边AC的中点．(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC．19.在三棱锥P－ABC中，点P在平面ABC中的射影为点O.(1)若P A＝PB＝PC，则点O是△ABC的________心；(2)若P A⊥PB，PB⊥PC，PC⊥P A，则点O是△ABC的________心.20.如图，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.求证：(1)EF∥平面ABC；(2)AD⊥AC.21..在正方体ABCD－A1B1C1D1中，M，N分别是BC1，CD1的中点，则()A.MN∥C1D1B.MN⊥BC1C.MN⊥平面ACD1D.MN⊥平面ACC122.如图，已知P A⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________.23.如图所示，已知六棱锥P－ABCDEF的底面是正六边形，P A⊥平面ABC，P A＝2AB，则下列结论正确的是()A．PB⊥AD B．平面P AB⊥平面PBCC．直线BC∥平面P AE D．直线PD与平面ABC所成的角为45°24.直角三角形ABC所在平面外有一点S，且SA＝SB＝SC，点D为斜边AC的中点．(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC.。
直线与平面垂直的判定和性质(典型例题解析1)
典例剖析【例1】 如图，设ABCD 是空间四边形，AB ＝AD ，CB ＝CD ，求证：BD ⊥AC.B证明：设BD 的中点为K ，连结AK 、CK ，∵AB ＝AD ，K 为BD 中点,∴AK ⊥BD .同理CK ⊥BD ，且AK ∩KC ＝K .∴BD ⊥平面AKC .∴BD 垂直于平面AKC 内的所有直线.∴BD ⊥AC .点评：证线面垂直，需先有线线垂直，而等腰三角形底边的中线垂直于底边是我们常常遇到的一种类型.做这种类型的题时，应注意抓住这一点.另一方面，线面垂直定义的逆命题是真命题，可作为线面垂直的一个性质来应用.【例2】 已知平面α∩平面β=EF ，且AB ⊥α，AC ⊥β.求证：EF ⊥平面ABC.证明：∵AB ⊥α,EF ⊂α,∴AB ⊥EF .AC ⊥β,EF ⊂β.∴AC ⊥EF .又AB 、AC 相交于A ，∴EF ⊥平面ABC .点评：本例的证法利用了直线和平面垂直的定义得到EF ⊥AB ，EF ⊥AC ，再用直线和平面垂直的定义得到EF ⊥平面ABC .【例3】 如图，正方体ABCD —A 1B 1C 1D 1中，AC ∩BD ＝O ，A 1C 1∩B 1D 1＝O 1.求证： OO 1⊥平面ABCD .A证明：∵ABCD —A 1B 1C 1D 1为正方体,∴AA 1⊥AB ，AA 1⊥AD .∵AB ∩AD ＝A ,∴AA 1⊥平面AC .∵AA 1BB 1，BB 1CC 1,∴AA 1CC 1.∴四边形AA 1C 1C 为平行四边形.∵O、O1分别为AC、A1C1的中点,∴OO1∥AA1，OO1⊥平面AC.点评：正方体是立体几何中重要的几何体，其中有许多重要的线线关系、线面关系，可用于求异面直线的角、距离及线面距离、点面距离等.。
直线、平面垂直的判定及其性质含练习答案
直线、平面垂直的判定及其性质知识点一、直线和平面垂直的定义与判定 定义判定语言描述如果直线l 和平面α内的任意一条直线都垂直，我们就说直线l 与平面互相垂直，记作l ⊥α一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直.图形条件 b 为平面α内的任一直线，而l 对这一直线总有l ⊥αl ⊥m ，l ⊥n ，m ∩n ＝B ，m ⊂α，n ⊂α 结论l ⊥αl ⊥α要点诠释：定义中“平面内的任意一条直线”就是指“平面内的所有直线”，这与“无数条直线”不同（线线垂直线面垂直）直线和平面垂直的性质 性质语言描述 一条直线垂直于一个平面，那么这条直线垂直于这个平面内的所有直线垂直于同一个平面的两条直线平行.图形条件结论1. 如图，直角ABC △所在平面外一点S ，且SA SB SC ==，点D 为斜边AC 的中点． （１） 求证：SD ⊥平面ABC ；（２） 若AB BC =，求证：BD ⊥面SAC ．知识点二、二面角 Ⅰ.二面角：：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle ）. 这条直线叫做二面角的棱，AS C B D这两个半平面叫做二面角的面. 记作二面角AB αβ－－. （简记P AB Q －－）二面角的平面角的三个特征:ⅰ. 点在棱上ⅱ. 线在面内 ⅲ. 与棱垂直Ⅱ.二面角的平面角：在二面角αβ－l －的棱l 上任取一点O ，以点O 为垂足，在半平面,αβ内分别作垂直于棱l 的射线OA 和OB ，则射线OA 和OB 构成的AOB ∠叫做二面角的平面角. 作用：衡量二面角的大小；范围：000180θ<<.例：已知四边形PABC 为空间四边形，∠PCA=90°，△ABC 是边长为32的正三角形，PC=2，D 、E 分别是PA 、AC 的中点，BD=10.试判断直线AC 与平面BDE 的位置关系，并且求出二面角P-AC-B 的大小.知识点三、平面和平面垂直的定义和判定 定义判定文字描述 两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.一个平面过另一个平面的垂线，则这两个平面垂直图形结果α∩β=l α-l-β=90oα⊥β（垂直问题中要注意题目中的文字表述，特别是“任何”“ 随意”“无数”等字眼）例：如图，△ABC 为正三角形，CE ⊥平面ABC ，BD ∥CE ，且CE=AC=2BD ，M 是AE 的中点 求证：①DE=DA;②平面BDM ⊥平面ECA ；③平面DEA ⊥平面ECA.知识点四：直线与方程一．直线的倾斜角定义：x轴正向与直线向上方向之间所成的角叫直线的倾斜角。
直线与平面垂直的判定经典例题
2.3直线、平面垂直的判定及其性质2.3.1直线与平面垂直的判定一、基础达标1．下列说法中正确的个数是()①若直线l与平面α内一条直线垂直，则l⊥α.②若直线l与平面α内两条直线垂直，则l⊥α；③若直线l与平面α内两条相交直线垂直，则l⊥α；④若直线l与平面α内任意一条直线垂直，则l⊥α；⑤若直线l与平面α内无数条直线垂直，则l⊥α.A．1 B．2C．3 D．4答案 B解析对①②⑤，均不能断定该直线与平面垂直，该直线与平面可能平行，可能斜交，也可能在平面内，所以是错误的．正确的是③④，故选B. 2．已知直线m，n是异面直线，则过直线n且与直线m垂直的平面() A．有且只有一个B．至多一个C．有一个或无数个D．不存在答案 B解析若异面直线m、n垂直，则符合要求的平面有一个，否则不存在．3．(2014·淮北高一检测)线段AB的长等于它在平面α内的射影长的2倍，则AB 所在直线与平面α所成的角为() A．30°B．45°C．60°D．120°答案 C解析如图，AC⊥α，AB∩α＝B，则BC是AB在平面α内的射影，则BC＝12AB，所以∠ABC＝60°，它是AB与平面α所成的角．4．空间四边形ABCD 的四边相等，则它的两对角线AC 、BD 的关系是( ) A ．垂直且相交 B ．相交但不一定垂直 C ．垂直但不相交 D ．不垂直也不相交答案 C解析 取BD 中点O ， 连接AO ，CO ， 则BD ⊥AO ，BD ⊥CO ， ∴BD ⊥面AOC ，BD ⊥AC ， 又BD 、AC 异面，∴选C.5．已知△ABC 所在平面外一点P 到△ABC 三顶点的距离都相等，则点P 在平面ABC 内的射影是△ABC 的________． 答案 外心解析 P 到△ABC 三顶点的距离都相等，则点P 在平面ABC 内的射影到△ABC 三顶点的距离都相等，所以是外心．6．(2014·舟山高一检测)如图所示，P A ⊥平面ABC ，△ABC 中BC ⊥AC ，则图中直角三角形的个数有________．答案 4 解析⎭⎬⎫P A ⊥平面ABC BC ⊂平面ABC ⇒⎭⎬⎫P A ⊥BCAC ⊥BC P A ∩AC ＝A ⇒BC ⊥平面P AC ⇒BC ⊥PC ， ∴直角三角形有△P AB 、△P AC 、△ABC 、△PBC . 7．在正方体ABCD －A 1B 1C 1D 1中，求证：A 1C ⊥平面BC 1D . 证明 如图，连接AC ，所以AC ⊥BD .又∵BD⊥A1A，AC∩AA1＝A，AC，A1A⊂平面A1AC，∴BD⊥平面A1AC.∵A1C⊂平面A1AC，∴BD⊥A1C.同理可证BC1⊥A1C.又∵BD∩BC1＝B，BD，BC1⊂平面BC1D，∴A1C⊥平面BC1D.二、能力提升8．(2014·青岛高一检测)如图，在长方体ABCD－A1B1C1D1中，AB＝BC＝2，AA1＝1，则BC1与平面BB1D1D所成角的正弦值为()A.63 B.265C.155 D.105答案 D解析如右图，在长方体ABCD－A1B1C1D1中，连接A1C1、B1D1，交于O点，连接OB，由已知A1B1C1D1是正方形，∴A1C1⊥B1D1.又∵BB1⊥平面A1B1C1D1，OC1⊂平面A1B1C1D1，∴OC1⊥BB1.而BB1∩B1D1＝B1，∴OC1⊥平面BB1D1D.∴OB是BC1在平面BB1D1D内的射影．∴∠C1BO是BC1与平面BB1D1D所成的角．在正方形A1B1C1D1中，OC 1＝12A 1C 1＝1222＋22＝ 2.在矩形BB 1C 1C 中，BC 1＝BC 2＋CC 21＝4＋1＝ 5. ∴sin ∠C 1BO ＝OC 1BC 1＝25＝105.9．在正方体ABCD －A 1B 1C 1D 1中，E 为A 1B 1的中点，则AE 与平面ABC 1D 1所成角的正弦值为________． 答案105解析 如图，取CD 的中点F ，连接EF 交平面ABC 1D 1于O ，连接AO .由已知正方体易知EO ⊥平面ABC 1D 1，所以∠EAO 为AE 与平面ABC 1D 1所成的角，设正方体棱长为1，在Rt △EOA 中，EO ＝12EF ＝12A 1D ＝22，AE ＝⎝ ⎛⎭⎪⎫122＋12＝52，sin ∠EAO ＝EO AE ＝105.所以直线AE 与平面ABC 1D 1所成的角的正弦值为105. 10.如图所示，在矩形ABCD 中，AB ＝1，BC ＝a (a >0)，P A ⊥平面AC ，且P A ＝1，若BC 边上存在点Q ，使得PQ ⊥QD ，则a 的取值范围是________．答案 [2，＋∞)解析 因为P A ⊥平面AC ，QD ⊂平面AC ， 所以P A ⊥QD .又因为PQ ⊥QD ，P A ∩PQ ＝P ， 所以QD ⊥平面P AQ ，所以AQ ⊥QD .①当0<a <2时，由四边形ABCD 是矩形且AB ＝1知，以AD 为直径的圆与BC 无交点，即对BC 上任一点Q ，都有∠AQD <90°，此时BC 边上不存在点Q ，使PQ ⊥QD ；②当a ＝2时，以AD 为直径的圆与BC 相切于BC 的中点Q ，此时∠AQD ＝90°，所以BC 边上存在一点Q ，使PQ ⊥QD ；③当a>2时，以AD为直径的圆与BC相交于点Q1，Q2，此时∠AQ1D＝∠AQ2D＝90°，故BC边上存在两点Q(即Q1与Q2)，使PQ⊥QD.11.(2014·南昌高一检测)如图所示，在棱长为1的正方体ABCD－A1B1C1D1中，点E是棱BC的中点，点F是棱CD上的动点．试确定点F的位置，使得D1E ⊥平面AB1F.解连接A1B，CD1，则A1B⊥AB1，A1D1⊥AB1，又A1D1∩A1B＝A1，∴AB1⊥面A1BCD1，又D1E⊂面A1BCD1，∴AB1⊥D1E.于是D1E⊥平面AB1F⇔D1E⊥AF.连接DE，则DE是D1E在底面ABCD内的射影．∴D1E⊥AF⇔DE⊥AF.∵ABCD是正方形，E是BC的中点，∴当且仅当F是CD的中点时，DE⊥AF，即当点F是CD的中点时，D1E⊥平面AB1F.三、探究与创新12．已知：α∩β＝AB，PQ⊥α于Q，PO⊥β于O，OR⊥α于R，求证：QR⊥AB.证明如图，∵α∩β＝AB，PO⊥β于O，∴PO⊥AB.∵PQ⊥α于Q，∴PQ⊥AB.∵PO∩PQ＝P，∴AB⊥平面PQO.∵OR⊥α于R，∴PQ∥OR.∴PQ与OR确定平面PQRO.即AB⊥平面PQRO.又∵QR⊂平面PQRD，∴QR⊥AB.13．已知四面体ABCD的棱长都相等，Q是AD的中点，求CQ与平面DBC所成的角的正弦值．解过点A作AO⊥平面BCD，连接OD，OB，OC，可知O是△BCD的中心．作QP⊥OD，如图所示．∵QP∥AO，∴QP⊥平面BCD.连接CP，则∠QCP即为CQ与平面DBC所成的角．设四面体的棱长为a，∵在正△ACD中，Q是AD的中点，∴CQ＝3 2a.∵QP∥AO，Q是AD的中点，O为△BCD的重心，∴QP＝12AO＝12a2－⎝⎛⎭⎪⎫23×32a2＝12×63a＝66a，即sin∠QCP＝QPCQ＝2 3.∴CQ与平面DBC所成角的正弦值为2 3.。
直线、平面垂直的判定及其性质经典例题
直线、平面垂直的判定及其性质经典例题经典例题透析类型一、直线和平面垂直的定义1．下列命题中正确的个数是( )①如果直线与平面内的无数条直线垂直，则；②如果直线与平面内的一条直线垂直，则；③如果直线不垂直于，则内没有与垂直的直线；④如果直线不垂直于，则内也可以有无数条直线与垂直．A．0B．1 C．2 D．3答案：B解析：当内的无数条直线平行时，与不一定垂直，故①不对；当与内的一条直线垂直时，不能保证与垂直，故②不对；当与不垂直时，可能与内的无数条直线垂直，故③不对；④正确．故选B．总结升华：注意直线和平面垂直定义中的关键词语．举一反三：【变式1】（2010 山东）在空间，下列命题正确的是A．平行直线的平行投影重合B．平行于同一直线的两个平面平行C．垂直于同一平面的两个平面平行D．垂直于同一平面的两条直线平行答案：D解析：A项，平行直线的平行投影也可以是两条平行线；B项，平行于同一直线的两个平面可平行、可相交；C项，垂直于同一平面的两个平面可平行、可相交；D项，正确．总结升华：本题主要考察对基础知识的掌握．类型二、直线和直线、平面垂直的判定2．（2011 广东理18）如图，在椎体P-ABCD中，ABCD是边长为1的菱形，且∠DAB=60，,PB=2, E,F分别是BC,PC的中点．（1）证明：AD 平面DEF;（2）求二面角P-AD-B的余弦值．解析：（1）证明：取AD中点G，连接PG，BG，BD．∵PA=PD，∴，在中，，∴为等边三角形，∴，∴AD⊥平面PBG，∴又PB//EF，得，又∵DE//GB，得AD⊥DE，又，∴AD⊥平面DEF．（2）为二面角P—AD—B的平面角，在，在中，总结升华：要判定一条已知直线和一个平面是否垂直，取决于在这个平面内能否找出两条相交直线和这条直线垂直，至于这两条相交直线是否和已知直线有公共点，则无关紧要.举一反三：【变式1】如图所示，直三棱柱中，∠ACB=90°，AC=1，，侧棱，侧面的两条对角线交点为D，的中点为M．求证：平面CBD ⊥平面BDM．证明：如下图，连接、、，则．∵，∴为等腰三角形．又知D为其底边的中点，∴．∵，，∴．又，∴．∵为直角三角形，D为的中点，∴，．又，，∴．．即CD⊥DM．∵、为平面BDM内两条相交直线，∴CD⊥平面BDM．又∵，∴平面CBD⊥平面BDM．总结升华：处理面面垂直问题转化为处理线面垂直问题，进一步转化为处理线线垂直问题.所以证明平面与平面垂直，只要在一个平面内找到两条相交直线和另一个平面内的一条直线垂直即可.类型三、直线和平面所成的角3．如图所示，已知∠BOC在平面内，OA是平面的斜线，且∠AOB=∠AOC=60°，OA=OB=OC=，BC=，求OA和平面所成的角．解析：∵，∠AOB=∠AOC=60°，∴△AOB、△AOC为正三角形，∴．∵，∴，∴△ABC为直角三角形．同理△BOC也为直角三角形．过A作AH垂直平面于H，连接OH，∵AO=AB=AC，∴OH=BH=CH，H为△BOC的外心．∴H在BC上，且H为BC的中点．∵Rt△AOH中，，∴，∴∠AOH=45°．即AO和平面所成角为45°．总结升华：(1)确定点在平面内的射影的位置，是解题的关键，因为只有确定了射影的位置，才能找到直线与平面所成的角，才能将空间的问题转化为平面的问题来解．(2)求斜线与平面所成的角的程序：①寻找过直线上一点与平面垂直的直线；②连接垂足和斜足得出射影，确定出所求解；③把该角放入三角形计算．(3)直线和平面所成的角，也应考虑到直线和平面垂直、直线和平面平行或在平面内诸情况，也就是直线和平面成90°角和0°角的情况，所以求线面所成角时，应想到以上两种情况．举一反三：【变式1】（2011 全国大纲19）如图，四棱锥中，,，侧面为等边三角形，．(Ⅰ)证明：；(Ⅱ)求与平面所成角的大小．解析：（I）取AB中点E，连结DE、SE，∴四边形BCDE为矩形，DE=CB=2，∵侧面为等边三角形∴又∵SD=1，，∴为直角．又∵，∴AB⊥平面SDE，∴．又SD与两条相交直线AB、SE都垂直．∴SD⊥平面SAB．（II）作垂足为F，FG⊥BC，垂足为G，连结SG∵AB⊥平面SDE，∴平面ABCD⊥平面SED．∴SF⊥平面ABCD，∵∴，又∵FG⊥BC，∴BC⊥平面SFG，∵∴平面SBC⊥平面SFG．作，H为垂足，则FH⊥平面SBC．又∵在中，，在中，∴，即F到平面SBC的距离为．∵ED//BC，∴ED//平面SBC，∴E到平面SBC的距离d也是．设AB与平面SBC所成的角为α，则．∴与平面所成的角为．【变式2】如图所示，在正三棱柱中，侧棱长为，底面三角形的边长为1，则与侧面所成的角是________．答案：解析：如下图．由题取AC中点O，连接BO．则BO⊥平面．故为与平面所成角．又在中，，．∴，∴．类型四、二面角4．如图所示，在四面体ABCD中，△ABD、△ACD、△BCD、△ABC都全等，且，，求以BC为棱，以面BCD和面BCA为面的二面角大小．解析：取BC的中点E，连接AE、DE，∵AB=AC，∴AE⊥BC．又∵△ABD≌△ACD，AB=AC，∴DB=DC，∴DE⊥BC．∴∠AED为二面角的平面角．又∵△ABC≌△BDC，∴AD=BC=2，在Rt△DEB中，DB=，BE=1，∴，同理．在△AED中，∵，，∴，∴∠AED=90°．∴以面BCD和面ABC为面的二面角大小为90°．总结升华：确定二面角的平面角，常常用定义来确定．举一反三：【变式1】已知D、E分别是正三棱柱的侧棱和上的点，且．求过D、E、C1的平面与棱柱的下底面所成的二面角的大小．解析：如图，在平面内延长DE和交于点F，则F是面与面的公共点，为这两个平面的交线，∴所求二面角就是的平面角．∵，且，∴E、分别DF和A1F的中点．∵，∴．又面，面，∴面，而面．∴．∴是二面角的平面角，由已知，∴．总结升华：当所求的二面角没有给出它的棱时，找出二面角的两个面的两个公共点，从而找出它的棱，进而求其平面角的大小即可．类型五、平面与平面垂直的判定5．在四面体ABCD中，，AB=AD=CB=CD=AC=，如图所示．求证：平面ABD⊥平面BCD．证明：∵△ABD与△BCD是全等的等腰三角形，∴取BD的中点E，连接AE、CE，则AE⊥BD，BD⊥CE，∴∠AEC为二面角A-BD-C的平面角．在△ABD中，，，∴．同理．在△AEC中，，，由于，∴AE⊥CE，即∠AEC=90°，即二面角A-BD-C的平面角为90°．∴平面ABD⊥平面BCD．总结升华：利用两个平面互相垂直的定义可以直接判定两个平面垂直，判定的方法是(1)找出两个相交平面的平面角；(2)证明这个平面角是直角；(3)根据定义，这两个平面互相垂直．举一反三：【变式1】如图所示，在空间四边形ABCD中，AB=BC，CD=DA，E、F、G分别为CD、DA和对角线AC的中点，求证：平面BEF⊥平面BGD．证明：∵AB=BC，CD=AD，G是AC的中点，∴BG⊥AC，DG⊥AC，∴AC⊥平面BGD．又EF∥AC，∴EF⊥平面BGD．∵EF平面BEF，∴平面BDG⊥平面BEF．总结升华：证面面垂直的方法：(1)证明两平面构成的二面角的平面角为90°；(2)证明一个平面经过另一个平面的一条垂线,将证明“面面垂直”的问题转化为证明线面垂直的问题.【变式2】如图所示，在Rt△AOB中，，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B-AO-C是直二面角．D是AB的中点．求证：平面COD⊥平面AOB；证明：由题意，CO⊥AO，BO⊥AO，∴∠BOC是二面角B-AO-C的平面角．又∵二面角B-AO-C是直二面角．∴CO⊥BO．又∵AO∩BO=O，∴CO⊥平面AOB．又CO平面COD，∴平面COD⊥平面AOB．【变式3】过点P引三条长度相等但不共面的线段PA、PB、PC，有∠APB=∠APC=60°，∠BPC=90°，求证：平面ABC⊥平面BPC．证明：如图，已知PA=PB=PC=a，由∠APB=∠APC=60°，△PAC，△PAB为正三角形，则有：PA=PB=PC=AB=AC=a，取BC中点为E直角△BPC中，，，由AB=AC，AE⊥BC，直角△ABE中，，，，在△PEA中，，，∴，平面ABC⊥平面BPC．类型六、综合应用6．如图所示，△ABC为正三角形，CE⊥平面ABC，BD∥CE，且CE=AC=2BD，M是AE的中点，求证：(1)DE=DA；(2)平面BDM⊥平面ECA；(3)平面DEA⊥平面ECA．证明：(1)取EC的中点F，连接DF．∵CE⊥平面ABC，∴CE⊥BC．易知DF∥BC，CE⊥DF．∵BD∥CE，∴BD⊥平面ABC．在Rt△EFD和Rt△DBA中，∵，，∴Rt△EFD≌Rt△DBA．故DE=AD．(2)取AC的中点N，连接MN、BN，MN CF．∵BD CF，∴MN BD．N平面BDM．∵EC⊥平面ABC，∴EC⊥BN．又∵AC⊥BN，∴BN⊥平面ECA．又∵BN平面MNBD，∴平面BDM⊥平面ECA．(3)∵DM∥BN，BN⊥平面ECA，∴DM⊥平面ECA．又∵DM平面DEA，∴平面DEA⊥平面ECA．总结升华：本题涉及线面垂直、面面垂直的性质和判定，这里证明的关键是BN⊥平面ECA，应充分体会线线垂直、线面垂直与面面垂直的关系．7．如图所示，已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点．(1)求证：MN∥平面PAD；(2)求证：MN⊥CD；(3)若∠PDA=45°，求证：MN⊥平面PCD．思路点拨：要证明MN∥平面PAD，须证MN平行于平面PAD内某一条直线．注意到M、N分别为AB，PC的中点，可取PD的中点E，从而只须证明MN∥AE即可．证明如下．证明：(1)取PD的中点E，连接AE、EN，则，故AMNE为平行四边形，∴MN∥AE．∵AE平面PAD，MN平面PAD，∴MN∥平面PAD．(2)要证MN⊥CD，可证MN⊥AB．由(1)知，需证AE⊥AB．∵PA⊥平面ABCD，∴PA⊥AB．又AD⊥AB，∴AB⊥平面PAD．∴AB⊥AE．即AB⊥MN．又CD∥AB，∴MN⊥CD．(3)由(2)知，MN⊥CD，即AE⊥CD，再证AE⊥PD即可．∵PA⊥平面ABCD，∴PA⊥AD．又∠PDA=45°，E为PD的中点．∴AE⊥PD，即MN⊥PD．又MN⊥CD，∴MN⊥平面PCD．总结升华：本题是涉及线面垂直、线面平行、线线垂直诸多知识点的一道综合题．(1)的关键是选取PD的中点E，所作的辅助线使问题处理的方向明朗化．线线垂直→线面垂直→线线垂直是转化规律．。
直线、平面垂直的判定及其性质_练习题1(答案)
直线、平面垂直的判定及其性质一、选择题1、“直线l垂直于平面α内的无数条直线”是“l⊥α”的（）A、充分条件B、必要条件C、充要条件D、既不充分也不必要条件2、如果一条直线l与平面α的一条垂线垂直，那么直线l与平面α的位置关系是（）A、l⊂αB、l⊥αC、l∥αD、l⊂α或l∥α3、若两直线a⊥b，且a⊥平面α，则b与α的位置关系是（）A、相交B、b∥αC、b⊂αD、b∥α，或b⊂α4、a∥α，则a平行于α内的( )A、一条确定的直线B、任意一条直线C、所有直线D、无数多条平行线5、如果直线a∥平面α，那么直线a与平面α内的 ( )A、一条直线不相交B、两条直线不相交C、无数条直线不相交D、任意一条直线都不相交6、若直线l上有两点P、Q到平面α的距离相等，则直线l与平面α的位置关系是( )A、平行B、相交C、平行或相交D、平行、相交或在平面α内二、填空题7、过直线外一点作直线的垂线有条；垂面有个；平行线有条；平行平面有个.8、过平面外一点作该平面的垂线有条；垂面有个；平行线有条；平行平面有个.9、过一点可作________个平面与已知平面垂直.10、过平面α的一条斜线可作_________个平面与平面α垂直.11、过平面α的一条平行线可作_________个平面与平面α垂直.三、解答题12、求证：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面13、过一点和已知平面垂直的直线只有一条14、有一根旗杆AB高8m，它的顶端A挂一条长10m的绳子，拉紧绳子并把它的下端放在地面上的两点（和旗杆脚不在同一直线上）,C D，如果这两点都和旗杆脚B的距离是6m，那么旗杆就和地面垂直，为什么？15、已知直线l⊥平面α，垂足为A，直线AP⊥l求证：AP在α内参考答案一、选择题1、B ；2、D ；3、D ；4、D ；5、D ；6、D二、填空题7、无数，一，一，无数8、一，无数，无数，一9、无数10、一个11、一个三、解答题12、已知：a∥b,a⊥α 求证：b⊥α证明：设m 是α内的任意一条直线αααα⊥⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫⊥⇒⎭⎬⎫⊂⊥b m m b b a m a m a //13、已知：平面α和一点P 求证：过点P 与α垂直的直线只有一条证明：不论P 在平面α内或外，设直线PA α⊥，垂足为A（或P ） 若另一直线PB α⊥，设,PA PB 确定的平面为β，且a αβ=I ∴,PA a PB a ⊥⊥又∵,PA PB 在平面β内，与平面几何中的定理矛盾 所以过点P 与α垂直的直线只有一条βαa P B A14、解：在ABC∆和ABD∆中，∵8,6,10=====AB m BC BD m AC AD m Array∴222222+=+==6810AB BC AC222222+=+==AB BD AD6810∴90ABC ABD∠=∠=o即,⊥⊥AB BC AB BD又∵,,B C D不共线∴AB⊥平面BCD，即旗杆和地面垂直；15、证明：设AP与l确定的平面为β如果AP不在α内，则可设α与β相交于直线AM∵l⊥α，∴l⊥AM又AP⊥l，于是在平面β内过点A有两条直线垂直于l，这是不可能的所以AP一定在α。
直线与平面垂直的判定
A 平行
B 垂直
L
C 相交
D 不确定
C
A
B
一条直线与一个平面内的两条相交直线都垂直，则 该直线与此平面垂直．
la
l
l b a
b
l
b
Aa
a b A
作用：
线不在多，相交就灵
判定直线与平面垂直． 记忆：线线垂直，则线面垂直
(2)a ,b a
（3）a b ， a b
上节思考题，你完成了吗？
（1）如图，点P 是平行四边
2. 线面角的概念及范围 范围：0，90 3．直线与平面垂直的判定
（1）利用定义；垂直于平面内任意一条直线
（2）利用判定定理．
线线垂直
线面垂直
3．数学思想方法：转化的思想
空间问题
平面问题
P
1、如图，圆O所在一平面为 ，
AB是圆O 的直径，C 是圆周上一点,
且PA AC, PA AB,求证：
（1）PA BC （2）BC 平面PAC
四、直线和平面所成的角：
如图所示，一条直线PA和平面 相交，但不垂直，这 条直线叫这个平面的斜线，斜线和平面的交点A叫做斜足。
过斜线上斜足以外的一点P向平面引垂线PO ，过垂 足O和斜足A的直线AO叫做斜线在这个平面上的射影。
斜线和射影所成的锐角叫做这条直线和平面所成的角。
P 斜线
斜足 A
O
范围：0，90
C
新课讲解：
画直线与平面垂直时，通常把直线画成与表 示平面的平行四边形的一边垂直，如图所示．
直线与平面的 一条边垂直
l
P
观察下面四个图，有什么结论？
l
l
直线与平面垂直的典型例题.doc
v1.0可编辑可修改直线与平面垂直的典型例题例 1 判断题：正确的在括号内打“√”号，不正确的打“×”号．(1) 一条直线和一个平面平行，它就和这个平面内的任何直线平行．（）(2) 如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直．（）(3) 垂直于三角形两边的直线必垂直于第三边．（）(4) 过点 A 垂直于直线a的所有直线都在过点 A 垂直于的平面内．（）(5) 如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面．（）例 2 在正方体ABCD A1 B1C1 D1中，E是 BB1的中点，O是底面正方形ABCD 的中心，求证： OE平面ACD1例 3 如图，在△ABC中， B 90，SA 平面 ABC ，点 A 在 SB 和 SC 上的射影分别为 M、N ，求证： MN SC例 4 如图，AB为平面的斜线，B为斜足，AH垂直平面于H点，BC为平面内的直线，ABH，HBC，ABC，求证：cos cos cos例 5 如图，已知正方形ABCD 边长为4，CG平面ABCD，CG 2 ， E、F 分别是AB、 AD 中点，求点 B 到平面 GEF 的距离例 6 如图所示，直角ABC 所在平面外一点S ，且 SA SB SC．(1) 求证：点 S 与斜边 AC 中点 D 的连线 SD 面 ABC ；(2) 若直角边 BA BC ，求证： BD 面 SAC．例 7 如图所示，BAC 90 ．在平面内，PA是的斜线，PAB PAC 60 ．求PA 与平面所成的角．例8如图，ABCD是正方形，SA ABCD，过A且垂直于SC的平面交SB SC、垂直于平面、SD分别于点 E 、 F 、 G ，求证： AE SB， AG SD ．例 9 如图，求证：如果一个角所在平面外一点到角的两边距离相等，那么这一点在平面内的射影在这个角的平分线上．例 10如图，已知空间四边形ABCD 的边 BC AC ， AD BD ，引 BE CD ， E 为垂足，作 AH BE 于 H ，求证：AH平面BCD．例 11如图，已知在ABC 中，BAC 60 ，线段AD平面ABC，AH平面DBC，H为垂足．求证： H 不可能是DBC 的垂心．例 12如图，在正方体ABCD A1 B1C1D1中，EF为异面直线A1 D 与AC的公垂线，求证：EF // BD1．。
直线与平面的垂直练习题
直线与平面垂直练习题
1.如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平
面ABC ，垂足O 落在线段AD 上．证明：AP ⊥BC ；
2如图, 在直三棱柱ABC －A 1B 1C 1中，AC BC ⊥，点D 是AB 的中点，111D A B 是中点
求证：（1）AC
1//平面CDB 1；
（2）11//AC D B CD 面面
（3）1AC BC ⊥
3.如图，四棱锥S ABCD -的底面是正方形，SD ⊥平面ABCD ，E 是SD 的中点．
（1）求证：//SB 平面EAC ；
（2）求证：AC BE ⊥．
4.如图2－36：已知PA ⊥⊙O 所在的平面，AB 是⊙O 的直径，C 是异于A 、B 的⊙O 上任意一点，过A 作AE ⊥PC 于E
求证：（1）BC PAC ⊥面 （2）PBC PAC ⊥面面 (3)AE ⊥平面PBC 。
5. 直三棱柱ABC －A 1B 1C 1中， AC =BC =AA 1=2，∠ACB =90︒.E 为BB 1的中点，D 点
在AB 上且DE = 3 .
（Ⅰ）求证：CD ⊥平面A
1ABB 1；
（Ⅱ）求三棱锥A 1－C DE 的体积.
6. 已知矩形ABCD 所在平面外一点P ，PA ⊥平面ABCD ，E 、F 分别
是 AB 、PC 的中点．
(1) 求证：EF ∥平面PAD ；
(2) 求证：EF ⊥CD ；
(3) 若∠PDA ＝45°，EF ⊥面PCD ．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.3直线、平面垂直的判定及其性质
2.3.1直线与平面垂直的判定
一、基础达标
1．下列说法中正确的个数是()
①若直线l与平面α内一条直线垂直，则l⊥α.
②若直线l与平面α内两条直线垂直，则l⊥α；
③若直线l与平面α内两条相交直线垂直，则l⊥α；
④若直线l与平面α内任意一条直线垂直，则l⊥α；
⑤若直线l与平面α内无数条直线垂直，则l⊥α.
A．1 B．2
C．3 D．4
答案 B
解析对①②⑤，均不能断定该直线与平面垂直，该直线与平面可能平行，可能斜交，也可能在平面内，所以是错误的．正确的是③④，故选B. 2．已知直线m，n是异面直线，则过直线n且与直线m垂直的平面() A．有且只有一个B．至多一个
C．有一个或无数个D．不存在
答案 B
解析若异面直线m、n垂直，则符合要求的平面有一个，否则不存在．3．(2014·淮北高一检测)线段AB的长等于它在平面α内的射影长的2倍，则AB 所在直线与平面α所成的角为() A．30°B．45°
C．60°D．120°
答案 C
解析如图，AC⊥α，AB∩α＝B，则BC是AB在平面α
内的射影，则BC＝1
2AB，所以∠ABC＝60°，它是AB与
平面α所成的角．
4．空间四边形ABCD 的四边相等，则它的两对角线AC 、BD 的关系是( ) A ．垂直且相交 B ．相交但不一定垂直 C ．垂直但不相交 D ．不垂直也不相交
答案 C
解析 取BD 中点O ， 连接AO ，CO ， 则BD ⊥AO ，BD ⊥CO ， ∴BD ⊥面AOC ，BD ⊥AC ， 又BD 、AC 异面，∴选C.
5．已知△ABC 所在平面外一点P 到△ABC 三顶点的距离都相等，则点P 在平面ABC 内的射影是△ABC 的________． 答案 外心
解析 P 到△ABC 三顶点的距离都相等，则点P 在平面ABC 内的射影到△ABC 三顶点的距离都相等，所以是外心．
6．(2014·舟山高一检测)如图所示，P A ⊥平面ABC ，△ABC 中BC ⊥AC ，则图中直角三角形的个数有________．
答案 4 解析
⎭
⎬⎫
P A ⊥平面ABC BC ⊂平面ABC ⇒
⎭
⎬⎫
P A ⊥BC
AC ⊥BC P A ∩AC ＝A ⇒BC ⊥平面P AC ⇒BC ⊥PC ， ∴直角三角形有△P AB 、△P AC 、△ABC 、△PBC . 7．在正方体ABCD －A 1B 1C 1D 1中，求证：A 1C ⊥平面BC 1D . 证明 如图，连接AC ，所以AC ⊥BD .
又∵BD⊥A1A，AC∩AA1＝A，
AC，A1A⊂平面A1AC，
∴BD⊥平面A1AC.
∵A1C⊂平面A1AC，∴BD⊥A1C.
同理可证BC1⊥A1C.
又∵BD∩BC1＝B，BD，BC1⊂平面BC1D，
∴A1C⊥平面BC1D.
二、能力提升
8．(2014·青岛高一检测)如图，在长方体ABCD－A1B1C1D1中，AB＝BC＝2，AA1＝1，则BC1与平面BB1D1D所成角的正弦值为()
A.
6
3 B.
26
5
C.15
5 D.
10
5
答案 D
解析如右图，在长方体ABCD－A1B1C1D1中，连接A1C1、B1D1，交于O点，连接OB，由已知A1B1C1D1是正方形，∴A1C1⊥B1D1.
又∵BB1⊥平面A1B1C1D1，OC1⊂平面A1B1C1D1，
∴OC1⊥BB1.而BB1∩B1D1＝B1，
∴OC1⊥平面BB1D1D.
∴OB是BC1在平面BB1D1D内的射影．
∴∠C1BO是BC1与平面BB1D1D所成的角．
在正方形A1B1C1D1中，
OC 1＝12A 1C 1＝1
222＋22＝ 2.
在矩形BB 1C 1C 中，BC 1＝BC 2＋CC 21＝4＋1＝ 5. ∴sin ∠C 1BO ＝OC 1BC 1＝25
＝105.
9．在正方体ABCD －A 1B 1C 1D 1中，E 为A 1B 1的中点，则AE 与平面ABC 1D 1所成角的正弦值为________． 答案
105
解析 如图，取CD 的中点F ，连接EF 交平面ABC 1D 1于O ，连接AO .
由已知正方体易知EO ⊥平面ABC 1D 1，所以∠EAO 为AE 与平面ABC 1D 1所成的角，设正方体棱长为1，在Rt △EOA 中，EO ＝12EF ＝12A 1D ＝2
2，AE ＝
⎝ ⎛⎭
⎪⎫122
＋12＝52，sin ∠
EAO ＝EO AE ＝105.所以直线AE 与平面ABC 1D 1所成的角的正弦值为10
5. 10.如图所示，在矩形ABCD 中，AB ＝1，BC ＝a (a >0)，P A ⊥平面AC ，且P A ＝1，若BC 边上存在点Q ，使得PQ ⊥QD ，则a 的取值范围是________．
答案 [2，＋∞)
解析 因为P A ⊥平面AC ，QD ⊂平面AC ， 所以P A ⊥QD .又因为PQ ⊥QD ，P A ∩PQ ＝P ， 所以QD ⊥平面P AQ ，所以AQ ⊥QD .
①当0<a <2时，由四边形ABCD 是矩形且AB ＝1知，以AD 为直径的圆与BC 无交点，即对BC 上任一点Q ，都有∠AQD <90°，此时BC 边上不存在点Q ，使PQ ⊥QD ；
②当a ＝2时，以AD 为直径的圆与BC 相切于BC 的中点Q ，此时∠AQD ＝90°，所以BC 边上存在一点Q ，使PQ ⊥QD ；
③当a>2时，以AD为直径的圆与BC相交于点Q1，Q2，此时∠AQ1D＝∠AQ2D
＝90°，故BC边上存在两点Q(即Q1与Q2)，使PQ⊥QD.
11.(2014·南昌高一检测)如图所示，在棱长为1的正方体ABCD－A1B1C1D1中，
点E是棱BC的中点，点F是棱CD上的动点．试确定点F的位置，使得D1E ⊥平面AB1F.
解连接A1B，CD1，则A1B⊥AB1，A1D1⊥AB1，又A1D1∩A1B＝A1，∴AB1⊥面A1BCD1，
又D1E⊂面A1BCD1，
∴AB1⊥D1E.
于是D1E⊥平面AB1F⇔D1E⊥AF.
连接DE，则DE是D1E在底面ABCD内的射影．
∴D1E⊥AF⇔DE⊥AF.
∵ABCD是正方形，E是BC的中点，
∴当且仅当F是CD的中点时，DE⊥AF，
即当点F是CD的中点时，D1E⊥平面AB1F.
三、探究与创新
12．已知：α∩β＝AB，PQ⊥α于Q，PO⊥β于O，OR⊥α于R，求证：QR⊥AB.
证明如图，∵α∩β＝AB，PO⊥β于O，
∴PO⊥AB.
∵PQ⊥α于Q，∴PQ⊥AB.
∵PO∩PQ＝P，∴AB⊥平面PQO.
∵OR⊥α于R，∴PQ∥OR.∴PQ与OR确定平面PQRO.
即AB⊥平面PQRO.
又∵QR⊂平面PQRD，∴QR⊥AB.
13．已知四面体ABCD的棱长都相等，Q是AD的中点，求CQ与平面DBC所成的角的正弦值．
解过点A作AO⊥平面BCD，
连接OD，OB，OC，可知O是△BCD的中心．作QP⊥OD，如图所示．∵QP∥AO，
∴QP⊥平面BCD.
连接CP，
则∠QCP即为CQ与平面DBC所成的角．
设四面体的棱长为a，
∵在正△ACD中，Q是AD的中点，
∴CQ＝
3 2a.
∵QP∥AO，Q是AD的中点，O为△BCD的重心，
∴QP＝1
2AO＝
1
2a
2－
⎝
⎛
⎭
⎪
⎫
2
3×
3
2a
2
＝1
2×
6
3a＝
6
6a，
即sin∠QCP＝QP
CQ＝
2 3.
∴CQ与平面DBC所成角的正弦值为
2 3.。