推荐-预应力框架梁计算书 精品
盖梁预应力张拉计算书

盖梁预应力张拉计算书一、工程概述本工程为_____桥梁盖梁预应力张拉施工。
盖梁采用预应力混凝土结构,以提高其承载能力和抗裂性能。
预应力钢束采用高强度低松弛钢绞线,规格为_____。
二、设计参数1、混凝土强度等级:_____2、预应力钢绞线规格:_____3、张拉控制应力:_____4、单根钢绞线截面积:_____5、钢绞线弹性模量:_____三、张拉力计算1、每束钢绞线的张拉力根据设计要求,张拉控制应力为σcon,单根钢绞线截面积为Ap,则每束钢绞线的张拉力P为:P =σcon × Ap × n其中,n 为每束钢绞线的根数。
2、千斤顶的张拉力考虑到千斤顶的摩阻等因素,千斤顶的张拉力应适当增大,通常乘以一个系数 k,k 一般取值为 105 左右。
千斤顶张拉力= k × P四、伸长量计算1、理论伸长量根据预应力钢绞线的弹性模量 Ep、预应力钢束的长度 L 和平均张拉力 Pp,理论伸长量ΔL 按下式计算:ΔL =(Pp × L)/(Ap × Ep)平均张拉力 Pp 的计算:Pp = P ×(1 e (kx +μθ))/(kx +μθ)其中,x 为从张拉端至计算截面的孔道长度,θ 为从张拉端至计算截面曲线孔道部分切线的夹角之和(rad),k 为孔道每米局部偏差对摩擦的影响系数,μ 为钢绞线与孔道壁的摩擦系数。
2、实际伸长量实际伸长量的测量应在初应力(一般为10%σcon)下测量伸长量ΔL1,然后在张拉到控制应力σcon 时测量伸长量ΔL2,则实际伸长量ΔL'为:ΔL' =ΔL2 ΔL1同时,还应考虑千斤顶内钢绞线的工作长度的伸长量。
五、千斤顶与油压表的校验在进行预应力张拉前,千斤顶和油压表必须进行配套校验。
通过校验得出千斤顶的油压与张拉力的关系曲线,以便在张拉过程中根据油压表读数准确控制张拉力。
六、预应力张拉施工步骤1、准备工作清理锚垫板上的杂物,检查锚垫板与孔道是否垂直。
梁板预应力张拉及计算书
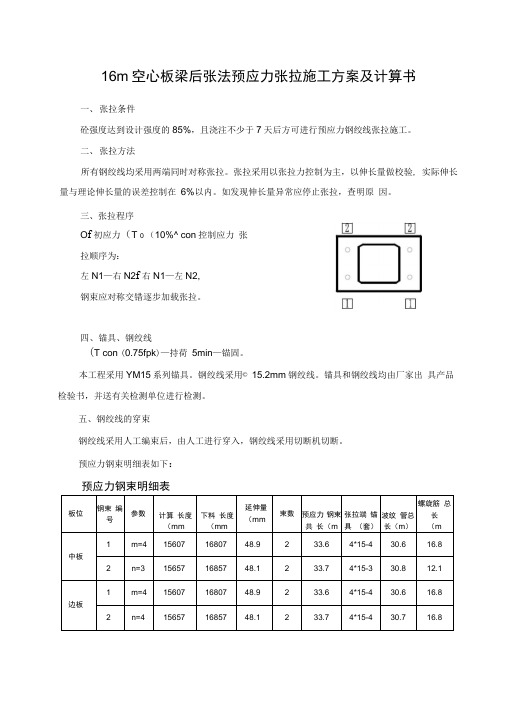
16m空心板梁后张法预应力张拉施工方案及计算书一、张拉条件砼强度达到设计强度的85%,且浇注不少于7天后方可进行预应力钢绞线张拉施工。
二、张拉方法所有钢绞线均采用两端同时对称张拉。
张拉采用以张拉力控制为主,以伸长量做校验, 实际伸长量与理论伸长量的误差控制在6%以内。
如发现伸长量异常应停止张拉,查明原因。
三、张拉程序拉顺序为:左N1—右N2f右N1—左N2,钢束应对称交错逐步加载张拉。
四、锚具、钢绞线(T con (0.75fpk)—持荷5min—锚固。
本工程采用YM15系列锚具。
钢绞线采用© 15.2mm钢绞线。
锚具和钢绞线均由厂家出具产品检验书,并送有关检测单位进行检测。
五、钢绞线的穿束钢绞线采用人工编束后,由人工进行穿入,钢绞线采用切断机切断。
预应力钢束明细表如下:预应力钢束明细表六、千斤顶、油表千斤顶、油表均经有关检测单位标定,千斤顶的工作架由钢管焊接而成,升降采用倒链进行抬升。
七、张拉操作采用柳州雷姆预应力机械有限公司生产的预应力智能张拉系统进行张拉。
千斤顶张拉进油升压必须缓慢、均匀、平稳,回油降压时应缓慢松开油阀,并使油缸回程到底。
梁端张拉工每张拉到整数时举手示意保持两端千斤顶力争同步工作。
八、实际伸长量的计算和测量初应力数值到达后,应在预应力钢束的两端精确的标以记号,预应力钢束的伸长量从记号起量,张拉力和伸长量的读数应在张拉过程中分阶段读出。
△L=S1+A L2式中:△L――为预应力筋的实际伸长量△L――为100%长拉力时预应力筋的实测伸长量△L2――为初应力时预应力筋的推算伸长量(本工程取值6mm 上式中△ L2= (c o/Ep)XL式中:c 0——为0.1 c con = 1860 X 0.75 X 0.1= 139.5MPaL――预应力筋长度其余各符号的含义与上述相同九、伸长率误差的计算(实测伸长量-理论伸长值)/理论伸长值X 100%,张拉过程中该误差应小于6%。
预应力梁计算书
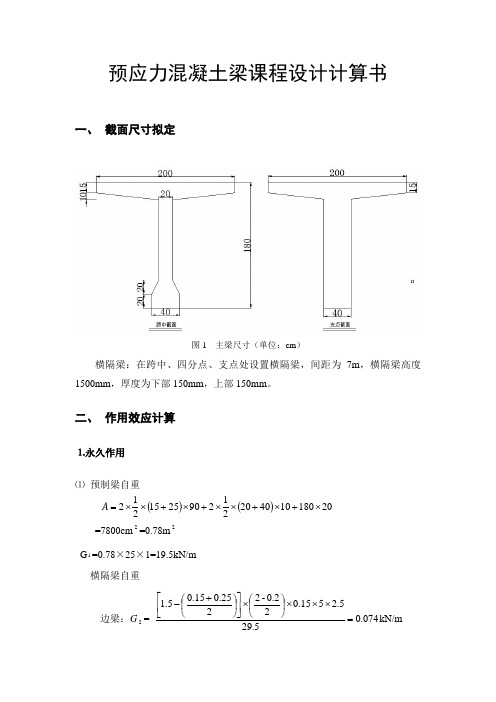
预应力混凝土梁课程设计计算书一、 截面尺寸拟定图1 主梁尺寸(单位:cm )横隔梁:在跨中、四分点、支点处设置横隔梁,间距为7m ,横隔梁高度1500mm ,厚度为下部150mm ,上部150mm 。
二、 作用效应计算⒈永久作用 ⑴ 预制梁自重()()20180104020212902515212⨯+⨯+⨯⨯+⨯+⨯⨯=A=7800cm 2=0.78m 2 G 1=0.78×25×1=19.5kN/m 横隔梁自重边梁:G 2= 074.05.295.2515.022.0-2225.015.05.1=⨯⨯⨯⎪⎭⎫⎝⎛⨯⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-kN/m中梁:G 3 =0.074×2=0.148kN/m ⑵ 二期恒载集度桥面铺装10cm 防水混凝土铺装:0.1×10×25=25kN/m2cm 沥青混凝土铺装:0.02×10×21=4.2kN/m 若将桥面铺装均摊给5片梁则: G 4=(25+4.2)/5=5.84kN/m 恒载集度边梁:g 1=19.5+0.074+5.84=25.414kN/m 中梁:g 2=19.5+0.148+5.84=25.488kN/m ⑶永久作用效应设x 为计算截面离左支座距离,令x l α=/,主梁弯矩和剪力的计算公式分别为:()2112M l gααα=- ()1122c Q l gα=-⋅表1 1号梁永久作用的弯矩和剪力位置作用效应跨中 α=0.5 四分点 α=0.25 支点 α=0.00 一期弯矩(kN m)⋅2009.75 1507.31 0 剪力 (kN) 0 140.25 280.50 二期弯矩 (kN m)⋅ 599.62 449.71 0 剪力()kN0 41.84 83.69 ∑弯矩 (kN m)⋅2609.37 1957.03 0 剪力()kN182.09364.19表2 2、3号梁永久作用的弯矩和剪力位置 作用效应跨中 α=0.5 四分点 α=0.25 支点 α=0.00 一期弯矩(kN m)⋅2017.75 1513.01 0 剪力 (kN) 0 140.78 281.56 二期弯矩 (kN m)⋅ 599.62 449.71 0 剪力()kN0 41.84 83.69 ∑弯矩 (kN m)⋅2616.97 1962.72 0 剪力()kN182.62365.25⒉可变作用 ⑴冲击系数简支梁桥的基频可采用下列公式估算: 22c c EI f l m π== 62.2590337.01045.366.28214.3102⨯⨯⨯⨯= 4.05 其中:62.259081.925414===g G m c 根据本桥的基频,可计算出汽车荷载的冲击系数为 μ=0.176ln f -0.0157=0.22按«桥规»规定两车道的车道折减系数为1 ⑵横向分布系数本算例横向分布系数计算跨中梁截面采用修正偏心压力法,支点截面采用杠杆原理法。
桥梁预应力计算书

引桥盖梁预应力张拉计算书第一章 设计伸长量复核一、计算公式及参数:1、预应力平均张拉力计算公式及参数:()()μθμθ+-=+kx e p p kx p 1式中:P p —预应力筋平均张拉力(N ) P —预应力筋张拉端的张拉力(N ) X —从张拉端至计算截面的孔道长度(m )θ—从张拉端至计算截面的曲线孔道部分切线的夹角之和(rad )k —孔道每米局部偏差对摩檫的影响系数,取0.002 μ—预应力筋与孔道壁的摩檫系数,取0.142、预应力筋的理论伸长值计算公式及参数:()P P p E A l p l =∆式中:P p —预应力筋平均张拉力(N ) L —预应力筋的长度(mm )A p —预应力筋的截面面积(mm 2),取140 mm 2E p —预应力筋的弹性模量(N/ mm 2),取1.95×105 N/ mm 2二、伸长量计算:1、N1束一端的伸长量:单根钢绞线张拉的张拉力P=0.75×1860×140=195300NX=15.812/2=7.906mθ=11.4×π/180=0.19897radkx+μθ=0.002×7.906+0.14×0.19897=0.0436678P p=195300×(1-e-0.0436678)/0.0436678=191097NΔL= P p L/(A p E p)=191097×7.906/(140×1.95×105)=55.3mm 与设计比较(55.3-57.1)/57.1=-3.15%2、N2束一端的伸长量:单根钢绞线张拉的张拉力P=0.75×1860×140=195300NX=15.821/2=7.9105mθ=12.8×π/180=0.2234radkx+μθ=0.002×7.9105+0.14×0.2234=0.047097P p=195300×(1-e-0.047097)/0.047097=190772NΔL= P p L/(A p E p)=190772×7.9105/(140×1.95×105)=55.27mm 与设计比较(55.27-57.1)/57.1=-3.2%第二章张拉时理论伸长量计算一、计算参数:1、K—孔道每米局部偏差对摩檫的影响系数:取0.0022、μ—预应力筋与孔道壁的摩檫系数:取0.143、A p—预应力筋的实测截面面积:140 mm24、E p—预应力筋实测弹性模量:2.02×105 N/ mm25、锚下控制应力:σk=0.75R y b=0.75×1860=1395 N/ mm26、锚圈口摩阻损失:3.3%σk7、单根钢绞线张拉端的张拉控制力:P=103.3%×σk A p=201745N8、千斤顶计算长度:56cm9、工作锚长度:7cm10、限位板计算长度:2.5cm11、工具锚计算长度:不计二、张拉时理论伸长量计算:1、N1束一端的伸长量:X=15.812/2=7.906mL=7.906+(0.56+0.07+0.025)=8.561mθ=11.4×π/180=0.19897radkx+μθ=0.002×7.906+0.14×0.19897=0.0436678P p=201745×(1-e-0.0436678)/0.0436678=197404NΔL= P p L/(A p E p)=197404×8.561/(140×2.02×105)=59.8mm 2、N2束一端的伸长量:X=15.821/2=7.9105mL=7.9105+(0.56+0.07+0.025)=8.566mθ=12.8×π/180=0.2234radkx+μθ=0.002×7.9105+0.14×0.2234=0.047097P p=201745(1-e-0.047097)/0.047097=197068NΔL= P p L/(A p E p)=197068×8.566/(140×2.02×105)=59.7mm 第三章千斤顶张拉力与对应油表读数计算一、钢绞线的张拉控制应力:12根钢绞线束:σcon=103.3σk=103.3%×2343=2420.32KN二、1523号千斤顶张拉、0050号油表时:千斤顶回归方程:P=-0.35+0.01035F式中:P——油压表读数(MP a)F——千斤顶拉力(KN)(1)、10%σcon=242.032 KN时:P=-0.35+0.01035F=-0.35+0.01035×242.032=2.16MP a(2)、40%σcon=968.13KN时:P=-0.35+0.01035F=-0.35+0.01035×968.13=9.67 MP a(3)、70%σcon=1694.22KN时:P=-0.35+0.01035F=-0.35+0.01035×1694.22=17.19 MP a (4)、100%σcon=2420.32KN时:P=-0.35+0.01035F=-0.35+0.01035×2420.32=24.7 MP a三、1524号千斤顶张拉、0054号油表时:千斤顶回归方程:P=0.21+0.01022F:式中: P——油压表读数(MP a)F——千斤顶拉力(KN)(1)、10%σcon=242.032KN时:P=0.21+0.01022F=0.21+0.01022×242.032=2.68 MP a (2)、40%σcon=968.13KN时:P=0.21+0.01022F=0.21+0.01022×968.13=10.10 MP a (3)、70%σcon=1694.22KN时:P=0.21+0.01022F=0.21+0.01022×1694.22=17.52 MP a (4)、100%σcon=2420.32KN时:P=0.21+0.01022F=0.21+0.01022×2420.32=24.95 MP a 四、1525号千斤顶张拉、0077号油表时:千斤顶回归方程:P=-0.47+0.01024F:式中: P——油压表读数(MP a)F——千斤顶拉力(KN)(1)、10%σcon=242.032KN时:P=-0.47+0.01024F=-0.47+0.01024×242.032=2.0 MP a (2)、40%σcon=968.13KN时P=-0.47+0.01024F=-0.47+0.01024×968.13=9.44 MP a (3)、70%σcon=1694.22KN时:P=-0.47+0.01024F=-0.47+0.01024×1694.22=16.88 MP a (4)、100%σcon=2420.32KN时:P=-0.47+0.01024F=-0.47+0.01024×2420.32=24.31 MP a 五、1526号千斤顶张拉、0064号油表时:千斤顶回归方程:P=-0.05+0.01021F:式中: P——油压表读数(MP a)F——千斤顶拉力(KN)(1)、10%σcon=242.032KN时:P=-0.05+0.01021F=-0.05+0.01021×242.032=2.42 MP a (2)、40%σcon=968.13KN时P=-0.05+0.01021F=-0.05+0.01021×968.13=9.83 MP a (3)、70%σcon=1694.22KN时:P=-0.05+0.01021F=-0.05+0.01021×1694.22=17.24 MP a (4)、100%σcon=2420.32KN时:P=-0.05+0.01021F=-0.05+0.01021×2420.32=24.66 MP a。
预应力梁计算书

YKL-1一、计算条件1、材料1)、预应力钢筋采用高强低松弛钢绞线Φs15.2,其强度为f ptk=1860N/mm22)、张拉控制应力为σcon(N/mm2)= 13023)、孔道成型采用预埋金属波纹管,直径(mm)为70.00 4)、锚具种类:夹片锚5)、非预应力钢筋采用HRB400级钢筋,箍筋采用HRB335级钢筋6)、混凝土强度等级为C40 fc(N/mm2)= 19.1 ftk(N/mm2)=2.517)、施加预应力时的混凝土强度为2、内力计算1)、跨中截面跨中设计弯矩M(KN.m):2287 恒荷载力作用下的弯矩标准值Mk(KN.m):891 活荷载力作用下的弯矩标准值Mk(KN.m):303 2)、支座截面支座设计弯矩M(KN.m):947 恒荷载力作用下的弯矩标准值Mk(KN.m):939 活荷载力作用下的弯矩标准值Mk(KN.m):285 3、结构信息1)、裂缝控制等级:三级2)、配筋情况:下部:2×6Φs15.2+9φ25上部:2×6Φs15.2+8φ254、张拉方式:一端张拉5、跨度L(mm)12.6二、截面验算2.1 截面设计参数梁截面宽度 b(mm) 400 梁截面高度 h(mm) 1000 上翼缘高度 h f(mm) 150 上翼缘宽度b f(mm) 2200 下翼缘高度h f'(mm) 0 下翼缘宽度b f'(mm) 400 支座截面加掖高度h a(mm) 0跨中截面面积A1(mm2) 6.700E+05支座截面面积A2(mm2) 6.700E+05跨中截面形心距上翼缘边缘的距离y11(mm) 329 跨中截面形心距下翼缘边缘的距离y12(mm) 671 支座截面形心距上翼缘边缘的距离y21(mm) 329 支座截面形心距下翼缘边缘的距离y22(mm) 671跨中截面惯性矩I1(mm4) 6.296E+10支座截面惯性矩I2(mm4) 6.296E+102.2 截面抗裂及承载力计算验算(三级)1、跨中截面1—1受拉区普通钢筋根数n1 9 受拉区普通钢筋直径d1(mm) 25 拉区预应力钢筋根数n2 12 弯矩标准值Mk(kN-m) 1194 次弯矩M2(kN-m) 469预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)147张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)33裂缝宽度验算受拉区纵向钢筋的公称直径d eq(mm) 26.56按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.03轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)1003.03纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)788.03等效应力σsk(N/mm2)74.06裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0)0.38裂缝宽度ωmax(mm)0.03 <0.2,满足要求承载力计算跨中计算弯矩包络值+1.2次弯矩M(KN.M)2287实际承载力Mu(KN.M)3313 >M,满足要求2、支座截面2—2受拉区普通钢筋根数n1 8受拉区普通钢筋直径d1(mm) 25拉区预应力钢筋根数n2 12弯矩标准值M k(kN-m) 647次弯矩M2(kN-m) -462预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)277张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)33 裂缝验算受拉区纵向钢筋的公称直径d eq(mm) 26.69按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.01轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)111.88纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)-7144.2等效应力σsk(N/mm2)-299.90裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0) 1.00裂缝宽度ωmax(mm)0.03 <0.2mm,满足要求抗震验算梁端的配筋强度比λ0.61 <0.75,满足要求截面换算配筋率ρ(%) 2.41 <2.5%,满足要求受压区高度比x/h0 0.23 <0.35,满足要求梁端底面与顶面普通钢筋面积比A s’/As 1.13 >0.3/(1-λ),满足要求梁底面普通钢筋配筋率0.66 >0.2%,满足要求承载力计算支座计算弯矩包络值+次弯矩M(KN.M)947(1.2恒荷弯矩+1.4活荷弯矩)*调幅系数+次弯矩M1(KN.M)263实际承载力Mu(KN.M)2710 >M1,满足要求支座计算配筋包络值A s(mm2) 5018支座换算实际配筋面积A s实(mm2) 9065 >As,满足要求支座抗剪设计值V(KN)977抗剪承载力V实(KN)1645 >V,满足条件施工阶段验算支座验算施工阶段上翼缘边缘砼法向压应力ócc(N/mm2) 2.61 <0.6fck,满足要求施工阶段下翼缘边缘砼法向拉应力ótp(N/mm2)-2.68 <0.95ftk,满足要求跨中验算施工阶段下翼缘边缘砼法向压应力ócc(N/mm2) 1.59 <0.6fck,满足要求施工阶段上翼缘边缘砼法向拉应力ócc(N/mm3)-3.14 <0.95ftk,满足要求施工阶段预应力伸长计算值(mm) 76施工阶段反拱验算0.06 0.05751219荷载长期作用下梁挠度验算9.25 满足要求<1/300一、计算条件1、材料1)、预应力钢筋采用高强低松弛钢绞线Φs15.2,其强度为f ptk=1860N/mm22)、张拉控制应力为σcon(N/mm2)= 13023)、孔道成型采用预埋金属波纹管,直径(mm)为80.004)、锚具种类:夹片锚5)、非预应力钢筋采用HRB400级钢筋,箍筋采用HRB335级钢筋6)、混凝土强度等级为C40 fc(N/mm2)= 19.1ftk(N/mm2)=2.517)、施加预应力时的混凝土强度为2、内力计算1)、跨中截面跨中设计弯矩M(KN.m):2364 恒荷载力作用下的弯矩标准值Mk(KN.m):788 活荷载力作用下的弯矩标准值Mk(KN.m):224 2)、支座截面支座设计弯矩M(KN.m):1474 恒荷载力作用下的弯矩标准值Mk(KN.m):1108 活荷载力作用下的弯矩标准值Mk(KN.m):274 3、结构信息1)、裂缝控制等级:三级2)、配筋情况:下部:2×8Φs15.2+9φ25上部:2×8Φs15.2+8φ254、张拉方式:一端张拉5、跨度L(mm)15.5二、截面验算2.1 截面设计参数梁截面宽度 b(mm) 400 梁截面高度 h(mm) 1200 上翼缘高度 h f(mm) 150 上翼缘宽度b f(mm) 2200 下翼缘高度h f'(mm) 0 下翼缘宽度b f'(mm) 400 支座截面加掖高度h a(mm) 0跨中截面面积A1(mm2) 7.500E+05支座截面面积A2(mm2) 7.500E+05跨中截面形心距上翼缘边缘的距离y11(mm) 411 跨中截面形心距下翼缘边缘的距离y12(mm) 789 支座截面形心距上翼缘边缘的距离y21(mm) 411 支座截面形心距下翼缘边缘的距离y22(mm) 789跨中截面惯性矩I1(mm4) 1.057E+11支座截面惯性矩I2(mm4) 1.057E+112.2 截面抗裂及承载力计算验算(三级)1、跨中截面1—1受拉区普通钢筋根数n1 9 受拉区普通钢筋直径d1(mm) 25 拉区预应力钢筋根数n2 16 弯矩标准值Mk(kN-m) 1012 次弯矩M2(kN-m) 692预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)156张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)44裂缝宽度验算受拉区纵向钢筋的公称直径d eq(mm) 26.89按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.03轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)777.51纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)868.11等效应力σsk(N/mm2)-34.20裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0) 1.00裂缝宽度ωmax(mm)0.04 <0.2,满足要求承载力计算跨中计算弯矩包络值+1.2次弯矩M(KN.M)2364实际承载力Mu(KN.M)4809 >M,满足要求2、支座截面2—2受拉区普通钢筋根数n1 8受拉区普通钢筋直径d1(mm) 25拉区预应力钢筋根数n2 16弯矩标准值M k(kN-m) 888次弯矩M2(kN-m) -680预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)292张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)44 裂缝验算受拉区纵向钢筋的公称直径d eq(mm) 27.04按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.01轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)95.45纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)-18520.95等效应力σsk(N/mm2)-355.74裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0) 1.00裂缝宽度ωmax(mm)0.03 <0.2mm,满足要求抗震验算梁端的配筋强度比λ0.68 <0.75,满足要求截面换算配筋率ρ(%) 2.41 <2.5%,满足要求受压区高度比x/h0 0.27 <0.35,满足要求梁端底面与顶面普通钢筋面积比A s’/As 1.13 >0.3/(1-λ),满足要求梁底面普通钢筋配筋率0.59 >0.2%,满足要求承载力计算支座计算弯矩包络值+次弯矩M(KN.M)1474(1.2恒荷弯矩+1.4活荷弯矩)*调幅系数+次弯矩M1(KN.M)310实际承载力Mu(KN.M)3902 >M1,满足要求支座计算配筋包络值A s(mm2) 5989支座换算实际配筋面积A s实(mm2) 11007 >As,满足要求支座抗剪设计值V(KN)895抗剪承载力V实(KN)1996 >V,满足条件施工阶段验算支座验算施工阶段上翼缘边缘砼法向压应力ócc(N/mm2) 4.51 <0.6fck,满足要求施工阶段下翼缘边缘砼法向拉应力ótp(N/mm2)-0.49 <0.95ftk,满足要求跨中验算施工阶段下翼缘边缘砼法向压应力ócc(N/mm2) 5.89 <0.6fck,满足要求施工阶段上翼缘边缘砼法向拉应力ócc(N/mm3)-1.69 <0.95ftk,满足要求施工阶段预应力伸长计算值(mm) 92施工阶段反拱验算 1.36 1.36165642荷载长期作用下梁挠度验算 6.72 满足要求<1/300一、计算条件1、材料1)、预应力钢筋采用高强低松弛钢绞线Φs15.2,其强度为f ptk=1860N/mm22)、张拉控制应力为σcon(N/mm2)= 13023)、孔道成型采用预埋金属波纹管,直径(mm)为55.004)、锚具种类:夹片锚5)、非预应力钢筋采用HRB400级钢筋,箍筋采用HRB335级钢筋6)、混凝土强度等级为C40 fc(N/mm2)= 19.1ftk(N/mm2)=2.517)、施加预应力时的混凝土强度为2、内力计算1)、跨中截面跨中设计弯矩M(KN.m):2058 恒荷载力作用下的弯矩标准值Mk(KN.m):788 活荷载力作用下的弯矩标准值Mk(KN.m):224 2)、支座截面支座设计弯矩M(KN.m):1729 恒荷载力作用下的弯矩标准值Mk(KN.m):1108 活荷载力作用下的弯矩标准值Mk(KN.m):274 3、结构信息1)、裂缝控制等级:三级2)、配筋情况:下部:2×5Φs15.2+7φ25上部:2×5Φs15.2+5φ254、张拉方式:一端张拉5、跨度L(mm)15.5二、截面验算2.1 截面设计参数梁截面宽度 b(mm) 400 梁截面高度 h(mm) 1200 上翼缘高度 h f(mm) 150 上翼缘宽度b f(mm) 2200 下翼缘高度h f'(mm) 0 下翼缘宽度b f'(mm) 400 支座截面加掖高度h a(mm) 0跨中截面面积A1(mm2) 7.500E+05支座截面面积A2(mm2) 7.500E+05跨中截面形心距上翼缘边缘的距离y11(mm) 411 跨中截面形心距下翼缘边缘的距离y12(mm) 789 支座截面形心距上翼缘边缘的距离y21(mm) 411 支座截面形心距下翼缘边缘的距离y22(mm) 789跨中截面惯性矩I1(mm4) 1.057E+11支座截面惯性矩I2(mm4) 1.057E+112.2 截面抗裂及承载力计算验算(三级)1、跨中截面1—1受拉区普通钢筋根数n1 7 受拉区普通钢筋直径d1(mm) 25 拉区预应力钢筋根数n2 10 弯矩标准值Mk(kN-m) 1012 次弯矩M2(kN-m) 433预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)156张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)44裂缝宽度验算受拉区纵向钢筋的公称直径d eq(mm) 26.64按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.02轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)1056.53纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)924.81等效应力σsk(N/mm2)40.15裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0)0.20裂缝宽度ωmax(mm)0.01 <0.2,满足要求承载力计算跨中计算弯矩包络值+1.2次弯矩M(KN.M)2058实际承载力Mu(KN.M)3320 >M,满足要求2、支座截面2—2受拉区普通钢筋根数n1 5受拉区普通钢筋直径d1(mm) 25拉区预应力钢筋根数n2 10弯矩标准值M k(kN-m) 888次弯矩M2(kN-m) -425预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)292张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)44 裂缝验算受拉区纵向钢筋的公称直径d eq(mm) 27.04按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.01轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)340.21纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)-544.20等效应力σsk(N/mm2)-575.16裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0) 1.00裂缝宽度ωmax(mm)0.05 <0.2mm,满足要求抗震验算梁端的配筋强度比λ0.68 <0.75,满足要求截面换算配筋率ρ(%) 1.51 <2.5%,满足要求受压区高度比x/h0 0.14 <0.35,满足要求梁端底面与顶面普通钢筋面积比A s’/As 1.40 >0.3/(1-λ),满足要求梁底面普通钢筋配筋率0.46 >0.2%,满足要求承载力计算支座计算弯矩包络值+次弯矩M(KN.M)1729(1.2恒荷弯矩+1.4活荷弯矩)*调幅系数+次弯矩M1(KN.M)565实际承载力Mu(KN.M)2622 >M1,满足要求支座计算配筋包络值A s(mm2) 5989支座换算实际配筋面积A s实(mm2) 6879 >As,满足要求支座抗剪设计值V(KN)895抗剪承载力V实(KN)1996 >V,满足条件施工阶段验算支座验算施工阶段上翼缘边缘砼法向压应力ócc(N/mm2) 1.65 <0.6fck,满足要求施工阶段下翼缘边缘砼法向拉应力ótp(N/mm2)-2.54 <0.95ftk,满足要求跨中验算施工阶段下翼缘边缘砼法向压应力ócc(N/mm2) 2.09 <0.6fck,满足要求施工阶段上翼缘边缘砼法向拉应力ócc(N/mm3)-1.88 <0.95ftk,满足要求施工阶段预应力伸长计算值(mm) 92施工阶段反拱验算0.11 0.10540212荷载长期作用下梁挠度验算9.24 满足要求<1/300YKL-4一、计算条件1、材料1)、预应力钢筋采用高强低松弛钢绞线Φs15.2,其强度为f ptk=1860N/mm22)、张拉控制应力为σcon(N/mm2)= 13023)、孔道成型采用预埋金属波纹管,直径(mm)为55.004)、锚具种类:夹片锚5)、非预应力钢筋采用HRB400级钢筋,箍筋采用HRB335级钢筋6)、混凝土强度等级为C40 fc(N/mm2)= 19.1ftk(N/mm2)=2.517)、施加预应力时的混凝土强度为2、内力计算1)、跨中截面跨中设计弯矩M(KN.m):1591 恒荷载力作用下的弯矩标准值Mk(KN.m):665 活荷载力作用下的弯矩标准值Mk(KN.m):15 2)、支座截面支座设计弯矩M(KN.m):518 恒荷载力作用下的弯矩标准值Mk(KN.m):773 活荷载力作用下的弯矩标准值Mk(KN.m):55 3、结构信息1)、裂缝控制等级:三级2)、配筋情况:下部:2×5Φs15.2+7φ25上部:2×5Φs15.2+5φ254、张拉方式:一端张拉5、跨度L(mm)15.5二、截面验算2.1 截面设计参数梁截面宽度 b(mm) 400 梁截面高度 h(mm) 1100上翼缘高度 h f(mm) 150 上翼缘宽度b f(mm) 2200 下翼缘高度h f'(mm) 0 下翼缘宽度b f'(mm) 400 支座截面加掖高度h a(mm) 0跨中截面面积A1(mm2) 7.100E+05支座截面面积A2(mm2) 7.100E+05跨中截面形心距上翼缘边缘的距离y11(mm) 369 跨中截面形心距下翼缘边缘的距离y12(mm) 731 支座截面形心距上翼缘边缘的距离y21(mm) 369 支座截面形心距下翼缘边缘的距离y22(mm) 731跨中截面惯性矩I1(mm4) 8.263E+10支座截面惯性矩I2(mm4) 8.263E+102.2 截面抗裂及承载力计算验算(三级)1、跨中截面1—1受拉区普通钢筋根数n1 7 受拉区普通钢筋直径d1(mm) 25 拉区预应力钢筋根数n2 10 弯矩标准值Mk(kN-m) 680 次弯矩M2(kN-m) 422预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)141张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)34裂缝宽度验算受拉区纵向钢筋的公称直径d eq(mm) 26.64按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.02轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)783.06纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)824.19等效应力σsk(N/mm2)-14.48裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0) 1.00裂缝宽度ωmax(mm)0.02 <0.2,满足要求承载力计算跨中计算弯矩包络值+1.2次弯矩M(KN.M)1591实际承载力Mu(KN.M)3013 >M,满足要求2、支座截面2—2受拉区普通钢筋根数n1 5受拉区普通钢筋直径d1(mm) 25拉区预应力钢筋根数n2 10弯矩标准值M k(kN-m) 561次弯矩M2(kN-m) -416预应力损失计算预应力钢筋与孔道壁之间的摩擦系数引起的预应力损失σl2(N/mm2)265张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)0预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)34 裂缝验算受拉区纵向钢筋的公称直径d eq(mm) 27.04按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.01轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)103.56纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)-11681.32等效应力σsk(N/mm2)-367.44裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0) 1.00裂缝宽度ωmax(mm)0.06 <0.2mm,满足要求抗震验算梁端的配筋强度比λ0.68 <0.75,满足要求截面换算配筋率ρ(%) 1.64 <2.5%,满足要求受压区高度比x/h0 0.15 <0.35,满足要求梁端底面与顶面普通钢筋面积比A s’/As 1.40 >0.3/(1-λ),满足要求梁底面普通钢筋配筋率0.48 >0.2%,满足要求承载力计算支座计算弯矩包络值+次弯矩M(KN.M)518(1.2恒荷弯矩+1.4活荷弯矩)*调幅系数+次弯矩M1(KN.M)197实际承载力Mu(KN.M)2356 >M1,满足要求支座计算配筋包络值A s(mm2) 2986支座换算实际配筋面积A s实(mm2) 6815 >As,满足要求支座抗剪设计值V(KN)495抗剪承载力V实(KN)1821 >V,满足条件施工阶段验算支座验算施工阶段上翼缘边缘砼法向压应力ócc(N/mm2) 2.54 <0.6fck,满足要求施工阶段下翼缘边缘砼法向拉应力ótp(N/mm2)-1.24 <0.95ftk,满足要求跨中验算施工阶段下翼缘边缘砼法向压应力ócc(N/mm2) 2.51 <0.6fck,满足要求施工阶段上翼缘边缘砼法向拉应力ócc(N/mm3)-1.90 <0.95ftk,满足要求施工阶段预应力伸长计算值(mm) 94施工阶段反拱验算0.52 0.51765696荷载长期作用下梁挠度验算8.91 满足要求<1/300一、计算条件1、材料1)、预应力钢筋采用高强低松弛钢绞线Φs15.2,其强度为f ptk=1860N/mm22)、张拉控制应力为σcon(N/mm2)= 13023)、孔道成型采用预埋金属波纹管,直径(mm)为55.004)、锚具种类:夹片锚5)、非预应力钢筋采用HRB400级钢筋,箍筋采用HRB335级钢筋6)、混凝土强度等级为C40 fc(N/mm2)=19.1ftk(N/mm2)=2.397)、施加预应力时的混凝土强度为2、内力计算支座截面支座设计弯矩M(KN.m):562 恒荷载力作用下的弯矩标准值Mk(KN.m):400 活荷载力作用下的弯矩标准值Mk(KN.m):213、结构信息1)、裂缝控制等级:三级2)、配筋情况:上部:2×5Φs15.2+7φ254、张拉方式:一端张拉5、跨度L(mm) 5二、截面验算2.1 截面设计参数梁截面宽度 b(mm) 500 梁截面高度 h(mm) 700 上翼缘高度 h f(mm) 150 上翼缘宽度b f(mm) 2300 下翼缘高度h f'(mm) 0 下翼缘宽度b f'(mm) 500 支座截面加掖高度h a(mm) 0支座截面面积A2(mm2) 6.200E+05支座截面形心距上翼缘边缘的距离y21(mm) 230 支座截面形心距下翼缘边缘的距离y22(mm) 470支座截面惯性矩I2(mm4) 2.632E+102.2 截面抗裂及承载力计算验算(三级)支座截面受拉区普通钢筋根数n1 7 受拉区普通钢筋直径d1(mm) 25 拉区预应力钢筋根数n2 10 弯矩标准值M k(kN-m) 421预应力损失计算张拉端锚具变形和钢筋内缩引起的预应力损失σl1(N/mm2)234预应力钢筋的应力松弛引起的应力损失σl4(N/mm2)33由于砼的收缩徐变引起的预应力损失σl5(N/mm2)43 裂缝验算受拉区纵向钢筋的公称直径d eq(mm) 26.64按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte0.03轴向压力作用点至纵向受拉钢筋合力点的距离e(mm)305.08纵向受拉钢筋合力点至截面受压区全力点的距离z(mm)218.83等效应力σsk(N/mm2)112.75裂缝间纵向受拉钢筋应变不均匀系数ψ(0.2<ψ<1.0)0.60裂缝宽度ωmax(mm)0.07 <0.2mm,满足要求抗震验算梁端的配筋强度比λ0.60 <0.75,满足要求截面换算配筋率ρ(%) 2.44 <2.5%,满足要求受压区高度比x/h0 0.26 <0.35,满足要求承载力计算支座计算弯矩包络值M(KN.M)5621.2恒荷弯矩+1.4活荷弯矩M1(KN.M)509实际承载力Mu(KN.M)1568 >M1,满足要求支座计算配筋包络值A s(mm2) 2700支座换算实际配筋面积A s实(mm2) 7814 >As,满足要求支座抗剪设计值V(KN)180抗剪承载力V实(KN)1468 >V,满足条件挠度验算挠度f(mm) 10.31 满足要求。
预应力框架梁计算书

预应力框架梁计算书预应力框架梁计算书1. 概述预应力框架梁是一种常用的结构形式,能够提高梁的承载能力和抗震性能。
本文档旨在提供一份详细的计算书范本,以便工程师们参考和使用。
2. 术语和定义在进行计算之前,我们首先需要了解一些术语和定义,以便更好地理解本文档的内容。
以下是一些常见的术语和定义:- 预应力:通过施加预先的拉力来改善结构的性能和耐久性。
- 梁:一种承受荷载并将其传递给支座的结构元素。
- 框架梁:由梁与柱组合构成的结构形式。
- 计算书:一份用于记录结构计算结果的文档。
3. 计算步骤在进行预应力框架梁的计算时,需要按照以下步骤进行:3.1. 确定梁的几何参数:包括长度、宽度和高度等几何特征。
3.2. 确定梁的材料参数:包括混凝土和预应力钢筋的强度等材料特性。
3.3. 计算梁的截面特性:根据几何参数和材料参数计算梁的截面特性,如惯性矩和截面模量等。
3.4. 计算梁的受力状态:根据梁所受的荷载和边界条件,计算梁的受力状态,包括弯矩、剪力和轴力等。
3.5. 根据受力状态计算各部分的尺寸:根据梁的受力状态和设计要求,计算各部分的尺寸,如预应力筋和箍筋的布置等。
3.6. 进行预应力计算:根据设计要求,确定预应力的大小和布置方式。
3.7. 进行梁的验算:根据计算结果,进行梁的验算,包括抗弯承载力和抗剪承载力等。
4. 附件本文档所涉及的附件如下:- 图纸:包括梁的平面图和剖面图等。
- 计算表格:用于记录计算过程和结果的表格。
- 验算报告:包括梁的受力状态和验算结果等。
5. 法律名词及注释在本文档中,可能涉及到一些法律名词和术语。
以下是一些常见的法律名词及其注释:- 建筑法:指规范和管理建筑活动的法律法规。
- 结构设计规范:包括建筑结构设计的相关规定和要求。
- 施工规范:包括建筑施工的相关规定和要求。
- 安全规定:指保障建筑结构安全的相关规定和要求。
本文档提供了一份详细的预应力框架梁计算书范本,希望能对工程师们在实际工作中提供参考和帮助。
预应力混凝土框架梁设计计算

预应力混凝土框架梁设计计算书二00六年四月目 录1. 设计荷载与内力计算 (1)1.1 梁截面几何特征 (1)1.2 柱截面几何特征 (1)1.3 荷载标准值 (2)1.4 内力计算 (2)2. 梁中预应力筋和普通钢筋的估算 (5)2.1 预应力筋线形的采用 (5)2.2 预应力筋的估算 (5)2.3 普通钢筋估算 (6)3. 第一批预应力损失计算 (7)3.1 孔道摩擦损失2l σ (7)3.2 锚具内缩损失1l σ: (7)3.3 第一批预应力损失lI σ: (8)4. 施工阶段抗裂验算 (9)4.1 第一批预应力损失完成后的预应力等效荷载 (9)4.2 第一批预应力损失完成后的预应力综合弯矩 (9)4.3 施工阶段恒载作用下的弯矩 (12)4.4 施工阶段正截面抗裂验算结果 (13)5. 第二批预应力损失计算 (15)5.1 钢筋应力松弛损失4l σ: (15)5.2 混凝土收缩徐变引起的预应力损失5l σ (15)5.3 预应力总损失l σ: (16)5.4 钢绞线平均有效预应力: (16)6. 预应力引起的次弯矩和次剪力计算 (17)6.1 预应力损失完成后的预应力等效荷载 (17)6.2 综合弯矩 (17)6.3 次弯矩、次剪力 (18)7. 正截面抗裂验算 (20)7.1 荷载标准组合、准永久组合下框架梁弯矩 (20)7.2 正截面抗裂验算结果 (20)7.3 抗裂验算小结 (21)8. 正截面承载力验算 (22)8.1 荷载基本组合下框架梁弯矩 (22)8.2 正截面受弯承载力计算结果 (22)9. 斜截面承载力验算 (25)9.1 荷载作用下框架设计剪力 (25)9.2 斜截面受剪承载力验算结果 (25)1. 设计荷载与内力计算1.1 梁截面几何特征1.2 柱截面几何特征1.3 荷载标准值屋面梁上的线荷载:(1)恒载:① 楼板自重、粉刷、吊顶、管道等:6.5kN/m2×6m=39kN/m② 次梁(250×500)自重:约为5.5kN/m③ 端支座处屋面梁自重:25×(0.45×1.5)=16.9kN/m内支座处屋面梁自重:25×(0.45×2.2)=24.8kN/m因此,恒载为(端支座)61.4~(内支座)69.3kN/m(2)活载:0.7kN/m2×6m=4.2kN/m1.4 内力计算由通用有限元程序SAP2000建立计算模型。
预应力梁计算书(按T 形截面)

二.内力设计值计算
Gk 为恒载内力标准值, Pk 为活载不利布置内力标准值, Ek 为地震内力标准值,Wk 为风载内力标准值 M k = Gk + Pk 为标准组合, M q = Gk + ϕ q Pk 为准永久组合, M d 为设计组合
1. 支座 A
Gk = −1379.5kN .m , Pk = −491.4kN .m , M k = −1870.9kN .m , M q = −1625.2kN .m M d = −2364.0kN .m
1478.0 × 106 × 651.7
则 Ap = max Ap , k , Ap ,q = 2676mm , n = Ap 139 = 19.3 根
2
(
)
5. 支座 E
Ap , k
Ap , q
− 2.39 10 9.964 10 × = ≈ 1952mm 2 976.5 0.3464 × 106 × 448.3 + 8.33 × 105 9.964 × 1010 1474.2 × 106 × 448.3 − 0.4 × 2.39 9.964 × 1010 = ≈ 2079mm 2 6 976.5 0.3464 × 10 × 448.3 + 5 8.33 × 10 9.964 × 1010
4. 跨中 D
M 主 = e p N pe = −461.7 × 3257.6 × 10
3
106
= −1053.9kN .m
M 次 = M p Ap − M 主 = −0.2550 × 3336 + 1053.9 = 653.3kN .m
5. 支座 E
M 主 = e p N pe = 148.3 × 3257.6 × 10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
预应力框架梁(YKL2)的计算书1.设计资料1. 混凝土强度等级:40C 219.1/c f N mm = 22.39/tk f N mm = 21.71/t f N mm = 240/cu f N mm = 423.2510/c E N mm =⨯2. 钢筋1).预应力筋采用低松弛(15.2)sφ钢绞线,每根钢筋截面面积为12139p A mm =21860/ptk f N mm = 21320/py f N mm = 521.9510/p E N mm =⨯2).非预应力纵向钢筋采用HRB335级钢筋:2300/y f N mm = 52210/s E N mm =⨯3).箍筋采用HPB235级钢筋: 2210/y f N mm =3. 锚具采用:柳州欧维姆机械股份有限公司的OVM.M15-14锚具4. 预应力梁的计算跨度取两端柱子的中心线距离: 26200mm 2预应力框架梁的计算 2.1设计资料图1:框架梁(YKL2)内力布置图2.1.1梁的几何特性:图2框架梁为T 形截面, 111900262001871,1900,600, 3.1741515600h h l mm h mm b mm b ==⨯=====<取120,12600121202040()f f f h mm b b h mm '''==+=+⨯=几何特征值为:522112040120 2.44810(),1900601840()A mm y mm =⨯=⨯=-= 52222600178010.6810(),1780/2890()A mm y mm =⨯=⨯==555212 2.4481010.681013.12810()A A A mm =+=⨯+⨯=⨯55112205512 2.44810184010.68108901067()2.4481010.6810A y A y y mm A A +⨯⨯+⨯⨯===+⨯+⨯111222I I A a I A a =+++3322114204012060017802040120(18401067)6001780(1067890)12124.6210()mm ⨯⨯=+⨯⨯-++⨯⨯-=⨯2.1.2内力组合: 支座处:弯矩设计值:38630.93476.7()M kN m =⨯=⋅(考虑次弯矩有利的影响) 短期效应组合:77430153789()s M kN m =+=⋅ 长期效应组合:30157740.73556.8()l M kN m =+⨯=⋅ 跨中:弯矩设计值:8788 1.210653.6()M kN m =⨯=⋅(考虑次弯矩不利的影响) 短期效应组合:496011636123()s M kN m =+=⋅ 长期效应组合:496011630.75774.1()l M kN m =+⨯=⋅2.2预应力筋的估算:混凝土强度等级:40C ,钢绞线(1X7):15.2sφ222119.1/,1860/,1320/c ptk py f N mm f N mm f N mm α===2.2.1预应力筋的估算:按正截面承载力要求估算预应力筋的数量 取预应力度PPR=0.7 (1)跨中按矩形截面来估算: 1.2878810545.6M kN m =⨯=⋅取95,35,120s p a mm a mm a mm ===01900951805(),1900351865(),s s h h a mm h h a mm =-=-==-=-= 19001201780()p p h h a mm =-=-=6220012210545.61018051805 1.019.1600c M x h h f b ⨯⨯=--=--α⨯⨯0614()0.350.351805632()mm h mm =<⨯=⨯=h 0——截面有效高度(预应力与非预应力筋的合力点距混凝土边缘的距离) M ——外荷载效应组合引起的弯矩设计值()62010545.6100.73733()132********/2()2p py MA mm x f h λ⨯==⨯=⨯--(其中:PPR :即预应力度,也可用λ表示)23733/13926.9,815.2,3892(mm )S p A φ==选配2 p p xz h 1780614/21473(mm)2=-=-= s s xz h 1865614/21558(mm)2=-=-=()6210545.610-3892132014731()6372()3001558s p py p y s A M A f z mm f z ⨯⨯⨯=-==⨯非预应力筋:6372/49113.114=,选配225,6874(mm )s A =总配筋率为:/687413203892/3002.22% 2.5%,6001805s py p yA f A f bh ++⨯ρ===<⨯满足要求。
(2)支座处:38630.93476.7.M kN m =⨯=按矩形截面计算:取181,35,210s p a mm a mm a mm ===019001811719(),1900351865(),s s h h a mm h h a mm =-=-==-=-= 19002101690()p p h h a mm =-=-=622001223476.71017191719 1.019.1600c M x h h f b ⨯⨯=--=--α⨯⨯0186()0.350.351719602()mm h mm =<=⨯=()6203476.7100.71131()132********/2()2p py MA PPR mm x f h ⨯==⨯=⨯--(其中:PPR :即预应力度,也可用λ表示)21131/1398.1,915.2,1251(mm )S p A φ==选配 p p xz h 1900-210186/21597(mm)2=-=-= s s xz h 1900-35186/21772(mm)2=-=-=6213476.710125113201597()1579()3001772s p py p y s A M A f z mm f z ⨯-⨯⨯=-==⨯1579/491 3.2,=选配4225,1964(mm )s A =由计算结果可知,预应力钢筋需要9根,但是考虑到预应力筋的连续性,其配筋同跨中截面的配筋,而支座处的的非预应力钢筋按构造要求进行配筋。
非预应力按照构造max{0.2%,45%t y f f }配筋 ,45%t y f f = 1.7145%0.26%30020.26%0.002660019002964sA Amm选配7225,3436(mm )s A =跨中截面的净截面的几何特征值表名称 b(mm) h(mm) A i (mm 2) y i (mm) A i*y i (mm 3) A i*y i 2(mm 4) I i (mm 4) 腹板 600 1780 1068000 890 950520000 8.46x1011 2.82 x1011 上翼缘 2040 120 244800 1840 450432000 8.29 x1011 2.94 x108 孔洞 d=110 3.14 -18997 120 -2279640 -2.74 x108 -2.2 x107AsE p /E c =6.15 6874 35401.1 35 1239038.5 43366348As' E p /E c =6.15343617695.4 186533001921 6.16 x1010合计 An13469001.433 x1091.74 x10122.82 x10119/ 1.43310/134********()n i i n y A y A mm ==⨯=∑2211122() 2.8210 1.741013469001064n i i i n n I I A y A y =+-=⨯+⨯-⨯∑1144.9410()mm =⨯2.2.2预应力筋的布置:图3 预应力筋布置图直线段AB 水平投影长度:00.250.25262006550l l mm ==⨯= 曲线(B-B ’)方程:2y Ax Bx C =++令坐标点定于曲线顶点C 点,再令曲线在B-B ’间的垂度为e,则B y e =,则由坐标推导而得,曲线方程为:22e y x l =(6550)l mm = 直线方程与曲线方程相切于B(B ’)点,抛物线的切线方程即为直线段AB 的直线方程,于是有 2e tg k l θ==,设直线方程坐标定于B 点,则直线方程为2e y kx x l== 22655036550A AB B e e y x y e e l =+=⨯+= 设直线方程为:19001202101570()A y mm =--=由预应力筋布置图可得,即15703,523.3()e e mm ==曲线方程:222523.30.0000126550e y x x x l === 直线方程:22523.30.166550e y kx x x x l ⨯====2.3预应力损失的计算:张拉控制应力:20.750.7518601395(/)con ptk f N mm σ==⨯=:con σ预应力钢筋的张拉控制应力2.3.1锚具变形和预应力钢筋内缩引起的预应力损失值1l σ5,0.25,0.0015a mm k μ===a :张拉端锚具变形和钢筋内缩值μ:预应力钢筋与孔道之间的摩擦系数k :考虑孔道每米长度局部偏差的摩擦系数 226.5541()220.523c l m e γ===⨯曲率半径为:9.6()f l m ∴=== 其中::f l 反向摩擦影响长度(m ):c γ圆弧形预应力钢筋的曲率半径(m ):x 张拉端距计算截面的距离 :p E 预应力钢筋的弹性模量A 点处:1l σ=2(/)(1/)con f c f l k x l σμγ+- 20.250.5213959.6(0.0015)(1)192.7(/)419.6N mm =⨯⨯⨯+⨯-= B 点处1l σ=2(/)(1/)con f c f l k x l σμγ+- 20.257.05213959.6(0.0015)(1)53.9(/)419.6N mm =⨯⨯⨯+⨯-= C 点处,113.69.6,0f l x m l m σ=>==1:l x σ距张拉端处的预应力损失4.2.3.2孔道摩擦损失2l σ20.25,0.0015,0.750.7518601395(/)con ptk k f N mm μσ====⨯= 表1 孔道摩擦损失计算表 2)l kx μθσσ+=con 1(1-第一批预应力损失l σI 为:22192.7 1.05193.75(/)82.49(/)l l A N mm C N mm σσI I =+==支座:跨中:2.3.3钢筋应力松弛损失4l σ 4l σ=0.2(0.575)concon ptkf σσ-213950.2(0.575)139548.83(/)1860N mm =⨯-⨯=2.3.4混凝土收缩和徐变引起的预应力损失5l σ 535280/115pc cul f σσρ'+=+跨中(C 点):12()(1395082.49)38925108289()p con l l p N A N σσσ=--=--⨯=nn()p p p G npc N N e M y A I σ-=+651125108289[5108289(1064120)496010](1064120)13.46910 4.94103.790.263.53(/)N mm ⨯--⨯⨯-=+⨯⨯=-=0.8%ρ==⨯5p s n (A +A )(3892+6874)=A 13.469102535280 3.53/4053.31(/)1150.008l N mm σ+⨯==+⨯其中:pc σ:受拉区预应力钢筋合力点处,由于预应力(扣除相应阶段预应力损失)和梁自重产生的混凝土法向压应力,其值不大于;cuf '0.5 :cuf '施加预应力时的混凝土立方体抗压强度 ρ:受拉区预应力钢筋和非预应力钢筋配筋率 对后张法构件,ρp s n(A +A )=A支座(A 点):(1395193.75)38924675265()p N N =-⨯=()p p p G npc nnN N e M y A I σ-=+651124675265[4675265(19001064210)301510](19001064210)13.46910 4.92103.470.113.36(/)N mm ⨯---⨯⨯--=+⨯⨯=-= 0.54%ρ==⨯5p s n (A +A )(3892+3436)=A 13.469102535280 3.36/4054.14(/)1150.0054l N mm σ+⨯==+⨯表2 预应力损失及有效预加应力p N 示意表:平均:2184.63296.7213951154.3(/)2pe N mm σ+=-=2.4次内力的计算:2.4.1等效荷载的计算:取支座和跨中截面有效预加力的平均值作为跨间的预应力值来计算等效荷载4088.54344.34216.4()22pA pC p kN N N N +=+== 端弯矩:4216.4(1.9 1.0640.21)2639.5()p M kN m =⨯--=⋅曲线范围内均布荷载:22884216.40.523103(/)(2 6.55)p N e q kN m l ⨯⨯===⨯ 水平力cos 4216.4()p p P N N N kN θ=⋅≈=水平垂直力sin tan 4216.40.16675()p p P N N N kN θθ=⋅≈⋅=⨯=竖向图4等效荷载分布图2.4.2综合弯矩:由PK 计算可得:平衡荷载产生的弯矩(综合弯矩)如下图所示:图5 综合弯矩(平衡荷载产生的弯矩)支座A 点的主弯矩:4216.4(1.9 1.0640.21)2640()M kN m =⨯--=⋅1跨中C 点的主弯矩:4216.4(1.0640.12)3980()M kN m =-⨯-=-⋅12.4.3次弯矩计算:M M M -次综主=(M 主__梁中预应力值对截面偏心距的乘积)次弯矩计算表(注:表中正值为梁下边缘受拉)表3次弯矩取平均为641.5kN.m,次剪力约为0 2.5承载力的计算:2.5.1相对受压区高度计算:541.951063.2510pE c E E α⨯===⨯ 100.0021b py p cus cuf E βξσεε=-++55,0.0033(50)100.0033(4050)100.00340.0033cu cu k f ε--=--⨯=--⨯=> 取0.0033cu ε=0p con l E pc σσσασ∏=-+2p p pn pc n n nnnN N e M y y A I I σ∏=±±:E α钢筋与混凝土弹性模量之比PC σ∏:第二批损失完成后,受弯构件受拉边缘处的混凝土预压应力0:p σ受拉区纵向预应力钢筋合力点处混凝土法向应力为0时的预应力钢筋应力:b ξ界限破坏时截面相对受压区高度 :cu ε 非均匀受压时的混凝土极限压应力支座处(A 点)4088.5P N kN ∏=55pe p pn l s snpn pe p l sA y A y e A A σσσσ-=-(1395296.72)3892(19001064210)54.143436(1900106435)(1395296.72)389254.143464-⨯⨯---⨯⨯--=-⨯-⨯ 618()mm =19001064210626()n y mm =--=65111140885004088500618626641.51062613.46910 4.9410 4.9410PC σ∏⨯⨯⨯⨯=++⨯⨯⨯ 23.04 3.20.817.05(/)N mm =++=0p con l E PC σσσασ∏=-+21395296.0167.051141.29(/)N mm =-+⨯=1050.80.420.00213201141.290.002110.0033 1.95100.0033py p cup cuf E βξσεε===--++++⨯⨯跨中(C 点)4344.3P N kN ∏=55pe p pn l s snpn pe p l sA y A y e A A σσσσ-=-(1395184.63)3892(1064120)53.316874(106435)(1395184.63)389253.316874-⨯⨯--⨯⨯-=-⨯-⨯937()mm =1064120944()n y mm =-=65111143443004344300937944641.51094413.46910 4.9410 4.9410PC σ∏⨯⨯⨯⨯=+-⨯⨯⨯23.237.78 1.239.78(/)N mm =+-=0p con l E PC σσσασ∏=-+21395184.6369.781269.1(/)N mm =-+⨯=1050.80.480.00213201269.10.002110.0033 1.95100.0033b py p cup cuf E βξσεε===--++++⨯⨯2.5.2正截面承载力计算:已知:23892p A mm =支座A 点:设计弯矩:38633863641.53221.5()M M kN m =-=-=⋅次38921320210346430035181()389213203464300p py p s y sp py s yA f a A f a a mm A f A f +⨯⨯+⨯⨯===+⨯+⨯ a-受拉区全部纵向钢筋合力点到截面受拉边缘的距离019001811719()h h a mm ===-=对预应力钢筋和非预应力钢筋的合力点取矩:20012c Mx h h f bα=--62023221.51017191719172(mm)0.421719722()19.1600b h mm ξ⨯⨯=--=<=⨯=⨯1119.160017238921320()0300s c p py y A f bx A f f α⨯⨯-⨯=-=<非预应力按照构造max{0.2%,45%t y f f }配筋 ,45%t y f f = 1.7145%0.26%30020.26%0.002660019002964sA Amm选配7225,3436(mm )s A =跨中(C 点):设计弯矩:87888788641.59429.5()M M kN m =+=+=⋅次3892132012068743003595()389213206874300p py p s y sp py s yA f a A f a a mm A f A f +⨯⨯+⨯⨯===+⨯+⨯01900951805()h h a mm =-=-=10120()19.12040120(1805)8159()9429.522f f c f f h M f b h h kN m M kN m α''=-=⨯⨯⨯-=⋅<=⋅ 属于第二类T 形截面对预应力钢筋和非预应力钢筋的合力点取矩:11((/2)c f f o f M M f b b h α'''=---)h h69429.51019.1(2040600120(1805120/2)=⨯-⨯-⨯⨯-)3670.2(.)kN m = 210012c M x h h f bα=--62023670.21018051805187()0.481805866.4()19.1600b mm h mm ξ⨯⨯=--=<=⨯=⨯ 1(c f f p pys yf bx b b A f A f α''⎡⎤+--⎣⎦=)h219.1[600187(2040600)120]389213201020()300mm ⨯⨯+-⨯-⨯==实配14225,6874(mm )s A =2.5.3斜截面承载力计算:图6:预应力梁剪力图因190012034600w h b -==< 验算截面尺寸:00.250.2519.160018055171()1671()c c f bh kN kN β=⨯⨯⨯=>故截面尺寸符合要求 验算是否需要计算配置箍筋:00.70.7 1.7160018051296.4()1671()t f bh kN V kN =⨯⨯⨯=<=故需要进行配筋计算 若只配置箍筋而不用弯起钢筋,0cs p p V V V V ≤+=忽略预应力的影响,故000.7 1.25scs t yvA V f bh f h s ∴=+ 即:1296.4 1.2521018051671s AKN s+⨯⨯⨯=故:0.79s As= ,取箍筋直径d=10mm则:78.54397()0.79s mm ⨯==,取200s mm =.min 78.54 1.710.26%0.240.240.2%600200210sv t sv sv yv A f bs f ρρ⨯===>==⨯=⨯ 满足要求.2.6使用阶段的验算: 2.6.1正截面的抗裂验算:支座A 点(上边缘)3789k M kN m =-⋅6211378910(19001064) 6.41(/)4.9410k ck M y N mm I σ⨯==⨯-=⨯65111140885004088500618626641.51062613.46910 4.9410 4.9410PC σ∏⨯⨯⨯⨯=++⨯⨯⨯ 23.04 3.20.817.05(/)N mm =++=226.417.050.64(/) 2.39/ck pc tk N mm f N mm σσ-=-=-<=,说明在支座A 点上部只产生压应力,不可能出现裂缝,故不需要进行裂缝宽度验算 跨中C 点(下边缘)62116123612310106413.12(/)4.9410k k ck M kN mM y N mm I σ=⋅⨯==⨯=⨯ 65111143443004344300937944641.51094413.46910 4.9410 4.9410PC σ∏⨯⨯⨯⨯=+-⨯⨯⨯ 23.237.78 1.239.78(/)N mm =+-=213.129.78 3.34(/)ck pc N mm σσ-=-=>22.39/tk f N mm =,需要进行裂缝宽度验算max t (1.90.08)epskcr s ed W c E σαψρ=+687438920.0190.51900600s pte teA A A ρ++===⨯⨯1.7cr α=(构件受力特征系数)2p0con l E pc =1395184.6369.781269.1(N/mm )σσσασ-+=-+⨯=0p0p p A ()A p con l E pc N σσσασ==-+(1395184.6369.78)3892=-+⨯⨯ 4939.14()kN =()(2040600)1200.166001805f ff b b h bh γ''--⨯'===⨯6230(6123641.5)1001370()4939.1410k p p M M e e mm N ++⨯=+=+=⨯200[0.870.12(1)()]f h z h eγ'=-- ()218050.870.1210.1618051255()1370mm ⎡⎤⎛⎫=-⨯-⨯⨯=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦20()()k p p sk p s M M N z e A A zσ+--=+6632612310641.5104939.1410(1255-0)41.9(/)(68743892)1255N mm ⨯+⨯-⨯⨯==+⨯0.650.65 2.391.1 1.10.850.2,0.20.01941.9tkte skf ψψρσ⨯=-=-=-<=⨯取22214252815.227(mm)14 1.020+280.515.2i i eqi i i n d d n v d ∑⨯+⨯===∑⨯⨯⨯⨯ 55225,(1.95 2.0)10/2 1.97510/, 1.7()s cr c mm E N mm α==+⨯=⨯=取预应力混凝土构件 max t (1.90.08)epskcr sed W c E σαψρ=+541.9271.70.2(1.9250.08)0.012()0.21.975100.019mm mm =⨯⨯⨯⨯+⨯=<⨯ 满足要求其中::ck σ标准组合下抗裂验算边缘的混凝土法向应力 :pc σ扣除全部预应力损失后边缘混凝土的预压应力:cr α构件受力特征系数ψ:裂缝间纵向受拉钢筋应变不均与系数 :sk σ按荷载效应的标准组合计算的预应力钢筋混凝土构件纵向受拉钢筋的等效应力:c 最外层纵向受拉钢筋外边缘至受拉区底边的距离:te ρ按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率:te A 有效受拉混凝土截面面积 :ep d 受拉区纵向钢筋的等效直径:f γ'受压翼缘截面面积与腹板有效截面面积的比值:e 轴向压力作用点至纵向受拉钢筋合力点的距离:p e 混凝土法向应力等于0时全部纵向预应力和非预应力的合力的作用点至受拉区纵向预应力钢筋和非预应力钢筋合力点的距离0:p N 混凝土法向应力等于0时,全部纵向预应力和非预应力筋的合力2.6.2挠度计算(1) 截面刚度计算0()cr pc tk M f w σγ=+120120(0.7)(0.7) 1.5 1.161600m h γγ=+=+⨯= 29.78/pc N mm σ=11834.9410 4.610()1064n n n I W mm y ⨯===⨯()cr pc tk n M f W σγ=+8(9.78 1.16 2.39) 4.6105774.1()kN m =+⨯⨯⨯=⋅5405774.10.946123210389268740.0613.25106001805cr cr k f p s s E c M k M A A E E bh γαρ====+⨯+=⋅=⨯=⨯⨯0.210.21(1)(10.45)0.7110.4500.7 3.740.061f E w γαρ=++-=+⨯+⨯-=()()0.85(1)c ns cr cr E I B k k w=+-4111515150.85 3.2510 4.941011.7100.94(10.94) 3.7410%11.7100.910.5310s s B B ⨯⨯⨯⨯==⨯+-⨯∴=⨯⨯=⨯考虑预拉区出现裂缝,故降低1515(1)0.749600.711635774.1()612310.5310 5.42105774.1(21)6123k sl q kq g l M B B M M M M M kN m B θ=-+=+=+⨯=⋅⨯⨯∴==⨯⨯-+ 其中::cr M 开裂弯矩γ:混凝土构件的截面抵抗塑性影响系数f γ:受拉翼缘截面面积与腹板有效截面面积的比值:m γ混凝土构件的截面抵抗塑性影响系数基本值s B :荷载短期作用下的截面弯曲刚度 l B :荷载长期作用下的截面弯曲刚度:q M 按荷载效应的准永久组合计算的弯矩,取计算区段内的最大弯矩值(2) 荷载作用下的挠度:跨中:612337899912()k M KN m =+=⋅ 等效荷载:22889912115.52(/)26.2M q KN m l ⨯=== 2453848q l lM lql f B B =-支座 46215155115.522620037891026200130.86070.8()384 5.42108 5.4210mm ⨯⨯⨯⨯=-=-=⨯⨯⨯⨯ (3) 预应力产生的反拱:跨中:328633436629()M M kN m =+=⋅ 等效荷载:2288662977.3(/)26.2M q kN m l ⨯=== 2453848q c n c nM l ql f E I E I =-支座 462411411577.32620032861026200384 3.2510 4.94108 3.2510 4.941029.517.612()mm ⨯⨯⨯⨯=-⨯⨯⨯⨯⨯⨯⨯⨯=-= 构件的挠度(考虑预压应力长期作用的影响,将预应力反拱值乘以增大系数2.0):26200270.821246.8()87.3()300300q p l f f f mm mm =-=-⨯=<== 满足要求 2.7施工阶段的验算: 2.7.1应力计算:施工阶段有效预加力为张拉控制应力减去第一阶段预应力损失3892(1395192.7 1.05)4675.3()pA p p N A kN σ==⨯--=3892(1395082.49)5108.3()pc p p N A kN σ==⨯--=4675.35108.34891.8()22pA pC p kN N N N +=+==端弯矩:4891.80.6263062.3()p M kN m =⨯=⋅曲线范围内均布荷载:22884891.80.523119.3(/)(2 6.55)p N e q kN m l ⨯⨯===⨯水平力cos 4891.8()p p P N N N kN θ=⋅≈=水平垂直力sin tan 4891.80.16782.7()p p P N N N kN θθ=⋅≈⋅=⨯=竖向图7 等效荷载分布图2图8 综合弯矩2(平衡荷载产生的弯矩)支座A 点的主弯矩:4891.80.6263062.3()M kN m =⨯=⋅1 跨中C 点的主弯矩:4891.80.9444617.9()M kN m =-⨯=-⋅1次弯矩计算表(注:表中正值为梁下边缘受拉)表四:次弯矩取平均为747.8kN.m考虑荷载的不利情况,即在施工预应力时可能的最小自重荷载为: 预应力梁的间距为6.0m,板厚h=120mm, 则由板传到梁上的线荷载为(6.00.6)(0.1225)16.2(/),16.5/g kN m kN m =-⨯⨯=取计算图9 最小自重荷载产生的弯矩图跨中C :()p A (1395082.49)38925108.3()p con l N kN σσI =-=--⨯=上边缘:2p p pn npc n nnnN N e y M y A I I σ=-+65111151083005108300937836747.81083613.46910 4.9410 4.9410⨯⨯⨯⨯=-+⨯⨯⨯ 23.798.10 1.273.04(/)N mm =-+=-611029*******3.04 3.044.914.9410k ct pc M W σσ⨯⨯=+=-+=-+⨯ 221.87(/)2 4.78(/)tkN mm f N mm '=<=>0(表明上边缘受压) 下边缘:2p p pn npc n nnnN N e y M y A I I σ=+-651111510830051083009371064747.810106413.46910 4.9410 4.9410⨯⨯⨯⨯=+-⨯⨯⨯23.7910.31 1.6112.49(/)N mm =+-=611022290010106412.4912.49 6.254.94106.25(/)0.80.826.821.44(/)k cc pc ckM w N mm f N mm σσ⨯⨯=-=-=-⨯'=<⨯==支座A :()p A (1395192.7 1.05)4675.3()p con l N kN σσI =-=--= 上边缘:2pp pn n pc n n n nN N e y M y A I I σ=++ 36511114675.3104675.3618836747.81083613.46910 4.9410 4.9410⨯⨯⨯⨯⨯=++⨯⨯⨯ 2=3.46+4.88+1.27=9.61(/)N mm611022*********.619.61 1.634.941011.24(/)0.80.826.821.44(/)k cc pc ckM w N mm f N mm σσ⨯⨯=-=-=-⨯'=<⨯== 下边缘:2pp pn n pc n n n nN N e y M y A I I σ=-- 36511114675.3104675.36181064747.810106413.46910 4.9410 4.9410⨯⨯⨯⨯⨯=--⨯⨯⨯ 2=3.46-6.21-1.61=-4.36(/)N mm6k 110022N 9621010644.36 4.36 2.07A 4.94102.28(/)2 4.78(/)k ct pc tkM W N mm f N mm σσ⨯⨯=++=-+=-+⨯'=-<=故:上下边缘均满足要求2.7.2梁端局部承压的计算采用OVM 锚具、垫板及局部承压钢筋等配套设备。
