文克勒地基上梁的计算课件
合集下载
文克尔地基上的龙门吊轨道基础梁计算
0． 90
三桩
3 218
27 899
3 218
2 930
0． 91
四桩
4 208
33 324
4 208
4 022
0． 96
六桩
6 072
43 885
6 072
5 296
0． 87
注：Nk 为荷载效应标准组轴心竖向力作用下，基桩或复合基桩的平均竖向力
2． 2 筏板设计
本工程上部结构的荷载由旋喷桩承担，筏板通过将相邻柱下 的承台连成整体，主要起到以下作用： 筏板与其上覆土的自重提供
M/kN·m
300 200 100
0 -100
-5 -3 -1 1 3 5 7 9 11 13 14 X/m
图 6 地基梁弯矩分布示意图
5 结语
运用文克尔地基上的无限长梁模型，可以计算如龙门吊轨道 基础梁等类似构件的内力、变形及基底反力。计算方法具有计算 过程简便，计算结 果 精 确 等 优 点。对 于 半 无 限 长 梁、有 限 长 梁 亦 可运用文克尔地基上的半无限长梁、文克尔地基上的有限长梁理
（ 2K） ，最终有：
θ=
－
P0 λ2 K
Bx
，M
=
P0 4λ
C
x
，Q
=
－
P0 2
Dx
（ 8）
其中， Ax = e － λx （ cosλx + sinλx） ； Bx = e － λx sinλx （ 9）
Cx = e － λx （ cosλx － sinλx） ； Dx = e － λx cosλx
建筑工业出版社，1993．
2 000，翼缘厚度 hf = 300，梁截面示意图见图 3。梁混凝土强度等 ［2］ GB 50007-2002，建筑地基基础设计规范［S］．
3.4文克勒地基上梁的计算[研究材料]
![3.4文克勒地基上梁的计算[研究材料]](https://img.taocdn.com/s3/m/a30d3497ccbff121dc36835a.png)
➢ 基底反力图形与竖向位移相似，如刚度大（基 础）受荷后基础底面仍保持平面，基底反力图 形按直线规律变化。
（a）
反力图 （b）
反力图 （c）
图3-8 文克勒地基模型
（a）侧面无摩阻力的土柱体系；（b）弹簧调模研型学；习（c）文克勒地基上的刚性基础
5
适用范围：
1）地基主要受力层为软土； 2）厚度不超过基础底面宽度之半的薄压缩层
dw
dx
dM
d 3w
V dx EI dx3
M
EI
d 2w dx2
p kw
调研学习
22
w ex C1 cos x C2 sin x ex C3 cos x C4 sin x
2 .集中荷载作用下的解答 (1)竖向集中力作用下
F0 x
边界条件：当x→∞时，w→0。将
O
此边界条件代入上式，得C１=C２=0。 梁的右半部，上式成为：
M
将上式连续对坐标x取两次导数，便得：
EI
d 4w dx4
d 2M dx2
dV dx
bp q
对于没有分布荷载作用（q = 0）的梁段，上式成为：
EI
d 4w dx4
bp
上式是基础梁的挠曲微分方程，对哪一种地基模型都适用。
调研学习
18
采用文克勒地基模型时
EI
d 4w dx 4
bp
p ks
sw
1）布辛奈斯科解，作用P时距r表面沉降s为
S p(1 2 ) / E0r
2）均荷作用下，矩形中心点沉降，可对上式 积分得
调研学习
7
按叠加法，网格i中点的沉降为所有n个网格上的基底 压力分别引起的沉降之和，即
调研学习
（a）
反力图 （b）
反力图 （c）
图3-8 文克勒地基模型
（a）侧面无摩阻力的土柱体系；（b）弹簧调模研型学；习（c）文克勒地基上的刚性基础
5
适用范围：
1）地基主要受力层为软土； 2）厚度不超过基础底面宽度之半的薄压缩层
dw
dx
dM
d 3w
V dx EI dx3
M
EI
d 2w dx2
p kw
调研学习
22
w ex C1 cos x C2 sin x ex C3 cos x C4 sin x
2 .集中荷载作用下的解答 (1)竖向集中力作用下
F0 x
边界条件：当x→∞时，w→0。将
O
此边界条件代入上式，得C１=C２=0。 梁的右半部，上式成为：
M
将上式连续对坐标x取两次导数，便得：
EI
d 4w dx4
d 2M dx2
dV dx
bp q
对于没有分布荷载作用（q = 0）的梁段，上式成为：
EI
d 4w dx4
bp
上式是基础梁的挠曲微分方程，对哪一种地基模型都适用。
调研学习
18
采用文克勒地基模型时
EI
d 4w dx 4
bp
p ks
sw
1）布辛奈斯科解，作用P时距r表面沉降s为
S p(1 2 ) / E0r
2）均荷作用下，矩形中心点沉降，可对上式 积分得
调研学习
7
按叠加法，网格i中点的沉降为所有n个网格上的基底 压力分别引起的沉降之和，即
调研学习
文克尔地基上的有限长梁计算
基础梁计算方法：
基础梁承受着整个建筑物的重量和外来荷载，所 以它的安全度关系着整个建筑物能否正常用。因 此建筑物的设计者对基础梁的研究十分重视，使 基础梁的计算内力尽可能与实际受力相接近, 从而 合理设计、合理配筋。
目前基础梁的实用工程分析法多采用两种方法: 完 全不考虑上部结构-基础-地基的共同作用或只考 虑基础-地基的共同作用。
w
M 02
K
Bx
M 03
K
Cx
其中
M
M0 2
Dx
Ax ex (cosx sin x)
V
M 0
2
Ax
Bx ex sin x
Cx ex (cosx sin x)
Dx ex cosx
Ax、Bx、Cx、Dx的数值可以查表确定
3、有限长梁的判定
实际工程中的梁是属于无限长梁还是有限长梁并非
以梁的绝对尺寸划分，而是通过荷载在梁端引起
文克尔地基上的有限 长梁计算
研究背景
土质地基上受多个集中力作用的有限长梁, 是工程实践中时常遇到的 一种力学模型。
基础梁： 工程中，结构物与地基的连接方式主要取决于地基的条件和荷载的大
小这两个方面。如果地基的条件比较好，荷载比较小，可以直接通过 墙柱的作用，将荷载传至地基，但是如果地基的条件比较差，荷载比 较大，就需要通过设置基础梁，基础梁的作用是把上部结构的重量、 荷载等外力比较均匀地传给地基，可以在一定程度上调节建筑物沉降， 使其均匀化，以减小地基所受压力的强度，使地基满足承载力的要求。 因此，基础梁被广泛应用在工业与民用建筑上。 常用的基础梁包括：柱下条形基础、柱下交叉条形基础、筏形基础和 箱型基础等。
1.建立文克尔地基上梁的挠曲微分方程：
地基基础讲义ppt课件(共139张PPT)
faE= afa ex、 Mx=（ Fk+ Gk）.
二、内力计算
1、简化计算方法
（1〕静定分析法
（2〕倒梁法
2、弹性地基梁法
（1〕对基础宽度不小于可压缩层厚度二倍的薄压 缩层地基，地基的压缩性比较均匀，可按文克勒地 基上梁的解析解。
（2） 对基础宽度不小于可压缩层厚度二倍的薄 压缩层地基，地基的压缩性不均匀，可按文克勒 地基上梁的数值分析法。
由式3-34节点i的竖向位移：
bx，by—分别为x，y方向基础的底面宽度
Sx，Sy —分别为x，y方向基础梁的特征长度
x， y—分别为x，y方向基础梁的柔度特征值 Ix，Iy—分别为x，y方向基础梁的截面惯性矩
根据变形协调条件
将静力平衡条件代入可解得：
对一端外伸的角柱节点
y=0，Zy=4
对无外伸的角柱节点
（2〕工程实测： （3〕物理模拟：根据相似理论推导相似准则
设计模型试验 （4〕数值模拟：将构件离散成有限个单元
数值模拟 （1〕有限元：ANSYS、ADINS、SAP、I-DIASD 等
（2〕有限差分法：FLAC
（3〕边界元： （4〕离散元：
ANSYS简介：
b、相邻柱荷载及柱距变化较大 Fk——作用于筏基上的竖向荷载总和
例题3-1
例题3-2
第六节、柱下条形基础
适用范围： （1〕地基较软弱，承载力低，地基压缩性
不均匀 （2〕荷载分布不均匀，不均匀沉降较大 （3〕上部结构对基础沉降较敏感
一、构造要求
1、为了使 与基础底面形心重合， 基底压力均匀分布， 基础梁的两端应外伸
2、肋梁的高h由计算定，以为柱距的〔1/4~1/8〕l1
3、翼板的高hf由计算定，当200mm<hf<250mm采用等 厚度，当hf>250mm采用宜采用变厚度翼板，i<1:3
二、内力计算
1、简化计算方法
（1〕静定分析法
（2〕倒梁法
2、弹性地基梁法
（1〕对基础宽度不小于可压缩层厚度二倍的薄压 缩层地基，地基的压缩性比较均匀，可按文克勒地 基上梁的解析解。
（2） 对基础宽度不小于可压缩层厚度二倍的薄 压缩层地基，地基的压缩性不均匀，可按文克勒 地基上梁的数值分析法。
由式3-34节点i的竖向位移：
bx，by—分别为x，y方向基础的底面宽度
Sx，Sy —分别为x，y方向基础梁的特征长度
x， y—分别为x，y方向基础梁的柔度特征值 Ix，Iy—分别为x，y方向基础梁的截面惯性矩
根据变形协调条件
将静力平衡条件代入可解得：
对一端外伸的角柱节点
y=0，Zy=4
对无外伸的角柱节点
（2〕工程实测： （3〕物理模拟：根据相似理论推导相似准则
设计模型试验 （4〕数值模拟：将构件离散成有限个单元
数值模拟 （1〕有限元：ANSYS、ADINS、SAP、I-DIASD 等
（2〕有限差分法：FLAC
（3〕边界元： （4〕离散元：
ANSYS简介：
b、相邻柱荷载及柱距变化较大 Fk——作用于筏基上的竖向荷载总和
例题3-1
例题3-2
第六节、柱下条形基础
适用范围： （1〕地基较软弱，承载力低，地基压缩性
不均匀 （2〕荷载分布不均匀，不均匀沉降较大 （3〕上部结构对基础沉降较敏感
一、构造要求
1、为了使 与基础底面形心重合， 基底压力均匀分布， 基础梁的两端应外伸
2、肋梁的高h由计算定，以为柱距的〔1/4~1/8〕l1
3、翼板的高hf由计算定，当200mm<hf<250mm采用等 厚度，当hf>250mm采用宜采用变厚度翼板，i<1:3
3.4文克勒地基上梁的计算解析
基 础 工 程
青岛理工大学 土木工程学院 地基教研室
3.3 地基计算模型
土的应力应变特性：非线性、弹塑性、土的各向异性、结构 性、流变性、剪胀性。 影响土应力应变关系的应力条件：应力水平、应力路径、 应力历史。
进行地基上梁和板分析时，必须解决基底压 力分布和沉降计算问题，它涉及土应力应变 关系，表达这种关系模式称为地基模型。
M0 M
q
M+dM V+dV
+q
x w bp
挠曲曲线
V bp x
+V
+M
w
(a)
(b)
(c)
图3-11 文克勒地基上基础梁的计算图式
（a）梁上荷载和挠曲；（b）梁的微单元；（c）符号规定
根据材料力学，梁挠度w的微分方程式为：
d2w EI 2 M dx
由梁的微单元的静力平衡条件∑M =0、∑V =0得到：
Wi Si
挠度=沉降量
解析解：指能以函数的形式解析地表达出 来地解答。如文克勒地基上梁的解答。 数值解：把梁或板微分方程离散化，最终 得到一组线性代数方程，从而求得近似地 数值解。
有限单元法 有限差分法
3.4 文克勒地基上梁计算
3.4.1 无限长梁的解答 一、微分方程
x F o
dx q
一、 文克勒地基模型 1867年捷克工程师文克勒提出如下假设： 地基上任一点所受的压力强度p与该点的地基 沉降量s成正比。
p=kS
K为基床反力系数，单位kN/m3
把地基划分许多竖直土柱，每条土柱可由一根 弹簧代替。压力与变形成正比。 基底反力图形与竖向位移相似，如刚度大（基 础）受荷后基础底面仍保持平面，基底反力图 形按直线规律变化。
青岛理工大学 土木工程学院 地基教研室
3.3 地基计算模型
土的应力应变特性：非线性、弹塑性、土的各向异性、结构 性、流变性、剪胀性。 影响土应力应变关系的应力条件：应力水平、应力路径、 应力历史。
进行地基上梁和板分析时，必须解决基底压 力分布和沉降计算问题，它涉及土应力应变 关系，表达这种关系模式称为地基模型。
M0 M
q
M+dM V+dV
+q
x w bp
挠曲曲线
V bp x
+V
+M
w
(a)
(b)
(c)
图3-11 文克勒地基上基础梁的计算图式
（a）梁上荷载和挠曲；（b）梁的微单元；（c）符号规定
根据材料力学，梁挠度w的微分方程式为：
d2w EI 2 M dx
由梁的微单元的静力平衡条件∑M =0、∑V =0得到：
Wi Si
挠度=沉降量
解析解：指能以函数的形式解析地表达出 来地解答。如文克勒地基上梁的解答。 数值解：把梁或板微分方程离散化，最终 得到一组线性代数方程，从而求得近似地 数值解。
有限单元法 有限差分法
3.4 文克勒地基上梁计算
3.4.1 无限长梁的解答 一、微分方程
x F o
dx q
一、 文克勒地基模型 1867年捷克工程师文克勒提出如下假设： 地基上任一点所受的压力强度p与该点的地基 沉降量s成正比。
p=kS
K为基床反力系数，单位kN/m3
把地基划分许多竖直土柱，每条土柱可由一根 弹簧代替。压力与变形成正比。 基底反力图形与竖向位移相似，如刚度大（基 础）受荷后基础底面仍保持平面，基底反力图 形按直线规律变化。
文克勒地基模型
文克勒地基模型文克勒地基模型：地基上任一点所受的压力强度p与该点的地基沉降S成正比，即p＝kS式中比例常数k称为基床系数，单位为kPa／m 。
﹙地基上某点的沉降与其它点上作用的压力无关，类似胡克定理，把地基看成一群独立的弹簧。
﹚﹙文克勒假设：假设每单位面积上所受的压力与地基沉陷成正比。
这一假设可以用于变宽度的基础梁，也可用于任何形状的基础板。
但按此假设，沉陷只发生在地基的受压部分。
﹚文克勒地基模型忽略了地基中的剪应力，而正是由于剪应力的存在，地基中的附加应力才能向旁扩散分布，使基底以外的地表发生沉降。
凡力学性质与水相近的地基，例如抗剪强度很低的半液态土﹙如淤泥、软粘土﹚地基或基底下塑性区相对较大时，采用文克勒地基模型就比较合适。
此外，厚度不超过梁或板的短边宽度之半的薄压缩层地基也适于采用文克勒地基模型。
﹙这是因为在面积相对较大的基底压力作用下，薄层中的剪应力不大的缘故。
﹚实际上，沉陷也发生在受压范围以外。
半无限大弹性体假设：假设地基是半无限大理想弹性体，采用弹性力学中半无限大弹性地基的沉陷公式来计算地基的沉陷。
显然一般土壤与理想弹性体是有区别的。
土壤是颗粒体，而且不能或几乎不能承受拉力。
因此，必须土壤中没有拉应力发生时，这个土壤地基才能当做连续体看待。
中厚度假设：假设地基是中等厚度的弹性层(有限压缩层)，用弹性力学导出地基的沉陷公式。
按照后两种假设计算基础梁时，必须把问题区分为平面问题和空间问题，前者又必须区分为平面应力问题和平面形变问题。
如果地基是均匀整岩，或是很厚的均匀土层，才能用半无限大弹性体假设来计算。
如果可压缩土层的厚度和基础的最大水平尺寸同阶大小，则须按照中厚度地基假设来计算。
如果地基的可压缩层较薄，与基础的最大水平尺寸相比，成为一个很薄的垫层，那就可以按照文克勒假设来计算。
基础梁的计算通常有两种方法:一种是导出基础梁的基本方程(微分方程和积分方程)，然后求解这些方程。
在文克勒假设下，基本方程成为四阶线性常系数的微分方程，可以用初参数法求解。
文克勒地基上梁的挠曲微分方程
由梁上竖向的静力平衡条件得：
F 0
dV Bp q dx
M 0
dM V dx
根据材料力学，梁挠度w的
微分方程式为：
Ec I
d 2w dx2
M
式中: Ec ——梁材料的弹性模量（kPa）; I ——截面惯性矩（m4）。
dM V dx
dV Bp q dx
将
Ec I
2、地基非均质性的影响
外荷载及基础相同，地基不同，基底反力不同
2、地基非均质性的影响
外地基及基础相同， 外载荷不同，基底 反力不同
二、地基变形对上部结构的影响
整个上部结构对基础不均匀沉降或挠曲的 抵抗能力，称为上部结构的刚度或整体刚度， 根据其大小分为：
柔性结构 敏感结构
刚性结构
1、柔性结构
∑F－作用在基础上的竖向外荷载和基底反力之和 ∑M－外荷载和基底反力对基础任一点的力矩之和
2、 变形协调条件（接触条件）
变形前后基础与地基总是保持接触，不得脱开， 即基础底面任一点的挠度wi应等于该点的地基
沉降si：
wi si
§3.4文克勒地基上梁的计算
一、微分方程式
从宽度为B的梁，取出长为dx为一小段梁元素， 其上作用着分布荷载q和基底反力p以及截面上的 弯矩M和剪力V。
(2)考虑基础—地基共同作用分析法 (3)考虑上部结构-基础-地基共同作用分析法
§3.3 地基计算模型
地基计算模型：在进行地基上梁和板的分析时， 能够表达基底压力分布和地基沉降的关系式， 最常用的三种线性弹性模型：
文克勒地基模型 弹性半空间地基模型
有限压缩层地基模型
一、文克勒地基模型 (又称“基床系数法”）
基础工程第3章3 连续基础3.4-3.6
w ex C3 cosx C4 sin x
对称性：在x=0处，dw/dx=0，代 入上式得C3－C4=0。令C3=C4=C， 则上式成为
w exCcosx sin x
静力平衡条件：再在O点处紧靠F0 的左、右侧把梁切开，则作用于O 点左右两侧截面上的剪力均等于F0 之半，且指向上方。根据符号规定， 在右侧截面有V=－F0 /2，由此得 C=F0λ/2kb 。 +V F0
解上述方程组得：
FA El Fl Dl Va El Fl Al M a Fl El Dl Vb Fl El Al M b Va M A El Fl Cl El Fl Dl M a 2 V Fl El Cl b Fl El Dl M b 2 FB Fl El Dl Va Fl El Al M a El Fl Dl Vb El Fl Al M b Va M B Fl El Cl Fl El Dl M a 2 Vb El Fl Cl El Fl Dl M b 2
3.4 文克勒地基上梁的计算
3.4.1 无限长梁的解答
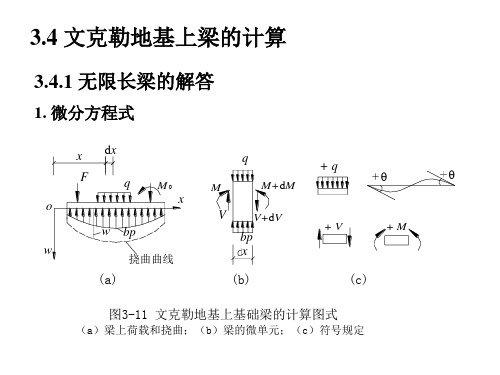
1. 微分方程式
x F o w w bp
挠曲曲线
dx q
M0 M
q
M+dM V+dV
+q
x
V bp x
+V
+M
(a)
(b)
(c)
图3-11 文克勒地基上基础梁的计算图式
（a）梁上荷载和挠曲；（b）梁的微单元；（c）符号规定
x F o
dx q
对短梁，可采用基底反力呈直线变化的简化方法计算；