专题五 解析几何1--1
专题五 解析几何 文科数学

专题五 文科数学 解析几何1.(2011·朝阳期末)已知圆的方程为086222=++-+y x y x ,那么下列直线中经过圆心的直线方程为( B )(A )012=+-y x (B )012=++y x (C )012=--y x (D )012=-+y x2.(2011·朝阳期末)设椭圆的两个焦点分别为1F ,2F ,过2F 作椭圆长轴的垂线与椭圆相交,其中的一个交点为P ,若△12F P F 为等腰直角三角形,则椭圆的离心率是( A )(A )1-(B )12(C ) (D )23.(2011·朝阳期末)经过点(2, 3)-且与直线250x y +-=垂直的直线方程为 280x y -+= .4.(2011·朝阳期末)(本小题满分13分)已知点(4, 0)M ,(1, 0)N ,若动点P 满足6||M N M P P N ⋅=.(Ⅰ)求动点P 的轨迹C 的方程;(Ⅱ)设过点N 的直线l 交轨迹C 于A ,B 两点,若181275N A N B -⋅- ≤≤,求直线l 的斜率的取值范围.解:(Ⅰ)设动点(, )P x y ,则(4, )M P x y =- ,(3, 0)M N =- ,(1, )P N x y =--. …………………2分 由已知得22)()1(6)4(3y x x -+-=--,化简得223412x y +=,得22143xy+=.所以点P 的轨迹C 是椭圆,C 的方程为13422=+yx. ………………………6分(Ⅱ)由题意知,直线l 的斜率必存在,不妨设过N 的直线l 的方程为(1)y k x =-,设A ,B 两点的坐标分别为11(, )A x y ,22(, )B x y .由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩消去y 得2222(43)84120k x k x k +-+-=. ………………8分因为N 在椭圆内,所以0∆>.所以212221228,34412.34kx x k k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩………………………………………………………10分 因为2121212(1)(1)(1)(1)(1)NA NB x x y y k x x ⋅=--+=+--]1)()[1(21212++-+=x x x x k222222243)1(943438124)1(kk k kkkk ++-=+++--+=, …………12分所以22189(1)127345k k-+--+≤≤. 解得213k ≤≤.所以1k -≤或1k ≤≤. …………………………………………13分5.(2011·丰台期末)过点(34)-,且与圆22(1)(1)25x y -+-=相切的直线方程为 43240x y -+= . 6.(2011·丰台期末) (本小题满分14分)已知O 为平面直角坐标系的原点,过点(20)M -,的直线l 与圆221x y +=交于P ,Q 两点.(Ⅰ)若PQ =,求直线l 的方程;(Ⅱ)若12M P M Q =,求直线l 与圆的交点坐标.解:(Ⅰ)依题意,直线l 的斜率存在,因为 直线l 过点(2,0)M -,可设直线l :(2)y k x =+. 因为PQ =,圆的半径为1,P ,Q 两点在圆221x y +=上,所以圆心O到直线l12 =.又因为12 =,所以15k=±,所以直线l的方程为20x-+=或20x++=.………………………7分(Ⅱ)设11(,)P x y,22(,)Q x y,所以22(2,)M Q x y=+,11(2,)M P x y=+.因为2M Q M P=,所以212122(2)2x xy y+=+⎧⎨=⎩即21212(1)2x xy y=+⎧⎨=⎩(*);因为P,Q两点在圆上,所以2211222211x yx y⎧+=⎪⎨+=⎪⎩把(*)代入,得2211221114(1)41x yx y⎧+=⎪⎨++=⎪⎩,所以11788xy⎧=-⎪⎪⎨⎪=±⎪⎩,22144xy⎧=⎪⎪⎨⎪=±⎪⎩,所以P点坐标为7(88-或7(88--,,Q点坐标为1(44,或1(44-,.………………………14分7. (2011·东莞期末)已知双曲线22221x ya b-=的一条渐近线方程为12y x=,则该双曲线的离心率为( A)A.25B.3C.5D.28.(2011·东莞期末)(本小题满分14分)已知椭圆E 的中心在坐标原点O ,两个焦点分别为)0,1(-A 、)0,1(B ,一个顶点为)0,2(H .(1)求椭圆E 的标准方程;(2)对于x 轴上的点)0,(t P ,椭圆E 上存在点M ,使得MH MP ⊥,求t 的取值范围.解:(1)由题意可得,1c =,2a =,∴b =∴所求的椭圆的标准方程为:22143xy+=.(2)设),(00y x M )20±≠x (,则2200143x y +=. ①且),(00y x t MP --=,),2(00y x MH --=, 由MH MP ⊥可得0=⋅MH MP ,即∴0)2)((2000=+--y x x t . ②由①、②消去0y 整理得3241)2(0200-+-=-x x x t .∵20≠x , ∴23411)2(4100-=---=x x t .∵220<<-x ,∴ 12-<<-t .∴t 的取值范围为)1,2(--. 9. (2011·佛山一检)已知双曲线22221(0,0)x y a b ab-=>>与抛物线28y x =有一个公共的焦点F ,且两曲线的一个交点为P ,若5PF =,则双曲线的离心率为( A )A .2B .C 2D10. (2011·佛山一检)若点P 在直线03:1=++y x l上,过点P 的直线2l 与曲线22:(5)16C x y -+=相切于点M ,则PM 的最小值为( D )AB .2C .D .411. (2011·佛山一检)已知直线22x y +=分别与x 轴、y 轴相交于,A B 两点,若动点(,)P a b 在线段A B 上,则a b 的最大值为____12______.12.(2011·广东四校一月联考)过圆224x y +=外一点(4,2)P 作圆的两条切线,切点分别为,A B ,则ABP ∆的外接圆方程是( D )A .22(4)(2)1x y -+-=B .22(2)4x y +-=C .22(2)(1)5x y +++=D .22(2)(1)5x y -+-=13.(2011·广东四校一月联考)设θ是三角形的一个内角,且1sin cos 5θθ+=,则方程22sin cos 1x y θθ-=表示的曲线是( D ) A .焦点在x 轴上的双曲线 B .焦点在x 轴上的椭圆C .焦点在y 轴上的双曲线D .焦点在y 轴上的椭圆14.(2011·广东四校一月联考)(本小题满分14分)设(1,0)F ,M 点在x 轴的负半轴上,点P 在y 轴上,且,M P PN PM PF=⊥.(1)当点P 在y 轴上运动时,求点N 的轨迹C 的方程;(2)若(4,0)A ,是否存在垂直x 轴的直线l 被以A N 为直径的圆截得的弦长恒为定值?若存在,求出直线l 的方程;若不存在,请说明理由.解:(1)(解法一)MP PN =,故P 为M N 的中点. -------1分设(,)N x y ,由M 点在x 轴的负半轴上,则(,0),(0,),(0)2yM x P x -> -------2分又(1,0)F ,(,),(1,)22y y PM x PF ∴=--=--------4分又PM PF ⊥ ,204yPM PF x ∴⋅=-+= -------6分 所以,点N 的轨迹C 的方程为24(0)y x x => -------7分(解法二)MP PN =,故P为M N 的中点. -------1分设(,)N x y ,由M 点在x 轴的负半轴上,则(,0),(0,),(0)2yM x P x -> -------2分又由,M P PN PM PF =⊥ ,故FN FM = ,可得22FNFM=-------4分由(1,0)F ,则有222(1)(1)x y x -+=--,化简得:24(0)y x x => -------6分 所以,点N 的轨迹C 的方程为24(0)y x x => -------7分 (2)设A N 的中点为B ,垂直于x 轴的直线方程为x a =, 以A N 为直径的圆交l 于,C D 两点,C D 的中点为H .12CB AN ==412422x B H a x a +=-=-+ -------9分22222211[(4)](24)44CH CB BHx y x a ∴=-=-+--+221[(412)416](3)44a x a a a x a a=--+=--+ -------12分所以,令3a =,则对任意满足条件的x , 都有29123C H=-+=(与x 无关),-------13分即C D = -------14分15.(2011·广州期末)已知直线l 经过坐标原点,且与圆22430x y x +-+=相切,切点在第四象限,则直线l 的方程为( C )A.y = B.y = C.3y x =- D.3y x=16.(2011·广州期末)(本小题满分14分)图4已知椭圆(222:13x yE a a+=>的离心率12e =. 直线x t =(0t >)与曲线E 交于不同的两点,M N ,以线段M N 为直径作圆C ,圆心为C . (1)求椭圆E 的方程; (2)若圆C 与y轴相交于不同的两点,A B ,求A B C ∆的面积的最大值.(本小题主要考查椭圆、圆、直线与圆的位置关系等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解:∵椭圆()222:133x yE a a+=>的离心率12e =,x=a∴12a=. …… 2分解得2a =.∴ 椭圆E 的方程为22143xy+=. …… 4分(2)解法1:依题意,圆心为.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=.∴ 圆C的半径为2r =. …… 6分∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即07t <<.∴弦长||A B ===. ……8分∴A B C ∆的面积12S =⋅ …… 9分)1=)2212712t +-≤7=. …… 12分=7t =时,等号成立.∴ A B C ∆的面积的最大值为7. …… 14分解法2:依题意,圆心为.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=.∴ 圆C的半径为2r =. …… 6分 ∴ 圆C 的方程为222123()4tx t y --+=.∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即07t <<.在圆C 的方程222123()4tx t y --+=中,令0x =,得2y =±,∴弦长||AB = 8分∴A B C ∆的面积12S =⋅ …… 9分)=)221272t +-≤7=. ……12分=7t =时,等号成立.∴ A B C ∆的面积的最大值为7. …… 14分17.(2011·哈九中高三期末)抛物线24x y =上一点到直线54-=x y 的距离最短,则该点的坐标是 ( )A .)2,1(B .)0,0(C .)1,21( D .)4,1(【答案】C【分析】根据题意,直线54-=x y 必然与抛物线24y x =相离,抛物线上的点到直线的最短距离就是与直线54-=x y 平行的抛物线的切线的切点。
解析几何-吕林根-课后习题解答一到五
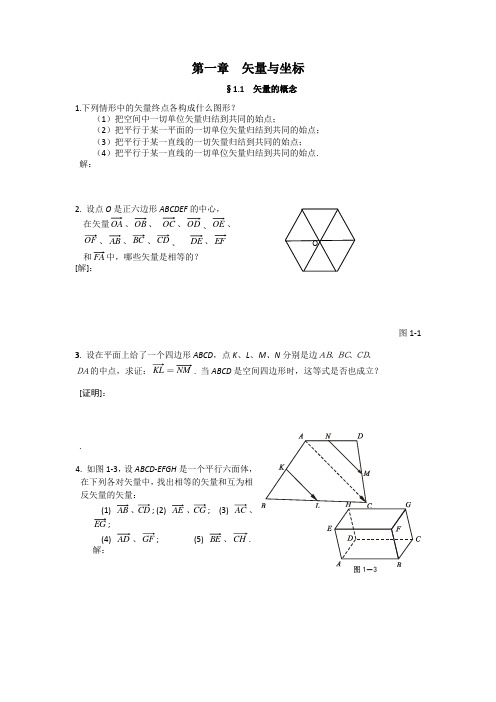
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。
老高考适用2023版高考数学二轮总复习第2篇经典专题突破核心素养提升专题5解析几何第1讲直线与圆课件

F=0,
则16+4D+F=0, 16+4+4D+2E+F=0,
F=0,
解得D=-4, E=-2,
所以圆的方程为 x2+y2-4x-2y=0,
即(x-2)2+(y-1)2=5; 若过(0,0),(4,2),(-1,1),
F=0,
则1+1-D+E+F=0, 16+4+4D+2E+F=0,
F=0Байду номын сангаас 解得D=-83,
因为 OP⊥OQ,故 1+ 2p×(- 2p)=0⇒p=12, 抛物线 C 的方程为:y2=x, 因为⊙M 与 l 相切,故其半径为 1, 故⊙M:(x-2)2+y2=1.
(2)设 A1(x1,y1),A2(x2,y2),A3(x3,y3).
当 A1,A2,A3 其中某一个为坐标原点时(假设 A1 为坐标原点时),
A2+B2
3.两条平行直线 l1:Ax+By+C1=0,l2:Ax+By+C2=0(A,B 不
同时为零)间的距离
d=
|C1-C2| . A2+B2
典例1 (1)(2022·辽宁高三二模)若两直线l1:(a-1)x-3y-2=0
与l2:x-(a+1)y+2=0平行,则a的值为
(A )
A.±2
B.2
C.-2
y0=-x0+5, 设所求圆的圆心坐标为(x0,y0),则x0+12=y0-x20+12+16. 解得xy00= =32, 或xy00= =1-1,6. 因此所求圆的方程为(x-3)2+(y-2)2=16 或(x-11)2+(y+6)2=144.
6.(2021·全国甲卷)抛物线C的顶点为坐标原点O,焦点在x轴上,直 线l:x=1交C于P,Q两点,且OP⊥OQ.已知点M(2,0),且⊙M与l相 切.
专题五 学生版

x 2 y2 变式训练 2 (2010· 天津)已知椭圆 2+ 2=1(a>b>0)的 a b 3 离心率 e= , 连接椭圆的四个顶点得到的菱形的面 2 积为 4. (1) 求椭圆的方程; (2)设直线 l与椭圆相交于不同的两点 A ,B ,已知点 A 的 坐标为(-a,0),点 Q (0,y0)在线段 AB 的垂直平分线上,且
题型二
圆锥曲线的性质 x2 y2 例 2 如图所示,椭圆 2+ 2=1 上的点 M a b 与椭圆右焦点 F1 的连线 MF1 与 x 轴垂直, 且 OM(O 是坐标原点)与椭圆长轴和短轴 端点的连线 AB 平行. (1)求椭圆的离心率; (2)F2 是椭圆的左焦点,C 是椭圆上的任一点, π 证明:∠F1CF2≤ ; 2 (3)过 F1 且与 AB 垂直的直线交椭圆于 P、 Q, 若△PF2Q 的面积是 20 3,求此时椭圆的方程.
变式训练 3 在平面直角坐标系 xOy 中, 已知圆 C1:(x+3)2+(y-1)2=4 和圆 C2:(x-4)2+(y-5)2=4. (1)判断两圆的位置关系,并求连心线 的方程; (2)求直线 m 的方程, 使直线 m 被圆 C1 截得的弦长为 4,被圆 C2 截得的弦长为 2.
知能提升演练
5.(2010· 湖南)若不同两点 P、Q 的坐标分别为(a,b), (3-b,3-a),则线段 PQ 的垂直平分线 l 的斜率为 ________; 圆(x-2)2+(y-3)2=1 关于直线 l 对称的 圆的方程为________________.
6. 设直线 ax-y+3=0 与圆(x-1)2+(y-2)2=4 相交于 A、B 两点,且弦 AB 的长为 2 3,则 a=________. 0
2.轨迹方程问题 (1)求轨迹方程的基本步骤: ①建立适当的平面直角坐标系,设出轨迹上任一点的坐 标——解析法(坐标法). ②寻找动点与已知点满足的关系式——几何关系. ③将动点与已知点的坐标代入——几何关系代数化. ④化简整理方程——简化. ⑤证明所得方程为所求的轨迹方程——完成其充要性.
(课标版)高考数学 原创预测题 专题五 解析几何 理

专题五:解析几何(新课标理)一、选择题1.若抛物线的焦点坐标为(2,0),则抛物线的标准方程是( )..28y x =.28y x =-.28x y =.24y x =2.已知直线1l :310ax y ++=,2l :2(1)10x a y +++=,若1l ∥2l ,则实数a 的值是( )..32a a =-=或.3a =-.2a =-.3a =3.已知抛物线212x y =的焦点是双曲线221mx ny -=(0mn ≠)的其中一个焦点,且双曲m =( ).8-.128-.8.128 4.对于集合{}22()|1A x y x y =+=,,()|100x y B x y a b a b ⎧⎫=+=>>⎨⎬⎩⎭,,,,如果A B =∅,则ab 的值为( )..正.负.0.不能确定5.连接椭圆22221(0)x y a b a b +=>>的一个焦点和一个顶点得到的直线方程为220x y -+=,则该椭圆的离心率为( )..12.. 236.定义:平面直角坐标系内横坐标为整数的点称为 “横整点”,过函数y =上任意两个“横整点”作直线,则倾斜角大于45︒的直线条数为( ).10.11.12.137.在直二面角AB αβ--中,PAB ∆在平面α内,四边形ABCD 在平面β内,且α⊥AD ,α⊥BC ,4=AD ,8=BC ,6=AB .若tan 2tan 1ADP BCP ∠=∠+,则动点P 在平面α内的轨迹是( ).椭圆的一部分 .线段.双曲线的一部分 .以上都不是8.双曲线)0,0(12222>>=-b a b y a x 中,F 为右焦点,为左顶点,点(0,)0B b AB BF ⋅=且,则此双曲线的离心率为( ).2 .3 .213+ .215+9.已知抛物线24,y x =焦点为F ,ABC ∆三个顶点均在抛物线上,若0FA FB FC ++=,则FA FB FC ++=( ).8 .6 .3 .010.如图,已知直线a ∥平面α,在平面α内有一动点P ,点A 是定直线a 上定点,且AP 与a 所成角为θ(θ为锐角),点A 到平面α距离为d ,则动点P 的轨迹方程为( ).2222tan x y d θ+= .2222tan x y d θ-=.22()tan d y d x θ=-.22()tan d y d x θ=--二、填空题11. 已知圆22430x y x +-+=的切线l 经过坐标原点,且切点在第四象限,则切线l 的方程为 .12.已知抛物线x y 42=的焦点为F ,在第一象限中过抛物线上任意一点P 的切线为l ,过P 点作平行于x 轴的直线m ,过焦点F 作平行于l 的直线交m 于M ,若4=PM ,则点P的坐标为 .13.已知点1F 、2F 分别是双曲线2222 1 (0,0)x y a b a b -=>>的左、右焦点,过F1且垂直于x 轴的直线与双曲线交于A ,B 两点,若2ABF ∆的最大角为锐角,则该双曲线离心率的取值范围是________.14.观察下图,类比直线方程的截距式和点到直线的距离公式,点(4,2,1)H 到平面ABC 的距离是.三、解答题15.已知直线l :4=x 与x 轴相交于点M ,P 是平面上的动点,满足0PM PO =(O 是坐标原点).⑴求动点P 的轨迹C 的方程;⑵过直线 l 上一点)(M D D ≠作曲线C 的切线,切点为E ,与x 轴相交点为F ,若12DE DF =,求切线DE 的方程.16.如图所示,双曲线的中心在坐标原点,焦点在x 轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P ,∠F1PF2=3π,且△PF1F2的面积为23,又双曲线的离心率为2,求该双曲线的方程.17.已知椭圆22221(0)x y a b a b +=>>的长半轴长为2,且点在椭圆上.(Ⅰ)求椭圆的方程;(Ⅱ)过椭圆右焦点的直线l 交椭圆于,A B 两点,若0OA OB =,求直线l 的方程.18.已知点(5,0)A ,抛物线24y x =的顶点在原点O ,倾斜角为4π的直线l 与线段OA 相交但不过,O A 两点,且交抛物线于,M N 两点,求AMN ∆的面积最大时直线l 的方程,并求AMN ∆的最大面积.19.设椭圆C :22221x y a b +=(0)a b >>的左、右焦点分别为12, F F ,上顶点为A ,过点A 与2AF 垂直的直线交x 轴负半轴于点Q ,且1222FFQF =,若过A ,Q ,2F 三点的圆恰好与直线l :30x -=相切.过定点(0, 2)M 的直线1l 与椭圆C 交于G ,H 两点(点G 在点M ,H 之间).(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线1l 的斜率0k >,在x 轴上是否存在点(, 0)P m ,使得以PG ,PH 为邻边的平行四边形是菱形.如果存在,求出m 的取值范围,如果不存在,请说明理由; (Ⅲ)若实数λ满足MG MH λ=,求λ的取值范围.20. 已知点(1,)M y 在抛物线2:2C y px =(0)p >上,抛物线的焦点为F ,且2MF =,直线:l 12y x b=-+与抛物线交于,A B 两点.(Ⅰ)求抛物线C 的方程;(Ⅱ)若x 轴与以AB 为直径的圆相切,求该圆的方程; (Ⅲ)若直线l 与y 轴负半轴相交,求AOB ∆面积的最大值.答案解析1.【解析】选,根据焦点坐标在x 轴上,可设抛物线标准方程为22y px =(0)p >,有22p =,4p =,所以抛物线的标准方程为28y x =.2.【解析】选,根据两直线平行得:321a a =+,解方程得32a a =-=或,当2a =时,两直线重合,不符合条件,故2a =舍去,所以3a =-.3.【解析】选C,根据先根据双曲线的一个焦点与抛物线22y x =的焦点重合求得焦点坐标,a ,然后对号入座求得m 的值.抛物线22y x =的焦点是1(,0)2F ,则12c =,c a e ==218m a ==.4.【解析】选,集合A 表示的图形是圆221x y +=;集合B 表示的图形是直线0(00)bx ay ab a b +-=>>,.由A B =∅可知,直线和圆没有公共点,所以,圆心到直线1>ab0ab <.5.【解析】选,直线220x y -+=与坐标轴的交点为(-2,0),(0,1),依题意得2,1c b a e ==⇒==.6.【解析】选,共有“横整点”()(()(()3,00,33,0---,其中满足条件的有()3,0与(()(0,3--连线共有5条;()3,0-与(1,--连线共有2条;(与(()(0,3-连线共有3条;(1, 与()0,3连线共有1条;综上共计11条.7.【解析】选C ,根据题意可知,又,tan ,tan BC PBBCP AD PA ADP =∠=∠AD=4,BC=8,.,6.4,1824轨迹为双曲线的一部分即∴==-=⨯-∴AB PB PA PBPA8.【解析】选D ,根据题意 0AB BF ⋅=,即2,,AB BF b ac ⊥∴=即,22ac a c =-故012=--e e ,又1>e ,所以.215+=e9.【解析】选B ,设A,B,C 三点的横坐标分别为321,,x x x ,根据已知0FA FB FC ++=,所以点F 为ABC ∆的重心,.3321=++∴x x x 根据抛物线的定义可知1233 6.2p FA FB FC x x x ++=+++=10.【解析】选B ,解决本题的关键是正确理解题意并正确的表示出tan θ,对于tan θ的表示将影响着整个题目的解决,至于如何想到表示tan θ,可以考虑选项里面的暗示,解题时需要先设动点坐标,然后表示tan θ找到关系.设(,)P x y ,则tan θ=,化简得2222tan x y d θ-=.11.【解析】设切线方程为y kx =,圆心坐标为()2,0,半径 1.r =所以直线l 与x 轴的夹角为30︒,所以tan150k =︒=即:.l y x =【答案】.3y x =-12.【解析】 设,1|,1,2),,(021000x y k x y x y y x P x x ='=='==所以l 方程为),(1200210x x x x y -=-与x 轴交点A 的坐标为),0,(0x -,1||||0+==x PM AF 所以)32,3(P【答案】)32,3(13.【解析】过F1且垂直于x 轴的直线与双曲线交于2(,)b A c a -,2(,)b Bc a --, 2ABF ∆是锐角三角形,等价于2145,AF F ∠<︒即21tan 1AF F ∠<.又因为双曲线中222b c a =-,所以222c a ac -<.不等式两边同时除以2a ,得:2()2101c c a a c a ⎧-⋅-<⎪⎪⎨⎪>⎪⎩,所以(1, 1c a ∈.【答案】(1, 114.【解析】 类比直线方程的截距式,直线的截距式是1x ya b +=,所以平面的截距式应该是1x y za b c ++=,然后是“类比点到直线的距离公式”应该转化为一般式,类比d =写出点到平面的距离公式,然后代入数据计算.平面ABC 的方程为1423x y z ++=--,即364120x y z +-+=,d ==15. 【解析】⑴依题意,)0 , 4(M ,设)40)( , (≠≠x x y x P 且,由0PM PO =,得PO PM ⊥得1-=⋅POPM k k ,即14-=⋅-xyx y ,整理得,动点P 的轨迹C 的方程为)40(2)2(222≠≠=+-x x y x 且.⑵DE 、DM 都是圆2222)2(=+-y x 的切线,所以DM DE =,因为DF 21=,所以DM DE DF 22==,所以6π=∠DFM ,设)0 , 2(C ,在CEF ∆中,2π=∠CEF ,6π=∠CFE ,2=CE ,所以4=CF ,)0 , 2(-F ,切线DE 的倾斜角6πα=或65π,所以切线DE 的斜率33=k 或33-,切线DE 的方程为)2(33+±=x y .16. 【解析】设双曲线方程为:x2a2-y2b2=1(a >0,b >0),F1(-c,0),F2(c,0),P(x0,y0). 在△PF1F2中,由余弦定理,得:|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos π3=(|PF1|-|PF2|)2+|PF1|·|PF2|. 即4c2=4a2+|PF1|·|PF2|. 又∵S △PF1F2=2 3. ∴12|PF1|·|PF2|·sin π3=2 3. ∴|PF1|·|PF2|=8.∴4c2=4a2+8,即b2=2. 又∵e =c a =2,∴a2=23.∴双曲线的方程为:3x22-y22=1.17. 【解析】(Ⅰ)由题意: 2a =.所求椭圆方程为22214x y b +=.又点在椭圆上,可得1b =.所求椭圆方程为2214x y +=.(Ⅱ)由(Ⅰ)知224,1a b ==,所以c =. 因为0OA OB ⋅=.若直线AB 的斜率不存在,则直线AB的方程为x =直线AB交椭圆于11)22-两点, 1304OA OB ⋅=-≠,不合题意.若直线AB 的斜率存在,设斜率为k ,则直线AB的方程为(y k x =.由22(440,y k x x y ⎧=-⎪⎨+-=⎪⎩可得2222(14)1240k x x k +-+-=. 由于直线AB 过椭圆右焦点,可知0∆>.设1122(,),(,)A x y B x y,则21212212414k x x x x k -+==+,222121212122([)3]14ky y k x x k x x x xk-==++=+.所以2221212222124114()141414k k kOA OB x x y yk k k---⋅=+=+=+++.由0OA OB⋅=,即2211414kk-=+,可得24,1111k k==±.所以直线l的方程为(11y x=±.18. 【解析】设直线l的方程为:(50)y x b b=+-<<联立24y xy x b⎧=⎨=+⎩消去x得:2440y y b-+=设1122(,),(,)M x y N x y,则21212416044by yy y b⎧∆=->⎪+=⎨⎪=⎩设直线l与OA的交点为P,则(,0)P b-1211||||(52(522AMNS PA y y b b∆=-=+=+2(5AMNS b∆=+≤=当且仅当522b b+=-,即1b=-时取“=”,此时直线l:1y x=-.故AMN∆的最大面积为19.【解析】(Ⅰ)因为1222F F QF=,所以1F为2F Q的中点.设Q的坐标为(3, 0)c-,因为2AQ AF⊥,所以2233b c c c=⨯=,2244a c c c=⨯=,且过2,,A Q F三点的圆的圆心为1(, 0)F c-,半径为2c. 因为该圆与直线l相切,所以|3|22cc--=.解得1c=,所以2a=,b=故所求椭圆方程为22143x y +=.(Ⅱ)设1l 的方程为2y kx =+(0k >),由222,143y kx x y =+⎧⎪⎨+=⎪⎩ 得22(34)1640k x kx +++=. 设11(,)G x y ,22(,)H x y ,则1221634kx x k +=-+.所以1122(, )(, )PG PH x m y x m y +=-+-=1212(2, )x x m y y +-+.=1212(2, () 4 )x x m k x x +-++21212121(, )(, ())GH x x y y x x k x x =--=--.由于菱形对角线互相垂直,则()PG PH +⋅0GH =.所以21122112()[()2] ()[()4]0x x x x m k x x k x x -+-+-++=.故2211212()[()2 ()4]0x x x x m k x x k -+-+++=.因为0k >,所以210x x -≠.所以21212()2 ()40x x m k x x k +-+++= 即212(1)()420k x x k m +++-=. 所以2216(1)()42034kk k m k +-+-=+解得2234km k =-+,即234m k k =-+.因为0k >,所以0m <.故存在满足题意的点P 且m的取值范围是[ 0).(Ⅲ)①当直线1l 斜率存在时,设直线1l 方程为2y kx =+,代入椭圆方程22143x y +=得22(34)1640k x kx +++=. 由0∆>,得214k >. 设11(, )G x y ,22(, )H x y , 则1221634k x x k +=-+,122434x x k =+. 又MG MH λ=,所以1122(, 2)=(, 2)x y λx y --. 所以12=x λx .所以122=(1+)x +x λx ,2122=x x λx . 所以2212122()==1+x +x x x x λλ. 所以2222164()3434(1)k k k λλ-++=+. 整理得2264(1)4k λλ+=+. 因为214k >,所以26441634k <<+,即2(1)416λλ+<<. 所以14216λλ<++<.解得1λ≠且77λ-<<+又01λ<<,所以71λ-<.②又当直线1l 斜率不存在时,直线1l 的方程为0x =,此时G,(0, H,2)MG =,(0, 2)MH =, 23MG MH-=,所以7λ=-所以71λ-<,即所求λ的取值范围是[7-.20. 【解析】:(Ⅰ)抛物线22y px = (0)p >的准线为2p x =-,由抛物线定义和已知条件可知||1()1222p p MF =--=+=,解得2p =,故所求抛物线方程为24y x =. (Ⅱ)联立2124y x b y x ⎧=-+⎪⎨⎪=⎩,消x 并化简整理得2880y y b +-=.依题意应有64320b ∆=+>,解得2b >-.设1122(,),(,)A x y B x y ,则12128,8y y y y b +=-=-,设圆心00(,)Q x y ,则应有121200,422x x y y x y ++===-.因为以AB 为直径的圆与x 轴相切,得到圆半径为0||4r y ==,又||AB 所以||28AB r =, 解得85b =-. 所以12124822224165x x b y b y b +=-+-=+=,所以圆心为24(,4)5-. 故所求圆的方程为2224()(4)165x y -++=.(Ⅲ)因为直线l 与y 轴负半轴相交,所以0b <,又l 与抛物线交于两点,由(Ⅱ)知2b >-,所以20b -<<,直线l :12y x b =-+整理得220x y b +-=,点O 到直线l的距离d ,所以1||42AOB S AB d ∆==-=令32()2g b b b =+,20b -<<,24()343()3g b b b b b '=+=+由上表可得()g b 的最大值为()327g -= . 所以当43b =-时,AOB ∆的面积取得最大值.。
高考数学备考艺体生辅导专题05《解析几何的第一问》(原卷版)

【高考备考艺体生文化课精选好题突围系列】专题五 解析几何的第一问圆的概念与方程【背一背基础知识】1. 标准方程:圆心坐标(,)a b ,半径r ,方程222()()x a y b r -+-=,一般方程:22x y Dx Ey ++++0F =(其中2240D E F +->);2.直线与圆的位置关系:相交、相切、相离 ,代数判断法与几何判断法; 3. 圆与圆的位置关系:相交、相切、相离、内含,代数判断法与几何判断法. 【讲一讲基本技能】 1. 必备技能:① 会用配方法把圆的一般方程化为标准方程;② 直线和圆的位置可用方程组的解来判断,但主要是应用圆心到直线的距离d 和圆半径r 比较,d r >⇔相离,d r =⇔相切,d r <⇔相交;③圆与圆的位置关系一般也是用圆心距12O O 与两圆的半径之和(或差)比较,12OO R r >+⇔相离,12OO R r =+⇔外切,12R r OO R r -<<+⇔相交,12OO R r =-⇔内切,12OO R r <-⇔内含. ④直线和圆的位置关系是这部分的重点考查内容.⑤对直线被圆截得弦长问题,求出圆的半径r ,圆心到直线的距离为d ,则直线被圆截得弦长为222r d -2.典型例题例1 在平面直角坐标系xOy 中,点)3,0(A ,直线42:-=x y l ,设圆C 的半径为1,圆心在l 上. 若圆心C 也在直线1-=x y 上,过点A 作圆C 的切线,求切线的方程;【分析】求圆的切线方程,一般设出直线方程为y kx b =+(斜率存在),再利用圆心到切线的距离等于圆的半径来求出其中的参数值. 【解析】例2 已知圆22:4230P x y x y +-+-=和圆外一点(4,8)M -.(1)过点M 作圆的割线交圆于,A B 两点,若||4AB =,求直线AB 的方程; (2)过点M 作圆的两条切线,切点分别为,C D ,求切线长及CD 所在直线的方程. 【答案】(1)4528440x y ++=或4x =;(2)27190x y --=.【分析】(1)先将圆的方程化成标准方程,求出圆心和半径,在根据弦长为4,结合垂径定理得到圆心到直线AB 的距离,则可以利用点到直线的距离公式求出直线AB 的斜率,求得直线方程;(2)利用切线的性质可知,切线长、半径、M 到圆心的距离满足勾股定理,则切线长可求;求出以PM 为直径的圆,与已知圆的方程,两式相减即可求得CD 所在的直线方程. 【解析】【练一练趁热打铁】1. 已知圆C 过点A (1,3),B (2,2),并且直线m: 320x y -=平分圆C 的面积. (Ⅰ)求圆C 的方程;2. 已知圆O 2:22460x y y +--=,求圆心在x-y-4=0,且过圆O 1与圆O 2交点的圆的方程。
高考数学(文)二轮复习专题五 解析几何 后 记 答题模板 Word版含答案
后记答题模板【范例赏析】后记答题模板(本讲对应学生用书第48~49页) 范例赏析典例如图,已知A,B分别为曲线C:22xa+y2=1(y≥0,a>0)与x轴的左、右两个交点,直线l过点B,且与x轴垂直,S为l上异于点B的一点,连接AS交曲线C 于点T.(1)若曲线C为半圆,点T为圆弧AB的三等分点,试求出点S的坐标.(2)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在a,使得O,M,S三点共线?若存在,求出a的值;若不存在,请说明理由.(典例)【规范解答】(1)当曲线C为半圆时,a=1,由点T为圆弧AB的三等分点,得∠BOT=60°或120°.2分①当∠BOT=60°时,∠SAB=30°.又AB=2,故在△SAB中,有SB=AB·tan 30°=23,所以S231⎛⎝⎭,. 4分②当∠BOT=120°时,同理可求得点S 的坐标为(1,).综上,点S 的坐标为S1⎛ ⎝⎭或S (1,2). 6分(2)切入点一:从点“T ”入手设点T (a cos θ,sin θ)(sin θ≥0),则直线AT 的方程为y=sin cos a a θθ+(x+a ), 8分令x=a ,得点S 2sin cos 1a θθ⎛⎫ ⎪+⎝⎭,,所以k OS =2sin (cos 1)a θθ+.又B (a ,0),所以k TB =sin cos -a a θθ. 10分假设存在a (a>0),使得O ,M ,S 三点共线,由于点M 在以SB 为直径的圆上,故BT ⊥OS.所以k OS ·k TB =sin cos -a a θθ·2sin (cos 1)a θθ+=-1,解得a 2=2.又因为a>0,所以. 15分经检验,当时,O ,M ,S 三点共线.故存在,使得O ,M ,S 三点共线. 16分切入点二:从点“S ”入手设点S (a ,m ),则直线SA 的方程为y=2m a (x+a ),联立方程组2221()2x y a m y x a a ⎧+=⎪⎪⎨⎪=+⎪⎩,,化简得(m 2+4)x 2+2m 2ax+m 2a 2-4a 2=0.8分设点T (x T ,y T ),因为A (-a ,0),所以x T ·(-a )=2222-44m a a m +,得x T =224-4a m am +,y T =244m m +,所以k TB =-2ma . 10分假设存在a (a>0),使得O ,M ,S 三点共线,由于点M 在以SB 为直径的圆上,故BT ⊥OS.12分又因为k OS =m a ,所以k OS ·k TB =m a ·2-ma ⎛⎫⎪⎝⎭=-1,解得a 2=2.又因为a>0,所以a=2.15分经检验,当a=2时,O ,M ,S 三点共线.故存在a=2,使得O ,M ,S 三点共线. 16分切入点三:从直线AS 的斜率入手 假设存在a (a>0),使得O ,M ,S 三点共线. 由于点M 在以SB 为直径的圆上,故BT ⊥OS.8分显然,直线AS 的斜率k 存在且k>0,可设直线AS 的方程为y=k (x+a ).由2221()x y a y k x a ⎧+=⎪⎨⎪=+⎩,,得(1+a 2k 2)x 2+2a 3k 2x+a 4k 2-a 2=0. 10分设点T (x T ,y T ),所以x T ·(-a )=42222-1a k a a k +.故x T =3222-1a a k a k +,从而y T =k (x T +a )=2221ak a k +,亦即T 322222-211a a k ak a k a k ⎛⎫ ⎪++⎝⎭,. 12分方法一:因为B (a ,0),所以BT u u u r =322222-2211a k aka k a k ⎛⎫⎪++⎝⎭,.由()x a y k x a =⎧⎨=+⎩,,得S (a ,2ak ),所以OS u u u r =(a ,2ak ).由BT ⊥OS ,可得BT u u u r ·OS u uu r =422222-241a k a k a k ++=0,即-2a 4k 2+4a 2k 2=0. 因为k>0,a>0,所以2. 15分经检验,当2时,O ,M ,S 三点共线.故存在2,使得O ,M ,S 三点共线. 16分方法二:因为B (a ,0),所以k BT =-TT y x a =-21a k ,故k SM =a 2k.由()x a y k x a =⎧⎨=+⎩,,得S (a ,2ak ),所以直线SM 的方程为y-2ak=a 2k (x-a ).O ,M ,S 三点共线当且仅当O 在直线SM 上,即-2ak=a 2k (-a ).因为k>0,a>0,所以2. 15分经检验,当2时,O ,M ,S 三点共线.故存在2,使得O ,M ,S 三点共线. 16分【总结提升】解题几何中的多动点问题,一直是学生难以逾越的障碍,究其原因:“多且动”,大有牵一发而动全身的感觉,各个点都丝丝相连,环环相扣.而恰恰正是点多且动,反而给我们一个启发,多且动的点中肯定有一个“核心点”,正是这个点牵动了其他点,使其他点始终围绕这个“核心点”运动.例题正是这类问题,其中点M 即为“核心点”,只要把握好这个“核心点”在圆上具有的性质,以其他的点或线为切入点,就可从多途径入手,让每个动点都可“一显身手”,以达到多解的目的.【拓展训练】拓 展 训 练变式 (2015·盐城二模)如图,在平面直角坐标系xOy 中,椭圆E :22x a+22y b =1(a>b>0)的离心率为2,直线l :y=12x 与椭圆E 相交于A ,B 两点,AB=25,C ,D 是椭圆E 上异于A ,B 两点,且直线AC ,BD 相交于点M ,直线AD ,BC 相交于点N.(1)求a ,b 的值;(2)求证:直线MN 的斜率为定值.(变式)【解答】(1)因为e=c a =2,所以c 2=12a 2,即a 2-b 2=12a 2,所以a 2=2b 2,故椭圆E 的方程为222x b +22y b =1.由题意,不妨设点A 在第一象限,点B 在第三象限.由22221212y x x y b b ⎧=⎪⎪⎨⎪+=⎪⎩,,解得A233⎫⎪⎪⎝⎭,. 又AB=5,所以5,即43b 2+13b 2=5,解得b 2=3.故a=6,3.(2)由(1)知椭圆E 的方程为26x +23y =1,从而A (2,1),B (-2,-1).①当CA ,CB ,DA ,DB 的斜率都存在时,设直线CA ,DA 的斜率分别为k 1,k 2,C (x 0,y 0),显然k 1≠k 2.从而k 1·k CB =00-1-2y x ·0012y x ++=2020-1-4y x =202031--16-4x x ⎛⎫ ⎪⎝⎭=20202-2-4x x =-12,所以k CB =-112k .同理k DB =-212k .于是直线AD 的方程为y-1=k 2(x-2),直线BC 的方程为y+1=-112k (x+2).由1211-(2)2-1(-2)y x k y k x ⎧+=+⎪⎨⎪=⎩,,解得12112122124-4-221-2-41.21k k k x k k k k k y k k ⎧=⎪+⎪⎨+⎪=⎪+⎩,从而点N 的坐标为12112212124-4-2-2-412121k k k k k k k k k k ⎛⎫+ ⎪++⎝⎭,. 用k 2代k 1,k 1代k 2得点M 的坐标为12212112124-4-2-2-412121k k k k k k k k k k +++,.所以k MN =12212112121211221212-2-41-2-41-21214-4-24-4-2-2121k k k k k k k k k k k k k k k k k k k k ++++++=12214(-)4(-)k k k k =-1.即直线MN 的斜率为定值-1.②当CA ,CB ,DA ,DB 中,有直线的斜率不存在时,根据题设要求,至多有一条直线斜率不存在,故不妨设直线CA 的斜率不存在,从而C (2,-1).仍然设DA 的斜率为k 2,由①知k DB =-212k .此时CA :x=2,DB :y+1=-212k (x+2),它们的交点坐标为M 222-1-k ⎛⎫⎪⎝⎭,.由BC :y=-1,AD :y-1=k 2(x-2),它们交点N 222--1k ⎛⎫⎪⎝⎭,,从而k MN =-1也成立. 由①②可知,直线MN 的斜率为定值-1.。
2014高考二轮复习解析几何专题(理科普通班)
肥东锦弘中学2014届高三数学二轮复习专题(理科普通班)专题五 解析几何 (一) 直线与方程类型一 直线斜率与倾斜角A.直线x sin α+y +2=0的倾斜角的取值范围是( ) A.[)0,πB.30,,44πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭ C. 0,4π⎡⎤⎢⎥⎣⎦D.0,,42πππ⎡⎤⎛⎫ ⎪⎢⎥⎣⎦⎝⎭ B. 已知两点A (-1,-5),B (3,-2),直线l 过点(1,1)且倾斜角是直线AB 倾斜角的两倍,则直线l 的方程为________类型二 两直线位置关系与点到直线的距离A.已知直线1L :ax +3y -1=0与直线2L :2x +(a -1)y +1=0垂直,则实数a =________B.若动点A ,B 分别在直线1L :x +y -7=0和2L :x +y -5=0上移动,则AB 的中点M 到原点的距离的最小值为( )A .3 2B .2 2C .3 3D .4 2C.“a =0”是“直线1L :(a +1)x +2a y -3=0与直线2L :2x +ay -2a -1=0平行”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件类型三 直线方程的综合A.已知直线l 经过直线2x +y -5=0与x -2y =0的交点.(1)点A (5,0)到l 的距离为3,求l 的方程; (2)求点A (5,0)到l 的距离的最大值.B.已知直线1L :x -y +3=0,直线l :x -y -1=0.若直线1L 关于直线l 的对称直线为2L ,求直线2L 的方程.C.已知直线x +2y =2分别与x 轴、y 轴相交于A ,B 两点,若动点P (a ,b )在线段AB 上,则ab 的最大值为________(二) 圆的方程类型一 求圆的方程A. 如果三角形三个顶点分别是O (0,0),A (0,15),B (-8,0),则它的内切圆方程为________B.(1)已知圆心在x 轴上,半径为5的圆O 位于y 轴左侧,且与直线x +y =0相切,则圆O 的方程是________(2)已知圆C 过点(1,0),且圆心在x 轴的正半轴上,直线l :y =x -1被该圆所截得的弦长为22,则圆C 的标准方程为________C.已知点P (2,1)在圆C :22x y ++ax -2y +b =0上,点P 关于直线x +y -1=0的对称点也在圆C 上,则圆C 的圆心坐标为_______类型二 直线与圆的位置关系A.设m ,n ∈R ,若直线(m +1)x +(n +1)y -2=0与圆(x -1)2+(y -1)2=1相切,则m +n 的取值范围是( )A .[1-3,1+3]B .(-∞,1-3,]∪[1+3,+∞)C .[2-22,2+22]D .(-∞,2-22]∪[2+22,+∞)B.若直线3x +4y +m =0与圆x 2+y 2-2x +4y +4=0没有公共点,则实数m 的取值范围是________C.已知圆M :22(2)x y +-=1,Q 是x 轴上的动点,QA ,QB 分别切圆M 于A ,B 两点. (1)若Q (1,0),求切线QA ,Q B 的方程. (2)求四边形QAMB 面积的最小值. (3)若|AB |=423,求直线MQ 的方程.类型三 圆与圆的位置关系A.若圆22xy +=4与圆22x y ++2ay -6=0(a >0)的公共弦的长为23,则a =B.当a 为何值时,圆C 1:22x y +-2ax +4y +2a -5=0和圆C 2:22x y ++2x -2ay +2a -3=0.(1) 外切;(2)相交;(3)外离;(4)内切.C.设直线3x +4y -5=0与圆C 1:22x y +=4交于A ,B 两点,若圆C 2的圆心在线段AB 上,且圆C 2与圆C 1相切,切点在圆C 1的劣弧AB 上,则圆C 2的半径的最大值是________类型四 综合问题A.已知实数x ,y 满足方程22x y +-4x +1=0.(1)求yx 的最大值和最小值; (2)求y -x 的最大值和最小值;(3)求22x y +的最大值和最小值.B.已知圆C :22(3)(4)x y -+-=1,点A (-1,0),B (1,0),点P 是圆上的动点,则d =22PA PB +的最大值为________,最小值为________C.已知平面区域⎪⎩⎪⎨⎧≤-+≥≥04200y x y x 恰好被面积最小的圆C :222()()x a y b r -+-=及其内部所覆盖,则圆C 的方程为________(三) 圆锥曲线类型一 概念应用A.已知点F ⎝⎛⎭⎫14,0,直线l :x =-14,点B 是l 上的动点.若过B 垂直于y 轴的直线与线段BF 的垂直平分线交于点M ,则点M 的轨迹是( )A .双曲线B .椭圆C .圆D .抛物线B.曲线C 是平面内与两个定点F 1(-1,0)和F 2(1,0)的距离的积等于常数2a (a >1)的点的轨迹.给出下列三个结论:①曲线C 过坐标原点; ②曲线C 关于坐标原点对称; ③若点P 在曲线C 上,则△F 1PF 2的面积不大于122a .其中,所有正确结论的序号是________类型二 圆锥曲线定义的应用A.如图所示,已知F (1,0),直线l :x =-1,P 为平面上的动点,过点P 作l 的垂线,垂足为点Q ,且QP QF FP FQ ⋅=⋅.求动点P 的轨迹C 的方程.B.一动圆与圆22x y ++6x +5=0外切,同时与圆22x y +-6x -91=0内切,求动圆圆心M 的轨迹方程,并说明它是什么曲线.C . 设圆22(1)x y ++=25的圆心为C ,A (1,0)是圆内一定点,Q 为圆周上任一点.线段AQ 的垂直平分线与CQ 的连线交于点M ,则M 的轨迹方程为( )A.22442125x y -=1B.22442125x y +=1C.22442521x y -=1D.22442521x y +=1 类型三 求离心率A.(1)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )A. 45B. 35C. 25D. 15(2)直线y =-3x 与椭圆C :2222x y a b+=1(a >b >0)交于A 、B 两点,以线段AB 为直径的圆恰好经过椭圆的右焦点,则椭圆C 的离心率为( ) A.32 B.3-12C.3-1 D .4-2 3 B.设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( ) A. 2 B. 3 C.3+12 D.5+12C.双曲线2222x y a b-=1(a >0,b >0)的左、右焦点分别为1F ,2F 渐近线分别为1l ,2l ,点P 在第一象限内且在1l 上,若2l ⊥1PF ,2l ∥2PF ,则双曲线的离心率是( ) A. 5 B .2 C. 3 D. 2类型四 椭圆的标准方程及其几何性质A.中心在原点,焦点在x 轴上的一椭圆与一双曲线有共同的焦点1F ,2F ,且|12F F |=213,椭圆的长半轴与双曲线半实轴之差为4,离心率之比为3∶7. (1)求这两曲线方程;(2)若P 为这两曲线的一个交点,求cos ∠12F PF 的值.B.设1F ,2F 分别是椭圆2222x y a b+=1(a >b >0)的左、右焦点,点P 在椭圆上,且1PF ⊥2PF ,|1PF |·|2PF |=2.当a =2b 时,求椭圆方程.类型五 抛物线的标准方程及其几何性质A.已知抛物线C :2y =2px (p >0)的准线l ,过M (1,0)且斜率为3的直线与l 相交于A ,与C 的一个交点为B ,若MB AM =,则p =_________B.已知过抛物线2y =2px 的焦点,斜率为22的直线交抛物线于()()1,12,2,A x y B x y 两点,且9AB =.(1)求该抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若λ+=,求λ的值.类型六 切线问题A. 如图,直线l :y =x +b 与抛物线C :2x =4y 相切于点A . (1)求实数b 的值;(2)求以点A 为圆心,且与抛物线C 的准线相切的圆的方程.B. 在平面直角坐标系xOy 中,已知点A (0,-1),B 点在直线y =-3上,M 点满足//,MA AB MB BA ⋅=⋅,M 点的轨迹为曲线C .(1)求C 的方程;(2)P 为C 上的动点,l 为C 在P 点处的切线,求O 点到l 距离的最小值.类型七 中点弦问题A.已知点M ⎪⎭⎫⎝⎛1,21在椭圆C :13422=+y x 内,则以点M 为中点的弦所在直线方程为 B.已知中心在原点,焦点在x 轴上的一椭圆与圆C:0252422=+--+y x y x 交与A 、B 两点,线段AB 恰是圆C 的直径,且AB 的斜率为21-,求此椭圆的方程. 类型八 对称问题A.已知抛物线C :x y =2与直线43:+=kx y l ,要使得C 上存在关于l 对称的两点,求实数k 的范围.B.已知椭圆C :,13422=+y x 直线l :m x y +=2,若椭圆C 上存在两点P 、Q 关于l 对称,求实数m 的范围.类型九 定值、定点、定直线问题A.椭圆C :13422=+y x ,过右焦点F 任作一直线交椭圆于A 、B 两点,问:x 轴上是否存在一点M ,使得⋅恒为定值.若存在,求出点M 坐标,若不存在,请说明理由.B.抛物线x y 42=上三点A 、B 、C 与焦点F 连线段依次成等差数列,且B (1,2),求证:线段AC 的中垂线过x 轴上一定点.C.已知抛物线()022>=p py x ,过点F 的直线与曲线交与A 、B 两点,过A 、B 作切线PA 、PB ,交点为P ,求证:P 点恒在一条直线上.类型十 最值问题(函数方程思想在解析几何中的应用)A.已知A 、B 是抛物线()022>=p px y 上的两点,且OB OA ⊥,则ABC ∆面积的最小值为 .B.设椭圆中心在坐标原点,A (2,0),B (0,1)是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点.(1)若6=,求k 的值; (2)求四边形AEBF 面积的最大值.C.设椭圆E :()012222>>=+b a by a x ,过点()()1,6,2,2N M 两点,O 为坐标原点。
专题五解析几何直线与圆教学课件2021届新高考数学二轮复习
故|MA|·|MB|≤225(当且仅当|MA|=|MB|=5 2 2时取“=”).
答案
(1)A
25 (2) 2
探究提高 1.求解两条直线平行的问题时,在利用A1B2-A2B1=0建立方程求出参 数的值后,要注意代入检验,排除两条直线重合的可能性. 2.求直线方程时应根据条件选择合适的方程形式利用待定系数法求解,同时要考虑 直线斜率不存在的情况是否符合题意.
【例 2】 (1)(2020·石家庄模拟)古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中
提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且
不等于 1 的常数,则该点轨迹是一个圆”.现在,某电信公司要在甲、乙、丙三地搭
建三座 5G 信号塔来构建一个特定的三角形信号覆盖区域,以实现 5G 商用,已知甲、
解析 (1)由题意知m(1+m)-2×1=0,解得m=1或-2,当m=-2时,两直线重 合,舍去;当m=1时,满足两直线平行,所以m=1.
(2)由题意可知,直线 l1:kx-y+4=0 经过定点 A(0,4),直线 l2:x+ky-3=0 经过 定点 B(3,0),注意到直线 l1:kx-y+4=0 和直线 l2:x+ky-3=0 始终垂直,点 M 又是两条直线的交点,则有 MA⊥MB,所以|MA|2+|MB|2=|AB|2=25.
热点三 直线(圆)与圆的位置关系
角度 1 圆的切线问题
【例 3】 (1)(2020·全国Ⅲ卷)若直线 l 与曲线 y= x和圆 x2+y2=15都相切,则 l 的方程
为( ) A.y=2x+1
B.y=2x+12
C.y=12x+1
D.y=12x+12
(2)(多选题)在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)
专题五 解析几何
时斜率不存在.
在涉
及 求直线方 程的题 型时,一 般可以用 待定系 数法,但
一定要弄清楚直线方程的各自适用范围. 同时注意灵
活 适用(如例 2,待 定系 数设 直线 方程 计算 量就 会很
大些).
热点二 圆及直线与圆的位置关系
理 解直线 与圆的 位置关 系、两圆 的位置 关系,会
用直线和圆的方程解决一些简单的问题. 掌握圆的标
4
A. 相切
B. 相离
C. 相交
D. 不能确定
解析 圆心到直线的距离为
| | d = sin αcos β+ cos αsin β+ 1 = sin(α+ β) + 1 ,
∵向量
a
与
b 的夹角为
2π 3
,
35
高三二轮复习专题·数学(理)
∴
-
1 2
=
cos 23π =
a
|a
b
|||b
| |
=
3
s
in
知 识. 例 1 平 面 上 有 相 异 的 两 点 A(cos θ, sin2θ) 和
B(0, 1),求经 过 A , B 两 点的 直线的 斜率及 倾斜角
的取值范围.
解析 ∵ A , B 是相异两点,
∴cos θ≠0, sin2θ≠1 .
设直线 AB 的倾斜角为 α,斜率为 k ,
则 k = tan α=
解 析 设 直 线 l 与 直 线 l1 ,l2 的 交 点 分 别 为 A, B , 点 A( x0, 2 - 3x0) ,
因为点 D(2, - 3) 是线段 AB 的中点,
所以点 B 的坐标为 (4 - x0, 3x0 - 8) . 又因为点 B 在直线 l2 上, 所以,(4 - x0) + 5(3x0 - 8) + 10 = 0 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题五解析几何1
(直线方程C级,圆方程C级,其他B级)
一、知识点整理
1.直线方程的五种形式
(1)点斜式:
(2)斜截式:
(3)两点式:
(4)截距式:
(5)一般式:
(6)第六式:
2.直线的两种位置关系
当不重合的两条直线l1和l2的斜率存在时:
(1)两直线平行
(2)两直线垂直
若有一条直线的斜率不存在,
3.三种距离公式
(1)A(x1,y1),B(x2,y2)两点间的距离:AB=.
(2)点到直线的距离:d=(其中点P(x0,y0),直线方程:Ax+By+C=0).
(3)两平行线间的距离:d=(其中两平行线方程分别为l1:Ax+By+C1=0,l2:Ax+By+C2=0).
4.圆的方程的两种形式
(1)圆的标准方程:
(2)圆的一般方程:
5.直线与圆、圆与圆的位置关系
(1)直线与圆的位置关系:代数判断法与几何判断法.
相交
相切
相离
(2)圆与圆的位置关系:代数判断法与几何判断法.
外离
外切
相交
内切
内含
二、回归课本,基础训练
1.(1)过点(5,2),且在y轴上的截距是在x轴上的截距的2倍的直线方程是______________.(2)“m=1”是“直线x-y=0和直线x+my=0互相垂直”的________条件.
2.已知A(3,1),B(-1,2),若∠ACB的平分线方程为y=x+1,则AC所在的直线方程为___ _ ____.
3.(1)若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的方程为____________________.(2)已知圆M的圆心在x轴上,且圆心在直线l1:x=-2的右侧,若圆M截直线l1所得的弦长为23,且与直线l2:2x-5y-4=0相切,则圆M的方程为___ _____.
4.(1)已知圆C:x2+(y-3)2=4,过点A(-1,0)的直线l与圆C相交于P、Q两点,若PQ=23,则直线l的方程为___________________________________.
(2)已知圆C的圆心与抛物线y2=4x的焦点关于直线y=x对称,直线4x-3y-2=0与圆C相交于A,B两点,且AB=6,则圆C的方程为____ ____________.
5.(1)(2014·重庆)已知直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=4相交于A,B 两点,且△ABC为等边三角形,则实数a=________.
(2)两个圆C1:x2+y2+2ax+a2-4=0(a∈R)与C2:x2+y2-2by-1+b2=0(b∈R)恰有三条公切线,则a+b的最小值为________.
6.在直角坐标系xOy中,已知A(-1,0),B(0,1),则满足P A2-PB2=4且在圆x2+y2=4上的点P的个数为________.
7.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,则实数a的取值范围是_____________________.
8.若圆x2+y2=r2(r>0)上有且只有两个点到直线x-y-2=0的距离为1,则实数r的取值范围是________.
9.设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是___ _____.。
