磁路中的欧姆定律
磁路欧姆定律

带负载后磁动势的平衡关系为:
铁芯中主磁通的最大值 在变压器空载或有负载
i1 N1 i2 N 2 i10 N
时基本不变 。
(3-31)
变压器工作原理
(变换电流作用)
由于变压器铁芯材料的导磁率高 、空载励磁电流 i10 很小,可忽略
i10 u1 e1
i2
e2
u20
原、2
(3-34)
阻抗变换举例:扬声器上如何得到最大输出功率?
(2)将负载通过变压器接到信号源上,使其阻抗匹配。 设变比 则:
RL 3.5 8 98
2
2
N1 K 3.5 : 1 N2
Rs U1
i1
N1 N 2
i2
u2 RL
输出功率为:
U 50 pL R R RL 100 98 98 6.25W L S (3-35)
(3-5)
二、铁磁材料的磁性能:
1、磁导率高
r
》1
磁畴结构
在物质内部电子绕原子核 旋转及电子本身自转形成 了分子电流,这个电流会 产生磁场。同时铁磁材料 内部的分子之间有一种相 互作用力,使得每个区域 内的分子磁场具有相同的 方向,组成许多小磁体, 具有磁性,这些小磁体称 为“磁畴”。
(3-6)
流一直很大,将会导致过热,把线圈烧坏。
磁路小结
直流磁路
U I R
(U不变,I不变)
IN Φ Rm
(Φ随Rm变化)
交流磁路
U Φm 4.44fN
( U不变时,
IN ΦRm
( I 随 Rm 变化)
(3-22)
Φ m基本不变)
§7-2 变压器
磁路的基本定律是什么?
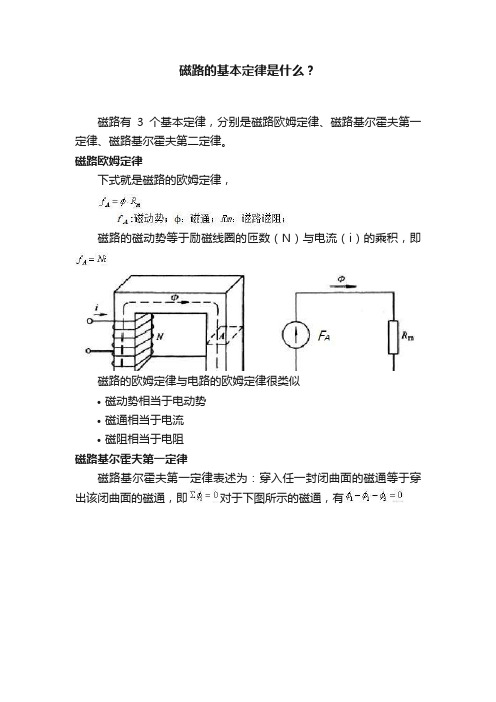
磁路的基本定律是什么?磁路有3个基本定律,分别是磁路欧姆定律、磁路基尔霍夫第一定律、磁路基尔霍夫第二定律。
磁路欧姆定律下式就是磁路的欧姆定律,磁路的磁动势等于励磁线圈的匝数(N)与电流(i)的乘积,即磁路的欧姆定律与电路的欧姆定律很类似•磁动势相当于电动势•磁通相当于电流•磁阻相当于电阻磁路基尔霍夫第一定律磁路基尔霍夫第一定律表述为:穿入任一封闭曲面的磁通等于穿出该闭曲面的磁通,即对于下图所示的磁通,有磁路基尔霍夫第二定律在磁路中沿任何闭合磁路径上,磁动势的代数和等于磁压降的代数和,即对于下图所示的磁通,有题主你好。
磁路是在理想情况下,仿照电路建立的一套理想化的物理模型。
理想化的原因从下面的讨论可以看出。
我们知道,线圈构造成的互感电路在理想情况下有这么几个性质:•不漏磁•电磁感应定律严格成立(如果存在磁荷,这条定律需要修正)•电磁场的变换比较缓慢,电路是似稳的主线圈输入电流是交变电流,那么该线圈就会产生交变的磁场,在不漏磁的假定下,次级线圈里的磁通量就等于主线圈发出的磁通量。
由于电磁场变化很慢,我们可以忽略电磁辐射带走那部分能量,那么这样我们可以用稳恒电路的磁感应强度-电流强度关系式近似表示这里的磁感应强度和电流强度的关系。
简单写为B=4πNI/L(高斯单位制)磁通量φ=BA=4πNIA/L,A是线圈的截面积。
由于主线圈的电流是驱动电流,次级线圈的电流是感应电流,所以我们定义主线圈里的电流与主线圈的匝数乘积为磁动势F,将磁动势与磁通量的比值定义为磁阻。
明显磁阻Rm在数值上等于L/(4πA),如果考虑铁芯等磁导率不等于真空磁导率的情况时,磁阻改写为L/(4πμA)。
对比电阻表达式,可以发现磁阻和电阻有很多相似的地方,比如都是正比于长度反比于截面积,比例系数是与材料性质有关。
下面我们来讨论磁路基本定律。
如果把φ=BA=4πNIA/L写成φ=F/Rm,那么这个公式就叫磁路的欧姆定律。
由于磁通量的性质,我们可以类比于电路的电流,所以对于串联的线圈之间的磁通量满足φ1=…=φn;对于并联情形有φ0=φ1+…+φn。
磁路欧姆定律

4.8.2磁路欧姆定律 4.8.2磁路欧姆定律 1 磁动势 通电线圈的匝数越多,电流越大,磁场 越强,磁通也就越多。我们把通过线圈的 电流I和线圈的匝数N的乘积称为磁动 (Fm)。
• • 单位A 单位A
F=NI
2.磁阻 2.磁阻
• • • • • •
电路中有电阻,磁路中也有磁阻。磁阻就是磁通通 过磁路时所受到的阻碍作用,用Rm表示。与导体的电阻 过磁路时所受到的阻碍作用,用Rm表示。与导体的电阻 相似,磁路中磁阻的大小与磁路的长度L 相似,磁路中磁阻的大小与磁路的长度L成正比,与磁 路的横截面积S 路的横截面积S成反比,并与组成磁路的磁导率有关, 其公式为:
N S N S
+ –
直流电机的磁路
交流接触器的磁路
• 磁路可以分为: • 1 无分支磁路 图4-51中a图磁电系仪表 51中
和b图变压器为无分支磁路。由于磁感线是 连续的,所以通过无分支磁路各处横截面 连续的,所以通过无分支磁路各处横截面 的磁通是相等的。 的磁通是相等的。
• 2 有分支磁路 图4-51中c图电动机线圈磁 51中
m
4.8.3 磁路与电路的比较
磁路
磁通势F 磁通势F 磁通Φ 磁感应强度B 磁感应强度B 磁阻 R m = I N
F Φ = = R m
电路
电动势 E 电流 I ຫໍສະໝຸດ 流密度 Jlµ S
Φ
电阻 + _
I =
R = γ S I
E
E = R
l
R
E l γ S
NI l µ S
4.8.4 电磁铁
•
将螺线管紧密地套在一个铁心上,就构 成了一个电磁铁。实际应用中的电磁铁一 成了一个电磁铁。实际应用中的电磁铁一 般由励磁线圈、铁心、 般由励磁线圈、铁心、衔铁三个主要部分 组成。 组成。 • 电磁铁按励磁电流性质的不同,分为直 电磁铁按励磁电流性质 励磁电流性质的不同,分为直 流电磁铁和交流电磁铁;按用途 用途的不同, 流电磁铁和交流电磁铁;按用途的不同, 可以分为起重电磁铁 控制电磁铁和 可以分为起重电磁铁、控制电磁铁和电磁 起重电磁铁、 吸盘等。 吸盘等。
磁路欧姆定律串联磁路

Y.Q.Xiong 2012 《电机学》第1章 导论
12
3. 自感和互感
① 自感
LΨ i
NΦ i
N (Fm ) i
N (Nim ) i
N 2m
N ——线圈匝数 Λm——自感磁通所经磁路的磁导
自感的大小与匝数的平方和磁路 的磁导成正比;
铁心线圈的自感要比空心线圈的 大得多;
E Em NΦm
2
2
2NπfΦm 4.44 fNΦm
感应电动势滞后磁通90度
4. 电磁力定律
f = Bli
f 左手定则
Y.Q.Xiong 2012 《电机学》第1章 导论
4
1.5 磁路基本定律及其计算方法
1. 磁路基
铁心线圈的电感不是常数,当磁 路饱和程度增加时,自感下降。
Y.Q.Xiong 2012 《电机学》第1章 导论
13
② 互感
M
Ψ 21 i1
N 2Φ21 i1
N2 (F1m ) i1
N2 ( N1i1m ) i1
N1N 2 m
N1 ——线圈1的匝数 N2 ——线圈2的匝数 Λm——互感磁通所经磁路的磁导
1.0 383 392 401 411 422 433 444 456 467 480 1.1 493 507 521 536 552 568 584 600 616 633 1.2 652 672 694 716 738 762 786 810 836 862 1.3 890 920 950 980 1010 1050 1090 1130 1170 1210 1.4 1260 1310 1360 1420 1480 1550 1630 1710 1810 1910 1.5 2010 2120 2240 2370 2500 2670 2850 3040 3260 3510 1.6 3780 4070 4370 4680 5000 5340 5680 6040 6400 6780 1.7 7200 7640 8080 8540 9020 9500 10000 10500 11000 11600 1.8 12200 12800 13400 14000 14600 15200 15800 16500 17200 18000
三、磁路及其基本定律 - 陕西师范大学网络教育学院首页
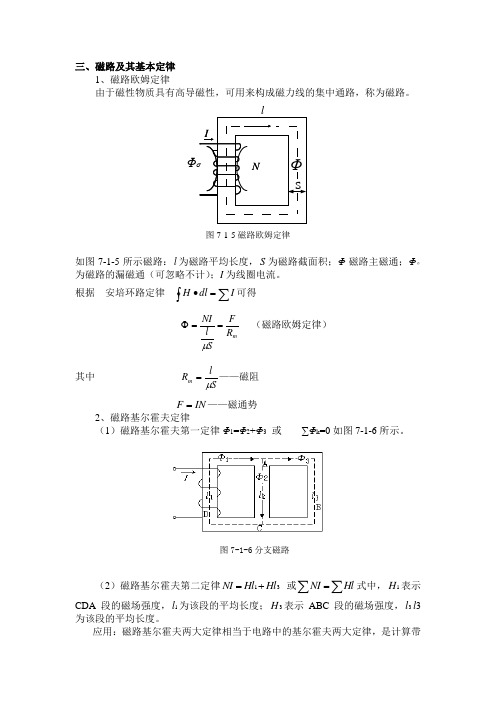
三、磁路及其基本定律1、磁路欧姆定律由于磁性物质具有高导磁性,可用来构成磁力线的集中通路,称为磁路。
Φ图7-1-5磁路欧姆定律如图7-1-5所示磁路:l 为磁路平均长度,S 为磁路截面积;Φ磁路主磁通;Φσ为磁路的漏磁通(可忽略不计);I 为线圈电流。
根据 安培环路定律⎰∑=∙I dl H 可得m R FSl NI ==Φμ (磁路欧姆定律) 其中 SlR m μ=——磁阻 IN F =——磁通势 2、磁路基尔霍夫定律(1)磁路基尔霍夫第一定律Φ1=Φ2+Φ3 或 ∑Φk =0如图7-1-6所示。
(2)磁路基尔霍夫第二定律13NI Hl Hl =+ 或NI Hl =∑∑式中,1H 表示CDA 段的磁场强度,1l 为该段的平均长度;3H 表示ABC 段的磁场强度,3l l 3为该段的平均长度。
应用:磁路基尔霍夫两大定律相当于电路中的基尔霍夫两大定律,是计算带图7-1-6分支磁路有分支的磁路的重要工具(本书对并联磁路不作要求)。
(3)如表7-1所示为磁路和电路的类比关系:(1)电路中有电流就有功率损耗。
磁路中恒定磁通下没有功率损耗;(2)电流全部在导体中流动,而在磁路中没有绝对的磁绝缘体,除在铁心的磁通外,空气中也有漏磁通;(3)电阻为常数,磁阻为变量;(4)对于线性电路可应用叠加原理,而当磁路饱和时为非线形不能应用叠加原理。
综上所述磁路与电路仅是数学形式上的类似,而本质是不同的。
4、磁路的计算:图7-1-7对图7-1-7所示分段均匀磁路应用基尔霍夫第二定律有 IN H l H l H =++δ02211 或∑=IN Hl将 μBH S B =Φ=,代入,有IN SS l S l =+Φ+Φ0222111μδμμ 或 IN R R R m m m =Φ+Φ+Φ021∑∑=Φ=ΦmmR FFR式中μ不是常数,因此公式并不能用于计算磁路,只可做定性分析用。
在磁路的分析中若已知磁通Φ求所需磁通势IN 则 (1)由11S B Φ=(查H B -曲线)得出111l H H →; (2)由22S B Φ=(查H B -曲线)得出222l H H →; (3)由δμ0000100H B H S S B →=→Φ=Φ=; (4)∑=IN Hl对交流磁路则可按幅值进行分析,即: 已知→Φ=Φ=→ΦS K S B C m C m m m 查H B -曲线∑=→=→→2m m m m II N I l H H C K 为叠片系数。
磁路的欧姆定律是

磁路的欧姆定律是
磁路的欧姆定律用来确定磁路的磁通Φ、磁动势F和磁阻Rm 之间的关系。
三者之间的定量关系可以表示为:Φ=F/Rm。
公式中:Rm是磁阻,单位为安培匝每韦伯,或匝数每亨利。
F 是磁动势,单位为安培匝。
Φ是磁通量,单位为韦伯。
即磁路中的磁通Φ等于作用在该磁路上的磁动势F除以磁路的磁阻Rm,这就是磁路的欧姆定律。
磁阻R与磁路的平均长度z成正比,与磁路的截面积S及构成磁路材料的磁导率口成反比,所以磁路磁阻的大小取决于磁路的几何尺寸和所采用材料的磁导率。
电工基础038.第38课时.磁路及磁路基本定律
a r b
(a)
(b)
空气隙有效面积计算
(a) 矩形截面; (b) 圆形截面
(3) 由已知磁通Φ, 算出各段磁路的磁感应强度B=Φ/S。
(4) 根据每一段的磁感应强度求磁场强度, 对于铁磁材 料可查基本磁化曲线。 对于空气隙可用以下公式:
B0 6 3 H0 0.8 10 B0 ( A / m) 8 10 B0 ( A / cm) 7 0 4 10
(5) 计算各段磁路的磁压Um(=HL)。
B0
(6) 根据基尔霍夫磁压定律, 求出所需的磁通势。
H1L1 H2 L2 H3 L3 NL
• 例10-1 图10-18为一无分支磁路,铁心线圈有200 匝。磁路尺寸如图所示。磁路用0.35mm厚D-41硅 钢片叠成,叠装系数k为0.91。若要在此磁路内建立 Φ=30×10-4Wb的磁通,求所需线圈电流值。
• 根据D-41电工硅钢片磁化数据表,铁心中各 段对应的磁场强度为: H1=2.85A/cm, H2=9.96A/cm • 空气隙中磁场强度H0按(10-13)式计算 H0≈0.8×106B0=0.8×106×0.909=727000 A/m 即H0=727000A/m=7270A/cm。
• 总的磁动势等于各段磁压之和,即: NI=H0L0+ H1L1+ H2L2 =(7270×0.5+2.85×19.5+9.96×47)A =4160A • 所以线圈电流I为 I=∑HL/N=4160/200A=20.8A
I
电 路
电动势
U R
电压降
+
E
_
E
I
U
磁路与电路的比较 (二)
磁路欧姆定律
若磁路不均匀,由不同材料构成, 若磁路不均匀,由不同材料构成,则磁 路的磁阻应由不同的几段串联而成, 路的磁阻应由不同的几段串联而成,即
IN = ΦRm1 + ΦRm2 +路欧姆定律
为了使励磁电流产生尽可能大的磁通,在电磁设备中 要放置一定形状的铁心。绝大部分磁通将通过铁心形 成闭合路径——磁路。 I v v Φ Q ∫ Hdl = ∑ I
∴
磁路欧 姆定律
Φ IN = Hl = l = l S B
l
IN F Φ= = l / S Rm F=IN 称为磁动势,此为产生磁通的激励 称为磁动势, Rm 称为磁阻是磁路对磁通具有阻碍作用的物理量; 称为磁阻是磁路对磁通具有阻碍作用的物理量; l 为磁路的平均长度; 为磁路的平均长度; S 为磁路的截面积。 为磁路的截面积。
l S
电路欧姆定律与磁路欧姆定律比较如下: 电路欧姆定律与磁路欧姆定律比较如下:
磁 路 磁动势 F 磁通 Φ 磁感应强度B 磁感应强度 磁阻 R= l / S 电 路 电动势E 电动势 电流 I 电流密度 J 电阻 R= l / γS I
+ –
I N
Φ
E
R
F Φ= Rm
E I= R
δ I 0 S0 ≈S1 1 l1 S1
链接五:磁路欧姆定律
链接五:磁路欧姆定律一磁路的基本概念在电工技术中不仅要讨论电路问题,还将讨论磁路问题。
因为很多电工设备与电路和磁路都有关系,如电动机、变压器、电磁铁及电工测量仪表等。
而磁路问题与磁场有关,与磁介质有关,磁场又往往与电流和电路相关联,所以下面我们研究磁路和电路的关系。
在电气设备中为了得到较强的磁场,通常利用磁导率很高的铁磁材料把电流产生的磁通集中在铁心这个限定的空间内。
这种集中的磁通所经过的路径称为磁路。
如图3—11所示为几种电气设备的磁路。
其中图3—11(a )中变压器的磁路是双回路方形磁路;图3—11(b )中电磁铁的磁路是单回路磁路,回路中有一小段空气隙;而图3—11(c )中是磁电式仪表的磁路,回路中有两小段空气隙。
线圈绕在由铁磁材料制成的铁心上,线圈通以电流,便产生磁通,故此线圈称为励磁线圈。
线圈中的电流称为励磁电流。
磁路的几何形状决定于铁心的形状和励磁线圈在铁心上安置位置。
图3—11 几种电气设备的磁路励磁线圈通过励磁电流会产生磁通,通过实验发现,线圈匝数越多,励磁电流越大,产生的磁通也就越多。
我们把励磁电流I 和线圈匝数N 的乘积称为磁动势,单位是安(A ),用F 表示,即 F N I = (3—18) 磁阻m R 表示磁介质对磁通的阻碍作用的大小。
磁介质的磁导率μ越大,横截面S 越大,则对磁通量φ的阻碍作用越小;而磁路L 越长,对磁路的阻碍作用越大。
m LR Sμ=(3—19)二 磁路欧姆定律(a)(b )(c)为了使励磁电流产生尽可能大的磁通,在电磁设备中要放置一定形状的铁心。
绝大部分磁通将通过铁心形成闭合路径——磁路。
磁路和电路在分析思路上基本一致,所以我们在分析磁路时,可以将全电路欧姆定律应用到磁路中来。
一个磁路中的磁阻等于磁动势与磁通量的比值。
这个定义可以表示为: mF R φ=(3—20)即磁路中的磁通Φ等于作用在该磁路上的磁动势 F 除以磁路的磁阻m R ,这就是磁路的欧姆定律。
磁路中的欧姆定律指的是
磁路中的欧姆定律指的是
一个磁路中的磁阻等于“磁动势”与磁通量的比值。
这个定义可以表示为:Φ=F/Rm
其中
Rm是磁阻,单位为安培匝每韦伯,或匝数每亨利。
F是磁动势,单位为安培匝。
Φ是磁通量,单位为韦伯。
即磁路中的磁通Φ等于作用在该磁路上的磁动势
F除以磁路的磁阻Rm,这就是磁路的欧姆定律。
这个定律有时称为霍普金森定律,又被称为磁路欧姆定律。
与电路欧姆定
律类似。
磁通量总是形成一个闭合回路,但路径与周围物质的磁阻有关。
它总是集
中于磁阻最小的路径。
空气和真空的磁阻较大,而容易磁化的物质,例如软铁,则磁阻较低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁路中的欧姆定律
磁路中的欧姆定律是电磁学中的一个重要定律,它描述了磁场中电流的行为。
欧姆定律是电学中的基本定律,它描述了电流通过导体时的行为。
在磁路中,欧姆定律同样适用,它描述了磁场中电流的行为。
磁路中的欧姆定律可以表示为:磁通量密度B与磁场中的电流I成正比,与磁路中的电阻R成反比。
即B=μNI/R,其中μ是磁导率,N是线圈匝数,I是电流,R是电阻。
磁路中的欧姆定律告诉我们,当电流通过磁路时,磁通量密度与电流成正比。
这意味着,如果电流增加,磁通量密度也会增加。
同样地,如果电流减少,磁通量密度也会减少。
这种关系可以用来计算磁路中的磁通量密度。
磁路中的欧姆定律还告诉我们,磁通量密度与磁路中的电阻成反比。
这意味着,如果电阻增加,磁通量密度会减少。
同样地,如果电阻减少,磁通量密度会增加。
这种关系可以用来计算磁路中的电阻。
磁路中的欧姆定律在电机、变压器等电磁设备的设计和分析中起着重要作用。
通过欧姆定律,我们可以计算出磁路中的磁通量密度和电阻,从而确定电磁设备的性能和效率。
此外,欧姆定律还可以用来优化电磁设备的设计,提高其效率和性能。
磁路中的欧姆定律是电磁学中的一个重要定律,它描述了磁场中电
流的行为。
通过欧姆定律,我们可以计算磁路中的磁通量密度和电阻,从而确定电磁设备的性能和效率。
磁路中的欧姆定律在电磁设备的设计和分析中起着重要作用,是电磁学中不可或缺的一部分。
