高中数学竞赛解题策略-几何分册第23章角元形式的梅涅劳斯定理
梅涅劳斯定理入门篇(最全)word资料

梅涅劳斯定理(入门篇)雷雨田 (广西师范大学附属外国语学校高50班 541004)梅涅劳斯定理这个定理怎么记最好呢?个人感觉“顶到分、分到顶、顶到分、分到顶、顶到分、分到顶”这样记忆来得非常容易不过找了很多资料,感觉仅仅是把这个定理(或者后面附一个逆定理)陈述然后证明完了之后,就直接给例题(或者直接讲赛瓦定理),看上去不怎么舒服,所以我把其他的一些东西附在这里,以供参考。
第一角元形式的梅涅劳斯定理(就是把线段比改为正弦值比)其表达式为:1=∠∠•∠∠•∠∠BA'B sin 'CBB sin CB 'C sin 'ACC sin AC 'A sin 'BAA sin证明如下:如图所示,由三角形面积公式(正弦定理)可得:AC 'A sin AC 'BAA sin AB AC 'A sin AC 'AA 'BAA sin 'AA AB S S C 'A 'BA C'AA 'ABA ∠⋅∠⋅=∠⋅⋅∠⋅⋅==∆∆2121同理可得CB'C sin BC 'ACC sin AC B 'C 'AC ,BA 'B sin AB 'CBB sin BC A 'B 'CB ∠⋅∠⋅=∠⋅∠⋅= 把这三个式子相乘,运用梅氏定理,就可得到这个式子怎么记最好呢?个人感觉根据梅涅劳斯定理中线段所对应的角来记忆最好。
第二角元形式的梅涅劳斯定理设O 是不在三角形ABC 三边所在直线上的任意一点,其他条件不变,则表达式为:1=∠∠•∠∠•∠∠OA'B sin 'COB sin OB 'C sin 'AOC sin OC 'A sin 'BOA sin现证明如下:AB C A’B ’C’如图,由C'A 'BA S S OC 'A 'BOA =∆∆ 可得A'B 'BA OB OC OC 'A sin 'OA B sin ⋅=∠∠同理得到另外两个对称式,相乘,运用梅氏定理即得证这个式子就这样记吧:先记住原来的梅涅劳斯定理形式,然后在每条线段表达式中间插一个O ,然后再在前面加上∠sin (比如BA'就变成'BOA sin ∠)梅氏定理的用处这个定理是平面几何的一个重要定理(好像所有竞赛书都把他与赛瓦定理放在第一节,不知是惯性还是怎么地),它大概有如下用处: 可以用来证明三点共线; 可以用来导出线段比例式;可以用来寻求一条线段是另一条线段的几分之几或几倍(即线段倍分);怎么用梅氏定理知道了这个定理,还要会用才行。
高二数学竞赛班二试平面几何讲义1

高二数学竞赛班二试平面几何讲义1梅涅劳斯定理和塞瓦定理一、知识要点:班级姓名1. 梅涅劳斯定理:若直线l不经过ABC的顶点,并且与ABC的三边BC,CA,AB或它们的延长线分别交于P,Q,R,则BPCQAR1 PCQARB证:设hA、hB、hC分别是A、B、C到直线l的垂BPCQARhBhChA线的长度,则:1PCQARBhChAhB2. 梅涅劳斯定理逆定理:设P、Q、R分别是ABC的三边BC、CA、AB上或它们的延长线上的三点,并且P、Q、R三点中,位于ABC边上的点的BPCQAR个数为0或2,若1,则P、Q、R三点共线;PCQARB证:设直线PQ与直线AB交于R',于是由定理1得:BPCQAR'__R'AR ' 1又1'=__RB由于在同一直线上的P、Q、R'三点中,位于ABC边上的点的个数也为0或2,因此R与R'或者同在AB线段上,或者同在AB的延长线上;若R与R'同在AB线段上,则R与R'必定重合,不然的话,设AR AR',ARAR'ARAR'这时AB AR AB AR,即BR BR,于是可得这与='矛盾'__R类似地可证得当R与R'同在AB的延长线上时,R与R'也重合''综上可得:P、Q、R三点共线;注:此定理常用于证明三点共线的问题,且常需要多次使用再相乘; 3. 塞瓦定理:设P、Q、R分别是ABC的BC、CA、AB边上的点,则APBP CQAR的充要条件是: 1PCQARB证:先证必要性:设AP、BQ、CR相交于点M,则:BPS ABPS BMPS ABMCQS BCMARS ACM,PCS ACPS CMPS ACMQAS ABMRBS __AR =1PCQARB1再证充分性:若BPCQAR‘1,设AP与BQ相交于M,且直线CM交AB于R,PCQARB BPCQAR’AR’AR‘ 1‘=因为R和R’都在线__BRB段AB上,所以R’必与R重合,故AP、BQ、CR相交于一点点M;二、例题精析例1:若直角ABC中,CK是斜边上的高,CE是ACK的平分线,E点在AK上,D是AC的中点,F是DE与CK的交点,证明:BF//CE。
高中数学竞赛辅导之——梅涅劳斯定理

梅涅劳斯定理定理1 若直线l 不经过的顶点,并且与的三边或它们的延长线分别交于,则证明1:设分别是A、B 、C 到直线l 的垂线的长度,则:。
证明2:作CN ∥BA ,交X Y于N,则错误!=错误!,错误!=错误!. 于是\f(AZ ,Z B)·\f(B X,XC )·CYY A=错误!·错误!·错误!·错误!=1. 证明3:如图,连AX ,BY ,记S ∆AYB =S 1,S∆BYC =S 2,S ∆CYX =S3,S ∆XYA =S 4.则错误!=错误!;错误!=错误!;错误!=错误!,三式相乘即得证. 注:此定理常运用求证三角形相似的过程中的线段成比例的条件。
1. 设AD是△A BC 的边BC 上的中线,直线CF 交A D于E.求证:AEED=\f(2AF , F B).证明由Me nelaus 定理得\f(AE , E D)·错误!·错误!=1 ,从而AEED=错误!. 2. 若直角中,CK 是斜边上的高,CE 是的平分线,E 点在AK 上,D 是AC 的中点,F 是D E与CK 的交点,证明:。
【解析】因为在中,作的平分线BH,则:,,即,所以为等腰三角形,作BC 上的高E P,则:,对于ZY XCBAS 1S 2 S 3S 4 ZYXCBANEACEZY XCBA和三点D、E、F根据梅涅劳斯定理有:,于是,即,根据分比定理有:,所以,所以。
3. 从点K引四条直线,另两条直线分别交直线与A、B、C、D和,试证:。
【解析】若,结论显然成立;若AD与相交于点L,则把梅涅劳斯定理分别用于和可得:,,,,将上面四个式子相乘,可得:,即:定理2设P、Q、R分别是的三边BC、CA、AB上或它们延长线上的三点,并且P、Q、R三点中,位于边上的点的个数为0或2,这时若,求证P、Q、R 三点共线。
证明:设直线PQ与直线AB交于,于是由定理1得:,又因为,则,由于在同一直线上P、Q、R三点中,位于边上的点的个数也为0或2,因此R与或者同在AB线段上,或者同在AB的延长线上;若R与同在AB线段上,则R与必定重合,不然的话,设,这时,即,于是可得,这与矛盾,类似地可证得当R 与同在AB的延长线上时,R与也重合,综上可得:P、Q、R三点共线。
个人精心整理!高中数学联赛竞赛平面几何四大定理-及考纲

个人精心整理!高中数学联赛竞赛平面几何四大定理-及考纲多面角,多面角的性质。
三面角、直三面角的基本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、表面展开图。
4、平面解析几何直线的法线式,直线的极坐标方程,直线束及其应用。
二元一次不等式表示的区域。
三角形的面积公式。
圆锥曲线的切线和法线。
圆的幂和根轴。
5、其它抽屉原理。
容斥原理。
极端原理。
集1.梅涅劳斯定理出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,(AZ/ZB)*(BX/XC)*(CY/YA)=1 。
证明:当直线交△ABC的AB、BC、CA的反向延长线于点D、E、F时,(AD/DB)*(BE/EC )*(CF/FA)=1逆定理证明:证明:X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1证明一过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC ,CE/EA=DC/AG三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/D C)×(DC/AG)=1证明二过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1证明四过三顶点作直线DEF的垂线,AA‘,BB',CC'有AD:DB=AA’:BB' 另外两个类似,三式相乘得1得证。
如百科名片中图。
※推论在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
高中数学联赛中常见的几何定理

高中数学联赛中常见的几何定理第一篇:高中数学联赛中常见的几何定理梅涅劳斯定理:梅涅劳斯(Menelaus)定理是由古希腊数学家梅涅劳斯首先证明的。
他指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么AF/FB×BD/DC×CE/EA=1。
证明:过点A作AG‖BC交DF的延长线于GAF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG三式相乘得:AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1它的逆定理也成立:若有三点F、D、E分别在的边AB、BC、CA或其延长线上,且满足AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
塞瓦定理:在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1证法简介(Ⅰ)本题可利用梅涅劳斯定理证明:∵△ADC被直线BOE所截,∴(CB/BD)*(DO/OA)*(AE/EC)=1 ①而由△ABD被直线COF所截,∴(BC/CD)*(DO/OA)*(AF/FB)=1②②÷①:即得:(BD/DC)*(CE/EA)*(AF/FB)=1(Ⅱ)也可以利用面积关系证明∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③同理CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤③×④×⑤得BD/DC*CE/EA*AF/FB=1利用塞瓦定理证明三角形三条高线必交于一点:设三边AB、BC、AC的垂足分别为D、E、F,根据塞瓦定理逆定理,因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA)/[(CD*ctgB)]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/[(BF*ctgA)]= 1,所以三条高CD、AE、BF交于一点。
高中数学竞赛平面几何中的几个重要定理

平面几何中几个重要定理及其证明一、 塞瓦定理1.塞瓦定理及其证明定理:在∆ABC 内一点P,该点与∆ABC 的三个顶点相连所在的三条直线分别交∆ABC 三边AB 、BC 、CA 于点D 、E 、F,且D 、E 、F 三点均不是∆ABC 的顶点,则有1AD BE CFDB EC FA⋅⋅=. 证明:运用面积比可得ADCADP BDP BDCS S AD DB S S ∆∆∆∆==. 根据等比定理有ADC ADC ADP APCADP BDP BDC BDC BDP BPCS S S S S S S S S S ∆∆∆∆∆∆∆∆∆∆-===-,所以APCBPC S AD DB S ∆∆=.同理可得APB APCS BE EC S ∆∆=,BPCAPB S CF FA S ∆∆=. 三式相乘得1AD BE CFDB EC FA⋅⋅=. 注:在运用三角形的面积比时,要把握住两个三角形是“等高”ABCD FP还是“等底”,这样就可以产生出“边之比”.2.塞瓦定理的逆定理及其证明定理:在∆ABC 三边AB 、BC 、CA 上各有一点D 、E 、F,且D 、E 、F均不是∆ABC 的顶点,若1AD BE CFDB EC FA⋅⋅=,那么直线CD 、AE 、BF 三线共点.证明:设直线AE 与直线BF 交于点P,直线CP 交AB 于点D /,则据塞瓦定理有//1AD BE CFD B EC FA⋅⋅=. 因为1AD BE CF DB EC FA⋅⋅=,所以有//AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线.注:利用唯一性,采用同一法,用上塞瓦定理使命题顺利获证. 二、 梅涅劳斯定理ABCD EFPD /3.梅涅劳斯定理及其证明ABCD EFG定理:一条直线与∆ABC 的三边AB 、BC 、CA 所在直线分别交于点D 、E 、F,且D 、E 、F 均不是∆ABC 的顶点,则有1AD BE CFDB EC FA⨯⨯=.证明:如图,过点C 作AB 的平行线,交EF 于点G .因为CG // AB,所以CG CFAD FA= ————1 因为CG // AB,所以CG ECDB BE= ————2 由1÷2可得DB BE CFAD EC FA=⋅,即得1AD BE CF DB EC FA ⋅⋅=. 注:添加的辅助线CG 是证明的关键“桥梁”,两次运用相似比得出两个比例等式,再拆去“桥梁”CG 使得命题顺利获证.4.梅涅劳斯定理的逆定理及其证明定理:在∆ABC 的边AB 、BC 上各有一点D 、E,在边AC 的延长线上有一点F,若1AD BE CFDB EC FA⋅⋅=, 那么,D 、E 、F 三点共线.ABCD EFD /证明:设直线EF 交AB 于点D /,则据梅涅劳斯定理有//1AD BE CFD B EC FA⋅⋅=. 因为1AD BE CF DB EC FA⋅⋅=,所以有//AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线.注:证明方法与上面的塞瓦定理的逆定理如出一辙,注意分析其相似后面的规律. 三、 托勒密定理5.托勒密定理及其证明定理:凸四边形ABCD 是某圆的内接四边形,则有 AB ·CD + BC ·AD = AC ·BD .证明:设点M 是对角线AC 与BD 的交点,在线段BD 上找一点,使得∠DAE =∠BAM .因为∠ADB =∠ACB,即∠ADE =∠ACB,所以∆ADE ∽∆ACB,即得AD DEAC BC=,即AD BC AC DE ⋅=⋅ ————1 由于∠DAE =∠BAM,所以∠DAM =∠BAE,即∠DAC =∠BAE;而∠ABD =∠ACD,即∠ABE =∠ACD,所以∆ABE ∽∆ACD .即得AB BEAC CD=,即AB CD AC BE ⋅=⋅ ————2 由1+2得AD BC AB CD AC DE AC BE AC BD ⋅+⋅=⋅+⋅=⋅. 所以AB ·CD + BC ·AD = AC ·BD .注:巧妙构造三角形,运用三角形之间的相似推得结论.这里的构造具有特点,不容易想到,需要认真分析题目并不断尝试.6.托勒密定理的逆定理及其证明定理:如果凸四边形ABCD 满足AB ×CD + BC ×AD = AC ×BD,那么A 、B 、C 、D 四点共圆.证法1同一法:在凸四边形ABCD 内取一点E,使得EAB DAC ∠=∠,EBA DCA ∠=∠,则EAB ∆∽DAC ∆.可得AB ×CD = BE ×AC ———1且 AE ABAD AC = ———2则由DAE CAB ∠=∠及2可得DAE ∆∽CAB ∆.于是有 AD ×BC = DE ×AC ———3由1+3可得 AB ×CD + BC ×AD = AC × BE + DE .据条件可得 BD = BE + DE,则点E 在线段BD 上.则由EBA DCA ∠=∠,得DBA DCA ∠=∠,这说明A 、B 、C 、D 四点共圆.证法2构造转移法延长DA 到A /,延长DB 到B /,使A 、B 、B /、A /四点共圆.延长DC到C /,使得B 、C 、C /、B /四点共圆.如果能证明A /、B /、C /共线,则命题获证那么,据圆幂定理知A 、C 、C /、A /四点也共圆. 因此,///A B A D AB BD=,///B C C D BC BD =. 可得 //////AB A D BC C D A B B C BD⨯+⨯+=.另一方面,///A C A D AC CD =,即///AC A D A C CD⨯=. 欲证//AB A D BC C D BD⨯+⨯=/AC A DCD ⨯,即证///AB CD A D BC CD C D AC BD A D ⨯⨯+⨯⨯=⨯⨯即 //()BC CD C D AC BD AB CD A D ⨯⨯=⨯-⨯.据条件有 AC BD AB CD AD BC ⨯-⨯=⨯,所以需证//BC CD C D AD BC A D ⨯⨯=⨯⨯,即证//CD C D AD A D ⨯=⨯,这是显然的.所以,//////A B B C A C +=,即A /、B /、C /共线.所以//A B B ∠与//BB C∠互补.由于//A B B DAB ∠=∠,//BB C DCB ∠=∠,所以DAB ∠与DCB ∠互补,即A 、B 、C 、D 四点共圆.7.托勒密定理的推广及其证明定理:如果凸四边形ABCD 的四个顶点不在同一个圆上,那么就有 AB ×CD + BC ×AD > AC ×BD证明:如图,在凸四边形ABCD 内取一点E,使得EAB DAC ∠=∠,EBA DCA ∠=∠,则EAB ∆∽DAC ∆.可得AB ×CD = BE ×AC ————1且AE ABAD AC = ————2则由DAE CAB ∠=∠及2可得DAE ∆∽CAB ∆.于是 AD ×BC = DE ×AC ————3由1+3可得 AB ×CD + BC ×AD = AC × BE + DE因为A、B、C、D四点不共圆,据托勒密定理的逆定理可知AB×CD + BC×AD≠AC×BD所以BE + DE≠BD,即得点E不在线段BD上,则据三角形的性质有BE + DE > BD.所以AB×CD + BC×AD > AC×BD.四、西姆松定理8.西姆松定理及其证明定理:从∆ABC外接圆上任意一点P向BC、CA、AB或其延长线引垂线,垂足分别为D、E、F,则D、E、F三点共线.证明:如图示,连接PC,连接 EF 交BC于点D/,连接PD/.因为PE⊥AE,PF⊥AF,所以A、F、P、Array E四点共圆,可得∠FAE =∠FEP.因为A、B、P、C四点共圆,所以∠BAC=∠BCP,即∠FAE =∠BCP.所以,∠FEP =∠BCP,即∠D/EP =∠D/CP,可得C、D/、P、E四点共圆.所以,∠CD/P +∠CEP = 1800;而∠CEP = 900,所以∠CD/P = 900,即PD/⊥BC.由于过点P 作BC 的垂线,垂足只有一个,所以点D 与D /重合,即得D 、E 、F 三点共线.注:1采用同一法证明可以变被动为主动,以便充分地调用题设条件.但需注意运用同一法证明时的唯一性.2反复运用四点共圆的性质是解决此题的关键,要掌握好四点共圆的运用手法. 五、 欧拉定理9.欧拉定理及其证明定理:设ΔABC 的重心、外心、垂心分别用字母G 、O 、H 表示.则有G 、O 、H 三点共线欧拉线,且满足3OHOG =.证明向量法:连BO 并延长交圆O 于点D;连接CD 、AD 、HC,设E 为边BC 的中点,连接OE 和OC .则→→→+=AH OA OH ——— ①因为 CD ⊥BC,AH ⊥BC,所以 AH // CD .同理CH // DA .所以,AHCD 为平行四边形.从而得→→=DC AH .而→→=OE DC 2,所以→→=OE AH 2.因为⎪⎪⎭⎫⎝⎛+=→→→OC OB OE 21,所以→→→+=OC OB AH ——— ②由①②得:→→→→++=OC OB OA OH ———— ③ 另一方面,→→→→→→→→++=+=+=GC GB OA GF OA AG OA OG 2.而→→→→→→+=+=OC GO GC OB GO GB ,,所以 ⎪⎪⎭⎫⎝⎛++=⇒+++=→→→→→→→→→OC OB OA OG OB OC GO OA OG 312 —— ④由③④得:→→=OG OH 3.结论得证.注:1运用向量法证明几何问题也是一种常用方法,而且有其独特之处,注意掌握向量对几何问题的表现手法;2此题也可用纯几何法给予证明. 又证几何法:连接OH,AE,两线段相交于点G /;连BO 并延长交圆O 于点D ;连接CD 、AD 、HC,设E 为边BC 的中点,连接OE 和OC,如图. 因为 CD ⊥BC,AH ⊥BC,所以 AH // CD .同理CH // DA .所以,AHCD 为平行四边形.可得AH = CD .而CD = 2OE,所以AH = 2OE .因为AH // CD,CD // OE,所以AH // OE .可得∆AHG /∽∆EOG /.所以////21AH AG HG OE G E G O ===. 由//21AG G E =,及重心性质可知点G /就是∆ABC 的重心,即G /与点G 重合.所以,G 、O 、H 三点共线,且满足3OH OG =.六、 蝴蝶定理10.蝴蝶定理及其证明定理:如图,过圆中弦AB 的中点M 任引两弦CD 和EF,连接CF 和ED,分别交AB 于P 、Q,则PM = MQ .证明:过点M 作直线AB 的垂线l ,作直线CF 关于直线l 的对称直线交圆于点C /、F /,交线段AB 于点Q /.连接FF /、DF /、Q /F /、DQ /.据圆的性质和图形的对称性可知:∠MF /Q /=∠MFP,∠F /Q /M =∠FPM ;且FF / // AB,PM = MQ /. 因为C 、D 、F /、F 四点共圆,所以A BCD EFP Q M C /F/ Q /∠CDF/ +∠CFF/ = 1800,而由FF/ // AB可得∠Q/PF +∠CFF/ = 1800,所以∠CDF/ =∠Q/PF,即∠MDF/ =∠Q/PF.又因为∠Q/PF =∠PQ/F/,即∠Q/PF =∠MQ/F/.所以有∠MDF/ =∠MQ/F/.这说明Q/、D、F/、M四点共圆,即得∠MF/Q/ =∠Q/DM.因为∠MF/Q/=∠MFP,所以∠MFP =∠Q/DM.而∠MFP =∠EDM,所以∠EDM =∠Q/DM.这说明点Q与点Q/重合,即得PM = MQ.此定理还可用解析法来证明:轴上的截距互为相反数.证:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立直角坐标系,M点是坐标原点.设直线DE、CF的方程分别为x = m1y + n 1,x = m2y + n 2;直线CD、EF的方程分别为y = k1 x ,y = k2 x.则经过C、D、E、F四点的曲线系方程为y –k1 x y–k2 x+λx–m1 y–n1x–m2 y–n2=0.整理得λ+k1k2x 2+1+λm1m2y 2–k1+k2+λm1+m2xy–λn1+n2x+λn1m2+n2m1y+λn1n2=0.由于C、D、E、F四点在一个圆上,说明上面方程表示的是一个圆,所以必须λ+ k1 k2 = 1 +λm1 m2≠ 0,且k1+k2+λm1+m2=0.若λ=0,则k1k2=1,k1+k2=0,这是不可能的,故λ≠0;又y轴是弦AB的垂直平分线,则圆心应落在y轴上,故有λn1+ n2 = 0,从而得n1 + n2 = 0.这说明直线DE、CF在x轴上的截距互为相反数,即得PM = MQ.。
中学数学竞赛中常用的几个重要定理
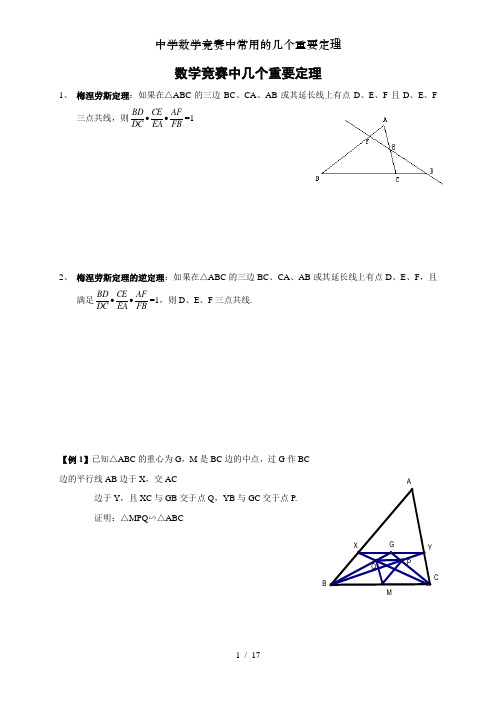
数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ,M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ,交AC边于Y ,且XC 与GB 交于点Q ,YB 与GC 交于点P. 证明:△MPQ ∽△ABCj MQGAC BXY P【例2】以△ABC的底边BC为直径作半圆,分别与边AB,AC交于点D和E,分别过点D,E作BC的垂线,垂足依次为F,G,线段DG和EF交于点M.求证:AM⊥BC【例3】四边形ABCD内接于圆,其边AB,DC的延长线交于点P,AD和BC的延长线交于点Q,过Q作该圆的两条切线,切点分别为E,F.求证:P,E,F三点共线.【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M ,过M 作AD 的平行线分别交AB ,CD于点E ,F ,交BC 的延长线于点O ,P 是以O 为圆心,以OM 为半径的圆上一点. 求证:∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900,点D 在AC 上,点E 在BD 上,AE 的延长线交BC 于F. 若BE :ED=2AC :DC ,则∠ADB=∠FDCD塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于N、P、M,则1=••PACPNCBNMBAM塞瓦定理的逆定理:设M、N、P分别在△ABC的边AB、BC、CA上,且满足1=••PACPNCBNMBAM,则AN、BP、CM相交于一点.【例1】B E是△ABC的中线,G在BE上,分别延长AG,CG交BC,AB于点D,F,过D作DN∥CG交BG于N,△DGL及△FGM是正三角形.求证:△LMN为正三角形.GCLMEDFN【例2】在△ABC 中,D 是BC 上的点DC BD =31,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比【练习1】设P 为△ABC 内一点,使∠BPA=∠CPA ,G 是线段AP 上的一点,直线BG ,CG 分别交边AC ,AB 于E ,F.求证:∠BPF=∠CPE【练习2】 在△ABC 中,∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点,且AD 平分∠BAC ,过点D 作垂线DP ⊥AB 于P ,DQ ⊥AC 于Q ,CP 于BQ 相交于K. 求证:AK ⊥BCCCC托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD【例1】 已知在△ABC 中,AB >AC ,∠A 的一个外角的平分线交△ABC 的外接圆于点E ,过E 作EF ⊥AB ,垂足为F.求证:2AF=AB -AC【例2】经过∠XOY 的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q.求证:OP 1+OQ1为定值HABCEFAXYPOQ【例3】 解方程42-x+12-x=x 7【练习1】 设AF 为⊙O1与⊙O2的公共弦,点B ,C 分别在⊙O1,⊙O2上,且AB=AC ,∠BAF ,∠CAF 的平分线交⊙O1,⊙O2于点D ,E. 求证:DE ⊥AF【练习2】⊙O 为正△ABC 的外接圆,AD 是⊙O 的直径,在弧BC 上任取一点P (与B ,C不重合).设E ,F 分别为△PAB ,△PAC 的内心.证明:PD=∣PE-PF ∣西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC ,PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线.【例1】过正△ABC 外接圆的弧AC 上点P 作P D ⊥直线AB 于D,作PE ⊥AC 于E,作PF ⊥BC 于F.求证:PF 1+PD 1=PE1【练习1】设P 为△ABC 外接圆周上任一点,P 点关于边BC ,AC 所在的直线的对称点分别为P 1,P 2.求证:直线P 1P 2经过△ABC 的垂心.CABPEFD HABP1P2CP三角形的五心内心【例1】设点M 是△ABC 的BC 边的中点,I 是其内心,AH 是BC 边上的高,E 为直线IM 与AH 的交点.求证:AE 等于内切圆半径r【例2】在△ABC 中,AB=4,AC=6,BC=5,∠A 的平分线AD 交△ABC的外接圆于K.O ,I 分别为△ABC 的外心,内心.求证:OI ⊥AK【练习】 在△ABC 中,∠BAC=300,∠ABC=700,M 为形内一点,∠MAB=∠MCA=200求∠MBA 的度数.B外心【例1】锐角△ABC的外心为O,线段OA,BC的中点为M,N,∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN【例2】在等腰△ABC中,AB=BC,CD是它的角平分线,O是它的外心,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,证明:BE=FD.【练习】1、⊙O 1与⊙O 2相交于P ,Q ,⊙O 1的弦PA 与⊙O 2相切,⊙O 2的弦PB 与⊙O 1相切.设△PAB 的外心为O ,求证:OQ ⊥PQ重心【例1】在△ABC 中,G 为重心,P 是形内一点,直线PG 交直线BC ,CA ,AB 于F ,E ,D.求证:FG FP +EG EP +DGDP=3【例2】已知△ABC 的重心G 和内心I 的连线GI ∥BC ,求证:AB+AC=2BCC【练习】1、设M 为△ABC 的重心,且AM=3,BM=4,CM=5,求△ABC 的面积.2、设O 是△ABC 的外心,AB=AC ,D 是AB 的中点,G 是△ACD 的重心,求证:OG ⊥CD垂心三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍.BCB【例1】△ABC 的外接圆为⊙O ,∠C=600,M 是弧AB 的中点,H 是△ABC 的垂心.求证:OM ⊥OH【例2】已知AD ,BE ,CF 是锐角△ABC 的三条高,过D 作EF 的平行线RQ ,RQ 分别交AB 和AC 于R ,Q ,P 为EF 与CB 的延长线的交点.证明:△PQR 的外接圆通过BC 的中点M.旁心【例1】在锐角∠XAY 内部取一点,使得∠ABC=∠XBD ,∠ACB=∠YCD.证明:△ABC 的外心在线段AD 上.CD【例2】AD是直角△ABC斜边BC上的高(AB<AC),I1,I2分别是△ABD,△ACD的内心,△A I1 I2的外接圆⊙O分别交AB,AC于E,F,直线FE与CB的延长线交于点M.证明:I1,I2分别是△ODM的内心与旁心.相交两圆的性质与应用【例1】证明:若凸五边形ABCDE中,∠ABC=∠ADE,∠AEC=∠ADB. 证明:∠BAC=∠DAEE【例2】已知⊙O1与⊙O2相交于A,B,直线MN垂直于AB且分别与⊙O1与⊙O2交于M,N,P 是线段MN的中点,Q1,Q2分别是⊙O1与⊙O2上的点,∠AO1Q1=∠AO2Q2求证:PQ1=PQ2【练习】梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,∠DAM=∠CBK,求证:∠DMA=∠CKBA其他的一些数学竞赛定理1、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和.推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b 、m c 则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+2、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ,则有ACABDC BD =3、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P4、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理: a 、b 、c 为△ABC 的边,则有: a 2=b 2+c 2-2bc ·cosA;b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;5、欧拉定理:△ABC 的外接圆圆心为O ,半径为R ,内切圆圆心为I ,半径为r,记OI=d,则有:d 2=R 2-2Rr.6、巴斯加线定理:圆内接六边形ABCDEF (不论其六顶点排列次序如何),其三组对边AB 与DE 、BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.。
数学竞赛--梅涅劳斯定理

梅涅劳斯定理16/3/5梅涅劳斯定理梅涅劳斯(Menelaus)定理(简称梅氏定理)最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica)。
任何一条直线截三角形的各边,都使得三条不相邻线段之积等于另外三条线段之积,这一定理同样可以轻而易举地用初等几何或通过应用简单的三角关系来证明. 梅涅劳斯把这一定理扩展到了球面三角形。
中文名梅涅劳斯定理外文名Menelaus别称梅氏定理表达式(AF/FB)×(BD/DC)×(CE/EA)=1提出者梅涅劳斯提出时间1678年应用学科数学,物理适用领域范围平面几何学适用领域范围射影几何学定理内容定理证明证明一过点A作AG∥DF交BC的延长线于点G.则证明二过点C作CP∥DF交AB于P,则两式相乘得证明三连结CF、AD,根据“两个三角形等高时面积之比等于底边之比”的性质有。
AF:FB =S△ADF:S△BDF…………(1),BD:DC=S△BDF:S△CDF…………(2),CE:EA=S△CDE:S△ADE=S△FEC:S△FEA=(S△CDE+S△FEC):(S△ADE+S△FEA)=S△CDF:S△ADF (3)(1)×(2)×(3)得证明四过三顶点作直线DEF的垂线AA‘,BB',CC',如图:充分性证明:△ABC中,BC,CA,AB上的分点分别为D,E,F。
连接DF交CA于E',则由充分性可得,(AF/FB)×(BD/DC)×(CE'/E'A)=1又∵2∴有CE/EA=CE'/E'A ,两点重合。
所以共线推论 在△ABC 的三边BC 、CA 、AB 或其延长线上分别取L 、M 、N 三点,又分比是λ=BL/LC 、塞瓦定理相区分,那里是λμν=1)此外,用该定理可使其容易理解和记忆:第一角元形式的梅涅劳斯定理如图:若E ,F ,D 三点共线,则 (sin ∠ACF/sin ∠FCB)(sin ∠BAD/sin ∠DAC)(sin ∠CBE/sin ∠ABE)=1 即图中的蓝角正弦值之积等于红角正弦值之积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第章 角元形式的梅涅劳斯定理
第一角元形式的梅涅劳斯定理设、、分别是的三边、、所在直线(包括三边的延长线)
上的点,则、、共线的充要条件是
证明如图,由
,
及
,
.
这三式相乘,运用梅涅劳斯定理及其逆定理,知结论成立. 第二角元形式的梅涅劳斯定理设、、分别是的三边、、所在直线上的点,点不在三边所在直线上,则、、三点共线的充要条件是
.
证明如图.注意到
C '
A'
B
O
C
B
A 图23-2
(其中),
,
. 所以
.
而由梅涅劳斯定理及逆定理知、、共线.
故知结论成立. 注:在上述两定理中,若采用有向角(规定角的终边绕逆时针方向时角为正值,否则为负值)时,两条件式的右端均为,有向角记为. 下面给出运用如上定理处理问题的例子. 例如图,设的三边、、所在的直线
E E'D F'F
D
C
B A
图23-3
上的点、、共线,并且直线、、关于、、平分线的对称直线、、分别与、、所在直
线交于、、,则、、也共线. 证明对及截线应用第一角元形式的梅涅劳斯定理,有
.
由题设知
,
,
,
,
,
,
.
从而有,
即
.
由第一角元形式的梅涅劳斯定理知,、、三点共线.
例若三角形的三条外角平分线皆与对边所在直线相交,则三交点共线. 证明如图,
设的三条外角平分线分别与对边所在直线相交于、、,则
知
,
,,
,
,
.
故有。
