多层和高层框架结构设计-竖向荷载作用
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
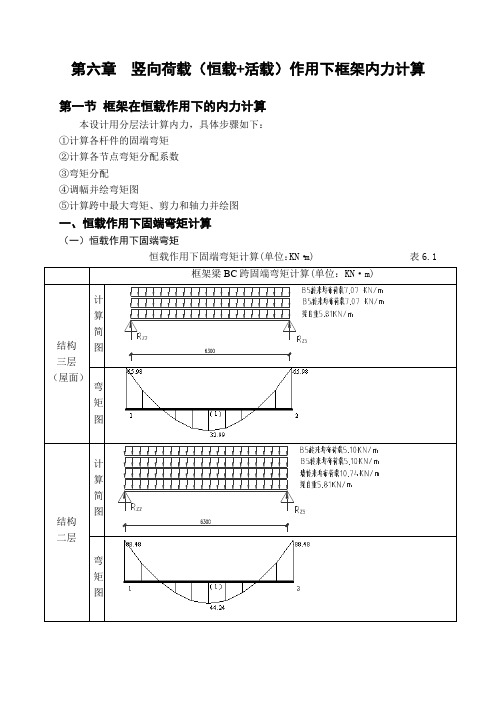
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
12.4多层框架结构在竖向荷载下的内力计算方法

12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
2.计算模型的确定 在计算简图中,框架节点多为刚接,柱子下端在基础顶面,也按刚接 考虑。杆件用轴线表示,梁柱的连接区用节点表示。等截面轴线取截面形 心位置,当上下柱截面尺寸不同时,则取上层柱形心线作为柱轴线。跨度 取柱轴线间的距离。计算简图中的柱高,对楼层取层高;对底层柱,现浇 楼板取基础顶面与二层楼板顶面之间的高度。 当各跨跨度不等但相差不超过10%时,可当作具有平静跨度的等跨框架。
12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
4.荷载计算
作用在多、高层建筑结构上的荷载有竖向荷载和水平荷载。竖向 荷载包括恒载和楼(屋)面活荷载、雪荷载,水平荷载包括风荷载和 水平地震作用。 活荷载大小见《建筑结构荷载规范》GB50009-2012第5.1.1条。
12.4竖向荷载作用下的内力近似计算
12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
由于计算时假定柱的远端为固定端,实际上除底层柱在基础处为固定 端外,其余各住的远端均有转角而非固定端。为减少由此引起的误差,除 底层柱外,其他各层柱的线刚度均乘以折减系数0.9,并取传递系数为1/3; 底层柱及梁的传递系数仍为1/2。 例12-2 用分层法计算例12-1框架的弯矩,并绘制弯矩图。
1转动刚度第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算2分配系数第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算3传递系数第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算4杆端弯矩第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算例121三跨二层钢筋混凝土框架各层框架梁所承受的竖向荷载设计值如图所示图中括号内数值为各杆件的相对线刚度
高层建筑的结构特点

高层建筑的结构特点一、高层建筑结构设计的特点高层建筑结构设计与低层、多层建筑结构相比较,结构专业在各专业中占有更重要的位置,不同结构体系的选择,直接关系到建筑平面的布置、立面体形、楼层高度、机电管道的设置、施工技术的要求、施工工期长短和投资造价的高低等。
其主要特点有:(一)水平力是设计主要因素在低层和多层房屋结构中,往往是以重力为代表的竖向荷载控制着结构设计。
而在高层建筑中,尽管竖向荷载仍对结构设计产生重要影响,但水平荷载却起着决定性作用。
因为建筑自重和楼面使用荷载在竖向构件中所引起的轴力和弯矩的数值,仅与建筑高度的一次方成正比;而水平荷载对结构产生的倾覆力矩、以及由此在竖向构件中所引起的轴力,是与建筑高度的两次方成正比。
另一方面,对一定高度建筑来说,竖向荷载大体上是定值,而作为水平荷载的风荷载和地震作用,其数值是随着结构动力性的不同而有较大的变化。
(二)侧移成为控指标与低层或多层建筑不同,结构侧移已成为高层结构设计中的关键因素。
随着建筑高度的增加,水平荷载下结构的侧向变形快速增大,与建筑高度H的4次方成正比(△=qH4/8EI)。
另外,高层建筑随着高度的增加、轻质高强材料的应用、新的建筑形式和结构体系的出现、侧向位移的快速增大,在设计中不仅要求结构具备足够的强度,还要求具备足够的抗推刚度,使结构在水平荷载下产生的侧移被控制在某一限度之内,否则会产生下述情况:1.因侧移产生较大的附加内力,尤其是竖向构件,当侧向位移增大时,偏心加剧,当产生的附加内力值超过一定数值时,将会导致房屋侧塌。
2.使居住人员感到不适或惊慌。
3.使填充墙或建筑装饰开裂或损坏,使机电设备管道损坏,使电梯轨道变型造成不能正常运转。
(三)抗震设计要求更高有抗震设防的高层建筑结构设计,除要考虑正常使用时的竖向荷载、风荷载外,还必须使结构具备良好的抗震性能,做到小震不坏、大震不倒。
(四)减轻高层建筑自重比多层建筑更为重要高层建筑减轻自重比多层建筑更有意义。
超高层建筑设计过程变形控制

超高层建筑变形控制1.竖向变形控制一般的多层利高层建筑相比,超高层结构的设计除了需要在结构体系选择、抗震设计、抗风设计等方面有更高的要求之外,还需要考虑非荷载作用下的结构变形和内力分析。
非荷载作用主要包括温度作用和混凝土的收缩、徐变以及地基的不均匀沉降等。
由于超高层结构高度可能在两三百米以上,以及不同竖向构件在压应力水平、材料等方面存在明显差异,还有混凝土材料的徐变、收缩等非荷载作用时,因此超高层结构必然产生不可忽视的竖向变形及差异。
在国外,二十世纪七十年代以后,高层建筑的竖向变形筹问题逐渐引起人们的注意。
美国的Russell H G等人对两幢钢筋混凝十高层建筑竖向变形进行了跟踪测试,其中高197m的Lake Point Tower,经过3年后柱的最大轴向变形超过了200mm;高262m的Water Tower Place经过五年后柱与墙的轴向变形差超过23mm,虽然该建筑在层13~14设有刚性转换层,第32层为刚度很大的设备层,但竖向构件间的轴向变形差异依然很明显。
这些与时间和环境相关的超高层结构竖向构件变形及差异,将使相邻的结构构件及非结构构件产生附加应力,还可能影响设备的安装使用。
国内外的研究者对结构的竖向变形及著异问题进行了分析和探讨。
杨丽、郭忠恭研究了钢筋泓凝土构件徐变和收缩的有关理论和公式,得竖向构件由于徐变和收缩产生的非弹性缩短,认为超过lOOm 的高层混凝十结构应该考虑徐变和收缩的影响。
高层建筑中,核心筒、角柱、边柱的竖向变形差异来自多个方面。
在竖向荷载作用下,各个部位垂直构件的截面轴向应力有高有低。
在结构施工时,核心筒施工往往先于周边框架柱施工,造成结构各部分受荷时间有先有后。
加上混凝土的弹性压缩、收缩、徐变以及温度变化等因素影响,最终会使得结构构件产生可观的竖向变形及变形差异。
这些变形将给设备安装带来不利影响,同时也会在结构中产生附加力矩。
一般而言,当结构超过30层或总高度大于100m时,在施工中就应当对此进行考虑。
第3章:多层和高层框架结构

帮 助
混凝土结构设计
第3章
竖向荷载作用下的内力计算方法
(1)分层法 基本假定 忽略垂直荷载作用下框架结构的侧移;
上一章 主 页 目 录
每层梁上的荷载只在本层梁及与其相连的上、 下层柱产生内力,不在其他层梁和其他层柱 上产生内力。
帮 助
混凝土结构设计
第3章
根据以上假定,多、高层框架可分层作为若干 个彼此互不关连的且柱端为完全固定的简单刚架近 似计算。简单刚架可用弯矩分配法计算,一般循环 2次。
主 页 目 录 上一章
帮 助
混凝土结构设计
第3章
框架梁内力
(1)弯矩
主 页
M
2 u ln
`
…3-13
目 录 上一章
式中, ——弯矩系数,查表3.6.1;
n ——框架梁上恒载与活载设计值之和;
ln ——净跨跨长,求支座弯矩时用相邻
两跨净跨跨长的均值。
帮 助
混凝土结构设计 表3.6.1
第3章
纵向布置
特点:
连系梁截面较小,框 架梁截面尺寸大,室 内有效净空高; 对纵向地基不均匀沉 降较有利; 房屋横向刚度小,侧 移大。 纵向承重
帮 助 主 页 目 录 上一章
混凝土结构设计
第3章
双向布置
主 页
特点: 整体性好,受力好;
目 录 上一章
适用于整体性要求
较高和楼面荷载较
e 钢筋的截断和弯起位置不对
f 框架梁柱的剖面图配筋和剖面位置对不上 g 剖面不能全面地反映框架的配筋情况等
混凝土结构设计
第3章
§3.1 概 述
房屋按高度和层数分类
低层
主 页 目 录 上一章
高层建筑 第三章荷载作用与组合

(3) 偶然荷载:在结构使用期间不一定出现,一旦出现, 其量值很大且持续时间较短的荷载。如地 震、爆炸力、撞击力等。 按作用方向:(1) 竖向荷载:荷载作用方向沿垂直方向的 荷载。如结构自重、楼屋面活荷载等。 (2)水平荷载:荷载作用方向沿水平方向的荷 载。如风荷载、水平地震作用等。 与多层建筑相比,高层建筑层数多、高度较大,其竖向荷 载的影响是与建筑高度成正比的线性关系,而水平作用所 产生的作用效应随建筑高度成非线性的增长。并逐渐成为 设计控制指标。 三、荷载代表值 荷载代表值是指为了方便设计给荷载规定以一定的量值。 包括:标准值、组合值、频遇值和准永久值。 其中标准值指正常情况下在设计基准期(如50年)内可能 出现的最不利荷载值,是荷载的基本代表值,而其他代表
离地面或海 平面高度
A 5 1.09 1.00 0.65 10 1.28 1.00 0.65 20 1.52 1.23 0.74 30 1.67 1.39 0.88 40 1.79 1.52 1.00 50 1.89 1.62 1.10 60 1.97 1.71 1.20 70 2.05 1.79 1.28 80 2.12 1.87 1.36 90 2.18 1.93 1.43 100 2.23 2.00 1.50 150 2.46 2.25 1.79 200 2.64 2.46 2.03
值是采用相应的系数乘以其标准值得出。系数查现行《建 筑结构荷载规范》(GB50009-2012)。 永久荷载应采用标准值作为代表值;可变荷载应根据设 计要求采用标准值、组合值、频遇值或准永久值作为代表 值;偶然荷载应按建筑结构使用特点确定其代表值。 建筑结构设计应根据使用过程中在结构上可能同时出现 的荷载,按承载能力极限状态和正常使用极限状态分别进 行荷载组合,并应取各自的最不利的效应组合进行设计。 对于承载能力极限状态,应按荷载效应的基本组合或偶 然组合进行荷载组合。对于正常使用极限状态,应根据不 同的设计要求,采用荷载的标准组合或偶然组合、频遇组 合或准永久组合进行荷载组合。
框架结构竖向荷载作用下的内力计算
框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的,在受到竖向荷载作用下,会引起构件内力的产生。
了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。
下面将详细介绍框架结构竖向荷载作用下的内力计算方法。
首先,通过建立结构模型来描述框架结构。
结构模型中包括构件、节点和连接关系。
构件可以是梁或柱,节点是构件之间的连接点,连接关系表示构件之间的刚性约束。
在竖向荷载作用下,框架结构的内力主要有两种情况:梁内力和柱内力。
1.梁内力计算:在竖向荷载作用下,梁会产生弯矩和剪力。
根据梁的基本理论,可以得出计算弯矩和剪力的公式。
-弯矩计算:弯矩是由竖向荷载作用在梁上引起的。
根据弯矩的定义,弯矩M等于施加在梁上的力乘以力臂。
当梁需要承受重力荷载时,弯矩的计算公式为M=w*l^2/8,其中w为荷载大小,l为梁的跨度。
-剪力计算:剪力是由竖向荷载作用在梁上引起的。
根据剪力的定义,剪力V等于施加在梁上的力。
当梁需要承受重力荷载时,剪力的计算公式为V=w*l/2,其中w为荷载大小,l为梁的跨度。
2.柱内力计算:在竖向荷载作用下,柱会产生压力和拉力。
根据柱的基本理论,可以得出计算压力和拉力的公式。
-压力计算:压力是由竖向荷载作用在柱上引起的。
根据力学平衡原理,压力P等于施加在柱上的荷载之和。
当柱需要承受多个重力荷载时,压力的计算公式为P=∑w,其中w为荷载大小。
-拉力计算:拉力是由竖向荷载作用在柱上引起的。
和压力类似,拉力T等于施加在柱上的荷载之和。
在实际计算过程中,需要考虑梁和柱的截面形状和材料性质,以及节点和连接部位的刚性约束等因素。
同时,还需要考虑结构的整体平衡条件和节点处的力的平衡条件。
在计算过程中,可以使用静力平衡原理和弹性力学理论来进行分析。
通过平衡方程和应变-位移关系等基本原理,可以建立结构方程组,并通过求解方程组得到内力的值。
总结起来,框架结构竖向荷载作用下的内力计算是一个复杂的过程,需要考虑多个因素和使用多种方法。
毕业设计指导书(框架结构设计)-内力计算及组合
计算杆件固端弯矩时应带符号,杆端弯矩一律以顺时针方向为正,如图3-6。
图 3-6 杆端及节点弯矩正方向
1)横梁固端弯矩:
(1)顶层横梁
自重作用:
板传来的恒载作用:
(2)二~四层横梁
自重作用:
板传来的恒载作用:
2)纵梁引起柱端附加弯矩:(本例中边框架纵梁偏向外侧,中框架纵梁偏向内侧)
顶层外纵梁
相交于同一点的多个杆件中的某一杆件,其在该节点的弯矩分配系数的计算过程为:
(1)确定各杆件在该节点的转动刚度
杆件的转动刚度与杆件远端的约束形式有关,如图3-1:
(a)杆件在节点A处的转动刚度
(b)某节点各杆件弯矩分配系数
图 3-1 A节点弯矩分配系数(图中 )
(2)计算弯矩分配系数μ
(3)相交于一点杆件间的弯矩分配
(3)求某柱柱顶左侧及柱底右侧受拉最大弯矩——该柱右侧跨的上、下邻层横梁布置活荷载,然后隔跨布置,其它层按同跨隔层布置(图3-4c);
当活荷载作用相对较小时,常先按满布活荷载计算内力,然后对计算内力进行调整的近似简化法,调整系数:跨中弯矩1.1~1.2,支座弯矩1.0。
(a)(b) (c)
图 3-4 竖向活荷载最不利布置
∑Mik/l
V1/A=gl/2+u-∑Mik/l
M=gl/2*l/4+u*1.05-MAB-V1/A*l/2
4
21.9
4.08
2.25
6
12.24
41.06
-30.54
2.55
50.75
-60.24
3
16.61
4.08
2.25
6
12.24
31.14
多层框架结构设计
非抗震设计
高度限制(m)
70
抗震设防烈度
6度
7度 8度 9度
60
55
45
25
高宽比限制
5
4
3
2
框架结构适用于非抗震时的多层及高层建筑,抗震设计时的 多层及小高层建筑(7度区以下)。7度区以下、小于等于3层的多 层建筑可不采用框架结构。
一般8度区高度超过20m采用框架结构不经济,因此6层以上 的建筑结构宜采用框架—剪力墙结构或剪力墙结构。
板或井字梁楼盖。 抗震设计时,不应采用部分由砌体墙承重、部分由框架承
重的混合承重形式。
横向框架梁 板 纵向框架梁
横向框架梁 板 纵向框架梁
框架梁 双向板
框架结构的承重方案
(3)柱网及层高 1)内廊式 2)等跨式
3)对称不等跨式
走廊及卫生间
走廊及卫生间
民用建筑柱网布置
结构布置情况是用图纸来表达的。结构布置图上要 将房屋中每一结构构件的类型、编号、平面和空间的位 置等明确地加以表示,它不但是结构设计人员用以进行 设计计算的依据,而且是施工人员进行施工时必不可少 的。
主梁截面宽度可取bb = (1/3~1/2)hb,且不宜小于200mm。 为了保证梁的侧向稳定性,梁截面的高宽比(hb/bb)不宜大 于4。(对于一般民用建筑,以选用下限为宜)
当一根框架梁的各跨跨度相差较大时,这种框架梁各 跨的截面宽度应该相同,以利于梁内上部纵筋的贯通和下 部纵筋的锚固;但梁各跨的截面高度应该取不同值。
为了降低楼层 高度,可将梁设计 成宽度较大而高度 较小的扁梁,扁梁 的截面高度可按
(1/25~1/18)lb 估算。扁梁的截面 宽度b(肋宽)与其 高度h的比值b/h不 宜超过3。
框架结构
板。为了避免框架节点纵横钢筋相互干扰,框架梁底部
通常较连系梁底部低50mm以A 上。
33
(2)、框架梁的构造要求
1).梁纵向钢筋的构造要求 梁纵向受拉钢筋的数量除按计算确定外,还必须考虑温度
、收缩应力所需要的钢筋数量,以防止梁发生脆性破坏和控制 裂缝宽度。纵向受拉钢筋的最小配筋百分率和最大配筋率需满 足要求。
A
27
第1 MGH=58.18kN·m MHG=28.09kN·m MHI=44.94 kN·m MIH=MIF+MIL=16.1+27.2=43.3kN·m
(5)根据以上结果,画出M图。
(单位: kN·m)
A
28
A
29
4 框架结构的构件设计与构造要求
竖向荷载和横向荷载根据分层法和反弯法计算内力, 然后进行组合、调幅、叠加,然后进行配筋计算。
第1层:∑P=10+19+22=51kN VGJ=17kN VHK=20.4kN VIL=13.6kN
A
25
(3) 计算柱端弯矩
第3
MAD=MDA=6.66kN·m MBE=MEB=8.9kN·m MCF=MFC=4.44kN·m
第2
MDG=MGD=24.18kN·m MEH=MHE=32.23kN·m MFI=MIF=16.1kN·m
A
21
§3 框架内力分析-水平荷载作用
水平荷载主要是风荷载及水平地震作用。
在水平荷载作用下框架结构的内力和侧移可用结构力学 方法计算,常用的近似算法反弯点法、D值法等。
23.04.2020
A
2222
三、例题
用反弯点法求图所示框架的弯矩图。
1)计算简图,图中括号内数字为各杆的相对线刚度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4) 将所有杆端的分配弯矩同时向其远端传递(对于刚接 框架,传递系数均取1/2);
(5) 将各节点因传递弯矩而产生的新的不平衡弯矩进行第 二次分配,使各节点处于平衡状态;
(6) 将各杆端的固端弯矩、分配弯矩和传递弯矩叠加,即 得各杆端弯矩。
2020/11/25
计算例题
右图括号中为梁、 柱线刚度的相对值
(0.9×4.21)
(0.9×4.21)
F I0 .9 1 .7 0 9 .9 1 1 2 ..7 7 9 7 3 .6 40 .0 8 9D
(9.53) E
(7.11) (4.84)
F C0 .9 1 .7 93 .1 6 2 4 .7 73 .6 40 .2 0 2 A
B
I (0.9×1.79)
2020/11/25
4400
3600
2.8 kN/m
G
(7.63) H
(4.21) (4.21)
3.8 kN/m
I (10.21)
(1.79)
3.4 kN/m
D
(9.53) E (12.77) F
(7.11) (4.84)
(3.64)
A
B
C
7500
5600
计算节点弯矩分配系数
节点 G:
≈
+
+
+
2020/11/25
竖向荷载作用下分层计算示意图
刚度系数: 传递系数:
3.竖向荷载作用下的内力计算方法
分层法 ✓ 计算要点
(1) 将多层框架沿高度分成若干单层无侧移的敞 口框架,每个敞口框架包括本层梁和与之相连的 上、下层柱。梁上作用的荷载、各层柱高及梁跨 度均与原结构相同,构件刚度可采用弹性刚度。
✓ 计算要点 (4) 用无侧移框架的计算方法(如弯矩分配法) 计算各敞口框架的杆端弯矩,由此所得的梁端弯 矩即为其最后的弯矩值;因每一柱属于上、下两 层,所以每一柱端的最终弯矩值需将上、下层计 算所得的弯矩值相加。
2020/11/25
3.竖向荷载作用下的内力计算方法 分层法
✓ 计算要点 (5) 在上、下层柱端弯矩值相加后,将引起新的 节点不平衡弯矩,如欲进一步修正,可对这些不 平衡弯矩在本节点再作一次分配,但不再传递。
-1.22
-0.13 -1.35
-1.55
-0.17 -1.72
-4.10 0.73 -0.46 -15.85
B -0.86
I
-0.20
左梁 下柱 上柱 0.709 0.202 0.089 8.89 F -6.30 -1.80 -0.79 -2.05 1.45 0.41 0.19 1.99 -1.39 -0.60
C -0.70 30
4.77 5.97 G
弯
矩
10.33
图
6.73 D 5.19
15.05 13.62
1.88 H
18.92 15.85
1.72 1.83 E
0.77 0.87
I 1.99
0.86 1.39 F
A 3.37 2020/11/25
0.86 B
0.70 C 31
M JK
q
M KJ
J
l0
H (0.9×4.21)
E H 9 .5 3 0 .9 0 4 .9 .2 1 4 .2 1 1 2 .7 7 4 .8 4 0 .1 2 3(0.9×4.21)
D
(9.53) E
E F 9 .5 3 0 .9 4 1 .2 2 .1 7 7 1 2 .7 7 4 .8 4 0 .4 1 3(7.11)
2020/11/25
6
3.竖向荷载作用下的内力计算方法
(1)分层法 ①基本假定
➢ 忽略竖向荷载作用下框架结构的侧移; ➢ 每层梁上的荷载只在本层梁及与其相连的上、
下层柱产生内力,不在其他层梁和其他层柱 上产生内力。 应当指出,上述假定中所指的内力不包 括柱轴力,因为某层梁上的荷载对下部 各层柱的轴力均有较大影响,不能忽略。
2020/11/25
计算节点弯矩分配系数
节点 D:
G
H
I
D G0 .9 4 .0 2 .1 9 9 4 ..5 2 3 17 .1 10 .1.79)
(0.9×4.21)
D E0.94.21 9 .5 9 3 .537.110.466D
(9.53) E
D
-17.81
3.31 6.20 8.30 -1.53
0.29 0.53 0.71 3.60 6.73 -10.33
A 3.37 2020/11/25
-0.45 H
左梁 上柱 下柱 右梁
0.308 0.123 0.156 0.413
17.81
E -8.89
4.15
-3.15
-3.06 0.36 -0.34 18.92
2.8 kN/m
G
M H F I2.81 2 5.62kN m 7.32kN m
H
I
M IF H2.81 2 5.62kN m 7.32kN mD
2020/11/25
E 7500
F 5600
计算杆件固端弯矩:底层
M D F E3 .81 2 7 .52k N m 17 .8 1k N m G 3.8 kN/m H
3600
2.8 kN/m
G
(7.63) H
(4.21) (4.21)
3.8 kN/m
I (10.21)
(1.79)
3.4 kN/m
D
(9.53) E (12.77) F
(7.11) (4.84)
(3.64)
A
B
C
7500
5600
注:内力及位移正负号规定
本章中,杆端弯矩以顺时针为正,剪力 以使隔离体产生顺时针转动趋势为正,轴力 以受压为正;杆端转角以顺时针为正,侧移 或相对侧移以向右为正。
✓ 计算步骤 (1) 画出分层框架计算简图; (2) 计算框架梁柱线刚度,注意折减系数; (3) 计算各分层框架梁、柱端弯矩; (4) 确定梁、柱端最终弯矩; (5) 计算梁跨中弯矩和剪力以及柱的剪力及轴力。
2020/11/25
计算例题 右图括号中为梁、 柱线刚度的相对值
2020/11/25
4400
(12.77) F (3.64) C
2020/11/25
计算杆件固端弯矩:顶层
M
F JK
q
M
F KJ
M G F H2 .8 1 2 7 .5 2k N m 1 3 .1 3k N mMJ
F JK
ql2 12
l
K
M
F KJ
ql2 12
M H FG2.81 2 7.52kN m 13.13kN m
K
Vl
Vr
梁端剪力的计算
q
M JK
Mx
Jx
Vl
Vx
梁跨中弯矩的计算
M JK
J Vu
h0
Vl
K M KJ
柱剪力的计算
Nu
Vl
Vr
Nl
柱轴力的计算
3.竖向荷载作用下的内力计算方法 弯矩二次分配法
✓ 基本假定 (1) 不考虑框架结构的侧移对其内力的影响; (2) 每层梁上的荷载仅对本层梁及其上、下柱的 内力产生影响,对其它各层梁、柱内力的影 响可忽略不计。 上述假定中所指的内力同样不包括柱轴力。
(4.84)
E B 9 .5 3 0 .9 4 .4 2 .1 8 4 1 2 .7 7 4 .8 4 0 .1 5 6 A
B
I (0.9×1.79)
(12.77) F (3.64) C
2020/11/25
计算节点弯矩分配系数
节点 F:
G
H
F E0 .9 1 .7 9 1 2 1 .7 2 7 .7 73 .6 40 .7 0 9
2020/11/25
3.竖向荷载作用下的内力计算方法 弯矩二次分配法
✓ 计算步骤 (1) 计算各节点弯矩分配系数; (2) 计算框架梁的固端弯矩; (3) 计算各节点不平衡弯矩,并对所有节点的不 平衡弯矩同时进行第一次分配(其间不进行 弯矩传递);
2020/11/25
3.竖向荷载作用下的内力计算方法 弯矩二次分配法
D
E
FD
(9.53) E (12.77) F
顶层计算简图
(7.11) (4.84)
(3.64)
A
B
C
2020/11/25
计算节点弯矩分配系数
G
(7.63) H (10.21) I
节点 G:
(0.9×4.21)
G H7.6370 .6 .9 34.210.668
D
(0.9×4.21) E
G D7.63 0. 90 .4 9. 21 4.210.332 节点 H:
恒载一次布置
活载分跨布置
(2)最不利荷载布置法 恒载一次布置,楼屋面活载根据影响线,
直接确定产生某一指定截面最不利内力的活 载布置。此法用手算方法进行计算很困难。
最不利荷载的布置
3.竖向荷载作用下的内力计算方法
在竖向荷载作用下,多、高层框架结构的内 力可用力法、位移法等结构力学方法计算。工程 设计中,如采用手算,可使用分层法、迭代法、 弯矩二次分配法及系数法等近似方法进行计算。
2020/11/25
3.竖向荷载作用下的内力计算方法 分层法
✓ 计算要点 (6) 在杆端弯矩求出后,可由静力平衡条件计算 梁端剪力及梁跨中弯矩;逐层叠加柱上的竖向荷 载(包括节点集中力、柱自重等)和与之相连的 梁端剪力,即得柱的轴力。
2020/11/25
3.竖向荷载作用下的内力计算方法 分层法
