世界第一公式:麦克斯韦方程组
最伟大的数学公式排名

最伟大的数学公式排名数学公式是数学的基础,它们用于描述各种概念、关系和规律。
但是,要评价哪个数学公式最伟大是主观的,因为每个公式都有其独特的背景和重要性。
以下是一些被广泛认为是非常重要和有影响的数学公式。
1. 欧拉公式(Euler's formula):这个公式将三角函数、指数函数和复数关联起来,是数学中最重要的公式之一。
2. 牛顿-莱布尼兹公式(Newton-Leibniz formula):这个公式用于计算定积分,是微积分的基础。
3. 泰勒公式(Taylor series):这个公式用于展开函数,是分析数学的重要工具。
4. 欧拉-麦克劳林公式(Euler-Maclaurin formula):这个公式将欧拉和麦克劳林两种求和的方法结合起来,用于求和和积分。
5. 贝叶斯定理(Bayes' theorem):这个公式用于概率推理和统计推断,是贝叶斯方法的基石。
6. 傅里叶变换(Fourier transform):这个公式将时间和空间域上的函数转换为频率域上的函数,是信号处理和图像处理领域的基础。
7. 拉普拉斯变换(Laplace transform):这个公式将时间域上的函数转换为复平面上的函数,用于求解偏微分方程。
8. 欧拉-雅可比公式(Euler-Jacobi formula):这个公式用于求解变分问题,是优化理论和力学中的重要工具。
9. 麦克斯韦方程组(Maxwell's equations):这个方程组描述了电磁场的运动规律,是电动力学的基础。
10. 薛定谔方程(Schrödinger equation):这个方程描述了量子力学中微观粒子的运动状态,是量子力学的基础。
这些公式都是数学中的重要工具,对于不同的领域有着不同的影响和应用。
因此,无法简单地评价哪个公式最伟大,它们各自在数学和科学中扮演着重要的角色。
世界第一公式麦克斯韦方程组

世界第一公式麦克斯韦方程组麦克斯韦方程组是描述电磁场的数学模型,也被称为世界第一公式。
它由一系列方程组成,总共有四个方程,分别是麦克斯韦方程的积分形式和微分形式。
麦克斯韦方程组的积分形式包括高斯定律、法拉第电磁感应定律和安培环路定律。
这些方程描述了电荷和电流是如何与电磁场相互作用的,以及通过对电磁场的积分来计算这些相互作用的结果。
首先,高斯定律是描述电场与电荷之间的相互作用的方程。
它的数学形式是通过对电场的通量进行积分得到的,公式为:∮E·dA=ε₀ΣQ其中,∮E·dA表示对电场E在闭合曲面上的法向通量进行积分,ε₀是真空介电常数,ΣQ是闭合曲面内的电荷总量。
其次,法拉第电磁感应定律描述了磁感应强度与电场变化率之间的关系。
它的数学形式是通过计算电场沿着闭合回路的线积分得到的,公式为:∮E·dl = - d(∮B·dA)/dt其中,∮E·dl表示对电场E沿闭合回路的线积分,∮B·dA表示磁感应强度B通过闭合曲面的法向通量,dt表示时间的微小变化。
最后,安培环路定律描述了磁场与电流之间的相互作用。
它的数学形式是通过计算磁场沿着闭合回路的线积分得到的,公式为:∮B·dl = μ₀I + μ₀ε₀(d∮E·dA)/dt其中,∮B·dl表示对磁感应强度B沿闭合回路的线积分,μ₀是真空磁导率,I是通过闭合曲面的电流总量,d∮E·dA/dt表示电场通过闭合曲面的法向通量的变化率。
除了积分形式,麦克斯韦方程组还有微分形式,用来描述电磁场如何随空间和时间的变化而变化。
对于电场和磁场的微分形式,可以用分别使用高斯定理和斯托克斯定理将积分形式转化为微分形式。
微分形式中的麦克斯韦方程组包括高斯定律的微分形式、法拉第电磁感应定律的微分形式和安培环路定律的微分形式。
总结起来,麦克斯韦方程组是描述电磁场的基本方程,是电磁学的核心理论。
世界著名的十大公式
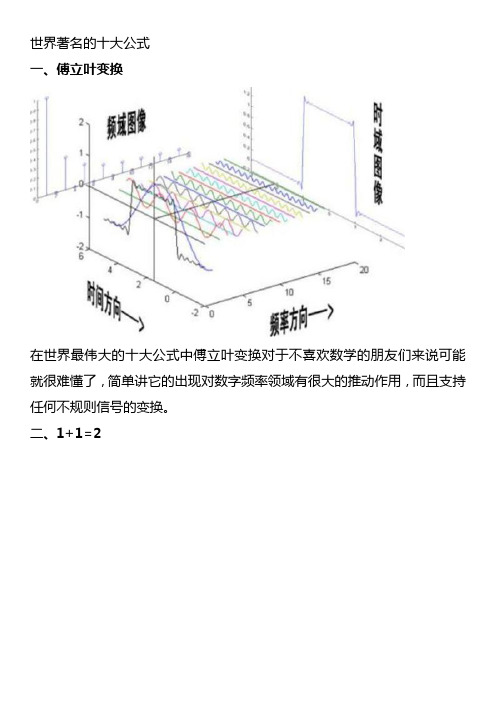
世界著名的十大公式一、傅立叶变换在世界最伟大的十大公式中傅立叶变换对于不喜欢数学的朋友们来说可能就很难懂了,简单讲它的出现对数字频率领域有很大的推动作用,而且支持任何不规则信号的变换。
二、1+1=21+1=2这个公式和上一个相比较应该就是无人不知了吧,从幼儿园开始它就伴随着我们,简单好理解,它的出现在整个数学领域可以说是引起轰动了的呢!三、毕达哥拉斯定理毕达哥拉斯定理也就是我们数学学习生涯中常见勾股定理,如今有四百多种图形被毕达哥拉斯定理给证明了,是非常伟大又典型的解决图形问题的公式。
四、麦克斯韦方程组人们评价说,如果没有麦克斯韦方程组就没有现代社会的文明,整个方程也是完美到无可挑剔,可以说宇宙间的任何电磁用这个方程组都能很好的被解释。
五、欧拉公式这个欧拉公式从形式上看非常的巧妙,没有任何多余的“杂质”,数学家们评论说凡是第一眼爱上这个公式的人必定会成为数学家,可见该公式的伟大之处。
六、质能方程在世界最伟大的十大公式中质能方程著名的物理学家爱因斯坦提出来的,该公式很好的揭示了质量和能量之间的关系,也正是质能方程的出现才有了当今的原子弹,氢弹等。
七、德布罗意方程组德布罗意方程组揭示出了任何物质都是有粒子性和波动性的,让波长和能量等之间有了一个很好的关系解释,提出者也在1929年获得了诺贝尔奖。
八、圆的周长公式圆的周长公式,这个伴随着整个数学学习生涯,如果用圆的周长公式来说计算太阳系包起来的周长,误差的直径不到百万分之一。
九、牛顿第二定律牛顿第二定律可以说是当下物理学的核心公式,它的出现可以是标志着真正物理学研究的开始,学习上好多的方程也都要依靠牛顿第二定律导出来。
十、薛定谔方程在世界最伟大的十大公式中薛定谔方程可谓是经典中的经典,它的出现很好的揭示了力学中位移和速度的关系,如今该公式在物理学的应用极为广泛,影响力也很大。
麦克斯韦方程组

麦克斯韦方程组麦克斯韦方程组是描述电磁场的四个基本方程,由苏格兰物理学家詹姆斯·克拉克·麦克斯韦在19世纪提出。
这四个方程求解了电磁场的本质,对于描述电磁波的传播以及电磁现象的研究起着重要的作用。
麦克斯韦方程组的第一个方程是高斯定律,它描述了电荷对电场产生的影响。
它的数学表达式为:∮E·dA = ε0∫ρdV其中,∮E·dA表示电场在截面A上的面积分,ε0为真空中的介电常数,ρ为电场中的电荷密度。
第二个方程是法拉第电磁感应定律,它描述了磁场通过闭合回路所产生的感应电场。
数学上可以表示为:∮B·dl = μ0(I + ε0d(∫E·dA)/dt)其中,∮B·dl表示磁场在环路l上的线积分,μ0为真空中的磁导率,I为环路中的电流强度,d(∫E·dA)/dt表示时间的变化率。
第三个方程是安培定律,它描述了环路中通过的电流对磁场产生的影响。
数学上可以表示为:∮B·dl = μ0I其中,∮B·dl表示磁场在环路l上的线积分,μ0为真空中的磁导率,I为环路中的电流强度。
最后一个方程是法拉第电磁感应定律的推广形式,也被称为麦克斯韦-安培定律。
它描述了变化的电场对磁场产生的影响,以及变化的磁场对电场产生的影响。
数学上可以表示为:∮E·dl = - d(∫B·dA)/dt其中,∮E·dl表示电场在环路l上的线积分,∮B·dA表示磁场通过闭合曲面的通量,d(∫B·dA)/dt表示时间的变化率。
麦克斯韦方程组是电磁学的基础,它描述了电荷和电流对电磁场产生的影响,以及电场和磁场对电荷和电流产生的影响。
通过这四个方程,我们可以推导出电磁波的存在和传播,解释电磁感应现象,研究电磁场的性质。
麦克斯韦方程组的研究也对电磁学的发展做出了巨大的贡献。
麦克斯韦方程组的理论和实验研究为电磁学的发展奠定了基础。
物理数学中10个最伟大公式

10个最伟大公式10 Greatest Formulae英国科学期刊《物理世界》曾让读者投票评选了“最伟大的公式”,最终榜上有名的十个公式既有无人不知的1+1=2,又有著名的E=mc2;既有简单的圆周公式,又有复杂的欧拉公式……这些公式美丽而精妙,这个地球上有多少伟大的智慧曾耗尽一生,才最终写下一个等号。
每当你解不开方程的时候,不妨换一个角度想,你正在见证的,是科学的美丽与人类的尊严。
让我们一起来看看这十个公式,你认识几个呢?No.10 圆的周长公式The Length of the Circumference of a CircleCπ=2r这个公式虽然简单,但却蕴含着深刻的智慧。
任何圆——不论大小——用它的周长比上直径,一定得到一个常数π。
你别小看圆周率π。
众所π是一个无限不循环小数,也是数学中最重要的常数周知,...=1415926.3之一。
许多数学家终其一生, 才能将圆周率计算到小数点后几十位. 而目前人类制造的超级计算机已经能得到圆周率的30万亿位,却仍然没有找到任何循环的迹象。
No.9 傅立叶变换The Fourier Transform[]dte tf t f F F t i ωω-∞∞-⎰== )()()(傅里叶变换是一种特殊的积分变换。
虽然这个公式复杂难懂,但是它在物理学、电子类科学、信号处理、统计学、密码学、声学、光学、海洋学等领域都有着广泛的应用。
另外,没有这个公式,就没有今天的电子计算机。
因此,你今天能够享受网上冲浪带来的乐趣,除了要感谢党和政府, 还要感谢傅里叶。
No.8德布罗意方程组The de Broglie Relationsp=ħk=h/λE=ħw=hv'这个方程组不仅指出了微观粒子波长和动量的关系,频率和能量的关系,还表明了粒子具有“波粒二象性”,彻底颠覆了牛顿的光粒子说,还否定了光的波动说。
德布罗意凭借这一发现荣获了1929年诺贝尔物理学奖。
No.71+1=2是不是感觉这个公式很简单? 然而,这个式子也有着深刻的含义。
物理学界最NB的十大方程

英国科学期刊《物理世界》曾让读者投票评选了“最伟大的公式”,最终榜上有名的十个公式既有无人不知的1+1=2,又有著名的E=mc2;既有简单的-圆周公式,又有复杂的欧拉公式……从什么时候起我们开始厌恶数学?这些东西原本如此美丽,如此精妙。
这个地球上有多少伟大的智慧曾耗尽一生,才最终写下一个等号。
每当你解不开方程的时候,不妨换一个角度想,暂且放下对理科的厌恶和对考试的痛恨。
因为你正在见证的,是科学的美丽与人类的尊严。
No.10 圆的周长公式(The Length of the Circumference of a Circle)圆的周长公式(The Length of the Circumference of a Circle).png这公式贼牛逼了,初中学到现在。
目前,人类已经能得到圆周率的2061亿位精度。
还是挺无聊的。
现代科技领域使用的-圆周率值,有十几位已经足够了。
如果用35位精度的-圆周率值,来计算一个能把太阳系包起来的一个圆的周长,误差还不到质子直径的百万分之一。
现在的人计算圆周率,多数是为了验证计算机的计算能力,还有就是为了兴趣。
No.9 傅立叶变换(The Fourier Transform)傅立叶变换(The Fourier Transform).png这个挺专业的,一般人完全不明白。
不多作解释。
简要地说没有这个式子没有今天的电子计算机(这个说法有待大家证实),所以你能在这里上网除了感谢党感谢政府还要感谢这个完全看不懂的式子。
另外傅立叶虽然姓傅,但是法国人。
No.8 德布罗意方程组(The de Broglie Relations)这个东西也挺牛逼的,高中物理学到光学的话很多概念跟它是远亲。
简要地说德布罗意这人觉得电子不仅是一个粒子,也是一种波,它还有“波长”。
于是搞啊搞就有了这个物质波方程,表达了波长、能量等等之间的关系。
同时他获得了1929年诺贝尔物理学奖。
No.7 1+1=2这个公式不需要名称,不需要翻译,不需要解释。
世界上最伟大的十大公式

世界上最伟大的十大公式1. 欧拉公式(Euler's formula):e^(iπ) + 1 = 0。
2. 相对论的质能方程(E=mc^2):能量和质量间的等价关系。
阐述了质量和能量之间的相互转化关系,揭示了相对论中的重要概念,改变了人们对能量和物质本质的理解。
3. 波尔兹曼熵公式(Boltzmann's entropy formula):S = k *ln(W)。
描述了热力学中的熵(entropy)概念,将微观粒子的状态数与系统的熵关联起来,阐明了熵作为热力学量的重要性。
4. 麦克斯韦方程组(Maxwell's equations):电磁场理论的基础。
5. 傅里叶变换(Fourier transform):信号处理和频谱分析的基础。
将时间域的信号转换为频域表示,使得我们可以更好地理解和处理各种周期性和非周期性信号。
6. 黑-斯科尔定律(Black-Scholes formula):金融选项定价模型。
这个公式描述了金融市场中期权(options)的评估和定价,为金融学和投资领域提供了重要的工具和理论基础。
7. 广义相对论场方程(Einstein field equations):描述引力场的方程。
描述了引力场的形成和演化,揭示了时空的弯曲和质量-能量分布之间的关系,极大地推动了现代宇宙学和天体物理学的发展。
8. 热力学第二定律(Second law of thermodynamics):熵的增加性原理。
说明了自然系统总是趋向于熵增加的状态,解释了各种热力学现象和自然过程中的方向性和不可逆性。
9. 斯特克斯-爱尔德方程(Navier-Stokes equations):流体力学的基本方程。
描述了流体的运动和流动规律,为理解和研究气体和液体的流动性质提供了关键的工具和方程。
10. 黄金分割(Golden Ratio):数学中的神秘与美感。
这个公式描述了两个分割比例之间的关系,被广泛应用于艺术、建筑、设计和自然界中,赋予各种事物以和谐和美感。
世界10大公式

世界10大公式一、麦克斯韦方程组(电磁学)1. 公式内容。
- 积分形式:- ∮_S →D· d→S=∫_Vρ dV(高斯定律,表示通过任意闭合曲面的电位移通量等于该闭合曲面所包围的自由电荷的代数和)。
- ∮_S →B· d→S = 0(高斯磁定律,表明通过任意闭合曲面的磁通量恒为零,即磁场是无源场)。
- ∮_L→E· d→l=-(d)/(dt)∫_S→B· d→S(法拉第电磁感应定律,感应电动势与磁通量变化率的关系)。
- ∮_L→H· d→l=∫_S(→J+(∂→D)/(∂ t))· d→S(安培 - 麦克斯韦定律,磁场强度沿闭合回路的线积分等于穿过该回路所限定面积的全电流)。
- 微分形式:- ∇·→D=ρ- ∇·→B = 0- ∇×→E=-(∂→B)/(∂ t)- ∇×→H=→J+(∂→D)/(∂ t)2. 意义。
- 它统一了电学和磁学,揭示了电场和磁场之间的相互联系、相互转化的规律。
麦克斯韦方程组的建立是经典电磁学理论的集大成者,并且预言了电磁波的存在,为现代通信、电子技术等众多领域奠定了理论基础。
- 在高中物理选修3 - 4中会初步涉及电磁感应现象(法拉第电磁感应定律部分内容),在大学物理教材(如电磁学部分)会详细讲解麦克斯韦方程组的积分形式和微分形式。
二、欧拉公式(复变函数等多领域)1. 公式内容。
- e^iθ=cosθ + isinθ,当θ=π时,有著名的等式e^iπ+1 = 0。
2. 意义。
- 它将数学中最重要的几个常数e(自然对数的底数)、i(虚数单位)、π(圆周率)、1(自然数的基本单位)和0(代表无或起点等多种数学概念)联系在一起,体现了数学的简洁性和统一性。
在复变函数、信号处理、量子力学等众多领域有着广泛的应用。
3. 在人教版教材中的体现。
- 在高中数学选修2 - 2中会简单介绍复数的概念,在大学的复变函数教材中会深入讲解欧拉公式及其应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
世界第一公式:麦克斯韦方程组麦克斯韦方程组,是英国物理学家詹姆斯·麦克斯韦在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。
从麦克斯韦方程组,可以推论出光波是电磁波。
麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。
从这些基础方程的相关理论,发展出现代的电力科技与电子科技。
麦克斯韦1865年提出的最初形式的方程组由20个等式和20个变量组成。
他在1873年尝试用四元数来表达,但未成功。
现在所使用的数学形式是奥利弗·赫维赛德和约西亚·吉布斯于1884年以矢量分析的形式重新表达的。
在英国科学期刊《物理世界》发起的“最伟大公式”中,麦克斯韦方程组力压勾股定理,质能转换公式,名列第一。
这里,不细谈任何具体的推导和数学关系,纯粹挥挥手扯扯淡地说一说电磁学里的概念和思想。
1力、能、场、势经典物理研究的一个重要对象就是力force。
比如牛顿力学的核心就是F=ma这个公式,剩下的什么平抛圆周简谐运动都可以用这货加上微积分推出来。
但是力有一点不好,它是个向量vector(既有大小又有方向),所以即便是简单的受力分析,想解出运动方程却难得要死。
很多时候,从能量的角度出发反而问题会变得简单很多。
能量energy说到底就是力在空间上的积分(能量=功=力×距离),所以和力是有紧密联系的,而且能量是个标量scalar,加减乘除十分方便。
分析力学中的拉格朗日力学和哈密顿力学就绕开了力,从能量出发,算运动方程比牛顿力学要简便得多。
在电磁学里,我们通过力定义出了场field的概念。
我们注意到洛仑兹力总有着F=q(E+v×B)的形式,具体不谈,单看这个公式就会发现力和电荷(或电荷×速度)程正比。
那么我们便可以刨去电荷(或电荷×速度)的部分,仅仅看剩下的这个“系数”有着怎样的动力学性质。
也就是说,场是某种遍布在空间中的东西,当电荷置于场中时便会受力。
具体到两个电荷间的库仑力的例子,就可以理解为一个电荷制造了电场,而另一个电荷在这个电场中受到了力,反之亦然。
类似地我们也可以对能量做相同的事情,刨去能量中的电荷(或电荷×速度),剩下的部分便是势potential。
一张图表明关系:积分力--->能||场<---势微分具体需要指出,这里的电场(标为E)和磁场(标为B)都是向量场,也就是说空间中每一个点都对应着一个向量。
如果我们把xyz三个分量分开来看的话,这就是三个标量场。
而能量和势是标量(电磁学中的势其实并不是标量,原因马上揭晓),放到空间中也就是一个标量场。
在力/场和能量/势之间互相转化的时候,我们是在31个标量场之间转化,必然有一些信息是丢掉了的。
怎么办?一个显而易见的答案是“保守力场”conservative force field。
在这样一个场中,能量(做功)不取决于你选择什么样的路径。
打个比方,你爬一座山,无论选择什么路径,只要起点和终点一样,那么垂直方向上的差别都是一样的,做的功也一样多。
在这种情况下,我们对力场有了诸多限制,也就是说,我假如知道了一个保守力场的x一个分量,那么另两个分量yz就随之确定了,我没得选(自由度其实只有一个标量场)。
有了保守力场这样的额外限制,向量场F(3个标量场)和(1个)标量场V之间的转化便不会失去信息了。
具体而言,二者关系可以写作F=-?V。
这里不说具体细节,你只要知道?是一种固定的、把一个标量场变成三个标量场的算法就可以了(叫做算符operator)。
那么我们想问,电场和磁场是不是保守力场呢?很不幸,不是。
在静电学中,静止的电场是保守的,但在电动力学中,只要有变化的电场和磁场,电场就不是一个保守力场了;而磁场从来都不是保守力场。
这也就是说明,在电磁学中,我们很少涉及能量这个概念,因为它不能完整地描述一个电磁场。
我们更多时候只关注“场”这个概念,尽管因此我们不得不涉足很多向量微积分,但我们没有办法,这是不让信息丢掉的唯一办法。
那么,既然势也是标量,它是否也是一个没什么用的概念呢?恰恰相反,在电动力学中我们定义出了“向量势”vector potential,以保留额外的自由度。
后面我会更具体地谈到这一点。
总而言之,我想说明一点,那就是电磁学的主要研究对象是电场和磁场,而麦克斯韦方程组就是描述电场和磁场的方程。
势(包括电势和磁向量势)也是有用的概念,而且不像引力势是一个标量,在电磁学中势不得不变成一个向量。
2麦克斯韦方程组前边说到,麦克斯韦方程组Maxwell equations是描述电场和磁场的方程。
前边也说到,因为电磁场不是保守力场,它们有三个标量场的自由度,所以我们必须用向量微积分来描述电磁场。
因此,麦克斯韦方程组每个式子都出现了向量微积分,而整个方程组也有积分形式和微分形式两种。
这两种形式是完全等价的,只是两种不同的写法。
这里我先全部写出。
积分形式:微分形式:这里E表示电场,B表示磁场,ε0和μ0只是两个常数暂时可以忽略。
积分形式中Q是电荷,I是电流,V表示一块体积,?V表示它的表面,而S表示一块曲面,?S 表示它的边缘。
微分形式中ρ是电荷密度(电荷/体积),J 是电流密度(电流/面积),?·和?×是两个不同的算符,基本可以理解为对向量的某种微分。
先不说任何细节,我们可以观察一下等式的左边。
四个方程中,两个是关于电场E的,两个是关于磁场B的;两个是曲面积分∫da或者散度?·,两个是曲线积分∫dl或者旋度?×。
不要管这些术语都是什么意思,我后面会讲到。
但光看等式左边,我们就能看出四个式子分别描述电场和磁场的两个东西,非常对称。
3电荷->电场,电流->磁场这一部分和下一部分中,我来简单讲解四个式子分别代表什么意思,而不涉及任何定量和具体的计算。
我们从两个电荷之间的库仑力讲起。
库仑定律Coulomb's Law是电学中大家接触到的最早的定律,有如下形式:其中Q是电荷,r是电荷之间的距离,r是表示方向的单位向量。
像我之前说的,把其中一个电荷当作来源,然后刨去另一个电荷,就可以得到电场的表达式。
高中里应该还学过安培定律Ampere's Law,也就是电流产生磁场的定律。
虽然没有学过具体表达式,但我们已经能看出它与库仑定律之间的区别。
库仑定律描述了“两个”微小来源(电荷)之间的“力”,而安培定律是描述了“一个”来源(电流)产生的“场”。
事实上,电磁学中也有磁场版本的库仑定律,描述了两个微小电流之间的力,叫做毕奥-萨伐尔定律Biot-Savart Law;反之,也有电场版本的安培定律,描述了一个电荷产生的磁场,叫做高斯定律Gauss's Law。
这四个定律之间有如下关系:电场磁场两个微小来源之间的力库仑定律毕奥-萨伐尔定律单个来源产生的场高斯定律安培定律数学上可以证明库仑定律(毕奥-萨伐尔定律)和高斯定律(安培定律)在静电学(静磁学)中是完全等价的,也就是说我们可以任意假设一个定律,从而推导出另一个定律。
然而如果我们想从静止的静电学和静磁学推广到电动力学,前者是非常不便的而后者很却容易,所以尽管库仑定律在中学中常常提到,麦克斯韦方程组中却没有它,有的是高斯定律和安培定律。
这两个定律分别是麦克斯韦方程组里的(1)和(4)的第一项,即:高斯定律(积分、微分形式):安培定律(积分、微分形式):我们继续推迟讲解数学关系,单看这几个式子本身,就能看到等式的左边有电场E(磁场B),而右边有电荷Q(电流I)或电荷密度ρ(电流密度J)。
看,电荷产生电场,电流产生磁场!4变化磁场->电场,变化磁场->电场然而这不是故事的全部,因为事实上电磁场是可以互相转化的。
法拉第发现了电磁感应,也就是说变化的磁场是可以产生电场的,这就是法拉第定律Faraday's Law。
类似地,麦克斯韦发现安培定律的描述并不完善,除了电流以外,变化的电场也可以产生磁场,这被称为安培-麦克斯韦定律Ampere-Maxwell Law。
这两个定律分别是麦克斯韦方程组里的(2)和(4)的第二项,即:法拉第定律(积分、微分形式):安培-麦克斯韦定律(积分、微分形式):同样地,等式的左边有电场E(磁场B),而右边有磁场B (电场E)的导数d/dt或偏导?/?t。
看,变化磁场产生电场,变化电场产生磁场!需要指出的是,我这样的说法其实是不准确的,因为并不是真的某一个场“产生”的另一个场。
这两个定律只是描述了电场(磁场)和磁场(电场)的变化率之间的定量关系,而不是因果关系。
小结一下,我们已经搞清楚了麦克斯韦方程组里每一项的意思,基本就是指出了电磁场的来源和变化电磁场的定量关系。
下一步便是往我们这些粗浅的理解中加入数学,具体看看这些方程到底说了什么。
在这之前,我们必须花一点时间了解一下向量微积分的皮毛。
5向量积分普通的单变量微积分基本可以理解为乘法的一种拓展。
我们想计算一个矩形的面积,我们用长x乘宽y,即xy。
如果宽不是一个定值而是根据长而变化的(也就是说宽是一个长的函数,即宽=y(x)),那么我们就需要积分,记为“∫y(x)dx”。
这样的想法也很容易推广到更高的维度,比如在一块体积V 内,若电荷密度为ρ,那么这块体积内的总电荷就是Q=ρV;如果ρ在空间中每一点都不一样,是个关于坐标的函数ρ(x),那么就要变成积分Q=∫∫∫ρ(x)dV(这里三个∫表示是一个三维的积分,很多时候也可以省略写为一个∫)。
在向量场中,这个事情比较麻烦。
首先两个向量的乘积的定义稍显复杂,必须使用点乘dot product,即u·v,它暗示着两个向量之间的角度,也就是有多么平行。
如果u和v完全平行,它们的点乘是一个正值;如果方向相反,则是一个负值;如果垂直,那么为0。
另一方面,我们不一定要像上一个电荷的例子一样积上整个体积V,我们可以只积一个曲面S或者一条曲线γ。
这就是所谓的曲面积分和曲线积分的概念。
曲面积分surface integral有如下形式:其中S表示我们需要积的曲面,F是我们想要积的向量场,·代表点乘,a指向垂直于S的方向。
因此,我们看到,如果F和S是平行的,那么点乘处处得0,这个曲面积分也为0。
换句话说,曲面积分表示着向量场F穿过曲面S的程度,因此也很形象地叫做通量flux。
下图为两个简单的例子(虚线----表示曲面所在的位置):曲面积分(通量)为0:→→→→→--------------------→→→→→曲面积分(通量)不为0:↑↑↑↑↑↑↑↑--------------------↑↑↑↑↑↑↑↑那么曲线积分line integral也很类似,只不过我们不积一个曲面S而是一个一维的曲线γ。
它有如下形式:其中γ表示我们需要积的曲线,·代表点乘,l指向曲线γ的方向。
