断裂力学期末考试题目及答案B卷 - 哈工大2008年秋季学期
《工程力学C》B卷附答案
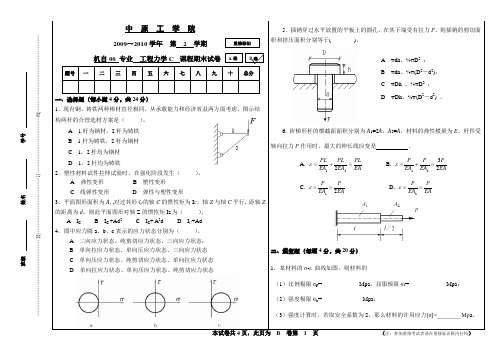
P m
T /Nmm
m 180P
M /Nmm
200P
故:
(3 分)
(3)最大剪应力值
; min 65 0 112 .5 。(3 分)
x
(3 分) 六、计算题(10 分) 解:(1)求支座反力:RA=2.5kN, RB=10.5kN
x
(1 分)
本试卷答案共 2 页,此页为第 1 页
(2)求危险截面
(3 分)
Q =30kN max
M =15kNm max
(2 分) (2 分)
(2)主应力值及主方向
(3 分)
四、计算题(15 分) 解:(1)外力:
扭转 m 180P Nmm 弯曲 P
(4 分)
(2)内力:
扭矩 T 180P Nmm
弯矩
M max
Pl 4
200PNmm
(4 分)
试校核此梁的强度。
本试卷共 4 页,此页为 B 卷第 4 页
姓名
班级
中原工学院
2009~2010 学年 第 2 学期
B卷
机自 08 专业 工程力学 C 课程期末试卷标准答案(即评分标准)
一、选择题(每小题 4 分,共计 24 分) 1.A 2.D 3.B 4.C
二、填空题(每题 4 分,共 20 分)
题1图
2.GIp 称为
,反映了圆轴抵抗扭转变形的能力。若一根空
心圆轴的外径为 D,内径为 d( D 2d ),则其抗扭截面模量Wp 为
。
3.刚性杆 AB 的左端铰支,1、2 两杆为长度相等、横截面面积相等的等直杆,
其弹性模量分别为 E1 和 E2,且有 E1=2E2,求两根拉杆的内力时,相应的变形协调
断裂力学试题

17.疲劳长裂纹扩展的规律和机理? 答:扩展速率受控于裂纹尖端的应力强度因子范围ΔK,ΔK=Kmax-Kmin;
随着应力比增大,疲劳裂纹扩展速率增大,疲劳门槛值减小。 组织对 Paris 区的 da/dN 影响不大, 而对门槛值区有较大影响。 18.分析疲劳断口的组成与影响因素; 答: (1) 疲劳断口的组成:一个典型的疲劳断口总是由疲劳源、疲劳裂纹扩展 区和最终断裂区三部分构成。 (2)影响因素:平均应力(拉伸平均应力降低疲劳强度,压缩平均应力提高疲 劳强度) 、表面加工与处理(疲劳裂纹通常起始于零件表面,因此,表面状况对 疲劳寿命有很大的影响,表面光洁度越高,形成疲劳裂纹的时间越长) 、加载型 式、缺口与应力集中、试样的尺寸。 19.分析疲劳应力应变曲线的特点;
e ae p
J J ae J
答: (1)在线弹性条件下,这三个参量可以互相替换,它们各自的断裂判据都是等效的,对 I 1 型裂纹: J K I2 GI E E E 1 2 E E 其中,平面应力: ;平面应变 : (2)在弹塑性条件下,应力强度因子已不在适用,主要是运用 J 积分和 COD 参量。在大范围 屈服的情况下二者之间的关系(采用 D-M 模型): J s ;考虑到实际材料,工程中可以 对其进行修正:J k
断裂力学复习要点与习题解析

此时 K1 < ;设计可行。
若设计护板材料受拉伸a应力皆为600 是否可行?
4103
4103
2021/1/4
22
例题6:
某构件由高强度钢板焊成,探伤发现在焊缝中
心存在一个20长的中心穿透裂纹。 残余应力测试
发现在裂纹周围存在残余应力场如图。最大残余应
力位于裂纹中心,其值为
,假如裂纹面上
的残余应力为直线型分布,材料的
● 所有的应力强度因子K都可以表示成什么形式?
● 平面应力情况下 与厚度有什么关系
●什么是能量(应变能)释放率G?能量释放率G与应力强度因子K有什么关系?
● S准则是怎样描述的? 与 K1c,K2c,K3c 有什么关系?
2021/1/4
3
S 准则假设为:
S 1、裂纹沿S最小的方向扩展,即由 确定开裂方向: m in
x r 1 0.02 0.6s
Kr0.6s2(a)0.5sin1a x0 a230s(a)0.5
2021/1/4
19
例题3
一高强钢 在380 ºC 回火, 在600 ºC 回火,
,
s 1 8 0 0 M P a,K 1 c ,5 0 M P am
假设这样处理的无限大板存在 单边裂s 纹 ,1 设5 0 计0 工M 作P 应a 力,K 为1 c 6 0 M P am
计算上述两种处理可以容许的临界裂纹尺寸为多少? 解:
,
在600 ºC 回火,
,
假设这样处理的无限大板存在 中心裂纹s1 ,1 设8 计0 0 工M 作P 应a 力,为K 1 c 5 0 M P am
计算那种处理可以满足要求?
s 1 5 0 0 M P a,K 1 c 6 0 M P am
第八章断裂力学习题及解

第八章 断裂力学习题及解习题1、已知I 型裂纹问题的应力函数为()()()z Z y z Z z I I I Im Re +=ϕ,其中()()z Z z Z I I ,分别为复变函数()z Z I 的二次积分和一次积分,试求出对应的应力分量。
解:令()()()y x iv y x u z Z I ,,+=,那么()udy v dx i v dy udx dz z Z CCC++-=⎰⎰⎰按C-R 条件有yux v y v x u ∂∂-=∂∂∂∂=∂∂,。
那么有如下关系式 y Zx Z Z ∂∂=∂∂='Im Re Re , xZy Z Z ∂∂=∂∂-='Im Re Im , 由应力函数可得应力()⎪⎪⎭⎫ ⎝⎛+∂∂+∂∂∂∂=+∂∂=∂∂=I I I I I 222I 2xx Z y Z y y Z y Z y Z y y σIm Im Re Im Re ϕ ()'Im Re Re Re Im Re Im I I I I I I I xx Z y Z Z yZ y Z Z y Z y -=+∂∂=++-∂∂=σ ()⎪⎪⎭⎫⎝⎛∂∂+∂∂∂∂=+∂∂=∂∂=x Z y xZ x Z y Z x x σI I I I 222I 2yyIm Re Im Re ϕ得 ()'Im Re Im Re I I I I yy Z y Z Z y Z x+=+∂∂=σ ()⎪⎪⎭⎫ ⎝⎛-∂∂-∂∂-∂∂=⎥⎦⎤⎢⎣⎡+∂∂-∂∂=∂∂∂-=I I I I I I 2xyZ y Z y y Z x Z y Z y x y x Im Im Re Im Re ϕτ ()'Re Re Im Re Im I I I I I xy Z y xZ y Z Z y Z x -=∂∂-=--∂∂=τ 习题2、如图8-1所示无限大板中含有一长度为2a 的中心贯穿裂纹,设I 型裂纹问题的应力函数为()()()z Z y z Z z I I I Im Re +=ϕ(双向拉伸),或为()()())(2Im Re 22y x A z Z y z Z z I I I --+=ϕ(单向拉伸)。
(完整版)断裂力学试题

一、简答题(本大题共5小题,每小题6分,总计30分)1、(1)数学分析法:复变函数法、积分变换;(2)近似计算法:边界配置法、有限元法;(3)实验标定法:柔度标定法;(4)实验应力分析法:光弹性法.2、假定:(1)裂纹初始扩展沿着周向正应力为最大的方向;(2)当这个方向上的周向正应力的最大值()max达到临界时,裂纹开始扩展•S3、应变能密度:W S,其中S为应变能密度因子,表示裂纹尖端附近应力场r密度切的强弱程度。
4、当应力强度因子幅值小于某值时,裂纹不扩展,该值称为门槛值。
5、表观启裂韧度,条件启裂韧度,启裂韧度。
二、推导题(本大题10分)D-B模型为弹性化模型,带状塑性区为广大弹性区所包围,满足积分守恒的诸条件。
积分路径:塑性区边界。
AB 上:平行于x1,有dx2 0 , ds dx1 , T22007断裂力学考试试题B卷答案BD上:平行于捲,有dx20 , ds dx1 , T2u iJ (Wdx2 T L ds)s V s V S(V A三、计算题(本大题共1、利用叠加原理:微段K]ABT2 V D)3小题,每小题集中力qdx U2dx1%BDT2U£dx1X120分,dK]总计60分)a 2q . a0 (2 2.(a x ) dx 10分sin cos — a cos sin a2b 2b 2b 2b— cos — a sin a 2b 2b2b(_ 2 2)cos — 2b a 2 cos a si n a2b2b 2b 2ba)2la sin 1(豎)a cosK i2qJ — 0 赢T d 当整个表面受均布载荷时,6 a .2、边界条件是周期的:a.zy0, xy 0c.所有裂纹前端又Z 应为2b 的周期函数si2z皿2冷 采用新坐标: z aZ % a)J (sin 七严2陶)20 时,sin —— ——,cos —2b 2b 2bK i 2qsin 1(a a ) q a10分令 x acos 一 a 2 x 2 a cosb.在所有裂纹内部应力为零.y0,x a, a 2b x a2b 在区间内单个裂纹时Zz z 2 a 210分d(sin -2b[吃(加sin ( a)2ba sin2b .2 a . a」 --------- cos——sin 】2b 2b0时,2 2帥莎(a)] (s^a)22b cos asin a 2b2b2bK I1吧0 F_Zsin2b1 a . a ——cos——sin —2b2b 2b2b ta n—a2ba tan—2b 10分注意行为规范3、当复杂应力状态下的形状改变能密度等于单向拉伸屈服时的形状改变能密度,材料屈服,即:2 2 2 2(1 2 ) ( 2 3) ( 3 1 ) 2 s对于I型裂纹的应力公式:(X2y)2xy1Kl cos-[1 sin-]2 2 r 2 2遵考场10分纪程•律0(平面应力,薄板或厚板表面)K I22scos2[1 3sin2—]2 2--平面应力下,I型裂纹前端屈服区域的边界方10分r、简答题1.断裂力学中, (80 分)按裂纹受力情况,裂纹可以分为几种类型?请画出这些类型裂纹的受力示意图。
哈尔滨工业大学历年材料力学试题及答案

哈尔滨工业大学学年第二学期材料力学试题(A 卷)一、 选择题(20分)1、图示刚性梁AB 由杆1和杆2支承,已知两杆的材料相同,长度不等,横截面积分别为A 1和A 2,若载荷P 使刚梁平行下移,则其横截面面积( )。
A 、A 1〈A 2B 、A 1 〉A 2C 、A 1=A 2D 、A 1、A 2为任意2、建立圆周的扭转应力公式τρ=M ρρ/I ρ时需考虑下列因素中的哪几个?答:( ) (1) 扭矩M T 与剪应力τρ的关系M T =∫A τρρdA (2) 变形的几何关系(即变形协调条件) (3) 剪切虎克定律(4) 极惯性矩的关系式I T =∫A ρ2dAA 、(1)B 、(1)(2)C 、(1)(2)(3)D 、全部 3、二向应力状态如图所示,其最大主应力σ1=( ) A 、σ B 、2σ C 、3σ D 、4σ4、高度等于宽度两倍(h=2b)的矩形截面梁,承受垂直方向的载荷,若仅将竖放截面改为平放截面,其它条件都不变,则梁的强度( )A 、提高到原来的2倍B 、提高到原来的4倍C 、降低到原来的1/2倍D 、降低到原来的1/4倍5. 已知图示二梁的抗弯截面刚度EI 相同,若二者自由端的挠度相等,则P 1/P 2=( ) A 、2 B 、4 C 、8 D 、16二、作图示梁的剪力图、弯矩图。
(15分) 题 号 一 二 三 四 五 六 总分 得 分题一、3图工程技术学院 _______________专业 班级 姓名____________ 学号---------------------------------------------------密 封 线 内 不 准 答 题-------------------------------------------------------------题一、5图题一、4题一、1图三、如图所示直径为d 的圆截面轴,其两端承受扭转力偶矩m 的作用。
设由实验测的轴表面上与轴线成450方向的正应变,试求力偶矩m 之值、材料的弹性常数E 、μ均为已知。
(完整版)断裂力学复习题(实际)解答(课件)
断裂力学复习题1.裂纹按几何特征可分为三类,分别是(穿透裂纹)、(表面裂纹)和(深埋裂纹)。
按力学特征也可分为三类,分别是(张开型)、(滑开型)和(撕开型)。
2.应力强度因子是与(外载性质)、(裂纹)及(裂纹弹性体几何形状)等因素有关的一个量。
材料的断裂韧度则是(应力强度因子)的临界值,是通过(实验)测定的材料常数。
3.确定应力强度因子的方法有:(解析法),(数值法),(实测法)。
4.受二向均匀拉应力作用的“无限大”平板,具有长度为2a 的中心贯穿裂纹,求应力强度因子ⅠK 的表达式。
【解】将x 坐标系取在裂纹面上,坐标原点取在裂纹中心,则上图所示问题的边界条件为:① 当y = 0,x → ∞时,σσσ==y x ;② 在y = 0,a x <的裂纹自由面上,0,0==xy y τσ;而在a x >时,随a x →,∞→y σ。
可以验证,完全满足该问题的全部边界条件的解析函数为22Ⅰ )(a z z z Z -=σ (1) 将坐标原点从裂纹中心移到裂纹右尖端处,则有z =ζ+a 或ζ= z -a ,代入(1),可得:)2()()(I a a Z ++=ζζζσζ于是有:aa a a a K πσζζσπζζζσπζζζ=++⋅=++⋅=→→)2()(2lim )2()(2lim 00Ⅰ5.对图示“无限大”平板Ⅱ型裂纹问题,求应力强度因子ⅡK 的表达式。
【解】将x 坐标系取在裂纹面上,坐标原点取在裂纹中心,则上图所示问题的边界条件为:① 当y = 0,x → ∞时,ττσσ===xy y x ,0;② 在y = 0,a x <的裂纹自由面上,0,0==xy y τσ;而在a x >时,随a x →,∞→xy τ。
可以验证,完全满足该问题的全部边界条件的解析函数为22Ⅱ )(a z z z Z -=τ (1) 将坐标原点从裂纹中心移到裂纹右尖端处,则有z =ζ+a 或ζ= z -a ,代入(1),可得: )2()()(Ⅱa a Z ++=ζζζτζ 于是有:a a a a a K πτζζτπζζζτπζζζ=++⋅=++⋅=→→)2()(2lim )2()(2lim 00Ⅱ6.对图示“无限大”平板Ⅲ型裂纹问题,求应力强度因子ⅢK 的表达式。
哈尔滨工业大学期末考试试题(B卷)
哈工大2002年春季学期题号-一--二二三四五六七八九附加分总分得分班级姓名一、单选或多选题(每小题3分,共8小题24分)1.某点为平面应力状态(如图所示),该点的主应力分别为A = 50MPa、二2 =0 、3=° -B二50MPa、二2=50 MPa、匚3= 0;C -1 =0、匚 2 二50 MPa、■T 3 = 0 -D -1 =0、二2 = 0、-3 : "50MPa。
正确答案是___________50er (MPtL)2.关于弹性体受力后某一方向的应力与应变关系有如下论述: 正确的是。
A 有应力一定有应变,有应变不一定有应力;B 有应力不一定有应变,有应变不一定有应力;C 有应力不一定有应变,有应变一定有应力;D 有应力一定有应变,有应变一定有应力。
3•下面有关体积应变的几个论述,正确的是________________A 与平均应力成正比;B与平均应力成反比;C与三个相垂直面上的正应力之和有关;D与平均应力无关。
4.下面有关应变能的几个论述,正确的是A与载荷的加载次序有关,与载荷的最终值无关;B与载荷的加载次序无关,与载荷的最终值无关;C与载荷的加载次序有关,与载荷的最终值有关;D 与载荷的加载次序无关,与载荷的最终值有关。
5•关于斜弯曲变形的下述说法,正确的是_________________A中性层与挠曲线所在的面正交;B中性轴过横截面的形心;C挠曲线在载荷作用面内;D挠曲线不在载荷作用面内。
A 单位力(广义)只能加在载荷作用点处;B单位力(广义)只能加在欲求位移的点处;C只能加单位集中力;D 只能加单位集中力偶。
正确的是_____________ 。
7 •压杆的稳定性,A 与压杆所承受的轴向压力大小有关;B与压杆的临界力大小有关;C 与压杆所承受的轴向压力大小无关;D 与压杆的临界力大小无关。
正确答案是___________& 自由落体冲击时的动荷系数,A 与被冲击物的刚度有关;B与自由落体下落的高度有关;C 与被冲击物的刚度无关;D 与冲击刚发生时,自由落体下落的速度有关。
哈尔滨工业大学理论力学试卷B卷答案
2005-2006学年第 一 学期期 终 考试试卷审批表一、填空题(每空1分,共10分)1.在静力学中主要研究三方面问题,即物体的受力分析、 力系的简化 、力系的平衡方程。
2.平面任意力系平衡方程可用三矩式表示,即,,0)(=∑F A M 0)(=∑F B M ,其中力系平衡的附加条件是 A 、B 、C 三点不共线 。
0)(=∑F CM3.点作圆周运动,加速度由切向加速度和法向加速度组成,其中切向加速度反映了 速度的大小随时间的变化率,方向是 该点的切线方向 ;法向加速度反映了 随时间的变化率,方向是 该点的法线方向 。
4.质点运动微分方程自然坐标投影形式为,,。
∑=n F m ρυ2∑=τυF dtd m∑=bF0二、选择题(每题2分,共10分)1、A ,B 为某平面力系作用面内任意两点,该力系向A 点简化的结果是主矢和主'RA F 矩,向B 点简化的主矩为,则下述哪种结论是正确的:(A ,C)A MB M A .当时,必有 B . 当时,可能有0'=RAF B A M M =0'=RA F B A M M ≠C .当时,可能有 D . 当时,必有0'≠RAF B A M M =0'≠RA F B A M M ≠2、当物体处于临界平衡状态时,静摩擦力的大小( C )s F A .与物体的重量成正比B .与物体的重力在支承面的法线方向的大小成正比C .与相互接触物体之间的正压力大小成正比D .由力系的平衡方程来确定第2 页3、满足下述哪个条件的运动是刚体的平面运动(C)A .刚体运动时,其上某直线始终与其初始位置保持平行B .刚体运动时,其上某两条相交直线始终与各自初始位置保持平行C .刚体运动时,其上所有点到某固定平面的距离始终保持不变D .刚体运动时,其上每一点都在某固定平面上运动。
4、质点系动量定理的微分形式为,式中指的是( C )dt d e i ∑=)(F P dt e i )(∑F A .所有主动力的元冲量的矢量和 B .所有约束力的元冲量的矢量和C .所有外力的元冲量的矢量和 D .所有内力的元冲量的矢量和5、下列说法中正确的是( D )A .若质点的动量守恒,则该质点对任一定点的动量矩也一定守恒B .若质点对某定点的动量矩守恒,则其动量也一定守恒C .若质点动量发生变化,则其动能一定发生变化D .若质点的动能发生变化,则其动量也一定发生变化三、构架由ABC 、CDE 、BD 三杆组成,尺寸如图所示。
断裂力学试卷(答案)2009
华中科技大学土木工程与力学学院《断裂力学》考试卷(半开卷)2009~2010学年度第一学期 成绩学号 专业 班级 姓名 一、简述下列概念(20分)1. 裂纹顶端应力强度因子描述Ⅰ、Ⅱ、Ⅲ型裂纹问题裂纹尖端附近区域的应力解,可统一表示为:()12ij mij K r f m I ,II ,III σθ-⎛⎫== ⎪⎝⎭。
K m 为场强度参量,称为应力强度因子或K 因子。
它表征裂纹尖端区域应力场的强弱程度,决定于裂纹体的几何形状、裂纹的尺寸及载荷。
⑤2. 能量释放率A 0G lim A A δδ∏∏δ→∂⎛⎫=-=- ⎪∂⎝⎭, 裂纹扩展单位面积所消耗的总势能。
它表示裂纹扩展单位面积时,提供给裂纹扩展所需的系统释放的能量(系统势能的减少)。
G 取决于裂纹体的载荷和几何形状。
⑤3. COD裂纹尖端沿垂直于裂纹方向所产生的位移。
它是裂纹顶端塑性应变的度量。
⑤4. J 积分J 积分的回路积分定义为:()i 2i1u J W dx T ds i 1,2x Γ∂⎛⎫=-= ⎪∂⎝⎭⎰该积分与积分路径无关,是弹塑性断裂力学中一个十分重要的参数, 反映了裂尖的某种力学特征或应力、应变场强度。
⑤二、回答下列问题(20分)1.为什么平面应变状态裂纹尖端塑性区尺寸比平面应力状态小?当0θ= 时,它们的塑性区尺寸分别等于多少?答:在平面应变状态下,沿板厚方向(z 方向)的弹性约束使裂纹尖端材料处于三向拉应力作用下。
而三向拉伸应力状态会对塑性流动起约束作用,即不易发生塑性变形。
所以平面应变状态裂纹尖端塑性区尺寸比平面应力状态小。
④当0θ= 时,平面应力状态:220ey s 1K 1K R 2r I I ππσσ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ③平面应变状态:220ey s 1K 1K R 2r I I πσσ⎛⎫⎫=== ⎪⎪⎭⎝⎭ ③ or ()220s 1K R 2r 12I νπσ⎛⎫==- ⎪⎝⎭2.何为R 阻力曲线?在工程实际中有何作用?答:R 是塑性变形和表面能消耗的能量,是裂纹扩展的阻力,R 越大,裂纹扩展就越不容易。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈工大2008年秋季学期
《断裂力学》试题B卷答案
一、简答题(70分)
1. 请简述线弹性断裂力学中裂纹尖端应力场的特点?(15)
答:裂纹尖端应力场有如下三个特点:
1)0
r处,应力趋于无穷大,即在裂尖出现奇异点;
=
2)应力强度因子在裂尖为有限量;
3)裂尖附近的应力分布是r和θ的函数,与无限远处应力和裂纹长无关。
2. 简述裂纹扩展的能量平衡理论?(15分)
答:对完全脆性材料,应变能释放率等于形成新表面所需要吸收的能量率。
对于金属等有一定塑性的材料,裂纹扩展中,裂尖附近发生塑性变形,裂纹扩展释放出来的应变能,不仅用于形成新表面所吸收的表面能,更主要的是克服裂纹扩展所吸收的塑性变形能,即塑性功。
对金属材料,能量平衡理论这时需要更广泛的概念。
这时,抵抗裂纹扩展能力=表面能+塑性变形能,对金属材料这是常数。
3. 断裂力学中,按裂纹受力情况,裂纹可以分为几种类型?(10分)
答:按裂纹受力情况把裂纹(或断裂)模式分成三类:张开型(I型)、滑开型(II型)和撕开型(III型)。
4. 请简述疲劳破坏过程的几个阶段?(5)
答:1)裂纹成核阶段
2)微裂纹扩展阶段
3)宏观裂纹扩展阶段
4)断裂阶段
5.试简要说明断裂力学与材料力学设计思想的差别?(10分)
答:
断裂力学和材料力学的研究对象不同,材料力学研究完整的材料,而断裂力学则研究带裂纹的材料。
虽然断裂力学是材料力学的发展和补充,但是断裂力学与材料力学的设计思想不同,其差别可从一下几方面来看:
1)静载荷情况
传统的强度条件要求最大计算应力小于材料强度指标,即: s s
n σσ≤max (屈服),s σ为屈服应力
b b n σσ≤max (破坏),b σ为强度极限
而断裂力学的裂纹失稳准则是:n K K IC I ≤
I K -裂纹尖端的应力强度因子
2)循环载荷情况
传统的疲劳设计,是用光滑试件作S -N 曲线,求出下界限应力1-σ疲劳极限。
如果最大工作应力满足下式
1
1max --≤n σσ 1-n 为循环载荷下的安全系数,并认为凡是有缺陷的构件都不能应用。
断裂力学认为:含裂纹构件,只有裂纹未达到临界长度仍可使用;在循环载荷作
用下,裂纹先缓慢扩展,直至达到临界长度,构件才失稳破坏。
并选用指标dN
da ——作用载荷每循环一周裂纹的扩展量,代表材料抵抗裂纹扩展的能力。
3)腐蚀介质下的情况
综上所述,断裂力学出现后,对宏观断裂有了进一步认识,对传统设计思想进行了改善与补充。
二、 推导题(20分)
在I-II 复合型裂纹问题中,裂纹尖端附近周向应力场由下式给出
[]
cos(/2)(1cos )3sin I II K K θσθθθ=+-
请简述最大应力准则的基本假定,并根据基本假定推导出开裂角的表达式?
答:
最大应力准则的基本假定:
1)裂纹沿最大周向应力方向开裂;
2)在该方向上周应力达到临界值时,裂纹开始扩展。
根据该假定有,
0=∂∂θσθ, 02
2<∂∂θσθ
把[]θθπθ
σθsin 3)cos 1(222cos II I K K r -+=带入上面两式 并利用 1cos sin 22=+θθ,可求得开裂角的表达式
2222420983arccos II
I II I I II ++±=K K K K K K θ 对于纯I 型,0=II K ,00=θ,故根号前必须取正,则
2222420983arccos II
I II I I II +++=K K K K K K θ
三、 证明题(25分)
定义J 积分如下, (/)J wdy T u xds Γ
=-⋅∂∂⎰,围绕裂纹尖端的回路Γ,始于裂纹下表面,终于裂纹上表面,按逆时针方向转动,其中w 是板的应变能密度,T 为作用在路程边界上的力,u 是路程边界上的位移矢量,ds 是路程曲线的弧元素。
证明J 积分值与选择的积分路程无关,并说明J 积分的特点。
答:1)由弹性力学公式
ij i i n T σ=, 2,1,=j i
i n ——弧元素法线的方向余弦。
利用2dx dy =,1dx dx =,带入⎰Γ∂∂⋅-= )(ds x
u T wdy J
可以得到 ⎰Γ∂∂⋅-= 1
2)(ds x u n wdx J i ij i σ i u ——位移分量。
由图(1)可知,ds dx n /21=,ds dx n /12-=
所以有,ds n ds n dx j j 112.δ==
则, ds n x u w J j i ij j ⎰Γ∂∂⋅-= 1
1)(σδ 作一封闭曲线*Γ,分四段1Γ、2Γ、3Γ、4Γ,如图(2),故*Γ内无奇异点。
由格林公式:⎰⎰⎰∂∂-∂∂=+A s dx dx x Q x Q Qdx Pdx ))()(212
121 令0=Q ,同时ds n dx .21-=,ds n dx .12=,则格林公式可改写成
⎰⎰⎰∂∂=A j s j dA x P ds Pn 则线积分
dA x u x x w dA x u w x ds n x u w A i ij j i ij j A j j i ij j ⎰⎰⎰⎰⎰⎪⎪⎭
⎫ ⎝⎛∂∂⋅∂∂-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂⋅-∂∂=∂∂⋅-Γ)()(1111 11*σσδσδ (a ) 利用:ij ij
w σε=∂∂,)(21i j j i ij x u x u ∂∂+∂∂=ε及jji ij σσ= 可以推出 11111)()(21x u x x u x x u x u x x w x w i j ij i ij j i j j i ij ij ij ∂∂∂∂-∂∂∂∂=⎥⎥⎦
⎤⎢⎢⎣⎡∂∂+∂∂∂∂=∂∂∂∂=∂∂σσσεε 利用平衡方程0,=j ij σ,可得
)(1
1x u x x w i ij j ∂∂∂∂=∂∂σ 将上式带入(a)式,有
0)(* 11=∂∂⋅-⎰
Γds n x u w j i ij j σδ 即0)(* =∂∂⋅-=⎰Γds x
u T wdy J 注意到,04321* =+++=⎰⎰⎰⎰ΓΓΓΓΓJ
又因为在路径2Γ、4Γ上,0=dy ,且由于2Γ、4Γ是自由表面,0=T 则有,⎰⎰⎰-ΓΓΓ=-=331
所以积分路径与选择的路线无关。
2)J 积分的局限性主要有:
a )积分中使用了全量理论,ij ij
w σε=∂∂,因此不允许卸载; b )用到了)(21i
j j i ij x u x u ∂∂+∂∂=ε,因此必须是小变形; c )用到了0,=j ij σ,指系统处于静平衡状态。
