单因素完全随机设计的方差分析
方差分析公式总结 1
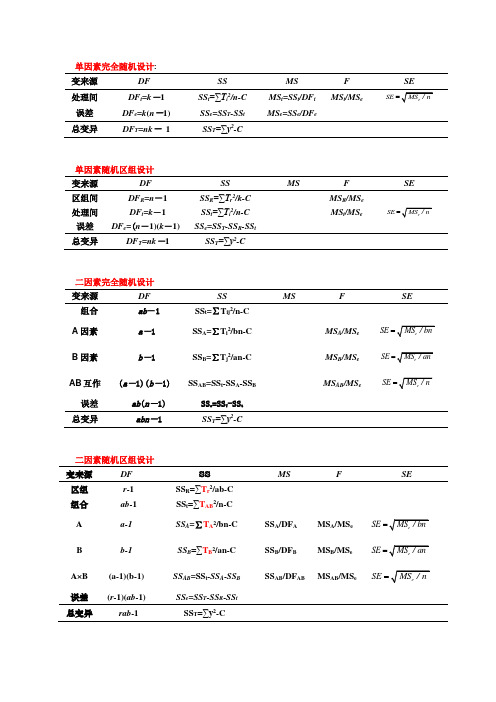
单因素完全随机设计:变来源DF SS MS F SE处理间DF t=k－1SS t=∑T i2/n-C MS t=SS t/DF t MS t/MS e SE误差DF e=k(n－1)SS e=SS T-SS t MS e=SS e/DF e总变异DF T=nk－1SS T=∑y2-C单因素随机区组设计变来源DF SS MS F SE 区组间DF R=n－1SS R=∑T r2/k-C MS R/MS e处理间DF t=k－1SS t=∑T i2/n-C MS t/MS e SE 误差DF e=(n－1)(k－1)SS e=SS T-SS R-SS t总变异DF T=nk－1SS T=∑y2-C二因素完全随机设计变来源DF SS MS F SE 组合 ab－1SS t=∑T ij2/n-CA因素 a－1SS A=∑T i2/bn-C MS A/MS e SE=B因素 b－1SS B=∑T j2/an-C MS B/MS e SEAB互作(a－1)(b－1) SS AB=SS t-SS A-SS B MS AB/MS e SE 误差 ab(n－1)SS e=SS T-SS t总变异 abn－1SS T=∑y2-C二因素随机区组设计变来源DF SS MS F SE 区组r-1SS=∑T r2/ab-CR组合ab-1SS=∑T AB2/n-CtA a-1 SS A=∑T A2/bn-C SS A/DF A MS A/MS e SE=B b-1 SS B=∑T B2/an-C SS B/DF B MS B/MS e SE=A×B (a-1)(b-1) SS AB=SS t-SS A-SS B SS AB/DF AB MS AB/MS e SE=误差(r-1)(ab-1) SS=SS T-SS R-SS te总变异rab-1SS=∑y2-CT裂区设计变异来源DF SS MS F SE 处理DFt=ab-1 SSt=∑T AB2/r-C主区部分区组DFR= r-1 SS R=∑T r2/ab-CA DFA= a-1 SS A=∑T A2/rb-C MS A F A=MS A/MS Ea误差a DFEa= (r-1)(a-1) SS Ea=SS M-SS R-SS A MS Ea主区总变异DF M= ra-1 SS M=∑T M2/b-C副区部分B DFB= b-1 SS B=∑T B2/ra-C MS B F B=MS B/MS EbA×B DFAB= (a-1)(b-1) SS AB=SS t-SS A-SS B MS AB F AB=MS AB/MS Eb误差b DFEb=a(r-1)(b-1)SS Eb=SS T-SS M-SS B-SS ABMS Eb总变异rab-1 SS T=∑y2-C拉丁方设计变来源DF SS MS F SE 横行区组DF R=k-1 SS R=∑T r2/k-C纵行区组DF C=k-1 SS C=∑T c2/k-C处理DF t=k-1 SS t=∑T t2/k-C MS t MS t/MS eSE误差DF e=(k-1)(k-2)SS e=SS T-SS R-SS C-SS t 总变异DF T=k2-1SS T=∑y2-C组内观察值数目不等的单向分组资料的方差分析(C=T2/∑n i)22 01i iin n nn k-=-∑∑∑()()()变异来源DF SS MS F误差DF e=∑n i－k SS e=SS T-SS t总变异DF T=∑n i－1SS T=∑y2-C巢式设计变异来源DF SS MS F SE 组间DF t=l-1 SS t=∑T i2/mn-C MS t MS t/MS e1亚组间DF e1=l(m-1) SS e1=∑Tij2/n-∑T i2/mnMS e1MS e1/MS e2亚组内DF e2=lm(n-1) SS e2=∑y2-∑T ij2/nMS e2总变异DF T=lmn-1 SS T=∑y2-CSESE无互作单个观测值正交试验资料的方差分析(C=T 2/n,SE A =SE B =SE C )变异DF SSMSFSEB DF B =b-1SS B =∑T B 2/rb-C SS B /DF B MSB /MS e CDF C =c-1SSC =∑T C 2/rc-C SS C /DF C MS C /MS e 误差 DF e =DF T -DF A -DF B -DF C SS e =SS T -SS A -SS B -SS C 总变 异DF T =n-1SS T =∑y 2-C无互作有重复观测值正交试验资料的方差分析变异来源 DF SS MS F SE 区组 n-1 SS R =∑T r 2/k-C 处理 k-1 SS t =∑T t 2/n-CA a-1 SS A =∑T A 2/ra-C SS A /DF A MS A /MS e (2)B b-1 SS B =∑T B 2/rb-C SS B /DF B MS B /Mse (2) Cc-1SS C =∑T C 2/rc-CSS C /DF C MS C /MS e (2)模误e1 DF t -DF A -DF B -DF C SS e1=SS t -SS A -SS B -SS C试误e2 DF T -DF R -DF tSS e2=SS T -SS R -SS t合误 DF e SS e 总 变 异 rab-1SS T =∑y 2-C有互作的正交试验资料的方差分析变异来源 DFSSMS F SE区组 r -1 SS R =∑T r 2/n-C 组合 ab-1 SS t =∑T AB 2/r-CA a-1 SS A =∑T A 2/ra-C MS A /MS e ;MS A /MS e2B b-1 SS B =∑T B 2/rb-C MS B /MS e ;MS B /MS e2 C c-1 SS C =∑T C 2/rc-C MS C /MS e ;MS C /MS e2A ×B (a-1)(b-1) SS AB =∑T AB 2/rab-C MS AB /MS e ;MS AB /MS e2 B ×C (b-1)(c-1) SS BC =∑T BC 2/rbc-CMS BC /MS e ;MS BC /MS e2模误DF t -DF A -DF B -D F C -DF AB -DF BC SS e1=SS t -SS A -SS B -SS C -SS AB -SS BC试误 DF T -DF R -DF t SS e2=SS T -SS R -SS t 合误 DF e SS e 总变 rab -1SS T =∑y 2-CB SEC SE 12e e MS F MS =A SE B SE C SE AB SE缺区处理（1）随机区组设计缺1区（2）随机区组设计缺2区n1,n2计算方法是：同一区组内，若比较的两处理都不缺区，则各记为1；若一处理缺区，另一处理不缺区，则缺区处理记0，不缺区处理记(k-2)/(k-1)，其中k 为试验的处理数目。
单因素方差分析公式研究单因素方差分析的公式
单因素方差分析公式研究单因素方差分析的公式单因素方差分析公式研究在统计学中，单因素方差分析是用于比较两个或多个组之间差异的一种方法。
它可以帮助我们确定因素对观测值的影响程度，并判断这种影响是否具有统计学上的显著性。
本文将对单因素方差分析的公式进行研究和解析，以帮助读者更好地理解和应用该方法。
一、方差的概念和计算公式方差是描述数据分散程度的统计量，用于衡量观测值与其均值之间的偏离程度。
对于一个样本数据集，方差的计算公式如下：\[S^2 = \frac{\sum{(X_i - \bar{X})^2}}{n-1}\]其中，\(S^2\)表示样本方差，\(\sum{(X_i - \bar{X})^2}\)表示所有观测值与均值之差的平方和，\(n\)表示样本容量。
二、单因素方差分析的公式在单因素方差分析中，我们将观测值按照某个因素分成两个或多个组，并比较这些组之间的差异。
单因素方差分析的计算公式如下：\[F = \frac{SSB}{SSW}\]其中，\(F\)表示方差分析的统计量，\(SSB\)表示组间平方和，\(SSW\)表示组内平方和。
三、组间平方和的计算方法组间平方和是一种衡量不同组之间差异的统计量，它的计算方法如下：\[SSB = \sum{\frac{T_i^2}{n_i}} - \frac{T^2}{N}\]其中，\(T_i\)表示第\(i\)组的总和，\(n_i\)表示第\(i\)组的样本容量，\(T\)表示所有观测值的总和，\(N\)表示总样本容量。
四、组内平方和的计算方法组内平方和是一种衡量同一组内观测值之间差异的统计量，它的计算方法如下：\[SSW = \sum{(X_{ij} - \bar{X_i})^2}\]其中，\(X_{ij}\)表示第\(i\)组的第\(j\)个观测值，\(\bar{X_i}\)表示第\(i\)组的均值。
五、方差分析的统计显著性检验通过计算得到方差分析的统计量\(F\)后，需要进行显著性检验来判断因素对观测值的影响是否具有统计学上的显著性。
第十三章单因素设计方差分析
第十三章单因素设计方差分析方差分析是由英国统计学家Ronald Fisher 研究出来的，并以他的名字命名的方法，称为F检验。
它可以解决单因素和多因素实验设计结果的数据处理问题。
早期的心理学实验是严格的实验室控制实验。
在实验中只允许研究者感兴趣的一种变量作为自变量，希望观察到自变量引起的因变量的变化。
自变量也称为因素(factor)，在实验中只安排一个自变量的实验叫做单因素实验。
经典心理学实验通常是单因素实验。
单因素的实验可以较明确的观察到自变量与因变量之间的因果关系，较适用于研究比较单纯的心理现象，但往往无法说明复杂的心理现象。
现代的实验设计将一些额外变量引入实验成为实验中新的因素，以期实验的结果更贴近真实的情景，从而发展了多因素的实验设计。
统计中用符号表示实验设计时，常用大写的英文字母表示因素，如因素A、因素B、因素C等；用S表示被试（subject）。
把S写在表示因素符号的后边、前面或中间，则表示不同的实验设计，例如：单因素被试间设计AS、单因素被试内设计SA、多因素被试间设计ABS、多因素被试内设计SAB、混合设计ASB。
第一节t检验与I类错误当两个总体没有差异，而统计推论的结论说有差异，就犯了I类错误；当两个总体存在差异，而统计推论的结论说没有差异，就犯了II类错误。
通常，I类错误的发生概率用α表示，II类错误发生的概率用β表示。
当采用多个两两t检验时，发生I类错误的概率就会增大。
I类错误的计算公式如下：I类错误发生的概率＝1－(1－α)C（13.1）所以当要比较3个或3个以上的总体平均数两两检验时，应采用方差分析（analysis of variance）的方法。
一个显著的F值表示，在所比较的总体平均数里至少有两个总体平均数存在着显著差异。
第二节方差分析的原理方差（V ariance）有时也称为变异数（V ariation），是表示一组数据离散程度的统计量。
方差的总体参数用符号σ2表示；方差的样本统计量用符号S2表示。
完全随机设计的方差分析(1)
.
21
.
22
方差分析(Analysis of variance，ANOVA)
方差分析的定义
又叫变量分析，是英国著名统计学家R . A . Fisher于20世纪提出的。它是用以检验两个或多个 均数间差异的假设检验方法。它是一类特定情况下 的统计假设检验，或者说是平均数差异显著性检验 的一种引伸。为纪念Fisher，以F命名，故方差分析 又称F检验 。
1.特点 单因素方差分析是按照完全随机设计的原则将处理 因素分为若干个不同的水平，每个水平代表一个样本，只 能分析一个因素对试验结果的影响及作用。其设计简单， 计算方便，应用广泛，是一种常用的分析方法，但其效率 相对较低。该设计中的总变异可以分出两个部分，
•
即SS总＝SS组间＋SS组内。
2.常用符号及其意义
.
29
end
第一节 完全随机设计资料的方差分析
完全随机设计：(completely random design)是采
用完全随机化的分组方法，将全部试验对象分配到g个
处理组（水平组），各组分别接受不同的处理，试验 结束后比较各组均数之间的差别有无统计学意义，推 论处理因素的效应。
.
30
end
第一节 完全随机设计资料的方差分析
离均差平方和 X2
总体方差 样本方差
2 X 2
N
S2XX2X2X2/n
n1
n1
方差—随机变量离散的重要衡量方法
.
13
试验指标（experimental index）： 为衡量试验
结果的好坏和处理效应的高低，在实验中具体 测定的性状或观测的项目称为试验指标。常用 的试验指标有：身高、体重、日增重、酶活性、 DNA含量等等。
单因素试验的方差分析
其中
r n i
2r
2
S S A X iX n i ii
i 1j 1
i 1
组间平方和（系
如果H0 成立，则SSA 较小。 统离差平方和）
反映的是各水平平均值偏离总平均值的偏离程度。
其中
1 r ni
ni1 j1
ij,
ni
i ij
j1
r ni
2 r ni
2
由P106定理5.1可推得：
S S 2 T~2 n 1 ,S S 2 A ~2 r 1 ,S S 2 E ~2 n r
将 分别SS记2T 作, SS2A
,
SSE
2
的自d由fT度,dfA,dfE
则 FSSA dfA~Fr1,nr
SSE dfE
（，称记作均S S 方A 和d f）A M S A ,S S Ed fE M S E
j1
i1
同一水平 下观测值 之和
所以观测 值之和
例2 P195 2 以 A、B、C 三种饲料喂猪，得一个月后每猪 所增体重（单位：500g）于下表，试作方差分析。
饲料
增重
A
51
40
43
48
B
23
ቤተ መጻሕፍቲ ባይዱ25
26
C
23
28
解：T1 51404348182, T2 232526 74, T3 232851
F0.012,610.92
1 5 .0 3
总和 1024.89 8
不同的饲料对猪的体重的影响极有统计意义。
例2的上机实现步骤
输入原始数 据列，并存 到A，B，C 列；
各水平数据放同一列
各水平数据 放在不同列
单因素试验的方差分析
单因素试验的方差分析
在方差分析中,我们将要考察的指标称为试验指标，影响 试验指标的条件称为因素(或因子),常用A、B、C, …来表示. 因 素可分为两类，一类是人们可以控制的；一类是人们不能控 制的。 例如，原料成分、反应温度、溶液浓度等是可以控制 的，而测量误差、气象条件等一般难以控制。 以下我们所说 的因素都是可控因素，因素所处的状态称为该因素的水平。 如果在一项试验中只有一个因素在改变，这样的试验称为单 因素试验，如果多于一个因素在改变，就称为多因素试验.
一、单因素试验方差分析的统计模型
例9.1 为求适应某地区的高产水稻的品种( 因素或因子) , 现选了 五个不同品种( 水平)的种子进行试验, 每一品种在四块试验田上进 行试种。假设这 20块土地的面积与其他条件基本相同, 观测到各块 土地上的产量( 单位: 千克) 见表9–1。
在这个问题目中, 要考察的指标是水稻的产量, 影响产量的因
分析的统计模型 .
方差分析的任务是对于模型(9. 1 ) , 检验 s 个总体 N ( 1 , 2) , …, N
( s , 2)的均值是否相等, 即检验假设
H0 : 1 2 s H1 : 1 , 2 , s , 不全相等。
（9.2）
为将问题( 9. 2 ) 写成便于讨论的形式, 采用记号
s nj
ST
(xij x)2
j1 i1
(9.3)
这里
x
1 n
s j 1
nj i1
xij ，
ST能反应全部试验数据之间的差异，又称
为总变差 Aj下的样本均值
x
j
1 n
nj i1
xij
(9.4)
注意到
(xij x )2 (xij x j x j x )2 =(xij x j )2 (x j x )2 2(xij x j )(x j x )
方差分析的应用范围单因素完全随机设计-随机化区组设计-拉丁方
方差分析(ANOVA)方差分析的应用范围单因素完全随机设计, 随机化区组设计,拉丁方设计多因素析因设计,裂区设计,交叉设计,正交设计多变量多元方差分析回归方程的假设检验第一节完全随机设计与资料分析方差分析目的：根据多个组间样本均数的差别推断总体均数是否存在差别。
一、方差分析的基本思想：1 / 162 / 16表12.2 红细胞沉降率(mm/h) 抗凝剂 红细胞沉降率 n i XS 2Σx Σx 2甲 17, 16, 16, 15 4 16.00.67 64 1026 乙 10, 11, 12, 12 4 11.3 0.92 45 509 丙 11, 9, 8, 9 4 9.3 1.58 37 347 合计1212.23.17146 1882观察值之间有变异，这变异可以用离均差平方和表示。
67.105)(112..=-=∑∑==Gi n j ij T ix x SS3 / 16进一步分析，总变异中有两类变异： 1. 组内变异，指各组内观察值的差异50.9)1()(12112.=-=-=∑∑∑===Gi ii Gi n j i ij W s n x x SS i2. 组间变异，指各组间样本均数与总均数的差异17.96)(12...=-=∑=Gi i i B x x n SS由于组内变异完全是个体间的差异，因此可以认为是随机误差。
而组间变异反映组间均数的差异，其可能仅仅包含随机误差，这时零假设成立。
也可能除随机误差外，还包含处理的效应，这时则备择假设成立。
组间变异和组内变异的自由度不同，无可比性。
计算均方，再进行比较：4 / 164 / 1637.4506.109.489/50.92/17.96)/()1/(====--=W B W B MS MS G n SS G SS F 二、方差分析的基本步骤 1. 方差分析的基本条件a. 各组观察值分别服从总体均数为μi 的正态分布。
b. 各组观察值总体方差相等。
单因素随机区组设计的方差分析
MSr Fr MSe MSb Fb MSe
变异来源 组间 区组
平方和 SSB SSR
自由度 k-1 n-1
均方 MSB MSR
F F=MSB/MSE F=MSR/MSE
p <0.05 或>0.05
误差
总变异
SSE
SST
（k-1）(n-1)
nk-1
MSE
例9-6：为研究听、触觉刺激对视觉的干扰效 果，随机抽取5名被试分别在5种不同的干扰下读
组内变异源于组内被试间的差异和实验误差，怎样
将被试间差异引起的变异从组内变异中分离出来，
从而提高F检验的精确度和灵敏度？
随机区组设计
单因素随机区组设计的方差分析
主要内容
随机区组设计（重点） 方差分析（重点）
1 随机区组设计
某研究要探讨文章的生字密度对学生阅读理解的影响， 生字密度有4个水平。由于考虑到学生的智力可能对阅读 理解测验分数产生影响，在实验实施之前，研究者首先 给32个学生做了智力测验，并按智力测验的分数将学生 分为8个区组，然后随机分配每个区组内的4个同质被试 分别阅读一种生字密度的文章，并回答阅读理解测验中 有关文章内容的问题。
k
( X ) 2
i 1
nj
nj
利用样本统计量进行方差分析（
SSB n ( X j X t )
j 1 k 2
X
k
2 ， ，n j ） S j j
SSB n j ( X j X t ) 2
j 1
SSW ( X ij X j ) n s 2 j
SST X
j 1 i 1
nj
k
nj
2
方差分析公式单因素方差分析多因素方差分析的计算公式
方差分析公式单因素方差分析多因素方差分析的计算公式方差分析公式计算单因素和多因素方差分析的方法是统计学中常用的数据分析技术。
方差分析可以用来比较两个或多个组之间的均值是否存在显著差异。
在本文中，将介绍单因素方差分析和多因素方差分析的计算公式和步骤。
一、单因素方差分析的计算公式单因素方差分析适用于只有一个自变量（因素）的情况下比较多个组的均值是否存在差异。
在进行单因素方差分析时，需要计算以下几个统计量。
1. 总平方和（SST）：总平方和表示各组数据与整体均值之间的偏差总和。
其计算公式如下：SST = Σ(xi - x)²其中，xi为每个观察值，x为所有观察值的均值。
2. 组内平方和（SSW）：组内平方和表示各组数据与各组均值之间的偏差总和。
其计算公式如下：SSW = Σ(xi - x i)²其中，xi为每个观察值，x i为各组观察值的均值。
3. 组间平方和（SSB）：组间平方和表示各组均值与整体均值之间的偏差总和。
其计算公式如下：SSB = Σ(ni * (x i - x)²)其中，ni为每个组的观察次数，x i为各组观察值的均值，x为所有观察值的均值。
4. 平均平方和（MSW和MSB）：平均平方和表示各组之间的平均差异程度。
其计算公式如下：MSW = SSW / (n - k)MSB = SSB / (k - 1)其中，n为总观察次数，k为组的个数。
5. F统计量：F统计量用于检验组间均值是否存在显著差异。
其计算公式如下：F = MSB / MSW二、多因素方差分析的计算公式多因素方差分析适用于两个或更多个自变量（因素）的情况下比较多个组的均值是否存在差异，并确定各因素之间的交互影响。
在进行多因素方差分析时，需要计算以下几个统计量。
1. 总平方和（SST）：总平方和的计算方式与单因素方差分析相同。
2. 组内平方和（SSW）：组内平方和的计算方式与单因素方差分析相同。
!!!)SPSS单因素方差分析
SPSS--单因素方差分析单因素方差分析也称作一维方差分析。
单因素方差分析是两个样本平均数比较的引伸，是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。
它是用来检验多个平均数之间的差异，从而确定因素对试验结果有无显著性影响的一种统计方法。
单因素方差分析（one-way ANOVA）,用于完全随机设计的多个样本均数间的比较，其统计推断是推断各样本所代表的各总体均数是否相等。
采用One-way ANOVA过程要求：因变量属于正态分布总体，若因变量的分布明显是非正态，应该用非参数分析过程。
若对被观测对象的试验不是随机分组的，而是进行的重复测量形成几个彼此不独立的变量，应该用Repeated Measure菜单项，进行重复测量方差分析，条件满足时，还可以进行趋势分析。
[例子]调查不同水稻品种百丛中“稻纵卷叶螟”幼虫的数量，数据如表1-1所示。
分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
表1-1不同水稻品种百丛中“稻纵卷叶螟”幼虫数（个/100丛）1建立因变量“虫数”和因素水平变量“品种”，然后在数据编辑窗口中输入对应的数值。
变量格式如表1－2和图1-1所示。
或者打开已存在的数据文件“虫数.sav”。
图1-12）启动分析过程从菜单中选择：分析 > 比较均值 > 单因素 ANOVA。
打开单因素方差分析对话框，如图1-2。
图1-2单因素方差分析窗口3）设置分析变量在这个对话框中，将因变量（观测变量）放到“因变量列表”框中，本例选择“虫数”。
将因素变量（自变量）放到“因子”框中。
本例选择“品种”。
4）设置多项式比较（一般选择缺省值）单击“对比”按钮，将打开如图1-3所示的对话框。
该对话框用于设置均值的多项式比较。
图1-3“对比”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。
例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。
单因素完全随机随机区组方差分析SPSS
2023.01
4
➢ 数据格式 n行2列 （指标变量、分组变量）
2023.01
5
➢ 检验环节
Analyze →Compare Means →One-Way ANOVA
2023.01
6
One-Way ANOVA 对话框
2023.01
多重比较
选项
7
Post Hoc Multiple Comparisons 对话框
单原因方差分析旳SPSS实现
2023.01
1
SPSS单原因方差分析过程名
完全随机设计方差分析： Analyze Compare Means
One－Way ANOVA
随机单位组设计方差分析： Analyze General Linear Models
Univariate
2023.01
2
1. 完全随机设计资料旳方差分析One-Way ANOVA
2023.01
3
表1 三组战士的第一秒用力肺活量(L)
对照组 锻炼组 药物组 合计 3.25 3.66 3.44 3.32 3.64 3.62 3.29 3.48 3.48 3.34 3.64 3.36 3.16 3.48 3.52 3.64 3.20 3.60 3.60 3.62 3.32 3.28 3.56 3.44 3.52 3.44 3.16 3.26 3.82 3.28
例1 某高原研究组将籍贯相同、年龄相同、身高 体重接近旳30名新战士随机分为三组，甲组为对 照组，按常规训练，乙组为锻炼组，每天除常规 训练外，接受中速长跑与健身操锻炼，丙组为药 物组，除常规训练外，服用抗疲劳药物，一月后 测定第一秒用力肺活量(L)，成果见表。试比较 三组第一秒用力肺活量有无差别。
方差分析单因素方差分析3篇
方差分析单因素方差分析第一篇：方差分析基础知识什么是方差分析？方差分析（ANOVA）是一种常用的数据分析方法，用于确定多个组或处理之间差异的检验方法。
方差分析的目的是比较各组之间的均值是否有显著差异，从而确定某种变量是否能够对观测结果产生统计显著影响。
方差分析的原理方差分析的基本原理是将总差异拆分为各个来源的差异，比较相对大小，进而确定各组均值之间是否存在显著差异。
方差分析原理中的总差异由于组内差异和组间差异组成，在计算统计检验时，需要根据样本数据计算出相应的方差分量。
方差分析的应用范围方差分析适用于多组数据的比较分析，通常用于以下场景：1. 不同处理方式对结果的影响是否显著；2. 产品的性能比较；3. 不同采样机构采样结果的差异性比较；4. 不同肥料对植物生长的影响比较等。
在研究中，方差分析也被广泛应用于实验设计和因子分析中，通过分析方差来确定影响观察结果的因素，以减少实验的时间和成本。
第二篇：单因素方差分析的步骤单因素方差分析是指数据来自同一总体下的不同组或处理之间的差异，其中只有一个因素起到决定性作用的方差分析。
对于一般的数据处理，单因素方差分析一般包括以下步骤。
1. 设定假设并确定显著性水平假设总体均值相等，等价于各组均值相等。
如果拒绝了该假设，则表明不同组之间均值存在显著差异。
同时，还需要确定显著性水平，通常为α=0.05或α=0.01。
2. 构建方差分析表构建方差分析表，并计算相关的方差分量，包括组内偏差平方和、组间偏差平方和、总偏差平方和和平均平方值。
3. 计算F值通过总偏差平方和、组内偏差平方和，以及各组样本容量计算F值。
4. 进行假设检验通过比较计算出的F值与参考F分布表中的临界值，以判断不同组之间差异是否显著。
5. 发现组之间差异的原因如果不同组之间均值存在显著差异，则需要通过多重比较或方差分析的分解来确定差异来源，以便进一步研究各组之间差异的原因。
第三篇：常用的单因素方差分析方法1. 单因素方差分析（One-way ANOVA）单因素方差分析是一种常见的数据分析方法，通常用于比较三个或三个以上组之间的差异。
单因素方差分析
其他选项（Options）对话框
统计量 描述性统计量 固定、随机效应模型标准差标准误置信区间 方差齐性检验 B-F近似方差分析法，一种稳健检验方法 Welch近似方差分析法，一种稳健检验方法
均数图（横轴为分类变量，纵轴为分析变量均数的线图）
剔除分析变量中含缺失值的观察单位 剔除所选变量中含缺失值的观察单位
大鼠烫伤后肝脏ATP含量（mg）的测量结果
A组 7.67 7.53 8.39 8.51 10.18 7.03 11.69 5.74 6.72 7.07 B组 11.24 11.70 11.52 13.65 13.43 14.19 7.21 12.87 13.89 16.93 C组 10.74 8.68 7.32 9.41 9.62 8.78 8.32 9.85 11.31 8.73
2、结果解释
ANOVA ATP Sum of Squares 114.065 97.663 211.729 df 2 27 29 Mean Square 57.033 3.617 F 15.767 Sig. .000
Between Groups Within Groups Total
2.双因素方差分析（two-way ANOVA） 称为随机区组设计的方差分析。该设计可以分 析两个因素。一个为处理因素，也称为列因素；一 个为区组因素，也称为行因素。
分析步骤如下： 1、建立假设，确定检验水准 H0:μ1=μ2=μ3 ，即不同时期切痂对大鼠肝脏 ATP含量无影响；
0.05
2、在SPSS中选择方法和计算统计量
4、 Dunnett’s C:基于学生化极差的多重比较方 法，是一种可信区间的方法。
均数趋势检验
多项式选项
线性组合比较 依次输入系数
心理统计SPSS-第五章 因素型实验设计及方差分析过程剖析
1 2
A1
8 12
A2
16 11
A3
21 16
3
4 5
11
7 13
15
10 12
18
19 22
6
9
14
18
练习
One Way方差分析程序的适用条件： 1.三个以上相等独立被试组在不同条件下接受观测得 到三组以上的独立数据组； 2.来自三个以上不同总体的独立被试组在相同条件下 接受同样的观测，得到三组以上的独立数据组； 3.一般要求因变量必须是连续测量的数据或近似于连
究会得到多组数据，而这些数据必然存在变异。被试差异、测量误 差、其他额外变量的变化等。因素型实验的目的就是考察自变量或准自
变量变化是否引起了因变量数据足够大的改变，以至于可以认为其不同
水平间因变量的差异性并非误差因素造成，而且这种评估是与误差因素 引起数据的变化量相比较而完成的。数据变异可以通过离差平方和或方 差来反映，所以关于数据变异的分析叫方差分析。
续变化的数据；
4.数据总体为正态分布、各数据样本方差齐性。
二、多因素完全随机实验设计方差分析（GLM 方差分析）
当研究的自变量或准自变量不只一个，每个自变量的水平在两个 以上时，就会结合出四个以上的实验处理。将选取来的被试分成四个 独立组，每个组被试只接受一种条件下的实验观察，则构成多因素完 全随机实验设计。其数据分析则要使用SPSS程序中的“General Linear Model-Univariate”模块。 如果进行简单效应检验，可执行类似于下的句法命令： MANOVA SCORE by A(1,2) B(1,2) /design（此句要求先输出完整的方差分析表） /design=A within B(1) A within B(2) B within A(1) B within A(2). （ANOVA命令中不能做简单效应检验）
单因素随机区组试验设计的方差分析
N-K法，也称q检验
q
(X X )
1
2
MS e
(
1
1
)
2nn
1
2
q值表的自由度为误差项的自由度
LSD法—最小有意义差法
H : H :
0
i
j
1
i
j
Y Y
i
j
~t
11
( df3 )
MS ( )
en n
i
j
自由度为误差项自由度
适用情况 研究中有两个试验变量，变量有两个或
多个水平 研究中还有一无关变量，也有两个或多
个水平 并且试验变量的水平和无关变量的水平
之间没有交互作用。
数据结构
A1 B1 A1 B2 A1 B3
区组一 X111… X121… …
X11r
X12r
A2 B1
A2 B2
A2 B3
X161… X16r
是不同的区组。
数据结构
A1
A2
A3
A4
区组一 x11
x12
x13
x14
区组二 x21
x22
x23
x24
区组三 x31
x32
x33
X34
区组四 x41
x42
x43
x44
研究假设H :1. 00j2. 0 为区组效应
i
i
H : , 不全为零
1
ji
x
ij
j
i
ij
双因素随机区组试验设计的方 差分析
多重比较法有许多种
几种常用多重比较方法
N-K法，也称q检验，由Newman-Keul提 出
LSD法—最小有意义差法 Bonfenomi不等式—a large number of
生物统计——单因素完全随机设计试验资料的方差分析
( LSR法) ( LSD法)
S xi x j
【例5-4】 5个玉米品种的盆栽试验， 调查了穗长(cm)性状，得资料如表5-17 所示。试比较品种穗长间有无差异。
1、计算各项平方和与自由度
x 460.5 C 8482.41 N 25
SST
2
2
x
2
2 ij
C
2
(21.5 19.5
3、多重比较
n 1 n0 [ ni ] k 1 ni
2 i
1 6 6 5 4 4 [25 ] 4.96 5 1 25
2 2 2 2 2
Sx S xi
MSe n0
1.94 0.625 4.96 2 1.94 0.884 4.96
(LSR法) (LSD法)
2 i
SSe SST SSt 85.34 46.50 38.84
dfT N 1 25 1 24 dft k 1 5 1 4 df e dfT dft 24 4 20
2、列出方差分析表，进行F检验。 F检验结果表明品种间穗长差异极显著。
3、多重比较
计算标准误
MSe 6.5333, df e 20, n 6
Sx MSe n 6.5333 1.0435 6
最小显著极差LSR值的计算
LSR0.05 SSR0.05( k ,dfe ) S x LSR0.01 SSR0.01( k ,dfe ) S x
多重比较结果表
SSe SST SSt 197.8333 67.1667 130.6666
dfT kn 1 4 6 1 23 dft k 1 4 1 3 df e dfT dft 23 3 20
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Start
制作人：李福建 娄文博 主讲人：
一。单因素完全随机设计
在实验中如果仅有一个实验因素，这个因素又分成k种 不同水平（k>2）或k种不同处理，将N名被试随机地分成 k个实验组，每个实验组又随机被指定接受一种实验处理， 这种实验设计就叫单因素完全随机设计。此时，k组不同 处理间是相互独立的。例如，研究识记得实验，按识记 材料的性质不同分为三种或四种处理，在同一教学内容 采用几种不同的教学方法等，都是单因素多个水平的实 验。
例1. 一批学生随机被分配在三 个组中，进行三种识记的实验， 结果如表10-3.问三种记忆方式 的效果是否有显著差异？
解题步骤详见 X1
课本P166-168
31
X2 58
X3 65
58
46 50 38 62 53 62
76
73 56 42 63 52
80
82 44 74 56 60 75
400
420
536
例2
从某班学习中等的学生中随机 抽出15名，把他们随机分成三 组，每组随机接受一种方式的 自学辅导实验，成绩如表，问 三种方式的效果是否有显著差 异？ 解题步骤详见课本P169-170
甲
75 83 78 79 81 396
乙
78 73 71 75 70 367
丙
83 85 81 88 90 427
(2)根据已知样本统计量进行方差分析
例3 把40名学生随机分成四组， 每组10人。每个组分别接受一 种方法的阅读训练，训练结束 测验成绩如表。已知训练成绩 服从正太分布，各组方差齐性， 问四种训练方法的效果是否有 显著差异? 解题步骤详见课本
训练方 法分组 每组人 数nj 每组平 均成绩 每组标 准差 A B C D
由于被试被随机选取又被随机分配到各组中，因此在理 论上认为各组被试在实验前其水平是相当的。如果接受 实验后，各组间在实验结果上存在显著差异，则可认为 这种差异是由于实验处理造成的。 教育实验中的单组实验或等组实验，就是单因素的实验。
二。单因素完全随机设计方差分析方法
（1）依据原始数据进行方差分析
P171-172
10
10
10
10
12
15
8
Hale Waihona Puke 13232
2.5