将军饮马问题讲
将军饮马问题的11个模型及例题
将军饮马问题的11个模型及例题将军饮马问题是一个经典的逻辑问题，涉及到将军如何用有限数量的马和酒到达目的地。
本文将介绍将军饮马问题的11个模型及相应的例题。
1. 直线模型将军与目的地之间没有障碍物，可以直线前进。
此时，将军只需将马拉到目的地即可。
例题1：将军与目的地之间距离为10公里，马的速度为每小时5公里，将军能否在2小时内到达目的地？2. 单个障碍物模型在将军与目的地之间存在一个障碍物，将军可以绕过该障碍物。
例题2：将军与目的地之间距离为15公里，马的速度为每小时4公里，障碍物位于距离将军起点5公里处，将军能否在3小时内到达目的地？3. 多个障碍物模型在将军与目的地之间存在多个障碍物，将军需要逐一绕过这些障碍物。
例题3：将军与目的地之间距离为20公里，马的速度为每小时6公里，障碍物位于距离将军起点分别为5公里、10公里和15公里的位置，将军能否在4小时内到达目的地？4. 跳跃模型将军可以让马跳过障碍物，从而直接到达目的地。
例题4：将军与目的地之间距离为12公里，马的速度为每小时8公里，将军在距离起点6公里处设置一个障碍物，将军能否在2小时内到达目的地？5. 限时模型将军需要在规定的时间内到达目的地。
例题5：将军与目的地之间距离为30公里，马的速度为每小时10公里，将军需要在3小时内到达目的地，是否可能？6. 守备模型目标地点有守备军，将军需要巧妙规避守备军。
例题6：将军与目的地之间距离为25公里，马的速度为每小时7公里，目的地有一支守备军位于距离目标地点10公里处，将军能否在4小时内到达目的地？7. 短平快模型将军不借助马匹，直接徒步走到目的地。
例题7：将军与目的地之间距离为8公里，将军的步行速度为每小时2公里，将军能否在4小时内到达目的地？8. 时间窗模型将军只能在规定时间范围内到达目的地。
例题8：将军与目的地之间距离为18公里，马的速度为每小时6公里，将军需要在3小时到4小时之间到达目的地，是否可能？9. 兵变模型将军需要利用敌军马匹达到目的地。
八年级将军饮马问题例题讲解
八年级将军饮马问题例题讲解哎呀，今天咱们聊聊八年级的将军饮马问题，听名字就觉得特别有意思，对吧？咱们先来个开门见山，将军带着他的军队，经过一条河，得给马喝水。
这问题看似简单，但其实里面藏着不少小玄机，真的是个大考验，脑袋瓜得动一动。
想象一下，这将军带着一帮士兵，行军走到河边，嗨，口渴得不行，马儿们更是想喝水。
可是，问题来了，河边的水不深，能让马儿们喝到，但不让它们掉进水里。
将军一边心急如焚，一边得想办法。
怎么让这些马儿在喝水的时候不掉进河里呢？这时候就得用到一些小技巧了。
咱们可以想象一下，马儿们得排队，得一个一个地喝水。
将军心里想着，得控制好马儿的喝水速度，别让它们都挤在一起，这样容易出事。
也许能用一些方法，比如说把马儿们牵得远一些，慢慢地让它们喝，像是在参加比赛一样，嘿嘿，真是有意思的场景。
想想马儿们排成一队，乖乖的，一个个慢慢走过来喝水，真是可爱。
这时候就得算一算了，马儿们得喝多少水，每匹马喝水的速度又有多快。
嘿，可能是三两口就满足了，也可能是急着想喝个痛快，一口气喝个干净。
将军得根据情况来调整策略，真是够麻烦的。
不过，思来想去，最好的办法还是得让马儿们分批来，排着队，井然有序。
然后，咱们再来想象一下，如果马儿们不听话，乱跑，那可就麻烦了。
想象一下将军那个急得直挠头的样子，心里想着：这马儿也太不听话了！要不就得用点小办法，比如说放一块香饽饽在河边，吸引它们过来，嘿嘿，果然，马儿们就乖乖走过来喝水了。
就像小朋友看到喜欢的玩具一样，立马就冲过去了，真是太可爱了。
接着咱们来讨论一下，假设这条河不宽，马儿们很快就能喝到水，那将军得加快速度，不能让马儿们等太久。
想想那画面，马儿们都急得不行，口水都快流下来了，哈哈，真是个搞笑的场景。
将军这时候就得使出浑身解数，调整路线，确保马儿们能尽快喝水。
但是，事情总是没那么简单。
马儿喝水喝得急，可能还会打架，踩到脚，这可就不好了。
所以，将军得一边指挥，一边安抚，真是一场心力交瘁的战斗。
将军饮马(最完整讲义)
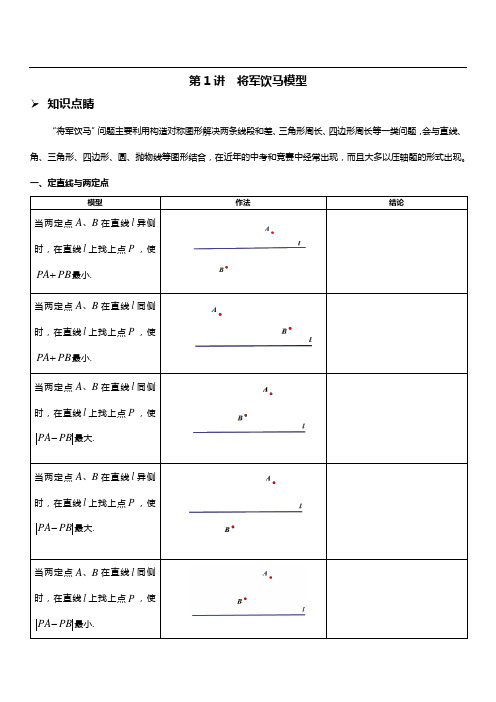
第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。
一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l异侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是，在OA 上找一点M ，在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、（M 在左），使NB MN AM ++最小,且d MN =.如图，21//l l ，21l l 、之间的距离为d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，且NB MN AM ++最小.如图，21//l l ，43//l l ,21l l 、之间的距离为1d ，43//l l 之间的距离为2d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，在43l l 、上分别找Q P 、两点，使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图，在⊙O 上找一点N ，在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1：如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值．P OBAMN例2：如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值．例3：如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( )A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)第3题图 第4题图 第5题图例4：如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( ) A ．4B ．5C ．6D ．7例5：如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________． PDCBAA BCDMNNMDCBA例6：如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值．例7：如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3 B ．4 C ． D ．第7题图 第8题图 第9题图例8：如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( ) A B ．2 C ．D ．4例9：如图，在菱形ABCD 中，AC =BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，连接PE 、PM ，则PE +PM 的最小值是( ) A ．6B ．C ．D ．4.5NMDBA E AFCDBNM DCBAEPDCBAM例10：如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)3第10题图 第11题图 第12题图例11：如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A ．B ．C ．D 例12：如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( )A ．B ．C ．D ．例13：如图，∠AOB =60°，点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是( )A B C ．6D ．3第13题图 第14题图 CBH FGEDCB AA BMOPN例14：如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为 ．例15：如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为___________．第15题图例16：如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．例17：如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．AB CD EFMx例18：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，求PD+PE 的最小值。
将军饮马(最完整讲义)
第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。
二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点（在左）, 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A ．例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A （4,4）, 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C ．,D ．第3题图 第4题图 第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5：如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________．A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图 第8题图 第9题图A ．例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA ．例10: 如图, 矩形ABOC 的顶点A 的坐标为（-4,5）, D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图 第11题图 第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图 第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N （3,0）是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15：如图, 已知正比例函数y=kx （k>0）的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为（0, 4）, P 为y 轴上的一个动点, M 、N 为函数y=kx （k>0）的图像上的两个动点, 则AM+MP+PN 的最小值为___________．第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为（6, 4）, E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17：如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值．x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。
第11讲 “将军饮马”问题探究(学生版)
知识导航
①作定点关于动点所在直线的对称点，构造轴对称图形
②等腰三角形、角分线模型是天然的轴对称模型
经典例题
1
三角板、刻度尺作图，保留作图痕迹，不写作法．
2
如图，正方形3
如图，正方形4
在
1
三角板、刻度尺作图，保留作图痕迹，不写作法：2
如图，在
3
如图，在
知识导航
经典例题1
如图，直线2
如图，
知识导航
经典例题
1
如图，在一组平行线2
如图，直线
3
如图，在正方形
设汽车行驶到公路上点的位置时，距离村庄最近，行驶到点的位置时，距离村庄上分别画出、的位置；
行驶时，在公路的哪一段上距离、两村都越来越近？在哪一段
巩固2
如图，、为的边、上的两个定点，在上求一点，使的周长最短．
巩固3
如图，，角内有点，在角的两边有两点、(均不同于点)，求作、，使得的周长的最小．
巩固4
如图，在中，若在，上各取一点，，使的值最小，试在图中画出，的位置．
巩固5
如图（1），、两单位分别位于一条封闭街道两旁（直线、是街道两边沿），现准备合作修建一座过街人行天桥．天桥应建在何处才能使由经过天桥走到的路程最短？在图（2）中作
如图，四边形中，，，在、上分别找一点、，使周长最小，求此时的度数以及的度数．。
将军饮马课件ppt
05
将军饮马问题的扩展和挑 战
变种问题
01
02
03
04
障碍物问题
在路径上设置障碍物，求最短 路径时需要避开障碍物。
多点折返问题
在路径上设置多个折返点，求 最短路径时需要多次折返。
限制条件问题
在求最短路径时加入限制条件 ，如步数限制、时间限制等。
动态变化问题
路径长度会随时间或其他因素 变化，需要求最短路径时考虑
这些变化。
计算复杂度
最坏情况下的时间复杂度
在最坏情况下，算法的时间复杂度可 能较高，需要优化算法以降低时间复 杂度。
空间复杂度
并行计算
为了提高算法的效率，可以考虑使用 并行计算来加速计算过程。
算法的空间复杂度也需要考虑，以评 估算法的内存消耗。
实际应用中的限制和优化
数据精度
在实际应用中，需要考虑 数据精度对算法的影响， 以避免误差累积导致结果 不准确。
在车辆调度方面，将军饮马问题同样 适用。通过优化车辆的出发时间和行 驶路线，物流公司可以最大化利用车 辆资源，提高运输效率。
计算机算法
图论算法
将军饮马问题作为图论中的经典问题，可以应用于计算机算法领域。通过解决将军饮马问题，可以开 发出更高效的图论算法，用于解决其他相关问题。
最短路径算法
最短路径算法是计算机算法中的重要组成部分。将军饮马问题可以作为最短路径算法的参考模型，帮 助开发人员找到图中两点之间的最短路径。
03
04
几何法是利用几何知识解决将 军饮马问题的方法。
它通过将问题转化为几何图形 ，利用几何定理和性质来找到
最短路径。
几何法适பைடு நூலகம்于具有明显几何特 征的问题，如两点之间的最短 距离、三角形中的最短路径等
将军饮马最短距离原理
将军饮马最短距离原理1.引言1.1 概述将军饮马最短距离原理是一种常见的数学问题，根据传说中的典故“将军饮马”，通过解决这个问题我们可以得到最短距离的最优解。
这个问题在数学领域中被广泛研究和应用，尤其在图论、最优路径规划、网络优化等领域中具有重要的意义。
将军饮马最短距离问题可以简单描述为：一个将军要从指定位置A饮马到指定位置B，同时他必须经过多个中间位置，并且需要选择经过这些中间位置的最短路径。
这个问题可以用图论中的有权有向图来模拟和解决。
每个位置可以看作图中的一个节点，将军的移动可以看作是节点之间的有向边，每条边的权值表示将军从一个位置到另一个位置的移动距离。
通过这个问题的求解，我们可以找到从起点到终点的最短路径，即将军饮马的最短距离。
将军饮马最短距离原理的研究不仅可以用于解决实际问题，还可以用来优化和改进一些相关算法和模型。
例如，在网络优化中，我们可以利用这个原理来找到网络中数据传输的最短路径，从而提高网络的传输效率。
此外，通过将军饮马问题的研究，还可以挖掘和发现一些潜在的规律和规划策略，进一步推动相关领域的发展。
本文将从将军饮马最短距离原理的背景和原理解析两个方面进行详细探讨，通过对相关理论和算法的介绍和分析，旨在增加对这一原理的理解和认识。
同时，本文还将探讨将军饮马最短距离原理的应用价值和未来发展方向，以期为相关领域的研究和实践提供一定的参考和指导。
1.2文章结构1.2 文章结构本文将按照以下结构进行叙述和分析将军饮马最短距离原理：1. 引言：为了引出将军饮马最短距离原理的背景和意义，概述本文将要介绍的内容。
2. 正文：2.1 将军饮马最短距离原理的背景：详细介绍将军饮马最短距离原理的起源和历史背景，包括相关的故事或传说，以便读者能够更好地理解该原理。
2.2 将军饮马最短距离原理的原理解析：深入分析将军饮马最短距离原理的具体原理，包括数学模型和算法等相关内容。
通过展示相关的数学推导或图表，让读者理解这一原理的运作机制。
将军饮马二次函数问题
将军饮马二次函数问题将军饮马是一道经典的二次函数问题，它涉及到求解一个关于时间和距离的函数关系。
这个问题在中国数学史上有着重要的地位，不仅因为它是求解一元二次方程的基础问题，还因为它体现了中国古代数学家高超的几何创造力和智慧。
将军饮马的问题可以概括为：一位将军从一座城市出发，骑着马奔向另一座城市。
在途中，将军发现一个河流横亘在他的路径上，他必须走一个弯曲的道路来绕过河流。
在整个过程中，将军骑马的速度是恒定的。
问题要求我们用数学方法来求解将军饮马的最短时间。
为了更好地理解问题，我们可以把这个问题绘制成图形。
假设河流是一条笔直的线段，将军出发点到河流的距离为a，河流的宽度为b，将军需要绕过河流走一段曲线，曲线的起点和终点都是河流的两端。
设曲线的长度为L，曲线与河流垂直相交。
将军的速度为v，问题要求我们求解将军饮马的最短时间。
为了解决这个问题，我们可以先考虑将军直接穿过河流的情况。
如果将军选择穿过河流，他需要经过一段距离为b的直行道路。
由于将军的速度是恒定的，所以他穿过河流的时间为t1=b/v。
接下来，我们可以考虑将军绕过河流走曲线的情况。
由于曲线是垂直相交于河流的，所以曲线与每个平行于河流的切线都有一个交点。
假设将军从某个切点出发，经过曲线走到另一个切点，然后再重新回到河流的对岸。
将军沿曲线行进的时间与他直行到达对岸的时间是相等的，因为他的速度是恒定的。
现在，我们需要找到一个与直行距离b相对应的最小曲线长度L。
假设将军在上游走曲线，然后沿着河流下游走直线到达对岸。
我们可以计算出将军顺时针绕过河流的距离，设为L1，将军逆时针绕过河流的距离，设为L2。
由于将军的速度是恒定的，所以他绕过河流的时间为t2=(L1+L2)/v。
接下来的问题是，如何确定使得t2最小的曲线长度L。
我们可以使用勾股定理来解决这个问题。
根据勾股定理，河流的宽度b和曲线长度L之间存在如下关系：L^2 = b^2 + a^2。
将这个关系带入到t2的公式中，我们可以得到t2 = (2L/v)v^2 / (v^2 + g)。
二次函数将军饮马问题解法及题目
二次函数将军饮马问题解法及题目二次函数将军饮马问题是高中数学中的经典问题之一，也是二次函数应用的一个重要例题。
下面将从问题的背景、解题思路和具体步骤三个方面来讨论这个问题的解法。
一、问题背景将军饮马问题的情境来源于古代传说。
据说，曹操在赤壁之战失败后，率领残部逃往华容道，途中骑着一匹名叫“赤兔”的战马。
此时在他身后不远处，有一支敌军紧追不舍。
为了摆脱敌人的追赶，曹操不得不冒着生命危险，在一座山顶上饮马止渴。
因为离敌军很近，他只敢让马尽量少喝。
问：如何确定曹操所饮马水的最大量和固定时间呢？二、解题思路将军饮马问题可以通过数学建模来解决。
具体来讲，这是一个面积最大的矩形问题，可利用函数极值来解决。
三、具体步骤1.根据题目要求，建立模型假设曹操饮马时间为$t$，此时马喝水的时间为$2t$。
设马每秒钟喝水$\Delta V$升，$t$秒钟后马喝的水量为$S=2t\Delta V$升，曹操饮马的体积为$V_S$，也就是可喝的水量。
现在需要求得曹操所饮马水的最大量和固定时间，秉承最优化原则，可以确定目标函数为：$S=2t\Delta V=2t\cdot\dfrac{V_S}{2t}=V_S$这个目标函数表明饮马次数越少、饮马时间越短，曹操所饮马水的体积越大。
2.建立关系式根据马喝水的过程，考虑将马喝水的水平面设为直线$y=kx$，其中$k=\Delta V$为斜率，$x$为时间，$y$为所喝的水量。
此时，曹操饮马水的体积为$x$轴上$x=2t$时直线$y=kx$与$x$轴之间的面积，可以表示为：$V_S=\displaystyle\int_0^{2t}kx\mathrm{d}x=\left[\dfrac{ k}{2}x^2\right]_0^{2t}=k\cdot(2t)^2=4k\Delta t^2$同时，由于直线$y=kx$经过原点，可以将直线的方程表示为：$y=kx$将$t$代入$x=2t$，得到：$y=4kt$即曲线上任意一点的坐标为$(2t,4kt)$。
将军饮马问题(讲)
将军饮马问题【2 】类型一.根本模式类型二.轴对称变换的应用（将军饮马问题）2.如图所示,假如将军从马棚M动身,先赶到河OA上的某一地位P,再立时赶到河OB上的某一地位Q,然后立刻返回校场N．请为将军从新设计一条路线(即选择点P和Q),使得总旅程MP＋PQ＋QN最短．【变式】如图所示,将军愿望从马棚M动身,先赶到河OA上的某一地位P,再立时赶到河OB 上的某一地位Q．请为将军设计一条路线(即选择点P和Q),使得总旅程MP＋PQ最短．3.将军要检阅一队士兵,请求(如图所示)：部队长为a,沿河OB排开(从点P到点Q);将军从马棚M动身到达队头P,从P至Q检阅部队后再赶到校场N．请问：在什么地位排队(即选择点P和Q),可以使得将军走的总旅程MP＋PQ＋QN最短?4. 如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M的距离与点P到OA边的距离之和最小5已知∠MON内有一点P,P关于OM,ON的对称点分离是和,分离交OM, ON于点A.B,已知＝15,则△PAB 的周长为（）A. 15 B 7.5 C. 10 D. 246. 已知∠AOB,试在∠AOB内肯定一点P,如图,使P到OA.OB的距离相等,并且到M.N两点的距离也相等.7.已知∠MON＝40°,P为∠MON内必定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.8. 如图,在四边形ABCD中,∠A＝90°,AD＝4,衔接BD,BD⊥CD,∠ADB＝∠C.若P是BC边上一动点,则DP长的最小值为______.演习1.已知点A在直线l外,点P为直线l上的一个动点,探讨是否消失一个定点B,当点P在直线l上活动时,点P与A.B两点的距离总相等,假如消失,请作出定点B;若不消失,请解释来由．2、 如图,在公路a 的同旁有两个仓库A .B ,现须要建一货色中转站,请求到A .B 两仓库的距离和最短,这个中转站M 应建在公路旁的哪个地位比较合理？aBA3. 已知：A .B 两点在直线l 的同侧, 在l 上求作一点M ,使得||AM BM -最小．4.如图,正方形ABCD 中,8AB =,M 是DC 上的一点,且2DM =,N 是AC 上的一动点,求DN MN +的最小值与最大值．NMD CB A5.如图,已知∠AOB 内有一点P ,试分离在边OA 和OB 上各找一点E.F,使得△PEF 的周长最小.试画出图形,并解释来由.6.如图,直角坐标系中有两点A.B,在坐标轴上找两点C.D,使得四边形ABCD 的周长最小.7.如图,村庄A.B 位于一条小河的两侧,若河岸a.b 彼此平行,如今要扶植一座与河.A. B岸垂直的桥CD,问桥址应若何选择,才能使A 村到B 村的旅程比来？8.4)9(122+-++=x x y ,当x 为何值时,y 的值最小,并求出这个最小值.9.在平面直角坐标系中,A(1,-3).B(4,-1).P(a,0).N(a+2,0),当四边形PABN 的周长最小时,求a 的值. 10.如图,在等腰梯形ABCD 中,AB=CD=AD=2,∠D=120°,点E.F 是底边AD 与BC 的中点,衔接EF,在线段EF 上找一点P ,使BP+AP 最短．演习1.不雅察下列银行标志,从图案看既是轴对称图形又是中间对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个 2.以下图形中,既是轴对称图形,又是中间对称图形的是（ ） A ．等边三角形 B ．矩形C ．等腰梯形D ．平行四边形3.鄙人列四个图案中既是轴对称图形,又是中间对称图形的是4.在等边三角形.正方形.菱形和等腰梯形这四个图形中,是中间对称图形的个数为（ ）A ．1个B ．2个C ．3个D ．4个5.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的偏向平移,我们把如许的图形变换叫做滑动对称变换．在天然界和日常生涯中,大量地消失这种图形变换（如图甲）．联合轴对称变换和平移变换的有关性质,你以为在滑动对称变换进程中,两个对应三角形（如图乙）的对应点所具有的性质是( )(A)对应点连线与对称轴垂直 (B)对应点连线被对称轴等分 (C)对应点连线被对称轴垂直等分 (D)对应点连线互相平行6.对右图的对称性表述,准确的是（ ）．A ．轴对称图形B ．中间对称图形C ．既是轴对称图形又是中间对称图形D ．既不是轴对称图形又不是中间对称图形7.如图,△A′B′C′是由△ABC 经由变换得到的,则这个变换进程是（A ）平移 （B ）轴对称 （C ）扭转 （D ）平移后再轴对称8.如图所示,四边形OABC 是矩形,点A.C 的坐标分离为（3,0）,（0,1）,点D 是线段BC 上的动点（与端点B.C 不重合）,过点D 作直线y ＝－12x ＋b 交折线OAB 于点E ． CBAB ′BA ′BC ′（1）记△ODE 的面积为S,求S 关于b 的函数关系式;（2）当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形OA1B1C1, 9.探讨OA1B1C1与矩形OABC 的重叠部分的面积是否产生变化,若不变,求出该重叠部分的面积;若转变,请解释来由.【答案】（1）由题意得B （3,1）．若直线经由点A （3,0）时,则b ＝32 若直线经由点B （3,1）时,则b ＝52若直线经由点C （0,1）时,则b ＝1①若直线与折线OAB 的交点在OA 上时,即1＜b≤32,如图25-a,此时E （2b,0）∴S ＝12OE·CO ＝12×2b×1＝b ②若直线与折线OAB 的交点在BA 上时,即32＜b ＜52,如图2此时E （3,32b -）,D （2b －2,1） ∴S ＝S 矩－(S △OCD ＋S △OAE ＋S △DBE)＝ 3－[12(2b －1)×1＋12×(5－2b)·(52b -)＋12×3(32b -)]＝252b b - ∴2312535222b b S b b b ⎧<≤⎪⎪=⎨⎪-<<⎪⎩（2）如图3,设O1A1与CB 订交于点M,OA 与C1B1订交于点N,则矩形OA1B1C1与矩形OABC 的重叠部分的面积即为四边形DNEM 的面积.本题答案由无锡市天一试验黉舍金杨建先生草制！由题意知,DM ∥NE,DN ∥ME,∴四边形DNEM 为平行四边形 依据轴对称知,∠MED ＝∠NED又∠MDE ＝∠NED,∴∠MED ＝∠MDE,∴MD ＝ME,∴平行四边形DNEM 为菱形． 过点D 作DH ⊥OA,垂足为H, 由题易知,tan ∠DEN ＝12,DH ＝1,∴HE ＝2, 设菱形DNEM 的边长为a,则在Rt △DHM 中,由勾股定理知：222(2)1a a =-+,∴54a = ∴S 四边形DNEM ＝NE·DH ＝54∴矩形OA1B1C1与矩形OABC 的重叠部分的面积不产生变化,面积始终为54． 10．如图,在平面直角坐标系中,△ ABC 的三个极点的坐标分离为A （0,1）,B （-1,1）,C （-1,3）.（1）画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;（2）画出△ABC绕原点O顺时针偏向扭转90°后得到的△A2B2C2,并写出点C2的坐标;,（3）将△A2B2C2平移得到△ A3B3C3,使点A2的对应点是A3,点B2的对应点是B3,点C2的对应点是C3（4,-1）,在坐标系中画出△ A3B3C3,并写出点A3,B3的坐标.【答案】（1）C1(-1,-3) (2)C2(3,1) (3)A3(2,-2),B3(2,-1)11.分离按下列请求解答：（1）在图1中,将△ABC先向左平移5个单位,再作关于直线AB的轴对称图形,经两次变换后得到△A1B1 C1.画出△A1B1C1;（2）在图2中,△ABC经变换得到△A2B2C2.描写变换进程.【答案】(1) 如图．(2) 将△ABC 先关于点A 作中间对称图形,再向左平移2个单位,得到△A2B2C2．（变换进程不独一）12.(1)不雅察发明0 1 2 3 4 5 6 7 8 9 10 1211 12 11 10 9 8 7 6 5 4 3 2 1ABC0 1 2 3 4 5 6 7 8 9 10 1211 12 11 10 9 8 7 6 5 4 3 2 1ACA 2B 2C 2如题26(a)图,若点A,B在直线l同侧,在直线l上找一点P,使AP+BP的值最小．做法如下：作点B关于直线l的对称点B',衔接AB',与直线l的交点就是所求的点P 再如题26(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小．做法如下：作点B关于AD的对称点,正好与点C重合,衔接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为．题18(a)图题18(b)图(2)实践应用如题26(c)图,已知⊙O的直径CD为4,AD的度数为60°,点B是AD的中点,在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值．题18(c)图题18(d)图(3)拓展延长如题26(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD．保留作图陈迹,不必写出作法．【答案】解：（13（2）如图：作点B关于CD的对称点E,则点E正好在圆周上,衔接OA.OB.OE,衔接AE交CD与一点P,AP+BP最短,因为AD的度数为60°,点B是AD的中点,所以∠AEB=15°,因为B关于CD的对称点E,所以∠BOE=60°,所以△OBE为等边三角形,所以∠OEB=60°,所以∠OEA=45°,又因为OA=OE,所以△OAE为等腰直角三角形,所以AE=22.（3）找B关于AC对称点E,连DE延长交AC于P即可,13.如图所示,A.B两村之间有一条河,河宽为a,现要在河上修一座垂直于河岸的桥,（Ⅰ）要使AB两村旅程比来,请肯定修桥的地点.（Ⅱ）桥建在何处才能使AB两村到桥的距离相等？。
数学将军饮马知识点总结
数学将军饮马知识点总结一、问题描述数学将军饮马问题的描述如下：一个将军率领一支骑兵队，要经过一片沙漠。
沙漠上有一口水井，水井的深度可以满足整支骑兵队的饮水需求。
将军骑着一匹马，可以携带一定数量的水。
现在问题来了，将军每小时可以骑马走一定的距离，而每匹马每小时可以喝一定的水。
现在需要确定将军携带多少水，才能保证整支骑兵队能够成功地跨越沙漠，而又不至于浪费水资源。
二、问题分析1. 数学模型建立数学将军饮马问题首先需要进行问题分析和建模，以确定针对这一问题的数学模型。
通过观察和分析可以得出，这是一个关于时间、距离和水量的问题，需要建立数学关系，建模求解。
2. 走距离与喝水在沙漠中骑马跋涉，对于骑马走的距离和喝水之间的关系需要进行合理的分析和计算。
根据数学将军饮马问题的描述，我们可以得知：将军每小时可以骑马走一定的距离，每匹马每小时可以喝一定的水。
3. 求解根据将军队伍的规模、马的喝水速度和水源的容量，我们需要求解将军携带多少水能够足够整支骑兵队顺利跨越沙漠的问题。
三、相关知识点总结1. 时间、距离与速度的关系在数学将军饮马问题中，时间、距离和速度是密不可分的。
根据题目描述，我们需要确定将军每小时可以骑马走的距离。
这就涉及到了时间、距离和速度的关系。
在实际生活和工作中，我们也经常会遇到时间、距离和速度的计算和关系问题，而这一问题正是数学知识在实际应用中的体现。
2. 水量的计算在数学将军饮马问题中，将军骑马携带的水量是一个重要的问题。
将军需要在保证整支骑兵队能够成功跨越沙漠的前提下，尽量减少携带的水量，避免浪费水资源。
因此，对于将军饮马问题，我们需要进行水量的计算和分析，以确定最合适的携带水量。
3. 最优化问题数学将军饮马问题可以理解为一个最优化问题，在保证整支骑兵队能够成功地跨越沙漠的前提下，需要尽量减少携带的水量，以达到最优化的效果。
这就涉及到了数学中的最优化问题的求解方法，需要通过建立数学模型、分析求解，找到最优的携带水量。
将军饮马问题讲义
将军饮马问题之阳早格格创做唐往诗人李颀的诗《古从军止》启头二句道:"黑日登山视烽火，薄暮饮马傍接河."诗中隐含着一个有趣的数教问题.如图所示，诗中将军正在瞅视烽火之后从山足下的A面出收，走到河边饮马后再到B面宿营.请问何如走才搞使总的路途最短?那个问题早正在古罗马时代便有了，传道亚历山大乡有一位粗通数教战物理的教者，名喊海伦.一天，一位罗马将军博程去考察他，背他请教一个百思不得其解的问题.将军每天从军营A出收，先到河边饮马，而后再去河岸共侧的B天启会，该当何如走才搞使路途最短?今后，那个被称为"将军饮马"的问题广大流传.将军饮马问题=轴对于称问题=最短距离问题（轴对于称是工具，最短距离是题眼）.所谓轴对于称是工具，即那类问题最时常使用的搞法便是做轴对于称.而最短距离是题眼，也便表示着归类那类的题手段缘由.比圆题目时常会出现线段a+b 那样的条件大概者问题.一往出现不妨赶快偶像到将军问题，而后利用轴对于称解题.一．六大模型1.如图，曲线l 战l 的同侧二面A、B，正在曲线l 上供做一面P，使PA+PB 最小.2.如图，曲线l 战l 的共侧二面A、B，正在曲线l 上供做一面P，使PA+PB 最小.3.如图，面P 是∠MON 内的一面，分别正在OM，ON 上做面A，B.使△PAB 的周少最小.4.如图，面P，Q 为∠MON 内的二面，分别正在OM，ON 上做面A，B.使四边形PAQB 的周少最小.5.如图，面A 是∠MON 中的一面，正在射线ON 上做面P，使PA 取面P 到射线OM 的距离之战最小6. .如图，面A 是∠MON 内的一面，正在射线ON 上做面P，使PA 取面P 到射线OM 的距离之战最小罕睹问题最先明黑几个观念，动面、定面、对于称面.动面普遍便是题目中的所供面，即那个大概的面.定面即为题目中牢固的面.对于称的面，做图所得的面，需要连线的面.1. 怎么对于称，做谁的对于称？.简朴道所有题目需要做对于称的面，皆是题手段定面.大概者道惟有定面才不妨去做对于称的.（不决定的面做对于称式不意思的）那么做谁的对于称面?最先要粗确闭于对于称的对于象肯定是一条线，而不是一个面.那么是哪一条线？普遍而止皆是动面天圆曲线.2. 对于称完以去战谁对接？一句话：战其余一个定面贯串.千万于不克不迭战一个动面贯串.粗确一个观念：定面的对于称面也是一个定面.比圆模型二战模型三.3. 所供面怎么决定？最先一定要明黑，所供面末尾反应正在图上一定是个接面.本量便是咱们所绘曲线战已知曲线的接面.底下咱们去瞅瞅将军饮马取二次函数分离的问题：1.如图，扔物线y=ax2+bx+c通过A（1，0）、B（4，0）、C（0，3）三面．（1）供扔物线的剖析式；（2）如图，正在扔物线的对于称轴上是可存留面P，使得四边形PAOC的周少最小？若存留，供出四边形PAOC周少的最小值；若不存留，请证明缘由．【分解】（1）设接面式为y=a（x﹣1）（x﹣4），而后把C面坐标代进供出a=，于是得到扔物线剖析式为y=x2﹣x+3；（2）先决定扔物线的对于称轴为曲线x=，连结BC接曲线x=于面P，如图，利用对于称性得到PA=PB，所以PA+PC=PC+PB=BC，根据二面之间线段最短得到PC+PA最短，于是可推断此时四边形PAOC的周少最小，而后估计出BC=5，再估计OC+OA+BC即可．【解问】解：（1）设扔物线剖析式为y=a（x﹣1）（x﹣4），把C（0，3）代进得a•（﹣1）•（﹣4）=3，解得a=，所以扔物线剖析式为y=（x﹣1）（x﹣4），即y=x2﹣x+3；（2）存留．果为A（1，0）、B（4，0），所以扔物线的对于称轴为曲线x=，连结BC接曲线x=于面P，如图，则PA=PB，PA+PC=PC+PB=BC，此时PC+PA最短，所以此时四边形PAOC的周少最小，果为BC==5，所以四边形PAOC周少的最小值为3+1+5=9．【面评】原题考查了待定系数法供二次函数的剖析式：正在利用待定系数法供二次函数闭系式时，要根据题目给定的条件，采用妥当的要领设出闭系式，进而代进数值供解．普遍天，当已知扔物线上三面时，常采用普遍式，用待定系数法列三元一次圆程组去供解；当已知扔物线的顶面大概对于称轴时，常设其剖析式为顶面式去供解；当已知扔物线取x轴有二个接面时，可采用设其剖析式为接面式去供解．也考查了最短路径问题．2．（2015•上乡区一模）设扔物线y=（x+1）（x﹣2）取x轴接于A、C二面（面A正在面C的左边），取y轴接于面B．（1）供A、B、C三面的坐标；（2）已知面D正在坐标仄里内，△ABD是顶角为120°的等腰三角形，供面D的坐标；（3）若面P、Q位于扔物线的对于称轴上，且PQ=，供四边形ABQP周少的最小值．【考面】二次函数概括题．【分解】（1）令x=0，供出取y轴的坐标；令y=0，供出取x 轴的坐标；（2）分三种情况计划：①当AB为底时，若面D正在AB上圆；若面D正在AB下圆；②当AB为腰时，A为顶面时，③当AB为腰时，A为顶面时；小心解问即可．（3）当AP+BQ最小时，四边形ABQP的周少最小，根据轴对于称最短路径问题解问．【解问】解：（1）当x=0时，y=﹣；当y=0时，x=﹣1大概x=2；则A（﹣1，0），B（0，﹣），C（2，0）；（2）如图，Rt△ABO中，OA=1，OB=，∴AB=2，∠ABO=30°，∠BAO=60°，∴△ABD是顶角为120°的等腰三角形．①当AB为底时，若面D正在AB上圆，由∠ABO=∠BAD=30°，AB=2，得D1（0，﹣），若面D正在AB下圆，由∠BAD=∠DBA=30°，AB=2，得D2（﹣1，﹣），②当AB为腰时，A为顶面时，∵∠DAB=120°，∠OAB=60°，AD=AB=2，∴面D正在y轴大概x轴上，若D正在y轴上，得D3（0，），若D正在x轴上，得D4（﹣3，0）；③当AB为腰时，A为顶面时，若面D正在第三象限，∵∠DBO=150°，BD=2，得D5（﹣1，﹣2）；若面D正在第四象限时，∵DB∥x轴，BD=2，得D6（2，﹣），∴切合央供的面D的坐标为（0，﹣），（﹣1，﹣），（0，），（﹣3，0），（﹣1，﹣2），（2，﹣）；（3）当AP+BQ最小时，四边形ABQP的周少最小，把面B进取仄移个单位后得到B1（0，﹣），∵BB1∥PQ，且BB1=PQ，∴四边形BB1PQ是仄止四边形，∴BQ=B1P，∴AP+BQ=AP+B1P，要正在曲线x=上找一面P，使得AP+B1P最小，做面B1闭于曲线x=的对于称面，得B2（1，﹣），则AB2便是AP+BQ的最小值，AB2==，AB=2，PQ=，∴四边形ABQP的周少最小值是+2．【面评】原题考查了二次函数概括题，波及二次函数取x轴的接面、取y轴的接面、等腰三角形的本量、勾股定理等真量，存留性问题的出现使得易度删大．。
[精选]将军饮马问题(讲)资料
![[精选]将军饮马问题(讲)资料](https://img.taocdn.com/s3/m/cfa30963aa00b52acec7ca14.png)
类型一、基本模式类型二、轴对称变换的应用（将军饮马问题） 2、如图所示，如果将军从马棚M 出发，先赶到河 0A 上的某一位置 P ,再马上赶到河 0B 上的某一位置Q,然后立即返回校场 N.请为将军重新设计一条路线 （即选择点P 和Q ）, 使得总路程M 卉PQ+ QN 最短.0B 上的某一位置 Q.请为将军设计一条路线（即选择点P 和Q ）,使得总路程 M 卉PQ 最短.3、将军要检阅一队士兵，要求 （如图所示）：队伍长为a ,沿河0B 排开（从点P 到点Q ）;将 军从马棚M 出发到达队头P ,从P 至Q 检阅队伍后再赶到校场 N.请问：在什么位置列队（即 选择点P 和Q ）,可以使得将军走的总路程 皿卉PQ^ QN 最短？将军饮马问题【变式】如图所示，将军希望从马棚4.如图，点 边的距离之和最小，再马上赶到河P 至 U 0A5已知/ MON内有一点P, P关于OM ON的对称点分别是召和R, 隅分别交OM, ON于点A B,已知=15,则厶PAB的周长为（A. 15 B 7.5 C. 10 D. 246. 已知/ AOB试在/ AOB内确定一点P,如图，使P到OA OB的距离相等，并且到M N 两点的距离也相等•7、已知/ MON= 40 ° , P为/ MON内一定点，OM上有一点A, ON上有一点B,当△ PAB的周长取最小值时，求/ APB的度数.8. 如图，在四边形ABCD中，/ A= 90°, AD= 4,连接BD, BD丄CD / ADB=Z C.若P是BC边上一动点，贝U DP长的最小值为_______.练习1、已知点A在直线I夕卜，点P为直线I上的一个动点，探究是否存在一个定点B，当点P在直线I上运动时，点P与A、B两点的距离总相等，如果存在，请作出定点 B ;若不存在，请说明理由.A■2、如图，在公路a 的同旁有两个仓库 A 、B ，现需要建一货物中转站，要求到 A 、B 两仓 库的距离和最短，这个中转站 M 应建在公路旁的哪个位置比较合理？A.■BA■----------------------------------------------------- a3、 已知：A 、B 两点在直线I 的同侧， 在I 上求作一点 M ，使得|AM -BM |最小.4、 如图，正方形 ABCD 中，AB =8, M 是DC 上的一点，且 DM =2 , N 是AC 上的一动 点，求DN MN 的最小值与最大值.A B,在坐标轴上找两点 C 、D,使得四边形ABCD 勺周长最小。
最短路径(将军饮马)问题(知识梳理与考点分类讲解)(人教版)(教师版) 24-25学年八年级数学上册
专题13.10最短路径（将军饮马）问题（知识梳理与考点分类讲解）第一部分【知识点归纳】【模型一：两定交点型】如图1，直线l和l的异侧两点A.B，在直线l上求作一点P，使PA+PB 最小；图1【模型二：两定一动型】如图2，直线l和l的同侧两点A.B，在直线l上求作一点P，使PA+PB 最小（同侧转化为异侧）；图2【模型三：一定两动型】如图3，点P是∠MON内的一点，分别在OM，ON上作点A，B。
使△PAB的周长最小。
图3【模型四：两定两动型】如图4，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。
使四边形PAQB的周长最小。
图4【模型五：一定两动（垂线段最短）型】如图5，点A是∠MON外的一点，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。
图5【模型六：一定两动，找（作）对称点转化型】如图6，点A是∠MON内的一点，在射线ON 上作点P，使PA与点P到射线OM的距离之和最小。
图6【考点1】两定一动型；【考点2】一定两动（两点之间线段最短）型；【考点3】一定两动（垂线段最短）型；【考点4】两定两动型；【考点5】一定两动（等线段）转化型；.第二部分【题型展示与方法点拨】【考点1】两定一动型；【例1】（23-24八年级上·全国·课后作业）如图，在ABC ∆中，3,4AB AC ==，EF 垂直平分BC ，交AC 于点D ，则ABP 周长的最小值是（）A ．12B ．6C ．7D ．8【答案】C 【分析】本题主要考查了，轴对称﹣最短路线问题的应用，解此题的关键是找出P 的位置．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，根据题意知点B 关于直线EF 的对称点为点C ，故当点P 与点D 重合时，AP BP +的值最小，即可得到ABP 周长最小．解：∵EF 垂直平分BC ，∴点B ，C 关于EF 对称．∴当点P 和点D 重合时，AP BP +的值最小．此时AP BP AC +=，∵3,4AB AC ==，ABP ∴ 周长的最小值是347AP BP AB AB AC ++=+=+=，故选：C ．【变式】（23-24八年级上·广东广州·期中）如图，在ABC V 中，1216AB AC ==，，20BC =．将ABC V 沿射线BM 折叠，使点A 与BC 边上的点D 重合，E 为射线BM 上的一个动点，则CDE 周长的最小值．【答案】24【详解】设BM 与AC 的交点为点F ，连接AE ，DF 先根据折叠的性质可得12BD AB ==，DF AF =，DE AE =，BDF BAF ∠=∠，再根据两点之间线段最短可得当点E 与点F 重合时，CDE 周长最小，进而求解即可．解：如图，设BM 与AC 的交点为点F ，连接AE ，DF ，由折叠的性质得：12BD AB ==，DF AF =，DE AE =，BDF BAF ∠=∠，20128CD BC BD ∴=-=-=，CDE ∴ 周长8CD DE CE AE CE =++=++，要使CDE 周长最小，只需AE CE +最小，由两点之间线段最短可知，当点E 与点F 重合时，最小值为AC ，∴CDE 周长为：681624AC +=+=．故答案为：24．【点拨】本题考查了折叠的性质等知识点，熟练掌握折叠的性质是解题关键．【考点2】一定两动（两点之间线段最短）型；【例2】（23-24八年级上·湖北省直辖县级单位·期末）如图，45MON ∠=︒，P 为MON ∠内一点，A 为OM 上一点，B 为ON 上一点，当PAB 的周长取最小值时，APB ∠的度数为（）A ．45︒B ．90︒C ．100︒D ．135︒【答案】B 【分析】本题主要考查了最短路线问题、四边形的内角和定理、轴对称的性质等知识点，掌握两点之间线段最短的知识画出图形是解题的关键．如图：作P 点关于OM ON 、的对称点A B ''、，连接A B ''，此时PAB 的周长最小为A B ''，求出A B ''即可．解：如图：作P 点关于OM ON 、的对称点A B ''、，然后连接A B ''，∵点A '与点P 关于直线OM 对称，点B '与点P 关于ON 对称，∴A P OM B P ON A A AP B B BP ''''⊥⊥==，，，，∴A APA B BPB ''''∠=∠∠=∠，，∵A P OM B P ON ''⊥⊥，，∴180MON A PB ''∠+∠=︒，∴18045135A PB ''∠=︒-︒=︒，在A B P ''△中，由三角形的内角和定理可知：18013545A B ''∠+∠=︒-︒=︒，∴45A PA BPB ''∠+∠=︒，∴1354590APB ∠=︒-︒=︒．故选：B ．【变式】（23-24八年级上·江苏无锡·期中）如图，45AOB ∠=︒，点M N 、分别在射线OA OB 、上，5MN =，15OMN S = ，点P 是直线MN 上的一个动点，点P 关于OA 的对称点为1P ，点P 关于OB 的对称点为2P ，连接1OP 、2OP 、12PP ，当点P 在直线MN 上运动时，则12OPP 面积的最小值是．【考点3】一定两动型（垂线段最短）；【例3】（22-23八年级上·湖北武汉·期末）如图，在ABC V 中，3AB =，4BC =，5AC =，AB BC ⊥，点P 、Q 分别是边BC 、AC 上的动点，则AP PQ +的最小值等于（）A ．4B ．245C ．5D ．275【答案】B 【分析】作A 过于BC 的对称点A '，过点A '作A Q AC '⊥，交AC 于点Q ，交BC 于点P ，根据对称可得：AP PQ A P PQ A Q ''+=+≥，得到当,,A P Q '三点共线时，AP PQ +最小，再根据垂线段最短，得到A Q AC '⊥时，A Q '最小，进行求解即可．解：作A 过于BC 的对称点A '，过点A '作A Q AC '⊥，交AC 于点Q ，交BC 于点P ，【变式】（23-24七年级下·陕西西安·阶段练习）如图，在Rt ABC △中，90ACB ∠=︒，3AC =，4BC =，5AB =，AD 是ABC V 的角平分线，若P Q 、分别是AD 和AC 边上的动点，则PC PQ +的最小值是．AD 是BAC ∠的平分线，1QAD Q AD∴∠=∠在AQD 与1AQ D 中【考点4】两定两动型；【例4】如图，已知24AOB ∠=︒，OP 平分AOB ∠，1OP =，C 在OA 上，D 在OB 上，E 在OP 上．当CP CD DE ++取最小值时，此时PCD ∠的度数为（）A ．36︒B ．48︒C ．60︒D ．72︒【答案】D 【分析】作点P 关于OA 的对称点P'，作点E 关于OB 的对称点'E ，连接'OP 、'PP 、'OE 、'EE 、''P E ，则由轴对称知识可知=''CP CD DE CP CD DE ++++，所以依据垂线段最短知：当''P C D E 、、、在一条直线上，且'''P E OE ⊥时，CP CD DE ++取最小值，根据直角三角形的两锐角互余及三角形外角的性质可以'P C PC =，'E D ED =，'1OP OP ==，=''CP CD DE CP CD DE ++++，'P OE ∠''P C D E 、、、在一条直线上，且''P E ''=9048=42OP E ∠︒-︒︒，'='''=7842CP P OP P OP E ∠∠-∠︒-︒=【答案】44βα-=︒【分析】本题考查轴对称—最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题．OQM OQM NQP '∴∠=∠=∠，OPQ ∠∴1(180)2PQN AOB α∠=︒-=∠+∠44βα∴-=︒，故答案为：44βα-=︒．【考点5】一定两动（等线段）转化型；【例5】（20-21八年级上·湖北鄂州·期中）如图，AD 为等腰△ABC 的高，其中∠ACB =50°，AC =BC ，E ，F 分别为线段AD ，AC 上的动点，且AE =CF ，当BF ＋CE 取最小值时，∠AFB 的度数为（）A ．75°B ．90°C ．95°D ．105°【答案】C 【分析】先构造△CFH 全等于△AEC ，得到△BCH 是等腰直角三角形且FH=CE ，当FH+BF 最小时，即是BF+CE 最小时，此时求出∠AFB 的度数即可．解：如图，作CH ⊥BC ，且CH=BC ，连接HB ，交AC 于F ，此时△BCH 是等腰直角三角形且FH+BF 最小，∵AC=BC ，∴CH=AC ，∵∠HCB=90°，AD ⊥BC ，∴AD//CH ，∵∠ACB=50°，∴∠ACH=∠CAE=40°，∴△CFH ≌△AEC ，∴FH=CE ，∴FH+BF=CE+BF 最小，此时∠AFB=∠ACB+∠HBC=50°+45°=95°．故选：C ．【点拨】本题考查全等三角形的性质和判定、等腰三角形的性质、最短路径问题，关键是作出辅助线，有一定难度．【变式】（23-24七年级下·四川宜宾·期末）在ABC V 中，80CAB ∠=︒，2AB =，3AC =，点E 是边AB 的中点，CAB ∠的角平分线交BC 于点D ．作直线AD ，在直线AD 上有一点P ，连结PC 、PE ，则PC PE -的最大值是．∵CAB ∠的角平分线交∴FAP ∠∠=∵AP AP =，∴APF APE ≌∴PF PE =，第三部分【中考链接与拓展延伸】1、直通中考【例1】（2020·湖北·中考真题）如图，D 是等边三角形ABC 外一点．若8,6BD CD ==，连接AD ，则AD 的最大值与最小值的差为．【答案】12【分析】以CD 为边向外作等边三角形CDE ，连接BE ，可证得△ECB ≌△DCA 从而得到BE=AD ，再根据三角形的三边关系即可得出结论．解：如图1，以CD 为边向外作等边三角形CDE ，连接BE ，∵CE=CD ，CB=CA ，∠ECD=∠BCA=60°，∴∠ECB=∠DCA ，∴△ECB ≌△DCA （SAS ），∴BE=AD ，∵DE=CD=6，BD=8，∴8-6<BE<8+6，∴2<BE<14，∴2<AD<14．∴则AD 的最大值与最小值的差为12．故答案为：12【点拨】本题考查三角形全等与三角形的三边关系，解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解，是一道较好的中考题．【例2】（2020·新疆·中考真题）如图，在ABC V 中，90,60,4A B AB ∠=∠=︒=︒，若D 是BC 边上的动点，则2AD DC +的最小值为．在Rt DFC △中，30DCF ∠=︒，12DF DC ∴=，122()2AD DC AD DC +=+2()AD DF =+，∴当A ，D ，F 在同一直线上，即此时，60B ADB ∠=∠=︒，2、拓展延伸【例1】（23-24八年级上·江苏镇江·阶段练习）如图，AC 、BD 在AB 的同侧，点M 为线段AB 中点，2AC =，8BD =，8AB =，若120CMD ∠=︒，则CD 的最大值为（）A ．18B ．16C ．14D ．12【答案】C 【分析】本题考查等边三角形的判定和性质，两点之间线段最短，解题的关键是学会添加常用辅助线，学会利用两点之间线段最短解决最值问题．如图，作点A 关于CM 的对称点A '，点B 关于DM 的对称点B '，证明'' A MB 为等边三角形，即可解决问题．解：如图，作点A 关于CM 的对称点A '，点B 关于DM 的对称点B '，∵120CMD ∠=︒，∴60∠+∠=︒AMC DMB ，∴60''∠+∠=︒CMA DMB ，∴60''∠=︒A MB ，∵MA MB MA MB ''===，∴'' A MB 为等边三角形∵14CD CA A B B D CA AM BD ''''<++=++=，∴CD 的最大值为14，故选：C ．【例2】（22-23八年级上·湖北武汉·期末）如图，锐角ABC V 中，302A BC ∠=︒=，，ABC V 的面积是6，D 、E 、F 分别是三边上的动点，则DEF 周长的最小值是（）A ．3B ．4C ．6D ．7∴AM AE AN ==，MF =∵BAC BAD DAC ∠=∠+∠∴MAN MAB BAD ∠=∠+∠∴(2MAN BAE EAC ∠=∠+∠。
将军饮马问题(讲)电子教案
将军饮马问题(讲)将军饮马问题类型一、基本模式类型二、轴对称变换的应用（将军饮马问题）2、如图所示，如果将军从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB上的某一位置Q，然后立即返回校场N．请为将军重新设计一条路线(即选择点P和Q)，使得总路程MP＋PQ＋QN最短．【变式】如图所示，将军希望从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB上的某一位置Q．请为将军设计一条路线(即选择点P和Q)，使得总路程MP＋PQ最短．3、将军要检阅一队士兵，要求(如图所示)：队伍长为a，沿河OB排开(从点P到点Q)；将军从马棚M出发到达队头P，从P至Q检阅队伍后再赶到校场N．请问：在什么位置列队(即选择点P和Q)，可以使得将军走的总路程MP＋PQ＋QN最短?4. 如图，点M在锐角∠AOB内部，在OB边上求作一点P，使点P到点M的距离与点P到OA边的距离之和最小5已知∠MON内有一点P，P关于OM，ON的对称点分别是和，分别交OM, ON于点A、B，已知＝15，则△PAB 的周长为（）A. 15 B 7.5 C. 10 D. 246. 已知∠AOB，试在∠AOB内确定一点P，如图，使P到OA、OB的距离相等，并且到M、N 两点的距离也相等.7、已知∠MON＝40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，求∠APB的度数.8. 如图，在四边形ABCD中，∠A＝90°，AD＝4，连接BD，BD⊥CD，∠ADB＝∠C.若P是BC边上一动点，则DP长的最小值为______.练习1、已知点A在直线l外，点P为直线l上的一个动点，探究是否存在一个定点B，当点P 在直线l上运动时，点P与A、B两点的距离总相等，如果存在，请作出定点B；若不存在，请说明理由．2、如图，在公路a 的同旁有两个仓库A 、B ，现需要建一货物中转站，要求到A 、B 两仓库的距离和最短，这个中转站M 应建在公路旁的哪个位置比较合理？aBA3、 已知：A 、B 两点在直线l 的同侧， 在l 上求作一点M ，使得||AM BM -最小．4、如图，正方形ABCD 中，8AB =，M 是DC 上的一点，且2DM =，N 是AC 上的一动点，求DN MN +的最小值与最大值．NMD CB A5、如图，已知∠AOB 内有一点P ，试分别在边OA 和OB 上各找一点E 、F ，使得△PEF 的周长最小。
将军饮马问题(解析版)
将军饮马问题模型的概述：唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B 点宿营。
问如何行走才能使总的路程最短。
模型一(两点在河的异侧)：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B 点宿营，将在何处渡河使行走距离最短并求最短距离。
方法：如右图，连接AB，与线段L交于点M,在M处渡河距离最短，最短距离为线段AB的长。
模型二(两点在河的同侧)：将军在观望烽火之后从山脚下的A点出发，需先走到河边让战马饮水后再到B点宿营，将在何处渡河使行走距离最短并求最短距离。
方法：如右图，作点B关于直线L的对称点B'，连接AB',与直线L的交点即为所求的渡河点，最短距离为线段AB'的长。
模型三：如图，将军同部队行驶至P处，准备在此驻扎，但有哨兵发现前方为两河AB、BC的交汇处，为防止敌军在对岸埋伏需派侦察兵到河边观察，再返回P处向将军汇报情况，问侦察兵在AB、BC何处侦查才能最快完成任务并求最短距离。
数学描述：如图在直线AB、BC上分别找点M、N，使得∆PMN周长最小。
方法：如右图，分别作点P关于直线AB、BC的对称点P'、P''，连接P'P''，与两直线的交点即为所求点M、N，最短距离为线段P'P''的长。
模型四如图，深夜为防止敌军在对岸埋伏，将军又派一队侦察兵到河边观察，并叮嘱观察之后先去存粮位置点Q处查看再返回P处向将军汇报情况，问侦察在AB、BC何处侦查才能最快完成任务并求最短距离。
数学描述：如图在直线AB、BC上分别找点M、N，使得四边形PQNM周长最小。
方法：如右图，分别作点P、点Q关于直线AB、BC的对称点P'、Q'，连接P'Q'，与两直线的交点即为所求点M、N，最短距离为线段(PQ+P'Q')的长。
将军饮马问题16大模型
将军饮马问题16大模型将军饮马问题源于中国古代的一个寓言故事，讲述的是三位将军跟随他们的军队来到一座河边准备渡河，但只有一条小船，这条小船一次只能搭载两人。
如果将军A和将军B在船上，将军C在岸边，将军C将会受到辱骂，如果将军A和将军C在船上，将军B在岸边，将军B也会受到辱骂，问题是如何让这三位将军都安全地渡河而不受辱骂。
这个问题启发了许多数学家和逻辑学家，有各种不同的解法。
下面将介绍将军饮马问题的16种不同模型。
模型1：最直接的解法最直接的解法是将将军A和将军B一同乘坐小船去对岸，然后将将军A带船返回，将将军C载到对岸。
模型2：穷举法穷举法是一种比较笨拙但可以解决问题的方法，即穷尽所有可能的情况。
这种方法虽然有效，但耗时较长。
模型3：递归法递归法是将问题分解成较小规模的子问题，并逐步解决。
这种方法可以节省时间和精力，但需要较高的逻辑思维能力。
模型4：数学推导法通过数学推导，可以将将军饮马问题转化为数学模型，从而得出解答。
这种方法需要较强的数学功底。
模型5：逻辑推理法逻辑推理法是通过逻辑推理和思维分析，得出解决将军饮马问题的方法。
这种方法强调思维的逻辑性和推理能力。
模型6：图论模型图论是数学的一个分支，可以用来描述将军饮马问题中的交叉关系和路径规划。
通过构建相应的图模型，可以更清晰地解决问题。
模型7：概率模型概率模型是通过概率计算和推测，找出解决将军饮马问题的可能性和概率分布。
这种方法适用于对问题进行全面分析和评估。
模型8：动态规划法动态规划法是针对多阶段决策问题的一种解决方法，可以在问题空间中寻找最优解。
这种方法适用于将军饮马问题的场景。
模型9：模拟法模拟法是通过模拟将军饮马问题的场景，以实验测算的方式找出最佳解决方案。
这种方法可以直观地展示问题的复杂性和解决路径。
模型10：启发式算法启发式算法是通过启发性的思考和优化方法，寻找将军饮马问题的最佳解决方案。
这种方法可以在复杂问题中找到较好的解决途径。
将军饮马问题讲义
将军饮马问题唐朝诗人李的诗开头两句说:"白日登山望烽火,黄昏饮马傍交河. "诗中隐含着一个有趣的数学问题.如图所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后再到B点宿营.请问怎样走才能使总的路程最短这个问题早在古罗马时代就有了,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短从此,这个被称为"将军饮马"的问题广泛流传.将军饮马问题=轴对称问题=最短距离问题轴对称是工具,最短距离是题眼;所谓轴对称是工具,即这类问题最常用的做法就是作轴对称;而最短距离是题眼,也就意味着归类这类的题目的理由;比如题目经常会出现线段 a+b 这样的条件或者问题;一旦出现可以快速联想到将军问题,然后利用轴对称解题;一．六大模型1.如图,直线l 和l 的异侧两点A、B,在直线l 上求作一点P,使PA+PB 最小;2.如图,直线l 和l 的同侧两点A、B,在直线l 上求作一点P,使PA+PB 最小;3.如图,点P 是∠MON 内的一点,分别在OM,ON 上作点A,B;使△PAB 的周长最小.4.如图,点P,Q 为∠MON 内的两点,分别在OM,ON 上作点A,B;使四边形PAQB 的周长最小;5.如图,点A 是∠MON 外的一点,在射线ON 上作点P,使PA 与点P 到射线OM 的距离之和最小6. .如图,点A 是∠MON 内的一点,在射线ON 上作点P,使PA 与点P 到射线OM 的距离之和最小常见问题首先明白几个概念,动点、定点、对称点;动点一般就是题目中的所求点,即那个不定的点;定点即为题目中固定的点;对称的点,作图所得的点,需要连线的点;1. 怎么对称,作谁的对称;简单说所有题目需要作对称的点,都是题目的定点;或者说只有定点才可以去作对称的;不确定的点作对称式没有意义的那么作谁的对称点首先要明确关于对称的对象肯定是一条线,而不是一个点;那么是哪一条线一般而言都是动点所在直线;2. 对称完以后和谁连接一句话：和另外一个定点相连;绝对不能和一个动点相连;明确一个概念：定点的对称点也是一个定点;例如模型二和模型三;3. 所求点怎么确定首先一定要明白,所求点最后反应在图上一定是个交点;实际就是我们所画直线和已知直线的交点;下面我们来看看将军饮马与二次函数结合的问题：1.如图,抛物线y=ax2+bx+c经过A1,0、B4,0、C0,3三点．1求抛物线的解析式；2如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小若存在,求出四边形PAOC周长的最小值；若不存在,请说明理由．分析1设交点式为y=ax﹣1x﹣4,然后把C点坐标代入求出a=,于是得到抛物线解析式为y=x2﹣x+3；2先确定抛物线的对称轴为直线x=,连结BC交直线x=于点P,如图,利用对称性得到PA=PB,所以PA+PC=PC+PB=BC,根据两点之间线段最短得到PC+PA最短,于是可判断此时四边形PAOC的周长最小,然后计算出BC=5,再计算OC+OA+BC即可．解答解：1设抛物线解析式为y=ax﹣1x﹣4,把C0,3代入得a﹣1﹣4=3,解得a=,所以抛物线解析式为y=x﹣1x﹣4,即y=x2﹣x+3；2存在．因为A1,0、B4,0,所以抛物线的对称轴为直线x=,连结BC交直线x=于点P,如图,则PA=PB,PA+PC=PC+PB=BC,此时PC+PA最短,所以此时四边形PAOC的周长最小,因为BC==5,所以四边形PAOC周长的最小值为3+1+5=9．点评本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解．一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解．也考查了最短路径问题．2．2015上城区一模设抛物线y=x+1x﹣2与x轴交于A、C两点点A在点C的左边,与y轴交于点B．1求A、B、C三点的坐标；2已知点D在坐标平面内,△ABD是顶角为120°的等腰三角形,求点D的坐标；3若点P、Q位于抛物线的对称轴上,且PQ=,求四边形ABQP周长的最小值．考点二次函数综合题．分析1令x=0,求出与y轴的坐标；令y=0,求出与x轴的坐标；2分三种情况讨论：①当AB为底时,若点D在AB上方；若点D在AB下方；②当AB为腰时,A 为顶点时,③当AB为腰时,A为顶点时；仔细解答即可．3当AP+BQ最小时,四边形ABQP的周长最小,根据轴对称最短路径问题解答．解答解：1当x=0时,y=﹣；当y=0时,x=﹣1或x=2；则A﹣1,0,B0,﹣,C2,0；2如图,Rt△ABO中,OA=1,OB=,∴AB=2,∠ABO=30°,∠BAO=60°,∴△ABD是顶角为120°的等腰三角形．①当AB为底时,若点D在AB上方,由∠ABO=∠BAD=30°,AB=2,得D10,﹣,若点D在AB下方,由∠BAD=∠DBA=30°,AB=2,得D2﹣1,﹣,②当AB为腰时,A为顶点时,∵∠DAB=120°,∠OAB=60°,AD=AB=2,∴点D在y轴或x轴上,若D在y轴上,得D30,,若D在x轴上,得D4﹣3,0；③当AB为腰时,A为顶点时,若点D在第三象限,∵∠DBO=150°,BD=2,得D5﹣1,﹣2；若点D在第四象限时,∵DB∥x轴,BD=2,得D62,﹣,∴符合要求的点D的坐标为0,﹣,﹣1,﹣,0,,﹣3,0,﹣1,﹣2,2,﹣；3当AP+BQ最小时,四边形ABQP的周长最小,把点B向上平移个单位后得到B10,﹣,∵BB1∥PQ,且BB1=PQ,∴四边形BB1PQ是平行四边形,∴BQ=B1P,∴AP+BQ=AP+B1P,要在直线x=上找一点P,使得AP+B1P最小,作点B1关于直线x=的对称点,得B21,﹣,则AB2就是AP+BQ的最小值,AB2==,AB=2,PQ=,∴四边形ABQP的周长最小值是+2．点评本题考查了二次函数综合题,涉及二次函数与x轴的交点、与y轴的交点、等腰三角形的性质、勾股定理等内容,存在性问题的出现使得难度增大．。
最新中考数学练习题-将军饮马问题 讲义
将军饮马(作对称点求最短线段终极版)背景知识：早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．常用知识点：两点之间线段最短，垂线段最短，三角形三边关系，轴对称，平移；解题思路：找对称点，变折线为直线。
常见模型：一、两定点一动点型：如图：在定直线l上找一个动点P，使动点P到两个定点A与B 的距离之和最小，即PA+PB最小。
解题思路：连接AB，与直线的交点为点Q，即此时点P运动到点Q处，最小值为AB.证明：运用三角形三边关系：两边之和大于第三边，当A、P、B三点共线可取等于。
在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.解题思路：作定点B关于直线l的对称点C,连接AC,交直线于点Q，当点P运动到点Q，最小值为AC.证明：关键是作其中一个定点的对称点，使得PB=PC，求PA+PB的最小值，即求PA+PC的最小值。
再转化为上述题型。
引申1：此题型也可以求PBPA-值最大。
解题思路：延长AB交直线l于点Q,当点P运动到点Q，PBPA-最大值为AB.证明：三角形任意两边之差小于第三边，当A、B、P三点共线可取等于.(提示：如果两定点不在直线的同侧，可以作其中一个定点关于直线l 的对称点)引申2：此题型也可以求PBPA-值最小。
解题思路：连接AB，作AB的垂直平分线角l于点P.证明：垂直平分线上的点到线段的两端距离相等，可得PA=PB二.两动点一定点型（两动点在角的两边上）如图，在∠MON的内部有一点A，在OM上找一点B，在ON 上找一点C，使得△BAC周长最短．解题思路：作点A关于OM的对称点'A，作点A关于ON的对称点''A，连接'''AA，与OM交于点B，与ON交于点C，连接AB，AC，此△ABC周长最短．证明：两点之间，线段最短变式1：如图：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得AB＋BC最短．解题思路:作点A关于OM的对称点'A，过点'A作CA'⊥ON，交OM 于点B，交ON于点C,即为所求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4. 如图，点 边的距离之和最小类型一、基本模式类型二、轴对称变换的应用（将军饮马问题）2、如图所示，如果将军从马棚 M 出发，先赶到河 OA 上的某一位置 P ，再马上赶到河 OB 上的某一位置 Q ，然后立即返回校场 N ．请为将军重新设计一条路线 （即选择点 P 和 Q ）， 使得总路程 MP ＋ PQ ＋QN 最短．3、将军要检阅一队士兵，要求 （如图所示 ） ：队伍长为 a ，沿河 OB 排开（从点 P 到点 Q ）；将 军从马棚 M 出发到达队头 P ，从 P 至 Q 检阅队伍后再赶到校场 N ．请问：在什么位置列队 （即 选择点 P 和 Q ），可以使得将军走的总路程 MP ＋PQ ＋ QN 最短?将军饮马问题变式】如图所示，将军希望从马棚 OB 上的某一位置 Q ．请为将军设计一条路线 MP ＋PQ 最短．，再马上赶到河P 到5 已知∠ MON内有一点 P，P 关于 OM，ON的对称点分别是和，分别交 OM, ON于点A、B，已知＝ 15，则△ PAB 的周长为( )A. 15 B 7.5 C. 10 D. 246. 已知∠ AOB，试在∠ AOB内确定一点 P，如图，使 P 到 OA、OB的距离相等，并且到 M、N两点的距离也相等 .7、已知∠ MON＝ 40， P为∠ MON内一定点， OM上有一点 A，ON上有一点 B，当△PAB的周边上一动点，则 DP长的最小值为练习1、已知点A在直线l 外，点P为直线l 上的一个动点，探究是否存在一个定点B，当点P在直线l 上运动时，点P 与A 、B 两点的距离总相等，如果存在，长取最小值时，求∠APB的度数 .8. 如图，在四边形ABCD中，∠ A＝90°，ADB＝∠ C.若 P 是请作出定点 B ；若不存在，请说明理由．2、 如图，在公路 a 的同旁有两个仓库 A 、 B ，现需要建一货物中转站，要求到 A 、B 两仓 库的距离和最短，这个中转站 M 应建在公路旁的哪个位置比较合理？ABa3、 已知： A 、B 两点在直线 l 的同侧， 在l 上求作一点 M ，使得 |AM BM |最小．4、如图，正方形 ABCD 中， AB 8， M 是DC 上的一点，且 DM 2， N 是 AC 上的一动 点，求 DN MN 的最小值与最大值．5、如图，已知∠ AOB 内有一点 最小。
试画出图形，并说明理由。
A 、B, 在坐标轴上找两点 C 、D,使得四边形 ABCD 的周长最小。
.A6、如图，直角坐标系中有两点 MP ，试分别在边7、如图，村庄 A 、B 位于一条小河的两侧，若河岸 a 、b 彼此平行，现在要建设一座与河岸 垂直的桥 CD ，问桥址应如何选择，才能使 A 村到 B 村的路程最近？最小时，求 a 的值 .10、如图，在等腰梯形 ABCD 中， AB=CD=AD=，2∠ D=120°，点 E 、F 是底边 AD 与 BC 的中点， 连接 EF ，在线段 EF 上找一点 P ，使 BP+AP 最短．练习1、观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有（ ）A ．1 个B ．2个C ．3个D ．4 个2、以下图形中，既是轴对称图形，又是中心对称图形的是（ ）3、在下列四个图案中既是轴对称图形，又是中心对称图形的是4 ,当 x 为何值时， y 的值最小， 并求出这个最小值9、在平面直角坐标系中， A(1，-3) 、B(4 ，-1) P(a,0) 、 N(a+2,0), 当四边形 PABN 的周长A ．等边三角形B ．矩形C ．等腰梯形D ．平行四边形8、y x 21(9 x)24、在等边三角形、 正方形、菱形和等腰梯形这四个图形中， 是中心对称图形的个数为 （ ） A ．1个 B ．2个 C ．3个 D ．4 个5、把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们 把这样的图形变换叫做滑动．对．称．变．换．． ．在自然界和日常生活中， 大量地存在这种图形变 换（如图甲）．结合轴对称变换和平移变换的有关性质， 你认为在滑．动．对．称．变．换． 过程中，两个对应三角形（如图乙）的对应点所具有的性质是 （ ） （A ） 对应点连线与对称轴垂直 （B ） （C ） 对应点连线被对称轴垂直平分 （D ）6、对右图的对称性表述，正确的是（ ）．D ．既不是轴对称图形又不是中心对称图形对应点连线被对称轴平分A ．轴对称图形B ．中心对称图形C ．既是轴对称图形又是中心对称图形7、如图，△ A ′ B ′ C′是由△ ABC 经过变换得到的，则这个变换过程是 A ）平移B ）轴对称 （C ）旋转D ）平移后再轴对称A ′BB ′BC ′AC8、如图所示，四边形OABC是矩形，点A、C 的坐标分别为（ 3，0），（0，1），点D 是线段1BC上的动点（与端点B、C不重合），过点D作直线y ＝－x＋b 交折线OAB 于点E．2（1）记△ ODE的面积为S，求S关于b 的函数关系式；（2）当点E 在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B1C1，9、探究OA1B1C1 与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由 .【答案】（1）由题意得 B（ 3，1）．3若直线经过点A（3， 0）时，则b＝25若直线经过点B（3， 1）时，则b＝2若直线经过点C（0， 1）时，则b＝13 ①若直线与折线OAB的交点在OA上时，即 1<b≤ ，如图 25-a，2此时E（ 2b，0）11∴S＝OE·CO＝×2b×1＝b22 35 ②若直线与折线OAB的交点在BA上时，即3<b< 5，如图 23此时E（3，b ），D（2b－2，1）25∴S 四边形 DNEM ＝ NE · DH ＝4∴矩形 OA 1B 1C 1 与矩形 OABC 的重叠部分的面积不发生变化，面积始终为10．如图，在平面直角坐标系中，△ABC 的三个顶点的坐标分别为 A （0,1），B （-1,1 ），C（-1,3 ）。
（1）画出△ ABC 关于 x 轴对称的△ A 1B 1C 1，并写出点 C 1 的坐标；（2）画出△ ABC 绕原点 O 顺时针方向旋转 90°后得到的△ A 2B 2C 2，并写出点 C 2 的坐标；，（3）将△ A 2B 2C 2 平移得到△ A 3B 3C 3，使点 A 2 的对应点是 A 3，点 B 2 的对应点是 B 3 ，点 C 2的对应点是 C 3（ 4， -1 ），在坐标系中画出△ A 3B 3C 3，并写出点 A 3， B 3的坐标。
∴S ＝S 矩－ ( S △OCD ＋ S △OAE ＋S △DBE )1 ＝ 3 － [ (2b 2－1）×1＋1 5 1 3 5 ×(5－2b )·( b )＋ ×3( b )] ＝ b b2b∴S5b2b23 2 5 2M ，OA 与 C 1B 1相交于点 N ，则矩形 OA 1B 1C 1 与矩形 DNEM 的面积。
本题答案由无锡市天一实验学校金杨建老师草制！2）如图 3，设 O 1A 1 与 CB 相交于点 的重叠部分的面积即为四边形OABC由题意知， DM ∥ NE ，DN ∥ ME ，∴四边形 DNEM 为平行四边形 根据轴对称知，∠ MED ＝∠ NED又∠ MDE ＝∠ NED ，∴∠ MED ＝∠ MDE ，∴ MD ＝ME ，∴平行四边形 过点 D 作 DH ⊥ OA ，垂足为 H ，1由题易知， tan ∠DEN ＝ ， DH ＝ 1，∴ HE ＝2，2DNEM 为菱形． 则在 Rt △DHM 中，由勾股定理知：2 2 2a2(2 a)2 12，∴ a答案】1) C1(-1,-3) (2)C2(3,1) (3)A3(2,-2),B3(2,-1) 11、分别按下列要求解答：（1）在图 1中,将△ ABC先向左平移 5个单位,再作关于直线AB的轴对称图形 ,经两次变换后得到△ A1B1 C1.画出△ A1B1C1；（2）在图 2 中, △ ABC经变换得到△ A2B2C2. 描述变换过程 .0 1 2 3 4 5 6 7 8 9 10 11 12答案】(1) 如图．(2) 将△ ABC 先关于点 A 作中心对称图形 , 再向左平移2 个单位 , 得到△ A 2B 2C 2．(变换过程不唯一)12、 (1) 观察发现如题 26(a) 图，若点 A ，B 在直线 l 同侧，在直线 l 上找一点 P ，使 AP+BP 的值最小． 做法如下：作点 B 关于直线 l 的对称点 B ，连接 AB ，与直线 l 的交点就是所求的点 P 再如题 26(b) 图，在等边三角形 ABC 中，AB=2，点 E 是 AB 的中点， AD 是高，在 AD 上找 一点 P ，使 BP+PE 的值最小．做法如下：作点 B 关于 AD 的对称点，恰好与点 C 重合，连接 CE 交 AD 于一点，则这 点就是所求的点 P ，故 BP+PE 的最小值为 ．题 18(a) 图(2) 实践运用 如题 26(c) 图，已知⊙ O 的直径 CD 为 4，AD 的度数为 60°，点 B 是 ?AD的题 18(b) 图中点，在直径 CD 上找一点 P，使 BP+AP的值最小，并求 BP+AP的最小值．（3） 拓展延伸 如题 26（d ） 图，在四边形 ABCD 的对角线 AC 上找一点 P ，使∠ APB=∠ APD ．保留 作图痕迹，不必写出作法．作点 B 关于 CD 的对称点 E ，则点 E 正好在圆周上，连接 一点 P ， AP+BP 最短，因为 AD 的度数为 60°，点 B 是 ?AD 的中点， 所以∠AEB=15°，因为 B 关于 CD 的对称点 E ，所以∠ BOE=60°，所以△ OBE 为等边三角形，所以∠ OEB=60°，所以∠ OEA=45°，又因为 OA=OE ，所以△ OAE 为等腰直角三角形，所以 AE=2 2 .（3）找 B 关于 AC 对称点 E ，连 DE 延长交 AC 于 P 即可，OA 、 OB 、 OE ，连接 AE 交 CD 与答案】2）如图：13、如图所示， A、B 两村之间有一条河，河宽为 a，现要在河上修一座垂直于河岸的桥，（Ⅰ）要使 AB两村路程最近，请确定修桥的地点。
（Ⅱ）桥建在何处才能使 AB 两村到桥的距离相等？。