华师大版-数学-九年级上册-第24章 解直角三角形检测题
华师大版九年级上册数学第24章 解直角三角形含答案(历年考试题)

华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,在正方形中,是等边三角形,,的延长线分别交于点,,连接,,与相交于点.有下列结论:① ;② ;③ ;④.其中正确的个数是()A.1B.2C.3D.42、如图,一艘船由港沿北偏东65°方向航行至港,然后再沿北偏西40°方向航行至港,港在港北偏东20°方向,则,两港之间的距离为().A. B. C. D.3、如图,中,,,,若,则的长为()A.6B.C.7.5D.104、如图,⊙O直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足M,OM:OD=3:5,则AB 的长是()A. cmB. cmC. cmD. cm5、等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )A.16B.18C.20D.16或206、△ABC中,∠B=90°,AC=,tan∠C=,则BC边的长为()A.2B.2C.D.47、以长为8cm、6cm、10cm、4cm的四条线段中的三条线段为边,可以画出三角形的个数为()A.1个B.2个C.3个D.4个8、如图,小明站在某广场一看台C处,测得广场中心F的俯角为21°,若小明身高CD=1.7米,BC=1.9米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10.5米,则看台底端A点距离广场中心F点的距离约为()米.(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)A.8.9B.9.7C.10.8D.11.99、如图,在直角坐标系中,四边形 OABC 为菱形,对角线 OB、AC 相交于 D 点,已知 A点的坐标为(10,0),双曲线 y= ( x>0 )经过 D 点,交BC 的延长线于 E 点,且OB•AC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=(x>0);②E 点的坐标是(4,6);③sin∠CO A= ;④EC= ;⑤AC+OB=8 .其中正确的结论有()A.4 个B.3 个C.2 个D.1 个10、如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是()A. B. C. D.11、如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是()A.①②③B.①②④C.①③④D.①②③④12、两根木棒分别长5cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长是偶数(单位:cm),则一共可以构成不同的三角形有()A.4个B.5个C.8个D.10个13、三角形两条边分别为3和7,则第三边可以为()A.9B.3C.2D.1014、下列长度的各组线段中可组成三角形的是( )A.1,2,3B.2,3,5C.3,3,6D. ,,15、以长为3cm,5cm,7cm,10cm的四条线段中的三条线段为边可以画出三角形的个数为( )A.1B.2C.3D.4二、填空题(共10题,共计30分)16、如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A 时,则点M运动路径的长为________.17、如图,在平面直角坐标系中,点A的坐标(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为________.18、如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为________米.19、如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为________米.20、如图△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若cos∠BDC= ,则BC的长为________.21、已知三角形的两边长是3和4,周长是偶数,则这样的三角形的第三边是________.22、如图,当太阳光与地面成角时,直立于地面的玲玲测得自己的影长为1.25m,则玲玲的身高约为________ m.(精确到0. 01m)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428).23、将一张长方形纸片ABCD如图所示折叠,使顶点C落在点,已知,,则折痕DE的长为________(用含a的式子表示).24、如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。
华师大版九年级上册数学第24章 解直角三角形含答案【完整版】

华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题,共计45分)1、下列各组长度的线段能构成三角形的是()A.1,2,4B.4,5,9C.4,6,8D.5,5,112、如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于,则sin∠CAB=()A. B. C. D.3、如图,已知菱形ABCD,DF1BC交AC于点,交C于点F,若tan∠BDF= ,AB=30,则CE的长是()A. B. C. D.4、在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为()(提示:可以构造平行四边形)A.2<AD<14B.1<AD<7C.6<AD<8D.12<AD<165、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,则AC长为()A.4B.2C.1D.6、如图,矩形ABCD的对角线AC、BD相交于点O,AB:BC=2:1,且BE∥AC,CE∥DB,连接DE,则tan∠EDC=()A. B. C. D.7、如图,小颖身高为160cm,在阳光下影长AB=240cm,当她走到距离墙角(点D)150cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为()A.50B.60C.70D.808、将下列长度的三根木棒首尾顺次连接,能组成直角三角形的一组是()A.2、4、6B.4、6、8C.8、10、12D.6、8、109、如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为()A. B. C. D.310、如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;② ;③当0<t≤5时,;④当秒时,△ABE∽△QBP;其中正确的结论是()A.①②③B.②③C.①③④D.②④11、在下面四根木棒中,选一根能与长为4cm,9cm的两根木棒首尾依次相接钉成一个三角形的是()A.4cmB.5cmC.9cmD.13cm12、下列是无理数的是()A. B. C.0.202002000… D.13、已知三角形两边长分别为2和9,第三边的长为二次方程x2-14x+48=0的一根,则这个三角形的周长为( )A.11B.17C.17或19D.1914、在△ABC中,∠C=90°,cosA=, AC=6,则AB的长度为()A.8B.10C.12D.1415、如图,⊙O的直径AB=2,点C在⊙O上,弦AC=1,则∠D的度数是()A.30°B.60°C.45°D.75°二、填空题(共10题,共计30分)16、如图,在△ABC中,AB=AC=5,BC=8.若∠BPC= ∠BAC,则tan∠BPC=________.17、如图,在Rt△ABC中,∠ACB=90°,,CM是斜边AB的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=________.18、点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°, 点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是________.19、一个直角三角形斜边上的高与中线分别是5㎝和6㎝,则它的面积是________ .20、等腰三角形的两边长为3 和,那么它的周长为________.21、如图,已知,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE.点P,C,E在一条直线上,,M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为________.22、在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则的长度为________.23、如图,Rt△ACB中,∠ACB=90°,AC=2BC=4,点P为AB边中点,点D为AC 边上不与端点重合的一动点,将△ADP沿着直线PD折叠得△PDE,若DE⊥AB,则AD的长度为________。
华东师大版九上数学24章《解直角三角形》单元测试题(含答案)

华东师大版九上数学24章《解直角三角形》单元测试题(含答案)解直角三角形测试题一. 选择题:(每小题2分,共20分)1. 在△EFG 中,∠G=90°,EG=6,EF=10,则cotE=() A.43 B.34 C. 53 D. 352. 在△ABC 中,∠A=105°,∠B=45°,tanC 的值是() A. 21 B. 33 C. 1 D. 3 3. 在△ABC 中,若22cos =A ,3tan =B ,则这个三角形一定是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形4. 如图18,在△EFG 中,∠EFG=90°,FH ⊥EG ,下面等式中,错误的是()A.EGEF G =sin B. EF EH G =sin C. FGGH G =sin D. FG FH G =sin 5. sin65°与cos26°之间的关系为()A. sin65°<cos26°< p="">B. sin65°>cos26°C. sin65°=cos26°D. sin65°+cos26°=16. 已知30°<α<60°,下列各式正确的是()A. B. C. D.7. 在△ABC 中,∠C=90°,52sin =A ,则sinB 的值是() A.32 B.52 C.54 D. 521 8. 若平行四边形相邻两边的长分别为10和15,它们的夹角为60°,则平行四边形的面积是()米2A. 150B.375C. 9D. 79. 如图19,铁路路基横断面为一个等腰梯形,若腰的坡度为i= 2∶3,顶宽是3米,路基高是4米,则路基的下底宽是()A. 7米B. 9米C. 12米D. 15米10. 如图20,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阻影部分)的面积为()A. αsin 1B. αcos 1 C. αsin D. 1 二. 填空题:(每小题2分,共10分) 11. 已知0°<α<90°,当α=__________时,21sin =α,当α=__________时,Cota=3.12. 若,则锐角α=__________。
【完整版】华师大版九年级上册数学第24章 解直角三角形含答案

华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为()A.3B.C.D.22、课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是()A.12米B. 米C.24米D. 米3、已知a、b、c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )A.2a+2b-2cB.2a+2bC.2cD.04、三角形两边的长是3和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为()A.12B.14C.12或14D.以上都不对5、在△ABC中,∠C=90°,BC=2,AB=3,则cosB的值为A. B. C. D.6、如图,在矩形纸片ABCD中,已知AB=,BC=1,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE折叠,得到多边形AFGE,点B,C的对应点分别为点F、G.在点E从点C移动到点D的过程中,则点F运动的路径长为()A.πB. πC. πD. π7、在Rt△ABC中,∠C=90°,AB=13,AC=12,则sinB的值是()A. B. C. D.8、已知锐角α,且sinα=cos38°,则α=()A.38°B.62°C.52°D.72°9、已知sinA= ,那么锐角等于()A.15°B.30°C.45°D.60°10、已知两条线段的长度分别为2cm、8cm,下列能与它们构成三角形的线段长度为()A.4cmB.6cmC.8cmD.10cm11、在△ABC中,若,则∠C的度数为( )A.30°B.60°C.90°D.120°12、下列长度的三条线段能组成三角形的是()A.1,2,3B.3,4,5C.3,1,1D.3,4,713、如图,是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=12m,∠A=30°,则立柱BC的长度为()A.4 mB.6 mC.8 mD.12 m14、平行四边形的对角线分别为x、y,一边长为 12,则x、y 的值可能是()A.8 与 14B.10 与 14C.18 与 20D.4 与 2815、如图是某河坝横断面示意图,迎水坡,为背水坡,过点A作水平面的垂线,设斜坡的坡度为,坡角为,斜坡的坡度为,坡角为,则下列结论正确的是( )A. B. C. D.二、填空题(共10题,共计30分)16、将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是________cm217、如图,将矩形绕点旋转至矩形位置,此时的中点恰好与点重合,交于点.若=1,则矩形的面积为________.18、纸片中,,将它折叠使与重合,折痕交于点,则线段的长为________.19、如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋楼底部的俯角为60°,热气球A与楼的水平距离为120 m,这栋楼的高度BC是________m(≈1.732,结果取整数).20、如图,在△ABC中,已知BC=5,,∠C=30°,EF 垂直平分BC,点 P 为直线EF上一动点,则 AP+BP 的最小值是________.21、在等腰△ABC中,AB=AC,如果cosC=,那么tanA=________.22、如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BC=3,则∠DCB的正切值为________.23、如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.24、在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=________25、如图一张长方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点M,将△ABM沿AM翻折后B至B′的位置,若B′为长方形纸片ABCD的对称中心,则的值为________.三、解答题(共5题,共计25分)26、计算:.27、为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入.(其中AB=9m,BC=0.5m)为标明限高,请你根据该图计算CE.(精确到0.1m)(参考数值,,)28、在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个直角三角形的其他元素。
华师大九年级上期末专题《第24章解直角三角形》单元试卷含解析

华师大版九年级数学上册期末专题:第24章解直角三角形单元检测试卷一、单选题(共10题;共30分)1.在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是()A. B. C. D.2.一个三角形的两边长分别是3和7,且第三边长为整数,这样的三角形周长最大的值为()A. 15B. 16C. 18D. 193.为测量某河的宽度,小军在河对岸选定一个目标点A,再在他所在的这一侧选点B,C,D,使得AB⊥BC,CD⊥BC,然后找出AD与BC的交点E.如图所示,若测得BE=90m,EC=45m,CD=60m,则这条河的宽AB等于()A. 120mB. 67.5mC. 40mD. 30m4.等腰三角形的周长为20cm,腰长为x cm,底边长为y cm,则底边长与腰长之间的函数关系式为()A. y=20﹣x(0<x<10)B. y=20﹣x(10<x<20)C. y=20﹣2x(10<x<20)D. y=20﹣2x(5<x<10)5.一段拦水坝横断面如图所示,迎水坡AB的坡度为i=1:,坝高BC=6m,则坡面AB的长度()A. 12mB. 18mC. 6D. 126.汶川地震后,抢险队派一架直升飞机去A、B两个村庄抢险,飞机在距地面450米上空的P点,测得A村的俯角为30°,B村的俯角为60°(如图)则A,B两个村庄间的距离是()米.A. 300B. 900C. 300D. 3007.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是()A. 4.5米B. 6米C. 7.2米D. 8米8.一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为()A. 10B. 12C. 14D. 169.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为()A. 5米B. 6米C. 8米D. (3+ )米10.如图,在□ABCD中,AB∶AD=3∶2,∠ADB=60°,那么cosA的值等于()A. B. C. D.二、填空题(共10题;共33分)11.小凡沿着坡角为30°的坡面向下走了2米,那么他下降________米.12.已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是________.13.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.14.如图,在直角坐标系中,P是第二象限的点,其坐标是(x,8),且OP与x轴的负半轴的夹角α的正切值是 ,则x=________,cosα=________.15.在Rt△ABC中,∠C=90°,如果AC=4,sinB=,那么AB=________16.高4 m的旗杆在水平地面上的影子长6 m,此时测得附近一个建筑物的影长24 m,则该建筑物的高是________m.17.tan________ °=0.7667.18.如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于________.19.如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC= +1,∠D=60°,则两条斜边的交点E到直角边BC的距离是________.20.已知当x1=a,x2=b,x3=c时,二次函数y= x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是________.三、解答题(共8题;共57分)21.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?22.小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B 两点的距离.23.如图,为了测量出楼房AC的高度,从距离楼底C处60 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53 °,求楼房AC的高度(参考数据:sin53 °= , cos53 °= , tan53 °= ,≈1.732,结果精确到0.1米)24.如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD 的高度(=1.7).25.“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)26.在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.(参考数据:sin37°≈ ,tan37°≈ ,sin21°≈ ,tan21°≈ )27.在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.(1)求证:四边形EFGH为平行四边形;(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.28.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).答案解析部分一、单选题1.【答案】B【考点】锐角三角函数的定义【解析】【解答】解:在△ABC中,∠C=90°,∵AC=4,BC=3,∴AB= =5.∴sinA= ,故答案为:B.【分析】先根据勾股定理算出AB,再根据正切定义得出结论。
最新华师大版九年级数学上册第24章解直角三角形单元测试题带答案
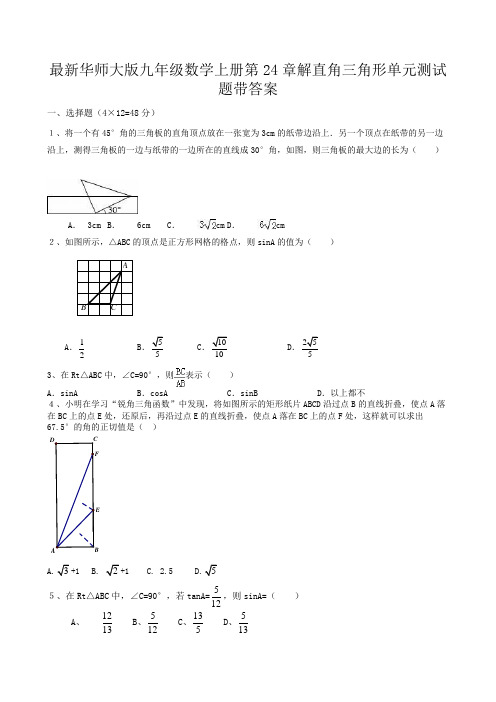
最新华师大版九年级数学上册第24章解直角三角形单元测试题带答案一、选择题(4×12=48分)1、将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为()A.3cm B.6cm C.cm D.cm2、如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.12BCD3、在Rt△ABC 中,∠C=90°,则表示()A.sinA B.cosA C.sinB D.以上都不4、小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°的角的正切值是()5、在Rt△ABC中,∠C=90°,若tanA=512,则sinA=()A、1213B、5 12C、135D、5136、已知∠A 为锐角,且sinA ≤21,则( ) A、0°≤A ≤60° B 、60°≤A <90° C 、0°<A ≤30° D 、30°≤A ≤90° 7、在Rt △ABC 中,斜边AB 的长为m ,∠A=55°,则直角边BC 的长是( )A .msin55°B .mcos55°C .sin 55m︒D .cos55m︒8、一座楼梯的示意图如图所示,BC 是铅垂线,CA 是水平线,BA 与CA 的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( ) A .米2B .米2C .(4+)米2D .(4+4tan θ)米29、在△ABC 中,若22cos =A ,3tan =B ,则这个三角形一定是( )A、锐角三角形; B、 直角三角形; C、钝角三角形; D、等腰三角形.10、如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD )急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF 的坡比i=1:2.下列说法正确的是( ) A、AB的长为400米; B、AF的长为10米; C、填充的土石方为19200立方米; D、填充的土石方为384立方米11、如图,△ABC 中AB=AC=4,∠C=72°,D 是AB 中点,点E 在AC 上,DE ⊥AB ,则cosA 的值为( )A .B .C .D .12、如图所示,某办公大楼正前方有一根高度是15米的旗杆ED ,从办公楼顶端A 测得旗杆顶端E 的俯角α是45°,旗杆底端D 到大楼前梯坎底边的距离DC 是20米,梯坎坡长BC 是12米,梯坎坡度i=1:,则大楼AB 的高度约为( )(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)A .30.6B .32.1C .37.9D .39.4二、填空题(4×6=24分)13、直角三角形斜边上的中线长是2.5,一直角边的长是3,则此直角三角形的面积为 .14、如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P ,则tan ∠APD 的值是 .15、若某人沿坡度i=3:4的斜坡前进10m ,则他所在的位置比原来的的位置 升高 m 。
A4版打印华师大版九年级上册数学第24章 解直角三角形含答案
华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题,共计45分)1、﹣sin60°的倒数为()A.﹣2B.C.﹣D.﹣2、如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA 与x轴正半轴的夹角α的正切值为,则y的值为()A.4B.C.5D.63、对于任意△ (见示意图).若是△ 的边上的中线,、的角平分线分别交、于点,连接,那么之间的数量关系正确的是()A. B. C. D.4、在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中正确的是()A.cosA=B.sinB=C.tanB=D.cotA=5、下列命题中,真命题有()①同旁内角互补;②长度为2、3、5的三条线段可以构成三角形;③平方根、立方根是它本身的数是0和1;④和﹣|﹣2|互为相反数;⑤4<<5;⑥在同一平面内,如果a∥b,a⊥c.那么b⊥c.A.0个B.1个C.2个D.3个6、tan35°•cotα=1,则α等于()A.65°B.35°C.75°D.55°7、△ABC中,∠ABC=30°,边AB=10,边AC可以从4,5,7,9,11取一值.满足这些条件的互不全等三角形的个数是()A.6B.7C.5D.48、sin45°的值等于( )A. B. C. D.9、以下列各组线段为边,能组成三角形的是()A.1cm,2cm,3cmB.2cm,5cm,8cmC.3cm,4cm,5cm D.4cm,5cm,11cm10、如图,已知△ABC,AB=5,∠ABC=60°,D为BC边上的点,AD=AC,BD=2,则DC=()A.0.5B.1C.1.5D.211、在△ABC中,若|sinB﹣|与(﹣cosA)2互为相反数,则∠C等于()A.120°B.90°C.60°D.45°12、如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ 是直角三角形时,t的值为()A.2sB.4sC.2s或4.5sD.2s或4s13、如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C 到航线AB的距离CD是()A.20海里B.40海里C.20 海里D.40 海里14、方程x2-9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为()A.12B.12或15C.15D.不能确定15、如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为()A. B.1 C. 或1 D. 或1 或二、填空题(共10题,共计30分)16、如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O 2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是________.17、下面是“作一个30°角”的尺规作图过程.已知:平面内一点A求作:,使得=30°做法:如图①作射线AB②在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C③以C为圆心,OC为半径作弧,与圆O交于点D,作射线AD,∠DAB即为所求的角请回答:该尺规作图的依据是________.18、如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是________ m.19、如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长________.20、位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间,周边风景秀丽.随着年代的增加,目前塔底低于地面约7米.某校学生先在地面处侧得塔顶的仰角为30°,再向古塔方向行进米后到达处,在处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么的值为________米.(结果保留根式)21、如图,在△ABC中,∠A=45°,AB= ,AC=6,点D,E为边AC上的点,AD=1,CE=2,点F为线段DE上一点(不与D,E重合),分别以点D、E为圆心,DF、EF为半径作圆.若两圆与边AB,BC共有三个交点时,线段DF长度的取值范围是________.22、如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=________.23、直角三角形两直角边的垂直平分线交于点P,则P点在________(填点P 的位置).24、某人沿坡度i=1:的坡面向上走50米,则此人离地面的高度为________米.25、如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=,则tan∠B的值为________三、解答题(共5题,共计25分)26、化简,并求值,其中a与2,3构成△ABC的三边,且a为整数.27、小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(B,F,D 在同一条直线上)。
九年级数学上册第24章解直角三角形检测题新版华东师大版(含参考答案)
九年级数学上学期:第24章检测题(时间:100分钟 满分:120分)一、选择题(每小题3分,共30分)1.在平面直角坐标系内有一点P(3,4),若OP 与x 轴正半轴的夹角为α,下列结论正确的是( A )A .tan α=43B .tan α=45C .sin α=35D .cos α=542.(三明中考)如图,在Rt △ABC 中,斜边AB 的长为m ,∠A =35°,则直角边BC 的长是( A )A .m sin35°B .m cos35° C.m sin35° D.mcos35° ,第2题图) ,第5题图),第7题图)3.计算6tan 45°-2cos 60°的结果是( D )A .4 3B .4C .5 3D .54.在Rt △ABC 中,∠C =90°,sin A =513,则tan B 的值为( D ) A.1213 B.512 C.1312 D.1255.如图,网格中的小正方形的边长均为1,点A ,B ,O 都在格点上,则∠A 的正弦值是( D )A.3510B.12C.255D.556.如果∠A,∠B 均为锐角,且2sin A -1+(3tan B -3)2=0,那么△ABC 是( B )A .锐角三角形B .直角三角形C .等边三角形D .钝角三角形 7.如图,河堤横断面迎水坡AB 的坡比是1∶3,堤高BC =10 m ,则坡面AB 的长度是( C )A .15 mB .20 3 mC .20 mD .10 3 m8.如图,CD 是平面镜,光线从A 点射出,经CD 上点E 反射后照射到B 点,若入射角为α,AC ⊥CD ,BD ⊥CD ,垂足分别为C ,D ,且AC =3,BD =6,CD =11,则tan α的值为( D )A.113B.311C.911D.119,第8题图) ,第9题图),第10题图)9.江津四面山是国家5A 级风景区,里面有一个景点被誉为亚洲第一岩——土地神岩,土地神岩壁画高度从石岩F 处开始一直竖直到山顶E 处,为了测量土地神岩上壁画的高度,小明从山脚A 处,沿坡度i =0.75的斜坡上行65米到达C 处,在C 处测得山顶E 处仰角为26.5°,再往正前方水平走15米到达D 处,在D 处测得壁画底端F 处的俯角为42°,壁画底端F 处距离山脚B 处的距离是12米,A ,B ,C ,D ,E ,F 在同一平面内,A ,B 在同一水平线上,EB ⊥AB ,根据小明的测量数据,则壁画的高度EF 为(精确到0.1米,参考数据:sin 26.5°≈0.45,cos 26.5°≈0.9,tan 26.5°≈0.5,sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.9)(A)A .49.5米B .68.7米C .69.7米D .70.2米10.如图,从点A 处观测一山坡上的电线杆PQ ,测得电线杆顶端P 的仰角是45°,向前走6 m 到达B 点,测得电线杆顶端P 和底端Q 的仰角分别是60°和30°,则该电线杆PQ 的高度(A) A .6+2 3 B .6+ 3 C .10- 3 D .8+ 3二、填空题(每小题3分,共24分)11.计算:tan 45°-13(3-1)0=__23__. 12.如图,某山坡的坡面AB =200米,坡角∠BAC=30°,则该山坡的高BC 的长为__100__米.13.如图,∠B =∠C,DE ⊥BC 于E ,EF ⊥AB 于F ,∠ADE 等于140°,∠FED =__50°__.,第12题图) ,第13题图),第14题图)14.如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE =6 cm ,sin A =35,则菱形ABCD 的面积是__60__cm 2.15.将一副三角尺按如图所示叠放在一起,则BE EC 的值是__33__. 16.如图,△ABC 的顶点A ,C 的坐标分别是(0,4),(3,0),且∠ACB=90°,∠B =30°,则顶点B 的坐标是__(3+43,33)__.,第15题图) ,第16题图),第18题图)17.在△ABC 中,AB =4,BC =3,∠BAC =30°,则△ABC 的面积为__23+5或23-5__.18.为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5 米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出__17__个这样的停车位.(2≈1.4)三、解答题(共66分)19.(8分)计算:(1)(-12)0+(13)-1·23-|tan 45°-3|; (2)24sin 45°+cos 230°-12·tan 60°+2sin 60°.解:2+3 解:1+53620.(8分)如图,△ABC 中,AD ⊥BC ,垂足是D ,若BC =14,AD =12,tan ∠BAD =34,求sin C 的值.解:121321.(8分)(2018·岳阳)图1是某小区入口实景图,图2是该小区入口抽象成的平面示意图.已知入口BC 宽3.9米,门卫室外墙AB 上的O 点处装有一盏路灯,点O 与地面BC 的距离为3.3米,灯臂OM 长为1.2米(灯罩长度忽略不计),∠AOM =60°.(1)求点M 到地面的距离;(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD 保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:3≈1.73,结果精确到0.01米)解:(1)如图,过M 作MN⊥AB 于N ,交BA 的延长线于N ,在Rt △OMN 中,∠NOM =60°,OM=1.2,∴∠M=30°,∴ON=12OM=0.6,∴NB=ON+OB=3.3+0.6=3.9,即点M到地面的距离是3.9米.(2)取CE=0.65,EH=2.55,∴HB=3.9-2.55-0.65=0.7,过H作GH⊥BC,交OM于G,过O作OP⊥GH于P.∵∠GOP=30°,∴tan30°=GPOP=33,∴GP=33OP=1.73×0.73≈0.404,∴GH=3.3+0.404=3.704≈3.70>3.5,∴货车能安全通过.22.(10分)(2018·铁岭)如图,某地质公园中有两座相邻小山.游客需从左侧小山山脚E处乘坐竖直观光电梯上行100米到达山顶C处,然后既可以沿水平观光桥步行到景点P 处,也可以通过滑行索道到达景点Q处,在山顶C处观测坡底A的俯角为75°,观测Q处的俯角为30°,已知右侧小山的坡角为30°.(图中的点C,E,A,B,P,Q均在同一平面内,点A,Q,P在同一直线上)(1)求∠CAP的度数及CP的长度;(2)求P,Q两点之间的距离.(结果保留根号)解:(1)∵PC∥AB,∴∠APC=∠PAB=30°,∴∠CAP=180°-75°-30°=75°,∴∠CAP=∠PCA,∴PC=AP,过P作PF⊥AB于F,则PF=CE=100,∴PA=2PF=200米,∴PC=PA=200米.(2)∵∠PCQ=∠QPC=30°,∴CQ=PQ.过Q作QH⊥PC于H,∴PH=12PC=100,∴PQ=PHcos30°=20033米.答:P,Q两点之间的距离是20033米.23.(8分)(2018·镇江)如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB的高度.(精确到0.1米,参考值:2≈1.41,3≈1.73)解:延长HF交CD于点N,延长FH交AB于点M,如右图所示,由题意可得,MB=HG=FE=ND=1.6 m,HF=GE=8 m,MF=BE,HN=GD,MN=BD=24 m,设AM=x m,则CN=x m,在Rt△AFM中,MF=AMtan45°=x1=x,在Rt△CNH中,HN=CNtan30°=x33=3x,∴HF=MF+HN-MN=x+3x-24,即8=x+3x-24,解得x≈11.7,∴AB=11.7+1.6=13.3 m,答:教学楼AB的高度AB长13.3 m.24.(12分)为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A ,B 两处巡逻,同时发现一艘不明国籍的船只停在C 处海域.如图所示,AB =60(6+2)海里,在B 处测得C 在北偏东45°的方向上,A 处测得C 在北偏西30°的方向上,在海岸线AB 上有一灯塔D ,测得AD =120(6-2)海里.(1)分别求出A 与C 及B 与C 的距离AC ,BC ;(结果保留根号)(2)已知在灯塔D 周围100海里范围内有暗礁群,我在A 处海监船沿AC 前往C 处盘查,途中有无触礁的危险?(参考数据:2≈1.41,3≈1.73,6≈2.45)解:(1)过点C 作CE⊥AB 于点E ,可得∠CBD =45°,∠CAD =60°,设CE =x ,在Rt△CAE 中,AE =CE·tan30°=33x ,在Rt △BCE 中,BE =CE =x ,∵AB =60(6+2)海里,∴x +33x =60(6+2),解得x =606,则AC =233x =1202,BC =2x =1203,答:A 与C 的距离为1202海里,B 与C 的距离为1203海里.(2)过点D 作DF⊥AC 于点F ,在△AD F 中,∵AD =120(6-2),∠CAD =60°,∴DF =ADsin60°=1802-606≈106.8>100,故海监船沿AC 前往C 处盘查,无触礁的危险.25.(12分)如图,已知斜坡AB 长602米,坡角(即∠BAC)为45°,BC ⊥AC ,现计划在斜坡中点D 处挖去部分斜坡,修建一个平行于水平线CA 的休闲平台DE 和一条新的斜坡BE.(1)若修建的斜坡BE 的坡比为3∶1,求休闲平台DE 的长是多少米?(2)一座建筑物GH 距离A 点33米远(即AG =33米),小亮在D 点测得建筑物顶部H 的仰角(即∠HDM)为30°,点B ,C ,A ,G ,H 在同一个平面内,点C ,A ,G 在同一条直线上,且HG⊥CG,问建筑物GH 高为多少米?解:(1)∵FM∥CG ,∴∠BDF =∠BAC =45°.∵斜坡AB 长602,D 是AB 的中点,∴BD =30 2.在△BDF 中,DF =BD ·cos ∠BDF =30,BF =DF =30.∵斜坡BE 的坡比为3∶1,∴BF EF =31,∴EF =103,∴DE =DF -EF =30-103,即休闲平台DE 的长是(30-103)米. (2)设GH =x 米,则MH =GH -GM =x -30,DM =AG +AP =33+30=63.在Rt △DMH 中,tan30°=MH DM ,即x -3063=33,解得x =30+213,则建筑物GH 的高为(30+213)米.。
九年级上册数学单元测试卷-第24章 解直角三角形-华师大版(含答案)
九年级上册数学单元测试卷-第24章解直角三角形-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )A.3B.1+C.1+3D.1+2、如图,直线AB与⊙O相切于点A,⊙O的半径为1,若∠OBA=30°,则OB长为()A.1B.2C.D.23、如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为()A.30,2B.60,2C.60,D.60,4、如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为()A.4 米B.(2 +2)米C.(4 ﹣4)米D.(4 ﹣4)米5、如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为()A.(,2)B.(,1)C.(,2)D.(,1)6、下面各组线段中,能组成三角形的是()A.2,3,4B.4,4,8C.5,4,10D.6,7,147、如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为()A.3cmB.4cmC.5cmD.8cm8、如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A. B. C. D.9、若一个三角形的两边长分别为2和6,第三边是方程x2-10x+21=0的一根,则这个三角形的周长为()A.7B.3或7C.15D.11或1510、一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是()A.第4张B.第5张C.第6张D.第7张11、如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,连接 AO并延长,交BC于点D,OH⊥BC于点H;若∠BAC=60°,OH=3cm,则OA=()A.6cmB.5cmC.4cmD.3cm12、如图,在平面直角坐标系中,O为坐标原点,将等边△ABC放在第一象限,其中边BC 的端点B、C分别在x轴的正半轴、y轴的正半轴上滑动,D是AC的中点,AB=4,连接OD,则线段OD长度的最大值是()A.2B.4C.2D.213、已知等腰三角形的腰和底的长分别是一元二次方程的根,则该三角形的周长是()A.5B.7C.5或7D.1014、在Rt△ABC中,∠C=90°,tanA= ,BC=4,则AC的值为()A.8B.2C.4D.415、如图,某同学在距离建筑中心B点m米的点A处,测得旗杆底部点C的仰角为α,旗杆顶部点D的仰角为β,则旗杆CD的长为()A. B.mtanβ﹣mtanα C. D.msinβ﹣msinα二、填空题(共10题,共计30分)16、如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧的中点,连接AE交BC于点F,若cosC= ,AC=6,则BF的长为________.17、如果cosA=0.8888,则∠A≈________ .(精确到″)18、如图,在高出海平面100m的悬崖顶A处,观测海平面上一艘小船B,测得它的俯角为30°,则船与观测者之间的水平距离约为________.(精确到1m.)19、计算:(﹣)﹣2﹣2cos60°=________.20、如图,已知线段AB=4,O是AB的中点,直线l经过点O,∠1=60°,P点是直线l上一点,当△APB为直角三角形时,则BP=________.21、如图,正方形的边长为,正方形的边长为.如果正方形绕点旋转,那么、两点之间的最小距离是________ .22、如果三条线段可组成三角形,且,,是奇数,则________.23、有两边相等的三角形的一边是7,另一边是4,则此三角形的周长是________.24、如图,四边形ABCD为菱形,AB=2,∠BCD=30°,点E在CD延长线上,且CD=DE,∠E=45°,点H是AC上的一个动点,则HD+HE的最小值为________25、如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为________.三、解答题(共5题,共计25分)26、计算:2tan60°﹣|1﹣|+(2015﹣π)0﹣()﹣1.27、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,求弦DC 的长.28、如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x轴上行驶,从原点O出发.(1)汽车行驶到什么位置时离A村最近?写出此点的坐标;(2)汽车行驶到什么位置时离B村最近?写出此点的坐标;(3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?29、如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HF与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米).(参考数据:cos75°≈0.2588, sin75°≈0.9659,tan75°≈3.732,,)30、如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B 两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)参考答案一、单选题(共15题,共计45分)1、D2、B3、C4、D5、A6、A7、B8、C9、C10、C11、A12、B13、B14、A15、B二、填空题(共10题,共计30分)16、17、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
九年级上册数学华师大版 第24章解直角三角形单元质检卷(A卷)(含详解)
解直角三角形一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)A. B. C.3.在中,,,,则的值是( )4.如图,在,,,D,E,F 分别是AB ,AC ,AD 的中点,,则EF 的长度为( )5.已知是锐角的内角,的值是( )6.周末,刘老师读到《行路难》中“闲来垂钓碧溪上,忽复乘舟梦日边.”邀约好友一起去江边垂钓.如图.钓鱼竿的长为4m.露在水面上的鱼线的长为,刘老师想看看鱼钩上的情况.把鱼竿逆时针转动15°到的位置,此时露在水面上的鱼线的长度是( )5tan 40︒5cos 40︒5sin 40Rt ABC △90C ∠=︒5BC =12AC =sin B Rt ABC △90ACB ∠=︒30A ∠=︒3BC =A ∠ABC △sin A ∠=A ∠AC BC AC AC 'BC ''A.3mB.C.D.7.如图, 中, , 延长CB 到点D , 使, 连接AD , 已知的值是( )A. B.9.我校数学兴趣小组的同学要测量建筑物的斜坡,用测角仪测得建筑物屋顶刚好到达坡底E 处,这时测到建筑物屋顶Rt ABC V 90C ∠=︒BD AB =tan D =tan ABC∠60︒75︒1:2i =BEA.38.5米B.39.0米C.40.0米D.41.5米10.如图,在中,,,,点P 为边上一动点,于点E ,于点F ,连接,则的最小值为( )A.二、填空题(每小题4分,共20分)11.课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB 在地面上的投影BC 的长为24米,则旗杆AB 的高度是______米.12.在中,,_______.13.如图,从航拍无人机A 看一栋楼顶部B 的仰角为,看这栋楼底部C 的俯角β为,无人机与楼的水平距离为,则这栋楼的高度为________m.ABC △45B ∠=︒60C ∠=︒6BC =AC PE AB ⊥PF BC ⊥EF EF Rt ABC △90C ∠=︒sin A =A =α30︒60︒60m14.如图,在中,,D是AB的中点,连接CD,过点B作CD的垂线,交CD延长线于点E,的值为______.15.如图,在中,,交_________.三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)16.(8分)计算(1)17.(8分)如图,在中,.Rt ABC△90C∠=︒Rt ABC△90ACB∠=︒tan A=DBE∠ABC△AB BC=tan B∠==DE AD⊥AC= 22cos45tan30sin60sin45︒+︒⋅︒-︒tan30cos60︒︒︒⋅︒(1)已知,,求BC 的长;(2)已知,求的度数.18.(10分)如图,在中,,垂足为D ,,.(1)求和的长;(2)求的值.19.(10分)图1为放在水平地面上的落地式话筒架实物图.图2为其示意图,支撑杆垂直于地面,,斜杆连接在支撑杆顶端A 处,,其中的长度可通过斜杆的滑动来进行调节,斜杆还可以绕着点A 旋转,且与支撑杆的夹角为.(1)当,时,求话筒C 到地面的高度;(2)落地式话筒可以根据使用者的身高需要调节的长度和夹角的度数,某运动员使用落地式话筒的适合高度是,请问该话筒的高度能否满足这名运动员的需要,并说明理)20.(12分)王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸人树的高度,他在点C 处测得大树顶端A 的仰角为,再从C 点出发沿斜坡走到达斜坡上D 点,在点D 处测得树顶端A 的仰角为,若斜坡的坡比为(点E ,C ,B 住同一水平线上).12AB =1sin 3A =BC =AC =B ∠ABC △BD AC ⊥6AB =AC =30A =︒BD AD sin C AB 115cm AB =CD 80cm CD =AC CD AB ()60150BAC BAC ∠︒≤∠≤︒50cm AC =120BAC ∠=︒CA BAC ∠183cm 1.73≈AB 45︒30︒CF 1:3i =(1)求王刚同学从点C 到点D 的过程中上升的高度;(2)求大树的高度(结果保留根号).21.(12分)如1图,在锐角三角形中,,,的对边分别为a ,b ,c .(1)用b ,c ,表示的面积S ;(3)如2图,若,于点D ,,求.AB ABC A ∠B ∠C ∠sin A ABC △sin b B ==:3:2AC BC =sin A =AB ⊥2BD =sin ACB ∠答案以及解析解析:,,,.故选:B.3.答案:D解析:如图所示:,,,故选:D.4.答案:C 解析:∵,,∴,∵点D 为斜边AB 的中点,∴,∵E ,F 分别是AD ,AC 的中点,∴90C ∠=︒ 12AC = 90C ∠=︒40B ∠=︒5AB =cos B ∠=∴cos 40︒=∴5cos 40BC =︒5BC =90ACB ∠=︒30A ∠=︒26AB BC ==Rt ABC △132CD AB ==12EF CD ==5.答案:C解析:如图,是锐角的内角,于点D,则设,,其中,则,故选:C.6.答案:C解析:∵∴,∴,∴,故选:C.7.答案:A解析:在中,. 设,, 则,. 在中, 由勾股定理, 得, 解得,sin CAB∠==A∠ABC△CD AB⊥5sin3A∠==3CD x=5AC x=0x>4AD x===5cos4AC xAAD x∴∠===45CAB∠=︒451560C AB=︒+︒=''︒sin60=︒=)4mB C==''Rt ACD△tan ACDCD==3CD AC= AC a=BC x=3CD a=3BD AB a x∴==-Rt ABC△222(3)a x a x+=-43x a=tanAC aABCBC x∴∠===在中,米,米,四边形是矩形,四边形,,在中,Rt BHE △45BE = 4BH ∴=8EH = AHDM AM DH ∴=AH DM =Rt CFN △解析:连接,取的中点G ,连接、,,,,,,,,为等腰直角三角形,,当时,取最小值,此时,的值也最小,,BP BP EG FG PE AB ⊥ PF BC ⊥90BEP BFP ∴∠=∠=︒12EG GF BG BP ∴===BEG EBG ∴∠=∠BFG FBG ∠=∠()2224590EGF BEG EBG BFG FBG EBG FBG B ∴∠=∠+∠+∠+∠=∠+∠=∠=⨯︒=︒EGF ∴△EF BP ∴===∴BP AC ⊥BP EF 60C ∠=︒,的最小值为此时,故选:C.11.答案:解析:旗杆、地面及太阳光线恰好构成直角三角形,故答案为解析:由,则,,.13.答案:解析:如图,作于点D,则,在中,,sin sin60BPCBC∴==︒·sin606BP BC∴=︒==BP∴EF=tan30ABBC∴=︒tan3024AB BC∴=⋅︒==sin A=4x=5c x=3b x=4tan3a xAb x∴===AD BC⊥60mAD=Rt ADB△tanBDADα=,在中,,,即这栋楼的高度为,故答案为:.解析:,设,,,D 是AB 的中点,,,又,,,,.)m BC CD BD =+=+=∴)tan 60tan 3060m BD AD α=⋅=⨯︒==Rt ADC △tan β=∴)tan 60tan 6060m CD AD β=⋅=⨯︒==∴90ACB =︒∠ tan A =∴3AC x =4BC x =5AB x ∴== 1522CD BD AD AB x ∴====ECB DBC ∴∠=∠BE CE ⊥ ACB BEC ∴∠=∠ACB BEC ∴∽△△BC AB ∴=431255x x BE x x ⋅∴==125cos 52x BE DBE BD x ∠===解析:如图,过点A 作垂足为H ,,,设,,,,,,,解得,,,,,,过点C 作垂足为M ,,,,,,AH CB ⊥ 85BD DC =AB BC=13AB BC x ==∴8BD x =5DC x = tan B ∠=AH CB ⊥∴512AH BH = 13AB BC x ==∴2222169AH BH AB x +==5AH x =12BH x =∴1284DH x x x =-=54HC x x x =-=∴AD ==AC ==∴cos DH ADC AD ∠==CM AD ⊥∴cos DM CD ADC x =⋅∠=AM AD DM x =-= DE AD ⊥CM AD ⊥∴//MC DE.(2)解析:(1)17.答案:(1)(2)解析:(1)在中,,.(2)在中,60B∠=︒Rt ABC△sin A=BCAB∴=Rt ABC△BC=AC=tan B∴==∴CE DMAC AM===512-22cos45tan30sin60sin45︒+︒⋅︒-︒22=+-12=tan30cos60︒︒︒⋅︒12=31146=--512=-4BC=12AB=4BC∴=.18.答案:(1);解析:(1),,在中,,,,(2)在中,,,19.答案:(1)(2)该话筒的高度能满足这名运动员的需要,理由见解析解析:(1)如图所示,过点C 作,于点E ,∵,∴,又,∴筒C 到地面的高度为;(2)依题意,当,点A ,D 重合时,,C 点离地面最高,此时如图所示,过点C 作,于点E ,60B ∴∠=︒150CAB ∠=︒3BD =AD =BD AC ⊥ 90ADB ∴∠=︒Rt ABD △6AB =30A ∠=︒sin 6sin303BD AB A ∴=⋅=︒⨯=cos 6cos30AD AB A ⋅=⨯︒==AC = AD =CD AC AD ∴=-=Rt CBD △90CDB =︒∠ 3BD =CD =BC ∴==sin BD C BC ∴===140cm//CE AB AE CE ⊥50cm AC =120BAC ∠=︒30CAE ∠=︒1sin 305025cm 2CE AC =︒⨯=⨯=115cm AB =11525140cm AB CE +=+=80cm AC CD ==//CE AB AE CE ⊥∴∴∴筒C 到地面的高度为∵某运动员使用落地式话筒的适合高度是,∴该话筒的高度能满足这名运动员的需要.20.答案:(1)4米(2)米解析:(1)过D 作于H ,如图所示:在中,∵斜坡的坡比为,∴,∵,∴,解得:或(舍去),∴王刚同学从点C 到点D 的过程中上升的高度为4米.(2)延长交于点G ,设米,由题意得,,∴(12+DH CE ⊥1509060CAE ∠=︒-︒=︒()sin 608069.2CE AC cm =⨯︒==≈()11569.2184.2cm AB CE +=+=183cm 183184.2<Rt DCH △CF 1:3i =3CH DH =222CH DH CD +=()(2223DH DH +=4DH =4DH =-AD CE AB x =30AGC ∠=︒tan 30DH GH ===︒∵斜坡的坡比为,∴,∴,在中,∵,∴,在中,∴解得:故大树的高度为米.21.答案:(1)(2)证明见解析解析:(1)如图1,过点C 作于点E ,在中,,.(2)证明:由(1)知,的面积,同理,,.CF 1:3i =312CH DH ==12CG GH CH =+=Rt ABC △45ACB ∠=︒AB BC =Rt ABG △tan 30AB BG ︒===12x =+AB (12+1sin 2S bc A =CE AB ⊥Rt AEC △sin sin CE CA A b A =⋅=111sin sin 222S AB CE c b A bc A ∴=⋅=⋅=ABC △1sin 2S bc A =1sin 2S ac B =in 12s S ab C =111sin sin sin 222bc A ac B ab C ∴==sin B b ==(3),设,则,即,.如图,在中,.由勾股定理可得,即,解得.在中,,,由勾股定理可得,即,解得.,..sin b B ==:3:2AC BC = 3AC x =2BC x =3b x =2a x =Rt ADC △sin 3CD CD A AC x ===CD ∴=222AD AC CD =-())2223AD x =-AD =Rt BDC △2BC x =CD =222BD CD BC +=222)(2)BD x +=2BD x ==2AB AD BD ∴=+=24BC x ===sin sin AB A ACB BC ⋅∴∠===。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形(时间:100分钟满分:120分)一、选择题(每小题3分,共30分)1.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( D )A.sin A=32B.tan A=12C.cos B=32D.tan B= 32.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( A )A.c sin A=a B.b cos B=c C.a tan A=b D.c tan B=b3.计算6tan45°-2cos60°的结果是( D )A.4 3 B.4 C.5 3 D.54.(·巴中)在Rt△ABC中,∠C=90°,sin A=513,则tan B的值为( D )A.1213B.512C.1312D.1255.如图,在下列网格中,小正方形的边长均为1,点A,B,O都在格点上,则∠A的正弦值是( D )A.3510B.12C.255D.556.如果∠A,∠B均为锐角,且2sin A-1+(3tan B-3)2,那么△ABC是( B )A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形7.(·凉山州)如图,河堤横断面迎水坡AB的坡比是1∶3,堤高BC=10 m,则坡面AB的长度是( C )A.15 m B.20 3 m C.20 m D.10 3 m,第7题图) ,第8题图),第9题图)8.如图,CD 是平面镜,光线从A 点射出,经CD 上点E 反射后照射到B 点,若入射角为α,AC ⊥CD ,BD ⊥CD ,垂足分别为C ,D ,且AC =3,BD =6,CD =11,则tan α的值为( D )A.113 B.311 C.911 D.1199.(·绵阳)如图,一艘海轮位于灯塔P 的北偏东30°方向,距离灯塔80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处,这时,海轮所在的B 处与灯塔P 的距离为( A )A .40 2 海里B .40 3 海里C .80海里D .40 6 海里10.如图,在两建筑物之间有一旗杆,高15米,从A 点经过旗杆顶点恰好看到矮建筑物的墙角C 点,且俯角α为60°,又从A 点测得D 点的俯角β为30°,若旗杆底点G 为BC 的中点,则矮建筑物的高CD 为( A )A .20米B .10 3 米C .15 3 米D .5 6 米二、填空题(每小题3分,共24分)11.(·锦州)计算:tan 45°-13(3-1)0=__23__.12.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sin A 的值是__74__. 13.如图,某山坡的坡面AB =200米,坡角∠BAC =30°,则该山坡的高BC 的长为__100__米.,第12题图) ,第13题图),第14题图)14.如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE =6 cm ,sin A =35,则菱形ABCD 的面积是__60__cm 2.15.将一副三角尺如图所示叠放在一起,则BE EC 的值是__33__. 16.如图,△ABC 的顶点A ,C 的坐标分别是(0,4),(3,0),且∠ACB =90°,∠B =30°,则顶点B 的坐标是__(3+43,33)__.,第15题图) ,第16题图),第18题图)17.△ABC 中,AB =4,BC =3,∠BAC =30°,则△ABC 的面积为__23+5或23-5__.18.(·宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5 米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出__17__个这样的停车位.(2≈1.4)点拨:如图,BC =2.2×sin45°≈1.54,CE =5×sin45°≈3.5,BE =BC +CE ≈5.04,EF =2.2÷sin45°≈3.14,(56-5.04)÷3.14+1≈16+1=17(个),故这个路段最多可以划出17个这样的停车位三、解答题(共66分) 19.(8分)计算:(1)(-2)2+|-3|+2sin60°-12; 解:4(2)6tan 230°-3cos30°-2sin45°. 解:12-220.(8分)(·重庆)如图,△ABC 中,AD ⊥BC ,垂足是D ,若BC =14,AD =12,tan ∠BAD =34,求sinC 的值.解:121321.(8分)如图,湖中的小岛上有一标志性建筑物,其底部为A ,某人在岸边的B 处测得A 在B 的北偏东30°的方向上,然后沿岸边直行4公里到达C 处,再次测得A 在C 的北偏西45°的方向上(其中A ,B ,C 在同一平面上).求这个标志性建筑物底部A 到岸边BC 的最短距离.解:过A 作AD ⊥BC 于点D ,则AD 的长度就是A 到岸边BC 的最短距离.在Rt △ACD 中,∠ACD =45°,设AD =x ,则CD =AD =x ,在Rt △ABD 中,∠ABD =60°,BD =x tan60°=33x ,又BC=4,即BD+CD=4,所以33x+x=4,解得x=6-23,则这个标志性建筑物底部A到岸边BC的最短距离为(6-23)公里22.(10分)(·乐山)如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E,若AD=1,AB=23,求CE的长.解:过点A作AH⊥BC于点H,则AD=HC=1,在△ABH中,BH=AB·cos30°=3,∴BC =BH+BC=4,∵CE⊥AB,∴CE=BC·sin30°=223.(10分)如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米;参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)解:过A点作AE⊥CD于点E,在Rt△ABE中,AE=AB·sin62°≈22,BE=AB·cos62°≈11.75,在Rt△ADE中,DE=AEtan50°≈18.33,∴DB=DC-BE≈6.58,故此时应将坝底向外拓宽大约6.58米24.(10分)(·泰州)图①,②分别是某型号跑步机的实物图与示意图,已知踏板CD长为1.6 m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8 m,∠ACD为80°,求跑步机手柄的一端A 的高度h.(精确到0.1 m ;参考数据:sin 12°=cos 78°≈0.21,sin 68°=cos 22°≈0.93,tan 68°≈2.48)解:过C 点作FG ⊥AB 于点F ,交DE 于点G.∵CD 与地面DE 的夹角∠CDE 为12°,∠ACD 为80°,∴∠ACF =90°+12°-80°=22°,∴∠CAF =68°,在Rt △ACF 中,CF =AC ·sin ∠CAF ≈0.744,在Rt △CDG 中,CG =CD ·sin ∠CDE ≈0.336,∴FG =FC +CG ≈1.1,故跑步机手柄的一端A 的高度约为1.1 m25.(12分)如图,已知斜坡AB 长602米,坡角(即∠BAC )为45°,BC ⊥AC ,现计划在斜坡中点D 处挖去部分斜坡,修建一个平行于水平线CA 的休闲平台DE 和一条新的斜坡BE .(1)若修建的斜坡BE 的坡比为3∶1,求休闲平台DE 的长是多少米?(2)一座建筑物GH 距离A 点33米远(即AG =33米),小亮在D 点测得建筑物顶部H 的仰角(即∠HDM )为30°,点B ,C ,A ,G ,H 在同一个平面内,点C ,A ,G 在同一条直线上,且HG ⊥CG ,问建筑物GH 高为多少米?解:(1)∵FM ∥CG ,∴∠BDF =∠BAC =45°,∵斜坡AB 长602,D 是AB 的中点,∴BD =302,∴DF =BD ·cos ∠BDF =30,BF =DF =30,∵斜坡BE 的坡比为3∶1,∴BF EF =31,∴EF =103,∴DE =DF -EF =30-103,即休闲平台DE 的长是(30-103)米 (2)设GH =x 米,则MH =GH -GM =x -30,DM =AG +AP =33+30=63,在Rt △DMH 中,tan30°=MHDM,x-30 63=33,解得x=30+213,则建筑物GH的高为(30+213)米即。
