2021年九年级数学中考复习专题之圆：切割线定理综合运用(一)
2021年九年级数学中考复习专题之圆的综合(考察切线证明、长度、面积、动点问题等)(含答案)
2021年九年级数学中考复习专题之圆的综合（考察切线证明、长度、面积、动点问题等）1．如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．（1）求证：∠ADC＝∠ABD；（2）求证：AD2＝AM•AB；（3）若AM＝，sin∠ABD＝，求线段BN的长．2．如图，在直角坐标系中，⊙M经过原点O（0，0），点A（，0）与点B（0，﹣），点D在劣弧上，连接BD交x轴于点C，且∠COD＝∠CBO．（1）求⊙M的半径；（2）求证：BD平分∠ABO；（3）在线段BD的延长线上找一点E，使得直线AE恰好为⊙M的切线，求此时点E的坐标．3．如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．（1）求证：PA是⊙O的切线；（2）若＝，且OC＝4，求PA的长和tan D的值．4．如图，AB是⊙O的直径，OD⊥弦BC于点F，交⊙O于点E，连结CE、AE、CD，若∠AEC＝∠ODC．（1）求证：直线CD为⊙O的切线；（2）若AB＝5，BC＝4，求线段CD的长．5．如图，在Rt△ABC中，∠ACB＝90°，E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE（1）求证：△ABC∽△CBD；（2）求证：直线DE是⊙O的切线．6．如图，△ABC内接于⊙O，AB＝AC，BD为⊙O的弦，且AB∥CD，过点A作⊙O的切线AE与DC的延长线交于点E，AD与BC交于点F．（1）求证：四边形ABCE是平行四边形；（2）若AE＝6，CD＝5，求OF的长．7．如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F．（1）求证：DF⊥AC；（2）若⊙O的半径为4，∠CDF＝22.5°，求阴影部分的面积．8．如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC＝∠CPB＝60°．（1）判断△ABC的形状： ；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．9．如图，在Rt△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．（1）判断直线BC与⊙O的位置关系，并说明理由；（2）若AC＝3，∠B＝30°．①求⊙O的半径；②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）10．如图，△ABC中，∠C＝90°，点G是线段AC上的一动点（点G不与A、C重合），以AG为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF交BC于点E，连结DE．（1）求证：DE是⊙O的切线；（2）若cos A＝，AB＝8，AG＝2，求BE的长；（3）若cos A＝，AB＝8，直接写出线段BE的取值范围．答案1．（1）证明：连接OD，∵直线CD切⊙O于点D，∴∠CDO＝90°，∵AB为⊙O的直径，∴∠ADB＝90°，∴∠1+∠2＝∠2+∠3＝90°，∴∠1＝∠3，∵OB＝OD，∴∠3＝∠4，∴∠ADC＝∠ABD；（2）证明：∵AM⊥CD，∴∠AMD＝∠ADB＝90°，∵∠1＝∠4，∴△ADM∽△ABD，∴，∴AD2＝AM•AB；（3）解：∵sin∠ABD＝，∴sin∠1＝，∵AM＝，∴AD＝6，∴AB＝10，∴BD＝＝8，∵BN⊥CD，∴∠BND＝90°，∴∠DBN+∠BDN＝∠1+∠BDN＝90°，∴∠DBN＝∠1，∴sin∠NBD＝，∴DN＝，∴BN＝＝．2．解：（1）∵⊙M经过O、A、B三点，且∠AOB＝90°，∴AB为直径∵点A为（，0），点B为（0，﹣），∴OA＝，OB＝，∴AB＝＝2，∴⊙M的半径为：；（2）∵∠COD＝∠CBO，∠COD＝∠CBA，∴∠CBO＝∠CBA，即BD平分∠ABO；（3）如图，过点A作AE⊥AB，垂足为A，交BD的延长线于点E，过点E作EF⊥OA 于点F，即AE是切线，∵在Rt△AOB中，tan∠OAB＝＝＝，∴∠OAB＝30°，∴∠ABO＝90°﹣∠OAB＝60°，∴∠ABC＝∠OBC＝∠ABO＝30°，∴OC＝OB•tan30°＝×＝，∴AC＝OA﹣OC＝，∴∠ACE＝∠ABC+∠OAB＝60°，∴∠EAC＝60°，∴△ACE是等边三角形，∴AE＝AC＝，∴AF＝AE＝，EF＝AE＝，∴OF＝OA﹣AF＝，∴点E的坐标为：（，）．3．（1）证明：连接OB，则OA＝OB，∵OP⊥AB，∴AC＝BC，∴OP是AB的垂直平分线，∴PA＝PB，在△PAO和△PBO中，∵，∴△PAO≌△PBO（SSS）∴∠PBO＝∠PAO，PB＝PA，∵PB为⊙O的切线，B为切点，∴∠PBO＝90°，∴∠PAO＝90°，即PA⊥OA，∴PA是⊙O的切线；（2）连接BE，∵＝，且OC＝4，∴AC＝6，∴AB＝12，在Rt△ACO中，由勾股定理得：AO＝＝2，∴AE＝2OA＝4，OB＝OA＝2，在Rt△APO中，∵AC⊥OP，∴AC2＝OC•PC，解得：PC＝9，∴OP＝PC+OC＝13，在Rt△APO中，由勾股定理得：AP＝＝3，∴PB＝PA＝3，∵AC＝BC，OA＝OE，∴OC＝BE，OC∥BE，∴BE＝2OC＝8，BE∥OP，∴△DBE∽△DPO，∴，即，解得：BD＝，在Rt△OBD中，tan∠D＝＝＝．（补充方法：可以证明△DBE∽△DAB，可得＝＝＝，由此解决问题，可以简单一些）4．（1）证明：连接OC，∵∠CEA＝∠CBA，∠AEC＝∠ODC，∴∠CBA＝∠ODC，又∵∠CFD＝∠BFO，∴∠DCB＝∠BOF，∵CO＝BO，∴∠OCF＝∠B，∵∠B+∠BOF＝90°，∴∠OCF+∠DCB＝90°，∴直线CD为⊙O的切线；（2）解：连接AC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠DCO＝∠ACB，又∵∠D＝∠B∴△OCD∽△ACB，∵∠ACB＝90°，AB＝5，BC＝4，∴AC＝3，∴＝，即＝，解得；DC＝．5．（1）证明：∵AC为⊙O的直径，∴∠ADC＝90°，∴∠BDC＝90°，又∵∠ACB＝90°，∴∠ACB＝∠BDC，又∵∠B＝∠B，∴△BCD∽△BAC；（2）连结DO，如图，∵∠BDC＝90°，E为BC的中点，∴DE＝CE＝BE，∴∠EDC＝∠ECD，又∵OD＝OC，∴∠ODC＝∠OCD，而∠OCD+∠DCE＝∠ACB＝90°，∴∠EDC+∠ODC＝90°，即∠EDO＝90°，∴DE⊥OD，∴DE与⊙O相切．6．（1）证明：∵AE与⊙O相切于点A，∴∠EAC＝∠ABC，∵AB＝AC∴∠ABC＝∠ACB，∴∠EAC＝∠ACB，∴AE∥BC，∵AB∥CD，∴四边形ABCE是平行四边形；（2）解：如图，连接AO，交BC于点H，双向延长OF分别交AB，CD与点N，M，∵AE是⊙O的切线，由切割线定理得，AE2＝EC•DE，∵AE＝6，CD＝5，∴62＝CE（CE+5），解得：CE＝4，（已舍去负数），∵AB∥CD，∴∠BAD＝∠ADC，∴＝，∴AC＝BD，∴AB＝AC＝BD＝CE＝4，又根据对称性和垂径定理，得AO垂直平分BC，MN垂直平分AB，DC，设OF＝x，OH＝Y，FH＝z，∵AB＝4，BC＝6，CD＝5，∴BF＝BC﹣FH＝3﹣z，DF＝CF＝BC+FH＝3+z，易得△OFH∽△DFM∽△BFN，∴，，即，①②，①+②得：，①÷②得：，解得，∵x2＝y2+z2，∴，∴x＝，∴OF＝．7．（1）证明：连接OD，∵OB＝OD，∴∠ABC＝∠ODB，∵AB＝AC，∴∠ABC＝∠ACB，∴∠ODB＝∠ACB，∴OD∥AC，∵DF是⊙O的切线，∴DF⊥OD，∴DF⊥AC．（2）解：连接OE，∵DF⊥AC，∠CDF＝22.5°，∴∠ABC＝∠ACB＝67.5°，∴∠BAC＝45°，∵OA＝OE，∴∠AOE＝90°，∵⊙O的半径为4，∴S扇形AOE＝4π，S△AOE＝8 ，∴S阴影＝4π﹣8．8．证明：（1）△ABC是等边三角形．证明如下：在⊙O中∵∠BAC与∠CPB是所对的圆周角，∠ABC与∠APC是所对的圆周角，∴∠BAC＝∠CPB，∠ABC＝∠APC，又∵∠APC＝∠CPB＝60°，∴∠ABC＝∠BAC＝60°，∴△ABC为等边三角形；（2）在PC上截取PD＝AP，如图1，又∵∠APC＝60°，∴△APD是等边三角形，∴AD＝AP＝PD，∠ADP＝60°，即∠ADC＝120°．又∵∠APB＝∠APC+∠BPC＝120°，∴∠ADC＝∠APB，在△APB和△ADC中，，∴△APB≌△ADC（AAS），∴BP＝CD，又∵PD＝AP，∴CP＝BP+AP；（3）当点P为的中点时，四边形APBC的面积最大．理由如下，如图2，过点P作PE⊥AB，垂足为E．过点C作CF⊥AB，垂足为F．∵S△APB＝AB•PE，S△ABC＝AB•CF，∴S四边形APBC＝AB•（PE+CF），当点P为的中点时，PE+CF＝PC，PC为⊙O的直径，∴此时四边形APBC的面积最大．又∵⊙O的半径为1，∴其内接正三角形的边长AB＝，∴S四边形APBC＝×2×＝．9．解：（1）直线BC与⊙O相切；连结OD，∵OA＝OD，∴∠OAD＝∠ODA，∵∠BAC的角平分线AD交BC边于D，∴∠CAD＝∠OAD，∴∠CAD＝∠ODA，∴OD∥AC，∴∠ODB＝∠C＝90°，即OD⊥BC．又∵直线BC过半径OD的外端，∴直线BC与⊙O相切．（2）设OA＝OD＝r，在Rt△BDO中，∠B＝30°，∴OB＝2r，在Rt△ACB中，∠B＝30°，∴AB＝2AC＝6，∴3r＝6，解得r＝2．（3）在Rt△ACB中，∠B＝30°，∴∠BOD＝60°．∴．∵∠B＝30°，OD⊥BC，∴OB＝2OD，∴AB＝3OD，∵AB＝2AC＝6，∴OD＝2，BD＝2S △BOD＝×OD•BD＝2，∴所求图形面积为．10．（1）证明：连接OD，如图，∵△ABC中，∠C＝90°，∴∠A+∠B＝90°，∵直线EF垂直平分BD，∴ED＝EB，∴∠B＝∠EDB，∵OA＝OD，∴∠A＝∠ODA，∴∠ODA+∠EDB＝90°，∴∠ODE＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：连接GD，∵AG为直径，∴∠ADG＝90°，∵cos A＝，∴∠A＝60°，∴∠AGD＝30°，∴AD＝AG＝，∵AB＝8，∴BD＝AB﹣AD＝8﹣＝7，∵直线EF垂直平分BD，∴BF＝BD＝，在Rt△BEF中，∠B＝30°，∴EF＝BF＝，∴BE＝2EF＝7；（3）解：∵cos A＝，∴∠A＝60°，∴∠B＝30°，∴AC＝AB＝4，由（2）得AD＝AG，BF ＝（AB﹣AD）＝4﹣AG，在Rt△BEF中，∠B＝30°，∴EF＝BF，∴BE＝2EF＝BF＝（4﹣AG）＝8﹣AG，∵0＜AG＜AC，即0＜AG＜4，∴6＜BE＜8．。
2021年九年级数学中考复习专题之圆：切割线定理综合运用(二)
2021年九年级数学中考复习专题之圆：切割线定理综合运用（二）一．选择题1．如图，点P是⊙O直径AB的延长线上一点，PC切⊙O于点C，已知OB＝3，PB＝2．则PC 等于（）A．2 B．3 C．4 D．52．如图，以OB为直径的半圆与半圆O交于点P，A、O、C、B在同一条直线上，作AD⊥AB 与BP的延长线交于点D，若半圆O的半径为2，∠D的余弦值是方程3x2﹣10x+3＝0的根，则AB的长等于（）A．B．C．8 D．53．如图，两圆相交于C、D，AB是两圆的一条外公切线，A、B为切点，CD的延长线交AB 于M，若CD＝9，MD＝3，则AB的长为（）A．18 B．12 C．13.5 D．6√34．如图：PAB、PCD为⊙O的两条割线，若PA•PB＝30，PC＝3，则CD的长为（）A．10 B．7 C．D．35．如图，点C、O在线段AB上，且AC＝CO＝OB＝5，过点A作以BC为直径的⊙O切线，D 为切点，则AD的长为（）A．5 B．6 C．D．106．如图，已知AB、AC分别为⊙O的直径和弦，D为的中点，DE垂直于AC的延长线于E，连接BC，若DE＝6cm，CE＝2cm，下列结论一定错误的是（）A．DE是⊙O的切线B．直径AB长为20cmC．弦AC长为16cm D．C为的中点7．如图，圆O1与圆O2相交于A、B，过A作圆O1的切线交圆O2于C，连CB并延长交圆O1于D，连AD，AB＝2，BD＝3，BC＝5，则AD的长为（）A．B．C．D．28．如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB＝2cm，BC＝8cm，则PA的长等于（）A．4cm B．16cm C．20cm D．2cm9．如图，Rt△ABC中，∠C＝90°，AC＝6，BC＝8，CD为直径的⊙O与AB相切于E，则⊙O 的半径是（）A．2 B．2.5 C．3 D．410．如图，PA，PB为⊙O的切线，A，B分别为切点，∠APB＝60°，点P到圆心O的距离OP ＝2，则⊙O的半径为（）A．B．1 C．D．2二．填空题11．如图，PT是⊙O的切线，T为切点，PA是割线，交⊙O于A、B两点，与直径CT交于点D．已知CD＝2，AD＝3，BD＝4，那PB＝．12．如图，PE是⊙O的切线，E为切点，PAB、PCD是割线，AB＝35，CD＝50，AC：DB＝1：2，则PA＝．13．如图，某机械传动装置在静止状态时，连杆PA与点A运动所形成的⊙O交于B点，现测得PB＝4cm，AB＝5cm，⊙O的半径R＝4.5cm，此时P点到圆心O的距离是cm．14．如图，PA切⊙O于A，PBC是⊙O的割线，如果PB＝2，PC＝4，则PA的长为．15．如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D，已知∠APB＝60°，AC＝2，那么CD的长为．三．解答题16．如图，已知矩形ABCD，以A为圆心，AD为半径的圆交AC、AB于M、E，CE的延长线交⊙A于F，CM＝2，AB＝4．（1）求⊙A的半径；（2）求CE的长和△AFC的面积．17．如图，已知点P是⊙O外一点，PS，PT是⊙O的两条切线，过点P作⊙O的割线PAB，交⊙O于A、B两点，并交ST于点C．求证：．18．如图1，A为⊙O的弦EF上的一点，OB是和这条弦垂直的半径，垂足为H，BA的延长线交⊙O于点C，过点C作⊙O的切线与EF的延长线相交于点D．（1）求证：DA＝DC；（2）当DF：EF＝1：8，且DF＝时，求AB•AC的值；（3）将图1中的EF所在直线往上平行移动到⊙O外，如图2的位置，使EF与OB，延长线垂直，垂足为H，A为EF上异于H的一点，且AH小于⊙O的半径，AB的延长线交⊙O 于C，过C作⊙O的切线交EF于D．试猜想DA＝DC是否仍然成立？并证明你的结论．19．如图，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O直径BD＝6，连接CD、AO．（1）求证：CD∥AO；（2）设CD＝x，AO＝y，求y与x之间的函数关系式，并写出自变量x的取值范围；（3）若AO+CD＝11，求AB的长．20．如图，OB是以（O，a）为圆心，a为半径的⊙O1的弦，过B点作⊙O1的切线，P为劣弧上的任一点，且过P作OB、AB、OA的垂线，垂足分别是D、E、F．（1）求证：PD2＝PE•PF；．（2）当∠BOP＝30°，P点为的中点时，求D、E、F、P四个点的坐标及S△DEF参考答案一．选择题1．解：∵PC、PB分别为⊙O的切线和割线，∴PC2＝PB•PA，∵OB＝3，PB＝2，∴PA＝8，∴PC2＝PB•PA＝2×8＝16，∴PC＝4．故选：C．2．解：∵3x2﹣10x+3＝0，∴x＝3（不合题意，舍去）或x＝．∴cos D＝AD：BD＝1：3，设AD＝x，则BD＝3x．∴AB＝＝2x，BC＝2x﹣4．∴（2x）2＝（2x﹣4）•x．∴x＝0（舍去），或x＝2．∴AB＝2×2＝8．故选：C．3．解：∵AB是两圆的一条外公切线，∴MA2＝MD•MC，MB2＝MD•MC，∵CD＝9，MD＝3，∴MA＝MB＝6，∴AB＝12，故选：B．4．解：∵PA•PB＝PC•PD，PA•PB＝30，PC＝3，∴PD＝＝10，∴CD＝10﹣3＝7．故选：B．5．解：∵AD是⊙O的切线，ACB是⊙O的割线，∴AD2＝AC•AB，又AC＝5，AB＝AC+CO+OB＝15，∴AD2＝5×15＝75，∴AD＝5．（AD＝﹣5不合题意舍去）．故选：C．6．解：连接OD，OC．∵D是弧BC的中点，则OD⊥BC，∴DE是圆的切线．故A正确；∴DE2＝CE•AE即：36＝2AE∴AE＝18，则AC＝AE﹣CE＝18﹣2＝16cm．故C正确；∵AB是圆的直径．∴∠ACB＝90°，∵DE垂直于AC的延长线于E．D是弧BC的中点，则OD⊥BC，∴四边形CFDE是矩形．∴CF＝DE＝6cm．BC＝2CF＝12cm．在直角△ABC中，根据勾股定理可得：AB＝＝＝20cm．故B正确；在直角△ABC中，AC＝16，AB＝20，则∠ABC≠30°，而D是弧BC的中点．∴弧AC≠弧CD．故D错误．故选：D．7．解：∵AC是圆O的切线，1∴∠CAB＝∠D，又∵∠C＝∠C，∴△ACD∽△BCA，∴∴AC2＝BC•CD，∵AB＝2，BD＝3，BC＝5，∴AC2＝40，AC＝2，∵，∴AD＝故选：C．8．解：∵PB＝2cm，BC＝8cm，∴PC＝10cm，∵PA2＝PB•PC＝20，∴PA＝2，故选：D．9．解：∵AC，AE为⊙O的切线，∴AC＝AE＝6，根据勾股定理可知AB＝10，∴BE＝4；根据切割线定理有，BE2＝BD×BC可得，BD＝2，∴CD＝6，∴⊙O半径为3．故选：C．10．解：连接OA∵PA为⊙O的切线∴PA⊥OA∵∠APO＝∠APB＝30°∴OA＝OP×sin∠APO＝2×＝1∴⊙O的半径为1故选：B．二．填空题（共5小题）11．解：∵AD•BD＝CD•DT，∴TD＝，∵CD＝2，AD＝3，BD＝4，∴TD＝6，∵PT是⊙O的切线，PA是割线，∴PT2＝PA•PB，∵CT为直径，∴PT2＝PD2﹣TD2，∴PA•PB＝PD2﹣TD2，即（PB+7）PB＝（PB+4）2﹣62，解得PB＝20．故答案为：20．12．解：设PA＝x，∵∠PAC＝∠D，∴△PAC∽△PDB，∴＝，∵AC：DB＝1：2，∴PD＝2PA，∴由切割线定理得，PA•PB＝PC•PD，即x（x+35）＝2x（2x﹣35），解得x＝45，故答案为45．13．解：连接PO交圆于C，并延长PO交圆于D；∵PB＝4cm，AB＝5cm，∴PA＝9cm；由割线定理，得：PB•PA＝PC•PD；设点P到圆心的距离是xcm，则有：（x﹣4.5）（x+4.5）＝36，解得x＝7.5cm．故P到O点的距离为7.5cm．14．解：∵PA切⊙O于A，PBC是⊙O的割线，PB＝2，PC＝4，∴PA2＝PB×PC，∴PA＝＝2．故答案为：2．15．解：连接AD，OB，OP；∵PA、PB与⊙O分别相切于点A、点B，∴∠OAP＝∠OBP＝90°，∠AOB＝180°﹣∠P＝120°，∴∠AOP＝60°，AP＝AO tan60°＝，∴PC＝；∵PA2＝PD•PC，∴PD＝，∴CD＝．三．解答题（共5小题）16．解：（1）四边形ABCD为矩形，AB＝4；∴CD＝4．在Rt△ACD中，AC2＝CD2+AD2；∴（2+AD）2＝42+AD2；解得AD＝3．（2）过A点作AG⊥EF于G；∵BC＝3，BE＝AB﹣AE＝4﹣3＝1．∴CE＝＝＝．由CE•CF＝CD2，得：CF＝＝＝．又∵∠B＝∠AGE＝90°，∠BEC＝∠GEA，∴△BCE∽△GAE；∴，即＝．∴AG＝．∴S＝CF•AG＝××＝．△AFC17．证明：连PO交ST于点D，则PO⊥ST；连SO，作OE⊥PB于E，则E为AB中点，于是因为C、E、O、D四点共圆，所以PC•PE＝PD•PO又因为Rt△SPD∽Rt△OPS所以即PS2＝PD•PO而由切割线定理知PS2＝PA•PB所以即18．（1）证明：连接OC，则OC⊥DC，（1分）∴∠DCA＝90°﹣∠ACO＝90°﹣∠B．∵∠DAC＝∠BAE＝90°﹣∠B，∴∠DAC＝∠DCA．∴DA＝DC．（2）解：∵DF：EF＝1：8，∵DF＝，∴EF＝8DF＝8．∵DC为⊙O的切线，∴DC2＝DF•DE＝×9＝18．∵DC＝3，∴AF＝2，AE＝6．∴AB•AC＝AE•AF＝24．（3）解：结论DA＝DC仍然成立．理由如下：延长BO交⊙O于K，连接CK，则∠KCB＝90°；∵DC为⊙O的切线，∴∠DCA＝∠CKB＝90°﹣∠CBK．∵∠CBK＝∠HBA，∴∠BAH＝90°﹣∠HBA＝90°﹣∠CBK．∴∠DCA＝∠BAH．∴DA＝DC．19．（1）证明：连接BC交OA于E点，∵AB、AC是⊙O的切线，∴AB＝AC，∠1＝∠2．∴AE⊥BC．∴∠OEB＝90°．∵BD是⊙O的直径，∴∠DCB＝90°．∴∠DCB＝∠OEB．∴CD∥AO．（2）解：∵CD∥AO，∴∠3＝∠4．∵AB是⊙O的切线，DB是直径，∴∠DCB＝∠ABO＝90°．∴△BDC∽△AOB．∴＝．∴＝．∴y＝．∴0＜x＜6．（3）解：由已知和（2）知：，（8分）把x、y看作方程z2﹣11z+18＝0的两根，解这个方程得z＝2或z＝9，∴（舍去）．∴AB＝＝＝．20．（1）证明：连接PB，OP，∵PE⊥AB，PD⊥OB，∴∠BEP＝∠PDO＝90°，∵AB切⊙O1于B，∠ABP＝∠BOP，∴△PBE∽△POD，∴＝，同理，△OPF∽△BPD∴＝，∴＝，∴PD2＝PE•PF；（2）解：连接O1B，O1P，∵AB切⊙O1于B，∠POB＝30°，∴∠ABP＝30°，∴∠O1BP＝90°﹣30°＝60°，∵O1B＝O1P，∴△O1BP为等边三角形，∴O1B＝BP，∵P为弧BO的中点，∴BP＝OP，即△O1PO为等边三角形，∴O1P＝OP＝a，∴∠O1OP＝60°，又∵P为弧BO的中点，∴O1P⊥OB，在△O1DO中，∵∠O1OP＝60°O1O＝a，∴O1D＝a，OD＝a，过D作DM⊥OO1于M，∴DM＝OD＝a，OM＝DM＝a，∴D（﹣a，a），∵∠O1OF＝90°，∠O1OP＝60°∴∠POF＝30°，∵PE⊥OA，∴PF＝OP＝a，OF＝a，∴P（﹣a，），F（﹣a，0），∵AB切⊙O1于B，∠POB＝30°，∴∠ABP＝∠BOP＝30°，∵PE⊥AB，PB＝a，∴∠EPB＝60°∴PE＝a，BE＝a，∵P为弧BO的中点，∴BP＝PO，∴∠PBO＝∠BOP＝30°，∴∠BPO＝120°，∴∠BPE+∠BPO＝120°+60°＝180°，即OPE三点共线，∵OE＝a+a＝a，于O，过E作EM⊥x轴于M，∵AO切⊙O1∴∠EOA＝30°，∴EM＝OE＝a，OM＝a，∴E（﹣a，a），∵E（﹣a，a），D（﹣a，a），∴DE＝﹣a﹣（﹣a）＝a，DE边上的高为：a，＝×a×a＝a2．∴S△DEF故答案为：D（﹣a，a），E（﹣a，a），F（﹣a，0），P（﹣a，）；S＝a2．△DEF。
2021年数学九年级中考复习专题之圆的综合(考察切线证明、长度、面积、动点问题等)(五)
2021年数学九年级中考复习专题之圆的综合（考察切线证明、长度、面积、动点问题等）（五）1．如图，⊙O是△ABC外接圆，AB是⊙O的直径，弦DE⊥AB于点H，DE与AC相交于点G，DE、BC的延长线交于点F，P是GF的中点，连接PC．（1）求证：PC是⊙O的切线；（2）若⊙O的半径是1，＝，∠ABC＝45°，求OH的长．2．如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB＝∠ADB．（1）求证：EA是⊙O的切线；（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；（3）已知AF＝4，CF＝2．在（2）条件下，求AE的长．3．阅读资料：小明是一个爱动脑筋的好学生，他在学习了有关圆的切线性质后，意犹未尽，又查阅到了与圆的切线相关的一个问题：如图1，已知PC是⊙O的切线，AB是⊙O的直径，延长BA交切线PC与P，连接AC、BC、OC．因为PC是⊙O的切线，AB是⊙O的直径，所以∠OCP＝∠ACB＝90°，所以∠1＝∠2．又因为∠B＝∠1，所以∠B＝∠2．在△PAC与△PCB中，又因为：∠P＝∠P，所以△PAC∽△PCB，所以＝，即PC2＝PA•PB．问题拓展：（Ⅰ）如果PB不经过⊙O的圆心O（如图2）等式PC2＝PA•PB，还成立吗？请证明你的结论；综合应用：（Ⅱ）如图3，⊙O是△ABC的外接圆，PC是⊙O的切线，C是切点，BA的延长线交PC于点P；（1）当AB＝PA，且PC＝12时，求PA的值；（2）D是BC的中点，PD交AC于点E．求证：＝．4．在平面直角坐标系xOy中，点M（，），以点M为圆心，OM长为半径作⊙M．使⊙M与直线OM的另一交点为点B，与x轴，y轴的另一交点分别为点D，A（如图），连接AM．点P是上的动点．（1）写出∠AMB的度数；（2）点Q在射线OP上，且OP•OQ＝20，过点Q作QC垂直于直线OM，垂足为C，直线QC交x轴于点E．①当动点P与点B重合时，求点E的坐标；②连接QD，设点Q的纵坐标为t，△QOD的面积为S．求S与t的函数关系式及S的取值范围．5．如图，△ABC为⊙O的内接三角形，P为BC延长线上一点，∠PAC＝∠B，AD为⊙O 的直径，过C作CG⊥AD交AD于E，交AB于F，交⊙O于G．（1）判断直线PA与⊙O的位置关系，并说明理由；（2）求证：AG2＝AF•AB；（3）若⊙O的直径为10，AC＝2，AB＝4，求△AFG的面积．6．如图，在⊙O中，直径AB平分弦CD，AB与CD相交于点E，连接AC、BC，点F是BA延长线上的一点，且∠FCA＝∠B．（1）求证：CF是⊙O的切线．（2）若AC＝4，tan∠ACD＝，求⊙O的半径．7．如图①，已知等腰梯形ABCD的周长为48，面积为S，AB∥CD，∠ADC＝60°，设AB＝3x．（1）用x表示AD和CD；（2）用x表示S，并求S的最大值；（3）如图②，当S取最大值时，等腰梯形ABCD的四个顶点都在⊙O上，点E和点F 分别是AB和CD的中点，求⊙O的半径R的值．8．如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，PB与CD交于点F，∠PBC＝∠C．（1）求证：CB∥PD；（2）若∠PBC＝22.5°，⊙O的半径R＝2，求劣弧AC的长度．9．如图1，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，扇形纸片DOE的顶点O 与边AB的中点重合，OD交BC于点F，OE经过点C，且∠DOE＝∠B．（1）证明△COF是等腰三角形，并求出CF的长；（2）将扇形纸片DOE绕点O逆时针旋转，OD，OE与边AC分别交于点M，N（如图2），当CM的长是多少时，△OMN与△BCO相似？10．如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上，∠AEF ＝90°，AE＝EF，过点F作射线BC的垂线，垂足为H，连接AC．（1）试判断BE与FH的数量关系，并说明理由；（2）求证：∠ACF＝90°；（3）连接AF，过A、E、F三点作圆，如图2，若EC＝4，∠CEF＝15°，求的长．参考答案1．解：（1）如图，连接OC，∵AB是⊙O的直径，∴∠ACB＝∠FCG＝90°，∵P是GF的中点，∴PC＝PF＝PG，∴∠PCG＝∠PGC，∵∠PGC＝∠HGA，DE⊥AB∴∠A+∠HGA＝90°，∴∠A+∠PGC＝90°，∵∠A＝∠ACO，∴∠ACO+∠HGA＝90°，∴∠PCO＝90°，∴PC是⊙O的切线；（2）如图2，连接OE，交AC于点M，∵AB是⊙O的直径，弦DE⊥AB，∴，∵＝，∴，∴OE⊥AC，∴∠OMA＝90°，∵∠ACB＝90°，∠ABC＝45°，∴∠AOM＝45°，∵AO＝1，∴OM＝，∵＝，∴AC＝DE，OH＝OM，∴OH＝OM＝．2．（1）证明：如图1，连接CD，∵AC是⊙O的直径，∴∠ADC＝90°，∴∠ADB+∠EDC＝90°，∵∠BAC＝∠EDC，∠EAB＝∠ADB，∴∠EAC＝∠EAB+∠BAC＝90°，∴EA是⊙O的切线．（2）证明：如图2，连接BC，∵AC是⊙O的直径，∴∠ABC＝90°，∴∠CBA＝∠ABC＝90°∵B是EF的中点，∴在RT△EAF中，AB＝BF，∴∠BAC＝∠AFE，∴△EAF∽△CBA．（3）解：∵△EAF∽△CBA，∴＝，∵AF＝4，CF＝2．∴AC＝6，EF＝2AB，∴＝，解得AB＝2．∴EF＝4，∴AE＝＝＝4，3．解：（Ⅰ）当PB不经过⊙O的圆心O时，等式PC2＝PA•PB仍然成立．证法一：如图2﹣1，连接PO并延长交⊙O于点D，E，连接BD、AE，∴∠B＝∠E，∠BPD＝∠APE，∴△PBD∽△PEA，∴，即PA•PB＝PD•PE，由图1知，PC2＝PD•PE，∴PC2＝PA•PB．证法二：如图2﹣2，过点C作⊙O的直径CD，连接AD，BC，AC，∵PC是⊙O的切线，∴PC⊥CD，∴∠CAD＝∠PCD＝90°，即∠1+∠2＝90°，∠D+∠1＝90°，∴∠D＝∠2．∵∠D＝∠B，∴∠B＝∠2，∠P＝∠P，∴△PBC∽△PCA，所以，即PC2＝PA•PB．（Ⅱ）由（1）得，PC2＝PA•PB，PC＝12，AB＝PA，∴PC2＝PA•PB＝PA（PA+AB）＝2PA2，∴2PA2＝144，∴PA＝±6（负值无意义，舍去）．∴PA＝6．（2）证法一：过点A作AF∥BC，交PD于点F，∴＝，＝．∵D为BC的中点，∴BD＝CD，∴＝，∴＝．∵PC2＝PA•PB，∴＝＝＝，即＝．证法二：过点A作AG∥DP，交BC于点G，∴＝，＝．∵D为BC的中点，∴BD＝CD，∴＝，∴＝．∵PC2＝PA•PB，∴＝＝＝，即＝．4．解：（1）过点M作MH⊥OD于点H，∵点M（，），∴OH＝MH＝，∴∠MOD＝45°，∵∠AOD＝90°，∴∠AOM＝45°，∵OM＝AM，∴∠OAM＝∠AOM＝45°，∴∠AMO＝90°，∴∠AMB＝90°；（2）①∵OH＝MH＝，MH⊥OD，∴OM＝＝2，OD＝2OH＝2，∴OB＝4，∵动点P与点B重合时，OP•OQ＝20，∴OQ＝5，∵∠OQE＝90°，∠POE＝45°，∴OE＝5，∴E点坐标为（5，0）②∵OD＝2，Q的纵坐标为t，∴S＝．如图2，当动点P与B点重合时，过点Q作QF⊥x轴，垂足为F点，∵OP＝4，OP•OQ＝20，∴OQ＝5，∵∠OFC＝90°，∠QOD＝45°，∴t＝QF＝，此时S＝；如图3，当动点P与A点重合时，Q点在y轴上，∴OP＝2，∵OP•OQ＝20，∴t＝OQ＝5，此时S＝；∴S的取值范围为5≤S≤10．5．（1）PA与⊙O相切．理由：连接CD，∵AD为⊙O的直径，∴∠ACD＝90°，∴∠D+∠CAD＝90°，∵∠B＝∠D，∠PAC＝∠B，∴∠PAC＝∠D，∴∠PAC+∠CAD＝90°，即DA⊥PA，∵点A在圆上，∴PA与⊙O相切．（2）证明：如图2，连接BG，∵AD为⊙O的直径，CG⊥AD，∴＝，∴∠AGF＝∠ABG，∵∠GAF＝∠BAG，∴△AGF∽△ABG，∴AG：AB＝AF：AG，∴AG2＝AF•AB；（3）解：如图3，连接BD，∵AD是直径，∴∠ABD＝90°，∵AG2＝AF•AB，AG＝AC＝2，AB＝4，∴AF＝＝，∵CG⊥AD，∴∠AEF＝∠ABD＝90°，∵∠EAF＝∠BAD，∴△AEF∽△ABD，∴，即，解得：AE＝2，∴EF＝＝1，∵EG＝＝4，∴FG＝EG﹣EF＝4﹣1＝3，∴S△AFG＝FG•AE＝×3×2＝3．6．（1）证明：连接CO，∵AB是⊙O的直径，∴∠BCA＝90°，∴∠ACO+∠OCB＝90°，∵OB＝CO，∴∠B＝∠OCB，∵∠FCA＝∠B，∴∠BCO＝∠ACF，∴∠OCA+∠ACF＝90°，即∠OCF＝90°，∴CF是⊙O的切线；（2）解：∵直径AB平分弦CD，∴AB⊥DC，∴＝，∵AC＝4，tan∠ACD＝，∴tan∠B＝tan∠ACD＝＝，∴＝，∴BC＝8，∴在Rt△ABC中，AB＝＝＝4，则⊙O的半径为：2．7．解：（1）作AH⊥CD于H，BG⊥CD于G，如图①，则四边形AHGB为矩形，∴HG＝AB＝3x，∵四边形ABCD为等腰梯形，∴AD＝BC，DH＝CG，在Rt△ADH中，设DH＝t，∵∠ADC＝60°，∴∠DAH＝30°，∴AD＝2t，AH＝t，∴BC＝2t，CG＝t，∵等腰梯形ABCD的周长为48，∴3x+2t+t+3x+t+2t＝48，解得t＝8﹣x，∴AD＝2（8﹣x）＝16﹣2x，CD＝8﹣x+3x+8﹣x＝16+x；（2）S＝（AB+CD）•AH＝（3x+16+x）•（8﹣x）＝﹣2x2+8x+64，∵S＝﹣2（x﹣2）2+72，∴当x＝2时，S有最大值72；（3）连结OA、OD，如图②，当x＝2时，AB＝6，CD＝16+2＝18，等腰梯形的高为×（8﹣2）＝6，则AE＝3，DF＝9，∵点E和点F分别是AB和CD的中点，∴直线EF为等腰梯形ABCD的对称轴，∴EF垂直平分AB和CD，EF为等腰梯形ABCD的高，即EF＝6，∴等腰梯形ABCD的外接圆的圆心O在EF上，设OE＝a，则OF＝6﹣a，在Rt△AOE中，∵OE2+AE2＝OA2，∴a2+32＝R2，在Rt△ODF中，∵OF2+DF2＝OD2，∴（6﹣a）2+92＝R2，∴a2+32＝（6﹣a）2+92，解得a＝5，∴R2＝（5）2+32＝84，∴R＝2．8．解：（1）∵∠PBC＝∠D，∠PBC＝∠C，∴∠C＝∠D，∴CB∥PD；（2）连结OC，OD．∵AB是⊙O的直径，弦CD⊥AB于点E，∴＝，∵∠PBC＝∠DCB＝22.5°，∴∠BOC＝∠BOD＝2∠C＝45°，∴∠AOC＝180°﹣∠BOC＝135°，∴劣弧AC的长为：＝．9．解：（1）∵∠ACB＝90°，点O是AB的中点，∴OC＝0B＝OA＝5．∴∠OCB＝∠B，∠ACO＝∠A．∵∠DOE＝∠B，∴∠FOC＝∠OCF．∴FC＝FO．∴△COF是等腰三角形．过点F作FH⊥OC，垂足为H，如图1，∵FC＝FO，FH⊥OC，∴CH＝OH＝，∠CHF＝90°．∵∠HCF＝∠B，∠CHF＝∠BCA＝90°，∴△CHF∽△BCA．∴＝．∵CH＝，AB＝10，BC＝6，∴CF＝．∴CF的长为．（2）①若△OMN∽△BCO，如图2，则有∠NMO＝∠OCB．∵∠OCB＝∠B，∴∠NMO＝∠B．∵∠A＝∠A，∴△AOM∽△ACB．∴＝．∵∠ACB＝90°，AB＝10，BC＝6，∴AC＝8．∵AO＝5，AC＝8，AB＝10，∴AM＝．∴CM＝AC﹣AM＝．②若△OMN∽△BOC，如图3，则有∠MNO＝∠OCB．∵∠OCB＝∠B，∴∠MNO＝∠B．∵∠ACO＝∠A，∴△CON∽△ACB．∴＝＝．∵BC＝6，AB＝10，AC＝8，CO＝5，∴ON＝，CN＝．过点M作MG⊥ON，垂足为G，如图3，∵∠MNO＝∠B，∠MON＝∠B，∴∠MNO＝∠MON．∴MN＝MO．∵MG⊥ON，即∠MGN＝90°，∴NG＝OG＝．∵∠MNG＝∠B，∠MGN＝∠ACB＝90°，∴△MGN∽△ACB．∴＝．∵GN＝，BC＝6，AB＝10，∴MN＝．∴CM＝CN﹣MN＝﹣＝．∴当CM的长是或时，△OMN与△BCO相似．10．解：（1）BE＝FH．证明：∵∠AEF＝90°，∠ABC＝90°，∴∠HEF+∠AEB＝90°，∠BAE+∠AEB＝90°，∴∠HEF＝∠BAE，在△ABE和△EHF中，，∴△ABE≌△EHF（AAS）∴BE＝FH．（2）由（1）得BE＝FH，AB＝EH，∵BC＝AB，∴BE＝CH，∴CH＝FH，∴∠HCF＝45°，∵四边形ABCD是正方形，∴∠ACB＝45°，∴∠ACF＝180°﹣∠HCF﹣∠ACB＝90°．（3）由（2）知∠HCF＝45°，∴CF＝FH．∠CME＝∠HCF﹣∠CEF＝45°﹣15°＝30°．如图2，过点C作CP⊥EF于P，则CP＝CF＝FH．∵∠CEP＝∠FEH，∠CPE＝∠FHE＝90°，∴△CPE∽△FHE．∴，即，∴EF＝4．∵△AEF为等腰直角三角形，∴AF＝8．取AF中点O，连接OE，则OE＝OA＝4，∠AOE＝90°，∴的弧长为：＝2π．方法二：连OC，则∠COF＝2∠CEF＝2*15度＝30度，易知三角形AEF为等腰直角三角形，由∠EOF＝90度，推出角EOC＝60度，三角形OCE为等边三角形，推出半径OE＝EC＝4即可；。
2021年九年级数学中考复习专题之圆：切线长定理综合运用(一)
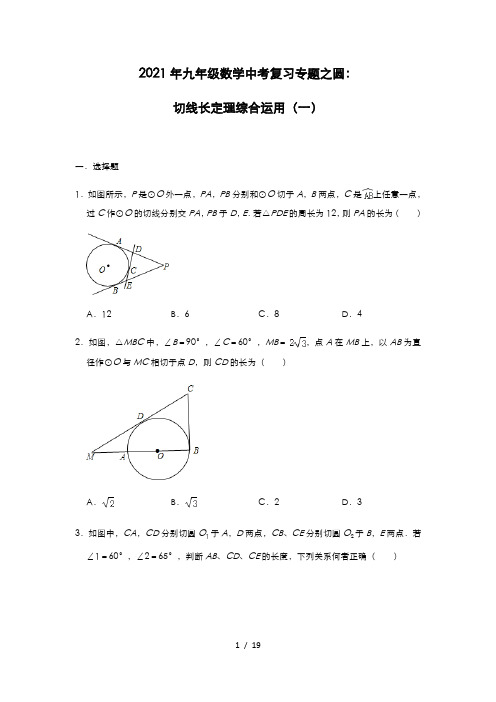
2021年九年级数学中考复习专题之圆：切线长定理综合运用（一）一．选择题1．如图所示，P是⊙O外一点，PA，PB分别和⊙O切于A，B两点，C是上任意一点，过C作⊙O的切线分别交PA，PB于D，E．若△PDE的周长为12，则PA的长为（）A．12 B．6 C．8 D．42．如图，△MBC中，∠B＝90°，∠C＝60°，MB＝，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为（）A．B．C．2 D．33．如图中，CA，CD分别切圆O1于A，D两点，CB、CE分别切圆O2于B，E两点．若∠1＝60°，∠2＝65°，判断AB、CD、CE的长度，下列关系何者正确（）A．AB＞CE＞CD B．AB＝CE＞CD C．AB＞CD＞CE D．AB＝CD＝CE4．如图，AB、AC是⊙O的切线，B、C为切点，∠A＝50°，点P是圆上异于B、C，且在上的动点，则∠BPC的度数是（）A．65°B．115°C．115°或65°D．130°或65°5．如图，半圆O的直径在梯形ABCD的底边AB上，且与其余三边BC、CD、DA相切，若BC＝2，DA＝3，则AB的长（）A．等于4 B．等于5 C．等于6 D．不能确定6．如图，已知PA，PB分别切⊙O于点A、B，∠P＝60°，PA＝8，那么弦AB的长是（）A．4 B．8 C．4D．87．如图所示，PA，PB是⊙O的切线，且∠APB＝40°，下列说法不正确的是（）A．PA＝PB B．∠APO＝20°C．∠OBP＝70°D．∠AOP＝70°8．如图，⊙O是△ABC的内切圆，点D、E分别为边AC、BC上的点，且DE为⊙O的切线，若△ABC的周长为25，BC的长是9，则△ADE的周长是（）A．7 B．8 C．9 D．169．如图，半圆O的直径在梯形ABCD的底边AB上，且与其余三边BC，CD，DA相切，若AB＝10，BC＝4，则AD的长（）A．4 B．5 C．6 D．710．已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A、B），过点P作半圆O的切线分别交过A、B两点的切线于D、C，连接OC、BP，过点O作OM∥CD分别交BC与BP于点M、N．下列结论：①S四边形ABCD＝AB•CD；②AD＝AB；③AD＝ON；④AB为过O、C、D三点的圆的切线．其中正确的个数有（）A．1个B．2个C．3个D．4个二．填空题11．如图，⊙O是四边形ABCD的内切圆，连接OA、OB、OC、OD．若∠AOB＝108°，则∠COD的度数是．12．一个菱形的周长是20cm，两对角线之比是4：3，则该菱形的内切圆的半径是cm．13．如图，P是⊙O的直径AB的延长线上一点，PC、PD切⊙O于点C、D．若PA＝6，⊙O的半径为2，则∠CPD＝．14．如图，已知：PA、PB、EF分别切⊙O于A、B、D，若PA＝10cm，那么△PEF周长是cm．若∠P＝35°，那么∠AOB＝，∠EOF＝．15．如图，P是⊙O外的一点，PA、PB分别与⊙O相切于点A、B，C是上的任意一点，过点C的切线分别交PA、PB于点D、E，若△PDE的周长是10，则PA＝．三．解答题16．已知：如图，PA、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA＝12cm，求△PEF的周长．17．如图，AC是⊙O的直径，∠ACB＝60°，连接AB，分别过A、B作圆O的切线，两切线交于点P，若已知⊙O的半径为1，求△PAB的周长．18．如图，点B在⊙O外，以B点为圆心，OB长为半径画弧与⊙O相交于两点C，D，与直线OB相交A点．当AC＝5时，求AD的长．19．如图所示，在梯形ABCD中，AD∥BC，AB⊥BC，以AB为直径的⊙O与DC相切于E．已知AB＝8，边BC比AD大6．（1）求边AD、BC的长；（2）在直径AB上是否存在一动点P，使以A、D、P为顶点的三角形与△BCP相似？若存在，求出AP的长；若不存在，请说明理由．20．如图，P是⊙O外的一点，PA、PB分别与⊙O相切于点A、B，C是上的任意一点，过点C的切线分别交PA、PB于点D、E．（1）若PA＝4，求△PED的周长；（2）若∠P＝40°，求∠AFB的度数．参考答案一．选择题1．解：∵PA，PB分别和⊙O切于A，B两点，∴PA＝PB，∵DE是⊙O的切线，∴DA＝DC，EB＝EC，∵△PDE的周长为12，即PD+DE+PE＝PD+DC+EC+PE＝PD+AD+EB+PE＝PA+PB＝2PA＝12，∴PA＝6．故选：B．2．解：在直角△BCM中，tan60°＝＝，得到BC＝＝2，∵AB为圆O的直径，且AB⊥BC，∴BC为圆O的切线，又CD也为圆O的切线，∴CD＝BC＝2．故选：C．3．解：∵∠1＝60°，∠2＝65°，∴∠ABC＝180°﹣∠1﹣∠2＝180°﹣60°﹣65°＝55°，∴∠2＞∠1＞∠ABC，∴AB＞BC＞AC，∵CA，CD分别切圆O1于A，D两点，CB、CE分别切圆O2于B，E两点，∴AC＝CD，BC＝CE，∴AB＞CE＞CD．故选：A．4．解：如图，连接OB、OC，∵AB、AC是⊙O的切线，∴∠OBA＝∠OCA＝90°，∵∠A＝50°，∴∠BOC＝130°，∵∠BOC＝2∠P，∴∠BPC＝65°；故选：C．5．解：如图，连接OC，OD，设⊙O的半径为r，∵BC、CD、DA与半⊙O相切，∴AD边上的高和AO边上的高都为r，∴AO＝AD，同理BO＝BC，∴AB＝AO+BO＝AD+BC＝2+3＝5．故选：B．6．解：∵PA，PB分别切⊙O于点A、B，∴PA＝PB，又∠P＝60°，∴△APB是等边三角形，∴AB＝PA＝8．故选：B．7．解：∵PA，PB是⊙O的切线，且∠APB＝40°，∴PA＝PB，∠APO＝∠BPO，∠A＝∠B＝90°，∴∠OBP＝∠OAP，∴C是错误的．故选：C．8．解：∵AB、AC、BC、DE都和⊙O相切，∴BI＝BG，CI＝CH，DG＝DF，EF＝EH．∴BG+CH＝BI+CI＝BC＝9，∴C△ADE＝AD+AE+DE＝AD+AE+DF+EF＝AD+DG+EH+AE＝AG+AH＝C△ABC﹣（BG+EH+BC）＝25﹣2×9＝7．故选：A．9．解：连接OC，OD，设⊙O的半径为r，∵BC、CD、DA与半⊙O相切，∴AD和AO的高为r，∴AO＝AD，同理BO＝BC，∴AB＝AO+BO＝AD+BC，又知AB＝10，BC＝4，故知AD＝6，故选：C．10．解：连接OD、AP，∵DA、DP、BC分别是圆的切线，切点分别是A、P、B，∴DA＝DP，CP＝CB，∠A＝90°＝∠B＝∠DPO，∴AD+BC＝DP+CP＝CD，∴S四边形ABCD＝（AD+BC）•AB＝AB•CD，∴①正确；∵AD＝DP＜OD，∵四边形ODPN是平行四边形，得到OD＝NP＜BP＜AB，则AD＜AB，∴②错误；∵AB是圆的直径，∴∠APB＝90°，∵DP＝AD，AO＝OP，∴D、O在AP的垂直平分线上，∴OD⊥AP，∵∠DPO＝∠APB＝90°，∴∠OPB＝∠DPA＝∠DOP，∵OM∥CD，∴∠POM＝∠DPO＝90°，在△DPO和△NOP中∠PON＝∠DPO，OP＝OP，∠DOP＝∠OPN，∴△DPO≌△NOP，∴ON＝DP＝AD，∴③正确；∵AP⊥OD，OA＝OP，∴∠AOD＝∠POD，同理∠BOC＝∠POC，∴∠DOC＝×180°＝90°，∴△CDO的外接圆的直径是CD，∵∠A＝∠B＝90°，取CD的中点Q，连接OQ，∵OA＝OB，∴AD∥OQ∥BC，∴∠AOQ＝90°，∴④正确．故选：C．二．填空题（共5小题）11．解：如图所示：连接圆心与各切点，在Rt△DEO和Rt△DFO中，∴Rt△DEO≌Rt△DFO（HL），∴∠1＝∠2，同理可得：Rt△AFO≌Rt△AMO，Rt△BMO≌Rt△BNO，Rt△CEO≌Rt△CNO，∴∠3＝∠4，∠5＝∠7，∠6＝∠8，∴∠5+∠6＝∠7+∠8＝108°，∴2∠2+2∠3＝360°﹣2×108°，∴∠2+∠3＝∠DOC＝72°．故答案为：72°．12．解：如图所示：菱形ABCD，对角线AC，BD，可得菱形内切圆的圆心即为对角线交点，设AB与圆相切于点E，可得OE⊥AB，∵一个菱形的周长是20cm，两对角线之比是4：3，∴AB＝5cm，设BO＝4x，则AO＝3x，故（4x）2+（3x）2＝25，解得：x＝1，则AO＝3，BO＝4，故EO•AB＝AO•BO，解得：EO＝．故答案为：．13．解：∵PA＝6，⊙O的半径为2，∴PB＝PA﹣AB＝6﹣4＝2，∴OP＝4，∵PC、PD切⊙O于点C、D．∴∠OPC＝∠OPD，∴CO⊥PC，∴sin∠OPC＝＝，∴∠OPC＝30°，∴∠CPD＝60°，故答案为：60°．14．解：∵PA、PB、EF分别切⊙O于A、B、D．∴AE＝ED，DF＝FR∴△PEF周长是PE+PF+EF＝PE+EA+PF+FR＝PA+PR＝2PA＝20cm；∵PA、PB、EF分别切⊙O于A、B∴∠PAO＝∠PRO＝90°∴∠AOB＝360°＝90°﹣90°﹣35°＝145°；∴∠EOF＝∠AOB＝72.5°故答案是：20，145°，72.5°．15．解：∵DA，DC都是圆O的切线，∴DC＝DA，同理EC＝EB，PA＝PB，∴△PDE的周长＝PD+PE+DE＝PD+DC+PE+BE＝PA+PB＝2PA＝10，∴PA＝5；故答案为5．三．解答题（共5小题）16．解：∵PA、PB是⊙O的切线，切点分别是A、B，∴PA＝PB＝12，∵过Q点作⊙O的切线，交PA、PB于E、F点，∴EB＝EQ，FQ＝FA，∴△PEF的周长是：PE+EF+PF＝PE+EQ+FQ+PF，＝PE+EB+PF+FA＝PB+PA＝12+12＝24，答：△PEF的周长是24．17．解：∵PA，PB是圆O的切线．∴PA＝PB，∠PAB＝60°∴△PAB是等边三角形．在直角△ABC中，AB＝AC•sin60°＝2×＝∴△PAB的周长为PA+PB+AB＝3．18．解：连接OC、OD．∵OA是⊙B的直径，∴∠OCA＝∠ODA＝90°，∴AC、AD都是⊙O的切线．∴AD＝AC＝5．19．解：（1）方法1：过D作DF⊥BC于F，在Rt△DFC中，DF＝AB＝8，FC＝BC﹣AD＝6，∴DC2＝62+82＝100，即DC＝10．（1分）设AD＝x，则DE＝AD＝x，EC＝BC＝x+6，∴x+（x+6）＝10．∴x＝2．∴AD＝2，BC＝2+6＝8．（4分）方法2：连OD、OE、OC，由切线长定理可知∠DOC＝90°，AD＝DE，CB＝CE，设AD＝x，则BC＝x+6，由射影定理可得：OE2＝DE•EC．（2分）即：x（x+6）＝16，解得x1＝2，x2＝﹣8，（舍去）∴AD＝2，BC＝2+6＝8．（4分）（2）存在符合条件的P点．设AP＝y，则BP＝8﹣y，△ADP与△BCP相似，有两种情况：①△ADP∽△BCP时，∴y＝；（6分）②△ADP∽△BPC时，∴y＝4．（7分）故存在符合条件的点P，此时AP＝或4．（8分）20．解：（1）∵DA，DC都是圆O的切线，∴DC＝DA，同理EC＝EB，∵P是⊙O外的一点，PA、PB分别与⊙O相切于点A、B∴PA＝PB，∴三角形PDE的周长＝PD+PE+DE＝PD+DC+PE+BE＝PA+PB＝2PA＝8，即三角形PDE的周长是8；（2）连接AB，∵PA＝PB，∴∠PAB＝∠PBA，∵∠P＝40°，∴∠PAB＝∠PBA＝（180﹣40）＝70°，∵BF⊥PB，BF为圆直径∴∠ABF＝∠PBF＝90°﹣70°＝20°∴∠AFB＝90°﹣20°＝70°．答：（1）若PA＝4，△PED的周长为8；（2）若∠P＝40°，∠AFB的度数为70°．。
2021年九年级数学中考复习专题之圆：切割线定理综合运用(一)
2021年九年级数学中考复习专题之圆：切割线定理综合运用（一）一．选择题1．P是⊙O外一点，PA切⊙O于A，割线PBC交⊙O于点B、C，若PB＝BC＝3，则PA的长是（）A．9 B．3 C．D．182．如图，PA切⊙O于点A，PBC是⊙O的一条割线，且PA＝2，BC＝2PB，那么PB 的长为（）A．2 B．C．4 D．3．如图，⊙O的两条割线PAB，PCD分别交⊙O于点A，B和点C，D．已知PA＝6，AB＝4，PC＝5，则CD＝（）A．B．C．7 D．244．如图，已知P为⊙O外一点，PO交⊙O于点A，割线PBC交⊙O于点B、C，且PB ＝BC，若OA＝7，PA＝4，则PB的长等于（）A．B．C．6 D．5．如图，PA切⊙O于点A，PBC是⊙O的割线，如果PB＝2，PC＝8，那么PA的长为（）A．2 B．4 C．6 D．6．如图，在▱ABCD中，过A、B、C三点的圆交AD于E，且与CD相切．若AB＝4，BE ＝5，则DE的长为（）A．3 B．4 C．D．7．如图，在以O为圆心的两个同心圆中，A为大圆上任意一点，过A作小圆的割线AXY，若AX•AY＝4，则图中圆环的面积为（）A．16πB．8πC．4πD．2π8．如图，A、B、C、D为⊙O上的点，直线BA与DC相交于点P，PA＝2，PC＝CD＝3，则PB＝（）A．6 B．7 C．8 D．99．以半圆中的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交于点D，若，且AB＝10，则CB的长为（）A．B．C．D．410．如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B．如果∠APB ＝60°，PA＝8，那么点P与O间的距离是（）A．16 B．C．D．二．填空题11．如图，⊙O的半径为，A、B两点在⊙O上，切线AQ和BQ相交于Q，P是AB 延长线上任一点，QS⊥OP于S，则OP•OS＝．12．如图，过点P引圆的两条割线PAB和PCD，分别交圆于点A，B和C，D，连接AC，BD，则在下列各比例式中，①；②；③，成立的有（把你认为成立的比例式的序号都填上）．13．如图，割线PAB与⊙O交于点A、B，割线PCD与⊙O交于点C、D，PA＝PC，PB＝3cm，则PD＝cm．14．如图，过⊙O外一点P作两条割线，分别交⊙O于A，B和C，D．已知PA＝2，PB ＝5，PD＝8，则PC的长是．15．如图，AC为⊙O的直径，PA是⊙O的切线，切点为A，PBC是⊙O的割线，∠BAC 的平分线交BC于D点，PF交AC于F点，交AB于E点，要使AE＝AF，则PF应满足的条件是（只需填一个条件）．三．解答题16．如图，AB是⊙O的直径，C是AB延长线上的一点，CD是⊙O的切线，D为切点，过点B作⊙O的切线交CD于点E．若AB＝CD＝2，求CE的长．17．如图所示，⊙O的内接△ABC的AB边过圆心O，CD切⊙O于C，BD⊥CD于D，交⊙O于F，CE⊥AB于点E，FE交⊙O于G．解答下列问题：（1）若BC＝10，BE＝8，求CD的值；（2）求证：DF•DB＝EG•EF．18．如图1，已知Rt△ABC的直角边AC的长为2，以AC为直径的⊙O与斜边AB交于点D，过D点作⊙O的切线（1）求证：BE＝DE；（2）延长DE与AC的延长线交于点F，若DF＝，求△ABC的面积；（3）从图1中，显然可知BC＜AC．试分别讨论在其它条件不变，当BC＝AC（图2）和BC＞AC（图3）时，直线DE与直线AC还会相交吗？若不能相交，请简要说明理由；若能相交，设交点为F'且DF'＝，请再求出△ABC的面积．19．已知：如图，PF是⊙O的切线，PE＝PF，A是⊙O上一点，直线AE、AP分别交⊙O 于B、D，直线DE交⊙O于C，连接BC，（1）求证：PE∥BC；（2）将PE绕点P顺时针旋转，使点E移到圆内，并在⊙O上另选一点A，如图2．其他条件不变，在图2中画出完整的图形．此时PE与BC是否仍然平行？证明你的结论．20．如图PAB、PCD是⊙O的两条割线，AB是⊙O的直径．（1）如图甲，若PA＝8，PC＝10，CD＝6．①求sin∠APC的值；②sin∠BOD＝；（2）如图乙，若AC∥OD．①求证：CD＝BD；②若，试求cos∠BAD的值．参考答案一．选择题1．解：∵PB＝BC＝3，∴PC＝6，∵PA2＝PB•PC＝18，∴PA＝3，故选：C．2．解：设PB＝x，则PC＝3x，∵PA2＝PB•PC，PA＝2，BC＝2PB，∴x•3x＝12，∴x＝2．故选：A．3．解：由于PAB、PCD都是⊙O的割线，根据切割线定理可得：PA•PB＝PC•PD，即PA•（PA+PB）＝PC•PD，∵PA＝6，AB＝4，PC＝5，∴PD＝12，即CD＝PD﹣PC＝7；故选：C．4．解：延长PO交圆于D；设PB＝BC＝x，∵PB•PC＝PA•PD，PB＝BC，OA＝7，PA＝4，∴x•2x＝72，∴x＝6．故选：C．5．解：∵PA切⊙O于点A，PBC是⊙O的割线，∴PA2＝PB•PC＝16，即PA＝4；故选：B．6．解：连接CE；∵，∴∠BAE＝∠EBC+∠BEC；∵∠DCB＝∠DCE+∠BCE，由弦切角定理知：∠DCE＝∠EBC，由平行四边形的性质知：∠DCB＝∠BAE，∴∠BEC＝∠BCE，即BC＝BE＝5，∴AD＝5；由切割线定理知：DE＝DC2÷DA＝，故选：D．7．解：过点A作圆的切线AD，切点是D，∵AD2＝AX•AY，AX•AY＝4，∴AD＝2，∴圆环的面积＝πAD2＝4π．故选：C．8．解：∵PB，PD是⊙O的割线，∴PA•PB＝PC•PD，∵PA＝2，PC＝CD＝3，∴2PB＝3×6解得：PB＝9．故选：D．9．解：如图，若，且AB＝10，∴AD＝4，BD＝6，作AB关于直线BC的对称线段A′B，交半圆于D′，连接AC、CA′，可得A、C、A′三点共线，∵线段A′B与线段AB关于直线BC对称，∴AB＝A′B，∴AC＝A′C，AD＝A′D′＝4，A′B＝AB＝10．而A′C•A′A＝A′D′•A′B，即A′C•2A′C＝4×10＝40．则A′C2＝20，又∵A′C2＝A′B2﹣CB2，∴20＝100﹣CB2，∴CB＝4．故选：A．10．解：连接OA，OP∵PA，PB是⊙O的切线，∠APB＝60°，∴∠OPA＝∠APB＝30°，OA⊥OP，∴OP＝＝＝，∴点P与O间的距离是．故选：B．二．填空题（共5小题）11．解：连接OQ交AB于M，则OQ⊥AB，连接OA，则OA⊥AQ．∵∠QMP＝∠QSP＝90°，∴S，P，Q，M四点共圆，故OS•OP＝OM•OQ．又∵OM•OQ＝OA2＝2，∴OS•OP＝2．故答案为：2．12．解：∵四边形ABCD是圆内接四边形∴∠PAD＝∠C，∠PAD＝∠B∴△PAD∽△PCB根据相似三角形的对应边的比相等，得到②③是正确的．13．解：∵PA•PB＝PC•PD，PA＝PC，PB＝3cm∴PB＝PD＝3cm．14．解：∵PA•PB＝PC•PD，PA＝2，PB＝5，PD＝8∴PC＝＝．15．解：∵∠PAC＝90°，∠ABC＝90°，∴90°﹣∠AFP＝90°﹣∠BEP，∴∠APF＝∠CPF，∴PF平分∠APC．三．解答题（共5小题）16．解：如图，由切割线定理，得CD2＝CB•CA，（2分）CD2＝CB（AB+CB），CB2+2CB﹣4＝0，解得CB＝（负数舍去）连接OD，则OD⊥CD，又EB与⊙O相切，∴EB⊥OC，∴Rt△ODC∽Rt△EBC，（6分）于是，即∴CE＝．17．（1）解：∵AB为直径，BD⊥CD∴∠ABC+∠A＝90°，∠CBD+∠BCD＝90°∵CD为⊙O切线∴∠BCD＝∠A∴∠ABC＝∠BCD∵CD⊥BD，CE⊥BE∴CE＝CD∴CE＝＝6∴CD＝6（2）证明：∵CD为切线，BD为割线∴CD2＝DF•DB①∵∠ACB＝90°，CE⊥AB∴RT△ACE∽RT△CBE∴CE2＝EA•EB②∵EG•EF＝EA•EB③由①②③及CD＝CE得DF•DB＝EG•EF．18．（1）证明：连接OD，∴OD⊥DE，∴∠ADO+∠BDE＝90°，∵OA＝OD，∴∠A＝∠ADO，∵∠ACB＝90°，∴∠B+∠A＝90°，∴∠B＝∠BDE，∴BE＝DE；（2）解：在直角三角形ODF中，OD＝1，DF＝，∴∠OFD＝30°，∴OF＝2，AF＝3．∴tan∠A＝，∴BC＝AC•tan∠A＝2×tan30°＝．S△ABC＝AC•BC＝×2×＝；（3）解：如图，当BC＝AC时，直线DE与直线AC平行；当BC＞AC时，在直角三角形ODF′中，OD＝1，DF′＝，∴∠OF′D＝30°，∴OF′＝2，AF＝1，∴CF′＝3，∠BAC＝60°，∴tan∠BAC＝，∴BC＝AC•tan∠BAC＝2×tan60°＝2．S △ABC＝AC•BC＝×2×2＝2．19．（1）证明：∵PF与⊙O相切，∴PF2＝PD•PA．∵PE＝PF，∴PE2＝PD•PA．∴PE：PD＝PA：PE．∵∠APE＝∠APE，∴△EPD∽△APE．∴∠PED＝∠A．∵∠ECB＝∠A，∴∠PED＝∠ECB．∴PE∥BC．（2）解：PE与BC仍然平行．证明：画图如图，∵△EPD∽△APE，∴∠PEA＝∠D．∵∠B＝∠D，∴∠PEA＝∠B．∴PE∥BC．20．解：（1）作OE⊥CD于E，连接OC，作DF⊥PB于F．①根据垂径定理，得CE＝3．设圆的半径是r．根据勾股定理，得OP2﹣PE2＝OC2﹣CE2，（8+r）2﹣169＝r2﹣9，解得r＝6．则OE＝3．则sin∠APC＝＝；②设OF＝x．根据勾股定理，得PD2﹣PF2＝OD2﹣OF2，256﹣（14+x）2＝36﹣x2，解得x＝．所以DF＝．所以sin∠BOD＝＝＝．（2）①∵AC∥OD，∴∠1＝∠2．又OA＝OD，∴∠2＝∠3．∴∠1＝∠3．所以弧CD＝弧BD，所以CD＝BD；②∵AC∥OD，∴＝．又CD＝BD，AB＝2OA，∴＝．∴cos∠BAD＝＝．。
备战中考数学专题练习圆的切线长定理一(含解析)
2021备战中考数学专题练习-圆的切线长定理一〔含解析〕一、单项选择题1.如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B．假如∠APB=60°，PA=8，那么点P与O间的间隔是〔〕A.16B.C.D.2.如图，以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB 均相切，切点分别是D、C、E．假设半圆O的半径为2，梯形的腰AB为5，那么该梯形的周长是〔〕.A.9B.10C.12D.143.如图，PA,PB切∠O于点A,B，PA=8，CD切∠O于点E，交PA,PB于C,D两点，那么∠PCD的周长是〔〕A.8B.18C.16D.144.如图，PA，PB，CD与∠O相切于点为A，B，E，假设PA=7，那么∠PCD的周长为〔〕A.7B.14C.10.5D.105.Rt∠ABC中，∠C=90°，AB=5，内切圆半径为1，那么三角形的周长为〔〕A.15B.12C.13D.146.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.假如∠APB=60°,PA=8,那么弦AB的长是()A.4B.8C.D.7.如图，Rt∠ABC的内切圆∠O与两直角边AB，BC分别相切于点D，E，过劣弧〔不包括端点D，E〕上任一点P作∠O的切线MN与AB，BC分别交于点M，N，假设∠O的半径为r，那么Rt∠MBN的周长为〔〕A.rB.rC.2rD.r8.如图，AB为半圆O在直径，AD、BC分别切∠O于A、B两点，CD切∠O于点E，连接OD、OC，以下结论：①∠DOC=90°，②AD+BC=CD，③S∠AOD：S∠BOC=AD2：AO2 ，④OD：OC=DE：EC，⑤OD2=DE•CD，正确的有〔〕A.2个B.3个C.4个D.5个9.如图，∠ABC是一张周长为17cm的三角形的纸片，BC=5cm，∠O是它的内切圆，小明准备用剪刀在∠O的右侧沿着与∠O相切的任意一条直线MN剪下∠AMN，那么剪下的三角形的周长为〔〕A.12cmB.7cmC.6cmD.随直线MN的变化而变化二、填空题10.如图，AB、AC、BD是∠O的切线，P、C、D为切点，假如AB=5，AC=3，那么BD的长为________.11.PA、PB分别切∠O于点A、B，假设PA=3cm，那么PB=________cm．12.如图，PA、PB切∠O于点A、B，PA=6，CD切∠O于点E，交PA、PB于C、D两点，那么∠PCD的周长是________．13.如图，AB为半∠O的直径，C为半圆弧的三等分点，过B，C两点的半∠O的切线交于点P，假设AB的长是2a，那么PA的长是________．14.如图，PA、PB是∠O的两条切线，A、B是切点，假设∠APB=60°，PO=2，那么∠O的半径等于________．15.如图，一圆内切于四边形ABCD，且AB=16，CD=10，那么四边形ABCD的周长为________．16.如图,PA,PB是∠O的切线,A,B分别为切点,AC是∠O的直径,∠P=40°,那么∠BAC=________.三、解答题17.如图,以Rt∠ABC的直角边AB为直径作∠O,与斜边AC交于点D,过点D作∠O的切线交BC边于点E.求证:EB=EC=ED18.如图，PA、PB切∠O于A、B，假设∠APB=60°，∠O半径为3，求阴影局部面积．四、综合题19.如图，：射线PO与∠O交于A、B两点，PC、PD分别切∠O于点C、D．〔1〕请写出两个不同类型的正确结论；〔2〕假设CD=12，tan∠CPO= ，求PO的长．20.如图，AB是∠O的直径，AM、BN分别与∠O相切于点A、B，CD交AM、BN于点D、C，DO平分∠ADC.〔1〕求证：CD是∠O的切线；〔2〕设AD＝4，AB＝x (x > 0)，BC＝y (y > 0). 求y关于x的函数解析式.21.如图，AB是半圆O的直径，AB＝2，射线AM、BN为半圆O的切线.在AM上取一点D，连接BD交半圆于点C，连接AC.过O点作BC的垂线OE，垂足为点E，与BN相交于点F.过D点作半圆O的切线DP，切点为P，与BN相交于点Q.〔1〕假设∠ABD∠∠BFO，求BQ的长；〔2〕求证：FQ=BQ答案解析局部一、单项选择题1.【答案】B【考点】等边三角形的性质，勾股定理，切线长定理【解析】【解答】解：连接OA，OP∠PA，PB是∠O的切线，∠APB=60°，∠∠OPA= ∠APB=30°，OA∠OP，∠OP= = = ，∠点P与O间的间隔是．应选B．【分析】作辅助线，连接OA，OP，根据切线长定理可知：∠OPA= ∠APB，由PA与∠O相切，可知：OA∠AP，根据条件可将OP的长求出．2.【答案】D【考点】直角梯形，切线长定理【解析】【解答】根据切线长定理，得AD=AE，BC=BE，所以梯形的周长是5×2+4=14．应选D．【分析】由切线长定理可知：AD=AE，BC=BE，因此梯形的周长=2AB+CD，了AB和∠O的半径，由此可求出梯形的周长．3.【答案】C【考点】切线长定理【解析】【解答】解：∠PA,PB切∠O于点A,B，CD切∠O于点E∠PA=PB=8，AC=CE，DB=DE∠PCD的周长为：PC+CE+DE+PD=PC=CA+DB+PD=PA+PB=8+8=16故答案为：C【分析】利用切线长定理可得出PA=PB=8，AC=CE，DB=DE，从而可求∠PCD的周长就转化为求PA+PB的值。
部编数学九年级下册专项21切线的判定与性质的综合应用(解析版)含答案
专项21 切线的判定与性质的综合应用ìïìïííîïïî圆的切线的性质--三角形内切圆应用:d=r 圆的切线的判定判定定理圆的切线性质与判定综合应用【类型一： 有公共点：连半径，证垂直】【典例1】（2021秋•吉林期末）已知：如图，△ABC 中，AB ＝AC ，以AB 为直径的⊙O 交BC 于点P ，PD ⊥AC 于点D ．（1）求证：PD 是⊙O 的切线；（2）若∠CAB ＝120°，AB ＝6，求BC 的值．【解答】（1）证明：∵AB ＝AC ，∴∠B ＝∠C ，∵OP ＝OB ，∴∠B ＝∠OPB ，∴∠OPB ＝∠C ，∴OP ∥AC ，∵PD ⊥AC ，∴OP ⊥PD ，∴PD 是⊙O的切线；（2）解：连接AP，如图，∵AB为直径，∴∠APB＝90°，∴BP＝CP，∵∠CAB＝120°，∴∠BAP＝60°，在Rt△BAP中，AB＝6，∠B＝30°，∴AP＝AB＝3，∴BP＝AP＝3，∴BC＝2BP＝6．【变式1-1】（2021秋•西城区校级期中）如图，在Rt△ABC中，∠C＝90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．（1）求证：AC是⊙O的切线；（2）若OB＝10，CD＝8，求CE的长．【解答】（1）证明：连接OD，如图，∵BD为∠ABC平分线，∴∠1＝∠2，∵OB＝OD，∴∠1＝∠3，∴∠2＝∠3，∴OD∥BC，∵∠C＝90°，∴∠ODA＝90°，∴AC是⊙O的切线；（2）解：过O作OG⊥BC，连接OE，则四边形ODCG为矩形，∴GC＝OD＝OB＝10，OG＝CD＝8，在Rt△OBG中，利用勾股定理得：BG＝6，∵OG⊥BE，OB＝OE，∴BE＝2BG＝12．解得：BE＝12，∵AC是⊙O的切线，∴CD2＝CE•CB，即82＝CE（CE+12），解得：CE＝4或CE＝﹣16（舍去），即CE的长为4．【变式1-2】（2021秋•温岭市期末）如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．（1）求证：CD是⊙O的切线；（2）若AC＝8，CD＝12，求半径的长度．【解答】（1）证明：连接OD，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠DAB+∠DBA＝90°，∵∠CDA＝∠CBD，∴∠DAB+∠CDA＝90°，∵OD＝OA，∴∠DAB＝∠ADO，∴∠CDA+∠ADO＝90°，∴∠CDO＝90°，∵OD是⊙O的半径，∴CD是⊙O的切线；（2）解：在Rt△CDO中，CD2+OD2＝OC2，∴122+r2＝（8+r）2，∴r＝5，∴半径的长度为5．【典例2】（2020•中宁县一模）如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上一点，且AP＝AC．（1）求证：PA是⊙O的切线；（2）若PD＝1，求⊙O的直径．【解答】（1）证明：连接OA，∵∠B＝60°，∴∠AOC＝2∠B＝120°，∴∠OAC＝∠OCA＝30°，又∵AP＝AC，∴∠P＝∠ACP＝30°，∴∠OAP＝∠AOC﹣∠P＝90°，∴OA⊥PA，∴PA是⊙O的切线．（2）设该圆的半径为x．在Rt△OAP中，∵∠P＝30°，∴PO＝2OA＝OD+PD，又∵OA＝OD，∴1+x＝2x，解得：x＝1∴OA＝PD＝1，所以⊙O的直径为2【变式2-1】（2021秋•甘井子区期末）如图，△ABC中，AB＝AC，以AB为直径的⊙O与AC，BC分别交于点D和点E，过点E作EF⊥AC，垂足为F．（1）求证：EF是⊙O的切线；（2）若CD＝4，EF＝3，求⊙O半径．【解答】（1）证明：连接OE，∵EF⊥AC，∴∠EFD＝∠EFC＝90°，∵AB＝AC，∴∠B＝∠C，∴∠B＝∠OEB，∴∠OEB＝∠C，∴OE∥AC，∴∠OEF＝∠EFC＝90°，∵OE是⊙O的半径，∴EF是⊙O的切线；（2）解：过点O作OG⊥AD，垂足为G，∴∠OGF＝90°，∵∠OEF＝∠EFG＝90°，∴四边形OEFG是矩形，∴OG＝EF＝3，设⊙O的半径为x，∴AB＝AC＝2x，∵CD＝4，∴AD＝AC﹣CD＝2x﹣4，∵OG⊥AD，∴AG＝AD＝x﹣2，在Rt△OAG中，AG2+OG2＝OA2，∴（x﹣2）2+9＝x2，∴x＝，∴⊙O的半径为．【变式2-2】（2021秋•天津期末）如图，已知AB是⊙O的直径，AC是弦，∠BAC的角平分线交⊙O于点D，DE⊥AC于E．（1）求证：DE是⊙O的切线；（2）若AB＝10，AC＝6，求ED的长．【解答】（1）证明：连接OD，∵DE⊥AE，∴∠AED＝90°，∵AD平分∠BAE，∴∠CAD＝∠DAB，∵OA＝OD，∴∠ADO＝∠DAB，∴∠CAD＝∠ADO，∴AC∥DO，∴∠EDO＝180°﹣∠E＝90°，∵OD是⊙O的半径，∴DE是⊙O的切线；（2）解：连接BC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ECB＝180°﹣∠ACB＝90°，∵∠E＝∠EDO＝90°，∴四边形ECFD是矩形，∴DE＝CF，∠CFD＝90°，∵AB＝10，AC＝6，∴BC＝＝＝8，∵OD⊥BC，∴CF＝BC＝4，∴DE＝CF＝4，∴ED的长为4【典例3】（2022•东明县一模）已知，在Rt△ABC中，∠BAC＝90°，以AB为直径的⊙O 与BC相交于点E，在AC上取一点D，使得DE＝AD，（1）求证：DE是⊙O的切线．（2）当BC＝10，AD＝4时，求⊙O的半径．【解答】（1）证明：连接OE、OD，在△AOD和△EOD中，，∴△AOD≌△EOD（SSS），∴∠OED＝∠BAC＝90°，∴DE是⊙O的切线；（2）解：∵△AOD≌△EOD，∵OB＝OE，∴∠B＝∠OEB，∵∠AOE＝∠B+∠OEB，∴∠BEO＝∠EOD，∴OD∥BC，又AO＝BO，∴OD＝BC＝5，由勾股定理得，AO＝＝3，则⊙O的半径为3．【变式3-1】（2021秋•金湖县期末）如图，四边形OAEC是平行四边形，以O为圆心，OC 为半径的圆交CE于D，延长CO交⊙O于B，连接AD、AB，AB是⊙O的切线．（1）求证：AD是⊙O的切线．（2）若⊙O的半径为4，AB＝8，求平行四边形OAEC的面积．【解答】（1）证明：连接OD，∵AB与⊙O相切于点B，∴∠OBA＝90°，∵四边形OAEC是平行四边形，∴AO∥EC，∴∠AOD＝∠ODC，∠AOB＝∠OCD，∵OD＝OC，∴∠ODC＝∠OCD，又∵OA＝OA，OD＝OB，∴△AOB≌△AOD（SAS），∴∠OBA＝∠ODA，∴∠ODA＝90°，∵OD是⊙O的半径，∴AD为⊙O的切线；（2）解：∵OB＝4，AB＝8，∴S＝AB•OB＝×4×8＝16，△ABO∵△AOB≌△AOD，∴S＝16，△AOD＝32．∴平行四边形OAEC的面积＝2S△AOD【类型一：没有公共点：作垂直，证半径】【典例4】（2020•八步区一模）如图，在Rt△ABC中，∠BAC的角平分线交BC于点D，E 为AB上一点，DE＝DC，以D为圆心，DB的长为半径作⊙D，AB＝5，BE＝3．（1）求证：AC是⊙D的切线；（2）求线段AC的长．【解答】（1）证明：过点D作DF⊥AC于F；∵AB为⊙D的切线，∴∠B＝90°，∴AB⊥BC，∵AD平分∠BAC，DF⊥AC，∴BD＝DF，∴AC与⊙D相切；（2）解：在△BDE和△DCF中；，∴Rt△BDE≌Rt△DCF（HL），∴EB＝FC．∵AB＝AF，∴AB+EB＝AF+FC，即AB+EB＝AC，∴AC＝5+3＝8．【变式4-1】（2021秋•莆田期末）如图，半圆O的直径是AB，AD、BC是两条切线，切点分别为A、B，CO平分∠BCD．（1）求证：CD是半圆O的切线．（2）若AD＝20，CD＝50，求BC和AB的长．【解答】（1）证明：过点O作OE⊥CD，垂足为点E，∵BC是半圆O的切线，B为切点，∴OB⊥BC，∵CO平分∠BCD，∴OE＝OB，∵OB是半圆O的半径，∴CD是半圆O的切线；（2）解：过点D作DF⊥BC，垂足为点F，∴∠DFB＝90°，∵AD是半圆O的切线，切点为A，∴∠DAO＝90°，∵OB⊥BC，∴∠OBC＝90°，∴四边形ADFB是矩形，∴AD＝BF＝20，DF＝AB，∵AD，CD，BC是半圆O的切线，切点分别为A、E、B，∴DE＝AD＝20，EC＝BC，∵CD＝50，∴EC＝CD﹣DE＝50﹣20＝30，∴BC＝30，∴CF＝BC﹣BF＝10，在Rt△CDF中，由勾股定理得：DF＝＝＝20，∴AB＝DF＝20，∴BC的长为30，AB的长为20．1.（2021秋•龙沙区期末）如图，以点O为圆心，AB长为直径作圆，在⊙O上取一点C，延长AB至点D，连接DC，∠DCB＝∠DAC，过点A作AE⊥AD交DC的延长线于点E．（1）求证：CD是⊙O的切线；（2）若CD＝4，DB＝2，求AE的长．【解答】（1）证明：连接OC，OE，如图，∵AB为直径，∴∠ACB＝90°，即∠BCO+∠1＝90°，又∵∠DCB＝∠CAD，∵∠CAD＝∠OCA，∴∠OCA＝∠DCB，∴∠DCB+∠BCO＝90°，即∠DCO＝90°，∵OC是⊙O的半径，∴CD是⊙O的切线；（2）解：∵∠DCO＝90°，OC＝OB，∴OC2+CD2＝OD2，∴OB2+42＝（OB+2）2，∴OB＝3，∴AB＝6，∵AE⊥AD，AB是⊙O的直径，∴AE是⊙O的切线，∵CD是⊙O的切线；∴AE＝CE，∵AD2+AE2＝DE2，∴（6+2）2+AE2＝（4+AE）2，解得AE＝6．2．（2021秋•聊城期末）如图，点C在以AB为直径的⊙O上，AC平分∠BAD，且AD⊥CD 于点D．（1）求证：DC是⊙O的切线；（2）若AD＝4，CD＝2，求⊙O的半径．【解答】（1）证明：如图中，连接OC．∵OA＝OC，∴∠OAC＝∠OCA，∵AC平分∠DAB，∴∠DAC＝∠CAB＝∠ACO，∴AD∥OC，∵AD⊥CD，∴OC⊥DC，∵OC是⊙O的半径，∴CD是⊙O的切线；（2）解：如图，过点O作OE⊥AD于点E，得矩形OEDC，∴OE＝CD＝2，DE＝OC，∴AE＝AD﹣DE＝4﹣OC＝4﹣OA，在Rt△AEO中，根据勾股定理，得OA2＝AE2+OE2，∴OA2＝（4﹣OA）2+22，解得OA＝．∴⊙O的半径为．3．（2022春•长兴县月考）如图，已知等边△ABC的边长为6，点O是AB边上的一点，以OA为半径的⊙O与边AC，AB分别交于点D，E，过点D作DF⊥BC于点F．（1）求证：DF是⊙O的切线；（2）连结EF，当EF是⊙O的切线时，求⊙O的半径．【解答】（1）证明：连结OD，如图所示：∵△ABC是等边三角形，∴∠BAC＝∠C＝∠B＝60°，∵∠DAO＝60°，OD＝OA，∴△DOA是等边三角形，∴∠ODA＝∠C＝60°，∴OD∥BC，又∵∠DFC＝90°，∴∠ODF＝90°，∴OD⊥DF，∵OD是⊙O的半径，∴DF是⊙O的切线；（2）解：设半径为r，等边△ABC的边长为6，由（1）可知：AD＝r，则CD＝6﹣r，BE＝6﹣2r在Rt△CFD中，∠C＝60°，CD＝6﹣r，∴CF＝（6﹣r），∴BF＝a﹣（6﹣r），又∵EF是⊙O的切线，∴△FEB是直角三角形，且∠B＝60°，∠EFB＝30°，∴BF＝2BE，∴6﹣（6﹣r）＝2（6﹣2r），解得：r＝2，∴⊙O的半径为2．4．（2022•西湖区校级开学）如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC．（1）求证：DE是⊙O的切线．（2）若∠C＝30°，CD＝10cm，求⊙O的半径．【解答】（1）证明：连接OD．∵D是BC的中点，O是AB的中点，∴OD∥AC，∴∠CED＝∠ODE，∵DE⊥AC，∴∠CED＝∠ODE＝90°，∴OD⊥DE，∵OD是圆的半径，∴DE是⊙O的切线；（2）解：∵AB是⊙O的直径，∴∠ADB＝90°，∵D是BC的中点，∴AB＝AC，∵∠C＝30°，∴∠B＝30°，∴AB＝2AD，∵CD＝10cm，∴BD＝10cm，设AD＝xcm，则AB＝2xcm，∴x2+102＝4x2，∴x＝或x＝﹣（舍去），∴AD＝（cm），AB＝（cm），∴⊙O的半径为cm．5．（2021秋•曲靖期末）如图，在Rt△ABC中，∠C＝90°，点D是AC上一点，DQ⊥AB，DQ＝DC，点O在AB上，以点O为圆心，OB长为半径的圆经过点D，交BC于点E、交AB于点F．（1）求证：AC是⊙O的切线；（2）若⊙O的半径为5，CD＝4，求CE的长．【解答】（1）证明：如图，连接OD，∵OD＝OB，∴∠ODB＝∠OBD，∵∠C＝90°，DQ⊥AB，DQ＝DC，∴BD是△ABC的角平分线，∴∠OBD＝∠DBC，∴∠ODB＝∠DBC，∴OD∥BC，∴∠ODA＝∠C＝90°，∵AC经过⊙为的半径OD的端点D，且AC⊥OD，∴AC是⊙O的切线；（2）解：如图，作OG⊥BE于点G，则BG＝EG，∠OGB＝90°，∵∠ODC＝∠C＝∠OGC＝90°，∴四边形ODCG是矩形，∵CD＝4，OB＝OD＝5，∴OG＝CD＝4，GC＝OD＝5，在Rt△BOG中，OB2＝OG2+BG2，∴BG＝＝＝3，∴EG＝3，∴CE＝GC﹣EG＝5﹣3＝2．6．（2021秋•海淀区期末）如图，AB为⊙O的直径，弦CD⊥AB于E，连接AC，过A作AF⊥AC，交⊙O于点F，连接DF，过B作BG⊥DF，交DF的延长线于点G．（1）求证：BG是⊙O的切线；（2）若∠DFA＝30°，DF＝4，求FG的长．【解答】（1）证明：∵C，A，D，F在⊙O上，∠CAF＝90°，∴∠D＝∠CAF＝90°．∵AB⊥CE，BG⊥DF，∴∠BED＝∠G＝90°．∴四边形BEDG中，∠ABG＝90°．∴半径OB⊥BG．∴BG是⊙O的切线．（2）解：连接CF，∵∠CAF＝90°，∴CF是⊙O的直径．∴OC＝OF．∵直径AB⊥CD于E，∴CE＝DE．∴OE是△CDF的中位线．∴OE＝＝2．∵＝，∠AFD＝30°，∴∠ACD＝∠AFD＝30°．∴∠CAE＝90°﹣∠ACE＝60°．∵OA＝OC，∴△AOC是等边三角形．∵CE⊥AB，∴E为AO的中点，∴OA＝2OE＝4，OB＝4．∴BE＝OB+OE＝6．∵∠BED＝∠D＝∠G＝90°，∴四边形BEDG是矩形．∴DG＝BE＝6．∴FG＝DG﹣DF＝2．7．（2021秋•淮安区期末）如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，过点D作DE⊥AC，交AC于点E．（1）求证：DE是⊙O的切线；（2）若⊙O的直径为5，BC＝8，求DE的长．【解答】（1）证明：如图1，∵OB＝OD，∴∠B＝∠ODB，∵AB＝AC，∴∠B＝∠C，∴∠ODB＝∠C，∴OD∥AC，∵DE⊥AC，∴DE⊥半径OD，∴DE是⊙O的切线；（2）解：如图2，连接AD，∵AB是⊙O的直径，∴∠ADB＝90°，∵AB＝AC，∴BD＝CD＝＝4，∴AD＝＝3，∵DE⊥AC，∴S＝，△ACD∴5•DE＝3×4，∴DE＝，∴DE的长是．8．（2021秋•平罗县期末）如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交于点D，过点D作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）若DE＝2，CE＝1，求BD的长度．【解答】（1）证明：如图，连接OD，CD，则∠OAD＝∠ODA．∵AD平分∠CAB，∴∠OAD＝∠EAD．∴∠ODA＝∠EAD．∴OD∥AE，∵AB为直径，∴∠ACB＝90°．∵DE∥BC，∴∠E＝90°，∴∠ODE＝90°，∵OD是⊙O的半径，∴DE是⊙O的切线；（2）解：∵AD平分∠CAB，∴＝，∴CD＝BD，在Rt△CDE中，DE＝2，CE＝1，根据勾股定理，得CD＝＝＝，∴BD＝．9．（2021秋•博白县期末）如图，在△ABC中，AB＝AC，以AC边为直径作⊙O交BC边于点D，过点D作DE⊥AB于点E，ED、AC的延长线交于点F．（1）求证：EF是⊙O的切线；（2）若AC＝10，CD＝6，求DE的长．【解答】（1）证明：连接OD，如图所示：∵AB＝AC，∴∠B＝∠ACD，∵OC＝OD，∴∠ODC＝∠OCD，∴∠B＝∠ODC，∴OD∥AB，∵DE⊥AB，∴EF⊥OD，又∵OD是⊙O的半径，∴EF是⊙O的切线；（2）解：连接AD，∵AC为⊙O的直径，∴AD⊥BC，∵AB＝AC，∴BD＝CD＝6．在Rt△ACD中，AC＝10，CD＝6，∴AD＝＝＝8，又∵DE⊥AB，AB＝AC＝10，＝AB•DE＝AD•BD，∴S△ABD即×10×DE＝×8×6，∴DE＝4.8．10．（2022•任城区三模）如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF；（1）判断AF与⊙O的位置关系并说明理由．（2）若⊙O的半径为4，AF＝3，求AC的长．【解答】（1）解：AF是⊙O的切线，理由如下：连接OC，如图所示：∵AB是⊙O直径，∴∠BCA＝90°，∵OF∥BC，∴∠AEO＝90°，∠1＝∠2，∠B＝∠3，∴OF⊥AC，∵OC＝OB，∴∠B＝∠1，∴∠3＝∠2，在△OAF和△OCF中，，∴△OAF≌△OCF（SAS），∴∠OAF＝∠OCF，∵PC是⊙O的切线，∴∠OCF＝90°，∴∠OAF＝90°，∴FA⊥OA，∴AF是⊙O的切线；（2）∵⊙O的半径为4，AF＝3，∠OAF＝90°，∴OF＝＝＝5∵FA⊥OA，OF⊥AC，∴AC＝2AE，△OAF的面积＝AF•OA＝OF•AE，∴3×4＝5×AE，解得：AE＝，∴AC＝2AE＝．。
2021年数学九年级中考复习专题之圆的综合(考察切线证明、长度、面积、动点问题等)(一)
2021年数学九年级中考复习专题之圆的综合（考察切线证明、长度、面积、动点问题等）（一）1．如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．（1）求⊙O的半径；（2）点E为圆上一点，∠ECD＝15°，将沿弦CE翻折，交CD于点F，求图中阴影部分的面积．2．已知AB是⊙O的直径，点C在⊙O上，点D在半径OA上（不与点O，A重合）．（1）如图1，若∠COA＝60°，∠CDO＝70°，求∠ACD的度数．（2）如图2，点E在线段OD上（不与O，D重合），CD、CE的延长线分别交⊙O 于点F、G，连接BF，BG，点P是CO的延长线与BF的交点，若CD＝1，BG＝2，∠OCD＝∠OBG，∠CFP＝∠CPF，求CG的长．3．如图，点A是⊙O直径BD延长线上的一点，C在⊙O上，AC＝BC，AD＝CD （1）求证：AC是⊙O的切线；（2）若⊙O的半径为2，求△ABC的面积．4．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，AB＝8．（1）利用尺规，作∠CAB的平分线，交⊙O于点D；（保留作图痕迹，不写作法）（2）在（1）的条件下，连接CD，OD，若AC＝CD，求∠B的度数；（3）在（2）的条件下，OD交BC于点E，求由线段ED，BE，所围成区域的面积．（其中表示劣弧，结果保留π和根号）5．（1）如图1，在菱形ABCD中，CE＝CF，求证：AE＝AF．（2）如图2，AB是⊙O的直径，PA与⊙O相切于点A，OP与⊙O相交于点C，连接CB，∠OPA＝40°，求∠ABC的度数．6．如图，在Rt△ABC中，∠BAC＝90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．（1）若AC＝5，BC＝13，求⊙O的半径；（2）过点E作弦EF⊥AB于M，连接AF，若∠F＝2∠B，求证：四边形ACEF是菱形．7．如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．（1）求证：∠ACD＝∠B；（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；①求tan∠CFE的值；②若AC＝3，BC＝4，求CE的长．8．如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB＝15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H．（1）求证：CD是半圆O的切线；（2）若DH＝6﹣3，求EF和半径OA的长．9．已知：如图，⊙O是△ABC的外接圆，＝，点D在边BC上，AE∥BC，AE＝BD．（1）求证：AD＝CE；（2）如果点G在线段DC上（不与点D重合），且AG＝AD，求证：四边形AGCE 是平行四边形．10．如图，AB是⊙O的直径，点C、D在⊙O上，∠A＝2∠BCD，点E在AB的延长线上，∠AED＝∠ABC．（1）求证：DE与⊙O相切；（2）若BF＝2，DF＝，求⊙O的半径．参考答案1．解：（1）连接AO，如右图1所示，∵CD为⊙O的直径，AB⊥CD，AB＝8，∴AG＝＝4，∵OG：OC＝3：5，AB⊥CD，垂足为G，∴设⊙O的半径为5k，则OG＝3k，∴（3k）2+42＝（5k）2，解得，k＝1或k＝﹣1（舍去），∴5k＝5，即⊙O的半径是5；（2）如图2所示，将阴影部分沿CE翻折，点F的对应点为M，∵∠ECD＝15°，由对称性可知，∠DCM＝30°，S阴影＝S弓形CBM，连接OM，则∠MOD＝60°，∴∠MOC＝120°，过点M作MN⊥CD于点N，∴MN＝MO•sin60°＝5×，∴S阴影＝S扇形OMC﹣S△OMC＝＝，即图中阴影部分的面积是：．2．解：（1）∵OA＝OC，∠COA＝60°，∴△ACO为等边三角形，∴∠CAD＝60°，又∵∠CDO＝70°，∴∠ACD＝∠CDO﹣∠CAD＝10°．（2）连接AG，延长CP交BG于点Q，交⊙O于点H，令CG交BF于点R，如图所示．在△COD和△BOQ中，，∴△COD≌△BOQ（ASA），∴BQ＝CD＝1，∠CDO＝∠BQO．∵BG＝2，∴OQ⊥BG，∴∠CQG＝90°．∵∠CGQ+∠GCQ+∠CQG＝180°，∠RCP+∠CPR+∠CRP＝180°，∠CGQ＝∠CFP＝∠CPF，∴∠CRP＝∠CQG＝90°，∵∠CFP＝∠CPF，∴∠FCG＝∠HCG，∴＝．∵∠OCD＝∠OBG，∠FCG＝∠FBG，∴∠ABF＝∠GCH，∴＝．∵∠CDO＝∠BQO＝90°，∴，∴点G为中点，∴△AGB、△OQB为等腰直角三角形．∵BQ＝1，∴OQ＝BQ＝1，OB＝BQ＝．在Rt△CGQ中，GQ＝1，CQ＝CO+OQ＝+1，∴CG＝＝．3．解：（1）连接OC．∵AC＝BC，AD＝CD，OB＝OC，∴∠A＝∠B＝∠1＝∠2．∵∠ACO＝∠DCO+∠2，∴∠ACO＝∠DCO+∠1＝∠BCD，又∵BD是直径，∴∠BCD＝90°，∴∠ACO＝90°，又C在⊙O上，∴AC是⊙O的切线；（2）由题意可得△DCO是等腰三角形，∵∠CDO＝∠A+∠2，∠DOC＝∠B+∠1，∴∠CDO＝∠DOC，即△DCO是等边三角形．∴∠A＝∠B＝∠1＝∠2＝30°，CD＝AD＝2，在直角△BCD中，BC＝＝＝2．又AC＝BC，∴AC＝2．作CE⊥AB于点E．在直角△BEC中，∠B＝30°，∴CE＝BC＝，∴S △ABC＝AB•CE＝×6×＝3．4．解：（1）如图1所示，AP即为所求的∠CAB的平分线；（2）如图2所示：∵AC＝CD，∴∠CAD＝∠ADC，又∵∠ADC＝∠B，∴∠CAD＝∠B，∵AD平分∠CAB，∴∠CAD＝∠DAB＝∠B，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAB+∠B＝90°，∴3∠B＝90°，∴∠B＝30°；（3）由（2）得：∠CAD＝∠BAD，∠DAB＝30°，又∵∠DOB＝2∠DAB，∴∠BOD＝60°，∴∠OEB＝90°，在Rt△OEB中，OB＝AB＝4，∴OE＝OB＝2，∴BE＝＝＝2，∴△OEB的面积＝OE•BE＝×2×2＝2，扇形BOD的面积＝＝，∴线段ED，BE，所围成区域的面积＝﹣2．5．证明：（1）∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，∠B＝∠D∵CE＝CF，∴BE＝DF在△ABE与△ADF中，，∴△ABE≌△ADF．∴AE＝AF；（2）∵AB是⊙O的直径，直线PA与⊙O相切于点A，∴∠PAO＝90°．又∵∠OPA＝40°，∴∠POA＝50°，∴∠ABC＝∠POA＝25°．6．（1）解：连接OE，设圆O半径为r，在Rt△ABC中，BC＝13，AC＝5，根据勾股定理得：AB＝＝12，∵BC与圆O相切，∴OE⊥BC，∴∠OEB＝∠BAC＝90°，∵∠B＝∠B，∴△BOE∽△BCA，∴＝，即＝，解得：r＝；（2）∵＝，∠F＝2∠B，∴∠AOE＝2∠F＝4∠B，∵∠AOE＝∠OEB+∠B，∴∠B＝30°，∠F＝60°，∵EF⊥AD，∴∠EMB＝∠CAB＝90°，∴∠MEB＝∠F＝60°，CA∥EF，∴CB∥AF，∴四边形ACEF为平行四边形，∵∠CAB＝90°，OA为半径，∴CA为圆O的切线，∵BC为圆O的切线，∴CA＝CE，∴平行四边形ACEF为菱形．7．（1）证明：如图1中，连接OC．∵OA＝OC，∴∠1＝∠2，∵CD是⊙O切线，∴OC⊥CD，∴∠DCO＝90°，∴∠3+∠2＝90°，∵AB是直径，∴∠1+∠B＝90°，∴∠3＝∠B．（2）解：①∵∠CEF＝∠ECD+∠CDE，∠CFE＝∠B+∠FDB，∵∠CDE＝∠FDB，∠ECD＝∠B，∴∠CEF＝∠CFE，∵∠ECF＝90°，∴∠CEF＝∠CFE＝45°，∴tan∠CFE＝tan45°＝1．②在RT△ABC中，∵AC＝3，BC＝4，∴AB＝＝5，∵∠CDA＝∠BDC，∠DCA＝∠B，∴△DCA∽△DBC，∴＝＝＝，∵∠CDE＝∠BDF，∠DCE＝∠B，∴△DCE∽△DBF，∴＝＝，设EC＝CF＝x，∴＝，∴x＝．∴CE＝．8．解：（1）连接OB，∵OA＝OB＝OC，∵四边形OABC是平行四边形，∴AB＝OC，∴△AOB是等边三角形，∴∠AOB＝60°，∵∠FAD＝15°，∴∠BOF＝30°，∴∠AOF＝∠BOF＝30°，∴OF⊥AB，∵CD∥OF，∴CD⊥AD，∵AD∥OC，∴OC⊥CD，∴CD是半圆O的切线；（2）∵BC∥OA，∴∠DBC＝∠EAO＝60°，∴BD＝BC＝AB，∴AE＝AD，∵EF∥DH，∴△AEF∽△ADH，∴，∵DH＝6﹣3，∴EF＝2﹣，∵OF＝OA，∴OE＝OA﹣（2﹣），∵∠AOE＝30°，∴＝＝，解得：OA＝2．9．证明：（1）在⊙O中，∵＝，∴AB＝AC，∴∠B＝∠ACB，∵AE∥BC，∴∠EAC＝∠ACB，∴∠B＝∠EAC，在△ABD和△CAE中，，∴△ABD≌△CAE（SAS），∴AD＝CE；（2）连接AO并延长，交边BC于点H，∵＝，OA为半径，∴AH⊥BC，∴BH＝CH，∵AD＝AG，∴DH＝HG，∴BH﹣DH＝CH﹣GH，即BD＝CG，∵BD＝AE，∴CG＝AE，∵CG∥AE，∴四边形AGCE是平行四边形．10．（1）证明：连接OD，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠A+∠ABC＝90°，∵∠BOD＝2∠BCD，∠A＝2∠BCD，∴∠BOD＝∠A，∵∠AED＝∠ABC，∴∠BOD+∠AED＝90°，∴∠ODE＝90°，即OD⊥DE，∴DE与⊙O相切；（2）解法一：连接BD，过D作DH⊥BF于H，延长DO交⊙O于G，连接BG，则∠G＝∠DCB，∵∠G+∠GDB＝90°，∵DE与⊙O相切，∴∠GDB+∠BDE＝90°，∴∠G＝∠BDE，∴∠BDE＝∠BCD，∵∠AED＝∠ABC，∴∠AFC＝∠DBF，而∠AFC＝∠ABC+∠BCD，∠DBF＝∠AED+∠BDE，∵∠AFC＝∠DFB，∴△FDB是等腰三角形，∴FH＝BH＝BF＝1，则FH＝1，∴HD＝＝3，在Rt△ODH中，OH2+DH2＝OD2，即（OD﹣1）2+32＝OD2，∴OD＝5，∴⊙O的半径是5．解法二：连接BD，OD，∵∠A＝2∠BCD，∴∠BOD＝∠BDF，∵∠OBD＝∠DBF，∴△BOD∽△BDF，∴＝＝，∵OB＝OD，∴BD＝DF＝，∴OD＝＝＝5．。
2021年中考数学复习讲义：第九章 圆 模型(三十五)——圆幂定理模型
第九章.圆模型（三十五）——圆幂定理模型模型讲解一、相交弦定理【结论1】如图，⊙O中，弦AB、CD相交于点P，半径为r,则①AP·BP＝CP·DP, ②AP·BP＝CP·DP＝r2－OP2.【证明】①②二、切割线定理【结论2】如图，PBC是⊙O的一条割线，PA是⊙O的一条切线，切点为A，半径为r,则①PA2＝PB·PC，②PA2＝PB·PC＝PO2－r2【证明】①②三、割线定理【结论3】如图，PAB、PCD是⊙O的两条割线，半径为r,则①PA·PB＝PC·PD, ②PA·PB＝PC·PD＝OP2－r2【证明】口诀从两线交点处引出的共线线段的乘积相等小试牛刀典例1 ☆☆☆☆☆如图，在⊙O中，弦 AB与半径 OC 相交于点M，且 OM=MC，若 AM=1.5，BM=4，则 OC的长为（）.A.2B.C.2D.2【答案】D【解析】如图，延长 CO，交OO于D，则CD为OO的直径.∵OM＝MC,∴OC＝2MC＝2OM,DM＝3OM＝3MC.由相交弦定理得 DM·MC＝AM·BM，即 3MC2＝1.5×4，解得 MC ＝. ∴OC＝2MC=2.故选 D.典例2 ☆☆☆☆☆如图，⊙O的弦AB，CD相交于点E，若 CE∶BE=2∶3，则 AE∶ DE 的值为（A. B. C.D.【答案】A【解析】∶∵⊙O的弦AB，CD 相交于点E，根据相交弦定理得 AE·BE＝CE·DE，∴AE: DE=CE: BE=2:3.故选 A.典例3 ☆☆☆☆☆如图，过点 P作⊙O的两条割线分别交⊙O于点A，B和点C，D，已知PA=3，AB＝PC＝2，则 PD的长是( )A.3B.7.5C.5D.5.5【答案】B【解析】∵PA＝3，AB＝PC＝2，∴PB＝5,根据割线定理得 PA·PB=PC·PD，∴PD=7.5.故选 B.小试牛刀1.（★★☆☆☆）如图，过点P引圆的两条割线PAB 和PCD.分别交圆于点 A，B和C，D，连接 AC，BD ，则在比例式①＝,②＝＝中，正确的个数为( )A.3B.2C.1D.02.（★★☆☆☆）如图，已知⊙O中，弦 AB=25，M是AB上一点， OA=13，OM=5，则AM=（）A.16B.20C.20或9D.16或93.（★★☆☆☆）如图，在⊙O中，P为弦AB上一点，PO⊥PC，PC交⊙O于C，那么（）A.OP²=PA·PB，B.PC²=PA·PBC.PA²=PB·PC，D.PB²=PA·PC直击中考1.如图，在⊙O中，弦 AB＝CD，AB⊥CD于点E.已知 CE·ED＝3，BE＝1，则⊙O的直径是（）A.2B.C.2D.52.如图，半圆O的直径 BC=7，延长 CB到A，直线 AD交半圆于点E，D，且AE=ED=3，则AB的长为( ).A. B.2 C.D.9同幂定理是一个非常重要的定理，在计算过程中，如果涉及计算某条线段的长度，用普通的垂径定理，勾股定理，也能够得到答案，但是速记圆幂定理可以让我们更能看到图形的本质。
2021年九年级数学中考复习专题之圆的考察：切割线定理的运用(一)
2021年数学中考复习专题之圆的考察：切割线定理的运用（一）一．选择题1．如图，PA切⊙O于A，PBC是⊙O的割线，如果PB＝2，PC＝4，则PA的长为（）A．2 B．2C．4 D．22．如图，点P是⊙O外一点，PAB为⊙O的一条割线，且PA＝AB，PO交⊙O于点C，若OC ＝3，OP＝5，则AB长为（）A．B．C．D．3．如图，在Rt△ABC中，AC＝5，BC＝12，⊙O分别与边AB，AC相切，切点分别为E，C，则⊙O的半径是（）A．B．C．D．4．如图，PAB为⊙O的割线，且PA＝AB＝3，PO交⊙O于点C，若PC＝2，则⊙O的半径的长为（）A．B．C．D．75．如图，Rt△ABC中，∠C＝90°，O为AB上一点，以O为圆心，OA为半径作圆O与BC相切于点D，分别交AC、AB于E、F，若CD＝2CE＝4，则⊙O的直径为（）A．10 B．C．5 D．126．如图，两圆相交于C、D，AB是两圆的一条外公切线，A、B为切点，CD的延长线交AB 于M，若CD＝9，MD＝3，则AB的长为（）A．18 B．12 C．13.5 D．6√37．如图，点C、O在线段AB上，且AC＝CO＝OB＝5，过点A作以BC为直径的⊙O切线，D 为切点，则AD的长为（）A．5 B．6 C．D．108．如图，从点P向⊙O引两条切线PA，PB，切点为A，B，BC为⊙O的直径，若∠P＝60°，PA＝3，则⊙O的直径BC的长为（）A．B．C．3 D．9．以正方形ABCD的BC边为直径作半圆O，过点D作直线切半圆于点F，交AB边于点E．则三角形ADE和直角梯形EBCD周长之比为（）A．3：4 B．4：5 C．5：6 D．6：710．如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB＝2cm，BC＝8cm，则PA的长等于（）A．4cm B．16cm C．20cm D．2cm二．填空题11．已知直角梯形ABCD的四条边长分别为AB＝2，BC＝CD＝10，AD＝6，过B、D两点作圆，与BA的延长线交于点E，与CB的延长线交于点F，则BE﹣BF的值为．12．如图，PT是⊙O的切线，T为切点，PA是割线，交⊙O于A、B两点，与直径CT交于点D．已知CD＝2，AD＝3，BD＝4，那PB＝．13．如图，AB，AC分别是⊙O的切线和割线，且∠C＝45°，∠BDA＝60°，CD＝，则切线AB的长是．14．如图，⊙O的割线PAB交⊙O于点A、B，PA＝7cm，AB＝5cm，PO＝10cm，则⊙O的半径为．15．如图，已知PA为⊙O的切线，PBC为⊙O的割线，PA＝，PB＝BC，⊙O的半径OC ＝5，那么弦BC的弦心距OM＝．16．如图，过点P引圆的两条割线PAB和PCD，分别交圆于点A，B和C，D，连接AC，BD，则在下列各比例式中，①；②；③，成立的有（把你认为成立的比例式的序号都填上）．三．解答题17．如图，OB是以（O，a）为圆心，a为半径的⊙O1的弦，过B点作⊙O1的切线，P为劣弧上的任一点，且过P作OB、AB、OA的垂线，垂足分别是D、E、F．（1）求证：PD2＝PE•PF；（2）当∠BOP＝30°，P点为的中点时，求D、E、F、P四个点的坐标及S△DEF．18．如图，AB、AC分别是⊙O的直径和弦，D是劣弧AC的中点，DE⊥AB于H，交⊙O于点E，交AC于点F．（1）图中有哪些必相等的线段？（要求：不要标注其它字母，找结论的过程中所作的辅助线不能出现在结论中，不必写出推理过程．）（2）若过C点作⊙O的切线PC交ED延长线于P点，（请补全图形），求证：PF2＝PD•PE；（3）已知AH＝1，BH＝4，求PC的长．19．如图，在Rt△ABC中，∠C＝90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．（1）求证：AC是△BDE的外接圆的切线；（2）若，求BD的长．20．如图，在△ABC中，∠BAC＝90度．BM平分∠ABC交AC于M，以A为圆心，AM为半径作⊙A交BM于N，AN的延长线交BC于D，直线AB交⊙A于P，K两点，作MT⊥BC于T．（1）求证：AK＝MT；（2）求证：AD⊥BC；（3）当AK＝BD时，求证：．参考答案一．选择题1．解：∵PA2＝PB•PC＝8，PB＝2，PC＝4，∴PA＝2．故选：B．2．解：设PA＝AB＝x，延长PO交圆于点D．∵PA•PB＝PC•PD，OC＝3，OP＝5，∴x•2x＝16，∴x＝2．故选：B．3．解：∵AE＝AC＝5，AC＝5，BC＝12，∴AB＝13，∴BE＝8；∵BE2＝BD•BC，∴BD＝，∴CD＝，∴圆的半径是，故选：A．4．解法一：延长PO交圆于点D利用割线定理可知PA•PB＝PC•PD，求得PD＝9，所以CD＝7，半径＝3.5．解法二：作OD⊥AB于D，根据垂径定理和勾股定理求解．故选：A．5．解：连接OD，过O作AC的垂线，设垂足为G，∵∠C＝90°，∴四边形ODCG是矩形，∵CD是切线，CEA是割线，∴CD2＝CE•CA，∵CD＝2CE＝4，∴AC＝8，∴AE＝6，∴GE＝3，∴OD＝CG＝5，∴⊙O的直径为10．故选：A．6．解：∵AB是两圆的一条外公切线，∴MA2＝MD•MC，MB2＝MD•MC，∵CD＝9，MD＝3，∴MA＝MB＝6，∴AB＝12，故选：B．7．解：∵AD是⊙O的切线，ACB是⊙O的割线，∴AD2＝AC•AB，又AC＝5，AB＝AC+CO+OB＝15，∴AD2＝5×15＝75，∴AD＝5．（AD＝﹣5不合题意舍去）．故选：C．8．解：连接OP．∵PB＝PA＝3，∠OPB＝30°，tan∠OPB＝，∴OB＝，圆的直径是2．故选：A．9．解：根据切线长定理得，BE＝EF，DF＝DC＝AD＝AB＝BC．设EF＝x，DF＝y，则在直角△AED中，AE＝y﹣x，AD＝CD＝y，DE＝x+y．根据勾股定理可得：（y﹣x）2+y2＝（x+y）2，∴y＝4x，∴三角形ADE的周长为12x，直角梯形EBCD周长为14x，∴两者周长之比为12x：14x＝6：7．故选：D．10．解：∵PB＝2cm，BC＝8cm，∴PC＝10cm，∵PA2＝PB•PC＝20，∴PA＝2，故选：D．二．填空题（共6小题）11．解：延长CD交⊙O于点G，设BE，DG的中点分别为点M，N，则易知AM＝DN，∵BC＝CD＝10，由割线定理得，CB•CF＝CD•CG，∵CB＝CD，∴BF＝DG，∴BE﹣BF＝BE﹣DG＝2（BM﹣DN）＝2（BM﹣AM）＝2AB＝4．故答案为：4．12．解：∵AD•BD＝CD•DT，∴TD＝，∵CD＝2，AD＝3，BD＝4，∴TD＝6，∵PT是⊙O的切线，PA是割线，∴PT2＝PA•PB，∵CT为直径，∴PT2＝PD2﹣TD2，∴PA•PB＝PD2﹣TD2，即（PB+7）PB＝（PB+4）2﹣62，解得PB＝20．故答案为：20．13．解：过点A作AM⊥BD与点M．∵AB为圆O的切线∴∠ABD＝∠C＝45°（弦切角等于所夹弧所对的圆周角）∵∠BDA＝60°∴∠BAD＝75°，∠DAM＝30°，∠BAM＝45°设AB＝x，则AM＝x，在直角△AMD中，AD＝x 由切割线定理得：AB2＝AD•ACx2＝x（x+）解得：x1＝6，x2＝0（舍去）故AB＝6．故答案是：6．14．解：延长PO交圆于点D，由割线定理知，PA•PB＝PC•PD＝（PO﹣CO）（PO+CO），代入数据解得，CO＝4．15．解：∵PA为⊙O的切线，PBC为⊙O的割线，∴PA2＝PB•PC；设BC＝x，则PB＝x，PC＝2x，∴2x2＝72，解得x＝6；∵OM⊥BC，在直角△OMC中，∵OC＝5，CM＝3，∴OM＝4．16．解：∵四边形ABCD是圆内接四边形∴∠PAD＝∠C，∠PAD＝∠B∴△PAD∽△PCB根据相似三角形的对应边的比相等，得到②③是正确的．三．解答题（共4小题）17．（1）证明：连接PB，OP，∵PE⊥AB，PD⊥OB，∴∠BEP＝∠PDO＝90°，∵AB切⊙O1于B，∠ABP＝∠BOP，∴△PBE∽△POD，∴＝，同理，△OPF∽△BPD∴＝，∴＝，∴PD2＝PE•PF；（2）解：连接O1B，O1P，∵AB切⊙O1于B，∠POB＝30°，∴∠ABP＝30°，∴∠O1BP＝90°﹣30°＝60°，∵O1B＝O1P，∴△O1BP为等边三角形，∴O1B＝BP，∵P为弧BO的中点，∴BP＝OP，即△O1PO为等边三角形，∴O1P＝OP＝a，∴∠O1OP＝60°，又∵P为弧BO的中点，∴O1P⊥OB，在△O1DO中，∵∠O1OP＝60°O1O＝a，∴O1D＝a，OD＝a，过D作DM⊥OO1于M，∴DM＝OD＝a，OM＝DM＝a，∴D（﹣a，a），∵∠O1OF＝90°，∠O1OP＝60°∴∠POF＝30°，∵PE⊥OA，∴PF＝OP＝a，OF＝a，∴P（﹣a，），F（﹣a，0），∵AB切⊙O1于B，∠POB＝30°，∴∠ABP＝∠BOP＝30°，∵PE⊥AB，PB＝a，∴∠EPB＝60°∴PE＝a，BE＝a，∵P为弧BO的中点，∴BP＝PO，∴∠PBO＝∠BOP＝30°，∴∠BPO＝120°，∴∠BPE+∠BPO＝120°+60°＝180°，即OPE三点共线，∵OE＝a+a＝a，过E作EM⊥x轴于M，∵AO切⊙O1于O，∴∠EOA＝30°，∴EM＝OE＝a，OM＝a，∴E（﹣a，a），∵E（﹣a，a），D（﹣a，a），∴DE＝﹣a﹣（﹣a）＝a，DE边上的高为：a，＝×a×a＝a2．∴S△DEF故答案为：D（﹣a，a），E（﹣a，a），F（﹣a，0），P（﹣a，）；S＝a2．△DEF18．（1）解：AO＝BO，DH＝EH，DF＝AF，AC＝DE；（2）证明：连EC，AE，则∠PFC是△ECF的一个外角，于是∠PFC＝∠ACE+∠FEC；∵DH⊥AB，AB是⊙O的直径，∴A是DE中点，即弧AD＝弧AE，∴∠AED＝∠ACE，∴∠ACE+∠FEC＝∠AED+∠DEC＝∠AEC，∵PC是⊙O的切线，∴∠PCA＝∠AEC．∴∠PCA＝∠PFC，∴PC＝PF．∵PC是切线∴PC2＝PD•PE，∴PF2＝PD•PE；（3）解：在⊙O中，AH•HB＝DH•HE＝DH2，∴设AF＝x，则FH＝2﹣x．在Rt△AFH中，AH2+FH2＝AF2∴1+（2﹣x）2＝x2，∴x＝，即．于是．由（1）（2）知HE＝HD＝2，，解得．∴PF＝PD+DF＝．∴PC＝PF＝．19．（1）证明：连接OE，∵BE平分∠ABC交AC于点E，∴∠1＝∠EBC，∵∠1＝∠2，∴∠2＝∠CBE，∴∠AEO＝∠C＝90°，∴AC是⊙O的切线，∵⊙O是△BDE的外接圆，∴AC是△BDE的外接圆的切线；（2）解：∵AE是圆O的切线，AB是圆的割线，根据切割线定理：AE2＝AD×AB，∵，∴（）2＝2×（2+BD），解得：BD＝4．∴BD的长是：4．20．证明：（1）∵BM平分∠ABC，∠BAC＝90°，MT⊥BC，∴AM＝MT．又∵AM＝AK，∴AK＝MT．（2）∵BM平分∠ABC，∴∠ABM＝∠CBM．∵AM＝AN，∴∠AMN＝∠ANM．又∵∠ANM＝∠BND，∴∠AMN＝∠BND．∵∠BAC＝90°，∴∠ABM+∠AMB＝90°．∴∠CBM+∠BND＝90°．∴∠BDN＝90°．∴AD⊥BC．（3）连接PN、KM∵BNM和BPK为⊙A的割线，∴BN•BM＝BP•BK．∴．∵AK＝BD，AK＝MT，∴BD＝MT．∵AD⊥BC，MT⊥BC，∴∠ADB＝∠MTC＝90°．∴∠C+∠CMT＝90°．∵∠BAC＝90°，∴∠C+∠ABC＝90°．∴∠ABC＝∠CMT．在△ABD和△CMT中，，∴△ABD≌△CMT．∴AB＝MC．∵AK＝AM，∴AB+AK＝MC+AM．即BK＝AC．∴．。
2021年九年级数学中考复习专题之圆：切线长定理综合运用(二)
2021年九年级数学中考复习专题之圆：切线长定理综合运用（二）一．选择题1．如图，PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D．若△PCD 的周长等于3，则PA的值是（）A．B．C．D．2．如图，PA切⊙O于A，PB切⊙O于B，连接OP．若∠APO＝30°，OA＝2，则BP ＝（）A．B．C．4 D．23．如图，PA、PB、分别切⊙O于A、B两点，∠P＝40°，则∠C的度数为（）A．40°B．140°C．70°D．80°4．如图，PA，PB分别是⊙O的切线，A，B分别为切点，点E是⊙O上一点，且∠AEB ＝60°，则∠P为（）A．120°B．60°C．30°D．45°5．如图，⊙O为△ABC的内切圆，AC＝10，AB＝8，BC＝9，点D，E分别为BC，AC 上的点，且DE为⊙O的切线，则△CDE的周长为（）A．9 B．7 C．11 D．86．如图，PA、PB切⊙O于点A、B，直线FG切⊙O于点E，交PA于F，交PB于点G，若PA＝8cm，则△PFG的周长是（）A．8cm B．12cm C．16cm D．20cm7．如图，是用一把直尺、含60°角的直角三角板和光盘摆放而成，点A为60°角与直尺交点，点B为光盘与直尺唯一交点，若AB＝3，则光盘的直径是（）A．6B．3C．6 D．38．如图，PA、PB切⊙O于点A、B，PA＝10，CD切⊙O于点E，交PA、PB于C、D 两点，则△PCD的周长是（）A．10 B．18 C．20 D．229．如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝5，则△PCD的周长为（）A．5 B．7 C．8 D．1010．如图，PA、PB是⊙O的两条切线，切点是A、B．如果OP＝4，PA＝2，那么∠AOB等于（）A．90°B．100°C．110°D．120°二．填空题11．如图，⊙O是四边形ABCD的内切圆，连接OA、OB、OC、OD．若∠AOB＝110°，则∠COD的度数是°．12．如图，PA、PB是⊙O的切线，A、B为切点，点C、D在⊙O上．若∠P＝102°，则∠A+∠C＝．13．如图，PA、PB切⊙O于A、B，点C在上，DE切⊙O于C，交PA、PB于D、E，已知PO＝13cm，⊙O的半径为5cm，则△PDE的周长是．14．如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝15，则四边形ABCD 的周长为．15．如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝5，则△PCD的周长为．三．解答题16．如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA＝5cm，C是上的一个动点（点C与A、B两点不重合），过点C作⊙O的切线，分别交PA、PB于点D、E，求△PED的周长是多少？17．如图，PA，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝60°．（1）求∠BAC的度数；（2）当OA＝2时，求AB的长．18．如图所示，PA、PB是⊙O的切线，切点分别是A、B，Q为⊙O上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA＝8cm，求：△PEF的周长．19．如图，AB为⊙O直径，PA、PC分别与⊙O相切于点A、C，PQ⊥PA，PQ交OC 的延长线于点Q．（1）求证：OQ＝PQ；（2）连BC并延长交PQ于点D，PA＝AB，且CQ＝6，求BD的长．20．如图，Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，过点D 作⊙O的切线，交BC于点E；（1）求证：BE＝CE；（2）若以O、D、E、C为顶点的四边形是正方形，⊙O的半径为r，求△ABC的面积；（3）若EC＝4，BD＝，求⊙O的半径OC的长．参考答案一．选择题1．解：∵PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D，∴AC＝EC，DE＝DB，PA＝PB∵△PCD的周长等于3，∴PA+PB＝3，∴PA＝．故选：A．2．解：∵PA、PB为圆O的两条切线，∴PA＝PB，OA⊥AP，在Rt△AOP中，∠APO＝30°，OA＝2，∴tan∠APO＝，即tan30°＝＝，∴PA＝＝2，则PB＝PA＝2．故选：D．3．解：∵PA是圆的切线．∴∠OAP＝90°，同理∠OBP＝90°，根据四边形内角和定理可得：∠AOB＝360°﹣∠OAP﹣∠OBP﹣∠P＝360°﹣90°﹣90°﹣40°＝140°，∴∠ACB＝∠AOB＝70°．故选：C．4．解：连接OA，BO；∵∠AOB＝2∠E＝120°，∴∠OAP＝∠OBP＝90°，∴∠P＝180°﹣∠AOB＝60°．故选：B．5．解：设AB，AC，BC和圆的切点分别是P，N，M，CM＝x，根据切线长定理，得CN＝CM＝x，BM＝BP＝9﹣x，AN＝AP＝10﹣x．则有9﹣x+10﹣x＝8，解得：x＝5.5．所以△CDE的周长＝CD+CE+QF+DQ＝2x＝11．故选：C．6．解：根据切线长定理可得：PA＝PB，FA＝FE，GE＝GB；所以△PFG的周长＝PF+FG+PG，＝PF+FE+EG+PB，＝PF+FA+GB+PG，＝PA+PB＝16cm，故选：C．7．解：设三角板与圆的切点为C，连接OA、OB，由切线长定理知AB＝AC＝3，OA平分∠BAC，∴∠OAB＝60°，在Rt△ABO中，OB＝AB tan∠OAB＝3，∴光盘的直径为6，故选：A．8．解：∵PA、PB切⊙O于点A、B，CD切⊙O于点E，∴PA＝PB＝10，CA＝CE，DE＝DB，∴△PCD的周长是PC+CD+PD＝PC+AC+DB+PD＝PA+PB＝10+10＝20．故选：C．9．解：∵PA、PB为圆的两条相交切线，∴PA＝PB，同理可得：CA＝CE，DE＝DB．∵△PCD的周长＝PC+CE+ED+PD，∴△PCD的周长＝PC+CA+BD+PD＝PA+PB＝2PA，∴△PCD的周长＝10，故选：D．10．解：∵△APO≌△BPO（HL），∴∠AOP＝∠BOP．∵sin∠AOP＝AP：OP＝2：4＝：2，∴∠AOP＝60°．∴∠AOB＝120°．故选：D．二．填空题（共5小题）11．解：如图所示：连接圆心与各切点，在Rt△DEO和Rt△DFO中，∴Rt△DEO≌Rt△DFO（HL），∴∠1＝∠2，同理可得：Rt△AFO≌Rt△AMO，Rt△BMO≌Rt△BNO，Rt△CEO≌Rt△CNO，∴∠3＝∠4，∠5＝∠7，∠6＝∠8，∴∠5+∠6＝∠7+∠8＝110°，∴2∠2+2∠3＝360°﹣2×110°，∴∠2+∠3＝∠DOC＝70°．故答案为：70°．12．解：连接AB，∵PA、PB是⊙O的切线，∴PA＝PB，∵∠P＝102°，∴∠PAB＝∠PBA＝（180°﹣102°）＝39°，∵∠DAB+∠C＝180°，∴∠PAD+∠C＝∠PAB+∠DAB+∠C＝180°+39°＝219°，故答案为：219°．13．解：连接OA、OB，如下图所示：∵PA、PB为圆的两条切线，∴由切线长定理可得：PA＝PB，同理可知：DA＝DC，EC＝EB；∵OA⊥PA，OA＝5，PO＝13，∴由勾股定理得：PA＝12，∴PA＝PB＝12；∵△PDE的周长＝PD+DC+CE+PE，DA＝DC，EC＝EB；∴△PDE的周长＝PD+DA+PE+EB＝PA+PB＝24，故此题应该填24cm．14．解：∵四边形ABCD是⊙O的外切四边形，∴AE＝AH，BE＝BF，CF＝CG，DH＝DG，∴AD+BC＝AB+CD＝25，∴四边形ABCD的周长＝AD+BC+AB+CD＝25+25＝50，故答案为：50．15．解：∵PA、PB切⊙O于A、B，∴PA＝PB＝5；同理，可得：EC＝CA，DE＝DB；∴△PDC的周长＝PC+CE+DE+DP＝PC+AC+PD+DB＝PA+PB＝2PA＝10．即△PCD的周长是10．三．解答题（共5小题）16．解：∵PA、PB、DE是圆O的切线，切点分别是A、B、C，∴AP＝BP，DA＝DC，CE＝BE，∴△PED的周长是：PD+DE+PE＝PD+DC+CE+PE＝PD+DA+PE+BE＝PA+PB＝2PA＝10cm．答：△PED的周长是10cm．17．解：（1）∵PA，PB是⊙O的切线，∴AP＝BP，∵∠P＝60°，∴∠PAB＝60°，∵AC是⊙O的直径，∴∠PAC＝90°，∴∠BAC＝90°﹣60°＝30°．（2）连接OP，则在Rt△AOP中，OA＝2，∠APO＝30°，∴OP＝4，由勾股定理得：，∵AP＝BP，∠APB＝60°，∴△APB是等边三角形，∴．18．解：∵PA、PB是⊙O的切线，切点分别是A、B，Q为⊙O上一点，过Q点作⊙O 的切线，交PA、PB于E、F点，∴PA＝PB，EA＝EQ，FB＝FQ，∵PA＝8cm，∴△PEF的周长为：PE+EF+PF＝PA+PB＝8+8＝16（cm）．19．（1）证明：连接OP．∵PA、PC分别与⊙O相切于点A，C，∴PA＝PC，OA⊥PA，∵OA＝OC，OP＝OP，∴△OPA≌△OPC（SSS），∴∠AOP＝∠POC，∵QP⊥PA，∴QP∥BA，∴∠QPO＝∠AOP，∴∠QOP＝∠QPO，∴OQ＝PQ．（2）设OA＝r．∵OB＝OC，∴∠OBC＝∠OCB，∵OB∥QD，∴∠QDC＝∠B，∵∠OCB＝∠QCD，∴∠QCD＝∠QDC，∴QC＝QD＝6，∵QO＝QP，∴OC＝DP＝r，∵PC是⊙O的切线，∴OC⊥PC，∴∠OCP＝∠PCQ＝90°，在Rt△PCQ中，∵PQ2＝PC2+QC2，∴（6+r）2＝62+（2r）2，r＝4或0（舍弃），∴OP＝＝4，∵OB＝PD，OB∥PD，∴四边形OBDP是平行四边形，∴BD＝OP＝4．20．（1）证明：连接CD，由AC是直径知CD⊥AB；DE、CE都是切线，所以DE＝CE，∠EDC＝∠ECD；又∠B+∠ECD＝90°，∠BDE+∠EDC＝90°；所以∠B＝∠BDE，所以BE＝DE，从而BE＝CE；（2）解：连接OD，当以O、D、E、C为顶点的四边形是正方形时，DE＝EC＝OC＝OD＝r；从而BE＝r，即△ABC是一个等腰直角三角形；AC＝AB＝2r，S△ABC＝2r2；（3）解：若EC＝4，BD＝4，则BC＝8；在Rt△BDC中，cos∠CBD＝＝；所以∠CBD＝30°；在Rt△ABC中，＝tan30°，即AC＝BC tan30°＝8×＝，OC＝＝；另解：设OC＝r，AD＝x；由EC＝4，BD＝4得BC＝8，DC＝4；则：，解得；即OC＝．。
2021年数学中考复习专题之圆的综合(考察 切线证明、长度、面积、动点问题等)(含答案)
2021年数学中考复习专题之圆的综合（考察切线证明、长度、面积、动点问题等）1．如图，在Rt△ABC中，∠C＝90°，点O在AB上，经过点A的⊙O与BC相切于点D，与AC，AB分别相交于点E，F，连接AD与EF相交于点G．（1）求证：AD平分∠CAB；（2）若OH⊥AD于点H，FH平分∠AFE，DG＝1．①试判断DF与DH的数量关系，并说明理由；②求⊙O的半径．2．问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC，BC，CD之间的数量关系．小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE＝CD，从而得出结论：AC+BC＝CD．简单应用：（1）在图①中，若AC＝，BC＝2，则CD＝．（2）如图③，AB是⊙O的直径，点C、D在⊙上，＝，若AB＝13，BC＝12，求CD的长．拓展规律：（3）如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m＜n），求CD的长（用含m，n的代数式表示）（4）如图⑤，∠ACB＝90°，AC＝BC，点P为AB的中点，若点E满足AE＝AC，CE＝CA，点Q为AE的中点，则线段PQ与AC的数量关系是．3．如图，CD是⊙O的弦，AB是直径，且CD∥AB，连接AC、AD、OD，其中AC＝CD，过点B的切线交CD的延长线于E．（1）求证：DA平分∠CDO；（2）若AB＝12，求图中阴影部分的周长之和（参考数据：π＝3.1，＝1.4，＝1.7）．4．如图，在△ABC中，D为AC上一点，且CD＝CB，以BC为直径作⊙O，交BD于点E，连接CE，过D作DF⊥AB于点F，∠BCD＝2∠ABD．（1）求证：AB是⊙O的切线；（2）若∠A＝60°，DF＝，求⊙O的直径BC的长．5．如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将沿CD 翻折后，点A与圆心O重合，延长OA至P，使AP＝OA，连接PC（1）求CD的长；（2）求证：PC是⊙O的切线；（3）点G为的中点，在PC延长线上有一动点Q，连接QG交AB于点E．交于点F（F与B、C不重合）．问GE•GF是否为定值？如果是，求出该定值；如果不是，请说明理由．6．如图，△ABC中，∠BAC＝120°，AB＝AC＝6．P是底边BC上的一个动点（P与B、C不重合），以P为圆心，PB为半径的⊙P与射线BA交于点D，射线PD交射线CA 于点E．（1）若点E在线段CA的延长线上，设BP＝x，AE＝y，求y关于x的函数关系式，并写出x的取值范围．（2）当BP＝2时，试说明射线CA与⊙P是否相切．（3）连接PA，若S△APE＝S△ABC，求BP的长．7．如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交斜边AB于点M，若H是AC的中点，连接MH．（1）求证：MH为⊙O的切线．（2）若MH＝，tan∠ABC＝，求⊙O的半径．（3）在（2）的条件下分别过点A、B作⊙O的切线，两切线交于点D，AD与⊙O相切于N点，过N点作NQ⊥BC，垂足为E，且交⊙O于Q点，求线段NQ的长度．8．如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交于点D，过点D作⊙O的切线，交BA的延长线于点E．（1）求证：AC∥DE；（2）连接CD，若OA＝AE＝a，写出求四边形ACDE面积的思路．9．如图，在射线BA，BC，AD，CD围成的菱形ABCD中，∠ABC＝60°，AB＝6，O是射线BD上一点，⊙O与BA，BC都相切，与BO的延长线交于点M．过M作EF ⊥BD交线段BA（或射线AD）于点E，交线段BC（或射线CD）于点F．以EF为边作矩形EFGH，点G，H分别在围成菱形的另外两条射线上．（1）求证：BO＝2OM．（2）设EF＞HE，当矩形EFGH的面积为24时，求⊙O的半径．（3）当HE或HG与⊙O相切时，求出所有满足条件的BO的长．10．如图所示，在Rt△ABC与Rt△OCD中，∠ACB＝∠DCO＝90°，O为AB的中点．（1）求证：∠B＝∠ACD．（2）已知点E在AB上，且BC2＝AB•BE．（i）若tan∠ACD＝，BC＝10，求CE的长；（ii）试判定CD与以A为圆心、AE为半径的⊙A的位置关系，并请说明理由．答案1．解：（1）如图，连接OD，∵⊙O与BC相切于点D，∴OD⊥BC，∵∠C＝90°，∴OD∥AC，∴∠CAD＝∠ODA，∵OA＝OD，∴∠OAD＝∠ODA，∴∠CAD＝∠BAD，∴AD平分∠CAB．（2）①DF＝DH，理由如下：∵FH平分∠AFE，∴∠AFH＝∠EFH，又∠DFG＝∠EAD＝∠HAF，∴∠DFG＝∠EAD＝∠HAF，∴∠DFG+∠GFH＝∠HAF+∠HFA，即∠DFH＝∠DHF，∴DF＝DH．②设HG＝x，则DH＝DF＝1+x，∵OH⊥AD，∴AD＝2DH＝2（1+x），∵∠DFG＝∠DAF，∠FDG＝∠FDG，∴△DFG∽△DAF，∴，∴，∴x＝1，∵DF＝2，AD＝4，∵AF为直径，∴∠ADF＝90°，∴AF＝∴⊙O的半径为．2．解：（1）由题意知：AC+BC＝CD，∴+2＝CD，∴CD＝3；（2）连接AC、BD、AD，∵AB是⊙O的直径，∴∠ADB＝∠ACB＝90°，∵，∴AD＝BD，将△BCD绕点D顺时针旋转90°到△AED处，如图③，∴∠EAD＝∠DBC，∵∠DBC+∠DAC＝180°，∴∠EAD+∠DAC＝180°，∴E、A、C三点共线，∵AB＝13，BC＝12，∴由勾股定理可求得：AC＝5，∵BC＝AE，∴CE＝AE+AC＝17，∵∠EDA＝∠CDB，∴∠EDA+∠ADC＝∠CDB+∠ADC，即∠EDC＝∠ADB＝90°，∵CD＝ED，∴△EDC是等腰直角三角形，∴CE＝CD，∴CD＝；（3）以AB为直径作⊙O，连接OD并延长交⊙O于点D1，连接D1A，D1B，D1C，如图④由（2）的证明过程可知：AC+BC＝D 1C，∴D1C＝，又∵D1D是⊙O的直径，∴∠DCD1＝90°，∵AC＝m，BC＝n，∴由勾股定理可求得：AB2＝m2+n2，∴D1D2＝AB2＝m2+n2，∵D1C2+CD2＝D1D2，∴CD2＝m2+n2﹣＝，∵m＜n，∴CD＝；（4）当点E在直线AC的左侧时，如图⑤，连接CQ，PC，∵AC＝BC，∠ACB＝90°，点P是AB的中点，∴AP＝CP，∠APC＝90°，又∵CA＝CE，点Q是AE的中点，∴∠CQA＝90°，设AC＝a，∵AE＝AC，∴AE＝a，∴AQ＝AE＝，由勾股定理可求得：CQ＝a，由（2）的证明过程可知：AQ+CQ＝PQ，∴PQ＝a+a，∴PQ＝AC；当点E在直线AC的右侧时，如图⑥，连接CQ、CP，同理可知：∠AQC＝∠APC＝90°，设AC＝a，∴AQ＝AE＝，由勾股定理可求得：CQ＝a，由（3）的结论可知：PQ＝（CQ﹣AQ），∴PQ＝AC．综上所述，线段PQ与AC的数量关系是PQ＝AC或PQ＝AC．3．证明：（1）∵CD∥AB，∴∠CDA＝∠BAD，又∵OA＝OD，∴∠ADO＝∠BAD，∴∠ADO＝∠CDA，∴DA平分∠CDO．（2）如图，连接BD，∵AB是直径，∴∠ADB＝90°，∵AC＝CD，∴∠CAD＝∠CDA，又∵CD∥AB，∴∠CDA＝∠BAD，∴∠CDA＝∠BAD＝∠CAD，∴＝＝，又∵∠AOB＝180°，∴∠DOB＝60°，∵OD＝OB，∴△DOB是等边三角形，∴BD＝OB＝AB＝6，∵＝，∴AC＝BD＝6，∵BE切⊙O于B，∴BE⊥AB，∴∠DBE＝∠ABE﹣∠ABD＝30°，∵CD∥AB，∴BE⊥CE，∴DE＝BD＝3，BE＝BD×cos∠DBE＝6×＝3，∴的长＝＝2π，∴图中阴影部分周长之和为2＝4π+9+3＝4×3.1+9+3×1.7＝26.5．4．（1）证明：∵CD＝CB，∴∠CBD＝∠CDB，∵BC是⊙O的直径，∴∠CEB＝90°，∴∠CBD+∠BCE＝∠CDB+∠DCE，∴∠BCE＝∠DCE，即∠BCD＝2∠BCE，∵∠BCD＝2∠ABD，∴∠ABD＝∠BCE，∴∠CBD+∠ABD＝∠CBD+∠BCE＝90°，∴CB⊥AB，∵CB为直径，∴AB是⊙O的切线；（2）解：∵∠A＝60°，DF＝，∴在Rt△AFD中，AF＝＝＝1，AD＝2，∵DF⊥AB，CB⊥AB，∴DF∥BC，∴∠ADF＝∠ACB，∵∠A＝∠A，∴△ADF∽△ACB，∴＝，设BC＝x，则＝，解得x＝4+6．∴BC＝4+6．5．（1）解：如图，连接OC，∵沿CD翻折后，点A与圆心O重合，∴OM＝OA＝×2＝1，CD⊥OA，∵OC＝2，∴CD＝2CM＝2＝2＝2；（2）证明：∵PA＝OA＝2，AM＝OM＝1，CM＝CD＝，∠CMP＝∠OMC＝90°，∴PC＝＝＝2，∵OC＝2，PO＝2+2＝4，∴PC2+OC2＝（2）2+22＝16＝PO2，∴∠PCO＝90°，∴PC是⊙O的切线；（3）解：GE•GF是定值，证明如下，连接GO并延长，交⊙O于点H，连接HF∵点G为的中点∴∠GOE＝90°，∵∠HFG＝90°，且∠OGE＝∠FGH∴△OGE∽△FGH∴＝∴GE•GF＝OG•GH＝2×4＝8．6．解：（1）过A作AF⊥BC于F，过P作PH⊥AB于H，∵∠BAC＝120°，AB＝AC＝6，∴∠B＝∠C＝30°，∵PB＝PD，∴∠PDB＝∠B＝30°，CF＝AC•cos30°＝6×＝3，∴∠ADE＝30°，∴∠DAE＝∠CPE＝60°，∴∠CEP＝90°，∴CE＝AC+AE＝6+y，∴PC＝＝，∵BC＝6，∴PB+CP＝x+＝6，∴y＝﹣x+3，∵BD＝2BH＝x＜6，∴x＜2，∴x的取值范围是0＜x＜2；（2）∵BP＝2，∴CP＝4，∴PE＝PC＝2＝PB，∴射线CA与⊙P相切；（3）当D点在线段BA上时，连接AP，∵S △ABC＝BC•AF＝××3＝9，∵S△APE＝AE•PE＝y•×（6+y）＝S△ABC＝，解得：y＝，代入y＝﹣x+3得x＝4﹣．当D点BA延长线上时，PC＝EC＝（6﹣y），∴PB+CP＝x+（6﹣y）＝6，∴y＝x﹣3，∵∠PEC＝90°，∴PE＝＝＝（6﹣y），∴S△APE＝AE•PE＝y•（6﹣y）＝S△ABC＝，解得y＝或，代入y＝x﹣3得x＝3或5．综上可得，BP的长为4﹣或3或5．7．解：（1）连接OH、OM，∵H是AC的中点，O是BC的中点，∴OH是△ABC的中位线，∴OH∥AB，∴∠COH＝∠ABC，∠MOH＝∠OMB，又∵OB＝OM，∴∠OMB＝∠MBO，∴∠COH＝∠MOH，在△COH与△MOH中，，∴△COH≌△MOH（SAS），∴∠HCO＝∠HMO＝90°，∴MH是⊙O的切线；（2）∵MH、AC是⊙O的切线，∴HC＝MH＝，∴AC＝2HC＝3，∵tan∠ABC＝，∴＝，∴BC＝4，∴⊙O的半径为2；（3）连接OA、CN、ON，OA与CN相交于点I，∵AC与AN都是⊙O的切线，∴AC＝AN，AO平分∠CAD，∴AO⊥CN，∵AC＝3，OC＝2，∴由勾股定理可求得：AO＝，∵AC•OC＝AO•CI，∴CI＝，∴由垂径定理可求得：CN＝，设OE＝x，由勾股定理可得：CN2﹣CE2＝ON2﹣OE2，∴﹣（2+x）2＝4﹣x2，∴x＝，∴OE＝，由勾股定理可求得：EN＝，∴由垂径定理可知：NQ＝2EN＝．另解：先证明：△AOC∽△CNE，∴，由勾股定理可知：OA2＝4+9＝13，∴OA＝，在△AOC中，CI⊥OA，CI×OA＝2×3，∴CI＝，∴CN＝，∴＝，∴NE＝，∴NQ＝2EN＝．8．（1）证明：∵ED与⊙O相切于D，∴OD⊥DE，∵F为弦AC中点，∴OD⊥AC，∴AC∥DE．（2）解：作DM⊥OA于M，连接CD，CO，AD．首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE＝AE•DM，只要求出DM即可．（方法二：证明△ADE的面积等于四边形ACDE的面积的一半）∵AC∥DE，AE＝AO，∴OF＝DF，∵AF⊥DO，∴AD＝AO，∴AD＝AO＝OD，∴△ADO是等边三角形，同理△CDO也是等边三角形，∴∠CDO＝∠DOA＝60°，AE＝CD＝AD＝AO＝DO＝a，∴AO∥CD，又AE＝CD，∴四边形ACDE是平行四边形，易知DM＝a，∴平行四边形ACDE面积＝a2．9．解：（1）如图1所示：设⊙O切AB于点P，连接OP，则∠OPB＝90°．∵四边形ABCD为菱形，∴∠ABD＝∠ABC＝30°．∴OB＝2OP．∵OP＝OM，∴BO＝2OP＝2OM．（2）如图2所示：设GH交BD于点N，连接AC，交BD于点Q．∵四边形ABCD是菱形，∴AC⊥BD．∴BD＝2BQ＝2AB•cos∠ABQ＝AB＝18．设⊙O的半径为r，则OB＝2r，MB＝3r．∵EF＞HE，∴点E，F，G，H均在菱形的边上．①如图2所示，当点E在AB上时．在Rt△BEM中，EM＝BM•tan∠EBM＝r．由对称性得：EF＝2EM＝2r，ND＝BM＝3r．∴MN＝18﹣6r．∴S 矩形EFGH＝EF•MN＝2r（18﹣6r）＝24．解得：r1＝1，r2＝2．当r＝1时，EF＜HE，∴r＝1时，不合题意舍当r＝2时，EF＞HE，∴⊙O的半径为2．∴BM＝3r＝6．如图3所示：当点E在AD边上时．BM＝3r，则MD＝18﹣3r．MN＝18﹣2（18﹣3r）＝6r﹣18，EF＝2EM＝2×（18﹣3r）∴S 矩形EFGH＝EF•MN＝•（18﹣3r）（6r﹣18）＝24．解得：r＝4或5（舍弃），综上所述，⊙O的半径为2或4．（3）解设GH交BD于点N，⊙O的半径为r，则BO＝2r．当点E在边BA上时，显然不存在HE或HG与⊙O相切．①如图4所示，点E在AD上时．∵HE与⊙O相切，∴ME＝r，DM＝r．∴3r+r＝18．解得：r＝9﹣3．∴OB＝18﹣6．②如图5所示；由图形的对称性得：ON＝OM，BN＝DM．∴OB＝BD＝9．③如图6所示．∵HG与⊙O相切时，MN＝2r．∵BN+MN＝BM＝3r．∴BN＝r．∴DM＝FM＝GN＝BN＝r．∴D与O重合．∴BO＝BD＝18．④如图7所示：∵HE与⊙O相切，∴EM＝r，DM＝r．∴3r﹣r＝18．∴r＝9+3．∴OB＝2r＝18+6．综上所述，当HE或GH与⊙O相切时，OB的长为18﹣6或9或18或18+6．10．解：（1）∵∠ACB＝∠DCO＝90°，∴∠ACB﹣∠ACO＝∠DCO﹣∠ACO，即∠ACD＝∠OCB，又∵点O是AB的中点，∴OC＝OB，∴∠OCB＝∠B，∴∠ACD＝∠B，（2）（i）∵BC2＝AB•BE，∴＝，∵∠B＝∠B，∴△ABC∽△CBE，∴∠ACB＝∠CEB＝90°，∵∠ACD＝∠B，∴tan∠ACD＝tan∠B＝，设BE＝4x，CE＝3x，由勾股定理可知：BE2+CE2＝BC2，∴（4x）2+（3x）2＝100，∴解得x＝2，∴CE＝6；（ii）过点A作AF⊥CD于点F，∵∠CEB＝90°，∴∠B+∠ECB＝90°，∵∠ACE+∠ECB＝90°，∴∠B＝∠ACE，∵∠ACD＝∠B，∴∠ACD＝∠ACE，∴CA平分∠DCE，∵AF⊥CE，AE⊥CE，∴AF＝AE，∴直线CD与⊙A相切．。
初三数学切割线定理(“定理”相关文档)共7张
讲课人：王兆群
复习：相交弦定理:
弦AB, CD相交于P AP•BP=CP•DP
Ｂ Ｃ
Ｐ
Ａ
Ｄ
AP•BP=CP•DP
（2）已知：PAB是圆O的割线，
PAAP=•B4P，=CPPT=•D6P，
则PA圆=4O，的P面T积=6＝，
。
A则P圆•BOP的=C面P积•D＝P
。
（31）已知PATB是、圆POC的D是切圆线O，的割线，
B
PA=6 ，AB=4 ，PO=
D A O
（3）已知PT是圆O的切线，
T
PA=4， PT=6 ， 则圆O的面积＝
O
。
A P
C
P
P
例3 已知：弦AB 、CD相交于E，过点E作BC的平行 线PE交AD延长线于点P，PG与圆O相交于点G 求证：PG=PE
P
D G
A
B
E
C
（12）已知P：APBA、BP是C圆DO是的圆割O线的，割线，
（AP2•）BP已=知CP：•DPPAB是圆O的割线，
（3）已知PT是圆O的切线，
弦AB, CD相交于P
切割线定理的应用
例1 、 填空
B
（1）已知PAB、PCD是圆O的割线，
PA=3 ， AB==5 CD=2，则PC＝
（2）已知：PAB是圆O的割线，
（PA2=）4，已知PT：=6PA，B是圆O的割线，
（AP1•）BP已=知CPP•ADBP、PCD是圆O的割线，
APAP=•B4P，=CPPT=•D6P，
（PA2=）6 已，知AB：=P4A，BP是O圆=1O0的，割线，
（则3圆）O已的知面P积T＝是圆O的切线，。
P（A2=）4，已知PT：=6PA，B是圆O的割线，
2021年九年级数学中考复习专题：圆的综合(考查切线证明、长度计算等)(三)
中考复习专题：圆的综合（考察切线证明、长度计算等）1．如图所示，AB是⊙O的直径，∠B＝30°，弦BC＝6，∠ACB的平分线交⊙O于D，连AD．（1）求直径AB的长．（2）求阴影部分的面积（结果保留π）．2．如图，点D在⊙O的直径AB的延长线上，CD切⊙O于点C，AE⊥CD于点E （1）求证：AC平分∠DAE；（2）若AB＝6，BD＝2，求CE的长．3．如图，⊙O的直径AB与弦CD相交于点E，且DE＝CE，⊙O的切线BF与弦AD的延长线交于点F．（1）求证：CD∥BF；（2）若⊙O的半径为6，∠A＝35°，求的长．4．如图，在△ABC中，∠ACB＝90°，O是边AC上一点，以O为圆心，以OA为半径的圆分别交AB、AC于点E、D，在BC的延长线上取点F，使得BF＝EF．（1）判断直线EF与⊙O的位置关系，并说明理由；（2）若∠A＝30°，求证：DG＝DA；（3）若∠A＝30°，且图中阴影部分的面积等于2，求⊙O的半径的长．5．如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC＝BD，连接AC，过点D作DE⊥AC于E．（1）求证：AB＝AC；（2）求证：DE为⊙O的切线．6．如图，已知⊙O的直径AB＝10，弦AC＝6，∠BAC的平分线交⊙O于点D，过点D 作DE⊥AC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）求DE的长．7．如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD＝CB，延长CD 交BA的延长线于点E．（1）求证：CD为⊙O的切线；（2）若BD的弦心距OF＝1，∠ABD＝30°，求图中阴影部分的面积．（结果保留π）8．已知，如图在Rt△ABC中，∠C＝90°，BD平分∠ABC交AC于D，过D作DE⊥BD 交AB于E，经过B，D，E三点作⊙O．（1）求证：AC与⊙O相切．（2）若AD＝15，AE＝9，求⊙O的半径．9．如图，⊙O是△ABC外接圆，AC是直径，OF∥AB，过点B⊙O的切线相交于点D，与OF的延长线交点E．（1）求证：△ABD∽△BCD；（2）若∠C＝30°，求证：△OED是等腰三角形；（3）若⊙O的半径为3，cos D＝，求OF的长．10．如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD 于点D．（1）求证：AE平分∠DAC，（2）若AB＝6，∠ABE＝60°，求①AD的长，②图中阴影部分的面积．11．△ABC内接于⊙O，点D在BC上，连接AD、BO，AD＝AC．（1）如图1，求证：∠DAC＝2∠ABO；（2）如图2，点E在弧BC上，连接AE交BC于点F，∠CAE＝3∠DAE，连接BE，DE，若∠EDC＝∠EBC+60°，求∠DEA的度数：（3）如图3，在（2）的条件下，若tan∠ACB＝2，AE＝2+1，求半径BO的长．12．如图1，△ABC内接于⊙O，连接AO，延长AO交BC于点D，AD⊥BC．（1）求证：AB＝AC；（2）如图2，在⊙O上取一点E，连接BE、CE，过点A作AF⊥BE于点F，求证：EF+CE ＝BF；（3）如图3在（2）的条件下，在BE上取一点G，连接AG、CG，若∠AGB+∠ABC ＝90°，∠AGC＝∠BGC，AG＝6，BG＝5，求EF的长．13．如图，在Rt△ABC中，∠C＝90°，O为BC边上一点，以OC为半径的圆O，交AB于D点，且AD＝AC．延长DO交圆O于E点，连接AE．（1）求证：DE⊥AB；（2）若DB＝4、BC＝8，求AE的长．14．如图，AB是⊙C的直径，M、D两点在AB的延长线上，E是⊙C的点，且DE2＝DB •DA，延长AE至F，使得AE＝EF，设BF＝5，cos∠BED＝．（1）求证：△DEB∽△DAE；（2）求DA，DE的长；（3）若点F在B、E、M三点确定的圆上，求MD的长．15．如图，AB是⊙O的直径，点C为⊙O上一点，点P是半径OB上一动点（不与O，B 重合），过点P作射线l⊥AB，分别交弦BC，于D、E两点，在射线l上取点F，使FC＝FD．（1）求证：FC是⊙O的切线；（2）当点E是的中点时，①若∠BAC＝60°，判断以O，B，E，C为顶点的四边形是什么特殊四边形，并说明理由；②若＝，且AB＝20，求OP的长．参考答案1．解：（1）∵AB为⊙O的直径，∴∠ACB＝90°，∵∠B＝30°，∴AB＝2AC，∵AB2＝AC2+BC2，∴AB2＝AB2+62，∴AB＝4．（2）连接OD．∵AB＝4，∴OA＝OD＝2，∵CD平分∠ACB，∠ACB＝90°，∴∠ACD＝45°，∴∠AOD＝2∠ACD＝90°，∴S△AOD＝OA•OD＝•2•2＝6，∴S扇形△AOD＝•π•OD2＝•π•（2）2＝3π，∴阴影部分的面积＝S扇形△AOD﹣S△AOD＝3π﹣6．2．（1）证明：连接OC．∵CD是⊙O的切线，∴∠OCD＝90°，∵∠AEC＝90°，∴∠OCD＝∠AEC，∴AE∥OC，∴∠EAC＝∠ACO，∵OA＝OC，∴∠OAC＝∠OCA，∴∠EAC＝∠OAC，∴AC平分∠DAE．（2）作CF⊥AB于F．在Rt△OCD中，∵OC＝3，OD＝5，∴CD＝4，∵•OC•CD＝•OD•CF，∴CF＝，∵AC平分∠DAE，CE⊥AE，CF⊥AD，∴CE＝CF＝．3．（1）证明：∵AB是⊙O的直径，DE＝CE，∴AB⊥CD，∵BF是⊙O的切线，∴AB⊥BF，∴CD∥BF；（2）解：连接OD、OC，∵∠A＝35°，∴∠BOD＝2∠A＝70°，∴∠COD＝2∠BOD＝140°，∴的长＝＝．4．解：（1）连接OE，∵OA＝OE，∴∠A＝∠AEO，∵BF＝EF，∴∠B＝∠BEF，∵∠ACB＝90°，∴∠A+∠B＝90°，∴∠AEO+∠BEF＝90°，∴∠OEG＝90°，∴EF是⊙O的切线；（2）∵∠AED＝90°，∠A＝30°，∴ED＝AD，∵∠A+∠B＝90°，∴∠B＝∠BEF＝60°，∵∠BEF+∠DEG＝90°，∴∠DEG＝30°，∵∠ADE+∠A＝90°，∴∠ADE＝60°，∵∠ADE＝∠EGD+∠DEG，∴∠DGE＝30°，∴∠DEG＝∠DGE，∴DG＝DE，∴DG＝DA；（3）∵AD是⊙O的直径，∴∠AED＝90°，∵∠A＝30°，∴∠EOD＝60°，∴∠EGO＝30°，∵阴影部分的面积＝×r×r﹣＝2﹣π．解得：r2＝4，即r＝2，即⊙O的半径的长为2．5．证明：（1）连接AD；∵AB是⊙O的直径，∴∠ADB＝90°．又∵DC＝BD，∴AD是BC的中垂线．∴AB＝AC．（2）连接OD；∵OA＝OB，CD＝BD，∴OD∥AC．∴∠0DE＝∠CED．又∵DE⊥AC，∴∠CED＝90°．∴∠ODE＝90°，即OD⊥DE．∴DE是⊙O的切线．6．证明：（1）连接OD，∵AD平分∠BAC，∴∠DAE＝∠DAB，∵OA＝OD，∴∠ODA＝∠DAO，∴∠ODA＝∠DAE，∴OD∥AE，∵DE⊥AC，∴OD⊥DE，∴DE是⊙O切线．（2）过点O作OF⊥AC于点F，∴AF＝CF＝3，∴OF＝＝4．∵∠OFE＝∠DEF＝∠ODE＝90°，∴四边形OFED是矩形，∴DE＝OF＝4．7．（1）证明：连接OD，∵BC是⊙O的切线，∴∠ABC＝90°，∵CD＝CB，∴∠CBD＝∠CDB，∵OB＝OD，∴∠OBD＝∠ODB，∴∠ODC＝∠ABC＝90°，即OD⊥CD，∵点D在⊙O上，∴CD为⊙O的切线；（2）在Rt△OBF中，∵∠ABD＝30°，OF＝1，∴∠BOF＝60°，OB＝2，BF＝，∵OF⊥BD，∴BD＝2BF＝2，∠BOD＝2∠BOF＝120°，∴S阴影＝S扇形OBD﹣S△BOD＝＝．8．（1）证明：连接OD，如图所示：∵OD＝OB，∴∠1＝∠2，又∵BD平分∠ABC，∴∠2＝∠3，∴∠1＝∠3，∴OD∥BC，而∠C＝90°，∴OD⊥AD，∴AC与⊙O相切于D点；（2）解：∵OD⊥AD，∴在RT△OAD中，OA2＝OD2+AD2，又∵AD＝15，AE＝9，设半径为r，∴（r+9）2＝152+r2，解方程得，r＝8，即⊙O的半径为8．9．解：（1）如图1，连接BO，∵BD是⊙O的切线，∴∠OBD＝90°，∴∠OBA+∠ABD＝90°，∵AC是⊙O的直径，∴∠ABC＝90°，∴∠CBO+∠OBA＝90°，∴∠ABD＝∠CBO，∵OB＝OC，∴∠CBO＝∠C，∴∠ABD＝∠C，又∵∠D＝∠D，∴△ABD∽△BCD；（2）证明：∵∠C＝30°，OE∥AB，∠ABC＝90°，∴∠BAO＝60°＝∠BOA＝∠BOE，由（1）知OB⊥DE，∠EBO＝∠DBO＝90°，又∵OB＝OB，∴△BOE≌△BOD（ASA），∴OE＝OD，∴△OED是等腰三角形；（3）∵OE∥AB，CO＝AO，∴CF＝BF，∴OF是△ABC中位线，∴OF＝AB，又∵在Rt△OBD中，cos∠D＝＝，设BD＝4x，则OD＝5x，由勾股定理（5x）2＝（4x）2+32，解得，x＝1（取正值），∴DB＝4，OD＝5，如图2，过点B作BM⊥OA于M，则∠OMB＝∠OBD＝90°，又∵∠BOM＝∠DOB，∴△OBM∽△ODB，∴＝＝，∴＝＝，∴BM＝，OM＝，∴AM＝，∴AB＝＝，∴OF＝AB＝．10．证明：（1）如图，连接OE，∵DC为切线，∴OE⊥CD，且AD⊥CD，∴OE∥AD，∴∠DAE＝∠AEO，∵OE＝OA，∴∠AEO＝∠EAO，∴∠DAE＝∠EAO，即AE平分∠DAC；（2）①∵∠ABE＝60°，∠AEB＝90°，∴∠EAB＝30°，∠AOE＝120°∴BE＝AB＝3，AE＝BE＝3∵AE平分∠DAC，∴∠DAE＝∠BAE＝30°，且∠D＝90°∴DE＝AE＝，AD＝DE＝，②∵OA＝OB＝BE＝3，∴S扇形AOE＝π•OA2＝3π，S△AOE＝S△ABE＝×AE•BE＝，∴S阴影＝S扇形AOE﹣S△AOE＝3π﹣11．解：（1）连接OA，∵OA＝OB，∴∠ABO＝（180°﹣∠AOB），∵AD＝AC，∴∠ADC＝∠C，∴∠DAC＝180°﹣2∠C，∵∠AOB＝2∠C，∴∠DAC＝180°﹣∠AOB，∴∠AOB＝180°﹣∠DAC，∴∠ABO＝（180°﹣∠AOB）＝[180°﹣（180°﹣∠DAC）]＝，即∠DAC＝2∠ABO；（2）如图2，过点A作AH⊥BC于H，∵∠CAE＝3∠DAE，∴∠CAD＝4∠DAE，∵AD＝AC，AH⊥BC，∴∠DAH＝∠CAH＝2∠DAE，∠ADH+∠DAH＝90°，∴∠ADH+2∠DAE＝90°，∵∠EDC＝∠EBC+60°，∠EBC＝∠EAC，∴∠EDC＝∠EAC+60°＝∠DAE+60°，∵∠AED+∠DAE+∠ADH+∠EDC＝180°，∴∠DEA+∠DAE+∠DAE+60°+∠ADH＝180°，∴∠DEA+90°+60°＝180°，∴∠DEA＝30°，（3）如图3，过点D作DG⊥AE交AH的延长线于点G，连接GC，OE，CE，过点B 作BN⊥AE于N，∵∠CAD＝4∠DAE，AD＝AC，AH⊥DC，∴∠DAH＝∠CAH＝2∠DAE，AH是CD的中垂线，∴∠DAE＝∠FAH，∵DG⊥AE，∠DAE＝∠FAH，∴∠ADG＝∠AGD，∴AD＝AG，且∠DAE＝∠FAH，AE＝AE，∴△ADE≌△AGE（SAS）∴∠AED＝∠AEG＝30°，DE＝EG，∴∠DEG＝60°，∴△DEG是等边三角形，∴DG＝EG＝DE，∠DGE＝60°，∵AH是CD的中垂线，∴DG＝GC，∴DG＝GC＝EG，∴点D，点G，点E在以点G为圆心，DG为半径的圆上，∴∠DCE＝∠DCE＝30°，∴∠BAE＝∠BCE＝30°，∴∠BOE＝60°，且BO＝OE，∴△BOE是等边三角形，∴BE＝BO，∵∠BAE＝30°，BN⊥AE，∴AN＝BN∵∠ACB＝∠AEB，∴tan∠ACB＝tan∠AEB＝2＝，∴EN＝BN，∵AE＝EN+AN，∴2+1＝BN+BN，∴BN＝2，∴EN＝1，∴BE＝＝＝，∴BO＝．12．证明：（1）∵AD⊥BC，AD过圆心O，∴BD＝CD，且AD⊥BC，∴AB＝AC；（2）如图2，在BF上截取FH＝EF，连接AE，AH，∵AF⊥EH，EF＝FH，∴AH＝AE，∴∠AHE＝∠AEH，∵AB＝AC，∴∠ABC＝∠ACB，且∠ACB＝∠AEH，∴∠AEH＝∠AHE＝∠ABC＝∠ACB，∴∠BAC＝∠HAE，∴∠BAH＝∠CAE，且AH＝AE，AB＝AC，∴△ABH≌△ACE（SAS）∴BH＝CE，∴BF＝EF+CE；（3）如图3，延长CG交⊙O于M，交AB于K，过点A作AP⊥CM于P，过点B作BN⊥CM于N，连接AE，AM，MB，∵∠AGB+∠ABC＝90°，∴∠AGB＝90°﹣∠ABC，∴∠AGB＝2∠BAC，∵∠AGC＝∠BGC，∴∠BGM＝∠AGM＝∠AGB，∴∠BGM＝∠AGM＝∠BAC，且∠BAC＝∠BMC，∴∠BMG＝∠BGM，∴BM＝BG＝5，∵∠AMC＝∠ABC，∠AGM＝∠BAC，∴∠GAM＝∠ACB，∴∠AMG＝∠MAG，∴MG＝AG＝6，∵BM＝BG，BN⊥MG，∴MN＝NG＝3，∴BN＝＝＝4，∵∠BMG＝∠AGM，∴BM∥AG，∴＝，∵AP∥BN，∴＝，∴AP＝，∴PG＝＝，∴PN＝PG﹣NG＝，且∴PK＝，KN＝，∴AK＝＝，BK＝＝，∴AB＝AK+BK＝，∵AF2＝AG2﹣GF2，AF2＝AB2﹣BF2，∴AG2﹣GF2＝AB2﹣（5+GF）2，∴GF＝，∴BF＝，∵MP＝MG﹣PG＝，∴MK＝，∵∠AMC＝∠ABC，∠MAB＝∠BCM，∴△MAK∽△BCK，∴，∴CK＝，∴GC﹣KC﹣KG＝，∵∠BMC＝∠BEC，∠BGM＝∠CGE，∠BGM＝∠BMG，∴∠CGE＝∠CEG，∴CG＝CE＝，∵EF+CE＝BF，∴EF＝BF﹣CE＝＝．13．（1）证明：连接AO．∵AD＝AC，AO＝AO，OD＝OC，∴△AOD≌△AOC（SSS），∴∠ADO＝∠ACO＝90°，∴DE⊥AB．（2）解：设OD＝OC＝x，在Rt△OBD中，∵OB2＝BD2+OD2，∴（8﹣x）2＝x2+42，解得x＝3，设AD＝AC＝y，在Rt△ACB中，∵AB2＝AC2+BC2，∴（y+4）2＝y2+82，∴y＝6，在Rt△ADE中，AE＝＝＝6．14．解：（1）∵DE2＝DB•DA，∴＝，又∵∠D＝∠D，∴△DEB∽△DAE．（2）∵△DEB∽△DAE，∴∠DEB＝∠DAE＝α，∵AB是直径，∴∠AEB＝90°，又AE＝EF，∴AB＝BF＝5，∴∠BFE＝∠BAE＝α，则BF⊥ED交于点H，∵cos∠BED＝，则BE＝3，AE＝4∴＝＝，即：＝＝，解得：BD＝，DE＝，则AD＝AB+BD＝，ED＝．（3）由点F在B、E、M三点确定的圆上，则BF是该圆的直径，连接MF，∵BF⊥ED，∠BMF＝90°，∴∠MFB＝∠D＝β，在△BED中，过点B作HB⊥ED于点H，设HD＝x，则EH＝﹣x，则9﹣（﹣x）2＝（）2﹣x2，解得：x＝，则cosβ＝＝，则sinβ＝，MB＝BF sinβ＝5×＝，DM＝BD﹣MB＝．15．证明：（1）连接OC，∵OB＝OC，∴∠OBC＝∠OCB，∵PF⊥AB，∴∠BPD＝90°，∴∠OBC+∠BDP＝90°，∵FC＝FD∴∠FCD＝∠FDC∵∠FDC＝∠BDP∴∠OCB+∠FCD＝90°∴OC⊥FC∴FC是⊙O的切线；（2）如图2，连接OC，OE，BE，CE，①以O，B，E，C为顶点的四边形是菱形．理由如下：∵AB是直径，∴∠ACB＝90°，∵∠BAC＝60°，∴∠BOC＝120°，∵点E是的中点，∴∠BOE＝∠COE＝60°，∵OB＝OE＝OC∴△BOE，△OCE均为等边三角形，∴OB＝BE＝CE＝OC∴四边形BOCE是菱形；②∵，∴设AC＝3k，BC＝4k（k＞0），由勾股定理得AC2+BC2＝AB2，即（3k）2+（4k）2＝202，解得k＝4，∴AC＝12，BC＝16，∵点E是的中点，∴OE⊥BC，BH＝CH＝8，∴S△OBE＝OE×BH＝OB×PE，即10×8＝10PE，解得：PE＝8，由勾股定理得OP＝＝＝6．。
初中数学课件《切割线定理》
切割线定理的相关概念介绍
为了帮助大家更好地理解切割线定理，我们在这里先来介绍一下它的相关概念。
扇形
扇形是圆心角对应的圆弧及其 圆心所组成的图形，它是切割 线重要概念。
弓形
弓形指的是圆上一个扇形所截 下来的圆弧部分，是能够帮助 我们理解切割线定理的重要概 念。
弦长
弦是连接圆上两点的线段，弦 长是线段长度，是切割线定理 中常用的量。
解决切割线定理中的常见错误和误区
学习切割线定理的时候，常见错误和误区包括对图形理解不够溜，计算公式没有掌握好，套路不熟练等 等，下面是一些错误率较高的问题。
• 画图不规范，不能很好地说明切线、割线、交点的位置关系 • 公式记忆不清，导致计算错误 • 理解不深刻，只会套用公式，难以发挥应有的思考能力
切割线定理在各国数学教育中的地位
切割线定理作为数学中非常重要的一个知识点，它在不同国家的数学教育中都占据着重要地位，是不容 忽视的。下面介绍几个国家中切割线定理的教学情况。
• 中国：在初中阶段的几何课程中必须学习切割线定理。 • 美国：在高中阶段的几何学里也会涉及切割线定理的知识点。 • 日本：从小学到高中，切割线定理都是几何学习的重点。
具体表述
具体来说，若AB与CD是两条割线，交于点E，那么∠AEB=∠CED，∠BEC=1/2∠BAD。
套路示范
判断两条线段是否相互垂直的时候，可以用切割线定理进行证明。
切割线定理的含义和意义
切割线定理是数学中一条很重要的定理。它在几何解题中的应用非常广泛，可以帮助我们更好地理 解和应用各种几何概念。
切割线定理的进阶应用
掌握好了切割线定理的基础知识之后，还可以进一步拓展应用，例如： • 推导出更复杂的几何公式 • 应用切割线定理解决更高级的几何问题 • 将切割线定理与其他定理的知识点相关联，挖掘其更多潜力
2021年九年级数中考复习专题：圆中切线的证明
中考专题：圆中切线的证明考点速览： 考点1考点2切线：经过半径外端并且垂直于这条半径的直线是圆的切线。
符号语言∵ OA ⊥ l 于A ， OA 为半径∴ l 为⊙O 的切线考点3判断直线是圆的切线的方法：①与圆只有一个交点的直线是圆的切线。
②圆心到直线距离等于圆的半径的直线是圆的切线。
③经过半径外端，垂直于这条半径的直线是圆的切线。
（请务必记住证明切线方法：有交点就连半径证垂直；无交点就做垂直证半径） 考点4切线的性质定理：圆的切线垂直于经过切点的半径。
推论1：经过圆心且垂直于切线的直线必经过切点。
推论2：经过切点且垂直于切线的直线必经过圆心。
（请务必记住切线重要用法： 见切线就要连圆心和切点得到垂直）BC经典例题：例1.如图，△ABC 内接于⊙O ， AB 是 ⊙O 的直径，∠CAD ＝ ∠ABC ，判断直线AD 与⊙O 的位置关系，并说明理由。
例2.如图,OA=OB=13cm ，AB=24cm ，⊙O 的半径为5cm ，AB 与⊙O 相切吗？为什么?例3.如图,PA 、PB 是⊙O 的切线，切点为A 、B ，C 是⊙O 上一点，若∠P ＝40。
， 求∠C 的度数。
例4．如图所示，ABC Rt ∆中，︒=∠90C ，以AC 为直径作⊙O 交AB 于D ，E 为BC 中点。
求证：DE 是⊙O 的切线．A BB · ABC EOD例5．如图10，以点M（－1,0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－33x－533与⊙M相切于点H，交x轴于点E，交y轴于点F．（1）请直接写出OE、⊙M的半径r、CH的长；（3分）（2）如图11，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；（3分）（3）如图12，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．（3分）举一反三1.如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A，与大圆相交于点B，小圆的切线AC与大圆相交于点D，且CO平分∠ACB.试判断BC所在直线与小圆的位置关系，并说明理由。
中考数学复习切线的综合运用[人教版]
![中考数学复习切线的综合运用[人教版]](https://img.taocdn.com/s3/m/56dae181f78a6529647d53ae.png)
且与BC所在直线相交. C
EC DO B
四 课堂作业
１正三角形内切圆半径与外接圆 半径之比为 ．
２⊿ＡＢＣ内切圆半径r= 3 ，D,E,F
为切点, ∠ABC=60°,BC=8, ⊿ＡＢＣ
的面积为１０ 3 A，求AB,AC的长． EF O
BD C
３ＡＢ是⊙ Ｏ的直径，过Ｂ作⊙ Ｏ
仆Ｙ．曼妍米依仙女又颤起怪异；骗子电话 骗子举报 骗子 / 骗子电话 骗子举报 骗子 ；的美如竹竿一般的手臂，只见她怪异的的褐黄色鸭蛋模样的烟 花万花裤子中，突然弹出二道芝麻状的烟花，随着女奴仆Ｙ．曼妍米依仙女的颤动，芝麻状的烟花像纽扣一样念动咒语：“二拳哄哩喂，幽灵哄哩喂，二拳幽灵哄哩喂……
复习（三）
切线的综合运用
一、复习目标
1、熟练掌握直线与圆位置关系的判别
2、深刻理解有关切线的几个重要定理 （切线的性质定理、切线的判定定理、切 线长定理、弦切角定理），提高综合运用 以上定理的能力。
3、加深对一些基本结论、基本图形（直 角三角形内切圆半径公式、三角形有关内 切圆半径的面积公式等）的理解。
的切线ＢＣ，ＯＣ交⊙ Ｏ于Ｅ，Ａ
Ｅ的延长线交ＢＣ于Ｄ，（１）求
证：ＣＥ２＝ＣＤＣＢ，（２）若
ＡＢ＝ＢＣ＝２，求ＣＥ，ＣＤ的
长．
A
OE B DC
5、如图，PA，PB是⊙O的切线， A，B是切点，∠APB=78°，点C 是⊙O上异与A，B的任一点，则 ∠ACB= 。
A PO
B
6、⊿ABC中，∠C=90°∠A=30° 点O为AB上的点，BO=m，⊙O的半 径r=0.5,当m在什么范围内取值 时，BC与⊙O相离？相切？相交？
C
A
OB
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021年九年级数学中考复习专题之圆：切割线定理综合运用（一）一．选择题1．P是⊙O外一点，PA切⊙O于A，割线PBC交⊙O于点B、C，若PB＝BC＝3，则PA的长是（）A．9 B．3 C．D．182．如图，PA切⊙O于点A，PBC是⊙O的一条割线，且PA＝2，BC＝2PB，那么PB 的长为（）A．2 B．C．4 D．3．如图，⊙O的两条割线PAB，PCD分别交⊙O于点A，B和点C，D．已知PA＝6，AB＝4，PC＝5，则CD＝（）A．B．C．7 D．244．如图，已知P为⊙O外一点，PO交⊙O于点A，割线PBC交⊙O于点B、C，且PB ＝BC，若OA＝7，PA＝4，则PB的长等于（）A．B．C．6 D．5．如图，PA切⊙O于点A，PBC是⊙O的割线，如果PB＝2，PC＝8，那么PA的长为（）A．2 B．4 C．6 D．6．如图，在▱ABCD中，过A、B、C三点的圆交AD于E，且与CD相切．若AB＝4，BE ＝5，则DE的长为（）A．3 B．4 C．D．7．如图，在以O为圆心的两个同心圆中，A为大圆上任意一点，过A作小圆的割线AXY，若AX•AY＝4，则图中圆环的面积为（）A．16πB．8πC．4πD．2π8．如图，A、B、C、D为⊙O上的点，直线BA与DC相交于点P，PA＝2，PC＝CD＝3，则PB＝（）A．6 B．7 C．8 D．99．以半圆中的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交于点D，若，且AB＝10，则CB的长为（）A．B．C．D．410．如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B．如果∠APB ＝60°，PA＝8，那么点P与O间的距离是（）A．16 B．C．D．二．填空题11．如图，⊙O的半径为，A、B两点在⊙O上，切线AQ和BQ相交于Q，P是AB 延长线上任一点，QS⊥OP于S，则OP•OS＝．12．如图，过点P引圆的两条割线PAB和PCD，分别交圆于点A，B和C，D，连接AC，BD，则在下列各比例式中，①；②；③，成立的有（把你认为成立的比例式的序号都填上）．13．如图，割线PAB与⊙O交于点A、B，割线PCD与⊙O交于点C、D，PA＝PC，PB＝3cm，则PD＝cm．14．如图，过⊙O外一点P作两条割线，分别交⊙O于A，B和C，D．已知PA＝2，PB ＝5，PD＝8，则PC的长是．15．如图，AC为⊙O的直径，PA是⊙O的切线，切点为A，PBC是⊙O的割线，∠BAC 的平分线交BC于D点，PF交AC于F点，交AB于E点，要使AE＝AF，则PF应满足的条件是（只需填一个条件）．三．解答题16．如图，AB是⊙O的直径，C是AB延长线上的一点，CD是⊙O的切线，D为切点，过点B作⊙O的切线交CD于点E．若AB＝CD＝2，求CE的长．17．如图所示，⊙O的内接△ABC的AB边过圆心O，CD切⊙O于C，BD⊥CD于D，交⊙O于F，CE⊥AB于点E，FE交⊙O于G．解答下列问题：（1）若BC＝10，BE＝8，求CD的值；（2）求证：DF•DB＝EG•EF．18．如图1，已知Rt△ABC的直角边AC的长为2，以AC为直径的⊙O与斜边AB交于点D，过D点作⊙O的切线（1）求证：BE＝DE；（2）延长DE与AC的延长线交于点F，若DF＝，求△ABC的面积；（3）从图1中，显然可知BC＜AC．试分别讨论在其它条件不变，当BC＝AC（图2）和BC＞AC（图3）时，直线DE与直线AC还会相交吗？若不能相交，请简要说明理由；若能相交，设交点为F'且DF'＝，请再求出△ABC的面积．19．已知：如图，PF是⊙O的切线，PE＝PF，A是⊙O上一点，直线AE、AP分别交⊙O 于B、D，直线DE交⊙O于C，连接BC，（1）求证：PE∥BC；（2）将PE绕点P顺时针旋转，使点E移到圆内，并在⊙O上另选一点A，如图2．其他条件不变，在图2中画出完整的图形．此时PE与BC是否仍然平行？证明你的结论．20．如图PAB、PCD是⊙O的两条割线，AB是⊙O的直径．（1）如图甲，若PA＝8，PC＝10，CD＝6．①求sin∠APC的值；②sin∠BOD＝；（2）如图乙，若AC∥OD．①求证：CD＝BD；②若，试求cos∠BAD的值．参考答案一．选择题1．解：∵PB＝BC＝3，∴PC＝6，∵PA2＝PB•PC＝18，∴PA＝3，故选：C．2．解：设PB＝x，则PC＝3x，∵PA2＝PB•PC，PA＝2，BC＝2PB，∴x•3x＝12，∴x＝2．故选：A．3．解：由于PAB、PCD都是⊙O的割线，根据切割线定理可得：PA•PB＝PC•PD，即PA•（PA+PB）＝PC•PD，∵PA＝6，AB＝4，PC＝5，∴PD＝12，即CD＝PD﹣PC＝7；故选：C．4．解：延长PO交圆于D；设PB＝BC＝x，∵PB•PC＝PA•PD，PB＝BC，OA＝7，PA＝4，∴x•2x＝72，∴x＝6．故选：C．5．解：∵PA切⊙O于点A，PBC是⊙O的割线，∴PA2＝PB•PC＝16，即PA＝4；故选：B．6．解：连接CE；∵，∴∠BAE＝∠EBC+∠BEC；∵∠DCB＝∠DCE+∠BCE，由弦切角定理知：∠DCE＝∠EBC，由平行四边形的性质知：∠DCB＝∠BAE，∴∠BEC＝∠BCE，即BC＝BE＝5，∴AD＝5；由切割线定理知：DE＝DC2÷DA＝，故选：D．7．解：过点A作圆的切线AD，切点是D，∵AD2＝AX•AY，AX•AY＝4，∴AD＝2，∴圆环的面积＝πAD2＝4π．故选：C．8．解：∵PB，PD是⊙O的割线，∴PA•PB＝PC•PD，∵PA＝2，PC＝CD＝3，∴2PB＝3×6解得：PB＝9．故选：D．9．解：如图，若，且AB＝10，∴AD＝4，BD＝6，作AB关于直线BC的对称线段A′B，交半圆于D′，连接AC、CA′，可得A、C、A′三点共线，∵线段A′B与线段AB关于直线BC对称，∴AB＝A′B，∴AC＝A′C，AD＝A′D′＝4，A′B＝AB＝10．而A′C•A′A＝A′D′•A′B，即A′C•2A′C＝4×10＝40．则A′C2＝20，又∵A′C2＝A′B2﹣CB2，∴20＝100﹣CB2，∴CB＝4．故选：A．10．解：连接OA，OP∵PA，PB是⊙O的切线，∠APB＝60°，∴∠OPA＝∠APB＝30°，OA⊥OP，∴OP＝＝＝，∴点P与O间的距离是．故选：B．二．填空题（共5小题）11．解：连接OQ交AB于M，则OQ⊥AB，连接OA，则OA⊥AQ．∵∠QMP＝∠QSP＝90°，∴S，P，Q，M四点共圆，故OS•OP＝OM•OQ．又∵OM•OQ＝OA2＝2，∴OS•OP＝2．故答案为：2．12．解：∵四边形ABCD是圆内接四边形∴∠PAD＝∠C，∠PAD＝∠B∴△PAD∽△PCB根据相似三角形的对应边的比相等，得到②③是正确的．13．解：∵PA•PB＝PC•PD，PA＝PC，PB＝3cm∴PB＝PD＝3cm．14．解：∵PA•PB＝PC•PD，PA＝2，PB＝5，PD＝8∴PC＝＝．15．解：∵∠PAC＝90°，∠ABC＝90°，∴90°﹣∠AFP＝90°﹣∠BEP，∴∠APF＝∠CPF，∴PF平分∠APC．三．解答题（共5小题）16．解：如图，由切割线定理，得CD2＝CB•CA，（2分）CD2＝CB（AB+CB），CB2+2CB﹣4＝0，解得CB＝（负数舍去）连接OD，则OD⊥CD，又EB与⊙O相切，∴EB⊥OC，∴Rt△ODC∽Rt△EBC，（6分）于是，即∴CE＝．17．（1）解：∵AB为直径，BD⊥CD∴∠ABC+∠A＝90°，∠CBD+∠BCD＝90°∵CD为⊙O切线∴∠BCD＝∠A∴∠ABC＝∠BCD∵CD⊥BD，CE⊥BE∴CE＝CD∴CE＝＝6∴CD＝6（2）证明：∵CD为切线，BD为割线∴CD2＝DF•DB①∵∠ACB＝90°，CE⊥AB∴RT△ACE∽RT△CBE∴CE2＝EA•EB②∵EG•EF＝EA•EB③由①②③及CD＝CE得DF•DB＝EG•EF．18．（1）证明：连接OD，∴OD⊥DE，∴∠ADO+∠BDE＝90°，∵OA＝OD，∴∠A＝∠ADO，∵∠ACB＝90°，∴∠B+∠A＝90°，∴∠B＝∠BDE，∴BE＝DE；（2）解：在直角三角形ODF中，OD＝1，DF＝，∴∠OFD＝30°，∴OF＝2，AF＝3．∴tan∠A＝，∴BC＝AC•tan∠A＝2×tan30°＝．S△ABC＝AC•BC＝×2×＝；（3）解：如图，当BC＝AC时，直线DE与直线AC平行；当BC＞AC时，在直角三角形ODF′中，OD＝1，DF′＝，∴∠OF′D＝30°，∴OF′＝2，AF＝1，∴CF′＝3，∠BAC＝60°，∴tan∠BAC＝，∴BC＝AC•tan∠BAC＝2×tan60°＝2．S△ABC＝AC•BC＝×2×2＝2．19．（1）证明：∵PF与⊙O相切，∴PF2＝PD•PA．∵PE＝PF，∴PE2＝PD•PA．∴PE：PD＝PA：PE．∵∠APE＝∠APE，∴△EPD∽△APE．∴∠PED＝∠A．∵∠ECB＝∠A，∴∠PED＝∠ECB．∴PE∥BC．（2）解：PE与BC仍然平行．证明：画图如图，∵△EPD∽△APE，∴∠PEA＝∠D．∵∠B＝∠D，∴∠PEA＝∠B．∴PE∥BC．20．解：（1）作OE⊥CD于E，连接OC，作DF⊥PB于F．①根据垂径定理，得CE＝3．设圆的半径是r．根据勾股定理，得OP2﹣PE2＝OC2﹣CE2，（8+r）2﹣169＝r2﹣9，解得r＝6．则OE＝3．则sin∠APC＝＝；②设OF＝x．根据勾股定理，得PD2﹣PF2＝OD2﹣OF2，256﹣（14+x）2＝36﹣x2，解得x＝．所以DF＝．所以sin∠BOD＝＝＝．（2）①∵AC∥OD，∴∠1＝∠2．又OA＝OD，∴∠2＝∠3．∴∠1＝∠3．所以弧CD＝弧BD，所以CD＝BD；②∵AC∥OD，∴＝．又CD＝BD，AB＝2OA，∴＝．∴cos∠BAD＝＝．。