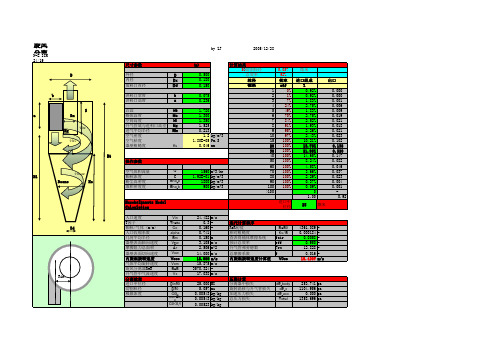
旋风分离器计算程序--Muschelknautz模型方法
旋风分离器计算程序
备注
6A.1示例中的计算值,HOFFMAN等2001年的实验数据,使用时将此 SHEET整体COPY成一个副本,进行计算
尺寸参数
(m)
计算结果
50切割粒径
8.07
微米
D
外径
D
0.075
总效率
26%
内径
Dx
0.030
粒径
效率 进口组成
出口
放料口直径
Dd
0.060
微米
eff
%
1
0%
13.50%
Vin Theta
Co alpha Rm Vzw
Ar Vow Vocs Vom ReR Vx
53.333 m/s 0.533333333 -
0.004 0.576 0.024 m 13.588 m/s 0.029 m^2 67.86 m/s 18.53 m/s 35.46 m/s 5695.8 56.62 m/s
Din50 D50 CC0>0=L0. C0<10.1
8.000 MU 8.07 mu
0.00578 kg/kg 0.01541 kg/kg 0.00578 kg/kg
迭代计算程序 相对粗糙度 插值得桶体摩擦系数 预计总效率 升气管弗劳德数 总摩擦系数
Ks/R fair eff Frx f
内旋涡旋转速度计算值 #NAME? #NAME?
0.000
b
进料口宽度
b
0.020
2
0%
16.50%
0.000
进料口高度
a
0.038
3
1%
14.00%
0.001
4
3%
9.00%
旋风分离器计算结果
旋风除尘器性能的模拟计算一、下图为旋风除尘器几何形状及尺寸，如图1所示，图中D、L及入口截面的长宽比在数值模拟中将进行变化与调整，其余参数保持不变。
图1 旋风分离器几何形状及尺寸（正视图）旋风分离器的空间视图如图2所示。
图2 旋风分离器空间视图二、旋风分离器数值仿真中的网格划分仿真计算时，首先对旋风除尘器进行网格划分处理，计算网格采用非结构化正交网格，如图3所示。
图3 数值仿真时旋风分离器的网格划分（空间）图4为从空间不同角度所观测到的旋风分离器空间网格。
图4 旋风分离器空间网格空间视图本数值仿真生成的非结构化空间网格数大约为125万，当几何尺寸（如D、L及长宽比）改变时，网格数会略有变化。
三、对旋风分离器的数值模拟仿真采用混合模型，应用Eulerian（欧拉）模型，欧拉方法，对每种工况条件下进行旋风分离器流场与浓度场的计算，计算残差<10-5，每种工况迭代约50000步，采用惠普工作站计算，CPU耗时约12h。
以下是计算结果的后处理显示结果。
由于计算算例较多，此处仅列出了两种工况条件下的计算后处理结果。
图5是L=1.3m，D=1.05m 入口长宽比1:3，入口速度10m/s时，在y=0截面（旋风分离器中心截面）上粒径为88微米烟尘的体积百分数含量分布图。
可以明显看出由于旋风除尘器的离心作用，灰尘被甩到外壁附近，而在靠近中心排烟筒下方筒壁四周，烟尘的体积浓度最大。
粒径88微米烟尘的空间浓度分布(空间)粒径88微米烟尘的浓度分布(旋风分离器中心截面)粒径200微米烟尘的空间浓度分布(空间)图5 L=1.3m、D=1.05m、长宽比1:3，入口速度10m/s时烟尘空间分布粒径88微米烟尘的空间浓度分布(空间)粒径88微米烟尘的浓度分布(旋风分离器中心截面)粒径200微米烟尘的空间浓度分布(空间)图6 L=2.3m、D=1.5m、长宽比1:1，入口速度15m/s时烟尘空间分布四、计算结果计算中，首先确定几何尺寸L，按照给定的两种烟尘颗粒，分别对L=2.3m、L=1.8m、L=1.3m、L=0.8m四种情况进行对比计算，对比计算结果为L=2.3m、L=1.3m时除尘效率较高。
旋风分离器计算程序--Muschelknautz模型方法
0.00543 kg/kg 0.00543 kg/kg 0.00523 kg/kg
迭代计算程序 ReR初值 相对粗糙度 查表得桶体摩擦系统 预计总效率 升气管弗劳德数 总摩擦系数 内旋涡旋转速度计算值
ReR0 Ks/R
fair eff Frx f
V0cs
压降计算 分离器中损失 旋转涡核与升气管损失 加速压力损失 总压力损失
Vin Theta
Co alpha Rm Vzw
Ar Vow Vocs Vom ReR Vx
Din50 D50 CC0>0=L0. C0<10.1
24.482 m/s 0.3 -
0.160 0.741 0.150 m 3.105 m/s 2.506 m^2 14.000 m/s 18.000 m/s 15.875 m/s 3570.324 17.038 m/s
Rho_p
1800 kg/m^3
90 100%
0.37%
0.004
堆积密度度
Rho_b
900 kg/m^3
100 100%
0.09%
0.001
>100
0
-
1.00
0.92
Muschelknautz Modeld Rin
入口速度 T因子 颗粒/气体 (m/m) 入口收缩系数 几何平均半径 器壁表面轴向速度 摩擦阻力总面积 器壁表面切向速度 内旋涡旋转速度 气体平均旋转速度 旋风分离器ReR 升气管中气流速度 分离效率 进口中位径 切割粒径 极限浓度
40 100%
14.65%
0.147
操作参数
50 100%
8.24%
0.082
旋风分离器数值模拟
精选课件
6
3 计算：模型选择
采用稳态，压力基求解器，不考虑重力。湍流模型采用k-epsilon(2 epn) 模型，激活Swirl Dominated Flow（强旋流）。离散相采用DPM模型。颗粒采 用煤粉，颗粒粒径为1um，密度为1000kg/m3
为何不采用Reynolds Stress模型？
精选课件
12
谢 谢！
精选课件
13
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
从其速度矢量图可以看出， 两侧的速度主要为周向速度，排 气管的速度主要为轴向速度，而 且速度逐渐减小，与已知相符。
精选课件
11
4 后处理
创建z=645截面的压力云图和速度矢量
从压力云图可以看出进口截面中间有个明显的低压区，其速度矢量图可 以明显的看出造旋运动，且中间区域有明显的空白，即周向速度分量很小。
由于旋风分离器内部流动非常复杂，用 试验或者解析的方法研究分离器内部的流动 状况比较困难。近年来，随着计算机硬件 CFD(计算流体动力学)技术的不断进步，数值 方法成为研究旋风分离器的一种重要手段。 通过对旋风分离器内气固两相进行数值模拟， 揭示旋风分离器内部流场，为优化旋风分离 器的结构提供思路，也为进一步提高分离性 能奠定基础。
因为旋风分离器内部流场是旋流占优， 所以采用Swirl Dominated Flow，不采用 Reynolds Stress模型是因为三维雷诺应力模 型需要求解七个方程，计算量大。
精选课件
7
3 计算：设置参数并求解
入口速度为30m/s，湍流强度为10%，水力直径为0.0543m。迭代3000， 并以出口质量流量判断其收敛与否。
超音速旋流分离器喷管的数值模拟-外文翻译
本科毕业设计（论文）外文翻译译文学生姓名：高勇红院（系）：机械工程学院专业班级：装备 0901指导教师：梁慧荣完成日期： 2013 年 3 月 21 日气—固旋风分离器在FLUENT中的流场数值模拟Flow-field Numerical Simulation of Gas-Solid CycloneSeparator based on FLUENT作者：DENG Qing-fang，Dongyi Zhou，SHEN Ai-ling起止页码：P740-P743出版日期（期刊号）：2010 IEEE DOI 10.1109/ICDMA.2010.88出版单位：2010 International Conference on Digital Manufacturing & Automation摘要：在本文中，利用fluent软件研究旋风分离器在各种条件下的气固两相流场，压力变化，速度变化和涡流特性。
研究结果表明，在旋流器中沿Y轴方向（切向速度）的速度和沿Z轴方向（轴向速度）的速度是主要因素；在旋风分离器中静压，每个方向的速度以及固体颗粒的分离率随着气体处理量的增加而增加；静态压力在旋风分离器的中心是最低的，固体颗粒被集中在内壁的中间段；气流的速度在各个方向上随着颗粒密度的增加而减少。
然而，旋风分离器因为颗粒度的增加而加剧管壁的磨损。
因此由经验可以推断出旋流器分离器在v=18 m/s，粉尘含量值为1％是被公认的计算结果。
关键词：fluent；数学模型；旋风分离器；数值模拟1 引言旋流分离器在除尘器和离心除尘设备之间是使用最广泛和最具代表性的设备，并且在水泥生产中有效地提高了粉尘的回收率，扮演了重要的角色。
典型的旋风分离器结构一般由进料口，圆柱段，圆锥段，溢流口和底流口组成。
在分离器内气流与颗粒沿切线方向从进气口进入分离器，旋转以及向下流动。
在离心力的作用下，固体颗粒被甩向筒壁并沿着椎体部分往下流动积累，同时气体旋流向上从出口管流出。
旋风分离器计算结果
旋风分离器计算结果标准化工作室编码[XX968T-XX89628-XJ668-XT689N]旋风除尘器性能的模拟计算一、下图为旋风除尘器几何形状及尺寸，如图1所示，图中D、L及入口截面的长宽比在数值模拟中将进行变化与调整，其余参数保持不变。
图1 旋风分离器几何形状及尺寸（正视图）旋风分离器的空间视图如图2所示。
图2 旋风分离器空间视图二、旋风分离器数值仿真中的网格划分仿真计算时，首先对旋风除尘器进行网格划分处理，计算网格采用非结构化正交网格，如图3所示。
图3 数值仿真时旋风分离器的网格划分（空间）图4为从空间不同角度所观测到的旋风分离器空间网格。
图4 旋风分离器空间网格空间视图本数值仿真生成的非结构化空间网格数大约为125万，当几何尺寸（如D、L及长宽比）改变时，网格数会略有变化。
三、对旋风分离器的数值模拟仿真采用混合模型，应用Eulerian（欧拉）模型，欧拉方法，对每种工况条件下进行旋风分离器流场与浓度场的计算，计算残差<10-5，每种工况迭代约50000步，采用惠普工作站计算，CPU耗时约12h。
以下是计算结果的后处理显示结果。
由于计算算例较多，此处仅列出了两种工况条件下的计算后处理结果。
图5是L=1.3m，D=1.05m 入口长宽比1:3，入口速度10m/s时，在y=0截面（旋风分离器中心截面）上粒径为88微米烟尘的体积百分数含量分布图。
可以明显看出由于旋风除尘器的离心作用，灰尘被甩到外壁附近，而在靠近中心排烟筒下方筒壁四周，烟尘的体积浓度最大。
粒径88微米烟尘的空间浓度分布(空间)粒径88微米烟尘的浓度分布(旋风分离器中心截面)粒径200微米烟尘的空间浓度分布(空间)粒径200微米烟尘的浓度分布(旋风分离器中心截面)图5 L=1.3m、D=1.05m、长宽比1:3，入口速度10m/s时烟尘空间分布粒径88微米烟尘的空间浓度分布(空间)粒径88微米烟尘的浓度分布(旋风分离器中心截面)粒径200微米烟尘的空间浓度分布(空间)粒径200微米烟尘的浓度分布(旋风分离器中心截面)图6 L=2.3m、D=1.5m、长宽比1:1，入口速度15m/s时烟尘空间分布四、计算结果计算中，首先确定几何尺寸L，按照给定的两种烟尘颗粒，分别对L=2.3m、L=1.8m、L=1.3m、L=0.8m四种情况进行对比计算，对比计算结果为L=2.3m、L=1.3m时除尘效率较高。
蜗壳式旋风分离器的原理与设计说明书
蜗壳式旋风分离器的原理与设计l0余热锅炉2007.4蜗壳式旋风分离器的原理与设计杭州锅炉集团股份有限公司王天春徐亦芳 1前言循环流化床锅炉的分离机构是循环流化床锅炉的关键部件之一,其主要作用是将大量高温,高浓度固体物料从气流中分离出来,送回燃烧室,以维持燃烧室一定的颗粒浓度,保持良好的流态化状态,保证燃料和脱硫剂在多次循环,反复燃烧和反应后使锅炉达到理想的燃烧效率和脱硫效率.因此, 循环流化床锅炉分离机构的性能,将直接影响整个循环流化床锅炉的总体设计,系统布置及锅炉运行性能.根据旋风分离器的入口结构类型可以分为:圆形或圆管形入口,矩形入口,"蜗壳式"入口和轴向叶片入口结构.本文重点分析在循环流化床锅炉中常用的"蜗壳式"入口结构.2蜗壳式旋风分离器的工作原理蜗壳式旋风分离器是一种利用离心力把固体颗粒从含尘气体中分离出来的静止机械设备.入口含尘颗粒气体沿顶部切向进入蜗壳式分离器后,在离心力的作用下,在分离器的边壁沿轴向作贴壁旋转向下运动,这时气体中的大于切割直径的颗粒被分离出来, 从旋风分离器下部的排灰口排出.在分离器锥体段,迫使净化后的气流缓慢进入分离器内部区域,在锥体中心沿轴向逆流向上运动,由分离器顶部的排气管排出.通常将分离器的流型分为"双旋蜗",即轴向向下外旋涡和轴向向上运动的内旋涡.这种分离器具有结构简单,无运动部件,分离效率高和压降适中等优点,常作为燃煤发电中循环流化床锅炉气固分离部件.图l蜗壳式旋风分离器示意图蜗壳式旋风分离器的几何尺寸皆被视为分离器的内部尺寸,指与气流接触面的尺寸.包括以下九个(见图1):a)旋风分离器本体直径(指分离器简体截面的直径),D;b)旋风分离器蜗壳偏心距离,; c)旋风分离器总高(从分离器顶板到排灰口),H;d)升气管直径,D;e)升气管插入深度(从分离器空间顶板算起),s;余热锅炉2007.4f)入口截面的高度和宽度,分别为a和 b;g)锥体段高度,H;h)排灰口直径,Dd;2.1旋风分离器中的气体流动图2为一种标准的切流式筒锥形逆流旋风分离器的示意图,图中显示了其内部的流态状况.气体切向进入分离器后在分离器内部空间产生旋流运动.在旋流的外部(外旋升气管涡),气体向下运动,并在中心处向上运动 (内旋涡).旋风分离器外部区域气体的向下运动是至关重要的.因为,依靠气体的向下运动,把所分离到器壁的颗粒带到旋风分离器底部.与此同时,气体还存在一个由外旋涡到内旋涡的径向流动,这个径向流动在升气管下面的分离器沿高度方向的分布并不均匀.轴向速度切向速度/图2切向旋风分离器及其内部流态示意图图2的右侧给出了气流的轴向速度和切向速度沿径向位置的分布图.轴向速度图表明气体在外部区域沿轴向向下运动.切向速度图表明气体在内部区域沿轴向向上运动. 轴向速度在中t2,线附近常常存在一个滞留区域,有时甚至出现气体轴向速度是向下的. 切向速度分布类似于兰金涡:外部的准自由涡(无摩擦流体的旋转运动,其涡流运动中的切向速度使得流体微元在所有径向位置上的动量矩相同)和内部的准强制涡(涡流内各点有相同的旋转角速度,就像刚体旋转一样).对于径向速度沿径向的分布规律,我们面面知道并不太多.一般来说,径向速度要比切向速度小得多,且很难精确测定.但升气管下口以下的径向速度通常是由外向内,但沿高度方向的分布是不均匀的.而且,升气管下口附近的向心径向速度最大,这与气体的二次流动有关.旋风分离器凹壁附近的旋流本身是不稳定的流动,因此旋流运动引起的压力梯度将造成旋风分离器内壁产生"二次流".静态压力沿旋流的外部区域是增加的.从顶板一直到下部的锥体整个壁面的边界层内部都存在压力梯度.另一方面,由于该边界层内的切向速度较低,其结果是在器壁附近区域的12余热锅炉2007.4气团存在向心的合力,于是沿旋风分离器顶板到锥体壁面出现图3所示的内流动.因此,这个向心的合力,是由器壁和气团之间的摩擦阻力来平衡.在顶板附近流动的气体沿升气管外壁向下流动.这就造成了升气管下口末端的径向速度增加,这常称为"升气管末端短路流", AiQ约占整个气团的10%.随着升气管的长度变短,比例还会提高.实验研究表明,除了以上边界层的二次流动外,在旋风分离器的涡核处还存在类似"面包卷"形状的二次流态.这种流态会使颗粒在旋风分离器内做循环运动.图3旋风分离器内气体运动三维示意图 Linden最早通过实验测量了旋风分离器内气体运动时的三维速度,即切向,径向和轴向速度.(1)切向速度切向速度对于粉尘颗粒的捕集与分离起着主导作用.含尘气体在切向速度的作用下,使尘粒由里向外离心沉降.排气管以下任一区域段上切向速度沿半径的变化规律可分为三个区域,靠近旋风分离器壁面为工区,切向速度Vow为常数,通常称为自由旋流区.图3所示分离器中,…一一一V.win:=一Ain一ab式中,Q是进入旋风分离器的流量;其余参数见图3所示.矩形入口旋风分离器的入口收缩系数 a:—一{一?+【(—{一)一—{一]/)t—)-一.一0.5D—R'c是旋风分离器入口气固两相流中的颗粒质量与气体质量的比值.在旋风分离器中心到"最大切向速度面",即排气管下部的中心区域,通常称为强制旋流区(?区).它类似刚体旋转运动, 其切向速度与旋转半径r之比为一常数, 即v0esr,=常数,此常数为角速度co.余热锅炉2007.4l3计算内旋涡半径Rcs处的气体切向速度, 其表达式为:(R/R)一式中,AR为有摩擦力存在的旋风分离器内部总面积,它包括顶板,简体和锥体表面以及升气管的外表面.AR=AD0f+Ab.1+Ac.+k :?【R2一畦+2II(H—Hc)+(R+lid)?曜+(R—lid)+2RxsJ是气体的几何平均旋转速度,它取决于近壁处的旋转速度和内旋涡的旋转速度V0cs.Muschelknautzt和Trefz定义旋风分离器雷诺数为:RiRiVp式中,p和分别表示气体的密度和绝对粘度;V0m是气体的几何平均旋转速度,=?vewv.c8,在大多数度情况下,式中 (v/v8rn)项是小于l的量,可以省略.这对于ReR值远远大于2000的工业用旋风分离器而言是可行的.在工区与?区之间气体的旋转则表现为另一种性质.通常称为半自由旋流区(II 区),其切向速度分布规律为v.rn=常数. 无损失时指数n为l,而刚体转动指数n为一l.在II区由于气体与器壁之间的摩擦产生一定的损失,在低浓度和光滑的器壁测得 n介于0.5,0.8之间,但在循环流化床锅炉的高浓度下并非如此.Mexander给出n的经验公式:,个,0.3n=l一(1一o.67D~?H)?{l,0, 式中,旋风分离器直径D的单位为m; 温度T为热力学温度,单位为K;T0为室内温度,283K.由于没有考虑器壁摩擦与入口浓度对旋流强度的影响,公式计算的n值偏低,影响 n值的因素是很复杂的.n与Re有关,Re 越大n值越趋近于l.最大切向速度面的位置,即强制旋流的半径主要取决于排灰管下口半径.经实验证明,与实际测定结果接近.(2)径向速度径向速度远远小于切向与轴向速度,大部分是向心的,只在中心涡核才有小部分的向外的径向速度.CS柱面是位于升气管下面,直径等于升气管的直径,长度止于分离器内表面的一个柱体.假设忽略器壁附近的径向速度,同时假设在CS柱面上的径向速度是均匀分布的,则有:llnJv(R)J;VrCS=式中,D是升气管的直径,也是CS柱面的直径;Hc.是CS柱面的高度;v(Rx) 是CS柱面的平均径向速度,绝对值为vrCs. 实际流动中,径向速度沿CS不是均匀分布的,分布十分复杂且不易测量.在升气管下口附近有一个径向向内的"短气流". 一部分气体在高度为Hc.,直径为D的假想简体上部区域短路进入升气管.这种现象是导致分级效率呈现非理想s形曲线分布的原因之一.柳绮年认为旋风分离器的径向气流速度分布是非轴对称的,尤其是锥体下部, 自然旋风长停止点处,靠近排灰口附近,有较明显的"偏流".此外,径向速度也不是均匀的,尤其在排气管下口附近,径向向心速度很大,有时甚至高达5,10m/s,出现 "短路"现象.这个气流会把颗粒拽到中心向上流动,很快进入排气管,对分离不利. (3)轴向速度轴向速度的分布也很复杂.在分离空间内,一般可将气流分为外侧下行流和内侧上行流两个区域.上下流的分界点与分离器的形状有关.在圆筒体部分,此分界面近似呈14余热锅炉2007.4圆柱形,其半径一般要稍大于排气管的半径.外侧下行流的流量沿轴向向下逐渐变小,约有15%,40%会进入排灰口.大部分气体是径向通过轴心逐渐变成向上的内旋涡流.在排灰口附近,分离出颗粒的气体还会通过中心返回旋风分离器.被分离下来的颗粒还会带回分离器,这也对分离不利.外侧向下的轴向速度一般总是大于颗粒的终端沉降速度,所以旋风分离器不是垂直放置也可以JI颐币0}jF灰.器壁表面的轴向速度Vzw::,R:,~/-R-xxR一丁亡(R—R2m)'一2.2旋风分离器中的颗粒流动循环流化床锅炉进入旋风分离器的颗粒浓度一般很高.当入口浓度co大于极限入口浓度c0L时,进入分离空间的颗粒超出极限浓度部分在进入旋风分离器时立即被甩到器壁上,以沉降的方式下行;而气体携带的那部分颗粒受到方向向内的阻力和方向向外的离心力作用,将在内旋涡流动中按照其粒径分布进行离心分离.因此,可以将旋风分离器的分离过程划分为沉降分离和离心分离两个过程的串联.coL=0.025《)?(10co)式中,X50为切割点粒径;Xmed为颗粒的质量平均粒径;当co?1时,k=0.15;当co <1时,k=一0.11,0.101nco 颗粒进入旋风分离器后,一部分被捕集,其余逃逸.进入,捕集和逃逸分别用符号M,,M和M.来表示它们的质量.旋风分离器中的颗粒质量平衡关系为:Mf=M.+M.总的分离效率可简单用旋风分离器捕集的颗粒质量与进入颗粒质量的比值来计算:M.,M.M.17瓦叫一一Mf—Me+—Me在工业过程中,总分离效率通常是一个最常用的评价指标.但是,对表征某个具体的旋风分离器本身性能而言,这个指标并不全面.因为它不仅取决于旋风分离器本身, 而且还取决于颗粒的粒径及密度.用分级效率更能全面反映旋风分离器的分离效果. 旋风分离器的分离性能最好用所谓的分级效率曲线(GEC)来表征,它是指在给定粒径或粒径范围的分离效率.对于进入,捕集及逃逸的粉料来说,如果相应的体积或质量密度分布分别是ff(X),fc(X)和fe(X), 则颗粒之间的颗粒质量平衡如下: ff(x)dx=1fc(x)d+(1—1)fe(x)fd =崛(x)=1(x)+(1—1)dF(x)因此,对于小于给定粒径的粉料,通过对上式逐项积分便得到其质量平衡方程: Ff(x)=(x)+(1—17)Fe(x)分级效率定义为,粒径在x—1dx和x +1dx间,被旋风分离器捕集的颗粒与进入颗粒的比值:M.fc(X)dx17利用上面的方程可得:,,(x)1717=1一(1_17)_l_(1-17)如果旋风分离器的分离是一个理想化的陡降切割,则在"临界"或"切割"粒径处的分级效率曲线是一条垂直线.在实际中得到的是一条光滑的s形的分离效率曲线(见图4).切割粒径或x50切割点(常指"dS0 切割粒径")被认为是分离效率等于0.5时的颗粒粒径.余热锅炉2007.4'150550X图4典型的呈S形的分级效率曲线示意图 X50粒径非常类似于普通纱网或筛子的筛孔.所有粒径大于X50的来料将被捕集或都被"截留"下来,而所有粒径小于X50的颗粒都不会被捕集.实际上,筛子本身也呈现某种非理想分离现象,对颗粒粒径不是一个理想化的陡降切割.分级效率曲线在切割粒径附近的陡降度反映了旋风分离器"切割锐度".用分级效率曲线在X50的斜率来表示.颗粒的雷诺数::式中,U啪是圆柱面CS上的切割粒径颗粒的终端速度U,啪-v赢如果ReD约小于O.5,则应用斯托克斯定律计算切割粒径:xso=5.18【RJ上式是在半径为Rx处利用一个简单的, 稳定状态下颗粒阻力与离心力的平衡关系式而得到的.这种情况下,阻力系数的经验公式:,当o.3<Rep<100oc.:当计算的颗粒粒径在斯托克斯范围内时,根据Barth(1956)模型,在圆柱面CS 上,旋转的颗粒所受到的作用力有:向外的离心力pp()和向内的斯托克斯阻力 3碌.在离心力的计算中,气体的密度与颗粒的密度相比可忽略.建立离心力和阻力的平衡方程,Barth关于旋风分离器切割粒径的着名表达式的修正式为: 厂——而一Xso一般在O.9—1.4的范围内.Muschelknautz和Trefz认为大约入口气量的 10%走旋风分离器的短环路,这部分气量沿着旋风分离器的顶板和升气管的外壁以螺旋方式进入升气管而排出.这部分气量一般占入口气量Q的4%16%,平均值是10%, 其余约90%的入口气量Q沿器壁内流动并由外旋涡进入内旋涡.确定切割粒径后,则用Dirgo和Leith (1985)函数来拟合分级效率这个曲线(参见Overcamp和Mantha,1998)有: 1(x)=—ITI常取6.4.()首先按照颗粒粒径分布划分为N个粒度级的质量组分,每个质量组分之和构成了全部颗粒质量;然后用每个质量百分数乘以该组分平均粒径下的捕集效率(分级效率), 分级效率是从分级效率曲线计算而得的.所有N个粒度级组分的总和就得到总效率. 其表达式为:=?r/i?zhMFi,式中,zhMFi是第i个组分的质量百分数.此时旋风分离器的总效率为:r/=(?一)+()i姗;式中,zhMFi是第i组分的质量百分数; r/i是第i粒度级组分的捕集效率. 2.3旋风分离器中的压降在旋风分离器中,当忽略流体摩擦时,16余热锅炉2007.4根据伯努利方程,流场中的静态压力和动态压力是可以转换的.在速度高的地方,静态压力低.反之,在速度低的地方,静态压力高.在实际流动中,由于摩擦的影响,机械能量的摩擦耗散损失将造成伯努利三项式之和沿流动方向减少.根据Muschelknautz模型,旋风分离器 "压降"指的是包括静压和动压之和的降低. 压降分为三部分:进口损失,旋风分离器本体分离空间的损失和升气管内的损失. 在旋风分离器进入通道内气固两相混合物必须从外部的低速区加速运动后,再进入旋风分离器本体中.假定在颗粒和气体之间的"滑移"速度忽略不计,则加速区的损失为::(1+c0)式中,(1+co)p是从加速区vl加速到 v2的气固混合物的密度.旋风分离器本体中的能量损失比较高, 主要是气固两相与器壁摩擦损失和旋风分离器的内部旋转损失造成的.壁面的摩擦损失越大,导致旋流强度越弱.在高含尘浓度的初级旋风分离器中,壁面摩擦阻力引起的壁面能量损失占总压力降的重要部分.气固两相与器壁摩擦损失,即旋风分离器中的损失表示为: ^DfARtO(VOwVOc8)y一2×O.9Q旋转涡核在升气管中的损失:Px:了]如因此,旋风分离器总压力损失是人口加速损失,器壁摩擦损失和旋转涡核在升气管中损失的总和:?P=?Pa+?Pbod+?PMuschelknautz基于实验给出摩擦系数f 的表达式,分为两部分,一部分是纯气流的旋风分离器摩擦系数fair;另外一部分是考虑了粉料影响的摩擦系数fd.总摩擦系数的表达式变为:f=+fdt+o.(是~//t%rp项表示器壁上流动颗粒灰带的堆积密度或器壁上流动颗粒层的堆积密度,它约等于O.3一O.5pbLI1k.k是颗粒静止状态下堆积密度.在缺乏资料时,可以设定p出 =O.4p.为弗劳得数,其表达式为:=—VI,vx是升气管进口气体的表观轴向进口速度.3标准切流式蜗壳,筒锥型旋风分离器设计要点循环流化床锅炉的分离机构必须满足下列几个要求:?能够在高温情况下正常连续工作;?能够满足极高浓度载粒气流的分离,因为进入分离装置的固体颗粒含量可达 550kg/m3;?具有低阻性,因为分离装置的阻力增大势必要提高风机的压头,增加能耗;?具有较高的分离效率,实际循环倍率在很大程度上是靠分离器的效率来保证的; ?能够与锅炉设计的流程相适应,使锅炉结构紧凑,易于设计.我们在设计循环流化床锅炉的旋风分离器时,不但要考虑含固体烟气的温度高,流量大及浓度高的特点,而且其结构还受锅炉柱子距离的限制,不能无限制加大旋风分离器的直径.所以蜗壳式旋风分离器是目前工业应用中常选择的型式.(1)人口设计旋风分离器的切向人口结构有矩形人口和圆管人口两种.由于圆管人口要过渡到旋风分离器筒体的矩形人口,设计时需要增加一个像文丘里流量计(收缩角不超过2l.,余热锅炉2007.417扩散角不超过15.)那样的过渡段,而且长度不能太短,否则导致颗粒的结垢及旋风分离器人口局部区域的冲蚀磨损加剧.所以常选用横截面是矩形的流通人口.这种矩形人口可以与旋风分离器筒体的外壁平齐地结合成一体.如果人口面积相当大或者粉料浓度比较高时,则最好在径向方向增加人口面积.为使人口与旋风分离器本体的外壁光滑地结合在一起,需要逐渐收缩使外半径逐渐过渡到与旋风分离器本体的外径一致,这就是"蜗壳"式人口结构.这种结构又分为圆筒环绕式蜗壳和"对数"螺旋式蜗壳.圆筒环绕式蜗壳分为90~,180.,270.和360~四种,后一种结构制造相对要复杂,所以在循环流化床锅炉中常选用前一种结构中的180. 蜗壳人口结构.这种蜗壳式人口结构紧凑,气流从人口进入到旋风分离器本体内部是一个较平稳的气体动力学过渡过程,同时也对人口高浓度气流中的颗粒提供了一定的预分离空间.在处理大气量时,能避免人口的气流直接冲刷升气管外壁,不但能防止流体流动的湍流扰动和可能产生的冲蚀问题,而且也减小了气流中颗粒对于旋风分离器壁的碰撞,降低了颗粒的反弹和返混.蜗壳式人口结构增大旋风分离器人口半径,导致进入流体的旋转动量增加,旋涡的旋转速度增加,切割粒径减小,同时导致总压力损失的增加.由于受空间和能耗的限制,"蜗壳式" 人口结构不能无限制扩大.由于旋风分离器的磨损与气体速度的四次方成正比,所以工程上设计速度一般在18m/s,26m/s.当处理的颗粒具有高磨损性时,选择过高的人口速度,会急剧增加冲蚀磨损,尤其是对旋风分离器本体或锥体段下部的磨损. (2)旋风分离器长度旋风分离器不能任意长.如果太长,旋涡就会在分离器本体的某一位置结束.这一点称为"自然转折点",或称为旋涡的"端点"或"尾端",而将这一点到分离器升气管末端之间的距离称为自然旋风长(如图5 所示),这一开拓性的工作是由Alexande (1949)来提出的.如果在透明旋风分离器的内壁上存在运动的颗粒,就可以清楚地看到旋涡端部的灰环.直到现在,还不能确定旋涡端点的准确特性.有关文献和旋风分离器研究人员对这一现象解释有以下两种:一是认为旋涡的端部是轴对称的,端部代表一种回流"气泡"运动;另一种观点认为旋涡的端点会附在侧壁上(即旋涡核是弯曲的), 且沿壁面高速旋转(见图5).在液体旋风分离器内,可以很容易观察到这种旋涡旋进现象,而涡核中存在气泡.尽管旋涡可能附在分离器下部壁面和旋转摆动,旋涡并不能在轴向某一点停止,准确地说,应是一个面.该主旋涡会在它的下游诱发一个二次旋涡.这种现象称为流体耦合.Ln图5自然旋风长示意图基于旋涡长度就是有限分离空间长度这一假设,有人会认为自然旋涡长度可以等同旋风分离器的实际长度,实际不全对.实验结果表明当旋涡端点位于筒锥形旋风分离器的锥体段时,有效长度减少引起的分离性能18余热锅炉2007.4下降要比预想的大得多.所以应避免旋涡端部位于锥体上.当旋涡位于分离器的底面时,这个平面的固体颗粒存在明显的返混现象,当然也影响到旋风分离器的切割直径. 除了对分离性能有不利影响外,旋涡端部在旋风分离器内也会引起结垢和堵塞现象,因为固体颗粒在旋涡端部以下位置的运动减弱.当进入旋风分离器内部时,可以确定旋涡端部的位置.如果在壁面,则会发现沿分离器的锥体或简体段出现壁面沉积物, 或抛光环或磨成环形沟槽,当然这与粉料的磨蚀性有关.磨损严重时会损坏旋风分离器的下部.旋涡端部的位置是难以通过模型进行分析确定的.到现在为止,最着名的计算自然旋风长的公式是由Alexander提出的: Lri=2.3Dx()Btitmer(1999)认为上式主要适用于直径很小的旋风分离器.当旋风分离器的直径为几米和整个雷诺数范围内如何确定旋涡末端位置仍然没有解决.旋风分离器长度是如何确定的,现在还不能给出一个一般性的回答.各个厂家选择也不一样.旋风分离器长度的选择是在可靠性(旋涡不应该在器壁上终止)和分离性能之间的一个折衷.在其他情况相同时,增加旋风分离器长度将能逐渐提高分离性能并降低压降.Maclean等人申请的专利(1978),声称使用这个长度的优点是使分离性能更好和磨损更小.旋风分离器最优设计长度为: :一1.09_/~1.X+4.49U^|n式中,Ax和Ai分别是升气管和烟气人口的横截面积.(3)升气管设计在旋风分离器的顶部设有升气管,它是一个简单的空心圆筒体,与外面的旋风分离器简体同心,它的内插长度大约延伸至人口中部左右.其作用是将分离后的"干净"气体从旋风分离器顶部排出,然后排人尾部的竖井烟道中.由于旋风分离器的切割直径和压力损失与升气管的直径密切相关,它常常被称为旋风分离器的核心参数.一般情况下是把升气管的长度延伸到人口的中部位置.这种升气管的优点是升气管短,制造费用较少,重量轻,通过旋风分离器切向人口检查和维修比较方便;由于升气管短,对升气管与旋风分离器顶板连接的焊缝所施加的应力较小;也会使总压力损失稍微减小.但是升气管插入长度是人口高度的一半,或者更小,一部分气固流体将从人口直接进入升气管走"短路",使旋风分离器的分离性能下降.反之,如果把升气管延伸到人口底板,关于费用,重量,检查的容易性,应力,压力损失和"短路"等一系列问题将产生与上述刚好相反的结果.由于绕升气管的流动气体将对升气管产生冲击,并引起升气管的侧向振动.在升气管与旋风分离器顶板连接的圆周部位,这个振动能导致疲劳裂缝.裂缝将造成气体"短路",即直接从旋风分离器顶板排出.如果不及时解决, 则会导致升气管与顶板的完全开裂,并掉人旋风分离器的底部.把升气管设计成下小上大的锥形结构, 可以把净化的气流的一部分旋转能量转换为静压力.基于Muschelknaum—Brunner (1967)提供的数据,采用这种结构,内旋涡压力损失减少15%,20%.(4)旋风分离器的磨损当旋风分离器分离煤,砂,飞灰,焦等磨蚀性颗粒时,磨损是造成非计划性停炉的主要原因之一.所以侵蚀磨损是工厂运行和维修部门最关心的问题.。
旋风分离器的工艺计算
旋风分离器的工艺计算》:*目录一.前言 ............................................................................................................. 错误!未定义书签。
应用范围及特点....................................................................................... 错误!未定义书签。
分离原理................................................................................................... 错误!未定义书签。
分离方法................................................................................................... 错误!未定义书签。
)性能指标 ................................................................................................. 错误!未定义书签。
二.旋风分离器的工艺计算.............................................................................. 错误!未定义书签。
旋风分离器直径的计算........................................................................... 错误!未定义书签。
由已知求出的直径做验算....................................................................... 错误!未定义书签。
旋风分离器旋风长度的分析计算
旋风分离器旋风长度的分析计算高翠芝;孙国刚;董瑞倩【摘要】认为当分离器外旋流中损耗的能量(即外旋流向内旋流传递的总能量)与内旋流旋转能量达到平衡,即内外旋流之间能量的传递达到稳定状态时,旋转气流到达旋涡尾端位置.由此,采用分离器内压降定量表征能量的损耗,推导得到旋风长度的计算公式.考察了排气管直径、入口尺寸、排气管插入深度、入口浓度、分离器长度、排尘口直径等因素对旋风长度的影响.将该公式计算结果与实验测量值进行对比,结果表明,该公式能较好地反映各因素对旋风长度的影响趋势,且数值差别较小.该公式通过旋风分离器能量传递的特性推导,具有明确的物理意义,适用性较强.%It was suggested that when the energy lost in the outer vortex (the overall energy transferred from outer vortex to inner vortex) and the rotation energy of the inner vortex reached equilibrium, the energy transfer between the inner and outer vortex reached a stable, and the vortex end could be obtained. Then, a calculation equation of the vortex length was obtained based on the analysis of the energy lost in the cyclone. The effects of the inlet dimension, vortex finder diameter, vortex finder length, cylinder length, dust outlet diameter, inlet concentration on the vortex length were investigated. In addition, the calculated and the measured vortex lengths were also compared. The results indicated that the equation could predict the effect tendency of the factors to vortex length, and the accuracy was generally satisfactory. The equation obtained through the investigation of the energy transfer possessed certain physics principlewith strong adaptability.【期刊名称】《石油学报（石油加工）》【年(卷),期】2012(028)001【总页数】5页(P94-98)【关键词】旋风分离器;旋风长度;压降【作者】高翠芝;孙国刚;董瑞倩【作者单位】中国石油大学重质油国家重点实验室,北京 102249;中国石油大学重质油国家重点实验室,北京 102249;中国石油大学重质油国家重点实验室,北京102249【正文语种】中文【中图分类】TQ051.8旋风分离器内流场为双涡旋转流动，内旋涡通常会在分离器本体的某一位置结束，称为旋涡“端点”或“尾端”，而排气管下口到旋涡尾端的距离定义为自然旋风长［1］。
旋风分离器的工艺计算
旋风分离器的工艺计算目录一.前言 (3)1.1应用范围及特点 (3)1.2分离原理 (3)1.3分离方法 (4)1.4性能指标 (4)二.旋风分离器的工艺计算 (4)2.1旋风分离器直径的计算 (5)2.2由已知求出的直径做验算 (5)2.2.1计算气体流速 (5)2.2.2计算旋风分离器的压力损失 (5)2.2.3旋风分离器的工作范围 (6)2.3进出气管径计算 (6)三.旋风分离器的性能参数 (6)3.1分离性能 (6)3.1.1临界粒径d pc (7)3.1.2分离效率 (8)3.2旋风分离器的压强降 (8)四.旋风分离器的形状设计 (9)五．入口管道设计 (10)六.尘粒排出设计 (10)七.算例（以天然气作为需要分离气体） (11)7.1工作原理 (11)7.2基本计算公式 (12)7.3算例 (13)八.影响旋风分离器效率的因素 (15)8.1气体进口速度 (15)8.2气液密度差 (15)8.3旋转半径 (15)参考文献 (15)旋风分离器的工艺计算摘要：分离器已经使用十分广泛无论在家庭生活中还是工业生产，而且种类繁多每种都有各自的优缺点。
现阶段旋风分离器运用比较广泛，它的性能的好坏主要决定于旋风分离器性能的强弱。
这篇文章主要是讨论旋风分离器工艺计算。
旋风分离器是利用离心力作用净制气体,主要功能是尽可能除去输送介质气体中携带的固体颗粒杂质和液滴，以达到气固液分离，以保证管道及设备的正常运行。
在本篇文章中，主要是对旋风分离器进行工艺计算。
关键字：旋风分离器、工艺计算一.前言旋风分离器设备的主要功能是尽可能除去输送介质气体中携带的固体颗粒杂质和液滴，达到气固液分离，以保证管道及设备的正常运行。
它是利用旋转气流产生的离心力将尘粒从气流中分离出来。
旋风分离器结构简单，没有转动部分制造方便、分离效率高，并可用于高温含尘气体的分离，而得到广泛运用。
旋风分离器采用立式圆筒结构，内部沿轴向分为集液区、旋风分离区、净化室区等。
第十二讲 旋风分离器的设计和非标设计方法
第十二讲旋风分离器的设计和非标设计方法旋风分离器是对流干燥系统的重要组成部分。
我们对此必须要足够地重视，有一些失败的对流干燥系统，不是干燥器设计不合理，而是旋风分离器设计或选用不合理。
在气流干燥和旋转闪蒸干燥系统中，有80～90%的产品是通过旋风分离器回收的，只有10～20%的产品是通过布袋除尘器回收的。
如果旋风分离器‘失灵’，大量的产品就‘拥挤’到布袋除尘器中，增加布袋除尘器的阻力，造成风机风压不够，以致干燥系统‘瘫痪’。
在喷雾干燥系统中，对于喷雾干燥塔底部作为主要回收产品的系统来说，也有将近30%的产品要通过旋风分离器回收；对于喷雾干燥塔底部不收集产品的系统（如中药浸膏喷雾干燥系统），就有全部或85%以上的产品要通过旋风分离器收集。
对于振动流化床干燥系统和转筒干燥系统也有5～10%的细微颗粒要通过旋风分离器回收。
一、旋风分离器的结构和工作原理：（一）、旋风分离器的结构：一般来说，旋风分离器由进风管，直筒，锥形筒，排灰管，锁风阀和排风管组成(见图1)。
（二）、工作原理：当含尘气流以14～22m/s速度由进风管进入旋风分离器时，气流将由直线运动变为圆周运动。
旋转气流的绝大部分沿直圆筒的内壁呈螺旋形向下，朝锥形筒体运动。
通常称此气流为‘外旋气流’。
含尘气流在旋转过程中产生离心力，将重度大于气体的尘粒甩向筒内壁。
尘粒一旦与筒壁接触，便失去惯性力，而靠入口速度的动量和向下的重力沿壁面下落，进入排灰管。
旋转下降的外旋气流在到达锥体时，因圆锥形的收缩而向除尘器中心靠拢。
根据‘旋转矩’不变原理，其切向速度不断提高。
当气流到达锥体下端某一位置时，即以同样的旋转方向从旋风分离器中部，由下反转而上，继续作螺旋运动，即为‘内旋气流’。
最后净化气体经排风内管排出器外,一部分未被捕获的尘粒也由此随排风排出旋风分离器。
自进气管流入的另一小部分气体，则向旋风分离器顶盖流动，然后沿排气管外侧向下流动。
当到达排气管下端时，即反转向上随上升的中心气流（内旋气流）一同从排气管排出。
锅炉烟气除尘系统设计 环境工程外文资料翻译
毕业论文外文资料翻译题目某燃煤采暖锅炉烟气除尘系统设计学院资源与环境学院专业环境工程班级学生学号指导教师张玲二〇一二年四月二十日济南大学- 1 -济南大学- 2 -济南大学- 3 -济南大学- 4 -- 5 -济南大学- 6 -济南大学- 7 -济南大学- 8 -济南大学- 9 -济南大学- 10 -济南大学Chemical Engineering and Processing 40 (2001) 245–254.新的旋风式分离器的计算方法与纷飞挡板和底部清洁的天然气 - 第二部分：实验验证Tomasz Chmielniak a,*, Andrzej Bryczkowskia,b煤化工Zamkowa1，41-803 Zabrze，波兰研究所化学和工艺设备，波兰西里西亚技术Uni6ersity，M. Strzody7，44-100格利维采1999年11月23日收到，在2000年6月6日修订后的形式;2000年6月6日采纳摘要派生模型预测研究所收集的效率和压力下降，煤化工（IChPW）与一个旋转挡板的旋风式分离器的设计测试和实验验证的结果。
试点工作包含测试气体流速和分离效率和压降转子转速的影响。
密封流除尘效率的影响进行了测试。
一个旋转挡板分隔的特点是高效率和低的压降。
挡板高度的扩展可以得到较高的除尘效率和更低的压降。
计算方法与实验结果显示了良好的实验预期。
©2001 Elsevier Science B.V.版权所有。
关键词粉尘分离；气旋；旋流挡板；收集效率；压降1介绍由于旋转分离元素的粉尘分离器的优势，致使过去几年对这类设备[1-5]建设的深入研究和理论描述。
它还涉及建设一个在化工、煤炭加工（IChPW）研究所开发的新型旋风式分离器旋流挡板[6]。
在这个问题上[6]前文推导的理论模型来预测一个旋转挡板分离器的收集效率和压力下降。
在本文章中，发达国家的计算方法的实验和实证检验的结果报告。
2 旋风式分离器的计算方法的理论与旋流挡板2.1收集效率级效率的模型来预测的基础上的Laith和利希特气旋的计算方法[7]。
旋风分离器计算程序--Muschelknautz模型方法
by ZJ
2005-12-28
计算结果 50切割粒径 总效率 粒径 微米 1 2 3 4 5 6 7 8 9 10 15 20 30 40 50 60 70 80 90 100 >100
b
a
DX
Dx V0w
V0cs
Hg
Ks
0.800 0.500 0.700 0.000 0.080 1.2 kg/m^3 1.80E-05 Pa.S 0.046 mm
Hi
m^3/hr kg/m^3 kg/m^3 kg/m^3
1.676 99% 效率 eff 7% 71% 95% 99% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100%
微米 进口组成 % 1.00% 1.00% 1.00% 1.00% 1.00% 1.00% 1.00% 1.00% 2.00% 3.00% 10.00% 15.00% 20.00% 15.00% 10.00% 9.00% 4.00% 2.00% 1.00% 1.00% 1.00 25 微米 出口 0.001 0.007 0.009 0.010 0.010 0.010 0.010 0.010 0.020 0.030 0.100 0.150 0.200 0.150 0.100 0.090 0.040 0.020 0.010 0.010 0.99
0025muschelknautzmodelcalculation进口中位径微米入口速度t因子颗粒气体mm入口收缩系数几何平均半径器壁表面轴向速度摩擦阻力总面积器壁表面切向速度内旋涡旋转速度气体平均旋转速度旋风分离器rer升气管中气流速度分离效率进口中位径切割粒径极限浓度vinthetacoalpharmvzwarvowvocsvomrervx10
旋风分离器计算模型
⎤ )⎥ ⎥ ⎥ ⎦
器壁表面轴向速度 0.9 ∙ 245000 = 5.57 m/s 5 3600 ∙ π ∙ 4 − 1.658 出风管（内筒）弗劳德数： 245000 F = = 3.86 π ∙ 2.2 2.2 3600 ∙ 4 ∙ 2 ∙ 9.8 ∙ 2 V = 雷诺准数初始值： Re 5 0.60 ∙ 5.57 ∙ 2 1.658 = ∙ = 30797 2.865 ∙ 10 15.7
效率% 0.1 0.5 2.5 4.3 6.9 14.9 18.0 20.0 15.0 6.0 4.0 2.0 94.2
讨论： 1）效率与内筒直经和深度的关系
为什么内筒高度增加后，效率反而下降呢？
2）压损与内筒直经和深度的关系
为什么内筒高度增加后，压损反而下降呢？
2. Leith 和 Licht 旋风筒模型
1.8、 内旋涡旋转速度 Vocs
V 其中： = V D ∙D m/s
1+
f∙A ∙V
Vow —— 器壁表面切向速度，m/s f —— 总摩擦系数 Ar —— 摩擦阻力总面积，m2
Q 2 ∙ 3600
D ∙ D
1.9、 50%切割粒径 d50
d = 10 ∙ 18 ∙ μ ∙ 0.9 ∙ 1 Q ∙ 3600 2 ∙ π ∙ (ρ − ρ ) ∙ V ∙H μm
1.11、 气体平均旋转速度 Vom
V = V ∙V m/s
Vow —— 器壁表面切向速度，m/s Vocs —— 内旋涡旋转速度,m/s
1.12、 旋风分离器雷诺数 ReR
Re = V H ∙μ ∙ 1+ V R ∙R ∙V ∙ρ
入口颗粒浓度对旋风分离器压力降影响的实验分析
入口颗粒浓度对旋风分离器压力降影响的实验分析李晓曼;宋健斐;魏志刚;孙国刚;魏耀东【摘要】T he feed concentration is the main parameters influencing the performance of cyclone . With the feed mass concentration range of 5 -550 g/m3 ,the experiments were conducted in the cyclone with a volute inlet for measuring pressure drop .The experimental results showed that the pressure drop decreased as feed concentration increasing , especially , at the beginning of experiment .In addition to the expansion loss at the cyclone inlet , the pressure drop is mainly composed of two parts ,the friction loss of gas‐solid surface in the separation zone depending on tangential velocity ,surface area and friction coefficient ,and the dynamic dissipation loss in the vortex finder determined by tangential velocities and mean axial velocity in the vortex finder .With the increase of feed concentration , the tangential velocities were reduced due to friction loss , resulting in the pressure going up in the vortex finder ,w hich may be the reason that the pressure drop was reduced . The change of pressure drop in cyclone separator led to the inlet flow rate varying ,as a consequence of which ,the inlet flow rate increased significantly with an increase of feed concentration .Finally ,a formula for calculating pressure drop of cyclone was developed based on the Muschelknautz model ,considering the particle effects on the tangential velocity ,which is suitable for predicting pressure drop under the condition of high feed concentration .%旋风分离器的入口气流颗粒浓度对旋风分离器的压力降有重要影响。
旋风分离器内部流场及分离效率的数值仿真_李仁年
mechanism o f separatio n , t hree-dimensi onal numeric simulati on of internal f low field of g aseous phase and the m oti on co ndi tion o f par ticles in it w as conducted by using the sof tw are F L UENT . RNG k-εmode w as used to sim ulat e t urbulent f low o f the g aseous phase and t he Lag range equatio n w as used t o sim ulated the part icles’ mo tion. T he result s sho wed that the f low field in gas cyclone could be divided into tw o part s :the i nner one and oute r one , and there w as great diff erence betw een the tw o part s w it h respect to the dist ribution of pressure and velocity of gas ;t he parti cles’ m ot ion w as co mplicated and random and thei r separation ef ficiency w as dependent on t he ent eri ng po sit ion at t he i nt ake.
旋风分离器的压力降计算
旋风分离器的压力降计算袁怡;孙国刚;周发戚;杨晓楠【摘要】以应用中最为常见的筒锥型切流返转式旋风分离器为对象,考察了旋风分离器各结构尺寸及人口气速对压力降的影响,评价了若干压力降模型的适用性.结果表明,Stairmand压力降计算模型的均方差最小,但由于其忽略了几何放大对压力降系数的影响,限制了该压力降模型的适用性.利用相似与模化的分析方法,在对文献给出的实验数据进行回归分析的基础上,修正了Stairmand压力降计算模型,并将修正式的计算结果与实验测量值及另外多篇文献中给出的切流返转式旋风分离器在不同结构尺寸及操作气速共计150种工况下的实验数据进行对比,结果表明,修正式的精度更高,适用范围更广,可以满足旋风分离器设计计算的要求.【期刊名称】《炼油技术与工程》【年(卷),期】2016(046)010【总页数】6页(P39-44)【关键词】旋风分离器;压力降模型;适用性;回归分析【作者】袁怡;孙国刚;周发戚;杨晓楠【作者单位】中国石油大学(北京)过程流体过滤与分离技术北京市重点实验室,北京市102249;中国石油大学(北京)过程流体过滤与分离技术北京市重点实验室,北京市102249;中国石油大学(北京)过程流体过滤与分离技术北京市重点实验室,北京市102249;中国石油大学(北京)过程流体过滤与分离技术北京市重点实验室,北京市102249【正文语种】中文旋风分离器是气固分离过程中一种常用的设备，因其结构简单，无运转部件，适用于高温高压等条件，目前在石油、化工、冶金、能源、环境等诸多领域得到广泛应用。
压力降是旋风分离器的主要性能指标之一，直接关系到能量消耗和风机的合理选择。
国内外学者对它进行了许多研究，提出了很多计算方法和计算公式，这些压力降模型为旋风分离器的工程应用提供了必要的设计依据，但不同压力降模型间的计算结果差异较大。
Linden，Alexander，Shepherd，First，Casal，Coker等认为，阻力系数主要取决于进出口尺寸，且可表示为进口面积和排气管直径的函数[1-6]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
旋风分离器计算程序--Muschelknautz模型方法
程序功能
按Muschelknautz模型方法计算旋风分离器在给定操作条件下的分离效率及压降
计算方法参见:
旋风分离器--原理,设计和工程应用第6章
[丹]A.C. 霍夫曼 [美]L. E. 斯坦恩著
彭维明等译, 化学工业版社, 2004,9ISBN 7-5025-5871-3
原书名: Gas Cyclones and Swirl tubes, Priciples, design and operation
by, Alex C. Hoffmann, Louis E. Stein, ISBN 3-540-43326-0
输入:
1旋风分离器尺寸参数
2操作参数
3进料粒径分布
输出:
150%切割粒径
2对进料粒径分布下总分离效率
3总压降
计算步骤
1输入尺寸参数
2输入操作参数
3输入进料粒径分布(可选)
4手工迭代计算:
1) 按雷诺数壁面相对粗糙度, 由雷诺数表格中的摩擦系数二元样条得 fair
2) 单元格(L41) 中计算出V0cs,
3) 将单元格 (H40) 中填入 L41 中的数值, 手工填入, 不可写成"=L41"
4) 重复上述操作,直至 单元格(L43) 的值小于 0.1
5) 如计算总效率与单元格(L36)中数值相差悬殊, 将计算的总效率填入L36,重复计算例题
6A.1Hoffman等(2001)测量数据
6A.2Obermair和Staudinger(2001)测量数据
6A.3Greif(1997)测量数据
技术支持
此程序由zjmche编制
技术答疑请联系:zjmche@
L36,重复计算。