有限元分析梁单元内力计算
有限元受力分析--结构梁-力-计算
有限元受力分析–结构梁-力-计算1. 前言受力分析是工程设计中至关重要的一环，能够帮助工程师完善设计并避免安全事故的发生。
在此，我们将介绍有限元受力分析在结构梁设计中的应用。
本文将重点讲解有限元受力分析的相关理论和计算方法。
2. 有限元受力分析有限元分析是数值计算的一种方法，可用于解决工程中的受力分析问题。
它把结构离散为有限个单元，然后对每个单元进行分析。
有限元分析可分为线性有限元分析和非线性有限元分析两种类型。
本文我们只讨论线性有限元分析。
在有限元分析中，结构被分解为离散的单元，每个单元都是基于解析解的一部分。
有限元的形状、尺寸和材料属性可以通过计算机程序进行定义。
使用数学模型和有限元方法，可以计算单元的应力、变形和应变，从而进行结构的受力分析。
3. 结构梁结构梁相信大家应该都知道，它是工程中最为常用的结构之一。
它具有一定的强度和刚度，可以支撑和传递载荷。
一般来说，结构梁通常由简单的杆件单元组成。
在进行结构梁受力分析时，我们需要考虑弯曲、剪切和挤压等不同形式的载荷，以及结构在工作条件下的应变和应力分布情况。
有限元受力分析对于这些问题的研究提供了很好的解决方案。
4.力的分析在受力分析中，载荷是非常关键的参数。
载荷可以是点载荷、均布载荷、集中荷载等。
在本文中，我们将分别介绍这些载荷类型的有限元分析方法。
4.1 点载荷分析点载荷通常是一个单点受到的载荷。
对于点载荷的有限元分析，我们可以通过构建一个网格模型，然后将点载荷作用在网格的节点上。
此外，还需要设定材料的弹性模量和截面的截面面积，以计算结构的应力和变形。
需要注意的是，点载荷分析过程中的网格划分应当尽量精细，以达到更为优秀的数值精度。
4.2 均布载荷分析均布载荷是沿着梁的长度方向均匀分布的载荷，例如一根梁的自重、荷载等。
在进行均布载荷的有限元分析时，我们可以在网格的中央位置放置均布载荷，然后将梁的边缘节点设置为固定的约束条件。
同样，需要设定材料的弹性模量和截面的截面面积以计算结构的应力和变形。
求简支梁受均布荷载跨中位移有限元分析步骤(平面梁单元)
K151 M O K 5151
对号入座，组合整体刚度矩阵，并将各个分块矩阵对应的数值代入， 组合成整体刚度矩阵
1
6l 12 6l 2l 2 −12 −6l 2 6l 2l 0 0 0 0 0 0 0 EI 0 K= 3 l M M 0 0 0 0 −12 −6l
ql RA − 12 2 6l −12 ql 2 − 6l 12 0 ql 0 0 0 EI 0 ql = l 0 M M ql RB − 2 0 ql 2 0 12
{Fpy }( 2 )
− ql / 2 − ql 2 / 12 2 = − ql / 2 3 2 ql / 12
……
1
2
3
….
51
ql Fpy = − 2
1
−
ql 12
2
ql 0 ql 0 L
−
ql 2
ql 12
根据
[ F ] = [ K ][δ ]
υ1 = 0
−12 −6l 24 0 −12 6l 0 0 0 0 M 6l 2l 2 −6l 2l 2 0 0 0 0
求出各节点的结点位移
[δ ]
0 θ 1 v2 θ2 v3 θ3 M 0 θ51
0 1 −
0 0
2 3 l l2 1 2 − 3 2 l l
δ1 1 δ 2 = N δ e − [ ] l δ3 1 δ 4 l2 0 0
弹簧单元与梁单元实例计算
弹簧单元与梁单元实例计算1.绪论有限元法也叫有限单元法（finite element method, FEM），是随着电子计算机的发展而迅速发展起来的一种弹性力学问题的数值求解方法。
五十年代初，它首先应用于连续体力学领域—飞机结构静、动态特性分析中，用以求得结构的变形、应力、固有频率以及振型。
由于这种方法的有效性，有限单元法的应用已从线性问题扩展到非线性问题，分析的对象从弹性材料扩展到塑性、粘弹性、粘塑性和复合材料，从连续体扩展到非连续体。
关键词：有限元方法，数值求解，动态分析2.有限元方法2.1有限元法概述有限元法是把要分析的连续体假想地分割成有限个单元所组成的组合体，简称离散化。
这些单元仅在顶角处相互联接，称这些联接点为结点。
离散化的组合体与真实弹性体的区别在于：组合体中单元与单元之间的联接除了结点之外再无任何关联。
但是这种联接要满足变形协调条件，即不能出现裂缝，也不允许发生重叠。
显然，单元之间只能通过结点来传递内力。
通过结点来传递的内力称为结点力，作用在结点上的荷载称为结点荷载。
当连续体受到外力作用发生变形时，组成它的各个单元也将发生变形，因而各个结点要产生不同程度的位移，这种位移称为结点位移。
在有限元中，常以结点位移作为基本未知量。
并对每个单元根据分块近似的思想，假设一个简单的函数近似地表示单元内位移的分布规律，再利用力学理论中的变分原理或其他方法，建立结点力与位移之间的力学特性关系，得到一组以结点位移为未知量的代数方程，从而求解结点的位移分量。
然后利用插值函数确定单元集合体上的场函数。
显然，如果单元满足问题的收敛性要求，那么随着缩小单元的尺寸，增加求解区域内单元的数目，解的近似程度将不断改进，近似解最终将收敛于精确解。
2.2有限元法的优点1、物理概念浅显清晰，易于掌握。
有限元法不仅可以通过非常直观的物理解释来被掌握，而且可以通过数学理论严谨的分析掌握方法的本质。
2、描述简单，利于推广。
用有限元法对悬臂梁分析的算例算例
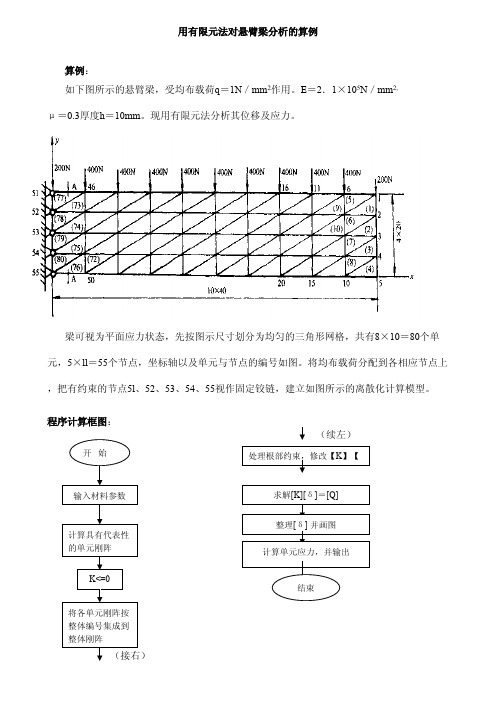
用有限元法对悬臂梁分析的算例算例：如下图所示的悬臂梁，受均布载荷q ＝1N ／mm 2作用。
E ＝2．1×105N ／mm 2,μ＝0.3厚度h ＝10mm 。
现用有限元法分析其位移及应力。
梁可视为平面应力状态，先按图示尺寸划分为均匀的三角形网格，共有8×10＝80个单元，5×ll ＝55个节点，坐标轴以及单元与节点的编号如图。
将均布载荷分配到各相应节点上，把有约束的节点5l 、52、53、54、55视作固定铰链，建立如图所示的离散化计算模型。
程序计算框图：（续左）程序中的函数功能介绍及源代码1.LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)――该函数用于计算平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)、第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)时的线性三角形元的单元刚度矩阵.该函数返回6×6的单位刚度矩阵k.2.LinearTriangleAssemble(K,k,i,j,m)――该函数将连接节点i,j,m的线性三角形元的单元刚度矩阵k集成到整体刚度矩阵K。
每集成一个单元，该函数都将返回2N×2N的整体刚度矩阵K.3.LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)-- 该函数计算在平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi, yi)第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)以及单元位移矢量为u时的单元应力。
该函数返回单元应力矢量。
函数源代码：function y = LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;%三角形单元面积，单元节点应该按逆时针排序，保证每个三角形单元的面积都为正值（也可作为一个小函数：LinearTriangleElementArea）betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);%B为应变矩阵，其中betai=yi-ym,betaj=ym-yi,betam=yi-yj.gammai=xm-xj, gammaj=xi-xm, gammam=xj-xi.D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%D为弹性矩阵，分为平面应力问题和平面应变问题对于平面应力问题D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];对于平面应变问题E1=E/（1-NU*NU），NU1=NU/（1-NU）y = t*A*B'*D*B;%单元刚度矩阵function y = LinearTriangleAssemble(K,k,i,j,m)K(2*i-1,2*i-1) = K(2*i-1,2*i-1) + k(1,1); K(2*i-1,2*i) = K(2*i-1,2*i) + k(1,2);K(2*i-1,2*j-1) = K(2*i-1,2*j-1) + k(1,3); K(2*i-1,2*j) = K(2*i-1,2*j) + k(1,4);K(2*i-1,2*m-1) = K(2*i-1,2*m-1) + k(1,5); K(2*i-1,2*m) = K(2*i-1,2*m) + k(1,6);K(2*i,2*i-1) = K(2*i,2*i-1) + k(2,1); K(2*i,2*i) = K(2*i,2*i) + k(2,2);K(2*i,2*j-1) = K(2*i,2*j-1) + k(2,3); K(2*i,2*j) = K(2*i,2*j) + k(2,4);K(2*i,2*m-1) = K(2*i,2*m-1) + k(2,5); K(2*i,2*m) = K(2*i,2*m) + k(2,6);K(2*j-1,2*i-1) = K(2*j-1,2*i-1) + k(3,1); K(2*j-1,2*i) = K(2*j-1,2*i) + k(3,2);K(2*j-1,2*j-1) = K(2*j-1,2*j-1) + k(3,3); K(2*j-1,2*j) = K(2*j-1,2*j) + k(3,4);K(2*j-1,2*m-1) = K(2*j-1,2*m-1) + k(3,5); K(2*j-1,2*m) = K(2*j-1,2*m) + k(3,6);K(2*j,2*i-1) = K(2*j,2*i-1) + k(4,1); K(2*j,2*i) = K(2*j,2*i) + k(4,2);K(2*j,2*j-1) = K(2*j,2*j-1) + k(4,3); K(2*j,2*j) = K(2*j,2*j) + k(4,4);K(2*j,2*m-1) = K(2*j,2*m-1) + k(4,5); K(2*j,2*m) = K(2*j,2*m) + k(4,6);K(2*m-1,2*i-1) = K(2*m-1,2*i-1) + k(5,1); K(2*m-1,2*i) = K(2*m-1,2*i) + k(5,2);K(2*m-1,2*j-1) = K(2*m-1,2*j-1) + k(5,3); K(2*m-1,2*j) = K(2*m-1,2*j) + k(5,4);K(2*m-1,2*m-1) = K(2*m-1,2*m-1) + k(5,5); K(2*m-1,2*m) = K(2*m-1,2*m) + k(5,6);K(2*m,2*i-1) = K(2*m,2*i-1) + k(6,1); K(2*m,2*i) = K(2*m,2*i) + k(6,2);K(2*m,2*j-1) = K(2*m,2*j-1) + k(6,3); K(2*m,2*j) = K(2*m,2*j) + k(6,4);K(2*m,2*m-1) = K(2*m,2*m-1) + k(6,5); K(2*m,2*m) = K(2*m,2*m) + k(6,6);K;%对号入座，如前所述，每集成一次都将返回2N×2N的整体刚度矩阵K.此题为110×110 function y = LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%平面应力和平面应变问题两种情况y = D*B*u;%单元应力计算主程序源代码E=21e7;NU=0.3;t=0.01;stifflike5=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.08,0.36,0.06,1) %选取2个基本单元，调用M文件stifflike1=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.06,0.4,0.06,1) K=sparse(110,110); %creat a xishu matrix for total stiff创建一个稀疏矩阵for i=1:49if rem(i,5)%模取余，bool型变量，非零即为真j=i;K=LinearTriangleAssemble(K,stifflike5,j,j+5,j+6);%节点编号K=LinearTriangleAssemble(K,stifflike1,j,j+6,j+1);endend%将每个单元刚度矩阵集成到总刚中K=full(K);%转化稀疏矩阵 k=K(1:100,1:100);k=[K,zeros(100,10);zeros(10,100),eye(10)];k=sparse(k);%利用边界条件简化基本方程Q=sparse(2:10:92,1,[-200,-400,-400,-400,-400,-400,-400,-400,-400,-400,],110,1);%外部荷载，此处不包括约束条件，通过形函数确定，是不是可以理解为梁的两端为中间的一半呢？d=k\Q;%高斯消元法，比克莱姆法则在计算速度上有绝对的优势！x=0:0.04:0.4;plot(x,d(106:-10:6))%基本绘图命令grid%带网格y=zeros(80,3);q=0;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.06;xn=0.4;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];xl=0.4;yl=0.06;xm=0.36;ym=0.04;xn=0.4;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.02;xn=0.4;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0;xn=0.4;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endendq=4;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.08;xn=0.36;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.06;xm=0.36;ym=0.06;xn=0.36;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.04;xn=0.36;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0.02;xn=0.36;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endend %y(i+q,:)这是实现什么的？没见过这种用法，算法上应该就是通过节点位移实现指定单元的内力，这部分本人看的也晕晕的，望高人指点N=y(73:80,1)结果图及数据输出悬臂梁轴线挠度图：一单元的单元刚阵1.0e+006 *0.8077 0 0 -0.4038 -0.8077 0.40380 2.3077 -0.3462 0 0.3462 -2.30770 -0.3462 0.5769 0 -0.5769 0.3462-0.4038 0 0 0.2019 0.4038 -0.2019-0.8077 0.3462 -0.5769 0.4038 1.3846 -0.75000.4038 -2.3077 0.3462 -0.2019 -0.7500 2.5096五单元的单元刚阵1.0e+006 *00.050.10.150.20.250.30.350.4x/m w /m0.5769 0 -0.5769 0.3462 0 -0.34620 0.2019 0.4038 -0.2019 -0.4038 0-0.5769 0.4038 1.3846 -0.7500 -0.8077 0.34620.3462 -0.2019 -0.7500 2.5096 0.4038 -2.30770 -0.4038 -0.8077 0.4038 0.8077 0-0.3462 0 0.3462 -2.3077 0 2.3077根部73-80各单元应力计算结果如下（n/m2）：1.0e+007 *2.1119 -0.0621 -2.2816 -4.8824 5.0479 2.4065 0.0352 -2.3753。
梁的有限元分析原理
梁的有限元分析原理梁的有限元分析原理是一种工程结构分析方法，广泛应用于建筑、桥梁、航空航天、汽车等领域。
它通过将连续的结构离散化为有限数量的小单元，通过数学模型进行计算，得出结构的力学性能和响应情况。
梁的有限元分析原理是有限元分析的基础，下面将对其进行详细介绍。
首先，梁的有限元分析原理基于梁理论，即在横向较小、纵向较长的情况下，结构可以近似为一维梁。
梁的有限元分析原理通过将梁划分为多个单元，每个单元内部可以看作两个节点之间的一段杆件，通过建立节点之间的力学关系方程，得到整个结构的力学性能。
其次，梁的有限元分析原理利用了变分原理，即将结构的势能取极小值，建立了结构的力学方程。
通过对于梁的弯曲、剪切和轴向力等方面的力学模型进行合理的假设与简化，可以得到结构的位移与力的关系，从而解决结构的力学问题。
在梁的有限元分析中，需要进行以下几个步骤：1.几何离散化：将梁结构划分为多个单元，每个单元具有相同的形状与尺寸，通常为矩形或三角形。
2.模型建立：根据梁理论以及力学方程的简化假设，建立节点的力学关系方程，包括位移、应力、应变等参数。
3.材料性能定义：确定梁材料的力学性能参数，如弹性模量、截面惯性矩等。
这些参数对梁结构的力学性能具有重要影响。
4.边界条件施加：根据实际问题设定边界条件，包括固定支座、约束条件等。
这些条件对于解决梁结构的位移、应力等问题至关重要。
5.方程求解：通过数学方法求解得到节点之间的力学关系方程，利用数值计算技术进行迭代求解，得到梁结构的位移、应力等参数。
6.结果分析：根据求解得到的结果，进行力学性能分析，如最大应力、挠度、模态分析等。
根据分析结果评估结构的强度与稳定性。
总结起来，梁的有限元分析原理是一种基于梁理论的工程结构分析方法，通过将结构离散化为多个小单元，利用力学关系方程和数值计算技术求解得到结构的力学性能。
通过梁的有限元分析原理，工程师可以更加准确地评估结构的强度与稳定性，对结构进行优化设计。
梁模型有限元计算_ANSYS Workbench有限元分析实例详解（静力学）_[共7页]
![梁模型有限元计算_ANSYS Workbench有限元分析实例详解（静力学）_[共7页]](https://img.taocdn.com/s3/m/ba2491b227d3240c8547ef2c.png)
4.2 梁单元静力学分析当结构长度对横截面的比率超过10:1，沿长度方向的应力为主要分析对象，且横截面始终保持不变时，即应用梁单元。
梁单元可用于分析主要受侧向或横向载荷的结构，如建筑桁架、桥梁、螺栓等。
在WB中默认为铁摩辛柯（Timoshenko）梁单元，即Beam188和Beam189，可计算弯曲、轴向、扭转和横向剪切变形。
其中Beam188采用线性多项式作为形函数，Beam189采用二次多项式作为形函数，当WB的Mesh设置中Mesh-Element Midside Nodes为Dropped 时，即为Beam188；Mesh-Element Midside Nodes为Kept时，即为Beam189。
有限元对单元特性的描述包括单元形状、节点数目、自由度和形函数。
表4-2-1为Beam 单元的对比。
在WB中默认设置为二次单元。
一般来说，线性单元需要更多的网格数才能达到二次单元的精度。
选用二次单元可提高计算精度，这是因为二次单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界，且二次插值函数可更高精度地逼近复杂场函数，所以当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多，在网格数量相同的情况下由高阶单元组成的模型规模要大得多，计算内存消耗也多，因此，在使用时应权衡考虑计算精度和时间。
表4-2-1 Beam单元对比4.2.1 梁模型有限元计算用ProE建立一桁架模型，导入WB进行分析计算。
（1）ProE建模。
在草绘界面绘制一边长为30mm、40mm、50mm的三角形，然后选择投影命令将草绘图形投影到基准面上，另存为x_t文件（其他3D软件操作方法类似）。
（2）导入模型。
如图4-2-1所示，在Import设置中，Operation设为Add Frozen，Line Bodies 设为Yes。
– 65 –– 66 – 图4-2-1 Import ProE模型文件设置（3）梁截面赋值，并定义截面方向，最后用Form New Part将三根梁合并为一个部件，如图4-2-2所示。
梁的有限元分析原理 - 考虑剪切变形影响的梁单元
代人
比较：弯曲梁 单元中的单刚
得到：
等截面梁单元有限元分析
8
长沙理工大学
小结
剪切变形的影响通过系数b反映在刚度矩阵中，使刚度减弱。 对矩形截面：
，当l >>h，b趋于0，可以忽略剪力变形的影响。
等截面梁单元有限元分析
9
长沙理工大学
Timoshenko梁单元
铁木辛柯梁单元——采用两个独立变量 挠度 w
几何关系，曲率
对比
等截面梁单元有限元分析
3
最小势能原理
长沙理工大学
k为截面剪切校正因子
1.经典梁单元 2.铁木辛柯梁单元
——C1型单元 ——C0型单元
等截面梁单元有限元分析
4
长沙理工大学
在经典梁单元基础上引入剪切变形的影响. 挠度叠加
结点位移
其中
采用不考虑剪切变形梁单元的w相同的Hermite插值； 采用2结点的Lagrange插值，即线性插值。
解决方法
假设剪切应变
代替插值函数
计算泛函的剪切应变能时，θ采用低一 阶，和dw/dx同阶插值函数代替原插值 函数
18
等截面梁单元有限元分析
长沙理工大学
等截面梁单元有限元分析
——考虑剪切变形的梁单元
2014.4.13
1
长沙理工大学
介绍.
轴力构件 axial elements 杆单元
受弯构件 flexural elements 梁单元
考虑剪切变形的梁单元
等截面梁单元有限元分析
2
长沙理工大学 假设：梁内的横向剪切力Q所产生的剪切变形将引起梁的附加挠度， 并使原来垂直于中面的截面变形后不再和中面垂直，而且发生翘曲。 考虑剪切变形的梁单元 但在这里，假设原来垂直于中面的截面变形后仍保持为平面。 几何描述
有限元分析梁单元内力计算
1.385 0 3.462 1.385 0 3.462 0 0 0
0 252 0 0 252 0 0 0 0
3.462 0 11.541 3.462 0 5.711 0 0 0
K
103
1.385 0
0 252
3.462 0
253.385 0 0 253.385
3.462 3.462
py3 m3
px3
6.25
5.208
py3 m3
6. 引入约束条件, 构成总体方程
2 px1 p y1
2.5 m1 3
4.25
1.385
0
3.462
103
1.385 0
0 252 0 0 252
3.462 0
11.541 3.462
0
1.385 0
0
0 1.385 3.462 0 1.385 3.462
[
K112
]
[
K
2 23
]
103
0 252
3.462 0
11.542 0
0 252
3.462 0
5.771 0
0 1.385 3.462 0 1.385 3.462
0 3.462 5.771 0 3.462 11.542
3. 单元刚度矩阵的座标变换
求：每根梁的内力。
P2 1kN P1 4kN
2.5m
解：
1.建座标系，对梁单元各节点编号 如图所示。
2.5m
2单元，三节点系统(即自然划分。也可以在集中 力作用处设一节点)。由于每一节点有3个自由度 ，故系统有9个自由度。总刚度矩阵[K]为9×9阶
y 2
5m
②3
杆结构 分析的有限元方法(有限元)
杆单元形状函数
杆单元刚度矩阵
平面问题中的坐标变换
梁结构分析的有限元方法
梁：承受横向荷载和弯矩的杆件。
梁的主要变形为挠度v
横截面变形前后都垂直于杆变形前的轴线x轴
中性层变形=0
纯弯曲没有剪力，只有弯矩
梁截面的惯性矩
杆结构分析的有限元方法
杆：承受轴向荷载的杆件
最基本的承力结构件：杆、梁
弹簧--简单的承受轴力的结构件
有限元方法中，每一个处理步骤都是标准化和规范化的，
因而可以在计算机上通过编程来自动实现。
F=kδ
k--刚性系数
位移的绝对变化量/杆件的伸长量δ=u2—u1
应力某截面上单位面积上的内力/内力的分布集度
应变相对伸长量单位长度的伸长量
杆单元的特性是节点位移及节点力的方向都是沿轴线方向。
杆结构的力学分析
铰接的杆结构----杆只受轴力-----杆件拉伸问题---可自然离散
两端为铰接的杆件只承受轴力。
各个单元研究（基于局部坐标系的表达)
各个单元研究
离散单元的集合、组装
杆单元及坐标变换
自由度：描述物体位置状态的每个独立变量。
对于杆单元，其节点位移有两个自由度。
abaqus梁单元线荷载
abaqus梁单元线荷载ABAQUS是一款常见的有限元分析软件，用于计算各种复杂结构的应力、应变和变形等。
在实际工程中，我们需要对一个梁进行线荷载的计算和分析，而ABAQUS中的梁单元可以很好地进行这种计算和分析。
本文将介绍在ABAQUS中如何对梁单元进行线荷载的计算和分析，让读者可以更好地理解和应用这些知识。
一、梁单元简介在ABAQUS中进行线荷载分析时，需要用到梁单元。
梁单元是一种具有三个节点的有限元，它的长度通常远大于其他两个维度，用于模拟长条状结构的应力和应变。
ABAQUS中有多种梁单元，常用的有BEAM188和BEAM189两种，其中BEAM188适用于线弹性分析，而BEAM189适用于非线性材料的分析。
在进行线荷载分析时，我们一般使用BEAM188单元。
二、梁单元线荷载的计算方法进行梁单元线荷载分析时，需要经过以下计算步骤：1. 定义模型在ABAQUS中，输入模型的方式有很多种，例如输入节点、单元等信息，或者使用建模软件生成模型然后导入到ABAQUS中等。
不过，不管用哪种方法，我们都需要先定义好模型的几何形状和材料属性等信息。
2. 定义截面属性对于一个梁单元而言，其承载能力与其截面形状和材料属性等有关。
在ABAQUS中，我们需要定义好梁单元的截面性质，如横截面积、惯性矩、截面形状等信息。
这些信息通常可以从设计图纸中获取。
3. 定义材料属性与截面属性类似，不同材料具有不同的力学性能，我们需要在ABAQUS中定义好梁单元所使用的材料属性。
例如，如果是钢梁，则其弹性模量、泊松比等参数可以通过查阅资料获得。
4. 定义节点荷载节点荷载是指作用在梁单元的节点上的荷载，通常会影响梁单元的应力与应变等信息。
在ABAQUS中，我们可以定义不同类型的节点荷载，例如单点荷载、区域荷载等。
5. 定义线荷载梁单元线荷载是指作用在梁单元上的力和/或力矩，通常是沿着梁的长度方向施加的荷载。
在ABAQUS中，我们可以定义不同类型的线荷载，例如均布荷载、单点荷载等。
《有限元理论与数值方法》第三讲-杆、梁结构有限元分析
Finite Element Theory and Numerical Method
一、杆、梁的物理力学模型
拉压杆单元如图3-6所示，已知等直杆件杆长为 l 横截面面积为 A 材料弹性模量为 E 所受轴向分布载荷集度为 p(x) 杆端位移分别为 u1 u2
杆端力分别记为 F1 F2
1、建立位移场
F1, u1 xa
1
a p(x)
2 F2 , u2
x
设局部坐标系下杆中任意点a的坐标为 xa
因为只有两个边界条件 u1
形函数具有如下性质： 1)本端为1，它端为0 2)单元内任意一点总和为1
N1(0) 1
N1(1) 0
N2 (0) 0 N2 (1) 1
N1() N2 () 1
2、应变分析
du dx
dN dx
ue
dN1 dx
B为应变矩阵或者几何矩阵。
dN2 dx
u
e
1 l
1 l
ue
[B1
B2 ]ue Bue
图示所示桁架 l 2m
EA 1.2106 kN
试求1-2杆和1-4杆单元的局部坐标单元 刚度矩阵
1-2杆：抗拉刚度 EA / l 6106 kN/m
F1 10N 3
1
F2 20N 4
2
ke1
EA l
1 1
1
1
6
105
1 1
1
1
kN
/
m
1-4杆：抗拉刚度 EA /( 2l) 4.24264 105 kN/m
有限元教程 梁单元的常用节点等效载荷
T
最后，求总的结点荷载矩阵
F Fd FE 20 10 10 5
T
（6）求解结构的整体刚度方程，计算未知的结点位移矩 阵 δ 。这里的整体刚度方程为：
312 0 30 0 u1 20 0 312 30 30 v 10 4 1 10 30 30 200 50 1 10 0 30 50 100 3 5
（1）单元划分、建立局部坐标系和整体坐标系，并对数 据进行整理，对单元和结点编号。
EA 300 10 4 l 6 EI 30 10 4 l2 4 EI 100 10 4 l 12 EI 12 10 4 l3
（2）求局部坐标系中的单元刚度矩阵 k ⓔ 。由于单元①、
②的尺寸完全一样，因此其单元刚度矩阵一样，根据局部坐 标系下单元刚度矩阵表达式，可以得到：
6.0654 0 11.919 kN 3.9729 30 28.196 kN 3.5865 25 19.594 kNm 6 10 0 0 11.919 kN 0 30 31.804 kN 0 25 28.613kNm
有限元分析
Finite Element Analysis
李建宇
天津科技大学
2
内容
补充内容
补充内容： 梁单元的常用节点等效载荷 （equivalent nodal load）
要求 了解：节点等效载荷的概念 理解：确定节点等效载荷的力学原理 掌握：常见梁外载荷的等效节点载荷
上节回顾
刚架结构
整体 离散
结构内力计算工具
结构内力计算工具引言：在工程设计和分析中，计算结构的内力是非常重要的。
结构内力是指在结构中各个构件上产生的力的分布情况。
通过计算结构的内力，可以评估结构的稳定性和安全性，为结构设计和优化提供依据。
本文将介绍几种常用的结构内力计算工具。
一、有限元软件有限元软件是目前工程领域最常用的结构分析工具之一。
通过有限元软件，可以将结构分割成许多小的单元，然后利用数值方法计算每个单元上的内力。
有限元软件可以模拟各种复杂的结构，包括钢结构、混凝土结构、土木工程等。
常用的有限元软件有ANSYS、ABAQUS、Nastran等。
二、桁架分析软件桁架是一种由杆件和节点组成的结构体系，广泛应用于桥梁、塔架等工程中。
桁架分析软件可以根据输入的结构参数和受力情况，自动计算桁架中各个构件上的内力。
这些软件通常提供直观的图形界面，方便用户输入结构参数和受力情况，并可以输出内力分布图和报告。
常用的桁架分析软件有STAAD Pro、SAP2000等。
三、数值计算软件数值计算软件可以通过数值方法求解结构的内力。
这些软件通常提供编程接口，用户可以编写自己的计算程序。
通过数值计算软件，可以灵活地定义结构的几何形状、材料性质和边界条件，并计算任意点上的内力。
常用的数值计算软件有MATLAB、Python等。
四、手工计算方法除了使用软件工具，还可以通过手工计算的方法来估算结构的内力。
手工计算方法通常适用于简单的结构，如梁、柱等。
通过应力平衡和力的平衡等原理，可以计算出结构中各个构件上的内力。
手工计算方法需要一定的理论基础和计算经验，但可以帮助工程师更好地理解结构的行为。
手工计算方法也有一些常用的公式和表格，可以简化计算过程。
结论：结构内力计算工具在工程设计和分析中具有重要的作用。
有限元软件、桁架分析软件、数值计算软件和手工计算方法是常用的结构内力计算工具。
根据不同的结构类型和计算要求，可以选择适合的工具进行内力计算。
通过准确计算结构的内力，可以评估结构的稳定性和安全性，为结构设计和优化提供依据。
有限元分析实例2
有限元分析梁的有限元分析试分析图中梁：梁承受均布载荷：1.0e5 P a图1 梁的载荷图梁截面分别采用以下三种截面（单位：m）：矩形截面：圆截面：工字形截面：B=0.1, H=0.15 R=0.1 w1=0.1，w2=0.1，w3=0.2,t1=0.0114，t2=0.0114，t3=0.0071.1进入ANSYS程序→ANSYSED 6.1 →Interactive →change the working directory into yours →input Initial jobname: beam→Run1.2设置计算类型ANSYS Main Menu: Preferences →select Structural → OK1.3选择单元类型ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete…→Add…→select Beam 2 node 188 →OK (back to Element Types window)→Close (the Element Type window)1.4定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear→Elastic→Isotropic→input EX:2.1e11, PRXY:0.3→ OK1.5定义截面ANSYS Main Menu: Preprocessor →Sections →Beam →Common Sectns→分别定义矩形截面、圆截面和工字形截面：矩形截面:ID=1,B=0.1，H=0.15 →Apply →圆截面：ID=2,R=0.1 →Apply →工字形截面：ID=3,w1=0.1，w2=0.1，w3=0.2，t1=0.0114，t2=0.0114，t3=0.007→OK1.6生成几何模型生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS→依次输入二个点的坐标：input:1(0,0),2(10,0)，3（5,1）→OK 生成梁ANSYS Main Menu: Preprocessor →Modeling →Create →Lines →lines →Straight lines →连接两个特征点，1(0,0),2(10,0) →OK1.7 网格划分ANSYS Main Menu: Preprocessor →Meshing→Mesh Attributes→Picked lines →OK→选择: SECT:1（根据所计算的梁的截面选择编号）；Pick Orientation Keypoint(s):YES→拾取：3#特征点(5,1) →OK→Mesh Tool →Size Controls) lines: Set →Pick All(in Picking Menu) →input NDIV:5→OK (back to Mesh Tool window) → Mesh →Pick All(in Picking Menu) → Close (the Mesh Tool window)1.8 模型施加约束✓最左端节点加约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→ On Nodes→pick the node at (0,0) → OK→select ALL DOF → OK✓最右端节点加约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→ On Nodes→pick the node at (10,0) → OK→select UY,UZ,ROTX → OK✓施加y方向的载荷ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Pressure→ On Beams→Pick All→VALI:100 → OK1.9 分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →OK1.10 结果显示ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape…→select Def + Undeformed→OK (back to Plot Results window) →Contour Plot→Nodal Solu →select: DOF solution, UY, Def + Undeformed, Rotation, ROTZ ,Def + Undeformed→OK。
有限元分析梁单元内力计算
迭代法
迭代法
通过迭代的方式逐步逼近梁 单元的内力。这种方法适用 于大型有限元模型，计算量 较小，但计算精度较低。
适用范围
适用于大型有限元模型，计 算量较小。
优点பைடு நூலகம்
计算量较小，适用于大型有 限元模型。
缺点
计算精度较低，不适用于对 精度要求较高的梁单元。
快速法
快速法
结合直接法和迭代法的优点，通过快速求解线性方程组来 得到梁单元的内力。这种方法适用于大型有限元模型，计 算精度较高，计算量相对较小。
有限元分析广泛应用于工程领域，如 结构力学、流体力学、电磁场等领域 ，用于解决复杂的问题和优化设计。
有限元分析的基本步骤
建立单元刚度矩阵
根据单元的物理特性和边界条 件，建立单元刚度矩阵。
施加外力
将外力施加到整体结构的节点 上。
离散化
将连续的结构或系统离散化为 有限个简单单元。
集成总刚度矩阵
将所有单元的刚度矩阵集成得 到整体结构的总刚度矩阵。
通过梁单元内力计算，可以发现潜在 的危险区域和薄弱环节，为改进设计 提供依据。
内力计算的结果还可以用于评估结构 的疲劳寿命和可靠性，为工程实际应 用提供重要的参考依据。
02
有限元分析基础
有限元分析概述
有限元分析是一种数值分析方法，通 过将复杂的结构或系统离散化为有限 个简单单元，利用数学近似方法对复 杂问题进行模拟和分析。
有限元分析梁单元内力计 算
• 引言 • 有限元分析基础 • 梁单元内力计算方法 • 梁单元内力计算的实例 • 结论
01
引言
目的和背景
有限元分析（FEA）是一种数值分析方法，用于解决复杂的工程问题，如结构强度、 刚度、稳定性等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 )}
节点1力矩平衡力方程 m2 m1 Q2l 0
m1 Q2l m2
m1
EJ l2
{6[(u2
u1 ) (v2
v1 )]
l ( 41
22 )}
二. 由单元刚度矩阵计算
{F e } [K e ]{ e } [K e ][T e ] { e }
0 0 0 0 u1 u1 v1
0 0
0 0
1 0
0 1
0 0
0 0
I
0 0 0 0 1 0
0 0 0 0 0 1
[
K
2 23
]
[T
2
]T
[
K
2 23
][T
2
]
[
K
2 23
]
若局部坐标与整体坐标方向一致, 则 [K e ] [K e ]
4. 求总刚度矩阵
节点号为i, j的单元, 其刚度矩 阵元素在总刚度矩阵中的位置
3i－2 3i－1 3i
k115 k215 k315
k116 k216 k316
k411 k511
k412 k512
k413 k513
k414 k514
k415 k515
k416 k516
k611 k612 k613 k614 k615 k616
2单元
kkk654222444
k425 k525 k625
k426 k526 k626
3.462 253.385
0
0 252
0 0 253.385
3.462 0
5.711 3.462 3.462
0 0 0 252 0
0 0 0 0 1.385
3.0000462uv00022
2.758
px3
6.25
5.208
py3 m3
3.462 0 0 0 0 0 0 0
u1
转换关系:
f ii
i
cos sin
0
sin cos
0
0 0 1
uvii
i
1
Fx1 x
1.轴向内力
N12
AE l
(2
1)
AE l
[cos (u2
u1) sin(v2
v1)]
AE [cos
l
sin
]uv22
u1 v1
AE [
l
]uv 22
u1 v1
2. 弯曲内力 y 向位移: 1节点: f1 sin u1 cos v1 u1 v1
3i－2 ＊＊＊
3i－1 ＊＊＊
3i
＊＊＊
3j－2 ＊＊＊ 3j－1 ＊＊＊
3j ＊＊＊
3j－2 3j－1 3j
＊＊＊ ＊＊＊ ＊＊＊
＊ ＊＊ ＊＊ ＊ ＊＊＊
单元刚度矩阵元素编号(相当于在总刚度矩阵中的位置)
1单元
kkk132111111
k112 k212 k312
k113 k213 k313
k114 k214 k314
y
1
b 2.5m a 2.5m
转换成整体座标:
故, ①单元的等效结点力:
0 2.0 {P121} 2202.5..05
{F e } [T ]{F e } {T }1 [T ]T
0 2 2 0
P121 T1 T 202.52.5 2022.5.5
1节点 2节点
②单元 N 2 N3 0
Al 2 0
J
0 0 u1 v1
12 6l
0
6l 2l 2
0
uuu2211vvv212
m2
0 0
12 6l 6l 2l 2
0 0
12 6l
6l 4l 2
2
矩阵相乘，求出各分量
N1
EA l
[u1
v1
u2
v2 ]
EA l
[
(u1
u2 )
(v1
v2 )]
N2
0 0 1 0 0 0
0 0 0 0 1 0
0 0 0 1 0 0
0 0 0 0 0 1
0 1 0 0 0 0
1 0 0 0 0 0
[T 1]T
0 0
0 0
1 0 0 0 0 0 1 0
0 0 0 1 0 0
0 0 0 0 0 1
[K112 ] [T 1]T [K112 ][T 1]
1.385 0 3.462 1.385 0 3.462
v1) 4l1
6(u2
v2 ) 2l2 }
EJ l2
{6[ ( u2
u1) (v2
v1)]
l ( 41
22 )}
m2
EJ l2
{6(u1
v1)
2l1
6(u2
v2 )
4l2 }
EJ l2
{6[ ( u2
u1) (v2
v1)]
l ( 21
42 )}
三 . 有非节点载荷时单元内力计算
252 0
0 252 0
0
0 1.385 3.462 0 1.385 3.462
0 3.462 11.542 0 3.462 5.771
252 0
0 252 0
0
0 1.385 3.462 0 1.385 3.462
0 3.462 5.771 0 3.462 11.542
单元刚度矩阵迭加成整体刚度矩阵
k427 k527 k627
k428 k528 k628
k429 k529 k629
kk872244
k725 k825
k726 k826
k727 k827
k728 k828
k729 k829
k924 k925 k926 k927 k928 k629
[
K e1 12
]
[K23e1]
1.385 0 3.462 1.385 0 3.462 0 252 0 0 252 0 3.462 0 11.542 3.462 0 5.771 1.385 0 3.462 1.385 0 3.462 0 252 0 0 252 0 3.462 0 5.771 3.462 0 11.542
2节点 3节点
总体载荷
2 0 2.5
0 0 0
px1
p y1 m1
2 px1
p y1 2.5 m1
2 0
0 6.25
1 2
3 4.25
2.5 5.208 0.05 2.758
0 0 0
0 6.25 5.208
px3
EJ l2
{6[(u2
u1) (v2
v1)] l(21
42 )}
Q2
EJ (12
f12 6l12 )
l3
EJ l3
{12[u(u1
u2 ) (v1
v2 )] 6l(1
2 )}
y方向平衡力方程 Q1 Q2 0
Q1 Q2
Q1
EJ l3
{12[u(u2
u1) (v2
v1)] 6l(1
0 6l 2l 2 0 6l 4l 2
252 0
0 252 0
0
0 1.385 3.462 0 1.385 3.462
[
K112
]
[
K
2 23
]
103
0 252
3.462 0
11.542 0
0 252
3.462 0
5.771 0
0 1.385 3.462 0 1.385 3.462
252 0 0 0 1.385 3.462
3.462 0 5.711 3.462 3.462 23.083 0 3.462 5.771
0 0 0 252 0 0 252 0 0
0 0 0 0 1.385 3.462 0 1.385 3.462
0 0 0 0 3.462 5.771 0 3.462 11.542
0 252 0 0 252 0
[
K121
]
103
3.462 1.385
0 0
11.542 3.462
3.462 1.385
0 0
5.771 3.462
0 252 0 0 252 0
3.462 0 5.771 3.462 0 11.542
②单元 0o , cos 1, sin 0
py3 m3
px3
6.25
5.208
py3 m3
6. 引入约束条件, 构成总体方程
2 px1 p y1
2.5 m1 3
4.25
1.385
0
3.462
103
1.385 0
0 252 0 0 252
3.462 0
11.541 3.462
0
1.385 0
[T 2 ]
0 0
0
0
0 0
0
0
0 0 1 0 0 0
0
0
0
0
0
0
0
0
0 0 000 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
I
1 0 0 0 0 0
0 1 0 0 0 0
[T 2 ]T
ql Q2 Q3 2 6.25kN
m2
m3
ql2 12
5.208 kN • m
转换成整体座标:
y
q 2.5kN / m