2018北师大版下册数学截长补短和半角模型[原创]

合集下载

2017_2018学年高中数学第三章三角恒等变形3.3三角函数的简单应用3.3.2半角公式及其应用课件北师大版必修4

α 2
cos +, +, -, + -, +
α 2Βιβλιοθήκη tan + + -
α 2
【做一做 1】 tan 15° =( A.2+ 3B. 2 − 3 C. 3 + 1D. 3 − 1
)
解析:tan 15° =
答案:B
1-cos30° = sin30°
3 1- 2 1 2
= 2 − 3.
【做一做 2】已知 cos 2θ=−
分析利用 tan 2 = ±
��
1-cos�� 或 ta n 1+cos�� 2
=
1-cos�� 进行求解. sin��
题型一
题型二
题型三
题型四
解(方法一)∵180° <θ<270° , ∴90° < 2 < 135° . ∴tan = −
�� 2 1-cos�� 1+cos�� 3 1+ 5 3 1-5
(2)若给出 α 的具体范围, 则先求出 2 所在的范围, 再根据 2 所在的范围确定符号. 若给出的角是某一象限的角,则根据下表确定符号.
��
��
α 第一象限第二象限第三象限第四象限
α 2 第一、三象限第一、三象限第二、四象限第二、四象限
sin +, +, +, +, -
=−
= − 2.
(方法二)∵180° <θ<270° , ∴sin θ=− 1-cos 2 �� = − 5 . ∴tan =

中考数学必会几何模型(含答案)

MATH微信：beijingdaxue777QQ:1456770148中考必会几何模型目录专题一角平分线相关问题模型 (3)模型1角平分线相关模型 (3)专题二8字模型与飞镖模型 (6)模型1：角的8字模型 (6)模型2：角的飞镖模型 (8)模型3边的“8”字模型 (10)模型4边的飞镖模型 (11)专题三半角模型 (15)专题四将军饮马模型 (23)模型1：直线与两定点 (23)模型2角与定点 (28)模型3两定点一定长 (31)专题五角平分线四大模型 (34)模型1角平分线的点向两边作垂线 (34)模型2截取构造对称全等 (35)模型3角平分线+垂线构造等腰三角形 (37)模型4角平分线+平行线 (39)专题六截长补短辅助线模型 (42)模型1截长补短 (42)专题七蚂蚁行程 (48)模型1立体图形展开的最短路径 (48)专题八三垂直全等模型 (55)模型1三垂直全等模型 (55)专题九手拉手模型 (62)模型1手拉手 (62)专题十相似模型 (68)模型1A、8模型 (68)模型2共边共角型 (72)模型3一线三等角型 (75)模型4倒数型 (79)模型5与圆有关的简单相似 (82)模型6相似和旋转 (85)专题十一圆中的辅助线 (89)模型1连半径构造等腰三角形 (89)模型2构造直角三角形 (90)模型3与圆的切线有关的辅助线 (94)专题十二中点四大模型 (97)模型1倍长中线或类中线（与中点有关的线段）构造全等三角形 (97)模型2已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”． (99)模型3已知三角形一边的中点，可考虑中位线定理 (102)模型4已知直角三角形斜边中点，可以考虑构造斜边中线 (107)专题一角平分线相关问题模型模型1角平分线相关模型（1）如图1，若点P是∠ABC和∠ACB的角平分线的交点，则∠P=90°+∠A；（2）如图2，若点P是外角∠CBF和∠BCE的角平分线的交点，则∠P=90°﹣∠A；（3）如图3，若点P是∠ABC和外角∠ACE的角平分线的交点，则∠P=∠A．图1图2图3针对训练1.（2016•枣庄）如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（）A．15°B．17.5°C．20°D．22.5°【小结】本题若不套用模型，则需要通过三角形的外角性质证明得到∠A、∠D的数量关系.2.（2018•巴中）如图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A=．【分析】由解题模型一中的（1）可知，∠BOC=90°+∠A，把∠BOC=110°代入计算可得到∠A的度数．【详解】∵∠BOC=90°+∠A，∠BOC=110°，∴90°+∠A=110°.∴∠A=40°．【小结】本题若不套用模型，需要利用三角形的内角和定理、角平分线的定义得到∠BO C、∠A的数量关系.3.（2018•济南历城区模拟）如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的角平分线，CA2是∠A1CD的角平分线，BA3是∠A2BD的角平分线，CA3是∠A2CD的角平分线，若∠A1=α，则∠A2018=．【详解】∵A1B是∠ABC的平分线，A1C是∠ACD的平分线，∴∠A1BC=∠ABC，∠A1CD=∠ACD，又∵∠ACD=∠A+∠ABC，∠A1CD=∠A1BC+∠A1，【小结】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，以及角平分线的定义，熟记性质然后推出后一个角是前一个角的一半是解题的关键。

北师大版七年级下册第11讲全等辅助线(二)--基础班

第11讲全等辅助线（二）知识点1 半角模型我们习惯把过等腰三角形顶角的顶点引两条射线，使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型. 常见的图形为正方形，正三角形等.（1）正方形内含半角:如图，在正方形ABCD中，E、F分别是BC、CD边上的点，∠EAF=45°，易证：EF=BE+DF. （2）正三角形内含半角:如图，在四边形ABCD中，AB=AC=BC,BD=DC，E、F分别是AB、AC边上的点，∠BDC=120° , ∠EDF=60°，易证：EF=FC+BE.【典例】1.已知：正方形ABCD 中，45MAN ∠=︒，它的两边分别交线段CB DC 、于点M N 、.求证BM DN MN +=.【解析】延长ND 到E 使DE BM = ∵四边形ABCD 是正方形 ∴AD=AB ，∠ADE=∠B=90° 在ADE △和ABM △中， =⎧⎪∠=∠⎨⎪=⎩AD AB ADE B DE BM ∴ADE ABM △≌△（SAS ） ∴AM=AE ∠=∠BAM DAE ∵45MAN ∠=︒∴45∠+∠=︒BAM NAD ∴45∠=∠=︒MAN EAN 在AMN △和AEN △中 =⎧⎪∠=∠⎨⎪=⎩MA EA MAN EAN AN AN ∴AMN AEN △≌△(SAS) ∴MN=EN∴DE+DN=BM+DN=MN 即BM DN MN +=【方法总结】本题考查了全等三角形的性质和判定，此题比较典型，具有一定的代表性，且证明过程类似，解题思路一般是将半角两边的三角形通过旋转到一边合并形成新的三角形，从而进行等量代NMD CBAENMD CBAOFEBA AFCO B EDHABCDO E换，然后证明与半角形成的三角形全等，再通过全等的性质得出线段之间的数量关系，从而解决问题.【随堂练习】1．（2018•旌阳区二模）如图，已知正方形ABCD E 、F 分别是AB 、BC 边上的点，且∠EDF=45°，将△DAE 绕点D 按逆时针方向旋转90°得到△DCM ．（1）求证：EF=MF ；【解答】（1）证明：∵△DAE 绕点D 逆时针旋转90°得到△DCM ， ∴DE=DM ，∠EDM=90°， ∵∠EDF=45°，∴∠FDM=45°， ∴∠EDF=∠FDM ．又∵DF=DF ，DE=DM ， ∴△DEF ≌△DMF ， ∴EF=MF ；知识点2 手拉手模型“手拉手”数学模型：【典例】AB1.如图，已知点C 为线段上一点，ACM △、BCN △是等边三角形．NMCBABNCACN⑴ 求证：AN BM =.⑵ 将ACM △绕点C 按逆时针方向旋转180°，使点A 落在CB 上，请你对照原题图在图中画出符合要求的图形；⑶ 在⑵得到的图形中，结论“AN BM =”是否还成立，若成立，请证明；若不成立，请说明理由；【解析】⑴ ∵ACM △、BCN △是等边三角形∴AC CM =，BC CN =60ACM BCN ∠=∠=° ∴∠=∠ACN MCB在ACN △和MCB △中 =⎧⎪∠=∠⎨⎪=⎩AC MC ACN MCB CN CB ∴ACN MCB △≌△（SAS ） ∴AN BM =⑵ 将ACM △绕点C 旋转如图：⑶ 在⑵的情况，结论AN BM =仍然成立．证明：∵60BCM NCA ∠=∠=°，CA CM =，CN CB =． ∴CAN CMB △≌△（SAS ）， ∴AN MB =．【方法总结】这是一个运动变化的探索题，是“手拉手”经典例题，证明方法类似，且在一定的条件下，探究原结论的存在性（不变性）；解决此类题，需要画图分析、判断、猜想、推理论证．【随堂练习】（2015秋•川汇区期末）如图，已知AB=AD ，AC=AE ，∠BAD=∠CAE=90°，试判断CD 与BE 的大小关系和位置关系，并进行证明．【解答】证明：CD=BE，CD⊥BE，理由如下：因为∠BAD=∠CAE=90°，所以∠BAD+∠DAE=∠CAE+∠DAE，即∠BAE=∠DAC．因为，所以△BAE≌△DAC（SAS）．所以BE=DC，∠BEA=∠DCA．如图，设AE与CD相交于点F，因为∠ACF+∠AFC=90°，∠AFC=∠DFE，所以∠BEA+∠DFE=90°．即CD⊥BE．知识点3 三垂模型常见三垂直模型【典例】1.如图（1），已知AB⊥BD，ED⊥BD，AB=CD，BC=DE，（1）试判断AC与CE的位置关系，并说明理由．（2）若将CD沿CB方向平移得到图（2）（3）（4）（5）的情形，其余条件不变，此时第（1）问中AC与CE的位置关系还成立吗？请任选一个说明理由．【解析】解：（1）AC⊥CE．理由：如图（1），∵AB⊥BD，ED⊥BD，∴∠B=∠D=90°，又AB=CD，BC=DE，∴△ABC≌△CDE（SAS），∴∠A=∠DCE，∵∠A+∠ACB=90°，∴∠DCE+∠ACB=90°，∴AC⊥CE；（2）不变．理由：如图（2），∵AB⊥BD，ED⊥BD，∴∠B=∠D=90°，又AB=C2D，BC1=DE，∴△ABC1≌△C2DE（SAS），∴∠A=∠EC2D，又∵∠A+∠AC1B=90°，∴∠EC2D+∠AC1B=90°，∴∠C2MC1=90°，∴AC1⊥EC2．【方法总结】本题主要考查全等三角形的判定、平移的性质，关键在于根据题意求证相关三角形全等．对于第一问，根据题意推出△ABC≌△CDE，即可推出AC⊥CE；对于第二问，主要是根据已知推出△ABC1≌△C2DE，即可推出结论．【随堂练习】1．（2017秋•乐陵市期末）如图，点A、D、E在直线l上，∠BAC=90°，AB=AC，BD⊥l于D，CE⊥l于E，求证：DE=BD+CE．【解答】证明：∵BD⊥l于D，CE⊥l于E，∴∠BDA=∠CEA=90°，∵∠BAC=90°，∴∠B=∠EAC=90°﹣∠DAB，在△BDA和△AEC中∴△BDA≌△AEC（AAS），∴BD=AE，AD=CE，∴DE=DA+AE=BD+CE．2．（2018春•槐荫区期末）已知：如图，∠DCE=90°，CD=CE ，AD ⊥AC 于A ，BE ⊥AC 于B ．求证：AB+AD=BE ．【解答】证明：∵∠ECB+∠DCA=90°，∠DCA+∠D=90°， ∴∠ECB=∠D ，在△ECB 和△CDA 中，，∴△ECB ≌△CDA （AAS ）， ∴BC=AD ，BE=AC ， ∴AD+AB=AB+BC=AC=BE ．综合运用1.在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ，D 为三角形ABC 外一点，且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究：当M 、N 分别在直线AB 、AC 上移动时，BM 、NC 、MN 之间的数量关系．图1 图2（1）如图1，当点M 、N 在边AB 、AC 上，且DM=DN 时，BM 、NC 、MN之间的数量关AM N BCDCBN M AF系是；（2）如图2，点M 、N 在边AB 、AC 上，且当DM ≠DN 时，猜想⑴问的结论还成立吗？写出你的猜想并加以证明.【解析】（1）如图1， BM 、NC 、MN 之间的数量关系 BM+NC=MN ．（2）猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE=BM ，连接DE ．BD=CD 且120BDC ∠=．∴ 30=∠=∠DCB DBC ．又△ABC 是等边三角形， ∴90MBD NCD ECD ∠=∠=∠=．在MBD △与ECD △中：BM CE MBD ECD BD CD =⎧⎪∠=∠⎨⎪=⎩∴MBD △≌ECD △(SAS) ． ∴DM=DE, BDM CDE ∠=∠ ∴60EDN BDC MDN ∠=∠-∠=在△MDN 与△EDN 中：⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ∴MDN EDN △≌△(SAS) ∴MN NE NC BM ==+2. 如图，等边三角形ABE 与等边三角形AFC 共点于A ，连接BF 、CE ，求证：BF =CE 并求出∠EOB 的度数.ENMDC BA【解析】∵△ABE、△AFC是等边三角形∴AE=AB，AC=AF，60EAB FAC∠=∠=︒∴∠+∠=∠+∠EAB BAC FAC BACEAC BAF即∠=∠∴AEC ABF△≌△（SAS）∴BF=EC∠=∠AEC ABF∠=∠又∵AGE BGO∴60∠=∠=︒BOE EAB∴60EOB∠=︒3. 如图，正五边形ABDEF与正五边形ACMHG共点于A，连接BG、CF，则线段BG、CF 具有什么样的数量关系并求出∠GNC的度数．【解析】解：结论：BG=CF．理由：如图，BG交CF于N，AG交CF于P，∵正五边形ABDEF与正五边形ACMHG共点于A，∴AB=AF，AC=AG，∠BAF=∠CAG=108°，∴∠BAG=∠FAC，在△ABG和△AFC中，，∴△ABG≌△AFC（SAS），∴CF=BG，∠BGA=∠FCA，∵∠GNC=180°﹣∠BGA﹣∠NPG，∵∠NPG=∠APC，∴∠GNC=180°﹣∠FCA﹣∠APC=∠CAG=108°．4. 如图，已知锐角△ABC中，以AB，AC为边向外作正方形ABDE和正方形ACFG，连结CE、BG，交点为O．（1）求证：EC=BG且EC⊥BG．（2）探究：△ABC与△AEG面积是否相等？并说明理由．【解析】解：（1）在正方形ABDE和正方形ACFG中，AE=AB，AC=AG，∵∠EAB=∠GAC=90°，∴∠EAC=∠BAG，在△EAC和△BAG中，，∴△EAC≌△BAG（SAS），∴CE=BG，∴∠AEC=ABG，∵∠AEC+∠1=90°，∠1=∠2，∴∠2+∠ABG=90°，∴∠BOE=180°﹣（∠2+∠ABG）=90°，∴CE⊥BG；（2）S△ABC=S△AEG成立．理由：作EH⊥GA交GA的延长线于点H，作BP⊥AC于点P，∴∠AHE=∠APB=90°．∵四边形ABDE和四边形ACFG都是正方形，∴AE=AB，AG=AC，∠EAB=∠GAC=90°，∵∠EAB+∠GAC+∠BAC+∠EAG=360°，∴∠EAG+∠BAC=180°．∵∠EAG+∠EAH=180°，∴∠EAH=∠BAP．在△AHE和△APB中，∴△AHE≌△APB（AAS），∴EH=BP．∵AG=AC，∴AG•EH=AC•BP，∴S△ABC=S△AEG．5. 如图①，△ABC和△ECD都是等边三角形，且点B、C、D在同一直线上，连接BE，AD．（1）求证：BE=AD；（2）如图②，点P为线段BE上一点，点F为线段AD上一点，AF=BP，连接AP，CP，PF，若PF⊥AD，求∠BPC的度数；【解析】证明：（1）∵△ABC和△ECD都是等边三角形，∴AC=BC，EC=DC，∠ACB=∠ECD=60°，∴∠ACB+∠ACE=∠ECD+∠ACE，即∠ACD=∠BCE，在△ACD于△BCE中，，∴△ACD≌△BCE（SAS），∴AD=BE；（2）解：如图②连接CF，∵AD=BE，AF=BP，∴AD﹣AF=BE﹣BP，∴PE=FD，∵△ACD≌△BCE，∴∠ADC=∠BEC，CE=CD，在△FDC与△PEC中，，∴△FDC≌△PEC（SAS），∴∠CPE=∠CFD，∵△ACD≌△BCE，∴∠DBE=∠CAD，∴∠BMA=∠EBD+∠ADB=60°，∴∠PCF=60°，∴△PCF是等边三角形，∴∠FPC=60°，∵PF⊥AD，∠FMP=60°，∴∠FPM=30°，∴∠CPM=30°，∴∠BPC=180°﹣30°=150°；6. 如图1所示，已知△ABC中，∠BAC=90°，AB=AC，AE是过点A的一条直线，且B点和C点在AE的异侧，BD⊥AE于D点，CE⊥AE与E点．（1）求证：BD=DE+CE（2）若直线AE绕点A旋转到图2所示的位置时（BD＜CE）其余条件不变，问BD 与DE，CE的关系如何？请予以证明．（3）若直线AE绕点A旋转到图3所示的位置时（BD＞CE）其余条件不变，问BD 与DE，CE的关系如何？直接写出结果，不需证明．【解析】证明：（1）∵BD⊥AE于D，CE⊥AE于E，∴∠ADB=∠AEC=90°．∵∠BAC=90°，∠ADB=90°，∵∠ABD+∠BAD=∠CAE+∠BAD=90°，∴∠ABD=∠CAE在△ABD 和△CAE中，∠ABD=∠CAE，∠ADB=∠CEA，AB=AC∴△ABD≌△CAE（AAS）∴BD=AE，AD=CE∵AE=AD+DE，∴BD=DE+CE（2）解：BD=DE﹣CE证明如下：∵BD⊥AE于D，CE⊥AE于E，∴∠DAB+∠DBA=90°∵∠BAC=90°，∴∠DAB+∠CAE=90°，∴∠DBA=∠CAE．在△DBA和△EAC中，∠D=∠E=90°，∠DBA=∠CAE，AB=AC △DBA≌△EAC（AAS）∴BD=AE，AD=CEBD=AE=DE﹣AD=DE﹣CE（3）∵BD⊥AE于D，CE⊥AE于E，∴∠DAB+∠DBA=90°∵∠BAC=90°，∴∠DAB+∠CAE=90°，∴∠DBA=∠CAE．在△DBA和△EAC中，∠D=∠E=90°，∠DBA=∠CAE，AB=AC △DBA≌△EAC（AAS）∴BD=AE，AD=CE又∵ED=AD+AE，∴DE=BD+CE．。

中考数学解题的基本模型半角模型

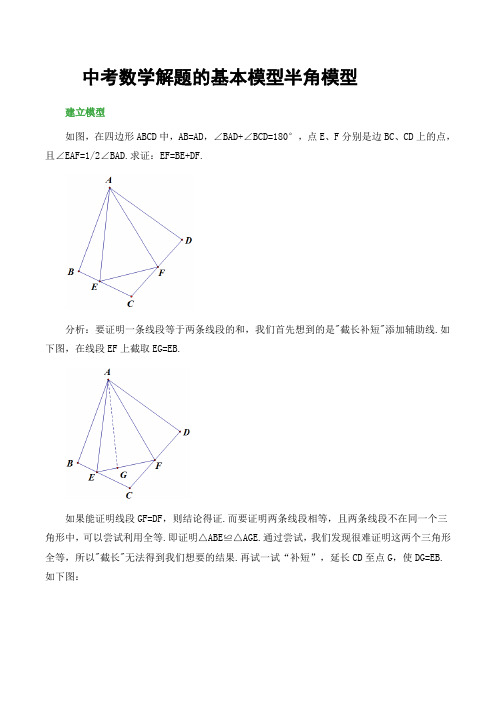
中考数学解题的基本模型半角模型建立模型如图，在四边形ABCD中，AB=AD，∠BAD+∠BCD=180°，点E、F分别是边BC、CD上的点，且∠EAF=1/2∠BAD.求证：EF=BE+DF.分析：要证明一条线段等于两条线段的和，我们首先想到的是"截长补短"添加辅助线.如下图，在线段EF上截取EG=EB.如果能证明线段GF=DF，则结论得证.而要证明两条线段相等，且两条线段不在同一个三角形中，可以尝试利用全等.即证明△ABE≌△AGE.通过尝试，我们发现很难证明这两个三角形全等，所以"截长"无法得到我们想要的结果.再试一试“补短”，延长CD至点G，使DG=EB.如下图：此时若能证明FG=FE，则FE=FG=FD+DG=FD+BE.结论得证.而要证明FE=FG，只需证明△AEF≌AGF即可.证明：延长FD至点G，使DG=BE.易证△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG.∴∠EAF=1/2∠BAD=∠BAE+∠FAD=∠DAG+∠FAD=∠GAF又∵AF=AF，∴△EAF≌△GAF.∴EF=GF=DF+DG=DF+BE反思：1、本题中的辅助线：延长DG=BE，也可以通过旋转来实现（实际上就是将三角形ABE绕点A逆时针旋转∠BAD的度数）.需要指出的是，如果用旋转，需说明C、D、G三点共线（证明∠ADG+∠ADC=180°即可）.2、题中有三个非常重要的元素：（1）∠EAF=1/2∠BAD（半角模型名称的由来）；（2）AB=AD. 共端点的两条线段相等，这点尤为关键，它为下一步的旋转提供了条件.当题中出现一个角等于另一角的一半，且共端点的线段相等时，常采用旋转，将分散的条件集中起来，为下一步的证明做好铺垫. （3）对角互补.由于对角互补的存在，通过旋转，两边的两个三角形可拼成一个大三角形，进而可证明三角形全等.一、半角结构之90°与45°先来看一道题目：如图，在正方形ABCD中，点E，F分别在BC，CD上，∠EAF=45°.求证：EF=BE+DF.证明：证明：∵四边形ABCD是正方形∴AB=AD且∠ABE+∠ADF=180°将△ABE绕点A逆时针旋转90°得到△ADG，此时点C、D、G三点共线.∴∠BAE=∠DAG，AE=AG. ∵∠EAF=45°∴∠BAE+∠DAF=∠DAG+∠DAF=∠GAF=45°∴∠EAF=∠GAF. 又∵AF=AF.∴△EAF≌△GAF.∴EF=GF=DF+DG=DF+BE.模型应用1：如图，在正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°.BE=2cm,DF=3cm.求正方形的边长.分析：根据上题的结论可知EF=BE+DF=5.设正方形的边长为x，那么CE=x-2，CF=x-3.在Rt△CEF中，根据勾股定理得，CE^2+CF^2=EF^2，即(x-2)^2+(x-3)^2=5^2，解得，x=6.所以正方形的边长为6以上的半角结构主要发生在四边形中，再次回顾半角结构中的重要元素：（1）半角（2）邻边相等（3）对角互补. 半角模型中经常通过旋转将分散的条件集中起来，进而通过三角形的全等进行证明.在三角形中同样存在半角模型，下面以一道题为例来说明三角形中的半角模型.如图，在△ABC中，∠BAC=90°，AB=AC.点D，E是BC边上两点且∠DAE=45°求证：BD^2+CE^2=DE^2分析：看到这个结论，相信大部分同学首先想到的是勾股定理，但DE,BD,CE不在同一个三角形中.所以要想办法将他们集中在一个三角形里面，根据题中条件AB=AC，共端点的两条线段相等，可以尝试旋转.证明：因为AB=AC，且∠BAC=90°.将△ABD绕点A逆时针旋转90°得到△ACG，连接EG. 如下图：由旋转的性质可知，△ABD≌△ACG.∴AD=AG，∠BAD=∠CAG，∠ABD=∠ACG=45°.∵∠DAE=45°，∴∠BAD+∠EAC=∠CAG+∠EAC=45°∴∠DAE=∠GAE∴△DAE≌△GAE(SAS)∴DE=GE在Rt△GCE中CE^2+CG^2=GE^2∵BD=CG，DE=CG∴BD^2+CE^2=DE^2反思：对于本题，我们通过旋转将分散的条件集中起来，进而得到结论。

全等三角形的六种模型全梳理(学生版)--初中数学专题训练

全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围，在三角形这一章，压轴题主要考查是证明三角形各种模型，或证明线段数量关系等，接来下我们针对其做出详细分析与梳理。

类型一、倍长中线模型目的：①构造出一组全等三角形；②构造出一组平行线。

将分散的条件集中到一个三角形中。

1【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB=8，AC=6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图2，延长AD到点E，使DE=AD，连接BE．请根据小明的方法思考：(1)如图2，由已知和作图能得到△ADC≌△EDB的理由是．A.SSSB.SASC.AASD.ASA(2)如图2，AD长的取值范围是．A.6<AD<8B.6≤AD≤8C.1<AD<7D.1≤AD≤7【感悟】解题时，条件中若出现“中点”、“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论转化到同一个三角形中．【问题解决】(3)如图3，AD是△ABC的中线，BE交AC于点E，交AD于F，且AE=EF．求证：AC=BF．2(培优)已知△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连接AD,BE，点F为BE中点．AD；(1)如图1，求证：BF=12(2)将△DCE绕C点旋转到如图2所示的位置，连接AE,BD，过C点作CM⊥AD于M点．①探究AE和BD的关系，并说明理由；②连接FC，求证：F，C，M三点共线．1.如图，△ABC中，BD=DC=AC，E是DC的中点，求证：AB=2AE．2.(1)如图1，已知△ABC中，AD是中线，求证：AB+AC>2AD；(2)如图2，在△ABC中，D，E是BC的三等分点，求证：AB+AC>AD+AE；(3)如图3，在△ABC中，D，E在边BC上，且BD=CE．求证：AB+AC>AD+AE．3.(1)阅读理解：如图①，在△ABC中，若AB=8，AC=5，求BC边上的中线AD的取值范围．可以用如下方法：将△ACD绕着点D逆时针旋转180°得到△EBD，在△ABE中，利用三角形三边的关系即可判断中线AD的取值范围是；(2)问题解决：如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF>EF；(3)问题拓展：如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=100°，以C为顶点作一个50°的角，角的两边分别交AB、AD于E、F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并说明理由．类型二、截长补短模型截长补短法使用范围：线段和差的证明(往往需证2次全等)3如图，在五边形ABCDE中，AB=AE，CA平分∠BCD，∠CAD=12∠BAE．(1)求证：CD=BC+DE；(2)若∠B=75°，求∠E的度数．4(培优)在△ABC中，BE，CD为△ABC的角平分线，BE，CD交于点F．(1)求证：∠BFC=90°+12∠A；(2)已知∠A=60°．①如图1，若BD=4，BC=6.5，求CE的长；②如图2，若BF=AC，求∠AEB的大小．1.如图，△ABC为等边三角形，若∠DBC=∠DAC=α0°<α<60°，则∠BCD=(用含α的式子表示)．2.如图，在四边形ABCD中，AB=AD,∠B+∠ADC=180°，点E、F分别在直线BC、CD上，且∠BAD．∠EAF=12(1)当点E、F分别在边BC、CD上时(如图1)，请说明EF=BE+FD的理由．(2)当点E、F分别在边BC、CD延长线上时(如图2)，(1)中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出EF、BE、FD之间的数量关系，并说明理由．3.阅读下面材料：【原题呈现】如图1，在△ABC中，∠A=2∠B，CD平分∠ACB，AD=2.2，AC=3.6，求BC的长．【思考引导】因为CD平分∠ACB，所以可在BC边上取点E，使EC=AC，连接DE．这样很容易得到△DEC≌△DAC，经过推理能使问题得到解决(如图2)．【问题解答】(1)参考提示的方法，解答原题呈现中的问题；(2)拓展提升：如图3，已知△ABC中，AB=AC，∠A=20°，BD平分∠ABC，BD=2.3，BC=2．求AD 的长．类型三、一线三等角模型应用：①通过证明全等实现边角关系的转化，便于解决对应的几何问题；②与函数综合应用中有利于点的坐标的求解。

中考数学复习满分突破(全国通用)：专题12 半角模型(原卷版)

专题12半角模型半角模型的概述：当一个角包含着该角的半角，如90°角包含着45°角，120°角包含着60°角，270°角倍角关系，且这两个角共顶点，共顶点的两条边相等，则该模型为半角模型。

解包含着135°角，即出现12题方法为：1）过公共点作旋转，2）截长补短的方法构造全等解题。

基本模型：1）90°的半角模型（常考）已知正方形ABCD中，E，F分别是BC、CD上的点，∠EAF=45°，AE、AF分别与BD相交于点O、P，则：①EF=BE+DF②AE平分∠BEF，AF平分∠DFE③C∆CEF=2倍正方形边长④S∆ABE+S∆ADF=S∆AEF⑤AB=AG=AD（过点A作AG⊥EF，垂足为点G）⑥OP2=OB2+OD2⑦若点E为BC中点，则点F为CD三等分点⑧∆APO∽∆AEF∽∆DPF∽∆BEO∽∆DAO∽∆BPA⑨ABEP四点共圆、AOFD四点共圆、OECFP五点共圆⑩∆APE、∆AOF为等腰直角三角形(11)EF=2OP(12)S∆AEF=2S∆APO(13)AB2=BP×OD(14)CE•CF=2BE•DF(15)∆EPC为等腰三角形(16)PX=BX+DP(过点E作EX⊥BD，垂足为点X)证明：①思路：延长CD到点M，使DM=BE，连接AM先根据已知条件∆ABE≌∆ADM(SAS)，由此可得AE=AM，∠BAE=∠DAM而∠BAE+∠FAD=45°，所以∠DAM+∠FAD=45°，可证明∆AEF≌∆AMF (SAS)，由此可得EF=MF，而MF=DM+DF=BE+DF，因此EF=BE+DF②思路：∵∆AEF≌∆AMF(SAS)∴∠AFM=∠AFE，∠AMF=∠AEF∴AF平分∠DFE又∵∠AMF=∠AEB∴∠AEB=∠AEF∴AE平分∠BEF③思路：C∆CEF=EF+EC+FC=(BE+DF)+EC+FC=（BE+EC）+（DF+FC）=BC+DC=2BC④、⑤思路：过点A作AG⊥EF，垂足为点G根据②证明过程可知AFG=∠AFD，∠AEB=∠AEG因此可以证明:∆ABE≌∆AGE(AAS),∆AGF≌∆ADF(AAS)所以AB=AG=AD，S∆ABE=S∆AGE，S∆AGF=S∆ADF则S∆AEF=S∆AGE+S∆AGF=S∆ABE+S∆ADF⑥思路：绕点A将∆APD逆时针旋转90°得到∆ANB,使AD，AB重合因为∆APD≌∆ANB(AAS)所以AN=AP，BN=DP，∠NAB=∠PAD，∠ADP=∠ABN因为∠ADB=∠ABD=45°，所以∠NBO=90°因为∠BAE+∠PAD=45°所以∠NAB+∠BAE=45°则∆ANO≌∆APO(SAS)所以NO=OP在Rt∆NBO中，由勾股定理可知：ON2=OB2+NB2，则OP2=OB2+OD2⑦思路：已知tan∠EAB=BEAB =12，且∠EAB+∠FAD=45°∴tan∠FAD=13（“12345型”），∴DF:AD=1:3，即点F为CD的三等分点。

第5讲角含半角模型(原卷版)

中考数学几何模型 5 ：角含半角模型st模型1：截长补短模型模型5：角含半角模型模型9：隐圆模型模型2：共顶点模型模型6：弦图模型模型10：胡不归最值模型模型3：对角互补模型模型7：轴对称最值模型模型11：阿氏圆最值模型名师点睛拨开云雾开门见山模型：中点模型模型8：费马点最值模型模型12：主从联动模型角含半角模型，顾名思义即一个角包含着它的一半大小的角。

它主要包含：等腰直角三角形角含半角模型；正方形中角含半角模型两种类型。

解决类似问题的常见办法主要有两种：旋转目标三角形法和翻折目标三角形法。

类型一：等腰直角三角形角含半角模型则：BD 2+CE 2=DE 2.3）如图，将等腰直角三角形变成任意等腰三角形时，亦可以进行两种方法的操作处理1）如图，在△ ABC 中，AB=AC ，∠BAC=90 ，点D，E在BC 上，且∠ DAE=45 ，则：BD 2+CE 2=DE 2.作法1：将△ ABD 旋转90作法2：分别翻折△ ABD, △ACE 2）如图，在△ ABC 中，AB=AC ，∠BAC=90 ，点 D 在BC 上，点E在BC 延长线上，且∠DAE=45 图示（1）名师点睛拨开云雾开门见山类型二：正方形中角含半角模型1）如图，在正方形 ABCD 中，点 E ，F 分别在边 BC ，CD 上，∠ EAF=45 °，连接 EF ，过点 A 作 AG ⊥ 于 EF 于点 G ，则： EF=BE+DF ， AG=AD.C=180 °，点 E ，F 分别在边 BC ， 1CD 上，∠ EAF= ∠BAD ，连接 EF ， 2图示（ 1）作法：将△ ABE 绕点 A 逆时针旋转 90°2）如图，在正方形 ABCD 中，点 E ，F 分别在边 CB ，DC 的延长线上， ∠EAF=45，连接 EF ，则：EF=DF-BE.图示（ 2）作法：将△ ABE 绕点 A 逆时针旋转 90°3）如图，将正方形变成一组邻边相等，对角互补的四边形，在四方形 ABCD 中， AB=AD ，∠ BAD+ ∠ 图示（ 3）作法：将△ ABE 绕点 A 逆时针旋转∠ BAD 的大小则： EF=BE+DF.典题探究启迪思维探究重点例题 1. 如图，正方形ABCD 的边长为4，点E，F分别在AB，AD 上，若CE＝5，且∠ECF＝45°，则CF变式练习>>> 1．如图四边形ABCD 中，AD∥BC，∠BCD＝90°，AB＝BC+AD，∠DAC＝45°，E为CD 上一点，且∠BAE＝45°．若CD ＝4，则△ ABE 的面积为(B．C．D．例题 2. 在正方形 ABCD 中，连接 BD ．（1）如图 1， AE ⊥ BD 于 E ．直接写出∠ BAE 的度数．（2）如图 1，在（ 1）的条件下，将△ AEB 以 A 旋转中心，沿逆时针方向旋转 30°后得到△ AB ′E ′，AB ′与 BD 交于 M ， AE ′的延长线与 BD 交于 N ．① 依题意补全图 1；② 用等式表示线段 BM 、 DN 和 MN 之间的数量关系，并证明．（ 3）如图 2，E 、F 是边 BC 、CD 上的点，△ CEF 周长是正方形 ABCD 周长的一半， AE 、AF 分别与 BD 交于 M 、 N ，写出判断线段 BM 、DN 、MN 之间数量关系的思路．变式练习 >>>2. （1）【探索发现】如图 1，正方形 ABCD 中，点 M 、N 分别是边 BC 、CD 上的点，∠ MAN ＝45°，若将△ DAN 绕点 A 顺时针旋转 90°到△ BAG 位置，可得△ MAN ≌△MAG ，若△MCN 的周长为 6，则正方形 ABCD 的边长为3 ．（2）【类比延伸】如图（ 2），四边形 ABCD 中，AB ＝AD ，∠BAD ＝120°，∠B+∠D ＝180°，点 M 、N 分别在边 BC 、CD 上的点，∠ MAN ＝60°，请判断线段 BM ，DN ，MN 之间的数量关系，并说明理由．（3）【拓展应用】如图 3，四边形 ABCD 中， AB ＝ AD ＝10，∠ ADC ＝ 120°，点 M ， N 分别在边 BC ，CD 上，连接 AM ，MN ，△ ABM 是等边三角形， AM ⊥AD ，DN ＝5（ ﹣1），请直接写出 MN 的长．不必写出完整推理过程）例题 3. 如图，在四边形 ABCD 中， AB=BC ，∠A=∠C=90°，∠B=135°，K ，N 分别是 AB ，BC 上的点，若△BKN 的周长为 AB 的 2倍，求∠ KDN 的度数 .变式练习 >>>3. 如图，正方形被两条与边平行的线段 EF ，GH 分割成四个小矩形， P 是EF 与 GH 的交点，若矩形的面积恰是矩形 AGPE 面积的 2 倍，试确定∠ HAF 的大小并证明你的结论 .PFCH例题 4. 如图，在四边形ABCD 中，AB＝AD，BC＝CD，∠ABC＝∠ADC＝90°，∠ MAN＝∠BAD．（1）如图1，将∠ MAN绕着A点旋转，它的两边分别交边BC、CD于M、N，试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系？直接写出结论，不用证明；（2）如图2，将∠ MAN 绕着A点旋转，它的两边分别交边BC、CD 的延长线于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？并证明你的结论；（3）如图3，将∠ MAN 绕着A点旋转，它的两边分别交边BC、CD 的反向延长线于M、N，试判断这一过程中线段BM、DN 和MN 之间有怎样的数量关系？直接写出结论，不用证明．达标检测领悟提升强化落实1. 请阅读下列材料：问题：正方形ABCD中，M，N分别是直线CB、DC上的动点，∠ MAN＝45°，当∠ MAN交边CB、DC 于点M、N（如图① ）时，线段BM 、DN 和MN 之间有怎样的数量关系？小聪同学的思路是：延长CB至E使BE＝DN，并连接AE，构造全等三角形经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题：（1）直接写出上面问题中，线段BM，DN和MN之间的数量关系；（2）当∠ MAN分别交边CB，DC的延长线于点M/N时（如图② ），线段BM，DN和MN之间的又有怎样的数量关系？请写出你的猜想，并加以证明；3）在图① 中，若正方形的边长为16cm，DN＝4cm，请利用（1）中的结论，试MN 的长．求2. （1）如图1，在四边形ABCD 中，AB＝AD，∠B＝∠D＝90°，E、F 分别是边BC、CD上的点，且∠ EAF＝∠ BAD ．试探究图中线段BE、EF、FD 之间的数量关系．（1）小王同学探究此问题的方法是：延长EB 到点G，使BG＝DF，连结AG，先证明△ ABG≌△ADF ，再证明△ AEG≌△ AEF，可得出结论，他的结论应是．（2）如图2，在四边形ABCD 中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD 上的点，且∠ EAF ＝∠ BAD ，上述结论是否仍然成立，并说明理由．（3）如图3，在四边形ABCD 中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD 延长线上的点，且∠ EAF ＝∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．3. 小曼和他的同学组成了“爱琢磨”学习小组，有一次，他们碰到这样一道题：“已知正方形ABCD ，点E、F、G、H 分别在边AB、BC、CD、DA 上，若EG⊥FH，则EG＝FH．”为了解决这个问题，经过思考，大家给出了以下两个方案：方案一：过点A作AM∥HF交BC于点M，过点B作BN∥EG交CD于点N；方案二：过点A作AM∥HF交BC于点M，过点A作AN∥EG交CD于点N．⋯（1）对小曼遇到的问题，请在甲、乙两个方案中任选一个加以证明（如图（1））．（2）如果把条件中的“正方形”改为“长方形” ，并设AB＝2，BC＝3（如图（2）），是探究EG、FH 之间有怎样的数量关系，并证明你的结论．（3）如果把条件中的“ EG⊥FH”改为“ EG与FH 的夹角为45°”，并假设正方形ABCD的边长为1，FH 的长为（如图（3）），试求EG 的长度．4. 已知：如图，正方形ABCD的边长为a，BM，DN 分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN ．（1）填空：与△ ABM 相似的三角形是________ ，BM?DN= ________ ；（用含 a 的代数式表示）（2）求∠ MCN 的度数；。

新北师大版八年级数学下册《线段和差证明的一点小技巧——截长补短法》教案_7

附件2
微课名称
线段和差证明的一点小技巧——截长补短法
教师单位
知识点来源
□学科：数学 □年级：八年级 □教材版本：北师大版
□所属章节：第一章
录制工具和方法
录屏软件+PPT
设计路
首先介绍截长补短法的概念，然后通过实例讲解如何利用截长补短法解决线段和差的证明问题。最后对线段和差证明中的截长补短法进行总结
结尾：最后对线段和差证明中截长补短法进行总结
应用说明
适用于八年级学生，已经有了三角形全等的判定及性质，等腰三角形的判定与性质，线段垂直平分线的判定与性质等基础后再学习
教学设计
内容
教学目的
通过线段和差证明中截长补短法的总结，让学生学会用截长补短法解决线段和差的证明
教学重点难点
如何利用截长补短法解决线段和差的证明问题
教学过程
导入：引入课题，并介绍截长补短法的概念及应用范围
内容讲解：以两个例子加以说明，其中例一采用了两种方法，即截长法和补短法，两种方法，两种不同的思路，通过实例引导学生认识在线段和差证明中究竟如何使用截长补短法，例二在例一的基础上难度有所增加，设计上采用了先从结论入手分析的方式，一步一步引导学生联系已知，分析出解决问题的方法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

32
H A B F E 1G
E
F D C B A
D C B A O G A
B C D
A B
C 初中几何之截长补短模型
模型截长补短如图①，若证明线段AB 、CD 、EF 之间存在 EF=AB+CD ，可以考虑截长补短法。

截长法：如图②，在EF 上截取EG=AB ，再证明 GF=CD 即可。

补短法：如图③，延长AB 至H 点，使BH=CD ，再证明AH=EF 即可。

模型分析
截长补短的方法适用于求证线段的和差倍分关系。

截长，指在长线段中
截取一段等于已知线段；补短，指将短线段延长，延长部分等于已知线段。

该类题目中常出现等腰三角形、角平分线等关键词句，可以采用截长补短法
构造全等三角形来完成证明过程。

模型实例
例1．如图，已知在△ABC 中，∠C=2∠B ，AD 平分∠BAC 交BC 于点D 。

求证：AB=AC+CD 。

例2．如图，已知OD 平分∠AOB ，DC ⊥OA 于点C ，∠A=∠GBD 求证AO+BO=2CO 。

精练1．如图，在△ABC 中，∠BAC=60°，AD 是∠BAC 的平分线，且
AC=AB+BD 。

求∠ABC 的度数。

E A
B
C D E A B C D F E
A B C D A
O E
A B C D 2．如图，∠ABC+∠BCD=180°，BE 、CE 分别平分∠ABC 、∠BCD 。

求证：AB+CD=BC 。

3．如图，在△ABC 中，∠ABC=60°，AD 、CE 分别平分∠BAC 、∠ACB 。

求证AC=AE+CD 。

4．如图，在△ABC 中，∠ABC=90°，AD 平分∠BAC 交BC 于点D ，∠C=30°，
BE ⊥AD 于点E 。

求证：AC-AB=2BE 。

5．如图，Rt △ABC 中，AC=BC ，AD 平分∠BAC 交BC 于点D ，CE ⊥AD 交AD 于F
点，交AB 于点E 。

求证：AD=2DF+CE 。

6．如图，五边形ABCDE 中，AB=AC ，BC+DE=CD ，∠B+∠E=180°。

求证：AD 平分∠CDE 。

D C B A M
N
初中几何之半角模型
模型1 倍长中线或类中线（与中点有关的线段）构造全等三角形已知如图：
①∠2=1
2∠AOB ；②OA=OB 。

连接F ′B ，将△FOB 绕点O 旋转至△FOA 的位置，连接F ′E 、FE ，可得△OEF ′≌△OEF 。

证明：
精品练习1．如图，已知正方形ABCD 中，∠MAN=45°，它的两边分别交线段
CB 、DC 于点M 、N 。

（1）求证：BM+DN=MN ；（2）作AH ⊥MN 于点H ，求证：AH=AB 。

图2A M B D C N 1图B A C D M N A F E B C D A B C D M
N
2．在等边△ABC 的两边AB 、AC 上分别有两点M 、N ，D 为△ABC 外一点，且∠MDN=60°，∠BDC=60°，BD=DC 。

探究：当M 、N 分别在线段AB 、AC
上移动时，BM 、NC 、MN 之间的数量关系。

（1）如图①，当DM=DN 时，BM 、NC 、MN 之间的数量关系是；
（2）如图②，当DM ≠DN 时，猜想（1）问的结论还成立吗？写出你的猜想并加以证明。

3．如图，在四边形ABCD 中，∠B+∠ADC=180°，E 、F 分别是BC 、CD 延长线上的点，且∠EAF=
12∠BAD 。

求证：EF=BE-FD 。

4、如图，正方形ABCD ，M 在CB 延长线上，N 在DC 延长线，∠MAN=45°。

求证：MN=DN-BM 。