复变函数柯西积分
复变函数_柯西积分公式
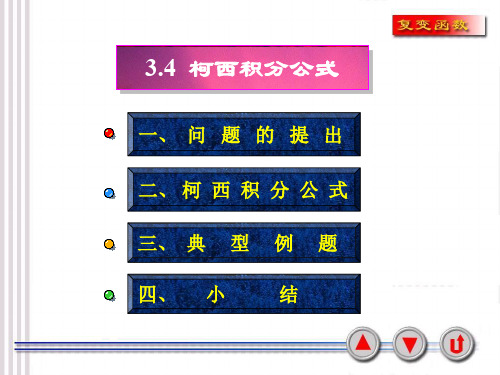
lim
z 0
f
'( z0
z) z
f
'(z0 )
2!
f (z)
2 i
C (z z0 )3 dz.
依次类推,用数学归纳法可得
f
(n)(z0 )
n!
2 i
f (z) C (z z0 )n1 dz.
18
例6 计算I
C
1 z3(z
1)
dz, 其中C为
|
16
f (z)在C上解析, f (z)在C上连续,
则M ,使得
f
(z)
M,d
min zC
z
z0
11
z z0
d, z z0
. d
取 z 1 d ,则有 2
d
1
2
z z0 z
I z
z z0
ML
d 3
z , 2 z z0 z
( L — C的 长 度 )
d
.
显 然 ,lim I 0,从 而 有 z 0
f '(z0 )
lim
z 0
f (z0
z) z
f (z0 )
1
2
i
f (z) C (z z0 )2 dz.
(*)
17
再利用()式及推导()的方法可证n 2的情形.
f
''(z0 )
f (z) dz 将接近于 f (z0 ) dz. ( 减小)
C z z0
C z z0
f (z0 ) dz
C z z0
复变函数的积分及柯西公式
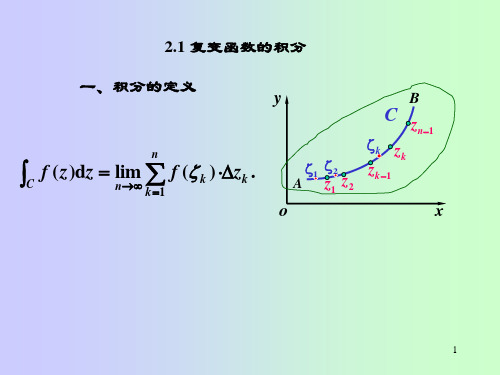
f z dz u iv dx idy
c c
udx vdy i vdx udy
c c
f x t iy t z t dt
2
三、复变函数积分的性质
(1) f ( z )dz
C Cdz;
( 2) kf ( z )dz k f ( z )dz; ( k为常数)
C
( 3) [ f ( z ) g( z )]dz f ( z )dz g( z )dz;
C C C
3
2.2 柯西定理
单连通区域的柯西定理:如果函数f(z)在闭单连通区域 中解析,则沿着中任何一个分段光滑的闭合围道c的积 分为:
2.1 复变函数的积分 一、积分的定义
y
C
f ( z )dz lim f ( k ) zk .
n k 1
n
A
1 2
z1 z2
k z k zk 1
C z n 1
B
o
x
1
二、复变函数积分公式
f z u x, y iv x, y z x iy , dz dx idy
复连通区域的柯西定理:如果函数f(z)是复连通区域中 的单值解析函数,则有:
4
2.3 不定积分
5
2.4 柯西公式
a,改记作z,积分变数用������表示,也可写作
推论: 1、模数原理:设f(z)在某闭区域上解析,则|f(z)|只 能在边界线 l 上取极大值。 2、刘维尔定理:如f(z)在全平面解析且有界,则f(z) 必为常数。
复变函数的积分 柯西定理

第三章 复变函数的积分§3-1复变函数的积分【刘连寿、王正清编著《数学物理方法》P 29-31】复变函数积分的定义:设C 为复平面上以0z 为起点,而以z 为终点的一段路径(即一根曲线),在C 上取一系列分点011,,,,n n z z z z z -=把C 分为n 段,在每一小段[1k k z z -]上任取一点k ξ作和数:()()()111nnn k k k k k k k S f z z f z ξξ-===-=∆∑∑, 其中1k k k z z z -∆=-如果当n →∞且每一小段的长度(1||||k k k z z z -∆=-)趋于零时, 和式()1nk kk f z ξ=∆∑的极限存在,并且其值与k z 及k ξ的选取方式无关,则称这一极限为()f z 沿路径C 由0z 到z 的积分:()()1limlim nn k k Cn n k fz dz S f z ξ→∞→∞===∆∑⎰,C 称为积分路径(()f z 在C 上取值,即z 在C 上变化)。
若C 为围线(闭的曲线),则积分记为: ()Cf z dz ⎰. (围道积分)几点说明:1. 复变函数的积分不仅与积分端点有关,还与积分路径有关。
(与我们以前在高等数学中学过的实变函数的线积分类似。
)2.因为 z x iy =+,dz dx idy =+,()()(),,f z u x y iv x y =+,于是()()()(),,CCf z dz u x y iv x y dx idy =++⎡⎤⎣⎦⎰⎰()()()(),,,,C C u x y dx v x y dy i v x y dx u x y dy ⎡⎤⎡⎤=-++⎣⎦⎣⎦⎰⎰,所以复变函数的积分可以归结为两个实变函数的线积分,它们分别是复变函数积分的实部和虚部。
3.从复变函数积分的定义出发,可以直接得出复变函数的积分具有如下简单性质:(1)0C dz z z =-⎰,z 、0z 分别为C 之起点、终点。
复变函数-柯西积分定理

显然, F(z)
z
f ( )d
是 f (z)的一个原函数。
z0
利用原函数的概念, 可以得出复积分的牛顿— 莱布 尼兹公式 :
定理 设 f (z) 在单连通区域D 内解析, F (z) 是 f (z) 的 一个原函数, 则对 a, b D, 有
b a
f
( z )dz
F(z)
b a
F(b)
F (a)
注:
(1) 本公式只用于计算与积分路径无关的积分;
(2) 在求原函数时, 实函数的换元积分法和分步 积分法仍成立。
例 计算积分 24i z 2dz 1 i
解:
z2
在 整 个 复 平 面 上 解 析, 且
1
z3
z2
3
24i z2dz 1 z3 24i 1 (86 18i)
1 i
3 1i
§3.2 柯西积分定理
问题 : f (z) 在什么条件下, C f (z)dz 仅与积分路径的起点
和终点有关, 而与积分路径无关呢?
定理(柯西积分定理) 若 f (z) 在单连通域 D 内处处解析, 那么 函数 f (z) 沿 D 内任意一条闭曲线C 的积分为零, 即
C f (z)dz 0
推论 如果 f (z) 在单连通域 D 内处处解析, 则 C f (z)dz
f (z0 ) 2i
dz or C z z0
1 f ( )
f (z)
d
2 i C z
称之为柯西积分公式。
说明: (1) 通过柯西积分公式, 可以把函数在C 内部任 一点z 的值用它在边界C 上的值通过积分来表示;
(2) 给出了解析函数的一个积分表达式:
C
复变函数课件:3_3柯西积分公式

使以Lρ 为边界的闭圆盘包含在D内(如图).
记 D ρ 为D挖去以Lρ 为边界的 开圆盘所得到的闭区域.
f (ξ ) 于是f (ξ )及 在 D ρ 上连续,在区域Dρ内解析. ξ −z
所以由定理3.2.7有,
f (ξ ) f (ξ ) ∫L ξ − z dξ = ∫Lρ ξ − z dξ .
证 作以z0心,以ρ (0 < ρ < ρ 0 )为半径的圆Lρ,
根据多连通区域上的柯西积分定理得
f ( z) f ( z) ∫L z − z0 dz = ∫Lρ z − z0 dz.
上式对满足0 < ρ < ρ 0的任何ρ 成立,于是
f ( z) f ( z) ∫L z − z0 dz = lim0 ∫Lρ z − z0 dz. ρ→ f ( z) 下证 lim ∫ dz=2π if ( z0 ). ρ →0 Lρ z − z 0 f ( z0 ) dz 由于2π if ( z0 ) = f ( z0 ) ∫ =∫ dz , 则 Lρ z − z Lρ z − z 0 0
π sin z 4 dz = ∫=2 z 2 − 1 z
∫
z +1 =
π sin z 4 dz + 2 1 z −1
2
∫
z −1 =
π sin z 4 dz z2 − 1 1
2
2 2 = πi + πi = 2πi . 2 2
3z − 1 dz. 例3 计算I = ∫ | z | = 2 ( z + 1)( z − 3) 3z − 1 解 显然f ( z ) = 只有一个奇点z = −1在 | z |< 2 ( z + 1)( z − 3) 3z − 1 内, 且函数g ( z ) = 在 | z |< 2内解析,在 | z |≤ 2内连续. z −3
柯西积分逆定理

柯西积分逆定理
柯西积分逆定理是复变函数中的一个基本定理,它指出如果一个函数在一个区域内的柯西积分都为零,则该函数在该区域内是全纯函数。
换句话说,只有全纯函数的柯西积分才能为零。
这个定理的逆定理同样成立,即如果一个函数在一个区域内是全纯函数,则该函数在该区域内的柯西积分都为零。
这个定理的证明需要用到格林公式和柯西—黎曼方程等一系列工具和技巧。
柯西积分逆定理在复变函数的研究中具有重要的应用价值,它为我们研究全纯函数提供了一个非常有力的工具。
同时,它也是复变函数理论中的一个重要定理,是我们学习和掌握复变函数知识的基础之一。
- 1 -。
复变函数柯西积分公式
复变函数柯西积分公式
柯西积分,即Cauchy Integral Formula,包括复变函数的一种重要的积分公式,是复变函数理论的基础。
柯西积分的出现极大地拓展了复变函数数学研究的视野,把它带入一个完整的复变函数空间,使科学家们能够有效地描述物理和复杂体系的运作。
柯西积分可以表示为:在复平面上的无界区域Ω中,若C为边界,a则是内部点,f(z)为一个连续的复变函数,则:
$$\oint_{C} f\left(z\right)dz=2 \pi i
\sum\left(f\left(a_{k}\right)\right)$$
其中,a_{k}为区域Ω内的根,且取出其中局部极小值。
因此,柯西积分也可以表述为,当根的改变对应的复变函数的值的积分之和。
此外,当区域Ω趋近于无界时,柯西积分也可以表示为简单的复变函数积分表达式。
柯西积分是复变函数研究中的基础,它被广泛用于使函数能够有效地描述物理和复杂体系的运作,以及用于解决合理的分析表示中的无限级数的和等问题。
由于柯西积分的出现,复变函数数学研究更加深入并常常被用于数学研究以及工程中,如信号处理、电磁学、电动学和更多其他领域。
复变函数柯西定理
复变函数柯西定理
柯西定理(Cauchy's Theorem)是复变函数论里极为重要的定理,其联系的柯西积分(Cauchy's Integral)应用于复平面单连通和复连通区域分别导致复变函数在某点附近的泰勒展开(Taylor Expansion)和洛朗展开(Laurent Expansion)。
柯西定理说:解析函数在复平面解析区域里的积分是路径独立的。
另一种表达是解析函数在其解析区域里的环路积分为零。
(I) 柯西定理的证明一般是结合联系面积分与线积分的格林定理(Green's Theorem):
[注:格林定理可以直接证明,亦可由联系面-线积分的旋度(Curl)公式给出。
]
以及解析函数的柯西-黎曼方程(Cauchy-Riemann Equation):
具体而言:
现在:1. 利用(1),对于实部和虚部分别取(P,Q)=(u,-v)和(P,Q)=(v,u); 2. 利用(2),环路积分为零得证。
(II) 另一个角度,可证明如下:
对于解析函数,由柯西-黎曼方程可知:(3)中的实部:udx-vdy 和虚部:vdx+udy 分别是全微分形式,可写作某实函数的全微分:
而实函数全微分的环路积分为零。
复变函数-柯西积分定理
z
1
i
dz
C
1 z
dz
1 2
C
zБайду номын сангаас
1
i
dz
1 2
C
z
1
dz i
2i 0 0 2i
(2)
I
C
1 z
dz
1 2
C
z
1
i
dz
1 2
C
z
1
i
dz
0 0 2 i
2
i
| z | 1 2
| z i | 1 2
例 不经计算, 验证下列积分值为零, 其中, C 为| z | 1。
1
1
(1) C z2 5z 6 dz (2) C (z2 2)( z3 3) dz
i(12z
2 0
2)
2(6z
2 0
1)i
Morera 定理 : 若函数 f (z) 在单连通域 D 内连续,且对 D 内任意封闭
曲线 C 有 ÑC f (z)dz 0,则 f (z) 在区域 D 内解析。
Liouville 定理 : 若 f (z) 在复平面上解析且有界,则 f (z) 恒为常数。
当 f (z) 有奇点时,不能直接应用该定理。
例 计算
1 C z(z2 1) dz
(1) C 为| z | 1 ; (2) C 为| z i | 1
2
2
解
:
由于
1 z(z2
1)
1 z
1 2
z
1
i
1 2
z
1
i
所以
| z | 1 2
| z i | 1 2
复变函数04
由C-R方程 - 方程
∂u ∂v ∂ u dy + g ( x ) ⇒v=∫ = ∂x ∂ y ∂x
再利用上式结果, 再利用上式结果,求v(x, y)的偏导数 的偏导数
∂v ∂ ∂u ∂u d y + g ′( x ) = − = ∫ ∂ x ∂ x ∂x ∂y
解出g 再求g 的积分, 解出 ′ (x), 再求 ′ (x)的积分 得到 的积分 得到v(x, y). 已知v(x, y), 求u(x, y)的方法基本相同 的方法基本相同. 已知 的方法基本相同
I = i∫
2π
0
f ( z0 + re )dθ
iθ
由于f 连续 连续, 由于 (z)连续 并且积分 I 在C上的值与 r 上的值与 无关, 无关 令 r → 0 得: f(z) → f(z0) 即
I = i∫
2π
0
f ( z0 )dθ = 2 πi f ( z0 )
4
f (z) dz = 2 π i f ( z 0 ) 即 ∫ C z−z 0 上式称为柯西积分公式 柯西积分公式 f(z)在区域 内解析; 在区域D内解析 若f(z)在区域D内解析; C为D内的任何一条正向简单闭曲线 内的任何一条正向简单闭曲线; 为 内的任何一条正向简单闭曲线 它的内部完全含于D; 它的内部完全含于 z0为C内的任意一点 则 内的任意一点. 内的任意一点 f (z) 1 f ( z0 ) = ∫C z − z0 dz 2 πi
15
部和虚部具有任意阶的连续偏导数, 部和虚部具有任意阶的连续偏导数,将上 式中的两个等式分别对x和 求偏导数 求偏导数, 式中的两个等式分别对 和y求偏导数,得
∂ u ∂ v ∂ u ∂ v , = =− 2 2 ∂x ∂y∂x ∂y ∂x∂y 2 2 ∂ v ∂ v 当二阶偏导数连续时 , = ∂y∂x ∂x∂y 2 2 2 2 ∂ u ∂ u ∂ v ∂ v 从而 2 + 2 = 0 ; 同理 2 + 2 = 0. ∂x ∂y ∂x ∂y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z0 , z1 为 D 内两个点,因为
f (z) g(z)' f '(z)g(z) f (z) g '(z)
而 f '(z) , g '(z) 仍为解析函数 , 所以有
f z1 z0
'(z)
g(z)
f (z) g '(z)dz
c1
c2
或 f (z)dz f (z)dz
c1
c2
即在区域内的一个解析函数沿闭曲线的积分,不
因闭曲线在区域内作连续变形而改变积分值 .
复合闭路定理: 设C为多连通域D内的一条简单闭曲线,
c1 , c2 ,..., cn为 C 内 n 条互不相交又互不包含的
简单闭曲线 .
c1 , c2 ,..., cn 所包围区域全含于D,f (z) 在 D
处处解析 ,则积分 f (z)dz 与连结起点及 c
终点的路线无关. 其逆命题是一莫瑞拉(Morcra) 定理;设D是复平面
上的单连通域,函数f (z) 在 D 上连续,若在D内任
一条闭曲线 C 上都有 f ( z)dz 0 c
则函数 f (z) 在 D 内解析.
6.复变函数积分的牛顿—莱布尼兹公式
c f (z)dz c f (z) ds ML
4.复变函数积分的计算 (1) 化为两个实二元函数的线积分计算
设 f (z) u(x, y) iv(x, y) 在 C上连续,
c f (z)dz c udx vdy ic vdx udy
(2) 若曲线 C 由方程 z(t) x(t) iy(t) , t t t
2.复变函数的积分
设函数 f (z) 在D内有定义,C 为 D内一条起点 为 终点为 的光滑有向曲线.将 C 任意分为
n 个小弧段,分点为 z0 , z1 ,..., zn
在每个小弧段上任取一点 k zk1zk
作积分和式 n f (k ) zk 其中 zk zk zk1 . k 1
如果 f (z) u iv 在单连通域 D 内处处解析
则变上限积分确定的函数 F(z)
z
f (z)d
z0
为 D 内的一个解析函数,并且 F '(z) f (z)
F(z) 是 f (z) 的一个原函数.
牛顿—莱布尼兹公式 若函数 f (z) 在单连通
域 D 内处处解析,G(z) 在 D 内的一个原函数,
2 i
c f (z) /(z z0 )n1 , n 1, 2,...
这点是与实变量函数有本质不同的.
一个实函数 f (x) 即使在 (a,b) 上可导, 其导数 f '(x) 不一定可导,甚至可能不连续.
第三章 哥西定理 哥西积分
2.学习与考试要求 4.本章疑难解析
1.本章知识提要
3. 重点与难点
5.本章典型例题
7.本章测试题
6.本章习题解答
第三章 哥西定理 哥西积分知识提要 一. 知识提要
c 设 是复平面上的一条曲线,其方程为
z z(t) x(t) iy(t) t
且满足
f (z) c (z z0 )n1 dz
n 1, 2,...
说明一个解析函数的导数仍是解析函数.
若 f (z) 在 D 内解析,C为闭曲线 z z0 r ,
z0 及 c 和 c 的内部都属于D, 则有 :
f
n ( z0 )
n
!
M rn
其中 M max f (z) 称柯西不等式.
如果不论对 C 的分法及 k 的取法如何,只要
max sk ( sk 是小弧段长度)趋于零时,
积分和式有唯一极限,则称这极限值为函数 f (z)
沿曲线 C 的积分.记为
n
n
k1
c
f
(z)dz
lim 0 k 1
f
(k )
zk
当 C 为闭曲线时 , 积分记为
c f (z)dz
6. 复变函数积分的牛顿-莱布尼兹公式与实一元 函数定积分的牛顿-莱布尼兹公式有何不同 ? 答:两者在形式和结果上都是类似的,只是复
变函数积分中对被积函数的要求更高一些 .在
一元实际分中,f (x) 只要在 a,b 上连续 ,
G(x) 是 f (x) 的一个源函数,就有公式成立; 而在复变函数积分中,除要求 f (x) 解析外 ,
f
(z)
g(z)
z1 z0
或
z1 f (z) g '(z) z0
f (z) g(z)
z1
z0
z1 f '(z) g(z)
z0
如
1i z ez dz
1
z ez
1i
1
1i ez dz
1
(z 1)ez
1i 1
ie1i
ie(cos1 i sin1)
单连通域时,定理的结论不成立.
如 f (z) 1 在圆环域 1 z 3 内解析,C
z
2
2
为城内以原点为圆心的正向圆周,但
c
1 z
dz
2
i
0
同时,要注意定理不能反过来用,即不能因为有某个
f (z)dz 0 , 而说 f (z) 在所包围区域 D 解析. c
如
c
f (z)dz
学习与考试要求 (1) 理解复变函数积分的概念,了解积分的性质,
会求复变函数的积分. (2) 理解柯西—古萨积分定理,掌握牛顿—莱布尼
兹公式、柯西积分公式 , 高阶导数公式和复合 闭路定理,能熟练运用来计算复变函数的积分.
(3) 理解 解析函数的导数 仍是解析函数 ,解析
函数无限次可导的概念 . (4) 理解调和函数与共轭调和函数的概念,会求它们
可以放宽到复连通域,若 c0 为外边界曲线 ,则:
c1,......., ck 全 部内边界曲线, f (z) 在
cc0 cc1 ck 所围区域内解析时,柯西积
分公式任然成立,即
1
f (z0 ) 2 i c f (z) /(z z0 )dz
n 1
i 1
外边界线 c0 取逆时针方向,内边界曲线取顺
时针方向,即
f (z)dz
f (z)dz 0
c
c0 c0 c1 c2 ck
其中 c0 为内边界曲线;
2) 内边界曲线 c1,......., ck 必须是互不相交,互
不包含的 ;
3)边界曲线必须是全部,这时才有
f (z)dz 0 c0 c0 c1 c2 ck
还要求 D 是单连同域 .
7. 如何应用复合闭路定理计算复变函数的积分 ? 应注意哪些问题 ? 答 : 应用复合闭路定理可以把沿区域外边界线 的回路积分化为沿区域内边界线的回路积分,使 积分变得易于计算 .对于积分回路的内部是 复 连通域的情形,显得尤为重要. 应用复合闭路定理时,要注意以下几个问属: 1) 边界曲线的方向.
2 i
ci f (z) /(z z0 )dz
9. 解析函数的高阶导数公式说明解析函数的导数 与实变函数的导数有何不同?
答: 解析函数的高阶导数公式说明:只要函数
f (z) 闭区域 D 内处处可微 ,就一定无限
次处处可微,且它的各阶导数均为 上的解 析函数,并有
f (n) (z) n!
内解析,则:
n
1) f (z)dz
f (z)dz
c
k 1 ck
c1 , c2 ,..., cn 均取正向 ;
2) f (z)dz 0
其中 为由 c1 , c2 ,..., cn 组成的复合闭路 .
8.柯西积分公式
若函数f (z) 在区域D内处处解析,C为D内的
任意一条正向筒单闭曲线,它的内部全部属于D.
1 z2
z 1
dz
0
,
但
f
(z)
1 z2
在 z 1 内并不处处解析.
莫瑞拉(Morcra)定理要求在 D 内任一条闭曲线上
都有 f (z)dz 0 时, f (z) 才在 D 内解析 . c
5. 复变函数积分法中是否有与实一元函数类似的 分部积分公式 ? 在什么条件下可以使用 ? 答 : 有.
给出,则 f (z)dz t f z(t)z '(t)dt
c
t
5.柯西—古萨(Cauchy-Goursat)定理
如果函数 f (z) 在单连通域 D 内处处解析,
则 f (z) 沿 D 内任一条闭曲线 C 的积分为
零.
即
f ( z)dz 0
c
其等价命题是:如果函数 f (z) 在单连通域 D 内
设 z0 为 C 内任意—点,则有
f
(z0 )
1
2 i
c
f (z) dz z z0
即一个解析函数 f (z) 在曲线 C 内任一点 z0 的值
可用它在边界上的值来表示.
当 C为圆周 z z0 R 时,z z0 Rei
公式可以写为
f
( z0
)
பைடு நூலகம்
1
2
2 0
f (z0
当 C 为连续函数时,积分 f (z)dz 一定存在. c
3.复变函数积分的性质
(1) 若 f (z) , g(z) 沿曲线 c 可积 a , b 为复常数,则
ca f (z) bg(z) dz a c f (z)dz bc g(z)dz
