人工智能-课后作业
人工智能课后习题

棋盘中棋子位置不同的个数。这里,综合数据库中的初始状态矩阵,能满足规则
R1、R2、
R4 的条件,所以有三条匹配规则。利用启发式函数决定哪一条规则为启用规则。因为规则
R4 的启发式函数值 h(x)=5 ,规则 R1 的 h(x)=6 ,规则 R2 的 h(x)=7 ,也就是说,规则 R4 所
得到的新状态与目标状态差距最小,所以启用规则
2.18,语义网络 2.7
2.12 解:首先建立棋盘变换的产生式规则。如果把棋盘的每一种布局看做是一个状态矩
阵,本题就变成了从初始状态矩阵到目标状态矩阵的一种变化。
所谓棋盘状态的变化
就是希望棋盘上空格周围的棋子能走进空格, 这也可以理解为移动空格, 只要实现空格的上、
下、左、右四种移动即可。 可通过建立四个条件一操作型的产生式规则, 来实现这四种移动。
R(f,j)表示从右岸将第 j 样东西带回左岸。
所以,所定义的算符组 F 中可能有 8 种算符:
F: L(f, 0),L(f ,1),L(f ,2),I(f,3), R(f,0),R(f ,1), R(f,2),R(f ,3)。
这里要指出的是,操作算符中的 f 可以不要,也就是说,完全可以把操作算符定义成
4*4*2=32 种。各状态的
形式描述如下:
So=(3,3,1), S1=(3, 2,1), S2=(3,1,1), S3=(3,0,1), S4=(3,3,0), S5=(3, 2,0), S6=(3,1,0), S7=(3,0,0), S8=(2,3,1), S9=(2, 2,1), S10=(2, 1,1),S11=(2,0,1), S12=(2,3, 0),S13=(2,2,0),S14=(2, 1,0),S15=(2,0, 0) S16=(1,3, 1),S17=(1,2,1),S18=(1, 1,1),S19=(1,0, 1),
人工智能课后作业
解:(1) :定义谓词P(x):x是人L(x, y):x喜欢y其中,y的个体域是{梅花,菊花}。
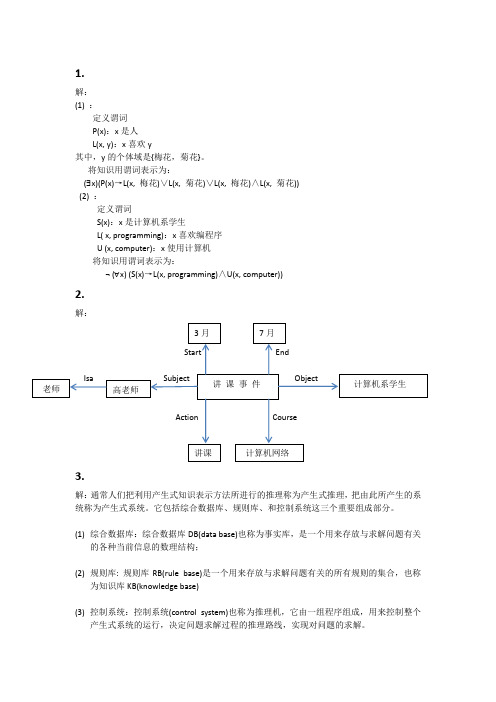
将知识用谓词表示为:(∃x)(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2) :定义谓词S(x):x是计算机系学生L( x, programming):x喜欢编程序U (x, computer):x使用计算机将知识用谓词表示为:¬ (∀x) (S(x)→L(x, programming)∧U(x, computer))2.解:3.解:通常人们把利用产生式知识表示方法所进行的推理称为产生式推理,把由此所产生的系统称为产生式系统。
它包括综合数据库、规则库、和控制系统这三个重要组成部分。
(1)综合数据库:综合数据库DB(data base)也称为事实库,是一个用来存放与求解问题有关的各种当前信息的数理结构;(2)规则库: 规则库RB(rule base)是一个用来存放与求解问题有关的所有规则的集合,也称为知识库KB(knowledge base)(3)控制系统:控制系统(control system)也称为推理机,它由一组程序组成,用来控制整个产生式系统的运行,决定问题求解过程的推理路线,实现对问题的求解。
解: 采用归结反演,存在如下归结树,故该子句集为不可满足5. 解: 证:先转化成子句集 对F ,进行存在固化,有 P(f(v))∧(Q(f(w)))得以下两个子句P(f(v)),Q(f(w))对﹁G ,有﹁ P(f(a))∨﹁P(y) ∨﹁先进行内部合一,设合一{f(a)/y} ﹁ P(f(a)) ∨﹁Q(f(a))再对上述子句集进行归结演绎推理。
其归结树如右图所示,即存在一个到空子句的归结过程。
因此G 为真。
人工智能课后习题第3章 参考答案

第3章确定性推理参考答案3.8 判断下列公式是否为可合一,若可合一,则求出其最一般合一。
(1) P(a, b), P(x, y)(2) P(f(x), b), P(y, z)(3) P(f(x), y), P(y, f(b))(4) P(f(y), y, x), P(x, f(a), f(b))(5) P(x, y), P(y, x)解:(1) 可合一,其最一般和一为:σ={a/x, b/y}。
(2) 可合一,其最一般和一为:σ={y/f(x), b/z}。
(3) 可合一,其最一般和一为:σ={ f(b)/y, b/x}。
(4) 不可合一。
(5) 可合一,其最一般和一为:σ={ y/x}。
3.11 把下列谓词公式化成子句集:(1)(∀x)(∀y)(P(x, y)∧Q(x, y))(2)(∀x)(∀y)(P(x, y)→Q(x, y))(3)(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y)))(4)(∀x) (∀y) (∃z)(P(x, y)→Q(x, y)∨R(x, z))解:(1) 由于(∀x)(∀y)(P(x, y)∧Q(x, y))已经是Skolem标准型,且P(x, y)∧Q(x, y)已经是合取范式,所以可直接消去全称量词、合取词,得{ P(x, y), Q(x, y)}再进行变元换名得子句集:S={ P(x, y), Q(u, v)}(2) 对谓词公式(∀x)(∀y)(P(x, y)→Q(x, y)),先消去连接词“→”得:(∀x)(∀y)(¬P(x, y)∨Q(x, y))此公式已为Skolem标准型。
再消去全称量词得子句集:S={¬P(x, y)∨Q(x, y)}(3) 对谓词公式(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y))),先消去连接词“→”得:(∀x)(∃y)(P(x, y)∨(¬Q(x, y)∨R(x, y)))此公式已为前束范式。
(完整版)人工智能课后习题

(完整版)人工智能课后习题第一章绪论1、什么是人工智能?试从学科和能力两方面加以说明。
答:学科:是计算机科学中涉及研究、设计和应用智能机器的一个分支,他的近期主要目标在于研究用机器来模仿和执行人脑的某些智力功能,并开发相关理论和技术。
能力:是智能机器所执行的通常与人类智能有关的智能行为,这些智能行为涉及学习、感知、思考、理解、识别、判断、推理、证明、通信、设计、规划、行为和问题求解等活动。
2、为什么能够用机器模仿人的智能?答:物理符号系统的假设:任何一个系统,如果它能够表现出智能,那么它就必定能执行输入符号、输出符号、存储符号、复制符号、建立符号结构、条件性迁移6种功能。
反之,任何系统如果具有这6种功能,那么它就能够表现出智能(人类所具有的智能)。
物理符号系统的假设伴随有3个推论。
推论一: 既然人具有智能,那么他(她)就一定是个物理符号系统。
推论二: 既然计算机是一个物理符号系统,它就一定能够表现出智能。
推论三: 既然人是一个物理符号系统,计算机也是一个物理符号系统,那么我们就能够用计算机来模拟人的活动。
3、人工智能研究包括哪些内容?这些内容的重要性如何?答:1)认识建模。
认识科学是人工智能的重要理论基础,涉及非常广泛的研究课题。
2)知识表示。
知识表示、知识推理和知识应用是传统人工智髓的三大核心研究内容其中,知识表示是基础,知识推理实现问題求解,而知识应用是目的。
知识表示是把人类知识概念化、形式化或模型化。
3)知识推理。
知识推理,包括不确定性推理和非经典推理等,似乎已是人工智能的一个永恒研究课题,仍有很多尚未发現和解决的问题值得研究。
4)知识应用。
人工智能能否获得广泛应用是衡量其生命力和检验其生存力的重要标志。
5)机器感知。
机器感知是机器获吹外部信息的基本途径。
6)机器思维。
机器思维是对传感信息和机器内部的工作信息进行有目的的处理。
7)机器学习。
机器学习是继专家系统之后人工智能应用的又一重要研究领域,也是人工智能和神经计算的核心研究课題。
人工智能课后习题第2章 参考答案

第2章知识表示方法参考答案2.8设有如下语句,请用相应的谓词公式分别把他们表示出来:(1)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
解:定义谓词P(x):x是人L(x,y):x喜欢y其中,y的个体域是{梅花,菊花}。
将知识用谓词表示为:(∃x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2) 有人每天下午都去打篮球。
解:定义谓词P(x):x是人B(x):x打篮球A(y):y是下午将知识用谓词表示为:(∃x )(∀y) (A(y)→B(x)∧P(x))(3)新型计算机速度又快,存储容量又大。
解:定义谓词NC(x):x是新型计算机F(x):x速度快B(x):x容量大将知识用谓词表示为:(∀x) (NC(x)→F(x)∧B(x))(4) 不是每个计算机系的学生都喜欢在计算机上编程序。
解:定义谓词S(x):x是计算机系学生L(x, pragramming):x喜欢编程序U(x,computer):x使用计算机将知识用谓词表示为:¬(∀x) (S(x)→L(x, pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。
解:定义谓词P(x):x是人L(x, y):x喜欢y将知识用谓词表示为:(∀x) (P(x)∧L(x,pragramming)→L(x, computer))2.9用谓词表示法求解机器人摞积木问题。
设机器人有一只机械手,要处理的世界有一张桌子,桌上可堆放若干相同的方积木块。
机械手有4个操作积木的典型动作:从桌上拣起一块积木;将手中的积木放到桌之上;在积木上再摞上一块积木;从积木上面拣起一块积木。
积木世界的布局如下图所示。
图机器人摞积木问题解:(1) 先定义描述状态的谓词CLEAR(x):积木x上面是空的。
ON(x, y):积木x在积木y的上面。
ONTABLE(x):积木x在桌子上。
HOLDING(x):机械手抓住x。
2020年《人工智能》--课后习题答案47

M(N)=2M(N-1)+1 最后可以解得 M(N)=2N-1
下面给出对梵塔问题给出产生式系统描述,并讨论 N 为任意时状态空间的规模。 (1)综合数据库
定义三元组:(A, B, C),其中 A, B, C 分别表示三根立柱,均为表,表的元素为 1~N 之 间的整数,表示 N 个不同大小的盘子,数值小的数表示小盘子,数值大的数表示大盘子。 表的第一个元素表示立柱最上面的柱子,其余类推。 (2)规则集
G(zhang,li)。
(2) 定义谓词 Marry(x,y):x 和 y 结婚,Male(x):x 是男的,Female(x):x 是女的。个体有
甲(A)、乙(B),将这些个体带入谓词中,得到 Marry(A,B)、Male(A)、Female(B)以及 Male(A)、
Female(B),根据语义用逻辑连接词将它们联结起来就得到表示上述知识的谓词公式:
题中各条推理则可以表示为:
P1: x DOG(X)
yBIT(X,Y)∨SOUND(X)
P2: :x(ANIMAL(X) ∧SOUND(X))
yBIT(X,Y)
P3: 猎犬是狗,即 DOG(X)种 X 的谓词样品是猎犬,同时也可得 ANIMAL(猎犬) 将 P3 带入 P1 可得 SOUND(猎犬),再将 SOUND(猎犬)和 ANIMAL(猎犬)带入 P2 可得
MaB))∨(Male(B)∧Female(A))
(3) 定义谓词 Honest(x):x 是诚实的,Lying(x):x 会说谎。个体有张三(zhang),将这些
个体带入谓词中,得到 Honest(x)、 Lying(x)、Lying(zhang)、 Honest(zhang),根
5.2《人工智能的应用》-课后作业-(2024)浙教版-信息技术-数据与计算必修1
《人工智能的应用》的作业题目及答案。
一、填空题(每题2分)1. 人工智能在医疗领域的应用之一是通过分析医学影像来辅助医生进行__________。
答案:诊断2. 自动驾驶汽车利用了多种传感器和__________技术来实现无人驾驶。
答案:机器学习3. 在金融服务中,AI可以用于检测和预防__________行为。
答案:欺诈4. 智能助手如Siri和Alexa是基于__________技术构建的。
答案:自然语言处理5. 在零售业中,AI被用来个性化推荐产品,这通常涉及到__________学习。
答案:协同过滤6. 人工智能在教育领域的应用包括自适应学习系统,这些系统能够根据学生的学习进度和风格调整教学内容,这种能力称为__________。
答案:个性化教学7. 在制造业中,机器人和AI系统合作完成复杂任务的过程被称为__________制造。
答案:智能制造8. 人工智能在农业中的应用包括使用无人机进行作物监测和__________喷洒。
答案:精准二、选择题(每题2分)1. 以下哪项不是人工智能在医疗领域的应用?A. 疾病诊断B. 药物研发C. 法律咨询D. 患者监护答案:C. 法律咨询解析:法律咨询不属于医疗领域,而是法律服务的范畴。
2. 自动驾驶汽车主要依赖于哪种类型的传感器?A. 温度传感器B. 光学传感器C. 压力传感器D. 湿度传感器答案:B. 光学传感器解析:自动驾驶汽车大量使用光学传感器(如摄像头和激光雷达)来感知周围环境。
3. 下列哪个是人工智能在金融领域的应用?A. 股市预测B. 农作物病虫害识别C. 交通流量控制D. 天气预测答案:A. 股市预测解析:股市预测是金融领域的典型应用,而其他选项分别属于农业和交通领域。
4. 自然语言处理(NLP)主要用于解决什么问题?A. 图像识别B. 语音到文本转换C. 硬件加速计算D. 网络安全答案:B. 语音到文本转换解析:自然语言处理专注于理解和生成人类语言,其中包括语音识别和语音合成等任务。
人工智能课后作业
人工智能课后作业1-1什么是人工智能?试从学科和能力两方面加以说明.答:人工智能(学科):人工智能(学科)是计算机科学中涉及研究、设计和应用智能机器的一个分支。
其近期的主要目标在于研究用机器来模仿和执行人脑的某些智力功能,并开发相关理论和技术。
人工智能(能力):人工智能(能力)是智能机器所执行的通常与人类智能有关的智能行为,如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习和问题求解等思维活动1-4为什么能用机器(计算机)恶搞人的智能?答:物理符号系统的假设:任何一个系统,如果它能够表现出智能,那么它就必的定能够继续执行输出符号、输入符号、存储符号、激活符号、创建符号结构、条件性搬迁6种功能。
反之,任何系统如果具备这6种功能,那么它就能整体表现出来智能(人类所具备的智能)。
物理符号系统的假设伴随有3个推论。
推断一:既然人具备智能,那么他(她)就一定就是个物理符号系统。
推断二:既然计算机就是一个物理符号系统,它就一定能整体表现出来智能。
推论三:既然人是一个物理符号系统,计算机也是一个物理符号系统,那么我们就能够用计算机来模拟人的活动。
1-5现在人工智能存有哪些学派?它们的心智观是什么?现在这些学派的关系如何?答:符号主义(symbolicism),又称为逻辑主义(logicism)、心理学派连结主义(connectionism),又称作仿生学派遣(bionicsism)或生理学派遣(physiologism)[其原理主要为神经网络及神经网络间的连接机制与学习算法]指出人的思维基元就是神经元,而不是符号处理过程。
指出人脑不同于电脑,并明确提出连结主义的大脑工作模式,用作替代符号操作方式的电脑工作模式。
行为主义(actionism),又称演化主义(evolutionism)或社会学学派(cyberneticsism)[其原理为社会学及认知-动作型控制系统]认为智能取决于感知和行动。
认为智能不需要知识、不需要表示、不需要推理;人工智能可以象人类智能一样逐步进化。
《人工智能》--课后习题答案
《人工智能》课后习题答案第一章绪论1.1答:人工智能就是让机器完成那些如果由人来做则需要智能的事情的科学。
人工智能是相对于人的自然智能而言,即用人工的方法和技术,研制智能机器或智能系统来模仿延伸和扩展人的智能,实现智能行为和“机器思维”,解决需要人类专家才能处理的问题。
1.2答:“智能”一词源于拉丁“Legere”,意思是收集、汇集,智能通常用来表示从中进行选择、理解和感觉。
所谓自然智能就是人类和一些动物所具有的智力和行为能力。
智力是针对具体情况的,根据不同的情况有不同的含义。
“智力”是指学会某种技能的能力,而不是指技能本身。
1.3答:专家系统是一个智能的计算机程序,他运用知识和推理步骤来解决只有专家才能解决的复杂问题。
即任何解题能力达到了同领域人类专家水平的计算机程序度可以称为专家系统。
1.4答:自然语言处理—语言翻译系统,金山词霸系列机器人—足球机器人模式识别—Microsoft Cartoon Maker博弈—围棋和跳棋第二章知识表达技术2.1解答:(1)状态空间(State Space)是利用状态变量和操作符号,表示系统或问题的有关知识的符号体系,状态空间是一个四元组(S,O,S0,G):S—状态集合;O—操作算子集合;S0—初始状态,S0⊂S;G—目的状态,G⊂S,(G可若干具体状态,也可满足某些性质的路径信息描述)从S0结点到G结点的路径被称为求解路径。
状态空间一解是一有限操作算子序列,它使初始状态转换为目标状态:O1 O2 O3 OkS0→−−−S1→−−−S2→−−−……→−−−G其中O1,…,Ok即为状态空间的一个解(解往往不是唯一的)(2)谓词逻辑是命题逻辑的扩充和发展,它将原子命题分解成客体和谓词两个部分。
与命题逻辑中命题公式相对应,谓词逻辑中也有谓词(命题函数)公式、原子谓词公式、复合谓词公式等概念。
一阶谓词逻辑是谓词逻辑中最直观的一种逻辑。
(3)语义网络是一种采用网络形式表示人类知识的方法。
人工智能课后习题答案
1.1 解图如下:(1) 1->2(2) 1->3(3) 2->3(6) 3->2(5) 3->1(4) 2->11.2h(n)=∑每个W 左边B 的个数;h(n)满足A*条件;h(n)满足单调限制(大家分析)。
1.3h1(n)= c ij ,一般情况不满足A*条件,但此题满足;ACDEBA=34; h2(n)=|c ij -AVG{(c ij )|,不满足A*条件;ACBDEA=42; 1.4此题最优步数已定,具有A*特征的启发函数对搜索无引导作用。
1.5此题启发式函数见P41。
1.10规定每次一个圆盘按固定方向(如逆时针)转动45°;可用盲目搜索算法构造搜索树;也可构造启发式函数如:h(n)=8个径向数字和与12的方差。
1.11状态空间数:9!=362880;有用的启发信息:1)平方数为3位数的数字:10~31;2)平方的结果数字各位不能重复:13,14,16,17,18,19,23,24,25,27,28,29,31; 只需校验313C =286种状态。
2.1 解图:2.5后手只要拿走余下棋子-1的个数即可。
第3章 3.18以下符号中□表示⌝(1)证明:待归结的命题公式为)(P Q P →⌝∧,求取子句集为},,{P Q P ⌝,对子句集中的子句进行归结可得可得原公式成立。
(2)证明:待归结的命题公式为())(()())P Q R P Q P R →→∧→→→ (,合取范式为:()()P Q R P Q P R ∨∨∧∨∧∧ ,求取子句集为{,,,}S P Q R P Q P R =∨∨∨ ,对子句集中的子句进行归结可得:① P Q R ∨∨ ② P Q ∨③ P ④ R ⑤ Q②③归结⑥ P R ∨ ①④归结 ⑦ R ③⑥归结 ⑧ ④⑦归结 由上可得原公式成立。
(3)证明:待归结的命题公式为()(())Q P Q P Q →∧→→ ,合取范式为:()()Q P Q P Q ∨∧∨∧ ,求取子句集为{,,}S Q P Q P Q =∨∨ ,对子句集中的子句进行归结可得:① Q P ∨ ② Q③ Q P ∨④ P ①②归结 ⑤ P ②③归结 ⑥ ④⑤归结由上可得原公式成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章:P23
1.人工智能
人工智能就是用人工的方法在机器(计算机)上实现的智能,或称机器智能
第二章:P51
5.(1)有的人喜欢打篮球,有的人喜欢踢足球,有的人既喜欢打篮球又喜欢踢足球。
定义谓词:LIKE(x,y):x喜欢y。
PLAY(x,y):x打(踢)y。
MAN(x):x是人。
定义个体域:Basketball,Soccer。
(x)(MAN(x) → LIKE(x,PLAY(x,Basketball))) ∨(y)(MAN(y) → LIKE(y,PLAY(y,Soccer))) ∨(z)(MAN(z) →LIKE(z,PLAY(z,Basketball)) ∧ LIKE(z,PLAY(z,Soccer))
(2)并不是每个人都喜欢花。
定义谓词:LIKE(x,y):x喜欢y。
P(x):x是人
定义个体词:flower
¬(x)(P(x) → LIKE(x,flower))
(3)欲穷千里目,更上一层楼。
定义谓词:S(x):x想要看到千里远的地方。
H(x):x要更上一层楼。
(x)(S(x) → H(x))
6. 产生式通常用于表示具有因果关系的知识,其基本形式是: P→Q
或者 If P Then Q [Else S]
其中,P是前件,用于指出该产生式是否可用的条件。
Q是一组结论或者操作,用于指出当前提P满足时,应该得出的结论或者应该执行的操作。
区别:蕴含式只能表示精确知识;而产生式不仅可以表示精确知识,还可以表示不精确知识。
产生式中前提条件的匹配可以是精确的,也可以是非精确的;而谓词逻辑蕴含式总要求精确匹配。
7.一个产生式系统一般由三部分组成:规则集、全局数据库、控制策略。
步骤:1)初始化全局数据库,把问题的初始已知事实送入全局数据库中
2)若规则库中存在尚未使用的规则,而且它的前提可与全局数据库中的已知事实匹配,则转3),若不存在则转5)
3)执行当前选中的规则,并对该规则做标记,把该规则执行后得到的结论送入全局数据库中。
如
果该规则的结论部分指出的是某些操作,则执行这些操作。
4)检查全局数据库中是否已经包含了问题的解,若已经包含,则求解结束,否则转2)5)要求用户提供进一步的关于问题的已知事实,若能提供,则转2),否则求解结束。
6)若规则库中不再有未使用过的规则,则求解过程结束。
11. 框架名:<教师>
姓名:单位(姓,名)
年龄:单位(岁)
性别:范围(男,女)缺省为男
职称:范围(教授,副教授,讲师,助教)
缺省我讲师
部门:单位(系,教研室)
住址:<地址框架>
工资:<工资框架>
开始工作时间:单位(年,月)
截止时间:单位(年,月)缺省为现在
框架名:<学生>
姓名:单位(姓,名)
年龄:单位(岁)
性别:范围(男,女)缺省为男
学院:单位(学院,系)
班级:单位(年级,班级)
入学时间:单位(年,月)
截止时间:单位(年,月)缺省为现在
13.
第三章:P83
6.(1) 由于(x)(
y)(P(x, y)∧Q(x, y))已经是Skolem 标准型,且P(x, y)∧Q(x, y)已经是合
取范式,所以可直接消去全称量词、合取词,得
{ P(x, y), Q(x, y)} 再进行变元换名得子句集:
S={ P(x, y), Q(u, v)}
(2)对谓词公式(x)(y)(P(x, y)→Q(x, y)),先消去连接词“→”得:
(
x)(
y)(¬P(x, y)∨Q(x, y))
此公式已为Skolem 标准型。
再消去全称量词得子句集:
S={¬P(x, y)∨Q(x, y)}
(3)对谓词公式(x)(y)(P(x, y)∨(Q(x, y)→R(x, y))),先消去连接词“→”得:
(
x)(
y)(P(x, y)∨(¬Q(x, y)∨R(x, y)))
此公式已为前束范式。
再消去存在量词,即用Skolem 函数f(x)替换y 得: (
x)(P(x, f(x))∨¬Q(x, f(x))∨R(x, f(x)))
此公式已为Skolem 标准型。
最后消去全称量词得子句集:
S={P(x, f(x))∨¬Q(x, f(x))∨R(x, f(x))}
(4)对谓词(x) (
y) (
z)(P(x, y)→Q(x, y)∨R(x, z)),先消去连接词“→”得:
(
x) (y) (z)(¬P(x, y)∨Q(x, y)∨R(x, z))
再消去存在量词,即用Skolem 函数f(x,y)替换z 得: (
x) (y) (¬P(x, y)∨Q(x, y)∨R(x, f(x,y)))
植物 树 AK O 有
根
有叶
AK
O
果树
苹果树
结果 结苹果
AK
O 草 海藻
AK
O
AK
O 长在水里
有叶 有根
Have
Have In
Have Have Get
Get
此公式已为Skolem标准型。
最后消去全称量词得子句集:
S={¬P(x, y)∨Q(x, y)∨R(x, f(x,y))}
7. (1)不可满足
(2)不是不可满足的,原因是不能由它导出空子句。
(3)不可满足
(5)不是不可满足的,原因是不能由它导出空子句。
8. (2)先将F和¬G化成子句集
由F得:S1={P(x),(Q(a)∨Q(b))}
由于¬G为:¬ (x) (P(x)∧Q(x)),即
(x) (¬ P(x)∨¬ Q(x)),
可得: S2={¬ P(x)∨¬ Q(x)}
因此,扩充的子句集为:
S={ P(x),(Q(a)∨Q(b)),¬ P(x)∨¬ Q(x)}
可得NIL;
9. 先定义谓词: F(x,y):x是y的父亲
GF(x,z):x是z的祖父
P(x):x是一个人
再用谓词把问题描述出来:
已知F1:(x) (y) (z)( F(x,y)∧F(y,z))→GF(x,z))
F2:(y)(P(x)→F(x,y))
求证结论G:(u) (v)( P(u)→GF(v,u))
然后再将F1,F2和¬G化成子句集:
①¬F(x,y)∨¬F(y,z)∨GF(x,z) ②¬P(r)∨F(s,r)
③ P(u) ④¬GF(v,u))
可得NIL;
第四章:P134
例5.1 设H1,H2,H3分别是三个结论,E是支持这些结论的证据,且已知: P(H1)=0.3 P(H2)=0.4 P(H3)=0.5
P(E/H1)=0.5 P(E/H2) =0.3 P(E/H3) =0.4
求: P(H1/E) ,P(H2/E) , P(H3/E)
由此可以看出,由于证据E 的出现,H1成立的可能性略有增加,H2,H3的可能性有不同程度的下降。
2.
设已知:
P(H1)=0.4 P(H2)=0.3 P(H3)=0.3
P(E1/H1)=0.5 P(E1/H2)=0.6 P(E1/H3)=0.3 P(E2/H1)=0.7 P(E2/H2)=0.9 P(E2/H3)=0.1 求:P(H1/E1E2), P(H2/E1E2), P(H3/E1E2)
由此可以看出,由于证据E1,E2的出现,H1,H2成立的可能性有不同程度的增加,H3的可能性下降了。
n
i H E P H P H E P H P E H P n
j j j i i i ,,2,1)
/()()
/()()/(1
=⨯⨯=
∑=03
.0)21/3(52.0)21/2(:
45
.0009.0162.014.014.0)3()3/2()3/1()2()2/2()2/1()1()1/2()1/1()
1()1/2()1/1()21/1(:===++=
⨯⨯+⨯⨯+⨯⨯⨯⨯=
E E H P E E H P H P H E P H E P H P H E P H E P H P H E P H E P H P H E P H E P E E H P 同理可得由公式可得解。
