高中数学典型例题任意角的三角函数1新课标
1.2.1任意角的三角函数(新授课)
1.2.1任意角的三角函数（新授课）【教学目标】1.复习三角函数的定义、定义域与值域、符号、及诱导公式；2.利用三角函数线表示正弦、余弦、正切的三角函数值；3.利用三角函数线比较两个同名三角函数值的大小及表示角的范围。
4.掌握用单位圆中的线段表示三角函数值，从而使学生对三角函数的定义域、值域有更深的理解。
5.学习转化的思想，培养学生严谨治学、一丝不苟的科学精神；.【教学重点】任意角的正弦、余弦、正切的定义（包括这三种三角函数的定义域和函数值在各象限的符号）；终边相同的角的同一三角函数值相等（公式一）【教学难点】任意角的正弦、余弦、正切的定义（包括这三种三角函数的定义域和函数值在各象限的符号）；三角函数线的正确理解..【教学过程】 一、知识回顾初中锐角的三角函数是如何定义的？在Rt △ABC 中，设A 对边为a ，B 对边为b ，C 对边为c ，锐角A 的正弦、余弦、正切依次为,,a b a sinA cosA tanA c c b===．角推广后，这样的三角函数的定义不再适用，我们必须对三角函数重新定义。
二、预习自学1.探究:结合上述锐角α的三角函数值的求法,我们应如何求解任意角的三角函数值呢?显然,我们只需在角的终边上找到一个点,使这个点到原点的距离为1,然后就可以类似锐角求得该角的三角函数值了.所以,我们在此引入单位圆的定义:在直角坐标系中,我们称以原点O 为圆心,以单位长度为半径的圆.2.思考:如何利用单位圆定义任意角的三角函数的定义?如图,设α是一个任意角,它的终边与单位圆交于点(,)P x y ,那么: (1)y 叫做α的正弦(sine),记做sin α,即sin y α=； （2）x 叫做α的余弦(cossine),记做cos α,即cos x α=； （3）y x叫做α的正切(tangent),记做tan α,即tan (0)y x xα=≠.注意:当α是锐角时，此定义与初中定义相同（指出对边，邻边，斜边所在）；当α不是锐角时，也能够找出三角函数，因为，既然有角，就必然有终边，终边就必然与单位圆有交点(,)P x y ，从而就必然能够最终算出三角函数值.3.思考:如果知道角终边上一点,而这个点不是终边与单位圆的交点,该如何求它的三角函数值呢?前面我们已经知道,三角函数的值与点P在终边上的位置无关，仅与角的大小有关.我们只需计算点到原点的距离r=,那么sinα=cosα=,tanyxα=.所以，三角函数是以为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数，又因为角的集合与实数集之间可以建立一一对应关系，故三角函数也可以看成实数为自变量的函数.1．三角函数定义在直角坐标系中，设α是一个任意角，α终边上任意一点P（除了原点）的坐标为(,)x y，它与原点的距离为(0)r r==>，那么（1）比值yr叫做α的正弦，记作sinα，即sinyrα=；（2）比值xr叫做α的余弦，记作cosα，即cosxrα=；（3）比值yx叫做α的正切，记作tanα，即tanyxα=；2．三角函数的定义域、值域三.典型例题例1.求53π的正弦、余弦和正切值.例2．已知角α的终边过点0(3,4)P--，求角α的正弦、余弦和正切值.例3．求证：当且仅当不等式组sin0{tan0θθ<>成立时，角θ为第三象限角.四、课堂练习6.探究:请根据任意角的三角函数定义,将正弦、余弦和正切函数的定义域填入下表；再将这三种函数的值在各个象限的符号填入表格中：五、课堂小结、本节课你学了哪些知识？有哪些收获？你已经正确理解、掌握它们了吗？六、课后作业1.确定下列三角函数值的符号,然后用计算器验证:(1)cos 250︒; (2)sin()4π-; (3)tan(672)︒-; (4)tan 3π2.求下列三角函数值:(1)'sin148010︒; (2)9cos 4π; (3)11tan()6π-。
2021_2022学年新教材高中数学第7章三角函数7.27.2.1任意角的三角函数学案苏教版必修第一
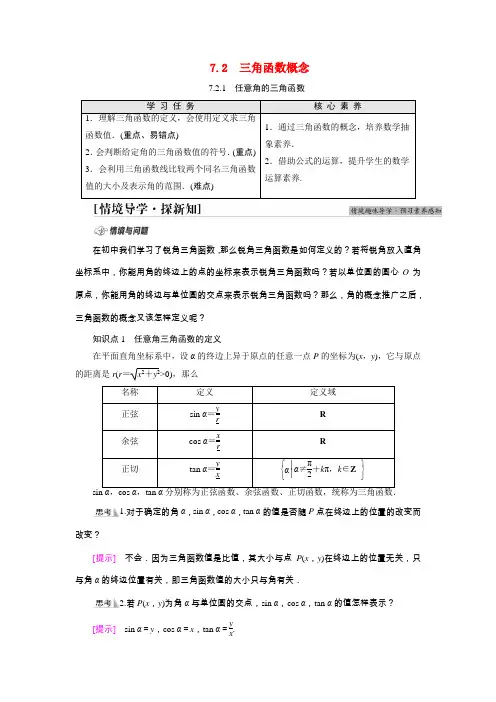
7.2 三角函数概念7.2.1任意角的三角函数学习任务核心素养1．理解三角函数的定义，会使用定义求三角函数值．(重点、易错点)2．会判断给定角的三角函数值的符号．(重点)3．会利用三角函数线比较两个同名三角函数值的大小及表示角的范围．(难点)1．通过三角函数的概念，培养数学抽象素养．2．借助公式的运算，提升学生的数学运算素养.在初中我们学习了锐角三角函数，那么锐角三角函数是如何定义的？若将锐角放入直角坐标系中，你能用角的终边上的点的坐标来表示锐角三角函数吗？若以单位圆的圆心O为原点，你能用角的终边与单位圆的交点来表示锐角三角函数吗？那么，角的概念推广之后，三角函数的概念又该怎样定义呢？知识点1任意角三角函数的定义在平面直角坐标系中，设α的终边上异于原点的任意一点P的坐标为(x，y)，它与原点的距离是r(r＝x2＋y2>0)，那么名称定义定义域正弦sin α＝yr R余弦cos α＝xr R正切tan α＝yx⎩⎨⎧⎭⎬⎫α⎪⎪α≠π2＋kπ，k∈Z1.对于确定的角α，sin α，cos α，tan α的值是否随P点在终边上的位置的改变而改变？[提示]不会．因为三角函数值是比值，其大小与点P(x，y)在终边上的位置无关，只与角α的终边位置有关，即三角函数值的大小只与角有关．2.若P(x，y)为角α与单位圆的交点，sin α，cos α，tan α的值怎样表示？[提示]sin α＝y，cos α＝x，tan α＝yx.1.若角α的终边经过点P ⎝ ⎛⎭⎪⎫22，－22，则sin α＝________；cos α＝________；tan α＝________.－2222－1 [由题意可知 |OP |＝⎝⎛⎭⎫22－02＋⎝⎛⎭⎫－22－02＝1， ∴sin α＝－221＝－22；cos α＝221＝22；tan α＝－2222＝－1.]知识点2 三角函数在各象限的符号2.(1)若α在第三象限，则sin αcos α________0；(填“＞”或“＜”)(2)cos 3tan 4________0.(填“>”或“<”) (1)＞ (2)＜ [(1)∵α在第三象限， ∴sin α＜0，cos α＜0，∴sin αcos α＞0. (2)∵π2<3<π，π<4<3π2，∴3是第二象限角，4是第三象限角． ∴cos 3<0，tan 4>0.∴cos 3tan 4<0.] 知识点3 三角函数线(1)有向线段：规定了方向(即规定了起点和终点)的线段；有向直线：规定了正方向的直线；有向线段的数量：若有向线段AB 在有向直线l 上或与有向直线l 平行，根据有向线段AB 与有向直线l 的方向相同或相反，分别把它的长度添上正号或负号，这样所得的数，叫作有向线段的数量，记为AB .(2)三角函数线3.思考辨析(正确的打“√”，错误的打“×”)(1)α一定时，单位圆的正弦线一定．( ) (2)在单位圆中，有相同正弦线的角必相等．( ) [答案] (1)√ (2)×类型1 三角函数的定义及应用【例1】 (1)在平面直角坐标系中，角α的终边在直线y ＝－2x 上，求sin α，cos α，tan α的值．(2)当α＝－π3时，求sin α，cos α，tan α的值．[解] (1)当α的终边在第二象限时，在α终边上取一点P (－1，2)，则r ＝(－1)2＋22＝5，所以sin α＝25＝255，cos α＝－15＝－55，tan α＝2－1＝－2.当α的终边在第四象限时， 在α终边上取一点P ′(1，－2)， 则r ＝12＋(－2)2＝5，所以sin α＝－25＝－255，cos α＝15＝55，tan α＝－21＝－2.(2) 当α＝－π3时，设α的终边与单位圆的交点坐标为P (x ，y )，(x >0，y <0)根据直角三角形中锐角π3的邻边是斜边的一半，得x＝12，由勾股定理得⎝⎛⎭⎫122＋y2＝1，y<0，解得y＝－32，所以P⎝⎛⎭⎫12，－32.因此sin α＝－321＝－32，cos α＝121＝12，tan α＝－3212＝－ 3.1．将本例(1)的条件“y＝－2x”改为“3x＋y＝0”其他条件不变，结果又如何？[解]直线3x＋y＝0，即y＝－3x，当α的终边在第二象限时，在α的终边上取一点P(－1，3)，则r＝2，所以sin α＝32，cos α＝－12，tan α＝－3；当α的终边在第四象限时，在α终边上取一点P′(1，－3)，则r＝2，所以sin α＝－32，cos α＝12，tan α＝－ 3.2．将本例(1)的条件“在直线y＝－2x上”，改为“过点P(－3a,4a)(a≠0)”，求2sin α＋cos α.[解]因为r＝(－3a)2＋(4a)2＝5|a|，①若a>0，则r＝5a，角α在第二象限，sin α＝yr＝4a5a＝45，cos α＝xr＝－3a5a＝－35，所以2sin α＋cos α＝85－35＝1.②若a<0，则r＝－5a，角α在第四象限，sin α＝4a－5a＝－45，cos α＝－3a－5a＝35，所以2sin α＋cos α＝－85＋35＝－1.1．已知角α终边上任意一点的坐标求三角函数值的方法(1)先利用直线与单位圆相交，求出交点坐标，然后再利用正、余弦函数的定义求出相应的三角函数值．(2)在α的终边上任选一点P (x ，y )，设P 到原点的距离为r (r >0)，则sin α＝y r ，cos α＝xr .当已知α的终边上一点求α的三角函数值时，用该方法更方便．2．已知特殊角α，求三角函数值的方法(1)先设出角α的终边与单位圆交点坐标，由锐角三角形的定义结合勾股定理求出该点的坐标．(2)利用三角函数的定义，求出α的三角函数值．(此时P 到原点的距离r ＝1)3．当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．[跟进训练]1．已知角θ终边上一点P (x,3)(x ≠0)，且cos θ＝1010x ，求sin θ，tan θ. [解] 由题意知r ＝x 2＋9，由三角函数定义得cos θ＝xr＝x x 2＋9.又∵cos θ＝1010x ， ∴xx 2＋9＝1010x . ∵x ≠0，∴x ＝±1. 当x ＝1时，P (1,3)， 此时sin θ＝312＋32＝31010， tan θ＝31＝3.当x ＝－1时，P (－1,3)， 此时sin θ＝3(－1)2＋32＝31010，tan θ＝3－1＝－3.2. 当α＝4π3时，求sin α，cos α，tan α的值．[解] 当α＝4π3时，设α的终边与单位圆的交点坐标为P (x ，y )，(x <0，y <0)根据直角三角形中锐角π3的邻边是斜边的一半，得x ＝－12，由勾股定理得⎝⎛⎭⎫－122＋y 2＝1，y <0，解得y ＝－32， 所以P ⎝⎛⎭⎫－12，－32.因此sin α＝－321＝－32，cos α＝－121＝－12，tan α＝－32－12＝ 3.类型2 三角函数值的符号【例2】 (1)若角θ同时满足sin θ<0且tan θ<0，则角θ的终边一定位于( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限(2)判断下列各式的符号． ①sin 2 015° cos 2 016° tan 2 017°； ②tan 191°－cos 190°； ③sin 2 cos 3 tan 4.(1)D [由sin θ<0，可知θ的终边可能位于第三或第四象限，也可能与y 轴的负半轴重合．由tan θ<0，可知θ的终边可能位于第二象限或第四象限，故θ的终边只能位于第四象限．](2)[解] ①∵2 015°＝1 800°＋215°＝5×360°＋215°， 2 016°＝5×360°＋216°，2 017°＝5×360°＋217°， ∴它们都是第三象限角，∴sin 2 015°<0，cos 2 016°<0，tan 2 017°>0， ∴sin 2 015° cos 2 016° tan 2 017°>0.②∵191°角是第三象限角，∴tan 191°>0，cos 191°<0， ∴tan 191°－cos 191°>0.③∵π2<2<π，π2<3<π，π<4<3π2，∴2是第二象限角，3是第二象限角，4是第三象限角， ∴sin 2>0，cos 3<0，tan 4>0， ∴sin 2 cos 3 tan 4<0.判断三角函数值在各象限符号的攻略(1)基础：准确确定三角函数值中各角所在象限． (2)关键：准确记忆三角函数在各象限的符号．(3)注意：用弧度制给出的角常常不写单位，不要误认为角度制导致象限判断错误．[跟进训练]3．判断下列式子的符号：(1)tan 108°·cos 305°；(2)cos 5π6·tan11π6sin2π3；(3)tan 120°·sin 269°.[解] (1)∵108°是第二象限角，∴tan 108°＜0. ∵305°是第四象限角，∴cos 305°＞0. 从而tan 108°·cos 305°＜0.(2)∵5π6是第二象限角，11π6是第四象限角，2π3是第二象限角，∴cos5π6＜0，tan 11π6＜0，sin 2π3＞0. 从而cos 5π6·tan11π6sin2π3＞0.(3)∵120°是第二象限角，∴tan 120°＜0， ∵269°是第三象限角，∴sin 269°＜0. 从而tan 120°·sin 269°＞0.类型3 应用三角函数线解三角不等式【例3】 在单位圆中画出适合下列条件的角α的终边的范围，并由此写出角α的集合： (1)sin α≥32；(2)cos α≤－12.1．在单位圆中，满足sin α＝32的正弦线有几条？试在图中明确． [提示] 两条，如图1所示，MP 1与NP 2都等于32. 2．在单位圆中，满足cos α＝－12的余弦线有几条？在图中明确．[提示] 一条，如图2所示，OM ＝－12.图1 图2[解] (1)作直线y ＝32交单位圆于A ，B 两点，连接OA ，OB ，则OA 与OB 围成的区域(图①阴影部分)即为角α的终边的范围，故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π＋π3≤α≤2k π＋2π3，k ∈Z .(2)作直线x ＝－12交单位圆于C ，D 两点，连接OC ，OD ，则OC 与OD 围成的区域(图②阴影部分)即为角α终边的范围，故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π＋23π≤α≤2k π＋43π，k ∈Z .利用三角函数线解三角不等式的方法(1)正弦、余弦型不等式的解法对于sin x ≥b ，cos x ≥a (sin x ≤b ，cos x ≤a )，求解的关键是恰当地寻求点，只需作直线y ＝b 或x ＝a 与单位圆相交，连接原点与交点即得角的终边所在的位置，此时再根据方向即可确定相应的范围．(2)正切型不等式的解法对于tan x ≥c ，取点(1，c )，连接该点和原点并反向延长，即得角的终边所在的位置，结合图象可确定相应的范围．[跟进训练]4．求函数f (x )＝1－2cos x ＋ln ⎝⎛⎭⎫sin x －22的定义域． [解] 由题意，自变量x 应满足不等式组⎩⎪⎨⎪⎧1－2cos x ≥0，sin x －22＞0，即⎩⎨⎧cos x ≤12，sin x ＞22.则不等式组的解的集合如图(阴影部分)所示，∴函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π＋π3≤x ＜2k π＋34π，k ∈Z .1．若sin α＜0，tan α＞0，则α终边所在象限是( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限C [由sin α＜0可知α的终边落在第三、四象限及y 轴的负半轴上． 由tan α＞0可知α的终边落在第一、三象限内． 故同时满足sin α＜0，tan α＞0的角α为第三象限角．] 2．(多选题)下列三角函数判断错误的是( ) A ．sin 165°>0 B ．cos 280°<0 C ．tan 170°>0D ．tan 310°>0BCD[∵90°<165°<180°∴sin 165°>0.又270°<280°<360°，∴cos 280°>0.又270°<310°<360°.∴tan310°<0,90°<170°<180°∴tan 170°<0.]3．已知角α终边过点P (1，－1)，则tan α的值等于________． －1 [由三角函数定义知tan α＝－11＝－1.]4．已知角α终边过P ⎝⎛⎭⎫32，12，则cos α等于________．32 [由三角函数定义可知，角α的终边与单位圆交点的横坐标为角α的余弦值，故cos α＝32.] 5．已知sin θ·tan θ<0，那么θ是第________象限角．二或三 [因为sin θ·tan θ<0，所以sin θ<0，tan θ>0或sin θ>0，tan θ<0，若sin θ>0，tan θ<0，所以θ在第二象限．若sin θ<0，tan θ>0，则θ在第三象限．]回顾本节知识，自我完成以下问题．1．三角函数值的大小与取点有关吗？与什么有关？[提示] 三角函数值的大小与终边所在的位置有关，与取点无关． 2．求一个角的三角函数值需确定几个量？分别是什么？[提示] 确定三个量，角的终边上异于原点的点的横、纵坐标及其到原点的距离． 3．已知角的大小，怎样利用定义求三角函数值？ [提示] 确定出角的终边与单位圆的交点坐标．。
高考数学专题《任意角和弧度制及任意角的三角函数》习题含答案解析
专题5.1 任意角和弧度制及任意角的三角函数1．（2021·宁夏高三三模（文））已知角α终边经过点()1,2,P-则cosα=（）A．12B．12-C D．【答案】D【解析】直接利用三角函数的定义即可.【详解】由三角函数定义，cos5α==-.故选：D.2.（2021·中牟县教育体育局教学研究室高一期中）已知角α的终边经过点()3,1P-，则cosα=（）A B．C．D【答案】C【解析】由三角函数的定义即可求得cosα的值．【详解】角α的终边经过点(3,1)P-，cosα∴==故选：C．3．（2020·全国高一课时练习）若α＝－2，则α的终边在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】练基础根据角的弧度制与角度制之间的转化关系可得选项.【详解】因为1 rad≈57.30°，所以－2 rad≈－114.60°，故α的终边在第三象限．故选：C.4．（2021·江苏高一期中）下列命题：①钝角是第二象限的角；②小于90︒的角是锐角；③第一象限的角一定不是负角；④第二象限的角一定大于第一象限的角；⑤手表时针走过2小时，时针转过的角度为60︒；⑥若5α=，则α是第四象限角．其中正确的题的个数是（）A．1个B．2个C．3个D．4个【答案】B【解析】结合象限角和任意角的概念逐个判断即可.【详解】对于①：钝角是大于90小于180的角，显然钝角是第二象限角. 故①正确；对于②：锐角是大于0小于90的角，小于90的角也可能是负角. 故②错误；对于③：359-显然是第一象限角. 故③错误；对于④：135是第二象限角，361是第一象限角，但是135361<. 故④错误；对于⑤：时针转过的角是负角. 故⑤错误；对于⑥：因为157.3rad≈，所以5557.3=286.5rad≈⨯，是第四象限角. 故⑥正确.综上，①⑥正确.故选：B.5．（2021·辽宁高三其他模拟）装饰公司制作一种扇形板状装饰品，其圆心角为23π，并在扇形弧上正面等距安装7个发彩光的小灯泡且在背面用导线将小灯泡串连（弧的两端各一个灯泡，导线接头忽略不计），已知扇形的半径为30厘米，则连接导线大致需要的长度约为（）A．55厘米B．63厘米C．69厘米D．76厘米【答案】B【解析】由于实际问题中扇形弧长较小，可将导线的长视为扇形弧长，利用弧长公式计算即可.【详解】因为在弧长比较短的情况下分成6等份，每部分的弦长和弧长相差很小， 所以可以用弧长近似代替弦长， 所以导线的长度为23020633ππ⨯=≈(厘米）． 故选：B6．（2021·上海格致中学高三三模）半径为2，中心角为3π的扇形的面积等于（ ） A ．43π B ．πC ．23π D ．3π 【答案】C 【解析】根据扇形的面积公式即可求解. 【详解】解：因为扇形的半径2r ，中心角3πα=，所以扇形的面积2211222233S r ππα==⨯⨯=， 故选：C.7．（2021·辽宁高三其他模拟）“数摺聚清风，一捻生秋意”是宋朝朱翌描写折扇的诗句，折扇出人怀袖，扇面书画，扇骨雕琢，是文人雅士的宠物，所以又有“怀袖雅物”的别号．如图是折扇的示意图，其中OA ＝20cm ，∠AOB ＝120°，M 为OA 的中点，则扇面（图中扇环）部分的面积是（ ）A ．50πcm 2B ．100πcm 2C ．150πcm 2D ．200πcm 2【答案】B 【解析】根据扇形面积公式计算可得； 【详解】解：扇环的面积为22211332400100222883r S r r παααπ⎛⎫=-==⨯⨯= ⎪⎝⎭．故选：B8．（2021·重庆八中高三其他模拟）如图所示，扇环ABCD 的两条弧长分别是4和10，两条直边AD 与BC 的长都是3，则此扇环的面积为（ ）A ．84B ．63C ．42D ．21【答案】D 【解析】设扇环的圆心角为α，小圆弧的半径为r ，依题意可得4αr =且()310αr +=，解得α、r ，进而可得结果. 【详解】设扇环的圆心角为α，小圆弧的半径为r ，由题可得4αr =且()310αr +=，解得2α=，2r ，从而扇环面积()221252212S =⨯⨯-=. 故选：D ．9．（2021·浙江高二期末）已知角α的终边过点(1,)P y ，若sin 3α=，则y =___________．【答案】【解析】利用三角函数的定义可求y . 【详解】由三角函数的定义可得sin α==y =故答案为：10．（2021·山东日照市·高三月考）已知函数()3sin,06log ,0xx f x x x π⎧≤⎪=⎨⎪>⎩，则13f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭______． 【答案】12- 【解析】利用分段函数直接进行求值即可． 【详解】∵函数()3,06log ,0xsinx f x x x π⎧≤⎪=⎨⎪>⎩， ∴311log 133f ⎛⎫=- ⎪⎝⎭＝， ∴611(1)sin 32f f f π⎛⎫⎛⎫⎛⎫=-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 故答案为：12-.1．（2021·河南洛阳市·高一期中（文））点P 为圆221x y +=与x 轴正半轴的交点，将点P 沿圆周逆时针旋转至点P '，当转过的弧长为2π3时，点P '的坐标为（ ）A ．1,2⎛ ⎝⎭B ．12⎛- ⎝⎭C ．21⎛⎫⎪ ⎪⎝⎭D ．122⎛⎫- ⎪ ⎪⎝⎭【答案】B 【解析】先求出旋转角，就可以计算点的坐标了. 【详解】设旋转角为θ，则22123θπππ⨯⨯=，得23πθ=，从而可得1(,22P '-. 故选：B.2．（2021·上海高二课时练习）若A 是三角形的最小内角，则A 的取值范围是（ ）练提升A ．0,2π⎛⎫⎪⎝⎭B ．0,3π⎛⎫ ⎪⎝⎭C ．,32ππ⎛⎫ ⎪⎝⎭D ．0,3π⎛⎤ ⎥⎝⎦【答案】D 【解析】由给定条件结合三角形三内角和定理即可作答. 【详解】设B ，C 是三角形的另外两个内角，则必有,A B A C ≤≤，又A B C π++=, 则3A A A A A B C π=++≤++=，即3A π≤，当且仅当3C B A π===，即A 是正三角形内角时取“=”，又0A >，于是有03A π<≤，所以A 的取值范围是(0,]3π.故选：D3．（2021·北京清华附中高三其他模拟）已知,R αβ∈．则“,k k Z αβπ=+∈”是“sin 2sin 2αβ=”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A 【解析】求解出sin 2sin 2αβ=成立的充要条件，再与,k k Z αβπ=+∈分析比对即可得解. 【详解】,R αβ∈，sin 2sin 2sin[()()]sin[()()]αβαβαβαβαβ=⇔++-=+--⇔2cos()sin()0αβαβ+-=，则sin()0αβ-=或cos()0αβ+=，由sin()0αβ-=得,k k k Z αβπαβπ-=⇔=+∈， 由cos()0αβ+=得,22k k k Z ππαβπαβπ+=+⇔=-+∈，显然s ,in 2sin 2k k Z απαββ=+∈=⇒，sin 2s ,in 2k k Z αβαβπ=+=∈，所以“,k k Z αβπ=+∈”是“sin 2sin 2αβ=”的充分不必要条件. 故选：A4．（2021·安徽池州市·池州一中高三其他模拟（理））已知一个半径为3的扇形的圆心角为()02θθπ<<，面积为98π，若()tan 3θϕ+=，则tan ϕ=（ ） A ．12-B ．34C ．12D ．43【答案】C 【解析】由扇形的面积公式得4πθ=,进而根据正切的和角公式解方程得1tan 2ϕ=. 【详解】解:由扇形的面积公式212S r θ=得9928πθ=,解得4πθ=, 所以()tan tan 1tan tan 31tan tan 1tan θϕϕθϕθϕϕ+++===--,解得1tan 2ϕ=故选:C5．（2021·新蔡县第一高级中学高一月考）一个圆心角为60的扇形，它的弧长是4π，则扇形的内切圆（与扇形的弧和半径的相切）的半径等于（ ） A ．2 B ．4 C ．2π D ．4π【答案】B 【解析】设扇形内切圆的半径为x ，扇形所在圆的半径为r ，求得3r x =，结合弧长公式，列出方程，即可求解. 【详解】如图所示，设扇形内切圆的半径为x ，扇形所在圆的半径为r ， 过点O 作OD CD ⊥， 在直角CDO 中，可得2sin 30ODCO x ==，所以扇形的半径为23r x x x =+=， 又由扇形的弧长公式，可得343x ππ⨯=，解得4x =，即扇形的内切圆的半径等于4. 故选：B.6．（2021·安徽合肥市·合肥一中高三其他模拟（文））已知顶点在原点的锐角α，始边在x 轴的非负半轴，始终绕原点逆时针转过3π后交单位圆于1(,)3P y -，则sin α的值为（ ）A ．6B C ．16D ．16【答案】B 【解析】根据任意角的三角函数的定义求出1cos()33πα+=-，然后凑角结合两角差的正弦公式求出sin α. 【详解】由题意得1cos()33πα+=-(α为锐角) ∵α为锐角，∴5336πππα，∴sin()03πα+>sin()sin sin ()3333πππααα⎡⎤⇒+=⇒=+-⎢⎥⎣⎦1132326⎛⎫=⨯--⨯=⎪⎝⎭ 故选：B7．（2020·安徽高三其他模拟（文））已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边经过点A (1，-3)，则tan()4πα+=（ ）A ．12B ．12-C ．1D ．-1【解析】根据终边上的点求出tan 3α=-，再结合正切和公式求解即可． 【详解】由题知tan 3α=-，则tan tan3114tan()41321tan tan 4παπαπα+-++===-+-. 故选：B8．（2021·合肥一六八中学高三其他模拟（理））已知顶点在原点，始边在x 轴非负半轴的锐角α绕原点逆时针转π3后，终边交单位圆于P x ⎛ ⎝⎭，则sin α的值为（ ） ABCD． 【答案】C 【解析】设锐角α绕原点逆时针转π3后得角β，由2113x +=，则x =，分x 的值结合三角函数的定义，求解即可，根据条件进行取舍. 【详解】设锐角α绕原点逆时针转π3后得角β，则3πβα=+，由α为锐角， 根据题意角β终边交单位圆于,3P x ⎛ ⎝⎭，则2113x +=，则3x =±若3x =，则sin ,cos 33ββ==所以sin sin sin cos cos sin 03336πππαβββ⎛⎫=-=-=< ⎪⎝⎭，与α为锐角不符合.若x =，则sin ββ==所以sin sin sin cos cos sin 0333πππαβββ⎛⎫=-=-=> ⎪⎝⎭,满足条件.9．（2021·安徽宣城市·高三二模（文））刘徽是中国魏晋时期杰出的数学家，他提出“割圆求周”方法：当n 很大时，用圆内接正n 边形的周长近似等于圆周长，并计算出精确度很高的圆周率 3.1416π≈．在《九章算术注》中总结出“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”的极限思想．运用此思想，当π取3.1416时，可得sin 2︒的近似值为（ ）A ．0.00873B ．0.01745C ．0.02618D ．0.03491【答案】D 【解析】由圆的垂径定理，求得2sin 2AB =︒，根据扇形对应的弦长之和近似于单位圆的周长，列出方程，即可求解. 【详解】将一个单位圆分成90个扇形，则每个扇形的圆心角度数均为4︒由圆的垂径定理，可得每个圆心角所对的弦长221sin 22sin 2AB AC ==⨯⨯︒=︒， 因为这90个扇形对应的弦长之和近似于单位圆的周长， 所以9021sin 2180sin 22π⨯⨯⨯︒=︒≈， 所以22 3.1416sin 20.03491180180π⨯︒≈=≈． 故选：D ．10．（2021·江苏南通市·高三其他模拟）某设计师为天文馆设计科普宣传图片，其中有一款设计图如图所示.QRT 是一个以点O 为圆心､QT 长为直径的半圆，QT =.QST 的圆心为P ，2dm PQ PT ==.QRT与QST 所围的灰色区域QRTSQ 即为某天所见的月亮形状，则该月亮形状的面积为___________2dm .6π 【解析】连接PO ，可得PO QT ⊥，求出23QPT π∠=，利用割补法即可求出月牙的面积. 【详解】解：连接PO ，可得PO QT ⊥，因为sin 2QO QPO PQ ∠==， 所以3QPO π∠=，23QPT π∠=，所以月牙的面积为2221121(21)dm 22326S πππ=⨯⨯-⨯⨯-⨯=.6π.1．（全国高考真题）已知角α的终边经过点(−4,3)，则cosα=（ ）A ．45B ．35C ．−35D ．−45 练真题【答案】D【解析】由题意可知x=-4，y=3，r=5，所以cosα=x r =−45.故选D. 2．（2020·全国高考真题（理））若α为第四象限角，则（ ）A ．cos2α>0B ．cos2α<0C ．sin2α>0D ．sin2α<0 【答案】D【解析】方法一：由α为第四象限角，可得3222,2k k k Z ππαππ+<<+∈， 所以34244,k k k Z ππαππ+<<+∈此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α<故选：D. 方法二：当6πα=-时，cos 2cos 03πα⎛⎫=-> ⎪⎝⎭，选项B 错误； 当3πα=-时，2cos 2cos 03πα⎛⎫=-< ⎪⎝⎭，选项A 错误； 由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确； 故选：D.3.（2015·上海高考真题（文））已知点的坐标为，将绕坐标原点逆时针旋转至，则点的纵坐标为（ ）. A ． B ． C ． D ．【答案】D【解析】由题意，设OA 与x 轴所成的角为，显然，，故，故纵坐标为4．（2018·全国高考真题（文））已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A(1 ， a)，B(2 ， b)，且cos2α=23，则|a −b |= A ．15 B ．√55 C ．2√55D ．1 【答案】B【解析】由O,A,B 三点共线，从而得到b =2a ，因为cos2α=2cos 2α−1=2⋅(√a 2+1)2−1=23， 解得a 2=15，即|a |=√55， 所以|a −b |=|a −2a |=√55，故选B.5.（2017·北京高考真题（理））在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则()cos αβ-=___________. 【答案】79- 【解析】因为α和β关于y 轴对称，所以2,k k Z αβππ+=+∈，那么1sin sin 3βα==，cos cos 3αβ=-=（或cos cos 3βα=-=）， 所以()2227cos cos cos sin sin cos sin 2sin 19αβαβαβααα-=+=-+=-=-. 6．（2021·北京高考真题）若点(cos ,sin )P θθ与点(cos(),sin())66Q ππθθ++关于y 轴对称，写出一个符合题意的θ=___． 【答案】512π（满足5,12k k Z πθπ=+∈即可） 【解析】根据,P Q 在单位圆上，可得,6πθθ+关于y 轴对称，得出2,6k k Z πθθππ++=+∈求解. 【详解】(cos ,sin )P θθ与cos ,sin66Q ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭关于y 轴对称， 即,6πθθ+关于y 轴对称，2,6k k Z πθθππ++=+∈， 则5,12k k Z πθπ=+∈， 当0k =时，可取θ的一个值为512π. 故答案为：512π（满足5,12k k Z πθπ=+∈即可）.。
2020-2021学年第一学期高中数学新教材必修第一册苏教版第七章第3课时 任意角的三角函数(1)
第3课时任意角的三角函数(1)一、学习目标1.掌握任意角的正弦、余弦、正切的定义.2.掌握正弦、余弦、正切函数的定义域和这三种函数的值在各象限的符号.二、问题导引预习教材P166——170的内容,思考下面的问题.在前面的学习中,我们在初中角的基础上将角的概念进行了推广,得到了任意角的概念,另外,还学习了角的另一种度量方法——弧度制.在初中学习了锐角后,我们研究了锐角的三角函数,现在,学习了任意角,那么我们能研究任意角的三角函数吗?如果能,又该如何研究呢?能通过锐角的三角函数来研究任意角的三角函数吗?三、即时体验1.填表:角正弦余弦正切2.已知角α的终边过点P(-3, 4),则sinα=, cosα=, tanα=.3.角-1328°的正弦值、余弦值、正切值的符号分别是、、.四、导学过程类型1由角的终边上的点求三角函数值【例1】已知角α的终边经过点P(2, -5),求α的正弦值、余弦值、正切值.类型2三角函数值的符号的判定【例2】确定下列三角函数值的符号:(1) cos; (2) sin(-565°); (3) tan.类型3由三角函数值求角的终边上的点的坐标【例3】已知角θ的顶点为坐标原点,始边为x轴的正半轴,若P(4, y)是角θ终边上一点, 且sinθ=-,求y的值.五、课堂练习1. (多选)若sinθcosθ<0,则角θ的终边在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.若<θ<π,则点P(cosθ, sinθ)位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.已知角α的终边经过点P(5, 12),则sinα+cosα=.4. sin1 cos2 tan3值的符号是.5.已知角α的终边经过点P(5t, 12t)(t≠0),求sinα+cosα的值.六、课后作业1. 若－<θ<－π,则点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.若角α的终边过点P(2sin30°, －2cos30°),则sinα的值等于 ()A. B. － C. － D. －3.若sinαcosα>0, cosαtanα<0,则角α的终边落在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. (多选)已知θ是第二象限角,则下列判断中正确的是()A. sin cos>0B. sin<0C. cos<0D. tan>05.已知角α的终边经过点P,则sinα=, tanα=.6. sin cos tan的值的符号是(填“正”或“负”).7. 已知角α的终边落在射线y=2x(x≥0)上,那么sinα·cosα=.8.设是第一象限角,且|cosα|=－cosα,则α可能是()A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角9. (多选)函数y=++的可能取值为()A. －3B. －1C. 1D. 310.已知角θ的终边过点P(x, 3)(x≠0),且cosθ=x,那么tanθ=.11.若角α的终边过点P(－4m, 3m)(m≠0),求2sinα+cosα的值.12.已知角α的终边在直线y=kx上,若sinα=－,且cosα<0,试求k的值.13.已知角α的终边上一点P到x轴、y轴的距离之比为4∶3,且cosα<0,求cosα－sinα的值.。
高中数学第一章知识点总结及典型例题
高中数学必修四 第一章知识点归纳第一：任意角的三角函数一：角的概念：角的定义，角的三要素，角的分类（正角、负角、零角和象限角），正确理解角，与角终边相同的角的集合}{|2,k k z ββπα=+∈ ，弧度制，弧度与角度的换算，弧长l r α=、扇形面积21122s lr r α==，二：任意角的三角函数定义：任意角α的终边上任意取一点p 的坐标是（x ，y ），它与原点的距离是22r x y =+(r>0)，那么角α的正弦r y a =sin 、余弦r x a =cos 、正切xya =tan ，它们都是以角为自变量，以比值为函数值的函数。
三：同角三角函数的关系式与诱导公式： 1.平方关系：22sin cos 1αα+=2. 商数关系：sin tan cos ααα=3．诱导公式——口诀：奇变偶不变，符号看象限。
正弦 余弦正切第二、三角函数图象和性质 基础知识:1、三角函数图像和性质1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyx解析式 y=sinxy=cosxtan y x =定义域值域和最值y ∈ 当x = ，1y 取最小值－当x = ，1y 取最大值y ∈当x = ，1y 取最小值－当x = ，1y 取最大值y ∈无最值周期性 π2=Tπ2=Tπ=T奇偶性奇函数 偶函数奇函数单调性在[]2222ππππ+-k k ，k Z ∈上是增函数在[]23222ππππ++k k ，k Z ∈上是减函数 在[]πππk k 22，-k Z ∈上是增函数在 []πππ+k k 22，k Z ∈上是减函数在⎪⎭⎫⎝⎛+-2,2ππππk k k Z ∈上为增函数对称性对称中心(,0) k k Z π∈对称轴方程2x k ππ=+，k Z ∈对称中心2(,0)k ππ+ k Z ∈对称轴方程x k π= ， k Z ∈对称中心(,0) k k Z π∈ 或者 对称中心2(,0)k ππ+k Z ∈2、熟练求函数sin()y A x ωϕ=+的值域，最值，周期，单调区间，对称轴、对称中心等 ，会用五点法作sin()y A x ωϕ=+简图：五点分别为：、 、 、 、 。
高中数学第一章三角函数1.2.1任意角的三角函数(1)课时提升作业1新人教A版必修4
任意角的三角函数(一）(15分钟30分）一、选择题（每小题4分，共12分)1。
求值sin750°=( ）A。
- B. — C.D。
【解析】选C.sin 750°= sin（2×360°+ 30°)=sin 30°=。
2.(2015·晋江高一检测）如果角θ的终边经过点(，-1），那么cosθ的值是( ）A.—B。
- C. D.【解析】选C。
点（，-1）到原点的距离r==2，所以cosθ=.【延伸探究】将本题中点的坐标改为(—1，），求sinθ-cosθ。
【解析】点（-1,）到原点的距离r==2，所以sinθ=，cosθ=-,所以sinθ-cosθ=—=。
3.(2015·北京高一检测）已知α∈（0,2π)，且sinα<0，cosα〉0,则角α的取值范围是( ）A。
B.C. D.【解析】选D。
因为sinα〈0，cosα〉0，所以角α是第四象限角，又α∈(0，2π），所以α∈.二、填空题（每小题4分，共8分)4。
求值：cosπ+tan=______【解析】cosπ=cos=cos=,tan=tan=tan=，所以cosπ+tan=+.答案：+5.(2015·南通高一检测)若角135°的终边上有一点(—4，a），则a的值是________.【解析】因为角135°的终边与单位圆交点的坐标为，所以tan 135°==-1，又因为点(—4，a)在角135°的终边上，所以tan 135°=,所以=-1,所以a=4.答案：4【补偿训练】如果角α的终边过点P(2sin 30°，—2cos 30°）,则cosα的值等于________。
【解析】2sin 30°=1,—2cos 30°=—，所以r=2，所以cosα=.答案：三、解答题6.（10分)判断下列各式的符号.（1)sinα·cosα（其中α是第二象限角）。
《任意角的三角函数》知识点总结及典型例题
任意角的三角函数模块一、角的概念及其推广要点一、角的相关概念 （1）角的概念角可以看成是由平面内一条射线（起始边）绕着端点旋转到一个新的位置（终边）所形成的图形。
（2）角的分类⎧⎪⎨⎪⎩正角:按逆时针方向旋转形成的角任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角要点二、终边相同角 （1）终边相同角的定义设α表示任意角，所有与α终边相同的角，包括α本身构成一个集合，这个集合可记为{},360|Z k k S ∈︒⋅+==αββ。
集合S 的每一个元素都与α的终边相等，当0=k 时，对应元素为α。
（2）注意①相等的角终边一定相同，但终边相同的角不一定相等；终边相同的角有无数个，它们相差︒360的整数倍。
②角的集合表示形式是不唯一的。
要点三、象限角与轴线角（1）象限角定义：角α顶点与原点重合，角的始边与x 轴非负半轴重合，终边落在第几象限，则称α为第几象限角． 第一象限角的集合为： 第二象限角的集合为：第四象限角的集合为：终边落在x 轴正半轴上角的集合： 终边落在x 轴负半轴上角的集合： 终边在x 轴上的角的集合为： 终边落在y 轴正半轴上角的集合： 终边落在y 轴负半轴上角的集合： 终边在y 轴上的角的集合为： 终边落在坐标轴上角的集合：（2）注意：终边落在同一条直线上的角相差︒180的整数倍，终边落在同一条射线上的角相差︒360的整数倍。
要点四、区间角、区域角区间角是介于两个角之间的角的集合，区域角是介于某两角终边之间的角的集合。
区域角是无数个区间角的集合。
注意：锐角都是第一象限角，但第一象限角不都是锐角；小于90°的角不都是锐角，它还包括零角和负角，只有小于90°的正角才是锐角。
考点一、求终边相同的角的集合例1.（1）写出所有与︒-650终边相同的角的集合，并在︒︒360~0范围内，找出与︒-650角终边相同的角。
（2）把︒-2011写成)3600(360︒≤≤︒+⋅ααk 的形式。
第5章-5.2.1-任意角三角函数的定义高中数学必修第一册湘教版
+ 2
2
3
cos sin = ± ．
4
1
− ，
2
=−
= 1，解得 = ±
3
，即cos
2
3
，即sin
2
=
=±
1
1
− .因为点 ,
2
2
3
，所以
2
在单
题型2 三角函数值的符号的判断
例7 判断下列各式的符号：
（1）tan 120∘ sin 269∘ ;
【解析】∵ 120∘ 是第二象限角,∴ tan 120∘ < 0.
方法帮丨关键能力构建
题型1 利用定义求三角函数值
例4 已知角 的终边经过点 2, −3 ，则sin
−
____．
−
=_______，cos
=_____，tan
=
【解析】因为 = 2， = −3，所以点到原点的距离 =
sin =
=
−3
13
=
3 13
（2）tan >
3
.
3
【解析】如图5.2.1-8，过单位圆与轴正半轴的交点作轴的
3
，过点和作一条直线，
3
3
此时终边落在直线上的角的正切值为 .在[0,2π)内，
3
π
7π
3
tan = tan = ，
6
6
3
垂线，在垂线上取一点，使得 =
由图可知，满足条件的角的终边在图中阴影部分（不包括边
π
由题意，知−
2
D.sin 2 < 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学新课标典型例题：任意角的三角函数 1
例1下列说法中，正确的是
[ ] A．第一象限的角是锐角
B．锐角是第一象限的角
C．小于90°的角是锐角
D．0°到90°的角是第一象限的角
【分析】本题涉及了几个基本概念，即“第一象限的角”、“锐角”、“小于90°的角”和“0°到90°的角”．在角的概念推广以后，这些概念容易混淆．因此，弄清
楚这些概念及它们之间的区别，是正确解答本题的关键．
【解】第一象限的角可表示为｛θ|k·360°＜θ＜90°＋k·360°，k∈Z｝，锐角可表示为｛θ|0°＜θ＜90°｝，小于90°的角为｛θ|θ＜90°｝，0°到90°的角为｛θ|0°≤θ＜90°｝．因此，锐角的集合是第一象限角的集合当k=0时的子集，故(A)，(C)，(D)均不正确，应选(B)．
(90°－α)分别是第几象限角？
【分析】由sinα·cosα＜0，所以α在二、四象限；由sinα·tanα＜0，所以α在二、三象限．因此α为第二象限的角，然后由角α的
【解】(1)由题设可知α是第二象限的角，即
90°＋k·360°＜α＜180°＋k·360°(k∈Z)，
的角．
(2)因为180°＋2k·360°＜2α＜360°＋2k·360°(k∈Z)，所以2α是第三、第四象限角或终边在y轴非正半轴上的角．
(3)解法一：因为90°+k·360°＜α＜180°＋k·360°(k∈Z)，
所以－180°－k·360°＜－α＜－90°－k·360°(k∈Z)．
故－90°－k·360°＜90°－α＜－k·360°(k∈Z)．
因此90°－α是第四象限的角．
解法二：因为角α的终边在第二象限，所以－α的终边在第三象限．
将－α的终边按逆时针旋转90°，可知90°－α的终边在第四象限内．
【说明】①在确定形如α＋k·180°角的象限时，一般要分k为偶数或奇数讨论；
②确定象限时，α＋kπ与α－kπ是等效的．
例3已知集合E=｛θ|cosθ＜sinθ，0≤θ≤２π｝，F=｛θ|tanθ＜sinθ｝，那么E∩Ｆ是区间
[ ]
【分析】解答本题必须熟练掌握各个象限三角函数的符号、各个象限的三角函
数值随角的变化而递增或递减的变化情况．可由三角函数的性质判断，也可由三角函数
线判断．用代入特殊值排除错误答案的方法解答本题也比较容易．
【解法一】由正、余弦函数的性质，
【解法二】由单位圆中的正弦线和正切线容易看出，对于二、四象限的角，AT＜MP，即tanα＜sinθ，由正弦线和余弦线可看出，当
应选(A)．
可排除(C)，(D)，得(A)．
【说明】本题解法很多，用三角函数线还可以有以下解法：因为第一、三象限均有AT＞MP，即tanθ＞sinθ，所以(B)，(C)，(D)均不成立．用排除法也有些别的方法，
可自己练习．
例 4 (1)已知角α终边上一点P(3k，－4k)(k＜0)，求sinα，cosα，tanα的值；
【分析】利用三角函数的定义进行三角式的求值、化简和证明，是
三两个象限，因此必须分两种情况讨论．
【解】(1)因为x＝3k，y=－4k，
例5一个扇形的周长为l，求扇形的半径、圆心角各取何值时，此扇形的面积最大．
【分析】解答本题，需灵活运用弧度制下的求弧长和求面积公式．本题是求扇形面积的最大值，因此应想法写出面积S以半径r为自变量的函数表达式，再用配方法求出
半径r和已知周长l的关系．
【解】设扇形面积为S，半径为r，圆心角为α，则扇形弧长为l－2r．所以
【说明】在学习弧度制以后，用弧度制表示的求弧长与扇形面积公
形的问题中，中心角用弧度表示较方便．本例实际上推导出一个重要公式，即当扇形周长为定值时，怎样选取中心角可使面积得到最大值．本题也可将面积表示为α的函数式，用判别式来解．
【分析】第(1)小题因α在第二象限，因此只有一组解；第(2)小题给了正弦函数值，但没有确定角α的象限，因此有两组解；第(3)小题角α可能在四个象限或是轴线角，因此需分两种情况讨论．
【解】
(3)因为sinα=m(|m|＜1)，所以α可能在四个象限或α的终边在x轴上．
例7(1)已知 tanα=m，求sinα的值；
【分析】(1)已知tanα的值求sinα或cosα，一般可将tanα
母都是sinα和cosα的同次式，再转化为关于tanα的式子求值，转化的方法是将分子、分母同除以cosα(或cos2α，这里cosα≠0)，即可根据已知条件求值．
【说明】由tanα的值求sinα和cosα的值，有一些书上利用公
很容易推出，所以不用专门推导和记忆这些公式，这类问题由现有的关系式和方法均可解决．
函数的定义来证明．
由左边=右边，所以原式成立．
【证法三】(根据三角函数定义)
设P(x，y)是角α终边上的任意一点，则
左边=左边，故等式成立．
例9化简或求值：
【分析】解本题的关键是熟练地应用正、余弦的诱导公式和记住特殊角的三角函数值．
=－sinα－cosα(因为α为第三象限角)．
例10 (1)若 f(cos x)=cos9x，求f(sin x)的表达式；
【分析】在(1)中理解函数符号的含义，并将f(sin x)化成f(cos(90°－x))是充分利用已知条件和诱导公式的关键．在(2)中必须正确掌握分段函数求值的方法．
【解】(1)f(sin x)＝f(cos(90°－x))＝cos9(90°－x)
=cos(2×360°＋90°－9x)＝cos(90°－9x)
=sin9x；
＝1．。