湘教版九年级数学上《相似三角形判定与性质》综合培优题
2018-2019学年最新湘教版九年级数学上册《相似三角形的判定与性质》同步测试及解析-精编试题

湘教版九年级数学上册第三章第四节《相似三角形的判定与性质》同步测试一.选择题(共10小题)1.如图,下列条件不能判定△ADB∽△ABC的是()A.∠ABD=∠ACB B.∠ADB=∠ABCC.AB2=AD•AC D.=2.如图,点P是▱ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有()A.0对B.1对C.2对D.3对3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A.∠ABP=∠C B.∠APB=∠ABCC.=D.=4.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.5.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于()A.B.C.D.6.若两个相似三角形的面积之比为1:4,则它们的最大边的比是()A.1:2 B.1:4 C.1:5 D. 1:167.若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为()A.16 B.8 C. 4 D. 28.(2015•呼伦贝尔)如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是()A.﹣1 B.C.1 D.9.在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则等于()A.B.C.D.10.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为()A.4 B.7C.3 D.12二.填空题(共8小题)11.在△ABC中,AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC 相似,且S△ADE:S四边形BCED=1:8,则AD= cm.12.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上中线的比为.13.如图,在△ABC中,D、E分别是AB、AC边上的点(DE不平行于BC),当时(写出一个答案即可),△ADE与△ABC相似.14.如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是.15.如图,已知矩形ABCD 的边长AB=3cm ,BC=6cm .某一时刻,动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动;同时动点N 从D 点出发沿DA 方向以2cm/s 的速度向A 点匀速运动.若以A 、M 、N 为顶点的三角形与△ACD 相似,则运动的时间 t 为 秒.16.如图,在△ABC 中,∠BAC=90°,∠B=30°,AD ⊥BC ,AE 平分∠BAD ,则△ABC ∽ ,△BAD ∽△ACD (写出一个三角形即可).17.如图,已知四边形ABCD 中,∠A=∠B=∠DEC ,且点E 为AB 边中点,则图中有 对相似三角形.18.如图,正方形ABCB 1中,AB=1.AB 与直线l 的夹角为30°,延长CB 1交直线l 于点A 1,作正方形A 1B 1C 1B 2,延长C 1B 2交直线l 于点A 2,作正方形A 2B 2C 2B 3,延长C 2B 3交直线l 于点A 3,作正方形A 3B 3C 3B 4,…,依此规律,则A 2014A 2015= .三.解答题(共6小题) 第15题图第16题图第17题图19.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求的值.20.如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,问△AOB与△COD 是否相似?有一位同学解答下:∵AD∥BC,∴∠ADO=∠CBO,∠DAO=∠BCO.∴△AOD∽△BOC.∴.又∵∠AOB=∠DOC,∴△AOB∽△COD.请判断这位同学的解答是否正确并说明理由.21.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.22.在平行四边形ABCD中,E为BC边上的一点.连结AE.(1)若AB=AE,求证:∠DAE=∠D;(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.23.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.(1)若△BMN与△ABC相似,求t的值;(2)连接AN,CM,若AN⊥CM,求t的值.24.在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC 向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:(1)当t=3秒时,这时,P,Q两点之间的距离是多少?(2)若△CPQ的面积为S,求S关于t的函数关系式.(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?第三章第四节《相似三角形的判定与性质》同步测试参考答案:一.选择题(共10小题)1.D 2.D 3.D 4.C 5.A 6.A 7.B 8.A 9.A 10.B二.填空题(共8小题)11.2或cm.12.2:3 .13.不唯一,如∠ADE=∠C 14.(3,6).15. 2.4或1.5 秒.16.△DBA (写出一个三角形即可).17. 3 18.2()2014.三.解答题(共6小题)19.解:∵DE∥BC,∴=,∵AD=3,AB=5,∴=.20.解:不正确,错误的原因是由△AOD∽△BOC得出,正解是:∵△AOD∽△BOC,∴,而就不能进一步推出△AOB∽△COD了.21.证明:∵∠BAC=90°,AB=AC=1,∴△ABC为等腰直角三角形,∴∠B=∠C=45°,∴∠1+∠2=180°﹣∠B=135°,∵∠ADE=45°,∴∠2+∠3=135°,∴∠1=∠3,∵∠B=∠C,∴△ABD∽△DCE.22.证明:(1)在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠B=∠EAD,∵∠B=∠D,∴∠DAE=∠D;(2)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△BEF∽△AFD,∴,∵E为BC的中点,∴BE=BC=AD,∴EF:FA=1:2.23.解:(1)由题意知,BM=3tcm,CN=2tcm,∴BN=(8﹣2t)cm,BA==10(cm),当△BMN∽△BAC时,,∴,解得:t=;当△BMN∽△BCA时,,∴,解得:t=,∴△BMN与△ABC相似时,t的值为或;(2)过点M作MD⊥CB于点D,由题意得:DM=BMsinB=3t=(cm),BD=BMcosB=3t=t(cm),BM=3tcm,CN=2tcm,∴CD=(8﹣)cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴,∴=,解得t=.24.解:由题意得AP=4t,CQ=2t,则CP=20﹣4t,(1)当t=3秒时,CP=20﹣4t=8cm,CQ=2t=6cm,由勾股定理得PQ=;(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,因此Rt△CPQ的面积为S=cm2;(3)分两种情况:①当Rt△CPQ∽Rt△CAB时,,即,解得t=3秒;②当Rt△CPQ∽Rt△CBA时,,即,解得t=秒.因此t=3秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似.。
湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案

湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.已知△ABC∽△A′B′C′且ABA′B′=12,则S△ABC∶S△A′B′C′为( )A.1∶2B.2∶1C.1∶4D.4∶12.如图,△ABC与△DE F相似,相似比为1∶2,BC的对应边是EF,若BC=1,则EF的长是( )A.1B.2C.3D.43.已知△ABC∽△DEF,且AB∶DE=1∶2,则△ABC的面积与△DEF的面积之比为( )A.1∶2B.1∶4C.2∶1D.4∶14.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF :S△ABF=4:25,则DE:EC=()A.2:3 B.2:5 C.3:5 D.3:25.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )A.1对B.2对C.3对D.4对6.如图,P是Rt△ABC的斜边BC上异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )A.1条B.2条C.3条D.4条7.如图,点P是△ABC的边AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )A.2条B.3条C.4条D.5条8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在格点为( )A.P1 B.P2C.P3D.P49.要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架乙共有( )A.1种B.2种C.3种D.4种10.如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是( )A.①②④B.②③④C.①②③④D.①③二、填空题11.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比值为.12.若两个相似三角形的周长比为2:3,则它们的面积比是.13.若△ABC∽△A′B′C′,且AB:A′B′=3:4,△ABC的周长为12 cm,则△A′B′C′的周长为____________.14.下图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是.(写出满足条件的所有的点)15.如图,平行四边形ABCD中,E是BC边延长线上一点,AE交CD于F,则图中相似三角形有对.16.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是.三、解答题17.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°. 求证:△ADC∽△DEB.18.如图,A、B、C、P四点均在边长为1的小正方形网格格点上.(1)判断△PBA与△ABC是否相似,并说明理由;(2)求∠BAC的度数.19.如图所示,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1) ∠EAF=∠B;(2) AF2=FE·FB.20.如图,在△ABC中,AD和BG是△ABC的高,连接GD.(1)求证△ADC∽△BGC;(2)求证CG·AB=CB·DG.21.如图,已知P是正方形ABCD边BC上一点,BP=3PC,Q是CD的中点(1)求证:△ADQ∽△QCP;(2)若AB=10,连接BD交AP于点M,交AQ于点N,求BM,QN的长.22.在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.(1)如图①,若BD=CE,求证:DF=EF.(2)如图②,若BD=1nCE,试写出DF和EF之间的数量关系,并证明.(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.答案1.C2.B3.B4.A5.C.6.C7.C.8.B9.C.10.C.11.答案为:1:4.12.答案为:4:9.13.答案为:16cm.14.答案为:Q.15.答案为:4.16.答案为(﹣3×4n﹣1,4n).17.证明:∵△ABC是等边三角形∴∠B=∠C=60°∴∠ADB=∠CAD+∠C=∠CAD+60°∵∠ADE=60°∴∠ADB=∠BDE+60°∴∠CAD=∠BDE∴△ADC∽△DEB.18.解:(1)△PBA与△ABC相似,理由如下:∵AB=5,BC=5,BP=1∴∵∠PBA=∠ABC∴△PBA∽△ABC;(2)∵△PBA∽△ABC∴∠BAC=∠BPA∵∠BPA=90°+45°=135°∴∠BAC=135°.19.证明:(1)∵AB∥CD∴∠B=∠C又∠C=∠EAF∴∠EAF=∠B(2)∵∠EAF=∠B,∠AFE=∠BFA ∴△AFE∽△BFA则AFBF=FEFA∴AF2=FE·FB20.解:(1) ∵在△ABC中,AD和BG是△ABC的高∴∠BGC=∠ADC=90°.又∠C=∠C∴△ADC∽△BGC.(2)∵△ADC∽△BGC∴CGDC=BCAC.∴CGBC=DCAC.又∠C=∠C∴△GDC∽△BAC.∴CGBC=DGAB.∴CG·AB=CB·DG.21.证明:(1)∵正方形ABCD中,BP=3PC,Q是CD的中点∴PC=14﹣BC,CQ=DQ=12CD,且BC=CD=AD∴PC :DQ =CQ :AD =1:2 ∵∠PCQ =∠ADQ =90° ∴△PCQ ∽△ADQ (2)∵△BMP ∽△AMD ∴BM :DM =BP :AD =3:4 ∵AB =10 ∴BD =10 2 ∴BM =同理QN =53 5.22.证明:(1)在题图①中作EG ∥AB 交BC 于点G 则∠ABC =∠EGC ,∠D =∠FEG. ∵AB =AC ,∴∠ABC =∠C. ∴∠EGC =∠C.∴EG =EC. ∵BD =CE ,∴BD =EG. ∵∠D =∠FEG ,∠BFD =∠GFE ∴△BFD ≌△GFE. ∴DF =EF. (2)解:DF =1nEF.证明:在题图②中作EG ∥AB 交BC 于点G ,则∠D =∠FEG.由(1)得EG =EC. ∵∠D =∠FEG ,∠BFD =∠EFG ∴△BFD ∽△GFE.∴BD EG =DF EF. ∵BD =1n CE =1n EG∴DF =1n EF.(3)解:成立.证明:在题图③中作EG ∥AB 交CB 的延长线于点G则仍有EG=EC,△BFD∽△GFE.∴BDEG=DFEF.∵BD=1nCE=1nEG,∴DF=1nEF.。
湘教版数学九年级上册第三章3.4《相似三角形的判定》解答题专项练习+解析.docx

湘教版九年级数学上册第三章3.4《相似三角形的判定》解答题专项练习+解析一.解答题(共12小题)1.如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;(2)选择(1)中一对加以证明.2.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,连接EF并延长交BC的延长线于点G.(1)求证:△ABE∽△DEF;(2)若正方形的边长为4,求BG的长.3.如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.4.如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.5.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.6.如图,在8×8的正方形网格中,△CAB和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.(1)填空:AC=,AB=.(2)求∠ACB的值和tan∠1的值;(3)判断△CAB和△DEF是否相似?并说明理由.7.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.(1)若BC=8,求FD的长;(2)若AB=AC,求证:△ADE∽△DFE.8.如图:方格纸中的每个小正方形边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.①判断△ABC和△DEF是否相似,并说明理由;②点P1,P2,P3,D,F都是△DEF边上的5个格点,请在这5个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似.(写出一个即可,并在图中连接相应线段,不必说明理由)9.如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,求证:△AEF∽△ACB.10.如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.(1)证明:△ABD∽△DCF;(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.11.如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.(1)求证:△ABD≌△BCE;(2)图中共有对相似三角形(全等除外).并请你任选其中一对加以证明.你选择的是.12.如图,△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)写出图中两对相似三角形(不得添加字母和线).(2)请选择其中的一对三角形,说明其相似的理由.湖南省澧县张公庙镇中学2015-2016学年湘教版九年级数学上册第三章3.4《相似三角形的判定》解答题专项练习+解析参考答案与解析一.解答题(共12小题)1.解:(1)△ADE≌△BDE,△ABC∽△BCD;(2)证明:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∴∠ABD=∠ABC=36°=∠A,在△ADE和△BDE中∵,∴△ADE≌△BDE(AAS);证明:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD为角平分线,∴∠DBC=∠ABC=36°=∠A,∵∠C=∠C,∴△ABC∽△BCD.2.(1)证明:∵ABCD为正方形,∴AD=AB=DC=BC,∠A=∠D=90°,∵AE=ED,∴,∵DF=DC,∴,∴,∴△ABE∽△DEF;(2)解:∵ABCD为正方形,∴ED∥BG,∴,又∵DF=DC,正方形的边长为4,∴ED=2,CG=6,∴BG=BC+CG=10.3.解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,有,∴AM=,∵BC=6,∴MN=3;②图2,作∠ANM=∠B,则△ANM∽△ABC,有,∵M为AB中点,AB=,∴AM=,∵BC=6,AC=,∴MN=,∴MN的长为3或.4.证明:∵AB=AC,D是BC中点,∴AD⊥BC,∴∠ADC=90°,∴∠FAE+∠AFE=90°,∵BE⊥AC,∴∠BEC=90°,∴∠CBE+∠BFD=90°,∵∠AFE=∠BFD,∴∠FAD=∠CBE,∴△AFE∽△BCE.5.证明:∵∠BAC=90°,AB=AC=1,∴△ABC为等腰直角三角形,∴∠B=∠C=45°,∴∠1+∠2=180°﹣∠B=135°,∵∠ADE=45°,∴∠2+∠3=135°,∴∠1=∠3,∵∠B=∠C,∴△ABD∽△DCE.6.解:(1)如图,由勾股定理,得AC==2.AB==2故答案是:2,2;(2)如图所示,BC==2.又由(1)知,AC=2,AB=2,∴AC2+BC2=AB2=40,∴∠ACB=90°.tan∠1==.综上所述,∠ACB的值是90°和tan∠1的值是;(3)△CAB和△DEF相似.理由如下:如图,DE=DF==,EF==.则===2,所以△CAB∽△DEF.7.解:(1)∵D、E分别是边AB、AC的中点,∴,DE∥BC.∴∠AED=∠C.∵∠F=∠C,∴∠AED=∠F,∴FD==4;(2)∵AB=AC,DE∥BC.∴∠B=∠C=∠AED=∠ADE,∵∠AED=∠F,∴∠ADE=∠F,又∵∠AED=∠AED,∴△ADE∽△DFE.8.解:①△ABC和△DEF相似.理由如下:∴===,∴△ABC∽△DEF;②△ACB∽△DP3P2.理由如下:∵由①知,△ABC∽△DEF,∴∠D=∠A.连接DP2P3,DP3=,DP2=,P2P3=.∵==,∴△ACB∽△DP3P2.9.证明:∵CE⊥AB,BF⊥AC,∴∠AEC=∠AFB=90°.∵∠A是公共角,∴△ABF∽△ACE.∴,∴,又∠A是公共角,∴△AEF∽△ACB.10.(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,∴∠1+∠2=∠DFC+∠2,∴∠1=∠DFC,∴△ABD∽△DCF;(2)解:∵∠C=∠E,∠AFE=∠DFC,∴△AEF∽△DCF,∴△ABD∽△AEF,故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.11.(1)证明:∵△ABC是等边三角形,∴AC=BA,∠ABD=∠C=60°,∴△ABD≌△BCE(SAS);(2)4对,分别是△BDF∽△BEC,△DBF∽△DAB,△AFE∽△ACD,△AFE∽△BAE,选择证明△AEF∽△BEA,∵△ABC是等边三角形,∴AC=BA,∠C=∠BAE=60°,AC=BC,∵BD=CE,∴AE=CD,∴△ACD≌△BAE(SAS),∴∠DAC=∠ABE,又∵∠AEF=∠BEA,∴△AEF∽△BEA.12.(1)解:△ABC∽△ADE,△ABD∽△ACE;(2)△ABD∽△ACE.证明:由(1)知△ABC∽△ADE,∴=,∴AB×AE=AC×AD,∴=,∵∠BAD=∠CAE,∴△ABD∽△ACE.初中数学试卷桑水出品。
九年级数学上册 3.3相似三角形的性质和判定同步练习 湘教版

九年级数学上册 3.3相似三角形的性质和判定同步练习湘教版九年级数学上册3.3相似三角形的性质和判定同步练习湘教版3.3关于相似三角形的性质和判断的同步实践一、仔仔细细,记录自信1.如图1所示,△ 牛津英语词典≓△ OCB,OE=6,EC=21,则△ OCB和△ 《牛津英语词典》是一本37b.52c。
85d.352.如图2,点e,f分别在矩形abcd的边dc,bc上,∠aef=90°,∠afb=2∠dae=72°,则图中甲、乙、丙三个三角形中相似的是()a.只有甲与乙b、只有b和Cc.只有甲与丙d、 A、B和C3.如图3,d是ab的中点,e是ac的中点,则△ade与四边形bced的面积比是()a.1c.13121d。
4b.4.在相同水压下,直径为4cm的水管出水量是直径为1cm的水管出水量的()a.4倍b.8倍c、 12次d.16倍5.以下声明:(1)相似且有一边为公共边的两个三角形全等;(2)相似且面积相等的两个三角形全等;(3)相似且周长相等的两个三角形全等.其中说法正确的有()a.0个b、一,c.2个d、三,6.我国国土面积约为960万平方千米,画在比例尺为1∶1000万的地图上的面积约是()a.960平方千米b、 960平方米c.960平方分米d、 960平方厘米二、认认真真,书写快乐7.已知△ 基础知识≓△ A.BCab呢?4,a?B6,b?C8那么BC=。
8.两个相似三角形,其中一个三角形的两个内角分别为40°和30°,则另一个三角形的最大内角为用心爱心专心一9.如图4,∠abc=∠cdb=90°,ac=a,bc=b,当bd与a、b满足关系时,△abc∽△cdb.10.如图5所示,P是等腰梯形ABCD上下ad上的一个点。
如果∠ a=∠ BPC,有一个类似于△ ABP11.相似三角形对应、、的比都等于相似比.12.相似多边形的周长比等于,面积比等于.13.如果三角形的三条边同时扩大四倍,则周长扩大几倍,面积扩大几倍。
湘教版-数学-九年级上册-数学3.4相似三角形的判定与性质
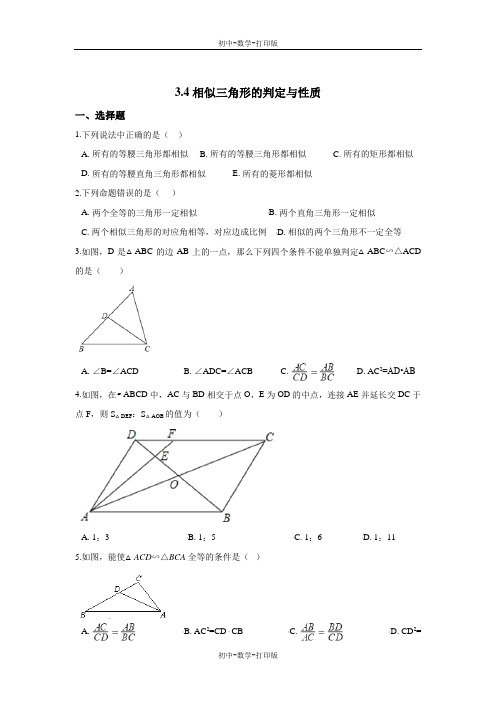
3.4相似三角形的判定与性质一、选择题1.下列说法中正确的是()A. 所有的等腰三角形都相似B. 所有的等腰三角形都相似C. 所有的矩形都相似D. 所有的等腰直角三角形都相似E. 所有的菱形都相似2.下列命题错误的是()A. 两个全等的三角形一定相似B. 两个直角三角形一定相似C. 两个相似三角形的对应角相等,对应边成比例D. 相似的两个三角形不一定全等3.如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD 的是()A. ∠B=∠ACDB. ∠ADC=∠ACBC.D. AC2=AD•AB4.如图,在▱ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为()A. 1:3B. 1:5C. 1:6D. 1:115.如图,能使△ACD∽△BCA全等的条件是()A. B. AC2=CD CB C. D. CD2=AD BD6.下列各组中的两个图形,不一定相似的是()A. 有一个角是120°的两个等腰三角形B. 两个等边三角形C. 两个直角三角形D. 两个等腰直角三角形7.设△ABC的面积为1,如图①,将边BC、AC分别2等分,BE1、AD1相交于点O,△AOB 的面积记为S1;如图②将边BC、AC分别3等分,BE1、AD1相交于点O,△AOB的面积记为S2;…,依此类推,则S n可表示为()(用含n的代数式表示,其中n为正整数)A. B. C. D.8.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是()A. =B. C. D.9.如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为()A. 2:3B. 2:5C. 4:9D. :10.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的()A. =B. =C. =D.=二、填空题11.若△ABC∽△DEF,相似比为2:3,则S△ABC:S△DEF=________.12.如图所示,△ABC中,DE∥BC ,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为________。
湘教版九年级上册数学相似三角形的判定定理同步测试题

3.4 相似三角形的判定与性质3.4.1 相似三角形的判定第2课时相似三角形的判定定理11. 有一个含有30°的两个直角三角形,一定( )A.相似B.全等C.既全等也相D.无法确定2.如图,在△ABC中.∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有()A.1对 B.2对 C.3对D.4对3. 如图,在Rt ABC∠=,E是AC的中点,且AB=5,AC=4,过E ∆中, C90作EF⊥AB于F,则AF=_______.4.如图,∠1=∠2=∠3,则图中相似三角形共有_____.5. 如图在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,那么与△ABC相似的三角形的个数有____.6. 如图,在△ABC中,AB=AC,BD=CD,CE⊥AB 于E.求证:△ABD∽△CBE.初中生提高做题效率的方法厚薄读书法:复习课本要厚薄结合著名数学家华罗庚先生说:“书要能从薄读到厚,还要能从厚读到薄。
”这就是厚薄读书法。
我们在复习功课时,也可以用这种方法,具体来说分为“由薄到厚”和“由厚读薄”两个部分由薄到厚第一步要“由薄到厚”地复习课本。
这就是说,我们在复习过程中对书本中的某些原理、定律、公式,不仅应该记住它的结论,而且还应该思考一下,这个定律是怎样发现的,这个公式是怎样推导的。
在阅读过程中对书中的每个概念、原理和观点要有自己的理解,对自己不懂的地方,还要查阅参考资料,通过充实书本的有关内容,使自己获得比书本上内容更为丰富、更为深刻的认识和见解,也就是把书“越读越厚”。
由厚到薄第二步可采用“由厚读薄”的方法。
在深入理解课本内容的基础上,经过自己的思考,对书中的内容加以归纳、综合和概括,抓住书中的精要、纲领,提高记忆效率。
具体来说,可采用提纲法和图表法进行归纳。
1.提纲法。
我们在复习的时候,一定要抓住纲要。
所以,在学完一个章节后,立即进行小结,总结归纳出一个复习提纲。
湘教版九年级上相似三角形性质与判定基础练习题

九上基础提高五 1、已知线段a 、b 有32a b a b +=-,则a:b 为 2、如图,两个三角形相似,AD =2,AE =3,EC =1,则BD = .第2题图 第3题图 第4题图3、如图,□ABCD 中,EF ∥AB ,DE:DA=2:5,EF=4,则CD 的长为 。
4、如图,电灯P 在横杆AB 的正上方,AB 在灯光下的影子为CD ,AB ∥CD,AB=2米,CD=5米,点P 到CD 的距离是3米,则P 到AB 的距离是 米。
5、如图,在河两岸分别有A 、B 两村,现测得A 、B 、D 在一条直线上,A 、C 、E 在一条直线上,BC//DE ,DE=90米,BC=70米,BD=20米。
则A 、B 两村间的距离为 。
第5题图 第6题图 第8题图6、如图,要使△ADB∽△ABC,还需要增添的条件是 _____ ____7、若△ABC ∽△'''C B A ,相似比为3∶2,则面积比为 ,若它们的周长差为40厘米,则△'''C B A 的周长为 厘米。
8、如图,在△ABC 中,CD ,AE 是三角形的两条高,写出图中所有 相似的三角形为 9、已知△ABC∽△A'B'C',S △ABC ∶S △A'B''C '=16∶9,AB=2,则A'B'= ___ 10、已知△ABC ∽△A′B′C′,AD 和A′D′是对应角平分线,且AD=8 A′D′=3 ,则△ABC 与△A′B′C′对应高的比为11、如图,D 、E 分别为AB 、AC 的中点,BE 、CD 交于点O , 则△ADE ∽△ ,相似比K 1= ; △ODE ∽△ ,相似比K 2= .12、如图,△ADE ∽△ABC ,21=BD AD ,△ABC 的面积为18, 则四边形BCED 的面积为 .13、已知:如图,ABCD 中,2:1:=EB AE ,(1)求AEF ∆与CDF ∆ 的周长的比,(2)如果2cm 6=∆AEF S ,求CDF S ∆.14、如图,已知ΔABC 中,AD 为BC 边中线,E 为AD 上一点,且CE=CD,∠EAC=∠B,求证:(1)ΔAEC ∽ΔBDA, (2) DC 2=AD •AE15、如图,在4×3的正方形方格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上. (1)填空:∠ABC= _________ °,BC= _________ ; (2)判断△ABC 与△DEC 是否相似,并证明你的结论.16、如图,∠ACB=∠ADC=90°,AC=6 ,AD=2.问当AB 的长为多少时,这两个直角三角形相似.17、如图,△ABC 是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?18、如图,在Rt ΔABC 中,∠ACB=90°,CD ⊥AB 于D ,AC=12,BC=9, 求AB 及BD 的长19、如图梯形ABCD 中,AD BC ∥,AC 与BD 相交于O 点,过点B 作BE CD ∥交CA 的延长线于点E . 求证:OE OA OC ⋅=220.如图,平行四边形ABCD 中,过点A 作AE ⊥BC 于为E ,连接DE ,F 为线段DE 上一点,且∠AFE =∠B.(1)求证:△ADF ∽△DEC (2)若AB =4,AD =33,AE =3,求AF 的长.21、如图、在等边⊿ABC 中,P 为BC 边的一点,D 为AC 上的一点,且∠APD= ︒06,(1)求证:ΔABP ∽ΔPCD; (2)若BP=1,CD=32,求⊿ABC 的边长.22、如图,在直角坐标系中,已知点A (2,0),B (0,4),在坐标轴上找到点C (1,0)和点D ,使△AOB 与△DOC 相似,求出D 点的坐标。
湘教版九年级数学上册测试题3.4 相似三角形的判定与性质3.4.1第4课时

第4课时 相似三角形的判定定理301 基础题知识点 三边成比例的两个三角形相似1.将一个三角形的各边都缩小12后,得到的三角形与原三角形(A) A .一定相似 B .一定不相似C .不一定相似D .不能判断是否相似2.甲三角形的三边分别为1,2,5,乙三角形的三边分别为5,10,5,则甲乙两个三角形(A)A .一定相似B .一定不相似C .不一定相似D .无法判断是否相似3.已知△ABC 的三边长分别为6 cm 、7.5 cm 、9 cm ,△DEF 的一边长为4 cm ,要使这两个三角形相似,则△DEF 的另两边长可以是(C)A .2 cm ,3 cmB .4 cm ,5 cmC .5 cm ,6 cmD .6 cm ,7 cm4.如图,两个三角形的关系是相似(填“相似”或“不相似”),理由是三边成比例的两个三角形相似.5.若△ABC 各边分别为AB =10 cm ,BC =8 cm ,AC =6 cm ,△DEF 的两边为DE =5 cm ,EF =4 cm ,则当DF =3cm 时,△ABC ∽△DEF.6.△ABC 和△A′B′C′符合下列条件,判断△ABC 与△A′B′C′是否相似.BC =2,AC =3,AB =4;B′C′=2,A′C′=3,A′B′=2.解:在△ABC 中,AB>AC>BC ,在△A′B′C′中,A′B′>A′C′>B′C′,BC B′C′=22=2,AC A′C′=33=3,AB A′B′=42=2. ∴BC B′C′≠AB A′B′≠AC A′C′. ∴△ABC 与△A′B′C′不相似.7.如图所示,根据所给条件,判断△ABC 和△DBE 是否相似,并说明理由.解:△ABC ∽△DBE.理由如下:∵AC DE =36=12,BC BE =48=12,AB DB =510=12, ∴AC DE =BC BE =AB DB. ∴△ABC ∽△DBE.02 中档题8.下列能使△ABC 和△DEF 相似的条件是(C)A .AB =c ,AC =b ,BC =a ,DE =a ,EF =b ,DF = cB .AB =1,AC =1.5,BC =2,DE =12,EF =8,DF =1C .AB =3,AC =4,BC =6,DE =12,EF =8,DF =6D .AB =2,AC =3,BC =5,DE =6,EF =3,DF =39.如图,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点,为使△ABC ∽△PQR ,则点R 应是甲、乙、丙、丁四点中的(C)A .甲B .乙C .丙D .丁10.(东营中考)如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的三条边长分别是3、4及x ,那么x 的值(B)A .只有1个B .可以有2个C .可以有3个D .有无数个11.如图,△ABC 中,点D 、E 、F 分别是AB 、BC 、AC 的中点,求证:△ABC ∽△EFD.证明:∵DE 、EF 、DF 是△ABC 的中位线,∴DE AC =EF AB =DF BC =12. ∴△ABC ∽△EFD.12.如图,正方形网格中每个小正方形的边长为1,△ABC 和△EDF 的顶点都在网格的格点上.(1)求证:△ABC ∽△EDF ;(2)求∠BAC 的度数.解:(1)证明:∵DE =2,DF =12+32=10,EF =2,AB =12+22=5,AC =12+32=10,BC =5,∴AB DE =AC EF =BC DF =102. ∴△ABC ∽△EDF.(2)∵△ABC ∽△EDF ,∴∠BAC =∠DEF.∵∠DEF =90°+45°=135°,∴∠BAC =135°.13.已知一个三角形框架的三边长分别为3米、4米、5米,现要做一个与其相似的三角形框架,已有一根长为2米的木条,问其他两根木条可选多长?共有多少种不同选法?解:(1)若2米的木条为最短边,设其他两根木条的长分别为x m 和y m ,则32=4x =5y ,解得x =83,y =103. (2)若2米的木条为第二长的边,设其他两根木条的长分别为x m 和y m ,则3 x=42=5y,解得x=32,y=52.(3)若2米的木条为最长边,设其他两根木条长分别为x m和y m,则3 x=4y=52,解得x=65,y=85.03综合题14.(菏泽中考)如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:(1)试证明△ABC是直角三角形;(2)判断△ABC和△DEF是否相似,并说明理由;(3)画一个三角形,使它的三个顶点为P1、P2、P3、P4、P5中的3个格点,并且与△ABC相似.解:(1)证明:根据勾股定理,得AB=25,AC=5,BC=5,∴AB2+AC2=BC2.∴△ABC为直角三角形.(2)△ABC和△DEF相似.理由:根据勾股定理,得AB=25,AC=5,BC=5,DE=42,DF=22,EF=210.∵ABDE=ACDF=BCEF=104,∴△ABC∽△DEF.(3)如图,△P2P4P5即为所求.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
C
P 九年级上培优五
1、如图RtΔABC中,∠ACB=90°,CD⊥AB与D,AC=6,BC=8,则
AB= ,CD= ,AD= ,BD=
第1题图第2题图
2、如图□ABCD中,EF∥AB,DE:DA=2:5,EF=4,则CD的长为。
3、如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD ,
AB∥CD,AB=2米,CD=5米,点P到CD的距离是3米,则P到
AB的距离是米。
第3题图第4题图
4、如图,在河两岸分别有A、B两村,现测得A、B、D在一条直线
上,A、C、E在一条直线上,BC//DE,DE=90米,BC=70米,BD=20
米,则A、B两村间的距离为。
5、如图,AC⊥AB,BE⊥AB,AB=10,AC=2,用一块三角尺进行如下
操作:将直角顶点P在线段AB上滑动,一直角边始终经过点C,
另一直角边与BE相交于点D,若BD=8,则AP的长为
第5题图第6题图
6、如图,在正方形ABCD中,F是AD的中点,BF与AC交于点G,
则△BGC与四边形CGFD的面积之比是
7、如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有对。
8、如图,梯形ABCD中,AD∥BC(AD<BC),AC、BD交于点O,若
S
S
OAB25
6
=
∆梯形ABCD
则△AOD与△BOC的周长之比为
第7题图第8题图
9、如图,D为△ABC的边AC上的一点,∠DBC=∠A,已知BC=2,
△BCD与△ABC的面积的比是2:3,
则CD的长是
第9题图第10题图
10、如图,已知AD∥BC,连结CD交AB于E,且AE∶EB=1∶3
EF∥BC交AC于F,S△ADE=2cm2,则S△BCE= ,S△AEF= .
11、如图,已知ΔABC中,AD为BC边中线,E为AD上一点,
且CE=CD,∠EAC=∠B,求证:ΔAEC∽ΔBDA, DC2=AD•AE
12、如图、在等边⊿ABC中,P为BC边的一点,D为AC上的一点,
且∠APD= ︒0
6,BP=1,CD=
3
2
,求⊿ABC的边长.
13、如图,∠ACB=∠ADC=90°,AC=6,AD=2.问当AB的长为
多少时,这两个直角三角形相似.
14、如图,在⊿ABC中,∠ACB = ︒0
6,点P是⊿ABC内的一点,
使得∠APB =∠BPC=∠CPA ,且PA=6,PB=8,求PC.
15、如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的
四个顶点分别在△ABC上。
求证:
EF
CD
AB
1
1
1
=
+.
16、已知□ABCD 中,过点B 的直线顺次与AC 、AD 及CD 的延长线相交于点E 、F 、G ,若BE=5,EF=2,求FG 的长
17、如图在⊿ABC 中,AB=AC ,AD 是中线,P 是AD 上一点,过C 作
CF ∥AB ,延长BP 交AC 交于E ,交CF 于F ,求证:BP 2
=PE.PF
18、如图,点M 是△ABC 内一点,过点M 分别作直线平行于△ABC 的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.求△ABC 的面积.
19、如图,有一批形状大小相同的不锈钢片,呈直角三角形,已知∠C=900,AB=5cm ,BC=3cm ,试设计一种方案,用这批不锈钢片裁出面积最大的正方形,并求出这种正方形的边长。
20、如图,在⊿ABC 中,BA=BC=20cm ,AC=30cm ,点P 从A 出发,沿AB 以4cm/秒的速度向点B 运动;同时点Q 从C 点出发,沿CA 以3cm/
秒的速度向A 点运动,设运动时间为x ,(1)当x 为何值时,PQ ∥BC (2)当
3
1
=∆∆ABC BCQ S S 时,求
ABC BPQ S S ∆∆的值 (3)ΔAPQ 能否与ΔCQB 相似?若能,求出AP 的长;若不能,
请说明理由。
F E
D A G。
