数学建模论文:高考志愿填报建议
数学建模——高考志愿选取的层次分析
高考志愿选取的层次分析一.引言大学是广大中学生心目中神圣的知识殿堂,对于每个拥有“大学梦”的中学毕业生来说,填报高考志愿是他们通向高等学府关键的一步。
在填报高考志愿时,学生和家长往往要考虑各种因素来权衡利弊以做出最优决策,但面对错综复杂的情况在紧迫的时间里又很难做出正确的选择,而如果他们填报志愿不得当,又势必会对今后的发展有所影响,甚至于终生遗憾。
因此在这里,我将综合学生在报考时最关心的几个因素,帮助他们进行定量分析,以便更合理地填报高考志愿。
二.问题的分析对于填报高考志愿这一事件,要想做出最优决策,需要考虑的因素很多,而在这些因素中有些可以定量化,有些只有定性关系。
为将半定性、半定量问题转化为定量问题,可以采用层次分析法。
这种方法可以将各种有关因素层次化,并逐层比较多种关联因素,为决策提供可比较的定量依据,所以针对填报高考志愿这一事件,我们将采取层次分析法。
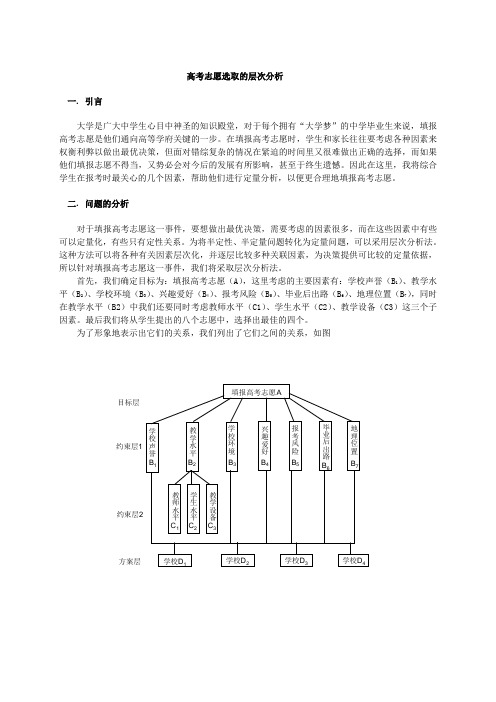
首先,我们确定目标为:填报高考志愿(A),这里考虑的主要因素有:学校声誉(B1)、教学水平(B2)、学校环境(B3)、兴趣爱好(B4)、报考风险(B5)、毕业后出路(B6)、地理位置(B7),同时在教学水平(B2)中我们还要同时考虑教师水平(C1)、学生水平(C2)、教学设备(C3)这三个子因素。
最后我们将从学生提出的八个志愿中,选择出最佳的四个。
为了形象地表示出它们的关系,我们列出了它们之间的关系,如图三. 建立模型 (一)构造成对比较阵面临的决策问题是:要比较n 个因素x 1,x 2…,x n ,对目标A 的影响,我们要确定它们在A 中所占的比重,即这n 个因素对目标A 的相对重要性。
我们用两两比较的方法将各因素重要性的定性部分数量化。
设有因素x 1,x 2…,x n 每次取两个因素x i x j ,用正数a ij 表示x i 与x j 的重要性之比。
由全部比较结果得到矩阵A=(a ij ),称作成对比较阵A 。
⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡nm n n n n a a a a a a a a a ,,,,,,,212,2221112,11 显然有n j i a a a ij ijij ≤≤>=,1,0,1。
高考志愿预测的数学模型研究

高考志愿预测的数学模型研究【摘要】本研究旨在探索利用数学模型预测高考志愿的可行性和有效性。
我们建立了一个基于历年高考成绩和志愿选择情况的数学模型,以预测考生的志愿排名。
接着,我们对大量数据进行收集和处理,确保模型的准确性和鲁棒性。
通过模型参数的优化和验证,我们提高了预测的准确率和稳定性。
我们还提出了一些改进策略,进一步提升模型性能。
结论部分讨论了数学模型在高考志愿预测中的应用前景和未来研究方向。
本研究为高考志愿预测领域提供了一种新的方法和思路,有望在实际应用中发挥重要作用。
【关键词】高考志愿预测、数学模型、研究背景、研究目的、研究意义、数据收集、模型参数优化、模型验证、模型评估、模型改进策略、应用前景、未来研究方向、总结。
1. 引言1.1 研究背景高考志愿预测一直是学生和家长们关注的焦点问题。
随着高考竞争日益激烈,学生们在填报志愿时往往面临着种种难题:应该选择哪些学校?哪些专业适合自己?如何合理安排志愿顺序?为了解决这些问题,研究者们开始利用数学建模的方法对高考志愿进行预测和优化。
传统的高考志愿填报通常基于学生的成绩和兴趣,但这种方法往往忽略了其他重要因素,如学校的声誉、专业的前景、学科交叉等。
建立一套科学的数学模型成为了解决这一问题的关键。
在这样的背景下,本文旨在探讨如何利用数学模型预测高考志愿,帮助学生和家长更好地选择适合自己的学校和专业。
通过收集和分析大量的数据,优化模型参数,验证和评估模型的准确性,并提出改进策略,以提高模型的预测能力和实用性。
本文也将展望数学模型在高考志愿预测中的应用前景,探讨未来的研究方向,并对本研究进行总结。
通过这些努力,希望能为解决高考志愿填报难题提供有力的支持和指导。
1.2 研究目的研究目的是为了探讨利用数学模型来预测高考志愿的可行性和准确性。
通过建立一个科学合理的数学模型,可以更好地帮助学生和家长了解考生的综合素质,从而为志愿填报提供更准确的参考。
通过对数据的收集和处理,可以进一步提高预测模型的准确性和可靠性,为考生提供更加个性化的志愿建议。
数学建模高考内容分析及复习建议

数学建模高考内容分析及复习建议一、数学建模高考内容分析数学建模是数学教育中的一门重要课程,也是高考中的一项重要内容。
通过对数学建模高考内容进行分析,可以帮助学生了解考试要求,有针对性地进行复备考。
1. 数学建模的考试形式:高考数学建模试题一般分为选择题和非选择题两部分。
选择题主要考察学生对数学模型的理解和应用能力,而非选择题则要求学生能够独立思考、分析和解决实际问题。
数学建模的考试形式:高考数学建模试题一般分为选择题和非选择题两部分。
选择题主要考察学生对数学模型的理解和应用能力,而非选择题则要求学生能够独立思考、分析和解决实际问题。
2. 数学建模的考试内容:数学建模的考试内容十分广泛,涉及了数学的各个领域,如代数、几何、概率与统计等。
在考试中,学生需要具备数学基础知识,并能够将这些知识运用到实际问题中进行建模和求解。
数学建模的考试内容:数学建模的考试内容十分广泛,涉及了数学的各个领域,如代数、几何、概率与统计等。
在考试中,学生需要具备数学基础知识,并能够将这些知识运用到实际问题中进行建模和求解。
3. 数学建模的考察重点:数学建模试题通常注重对学生的综合能力的考察,包括数学建模思维能力、数学分析和推理能力、问题建模和解决能力等。
因此,学生在备考过程中应注重培养综合素质和综合运用数学知识的能力。
数学建模的考察重点:数学建模试题通常注重对学生的综合能力的考察,包括数学建模思维能力、数学分析和推理能力、问题建模和解决能力等。
因此,学生在备考过程中应注重培养综合素质和综合运用数学知识的能力。
二、数学建模高考复建议为了顺利备考数学建模高考,学生们可以采取以下复建议:1. 全面复数学基础知识:数学建模考试需要学生具备扎实的数学基础知识,因此,学生们应该全面复数学各个领域的知识点,并理解它们之间的联系。
全面复习数学基础知识:数学建模考试需要学生具备扎实的数学基础知识,因此,学生们应该全面复习数学各个领域的知识点,并理解它们之间的联系。
高考选择志愿层次分析 数学建模

高考选择志愿本论文针对中学毕业生填报高考志愿问题设计一个根据学校的和个人的若干因素排出各个大学志愿的名次模型。
对于志愿的选择排名,我们采用层次分析法给出各志愿的排名。
用层次分析法,我们先确定各因素的的权系数,再建立层次机构模型,最后进行层次分析,确定ABCD四个志愿的顺序。
关键词:层次分析、确定系数、层次结构模型一、提出问题建立数学模型,对各个高校的志愿进行排名。
排名的目的是根据考虑因素排出各个志愿的的一个顺序,所以说一个好的排名算法应满足下面的一些基本要求:保序性、稳定性、对数据可依赖程度给出较为精确的描述。
二、问题重述某中学毕业生填报高考志愿,要考虑到报考学校的名声誉、教学、科研、文体及教学环境,同时又要结合本人的兴趣、考试成绩和毕业后的出路等因素。
在每一因素内还有若干子因素,如在教学因素中要考虑到教师的水平、学生的水平、深造条件等。
考生可填A、B、C、D四个志愿。
A B C D名校自豪感0.8 0.75 0. 7 0.65录取风险0.7 0.75 0.8 0.85校誉奖学金0.6 0.8 0.7 0.75就业前景0.8 0.77 0.81 0.75科研成果0.7 0.65 0.7 0.71实验室水平0.8 0.81 0.76 0.77科研教师论文0.7 0.65 0.71 0.69国家科学奖0.8 0.78 0.77 0.81教师水平0.78 0.79 0.76 0.8教学学生水平0.8 0.79 0.78 0.79深造条件0.4 0.2 0.45 0.3文体校园文化0.8 0.79 0.81 0.8体育设施0.65 0.7 0.64 0.65个人兴趣0.78 0.84 0.76 0.77考试成绩0.7 0.75 0.8 0.85毕业出路0.8 0.77 0.81 0.75三、符号说明A 学校选择B1校誉B2科研B3教学B4文体B5个人兴趣B6考试成绩B7毕业出路C1名校自豪感C2录取风险C3年奖学金C4就业前景C5 科研成果C6实验室水平C7教师论文C8国家科学奖C9教师水平C10学生水平C11深造条件C12校园文化C13体育设施CI 一致性指标四、 建立模型(二)构造成对比较阵面临的决策问题是:要比较n 个因素x 1,x 2…,x n ,对目标A 的影响,我们要确定它们在A 中所占的比重,即这n 个因素对目标A 的相对重要性。
关于高考志愿填报的建议有什么

关于高考志愿填报的建议有什么高考志愿填报的建议有什么志愿填报首选城市,不是学校、更不是专业:为了四年甚至更久的生活,为了谋得更好的发展空间,请记住,志愿要一定首选城市。
城市的选择必须和家庭情况相互配合,考生应接纳但不盲从家长建议。
海阔凭鱼跃,天高任鸟飞,高分者城市选择中必选“北上广深”,低分者则应当选择省内经济发达的城市,再次是临近省份经济发达城市。
重院校、轻专业,是错的,重院校、轻专业,是贻害无穷的馊主意。
分高者,应该“重院校、轻专业”。
报考6类及以下院校,应该“重专业、轻院校”,按照专业技术配比志愿与高校,找到就业前景最优的志愿填报方式。
高考志愿填报的注意事项一、高考志愿填报注意考生未来职业选择和方向考生及家长在填报高考志愿时要结合自己的高考分数和兴趣爱好综合考量之后再进行选择,确定好报考专业的范围和培养目标,并对自己的未来职业生涯和规划有一个准确的认识。
二、掌握一些高考志愿填报的系统知识高考志愿对于考生来说的重要作用并不次于高考,高考志愿填报决定了未来被哪一个专业录取,以及毕业以后的工作选择和方向。
因此考生和家长需要多方了解高考志愿的系统,掌握其中的各方面信息和渠道,参考一些准确的信息,运用科学的方法进行合理决策并成功填报高考志愿。
三、高考志愿填报要选择好院校和专业顺序,并决定是否服从调剂考生在高考志愿填报时的排列顺序是:院校、专业、是否调剂。
在院校的顺序选择上一般是吧最喜欢并且最想要报考的排在最前面的志愿;专业顺序的选择也是把自己想要报考的专业并且比较有优势地位的专业排在前面一些;对于是否服从调剂的问题要结合自身的高考分数,不要过高估计自己的分数,但是也要合理确定院校分数线。
选择冷门专业有哪些注意事项1、要有足够的学习动力不管你选择这专业是因为调剂、还是因为兴趣,都要对学习这学科有足够的动力。
你不一定非要对这学科有浓厚的兴趣,但一定要有好感,而且这个好感可以促使你认真完成未来四年的学业。
高考填报志愿的建议(最新)

高考填报志愿的建议(最新)高考填报志愿的建议有哪些高考填报志愿是一项复杂的决策过程,需要考虑到诸多因素,如专业兴趣、职业规划、学校实力、地理位置、录取概率等等。
以下是一些填报志愿的建议:1.了解政策:首先要了解高考政策,包括录取批次、志愿数量、投档方式、加分政策等。
2.分析录取数据:这是填报志愿的基础,需要收集并分析目标大学和专业的录取数据,包括历年录取分数线、位次、招生人数等信息。
同时也要参考当地招生办公布的录取数据。
3.考虑专业兴趣:高考填报志愿应该基于自己的兴趣和专业前景分析,做好职业规划。
4.合理分配志愿:在填报志愿时,要合理分配平行志愿学校数量,可适当填报自己想要冲刺的学校,也要填报能保底的学校。
5.注意专业和城市:在选择专业和学校时,要综合考虑专业、学校和城市之间的关系。
一些热门专业可能就业前景好,但竞争也大,而一些城市的教育资源也相对丰富。
6.咨询专家意见:在做出决策之前,咨询一些专业的教育机构或大学招生顾问,他们可以提供更多有关志愿填报的意见和建议。
7.考虑自身情况:在填报志愿时,也要考虑自己的家庭情况、经济能力等因素,避免因学费过高而影响后续学业。
总的来说,高考填报志愿是一项需要理性分析和权衡的事情,需要综合考虑各种因素,做好充分的准备和规划。
高考填报志愿的后悔对于高考填报志愿后感到后悔的情况,可以参考以下建议:1.不要过分纠结于过去:高考志愿的填报并不能完全决定一个人的未来,大学和学业生涯只是人生中的一个阶段,而非决定因素。
2.审视自己的后悔情绪是否合理:需要思考自己是因为对学校、专业的不满而感到后悔,还是因为其他原因。
不同原因导致的后悔情绪有不同的解决方法。
3.考虑复读等其他选择:如果对当前的专业和学校真的非常不满意,可能需要考虑复读或者转学等其他选择。
但是,这种选择需要谨慎考虑,因为改变一次考试结果需要付出巨大的努力和风险。
4.积极面对当前情况:如果无法改变过去,那么就需要学会接受现实,积极面对当前的情况。
高考志愿报考模型的研究
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):山东大学参赛队员(打印并签名) :1. 青城霖傲2. 刘永轩3. 柳吟轩指导教师或指导教师组负责人(打印并签名):张清华日期: 2011 年 8 月 20日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号)关于高考志愿报考模型的研究摘要在每一年的高考志愿填报中涉及到很多随机因素和策略,考生往往不知道如何科学的填报志愿,本文在提取大量数据的基础上,主要解决的是在考生的分数、想报考的专业及院校所在地区都已经确定了的情况下为考生找到那个某专业的层次水平较高且被录取的概率较大院校。
首先,我们通过查阅资料并结合实际确定影响报考志愿的因素为录取把握(B1)、发展前景(B2)、兴趣特长(B3)及他人意见(B4)。
然后我们通过层次分析法将半定量、办定性的问题转化为定量分析问题,并用Matlab软件求得权向量,即得到各自权重分别为0.4914、0.2689、0.1460、0.0937。
在描点画出每年的各高校的录取分数线与投档线的离散图形的基础上,观察出录取分数线与投档线存在线性关系,经过拟合发现其与线性回归符合的很好,以此线性回归模型预测出今年华东地区各院校工商管理专业在山东省的录取分数线,由于预测出来的分数与实际都有一定的偏差,为了保险起见并且在追求好的专业层次水平的基础上,求最好的报考院校时引入了修正值。
关于高考志愿如何填报的数学建模题
高考志愿如何填报的数学建模题高考志愿如何填报的数学建模题随着高考日益临近,填报志愿成为广大考生和家长关注的焦点。
在高考志愿填报中,数学建模题也成为了重要的考察内容之一。
本文将综合多地高考信息,从不同角度出发,为考生和家长提供有关高考志愿如何填报的数学建模题的相关建议。
一、数学建模题的分类和特点数学建模题是高考数学中的一大难点,因此必须对其进行分类和了解其特点。
数学建模题可以分为实际问题和虚拟问题两种类型。
实际问题是指与现实生活相关的问题,如交通、环境、经济等方面的问题。
虚拟问题则是指与现实生活无关的问题,如抛物线、三角函数等数学专业问题。
数学建模题的特点是综合性强,涉及多个知识点,需要考生在解题过程中进行综合运用。
因此在考察数学建模题时,不仅要考察考生的数学知识,还要考察考生的数学思维能力和解决实际问题的能力。
二、数学建模题在高考志愿填报中的作用数学建模题在高考志愿填报中的作用是非常重要的。
在填报志愿时,数学建模题的考试成绩也被列入了志愿填报的参考范围。
因此,考生应该在高考前认真对待数学建模题,切实提高自己的成绩,以便更好地填报自己的志愿。
三、如何提高数学建模题的成绩提高数学建模题的成绩需要考生在平时的学习中进行积累和总结。
首先,考生要熟练掌握基本的数学知识和公式,例如函数、导数、积分等。
其次,考生要注重实际问题的解决过程,学会运用数学知识解决实际问题。
最后,考生还要注重练习,通过大量的练习和模拟考试来提高自己的数学建模能力。
四、高考志愿填报中数学建模题的策略在高考志愿填报中,数学建模题的策略也非常重要。
首先,考生要了解自己的数学建模水平和所报考专业的要求,确定自己的志愿填报方向。
其次,考生要注意填报的志愿之间的差距,尽可能地提高自己的上榜率。
最后,考生还要注意填报志愿时的时间控制,尽可能地合理分配填报志愿的时间,避免错过填报的机会。
五、高考志愿填报中数学建模题的注意事项在高考志愿填报中,考生还需注意以下事项。
数学建模论文(精选4篇)
数学建模论文(精选4篇)数学建模论文模板篇一1数学建模竞赛培训过程中存在的问题1.1学生数学、计算机基础薄弱,参赛学生人数少以我校理学院为例,数学专业是本校开设最早的专业,面向全国28个省、市、自治区招生,包括内地较发达地区的学生、贫困地区(包括民族地区)的学生,招收的学生数学基础水平参差不齐.内地较发达地区的学生由于所处地区的经济文化条件较好,教育水平较高,高考数学成绩普遍高于民族地区的学生.民族地区由于所处地区经济文化较落后,中小学师资力量严重不足,使得少数民族学生数学基础薄弱,对数学学习普遍抱有畏难情绪,从每年理学院新生入学申请转系的同学较多可以窥见一斑.虽然学校每年都组织学生参加全国大学生数学建模竞赛,但人数都不算多.从专业来看,参赛学生主要以数学系和计算机系的学生为主,间有化学、生科、医学等理工科学生,文科学生则相对更少.理工科类的学生基本功比较扎实,他们在参赛过程中起到了重要作用.文科学生数学和计算机功底大多薄弱,更多的只是一种参与.从年级来看,参赛学生以大二的学生居多;大一的学生已学的数学和计算机课程有限,基本功还有些欠缺;大三、大四的学生忙着考研和找工作,对数学建模竞赛兴趣不大.从参赛的目的来看,有20%左右的学生是非常希望通过数学建模提高自己的综合能力,他们一般能坚持到最后;还有50%的学生抱着试试看的态度参加培训,想锻炼但又怕学不懂,觉得可以坚持就坚持,不能则中途放弃;剩下的30%的学生则抱着好奇好玩的态度,他们大多早早就出局了.学生的参赛积极性不高,是制约数学建模教学及竞赛有效开展的不利因素.1.2无专职数学建模培训教师,培训教师水平有限,培训方法落后数学建模的培训教师主要由理学院选派数学老师临时组成,没有专职从事数学建模的教师.由于学校扩招,学生人数多,教师人数少,数学教师所承担的专业课和公共课课程多,授课任务重;备课、授课、批改作业占用了教师的大部分工作时间,并且还要完成相应的科研任务.而参加数学建模教学及竞赛培训等工作需要花费很多时间和精力,很多老师都没有时间和精力去认真从事数学建模的教学工作.培训教师队伍整体素质不够强、能力欠缺,指导起学生来也不是那么得心应手,且从事数学建模教学的老师每年都在调整,不利于经验的积累.另外,学校对参与数学建模教学及竞赛培训的教师的鼓励措施还不是十分到位和吸引人,培训教师对数学建模相关的工作热情不够,缺乏奉献精神.在2011年以前,数学建模培训主要采用教师授课的方式进行,但各位老师授课的内容互不联系.比如说上概率论的老师就讲概率论的内容,上常微分方程的老师就讲常微分的内容.学生学习了这些知识,不知道有什么用,怎么用,不能将这些知识联系起来转化为数学建模的能力.这中间缺少了很重要的一个环节,就是没有进行真题实训.结果就是学生既没有运用这些知识构建数学模型的能力,也谈不上数学建模论文写作的技巧.虽然学校年年都组织学生参加全国大学生数学建模竞赛,但结果却不尽如人意,获奖等次不高,获奖数量不多.1.3学校重视程度不够,相关配套措施还有待完善任何一项工作离开了学校的支持,都是不可能开展得好的,数学建模也不例外.在前些年,数学建模并没有引起足够的重视,学校盼望出成绩但是结果并不理想,对老师和学生的信心不足.由于经费紧张,并未专门对数学建模安排实验室,图书资料很少,学生用电脑和查资料不方便,没有学习氛围.每年数学建模竞赛主要由分管教学的副院长兼任组长,没有相应专职的负责人,培训教师去参加数学建模相关交流会议和学习的机会很少.学校和二级学院对参加数学建模教学、培训的老师奖励很少,学生则几乎没有.在课程的开设上也未引起重视,虽然理学院早在1997年就将数学实验和数学建模课列为专业必修课,但非数学专业只是近几年才开始列为公选课开设,且选修率低.2针对存在问题所采取的相应措施2.1扩大宣传,重视数学和计算机公选课开设,举办数学建模学习讨论班最近两年,学院组建了数学建模协会,负责数学建模的宣传和参赛队员的海选,通过各种方式扩大了对数学建模的宣传和影响,安排数学任课教师鼓励数学基础不错的学生参赛.同时邀请重点大学具有丰富培训经验的老师来做数学建模专题讲座,交流经验.学院重视数学专业的基础课程、核心课程的教学,选派经验丰富的老教师、青年骨干教师担任主讲,随时抽查教学质量,教学效果.严抓考风学风,对考试作弊学生绝不姑息;学生上课迟到、早退、旷课一律严肃处理.通过这些举措,学生学习态度明显好转,数学能力慢慢得到提高.学校有意识在大一新生中开设数学实验、数学建模和相关计算机公选课,让对数学有兴趣的学生能多接触这方面的知识,减少距离感.选用的教材内容浅显而有趣味,主要目的是让同学们感受到数学建模并非高不可攀,数学是有用的,增加学生学习数学的热情和参加数学建模竞赛的可能性.为了解决学生学习数学建模过程中的遇到的困难,学院组织老师、学生参加数学建模周末讨论班,老师就学生学习过程中遇到的普遍问题进行讲解,学生分小组相互讨论,尽量不让问题堆积,影响后续学习积极性.通过这些措施,参赛学生的人数比以往有了大的改观,参赛过程中退赛的学生越来越少,参赛过程中的主动性也越来越明显.2.2成立数学建模指导教师组,分批培养培训教师,改进培训方法近年来,学院开始重视对数学建模培训教师的梯队建设,成立了数学建模指导教师组.把培训教师分批送出去进修,参加交流会议,学习其它高校的经验,并安排老教师带新教师,培训教师队伍越来越稳定、壮大.从去年开始,理学院组织学生进行了为期一个月的暑期数学建模真题实训,从8月初到8月底,培训共分为7轮.学生首先进行三天封闭式真题训练———其次答辩———最后交流讨论.效果明显,学生的数学建模能力普遍得到了提高,学习积极性普遍高涨.9月份顺利参加了全国大学生数学建模竞赛.从竞赛结果来看,比以前有了比较大的进步,不管是获奖的等次还是获奖的人数上都取得了历史性突破.有了这些可喜的变化,教师和学生的积极性都得到了提高,对以后的数学建模教学和培训工作将起着极大的促进作用.除了这种集训,今后,数学建模还需要加强平时的教学和培训工作.2.3学校逐渐重视,加大了相关投入,完善了激励措施最近几年,学校加大了对数学建模教学和培训工作的相关投入和鼓励措施.安排了专门的数学建模实验室,配备了学院最先进的电脑、打印机等设备,购买了数学建模相关的书籍.划拨了数学建模教学和培训专项经费.虽然数学建模教学还没有计入教学工作量,但已经考虑计入职称评定的相关工作量中,对参加数学建模教学和培训的老师减少了基本的教学工作量,使他们有更多的时间和精力投入到数学建模的相关工作中去.对参加全国大学生数学建模竞赛获奖的老师和学生的奖励额度也比以前有了很大的提高,老师和学生的积极性得到了极大的提高.3结束语对我们这类院校而言,最重要的数学建模赛事就是一年一度的全国大学生数学建模竞赛了.竞赛结果大体可以衡量老师和学生的付出与收获,但不是绝对的,教育部组织这项赛事的初衷主要是为了促进各个院校数学建模教学的有效开展.如果过分的看重获奖等次和数量,对学校的数学建模教学和组织工作都是一种伤害.参赛的过程对学生而言,肯定是有益的,绝大多数参加过数学建模竞赛的学生都认为这个过程很重要.这个过程可能是四年的大学学习过程中体会最深的,它用枯燥的理论知识解决了活生生的现实中存在的问题,虽然这种解决还有部分的理想化.由于我校地处偏远山区,教育经费相对紧张,投入不可能跟重点院校的水平比,只能按照自身实际来.只要学校、老师、学生三方都重视并积极参与这一赛事,数学建模活动就能开展的更好.数学建模论文模板篇二培养应用型人才是我国高等教育从精英教育向大众教育发展的必然产物,也是知识经济飞速发展和市场对人才多元化需求的必然要求。
高考志愿填报建议
高考志愿填报建议高考是每个考生人生中的重要时刻,它决定着一个人未来的发展方向。
而高考志愿填报是高考过程中至关重要的一环,它直接关系到每个考生的进一步深造和未来职业发展。
因此,正确而明智地填报志愿是每个考生都应该认真对待的事情。
下面,我将为大家提供一些高考志愿填报的建议和指导。
首先,了解自己的兴趣和专长是选择专业的重要依据。
每个人都有自己的兴趣爱好和特长,比如文科、理科、艺术、体育等。
考生应该根据自己的兴趣和特长来选择适合自己的专业或学科。
这样不仅能够提高学习的积极性和主动性,还能够提高学习效果和成绩。
其次,了解专业的就业前景和发展方向。
随着社会的不断发展,一些新的专业和学科逐渐受到关注。
考生应该了解各个专业和学科的就业前景和发展方向,从而选择一个更具有发展潜力的专业。
此外,还应该了解一些热门专业和学科的就业竞争情况,避免选择就业竞争激烈的专业。
第三,多方面地了解学校的情况。
高考志愿填报不仅涉及到专业的选择,还涉及到学校的选择。
考生应该多方面地了解学校的情况,包括学校的办学理念、学科设置、师资力量、科研实力等。
可以通过参加招生宣讲会、学校开放日等活动来亲身感受学校的氛围和环境。
还可以通过查阅学校的官方网站、学生交流平台等来了解学校的相关信息。
第四,要灵活填报志愿。
考生填报志愿时应该根据自己的实际情况和分数来合理安排。
首先要结合自己的兴趣和专长来有针对性地选择专业和学校。
其次要根据自己的分数段来充分运用平行志愿、循环志愿等填报策略,灵活地进行志愿填报。
同时,还要注意合理安排专业的选择顺序,确保第一志愿和后备志愿之间的差距不要过大。
最后,填报志愿时要遵循自己的内心真实想法。
有些考生为了得到家庭或社会的认可,或是为了追求名利地填报志愿。
但这样做很容易迷失自己。
因此,考生应该坚持填报志愿时的内心真实想法。
只有选择自己真正感兴趣并且适合自己的专业和学校,才能更好地发挥自己的优势,实现自己的梦想。
总之,高考志愿填报是一个严肃而复杂的过程,需要考生理性、科学地进行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):X 我们的参赛报名号为(如果赛区设置报名号的话):xxxxxxxx 所属学校(请填写完整的全名):集美大学参赛队员(打印并签名) : 1. 吴培基光电0913 20095360282. 刘伟权数学0912 20095300553. 陈巧婷数学0912 2009530035指导教师或指导教师组负责人(打印并签名):日期: 2011 年 7 月 31 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):2011年福建高考志愿填报建议摘要:在每一年的高考志愿填报中涉及到很多随机因素和策略,考生往往不知道如何科学的填报志愿,本文在提取大量数据的基础上,主要解决的是计算出考生对应分数填报其感兴趣的高校被录取的概率。
在综合考虑每年的各高校的录取分数线及平均分,运用概率统计和模糊数学的方法,将学校往年的录取分和考生的原始分转化为标准分,以排除每年考试的难易程度带来分数波动的影响。
另外,运用层次分析法将各种因素纳入考虑算出权重。
最后计算被录取的概率。
最后,根据我们的研究分析,对考生填报志愿给出建议。
关键词:高考志愿概率统计模糊数学层次分析标准分权重目录一、问题重述二、问题分析三、模型假设四、模型建立五、模型应用六、给考生的建议七、模型推广与评价八、参考文献一、问题重述在每年的高考结束后,考生和家长就投入到了紧张的志愿填报之中。
福建省是知分填报志愿的,也就是考生是在知道了自己的成绩、排名以及本一、本二线后才填报志愿的。
考生和家长往往通过多种渠道去了解当年招生政策及高校的招生信息,特别是往年招生院校的招生数量、报考人数、录取的最高成绩、平均成绩、最低成绩及录取情况,找到与自己分数相差较小的高校,作为自己填报志愿的重要参考。
最后再通过学校的声誉、地理位置、专业好坏及难度、就业等情况最后确定报考志愿。
根据最近5年各个高校的录取情况,给2011年考生提出一个合理的填报志愿(以福建省为例),分别根据文理科情形从500分至650分,分10分给出建议。
二、问题分析每年都会有考生因为错估自己进入某高校的概率而落榜,所以我们要通过建立关于高考志愿填报的数学模型,来帮助考生计算自己进入心仪的学校的概率。
在志愿的填报过程中,往年的信息是最重要的参考,我们需要根据往年的数据来得出今年自己考上想要报考的学校的概率大小。
数据来源和初步处理这个数学模型的构造的特点是数据量分散,而且数据量大,所以我们建立该模型时最先考虑的问题是数据的查找和筛选。
我们选取了23个省、直辖市的47所高校,对其2006-2010年5年的文理科方面在福建省的招生人数、最高分、最低分、平均分进行分析。
我们选取的高校见以下分布图:关于学校的选取,我们认为清华、北大这两所高校每年在福建省的招生人数及分数较为稳定,我们没将他们列入讨论范围;另外,由于我们所建立的模型是针对福建考生的,所以我们选取的高校中,福建省的高校占有率相比于其它省份会高出一点;再次,我们尽量选取了沿海与内陆的大学等同比例。
这样就可以使我们选择的高校更具有代表性。
由于,考生的考试成绩是基本符合正态分布的,所以我们选取了各个高校的最高分、最低分、平均分以及福建省当年的重点线和当年的最高分,用来对正态当年福建省的考生的成绩分布作个大概的估计。
从而建立数学模型,从而估计某一学生进入某高校的概率。
三、模型假设1.这5年来各高校的相对录取分数没有受到录取比例、招生政策的影响;2.这5年来各校对考生的吸引力没有发生变化;3.考生通过网络获取各高校的信息是全面和权威的;4.考试根据各高校的信息做出的主管数据可以真实的反映考生的意愿。
四、模型建立(一)基于概率统计的估计录取概率模型:1)我们考查福建省2010年的高考理科分数段与人数分布:绘出分段人数统计图通过分段人数统计图,我们可以看出图像较符合正态分布的概率密度图像。
进行标准正态化2)进行标准化由标准化公式:(,)(0,1)XN Z N x z μσμσ→-=知道进行标准化最重要的是两个参数,即期望μ和标准差σ。
对于进行数据分析,比较容易得到的数据是省重点线key x 和省最高分max x 。
由于划重点线对应的是重点院校的招生比例,大体上比较稳定。
以福建为例,基本上是总人数的14%,大体上比μ高出1.3σ,而根据3σ法则,状元的分数比μ高3σ,实际上由于有最高分数的约束,不会达到,所以设置为2.8σ。
于是,5.1max 'keyx x -=σσμ3.1'-=key x 所以得到粗略的标准化公式:3.15.15.1)5.13.1('max max max ''+⨯--=--⨯--=-=keykey keykeykey x x x x x x x x x x x z σμ由于我们所关心的仅仅是不同x 标准化后的大小,所以略去常数1.3,并且为观察方便我们将区间平移并放大到以500为中心的区域,即修改标准化公式为:'max 500500key keyx x z x x η-=⨯⨯+-设置的参数max keyx x ησ-=,表示该省上重点线的难度。
考查几组得到分数分布的考生情况,验证了标准化公式的正确性,我们可以估计福建省的η值,η=1.5。
进行标准化的最大好处是去处了某省某年由于考题难易造成的分数线的波动,从而可以进行某校在某地区各年录取情况的横向比较。
对录取平均分也进行如此处理,对各高校数据依次进行如下处理1.分布假设检验由于排除难易程度造成的波动,标准化后的成绩大体上符合正态分布。
使用Jarque-Bera检验可以看出,百分之九十五以上的数据均符合正态分布。
2.均值方差分析对于填报学校最重要的指标就是分数线的均值和标准差了,特别是标准差表明了该学校录取成绩的随机变化程度,显得更加重要。
对大量数据进行处理,发现不同学校在不同省市的标准差与该校的招生人数、以及均值有一些规律性的联系。
经过分析可以发现有以下几点规律:(1)平均分比录取线有更好的稳定性。
这一方面是正态分布固有的特点,同时也说明每个学校每年的整体生源情况并不像录取分数线所显示的那样大。
所以对于追求该校好的专业的同学更应该关注平均分数的变化。
(2)分数越高分数波动越大,分数较低时招生人数多少不太影响分数的波动。
这是由于低分数的学校由于有录取分数线的限制,其波动有一个下限。
(二)基于模糊判决的院校选择:对于院校的选择,我们用模糊层次分析法:图2 高考志愿模型层次图说明:决策层A:通过对个人因素的分析,考虑到各方面的社会因素,再广泛地征询家长、教师、朋友同学等最后作出填报或不填报某一学校(或专业)的决策。
因素层B:B1 个人因素(包括子因素层:C1、C2);B2:他人因素(包括自因素层C3、C4);B3 社会因素(包括子因素层C5、C6、C7)。
子因素层C:C1:个人兴趣、爱好;C2:该(院校)专业容易学;C3:家长的影响;C4:老师的影响;C5:学校的声誉(办学条件、知名度);C6:专业对口、工作岗位收入高、社会地位高、工作舒适;C7:该学校处于大中城市,校园环境幽雅。
模糊多级综合评判的数学描述我们利用模糊综合评判法对选报高考志愿进行二级综合评判。
所谓模糊综合评判是指运用模糊数学中模糊统计的方法,通过影响某事物各个因素的综合考虑,对其做出科学的评判。
图3 模糊推理示意图确定因素集设评判对象具有n 种属性,把影响评判对象的每一属性称为一个因素, n 个因素组成集合称为因素集。
令总目标的因素集为A ,即A = ( B1 ,B2 , ……, Bn) (此模型中n = 3) , Bi ∩Bj =φ( i ≠j) ;各一级指标的因素集为Bk ,即Bk = ( Ck1 , Ck2 , ……,Ckmk) ( mk 为第k 个一级指标的二级指标数) ( k =1 ,2 , ⋯, n) 。
确定评语集模糊综合评价结果一般是用一个模糊集V 表示,各评价结果组成的分明集称为评语集,文中指方案层组成集合, 记V = ( V1 , V2 , ……, Vi , ……Vm) , Vi 表示第i 个方案。
指标体系权重的确立为确立各因素的权重,可采用直接评分法、功能评分法、二项系数法、AHP 法或DELPHI 等方法。
设A = ( B1 , B2 , ……Bi , ……, Bn) 的权重为W =( W1 , W2 , ……, Wi , ……, Wn) ( Wi 为因素Xi 在X 中的比重) ,0 ≤Wi ≤1 ,11nii W==∑ , Bk = ( Ck1 , Ck2 , ……,Cki , ……, Ckmk) , 相应权重为Wk = ( Wk1 ,Wk2 , ……, Wki , ……, Wkmk) ( Wki 为指标Cki 在Bk 中的比重),101,1km ki ki i W W =≤≤=∑,k = 1 ,2 ,……, n 。
隶属度及模糊评判矩阵的确定定出Xk 的每个因素Ckj 对于m 个评判集的隶属度( kj1r , kj2r , ⋯, kjm r ) , mk 个因素的隶属度可用mk ×m 阶模糊评判矩阵k R 表示。
确定kji r :由s 个专家组成评判组, 其权向量W = ( W1 , W2 , ⋯,Wi , ⋯, Ws) , 11si Wi ==∑, 每人针对评判集给Bk 的每个因素Ckj 一个评定值()[0,1](1,2,,)t ji r t s ∈=,对所有专家的评定值进行如下加权处理:()1st ji ji k i r Wi r ==⨯∑,由此可得到Bk 的模糊评判矩阵Rk111212122212(1,2,,,)ji k rk rk rk m rk rk rk m Rk r m rkmk rkmk rkmkm k i n ⎡⎤⎢⎥⎢⎥=⨯=⎢⎥⎢⎥⎣⎦=模糊评判一级评判先由最低层指标开始,以Bk 的二级指标的权重向量Wk 与其模糊评判矩阵Rk 进行模糊矩阵合成运算,可得出对Bk 的二级指标集的判断向量12*(,,,)(1,2,,,,)k k k k k km P W R p p p k i n ===这里*代表模糊合并运算算子,可根据实际情况选择主因素决定型、主因素突出型、加权平均型等。
