1--专题一:基本初等函数图像及其性质
六大基本初等函数图像及其性质
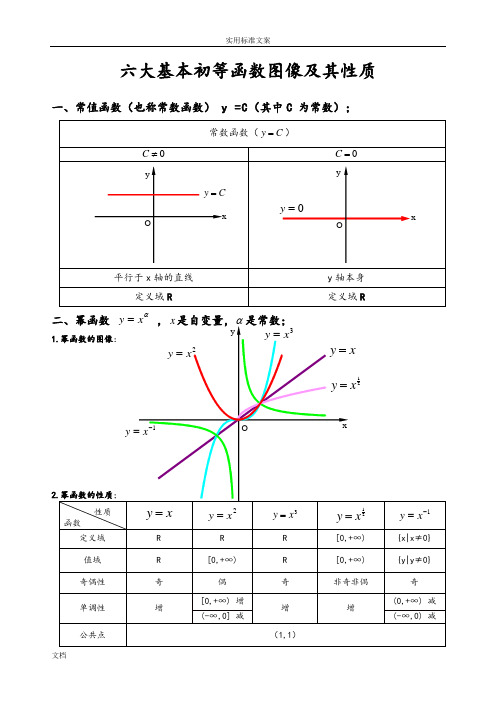
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
高数总结:基本初等函数图像及其性质
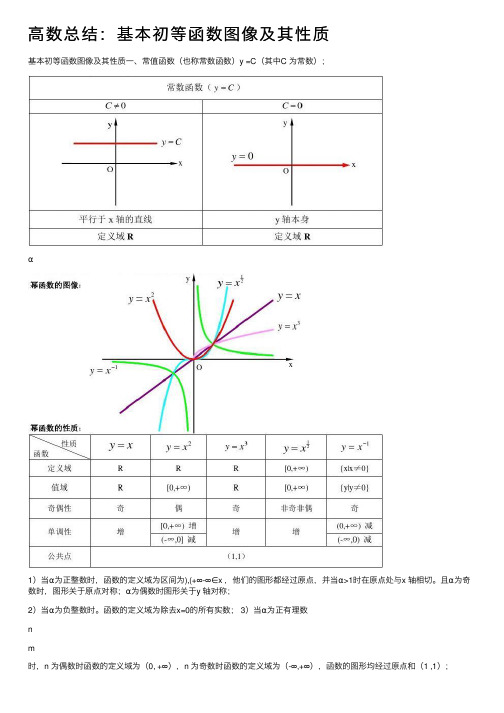
⾼数总结:基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数n4)如果m>n 图形于x 轴相切,如果m5)当α为负有理数时,n 为偶数时,函数的定义域为⼤于零的⼀切实数;n 为奇数时,定义域为去除x=0以外的⼀切实数。
三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ,1≠a ),定义域是R ;[⽆界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上⽅; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的⼤⼩⽐较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ?=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越⼤,xa y =的图像越靠近y 轴;b.2.当10<的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [⽆界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式⼦N a log 叫做对数式。
六大基本初等函数图像及其性质
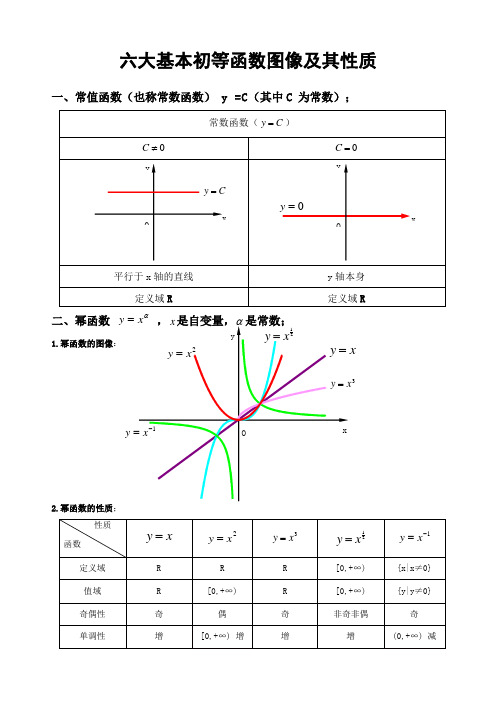
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像与其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C (其中 C 为常数);常数函数( y C )C 0yy Cy 0xO平行于 x 轴的直线定义域 R二、幂函数 y x, x 是自变量,是常数;1. 幂函数的图像:y y x3y x2y x1O2.幂函数的性质;性质y x y x2y x3函数定义域R R R值域R[0,+ ∞ )R奇偶性奇偶奇单调性增[0,+ ∞) 增增(-∞ ,0]减公共点( 1,1)C 0yOy轴本身定义域 Ry x1y x 2x1y x 2[0,+ ∞ )[0,+ ∞ )非奇非偶增xy x 1{x|x ≠ 0}{y|y ≠ 0}奇(0,+∞) 减(-∞ ,0) 减第 1 页1)当 α 为正整数时,函数的定义域为区间为x ( ,),他们的图形都经过原点,并当α >1 时在原点处与 x 轴相切。
且 α为奇数时,图形关于原点对称;α 为偶数时图形关于 y 轴对称;2)当 α 为负整数时。
函数的定义域为除去 x=0 的所有实数;3)当 α 为正有理数m时, n 为偶数时函数的定义域为(0, +∞), n 为奇数时函数的定义域为( -n∞ ,+∞),函数的图形均经过原点和( 1 ,1);4)如果 m>n 图形于 x 轴相切,如果m<n,图形于 y 轴相切,且 m 为偶数时,还跟y 轴对称; m , n均为奇数时,跟原点对称;5)当 α 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数ya x(x 是自变量,a 是常数且a0 , a1 ),定义域是R ;[ 无界函数 ]1. 指数函数的图象 :yaxyyy ax(a 1)(0 a1)(0,1)y 1(0,1)y 1OxOx2. 指数函数的性质 ;性质y a x(a 1)y a x(0 a 1)函数定义域 R值域(0,+∞)奇偶性非奇非偶公共点过点 (0,1),即 x 0 时, y1单调性 在(, )是增函数 (, )在是减函数1 ) 当 a1时 函 数 为 单 调 增 , 当 0 a 1时函数为单调减;2 ) 不 论 x 为 何 值 , y 总 是 正 的 , 图 形 在 x 轴 上 方 ;3 ) 当 x 0 时 , y1,所以它的图形通过(0,1)点 。
1- 专题一基本初等函数图像及其性质
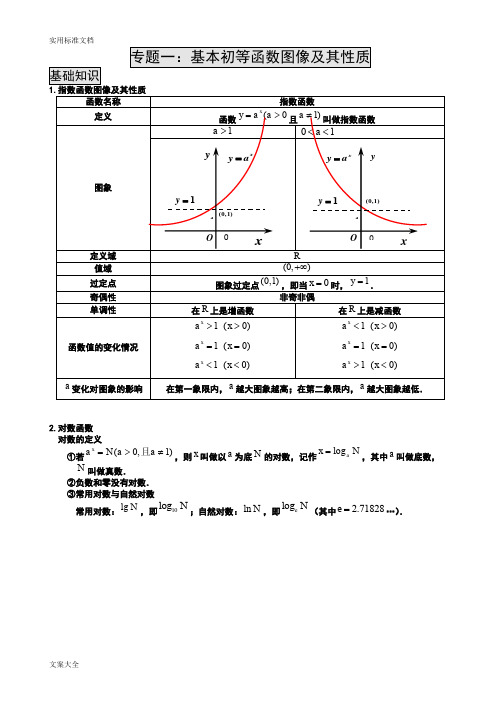
2.对数函数对数的定义①若(0,1)xa N a a=>≠且,则x叫做以a为底N的对数,记作logax N=,其中a叫做底数,N叫做真数.②负数和零没有对数.③常用对数与自然对数常用对数:lg N,即10log N;自然对数:ln N,即logeN(其中 2.71828e=…).4.幂函数(1)幂函数的定义:一般地,函数y xα=叫做幂函数,其中x为自变量,α是常数.(2(3)幂函数的性质①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象 分布在第一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限 (图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限. ②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则 幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴. ④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当qp α=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则q py x =是奇函数,若p 为 奇数q 为偶数时,则q py x =是偶函数,若p 为偶数q 为奇数时,则q py x =是非奇 非偶函数.⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x = 上方,若1x >,其图象在直线y x =下方.5.二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (3)二次函数图象的性质①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线, 对称轴方程为,2b x a =-顶点坐标是24(,)24b ac b a a --.6.7.一元二次函数表达式形式顶点式:f(x)=a(x -h)2+k ,定点坐标(h,k )分解式:f(x)=a(x -x1)(x -x2), 一元二次方程的两根为x1,x2 一般式:f(x)=ax2+bx +c ,(a ≠0).8.反函数互为反函数的两个图像关于y=x 成轴对称关系;原函数的定义域是其反函数的值域,原函数的值域是其反函数的定义域专题一 基本初等函数图像及其性质 练习一一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,选出符合题目要 求的一项填在答题卡上.1.(新课标全国卷)下列函数中,既是偶函数,又是在(0,+∞)上单调递增的函数是( )A .y =x 3B .y =|x |+1C .y =-x 2+1D .y =2-|x |2.(广东卷)设函数f (x )和g (x )分别是R 上的偶函数和奇函数,则下列结论恒成立的是( )A .f (x )+|g (x )|是偶函数B .f (x )-|g (x )|是奇函数C .|f (x )|+g (x )是偶函数D .|f (x )|-g (x )是奇函数3.(湖北卷)已知定义在R 上的奇函数f (x )和偶函数g (x )满足下列关系f (x )+g (x )=a x -a -x+2(a >0,且a ≠1).若g (2)=a ,则f (2)=( )A .2 B.154 C.174D .a24.(山东卷)对于函数y =f (x ),x ∈R ,“y =|f (x )|的图象关于y 轴对称”是“y =f (x )是奇函数”的(B)A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件5.(全国卷)设f (x )是周期为2的奇函数,当0≤x ≤1时,f (x )=2x (1-x ),则f ⎝ ⎛⎭⎪⎫-52=( ) A .-12 B .-14 C.14 D.126.在实数集R 中定义一种运算“*”,对任意给定的a ,b ∈R ,a *b 为唯一确定的实数,且具有性质:(1)对任意a ,b ∈R ,a *b =b *a ; (2)对任意a ∈R ,a *0=a ;(3)对任意a ,b ∈R ,(a *b )*c =c *(ab )+(a *c )+(c *b )-2c .关于函数f (x )=(3x )*13x的性质,有如下说法:①函数f (x )的最小值为3;②函数f (x )为奇函数;③函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫-∞,-13,⎝ ⎛⎭⎪⎫13,+∞.其中所有正确说法的个数为( ) A .0 B .1 C .2 D .3二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上. 7.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x x >00 x =0x 2+mx x <0为奇函数,若函数f (x )在区间[-1,|a |-2]上单调递增,则a 的取值范围是 .8.(上海卷)设g (x )是定义在R 上,以1为周期的函数,若函数f (x )=x +g (x )在区间[3,4]上的值域为[-2,5],则f (x )在区间[-10,10]上的值域为 .9.对方程lg(x +4)=10x根的情况,有以下四种说法:①仅有一根;②有一正根和一负根;③有两个负根; ④没有实数根.其中你认为正确说法的序号是 .三、解答题:本大题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.10.(12分)已知函数f(x)=ax2+bx+c,x∈[0,6]的图象经过(0,0)和(6,0)两点,如图所示,且函数f(x) 的值域为[0,9].过动点P(t,f(t))作x轴的垂线,垂足为A,连接OP.(1)求函数f(x)的解析式;(2)记△OAP的面积为S,求S的最大值.12.(13分)(上海卷)已知函数f(x)=a·2x+b·3x,其中常数a,b满足a·b≠0.(1)若a·b>0,判断函数f(x)的单调性;(2)若a·b<0,求f(x+1)>f(x)时的x的取值范围.专题一 基本初等函数图像及其性质 练习二一、选择题:本大题共12小题。
基本初等函数图像及性质大全

一、一次函数与二次函数(一)一次函数(二)二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠②顶点式:2()()(0)f x a x h k a =-+≠③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便.(3)二次函数图象的性质①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2b a -+∞上递增,当2bx a=-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2ba -+∞上递减,当2bx a=-时,2max 4()4ac b f x a -=.二、幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.(2)幂函数的图象过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).三、指数函数(1)根式的概念:如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,mna a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.(3)运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈(4)指数函数四、对数函数(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).(4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a M M N N-= ③数乘:log log ()n a a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b=≠∈⑥换底公式:log log (0,1)log b a b NN b b a=>≠且(5)对数函数五、反函数(1)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y f x -=.(2)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x f y -=改写成1()y f x -=,并注明反函数的定义域.(3)反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称. ②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数.六、三角函数的图像和性质(一)正弦与余函数的图像与性质2. 正切与余切函数的图像与性质七、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质2. 反正切与反余切函数的图像与性质。
基本初等函数性质&图像

基本初等函数. 幂函数(a为实数)要记住最常见的几个幂函数的定义域及图形.. 指数函数定义域:,值域:,图形过(0,1)点,a>1时,单调增加;a时,单调减少。
今后用的较多。
. 对数函数定义域:,值域:,与指数函数互为反函数,图形过(1,0)点,a>1时,单调增加;a<1时,单调减少。
. 三角函数,奇函数、有界函数、周期函数;,偶函数、有界函数、周期函数;,的一切实数,奇函数、周期函数,的一切实数,奇函数、周期函数;,. 反三角函数;;;。
以上是五种基本初等函数,关于它们的常用运算公式都应掌握。
注:(1)指数式与对数式的性质由此可知,今后常用关系式,如:(2)常用三角公式复合函数设y是u的函数,,而u是x的函数,如果,则称为由和复合而成的复合函数,u 叫中间变量。
注:(1)的定义域或者和的定义域相同,或者只是的定义域的一部分,并且不是任何两个函数都可以构成复合函数。
如:,则的定义域是,是的定义域的一部分,不能构成复合函数。
例 1 设的定义域是[0,1],求的定义域。
解所以的定义域为(2)复合函数也可以由更多个函数复合而成。
如:,则要求:能够判断一个复合函数是由哪些简单函数符合而成的,这一点对今后的学习非常重要,方法是:从外向里,层层剥皮。
例2判断下列函数是由那些简单函数复合而成的(1)(2)(3)(4)解(1)(2)(3)(4)初等函数由基本初等函数和常数经过有限次的四则运算及有限次复合构成的能用一个解析式表出的函数叫初等函数。
说明:一般情况下,大多数分段函数不是初等函数,但能用一个解析式表达的分段函数仍为初等函数。
双曲函数与反双曲函数双曲正弦:,奇函数,单调增函数;双曲余弦:,偶函数,时,单调减,时,单调增;双曲正切:,奇函数,单调增函数。
函数的图形见书P27~P28。
下面公式成立,,,。
反双曲正弦反双曲余弦,反双曲正切函数图形的变换平移①由的图形,作的图形。
图形右移,,图形左移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非偶函数.
⑤图象特征:幂函数 y x , x (0, ) ,当 1 时,若 0 x 1 ,其图象在直线 y x 下方,
若 x 1 ,其图象在直线 y x 上方,当
1时,若 0 x 1
yx
,其图象在直线
上方,若 x 1 ,其图象在直线 y x 下方.
5.二次函数
(1)二次函数解析式的三种形式
①一般式: f (x) ax2 bx c(a 0)
4.幂函数
(1)幂函数的定义: 一般地,函数 y
(2)幂函数的图象
x
x
叫做幂函数-
大德教育 高考课外辅导 孙老师 187 8906 2361
(3)幂函数的性质 ①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象
分布在第一、二象限(图象关于 y 轴对称);是奇函数时,图象分布在第一、三象限
④奇偶性:当 为奇数时,幂函数为奇函数,当 为偶数时,幂函数为偶函数.当
p (其
q
中 p, q 互质, p 和 q Z ),若 p 为奇数 q 为奇数时,则 y x p 是奇函数,若 p 为
-4-
大德教育 高考课外辅导 孙老师 187 8906 2361
q
q
奇数 q 为偶数时,则 y x p 是偶函数,若 p 为偶数 q 为奇数时,则 y x p 是非奇
8.反函数 互为反函数的两个图像关于 y=x 成轴对称关系; 原函数的定义域是其反函数的值域,原函数的值域是其反函数的定义域
-7-
大德教育 高考课外辅导 孙老师 187 8906 2361
专题一 基本初等函数图像及其性质 练习一
一、选择题:本大题共 6 小题,每小题 5 分,共 30 分.在每小题给出的四个选项中,选出符合题目要
3.对数函数图像及其性质 函数名称 定义 图象
对数函数
y log x(a 0 a 1) 叫做对数函数
函数
a
且
a1
0 a1
-2-
大德教育 高考课外辅导 孙老师 187 8906 2361
定义域
(0, )
值域 过定点
R 图象过定点 (1,0) ,即当 x 1 时, y 0 .
奇偶性 单调性
函数值的变化情况
图象
定义域 值域
(-∞,+∞) 4ac-b2 [ 4a ,+∞)
(-∞,+∞)
4ac-b
4a
]
2
(-∞,
6.二次函数图像及其性质 单调性
奇偶性
b 在 x∈(-∞,-2a]上单调递 减
b 在 x∈[-2a,+∞)上单调递 增
b 在 x∈(-∞,-2a]上单调递增
b 在 x∈[-2a,+∞)上单调递减
当 b=0 时为偶函数,b≠0 时为非奇非偶函数
在 R 上是增函数
ax 1 (x 0) ax 1 (x 0) ax 1 (x 0)
非奇非偶
在
R 上是减函数 ax 1 (x 0)
ax 1 (x 0)
ax 1 (x 0)
a
a
在第一象限内, 越大图象越高;在第二象限内, 越大图象越低.
-1-
大德教育 高考课外辅导 孙老师 187 8906 2361
2.对数函数
求的一项填在答题卡上.
1.(新课标全国卷)下列函数中,既是偶函数,又是在(0,+∞)上单调递增的函数是(
)
A.y=x3
B.y=|x|+1
C.y=-x2+1
D.y=2-|x|
2.(广东卷)设函数 f(x)和 g(x)分别是 R 上的偶函数和奇函数,则下列结论恒成立的是( )
A.f(x)+|g(x)|是偶函数
(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
②过定点:所有的幂函数在 (0, ) 都有定义,并且图象都通过点 (1,1) .
③单调性:如果 0 ,则幂函数的图象过原点,并且在[0, ) 上为增函数.如果 0 ,则
幂函数的图象在 (0, )
y 轴. x
上为减函数,在第一象限内,图象无限接近 轴与 q
对数的定义
①若 ax N (a 0,且a N 叫做真数.
1) x
a
N 的对数,记作 x
,则 叫做以 为底
loga N
a
,其中 叫做底数,
②负数和零没有对数. ③常用对数与自然对数
常用对数: lg N ,即 log10 N ;自然对数: ln N ,即 log N (其中 e 2.71828 …). e
(3)二次函数图象的性质
①二次函数 f (x) ax2 bx c(a 0)的图象是一条抛物线,
x
对称轴方程为
b 2a
,
顶点坐标是
(
b 4ac b 2a , 4a 2 ) .
-5-
解析式
大德教育 高考课外辅导 孙老师 187 8906 2361
f(x)=ax2+bx+c(a>0)
f(x)=ax2+bx+c(a<0)
B.f(x)-|g(x)|是奇函数
大德教育 高考课外辅导 孙老师 187 8906 2361
专题一:基本初等函数图像及其性质
基础知识
1.指数函数图像及其性质 函数名称 定义
指数函数
函数 y ax (a 0 且 a 1) 叫做指数函数
a1
0 a1
图象
定义域 值域
过定点 奇偶性 单调性
函数值的变化情况
a 变化对图象的影响
R (0, )
图象过定点 (0,1) ,即当 x 0 时, y 1.
-6-
顶点 对称性
大德教育 高考课外辅导 孙老师 187 8906 2361
b 4ac-b2 (-2a, 4a )
b
图象关于直线
x=- 2a
成轴对称图形
7.一元二次函数表达式形式 顶点式:f(x)=a(x-h)2+k,定点坐标(h,k) 分解式:f(x)=a(x-x1)(x-x2), 一元二次方程的两根为 x1,x2 一般式:f(x)=ax2+bx+c,(a≠0).
a 变化对图象的影响
非奇非偶
在 (0, ) 上是增函数
loga x loga x loga x
0 (x 0 (x 0 (0
1) 1) x 1)
在
(0, loga x loga x loga x
) 上是减函数 0 (x 1) 0 (x 1) 0 (0 x 1)
a
a
在第一象限内, 越大图象越靠低;在第四象限内, 越大图象越靠高.
②顶点式: f (x) a(x h)2 k(a 0)
③两根式: f (x) a(x x1 )(x x2 )(a 0)
(2)求二次函数解析式的方法
①已知三个点坐标时,宜用一般式.
②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.
③若已知抛物线与 x 轴有两个交点,且横线坐标已知时,选用两根式求 f (x) 更方便.
