实数复习课件(新人教版)
合集下载
人教版七年级下册数学《平方根》实数教学说课复习课件(第3课时)
人教版 数学 七年级 下册
6.1 平方根
第3课时
课件
导入新知
1.什么叫做算术平方根？
如果一个正数x的平方等于a,那么这个正数x叫做a的
算术平方根.
2.判断下列各数有没有算术平方根，如果有，请求出它
们的算术平方根.
36
100； 1；
;
121
0; －0.0025; (-3)2 ; －25.
导入新知
3. 填空:
例如：
4的平方根表示为 ：
4，
4 2
5的平方根表示为 ：
5，
25
25
25
5
，
：
的平方根表示为
36
36
36
6
0的平方根表示为: 0
规定
：
0 0. 0 0
0的平方根为0.
探究新知
考 点 1
利用平方根的表示求平方根
分别求下列各数的平方根：
（1）36 ;
25
（2）
典例精析
例2 下列说法正确的是( A
)
A．因为62＝36，所以6是36的算术平方根
B．因为(－6)2＝36，所以－6是36的算术平方根
C．因为(±6)2＝36，所以6和－6都是36的算术平方根
D．以上说法都不对
例3 16的算术平方根是
4
例4 下列说法正确的是
①
①4是25的算术平方根.
② 0.01是0.1的算术平方根.
边长是多少分米？
实际上就是要求出一个数，使
它的平方等于9，即：
(
)
2
9
9平方分米
显然，括号里应是±3，但－3不符
6.1 平方根
第3课时
课件
导入新知
1.什么叫做算术平方根？
如果一个正数x的平方等于a,那么这个正数x叫做a的
算术平方根.
2.判断下列各数有没有算术平方根，如果有，请求出它
们的算术平方根.
36
100； 1；
;
121
0; －0.0025; (-3)2 ; －25.
导入新知
3. 填空:
例如：
4的平方根表示为 ：
4，
4 2
5的平方根表示为 ：
5，
25
25
25
5
，
：
的平方根表示为
36
36
36
6
0的平方根表示为: 0
规定
：
0 0. 0 0
0的平方根为0.
探究新知
考 点 1
利用平方根的表示求平方根
分别求下列各数的平方根：
（1）36 ;
25
（2）
典例精析
例2 下列说法正确的是( A
)
A．因为62＝36，所以6是36的算术平方根
B．因为(－6)2＝36，所以－6是36的算术平方根
C．因为(±6)2＝36，所以6和－6都是36的算术平方根
D．以上说法都不对
例3 16的算术平方根是
4
例4 下列说法正确的是
①
①4是25的算术平方根.
② 0.01是0.1的算术平方根.
边长是多少分米？
实际上就是要求出一个数，使
它的平方等于9，即：
(
)
2
9
9平方分米
显然，括号里应是±3，但－3不符
实数复习课课件人教版ppt
实数的分类
有理数和无理数统称实数.
无理数的特征:
１．圆周率及一些含有的数
２．开不尽方的数 ３．无限不循环小数
火灾袭来时要迅速疏散逃生，不可蜂 拥而出 或留恋 财物， 要当机 立断， 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
把下列各数分别填入相应的集合内：
3 4 , 7 , 8 , 2 1, 1 , 0,
说明:立方根的性质可以概括为立方根 的唯一性,即一个数的立方根是唯一的.
火灾袭来时要迅速疏散逃生，不可蜂 拥而出 或留恋 财物， 要当机 立断， 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
6、开平方：
求一个数的平方根的运算，叫做开平方 .
开平方与平方互为逆运算。
我们可以运用平方运算来求一个数的平方根。
火灾袭来时要迅速疏散逃生，不可蜂 拥而出 或留恋 财物， 要当机 立断， 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
已知 1.72011.31, 11.72014.14,7
那0么 .0017的 20平 1 方根 0.0是 4147
已知 2.361.53,623.64.85,8
掌
若x0.485,则 8x是 0.236
不 要 遗 漏
解下列方程：
1. 9(3y)2
解: (3 y)2
3 y
2
4
4
9
49Biblioteka 2. 2（ 7x2） 31250
解: 27(3x2)3 125
3
(x2)3 125
3
27
x 2 3 125
y 3
3
y21或y32
3
3
3
27
x 25
有理数和无理数统称实数.
无理数的特征:
１．圆周率及一些含有的数
２．开不尽方的数 ３．无限不循环小数
火灾袭来时要迅速疏散逃生，不可蜂 拥而出 或留恋 财物， 要当机 立断， 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
把下列各数分别填入相应的集合内：
3 4 , 7 , 8 , 2 1, 1 , 0,
说明:立方根的性质可以概括为立方根 的唯一性,即一个数的立方根是唯一的.
火灾袭来时要迅速疏散逃生，不可蜂 拥而出 或留恋 财物， 要当机 立断， 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
6、开平方：
求一个数的平方根的运算，叫做开平方 .
开平方与平方互为逆运算。
我们可以运用平方运算来求一个数的平方根。
火灾袭来时要迅速疏散逃生，不可蜂 拥而出 或留恋 财物， 要当机 立断， 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
已知 1.72011.31, 11.72014.14,7
那0么 .0017的 20平 1 方根 0.0是 4147
已知 2.361.53,623.64.85,8
掌
若x0.485,则 8x是 0.236
不 要 遗 漏
解下列方程：
1. 9(3y)2
解: (3 y)2
3 y
2
4
4
9
49Biblioteka 2. 2（ 7x2） 31250
解: 27(3x2)3 125
3
(x2)3 125
3
27
x 2 3 125
y 3
3
y21或y32
3
3
3
27
x 25
第六章 实数(复习课件)七年级数学下册(人教版)
举一反三
【7-2】如图，用两个边长为 18cm的小正方形纸片拼成一个大的正方形纸
片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长
方形纸片长宽之比为3:2，且面积为30cm2?请说明理由.
解:不能.理由如下：因为大正方形纸片的面
积为( 18)2+( 18)2=36(cm2) ，
高频考点
高频考点七 实数的综合运用
(3)如果2+ 5的整数部分是a，小数部分是b，求出a-b的值.
(3)因为 4< 5< 9，即2< 5<3，
所以4<2+ 5<5，
所以2+ 5的整数部分为4，小数部分为2+ 5-4= 5-2，即a=4，b= 5-2，
所以a-b=4-( 5-2)= 6- 5.
举一反三
【7-1】若 2的整数部分为x，小数部分为y，则 2x-y的值是( C )
A.2 2-2
B.2
C.1
D. 2
【7-2】如图，用两个边长为 18cm的小正方形纸片拼成一个大的正方形纸
片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长
方形纸片长宽之比为3:2，且面积为30cm2?请说明理由.
0
一个，为负数
3
a
可以为任何数
知识梳理
四、实数及其运算
有理数包括整数和分数，它们都可以写成有限小数或者无限循环小数的形
式.
5 3 27 11 9
, , , , .
2 5 4 9 11
5
2.5
2
3
0.6
5
27
6.75
4
.
11
七年级数学人教版下册第六章6.3.1实数及其分类课件
101 001 000 1…(相邻两个1之间0的个数逐次加1)， A．无理数包括正无理数、0和负无理数
正有理数
有
理
数
0
负 有 理 数
8， ，-4.
限小数或无限循环小数的形式.
正数：{ ，…}；
∵
，∴
是有理数．∵
，
8， ，…}；
合作探究
知识点 1 无理数
探究 我们知道有理数包括整数和分数，请把下列分数写成 小数的形式，你有什么发现？
3
2
(相邻两个1之间0的个数逐次加1)， 3 9
，－
.
有理数：{ －7，0.32， 1 ，3.14·，0，…}； 2
3
无理数：{ 8 ， 1 ，0.101 001 000 1…(相邻两个1 2
之间0的个数逐次加1)， 3 9 ，－ ，…}； 2
正实数：{ 0.32，1 3
，3.14·，
8
，
1 2
这样的无限不循环小数．
例1 下列各数：3.141 59， 3 8 ，0.131 131 113…(每相
邻两个3之间依次多1个1)，－π，
2 5 ，
1 7
中，无
理数有( B )
A．1个
B．2个
C．3个
D．4个
导引：∵3.141 59是有限小数，∴3.141 59是有理数．
∵ 3 8 2 ，∴ 3 8 是有理数．∵ 25 5 ，
人教版数学七年级下册
第六章
6.3.1 实数及其分类
学习目标
1.了解无理数和实数的概念以及实数的分 类。
2.知道实数与数轴上的点具有一一对应的 关系。
复习导入
…}；
(1)如图，OA=OB,数轴上点A对应的数是什么？它介
正有理数
有
理
数
0
负 有 理 数
8， ，-4.
限小数或无限循环小数的形式.
正数：{ ，…}；
∵
，∴
是有理数．∵
，
8， ，…}；
合作探究
知识点 1 无理数
探究 我们知道有理数包括整数和分数，请把下列分数写成 小数的形式，你有什么发现？
3
2
(相邻两个1之间0的个数逐次加1)， 3 9
，－
.
有理数：{ －7，0.32， 1 ，3.14·，0，…}； 2
3
无理数：{ 8 ， 1 ，0.101 001 000 1…(相邻两个1 2
之间0的个数逐次加1)， 3 9 ，－ ，…}； 2
正实数：{ 0.32，1 3
，3.14·，
8
，
1 2
这样的无限不循环小数．
例1 下列各数：3.141 59， 3 8 ，0.131 131 113…(每相
邻两个3之间依次多1个1)，－π，
2 5 ，
1 7
中，无
理数有( B )
A．1个
B．2个
C．3个
D．4个
导引：∵3.141 59是有限小数，∴3.141 59是有理数．
∵ 3 8 2 ，∴ 3 8 是有理数．∵ 25 5 ，
人教版数学七年级下册
第六章
6.3.1 实数及其分类
学习目标
1.了解无理数和实数的概念以及实数的分 类。
2.知道实数与数轴上的点具有一一对应的 关系。
复习导入
…}；
(1)如图，OA=OB,数轴上点A对应的数是什么？它介
【2014】(包头专版)中考数学复习方案专题课件_第1单元实数【新课标人教版】
a（a>0）， |a|＝0（a＝0）， －a（a<0）
包考探究
考点聚焦
第1节┃考点聚焦
名称 科学记 数法
定义
性质
把一个数写成________ a³10n 的 设这个数为m，①当|m|≥10时， 形式(其中1≤|a|<10，n为 n等于原数的整数位数减1；②当 整数)，这种记数法叫做科 |m|＜1时，|n|等于原数左起第一 学记数法 个非零数字前所有零的个数
实数的有关概念
定义 性质 规定了_______ _______ 原点 、 正方向 数轴 数轴上的点与实数一一对应 单位长度 和 ________的直线 符号 不同的两个 若 a，b 互为相反数，则有 a＋b＝0， 只有______ 相反数 数互为相反数 |a|＝|b|.0 的相反数是 0 乘积 为 1 的两个数互 若 a，b 互为倒数，则 ab＝1.0 没有 ________ 倒数 为倒数 倒数．倒数等于本身的数是 1 或－1 数轴上表示数 a 的点与原 绝对值 距离 ，记作|a| 点的________
考点聚焦
包考探究
第1节┃包考探究
方法点析
(1)求一个数的相反数，直接在这个数的前面加
上负号，有时需要化简得出． (2)一个负数的绝对值等于它的相反数，反过来，一个数的绝 对值等于它的相反数，则这个数是非正数． (3)解含有绝对值或和数轴有关的问题时常用到字母表示数的
思想、分类讨论思想和数形结合思想．
考点聚焦
包考探究
第1节┃考点聚焦
考点6
差值 比较法 商值 比较法 绝对值 比较法 其他方法
比较实数大小的常用方法
设 a, b 是任意两实数，则 a－b>0↔ a>b；a－b<0↔a<b； a－b＝0↔a＝b a 设 a, b 是两个正实数，则 >1↔a>b； b a a ＝1↔a＝b； <1↔a<b b b 设 a, b 是两个负实数，则|a|>|b|↔a<b；|a|＝|b|↔a＝b； |a|<|b|↔a>b 除此之外，还有平方法、倒数法等
第六章实数复习(公开课)ppt课件
19世纪
数学家逐步完善实数理论 ，形成了完备的实数体系 ，为数学分析、连续函数 等研究奠定了基础。
减法运算
总结词
减法运算的基本性质
详细描述
实数的减法运算可以转化为加法运算，即a-b=a+(-b)。
总结词
减法运算的运算律
详细描述
减法运算同样满足交换律和结合律，即a-b=b-a和(ab)-c=a-(b+c)。
总结词
减法运算的运算性质
详细描述
减法的可逆性也是减法的一个重要性质，每一个数都有 唯一的相反数；另外，0是减法的单位元，任何数与0 相减都等于它本身。
总结词
加法运算的运算律
详细描述
加法运算还有一些特殊的运算律，例如，任何数与0相加 都等于它本身，即a+0=a；相反数相加等于0，即a+(a)=0。
总结词
加法运算的运算性质
详细描述
加法运算还有一些重要的运算性质，例如，加法的可逆性 ，即每一个数都有加法逆元，与它相加等于0；加法的单 位元，即有一个特殊的数0，任何数与它相加都等于它本 身。
实数在几何学中有着广泛的应用，例如在计算长度 、面积和体积时，需要使用实数表示测量值。
函数定义域与值域
实数可以用来定义各种数学函数，包括代数函数、 三角函数、指数函数和对数函数等，同时函数的值 域也由实数构成。
数学分析基础
实数对于数学分析来说是必不可少的基础，极限、 连续性和可微性的定义都离不开实数。
在物理中的应用
80%
测量与计算
在物理学中，实数常被用于表示 和计算各种物理量，如长度、时 间、质量、电荷等。
100%
物理定律的数学表达
许多物理定律可以用实数表示的 数学公式来描述，例如牛顿第二 定律 F=ma。
人教新课标八年级课件实数复习课
平数数PJ你知道算术平方根、平方根、立方根联系和区别吗?1 •说出下列各数的平方根和算术平方根:(2) 0.512 0.8(4) -15---8 2(1) 169(2)±13和 13 (4)102 1 ±10和 100. 16 ⑶±0.4和0.4 2芸±|和I7(5)—2—93•说出下列各式的值:(3)±2536±26(6)(4)^125 5(5)-球0.027 -0.352 (6)I 负分数厂正无理数 负无理数无限不循环小数I 1.圆周率兀及一些含有龙的数 _般有三种情况2 .开不尽方的数有限小数及无限循环小数< 厂整数 分数正整数 负整数正分数｝自然数3 .有一定的规律，但不循环的无限小数把下列各数分别填入相应的集合内:-亦， -編， 0.3737737773 • •（相邻两个3之间的7的个数逐次加1）判断：下列说法是否正确:1 •实数不是有理数就是无理数。
2 •无限小数都是无理数。
3 •无理数都是无限小数。
(\/ )) 2 )4 ■带根号的数都是无理数。
(% )5 •两个无理数之和一定是无理数。
(7 )6•所有的有理数都可以在数轴上表示，反过来, 数轴上所有的点都表示有理数。
（H?=4 所以心=』第一値龜冃/（1）—插換着意义（）%（2） 0.01是0.1的算数平方根（）* 2.填空：（1）嗣立方根是（）2 的寿护是（^^3⑵ V? = 3 J（-3严二3 所以== a （Q 为任何数）=a （Q 为任何数）>660V第二饱龜貝/1. 计算：f (1).7144 + ^16-0-^(2)苗_塚—逅_百2. 解方程：(1)(x-1)—125(2)2(3兀-厅=8第三饱龜貝/1.当X X渝5 2X-1没有平方根2•若&X-7)0期？的缜是x=7 3.—个正数x的两个平方根分别是a+1和a-3侧a= 專二4a已知:y — Jx _ 2 +守2 -兀+ 3 ,求y—x的算数平方根A已知：X、歹满足J-2y-3+(2x-3y-5)~0，求x-Sy 的平方根A >. >. >. >.y/x — 2,且(y -1)2 + &-3二0,求右+y3 + z3的值o(1) -0・ 008 —0.22764。
最新人教版初中九年级下册数学【总复习第一讲 实数】教学课件
7、(2019河南）成人每天维生素D的摄入量约为0.0000046克.
数据“0.0000046”用科学记数法表示为( C )
（A）46×10-7
（B）4.6×10-7
（C）4.6×10-6
（D）0.46×10-5
知识点4：平方根、算术平方根、立方根
即时演练
8、16的平方根是±4 ，算术平方根是 4 ，－27的立方根是 －3 ；
)
（C）
1
6
（D）1 6
4、(2019玉林) 9的倒数是 ( A )
1
（A）
9
（B） 1 9
（C）9
（D）－9
5、(2017广州)如图，数轴上两点A，B表示的数互为相反数，则点）6
（C）0
（D）无法确定
知识点3：科学记数法与近似数
1. 科学记数法 把一个数记成 a×10n 的形式，其中1≤|a|＜10，且
n为整数．
2. 近似数 一个近似数四舍五入到哪一位，就说这个近似数
精确到哪一位．
即时演练
6、(2019广东)某网店2019年“母亲节”这天的营业额为 221 000元，将数221 000用科学记数法表示为( B )
（A）2.21×106
（B）2.21×105
（C）221×103
（D）0.221×106
本节课复习的主要内容
1、实数的相关概念; 2、实数的大小比较; 3、实数的运算。
知识点1：实数的分类
正整数
整数零
有理数 负整数
实数
分数负正分分数数
无理数负正无无理理数数
即时演练
1、（2019桂林）若海平面以上1045米，记作＋1045米，则海 平面以下155米，记作（ B ）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
算术平方根 开平方
乘 方
互为逆运算
开 方
平方根 立方根
负的平方根
开立方
一般地，如果一个数的平方等于a，这个数叫做a的平方根。（也叫二次方根）
若x2＝a a≥0 则x a
一个正数有两个平方根，它们互为相反数，零的平方根还是 零。负数没有平方根。 求一个数的平方根的运算，叫做开平方。
正数a的正的平方根和零的平方根,统称算术平方根 。
(C )
- 13
（3） 下列各组数中，互为相 反数的是（ B ） 1 2 3 2与 （B） （A） （ 2 ）与 8 2
（C）
3 3 2与 2 （D）8与 8
7.判断题 （1） 7 3 7 3 2
1 1 （ 2） 2 3 3 2 2 2
1.计算 5 5 2 3 3 3
2.求式子中 x 的值：3( x 2)
2
11 16
3.若 a b 4与 a b 14 互为相反数，求 a 2 b2 的值
（8）两个无理数的和一定是 无理数 （9）两个无理数的积一定是 无理数 （10）若正数a的一个平方根 是b，那么a的另一个平方 根是-b. （11）正数的两个平方根的和为0 （12）没有平方根的数也没有立方根
6.选择题： (1).(-3)2的算术平方根是（ D ）
（A）无意义 （B）±3 （ D） 3 （C）-3 (2).下列运算正确的是（ A ） 3 3 ( A) 6 6 (B) 3.6 0.6
• 有理数和无理数统称实数. 正有理数 有限小数和 有理数 0 无限循环小 数 负有理数 实 数 正无理数 无限不循 无理数 负无理数 环小数 实 数
正实数
0
负实数
实数的性质：
• 数a的相反数是-a. 一个正实数的绝对值是它本身； 一个负实数的绝对值是它的相反数； 0的绝对值是0.
1、求下列各数的相反数、倒数和绝 对值： (1) 7 的相反数是 ； 倒数是 ；
例：
32 2 2 3 2 3
分析： 3 2 2
2 3 2 3
2 3
2 2 3
3 2
原式 2 2 3 2 3 （ 3 2） 2 2 3 2 3 3 2 2 2 2 2 3 3 3
4 2 3
练习
；
2 3 ； （2） 3 －2的绝对值是_________
（3）若 x 1, y 2 ，且xy>0，x+y= 3或－ 3 。
练习：1. x为何值时，下面各式有意义？ x （1） 2 x （2） x （3） x 1
2.如图，在数轴上表示实数 15的点可能是（C） P Q M N 0 1 2 3 4 A.点P B. 点Q C.点M D.点N
64 的值是
8
64 的平方根是
8
4
64 的立方根是
填空
5 （1） 25 的算术平方根是______;
(2)若 x =3,则
2
3 x 的值是_____;
(3) a 的平方根是 3 ,则
(4)
a
81 =_____;
8 7 82 _____, ( 7) 2 ______ 。
对于 a2 的值得讨论
例题
(1)π的整数部分为3，则它 的小数部分是 ；
(2) 5的整数部分是多少?小数部 分是多少?
6、在 3 ， 2 8 ， 0.3333 ，
3
2 1 3 ， ， 3.14 ， 1 ，8 ， 中， 2 整数是： 有理数是： 无理数是： 实数是：
填空
1 3 的倒数是 3 （ 1）
你知道算术平方根、平方根、立方根的 区别吗？
平方根
立方根
3
a的取值
性 质
正数 0 负数
a a≥
0 没有 0,1
≠
0
a a≥ 0
0 没有 0
a
a 是任何数
0 负数（一个） 0,1,-1
正数（一个） 互为相反数（两个） 正数（一个）
是其本 身
填一填，更深入了解！
8是
64
的平方根
64的平方根是 ±8
非负数a的算术平方根是非负数， 即 a≥0 。 一般地，如果 ，那么 x 叫 a 的立方根 x a
3
数a的立方根用符号 3
a 表示。
一个正数有一个正的立方根；一个负数有一个负的立方根，零的立方根是零。
求一个数的立方根（三次方根）的运算，叫做开立 方，开立方与立方互为逆运算。
区别
算术平方根 表示方法
a a
2
a , ( a 0) 0, ( a 0) a , ( a 0)
1.无理数有几个？ 2.无理数都是用根号表示的数吗？
3.无理数都是开方开不尽的数吗？
4.用根号表示的数都是无理数吗？ 注意： 1.无理数的个数是无限多个. 2.无理数不都是用根号表示的. 3.用根号形式表示的数不都是无理数.
绝对值是
(2)
3
。
；
；
- 8 的相反数是 2 ； 倒数是
； 倒数是
绝对值是 2 . (3) 49 的相反数是
绝对值是 .
2. 169的平方根是_____ 3. -0.216的立方根是_____ 4. 64的立方根的算术平 方根是______
5.下列说法正确的是： （1）无限小数是无理数 （2）有理数都是有限小数 （3）一个数的立方根不一定是 无理数 （4）任何实数都有唯一的立方根 （5）只有正实数才有算术平方根 （6）任何数的平方根有两 个，它们互为相反数 （7）不带根号的数都是有理数
（3） ( 3) 2 3 2 （4） ( 11) 11 （5） ( 7) 7
3 3
错题集
• （1）求 3 64 的绝对值; • （2）已知一个数的平方根 是 2，求这个数及它的另 外一个平方根.
例：比较下列各组里两个数的大小.
（1）1.7 和
3
（2） 6和 7
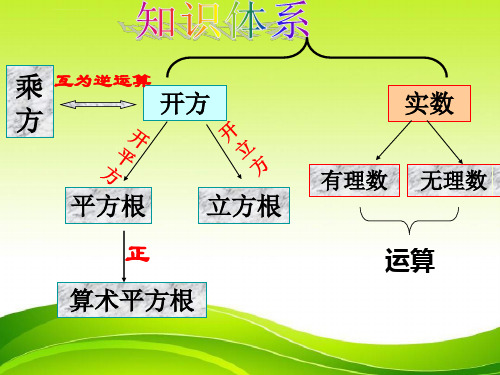
乘 方
互为逆运算
开 方
平方根 立方根
负的平方根
开立方
一般地，如果一个数的平方等于a，这个数叫做a的平方根。（也叫二次方根）
若x2＝a a≥0 则x a
一个正数有两个平方根，它们互为相反数，零的平方根还是 零。负数没有平方根。 求一个数的平方根的运算，叫做开平方。
正数a的正的平方根和零的平方根,统称算术平方根 。
(C )
- 13
（3） 下列各组数中，互为相 反数的是（ B ） 1 2 3 2与 （B） （A） （ 2 ）与 8 2
（C）
3 3 2与 2 （D）8与 8
7.判断题 （1） 7 3 7 3 2
1 1 （ 2） 2 3 3 2 2 2
1.计算 5 5 2 3 3 3
2.求式子中 x 的值：3( x 2)
2
11 16
3.若 a b 4与 a b 14 互为相反数，求 a 2 b2 的值
（8）两个无理数的和一定是 无理数 （9）两个无理数的积一定是 无理数 （10）若正数a的一个平方根 是b，那么a的另一个平方 根是-b. （11）正数的两个平方根的和为0 （12）没有平方根的数也没有立方根
6.选择题： (1).(-3)2的算术平方根是（ D ）
（A）无意义 （B）±3 （ D） 3 （C）-3 (2).下列运算正确的是（ A ） 3 3 ( A) 6 6 (B) 3.6 0.6
• 有理数和无理数统称实数. 正有理数 有限小数和 有理数 0 无限循环小 数 负有理数 实 数 正无理数 无限不循 无理数 负无理数 环小数 实 数
正实数
0
负实数
实数的性质：
• 数a的相反数是-a. 一个正实数的绝对值是它本身； 一个负实数的绝对值是它的相反数； 0的绝对值是0.
1、求下列各数的相反数、倒数和绝 对值： (1) 7 的相反数是 ； 倒数是 ；
例：
32 2 2 3 2 3
分析： 3 2 2
2 3 2 3
2 3
2 2 3
3 2
原式 2 2 3 2 3 （ 3 2） 2 2 3 2 3 3 2 2 2 2 2 3 3 3
4 2 3
练习
；
2 3 ； （2） 3 －2的绝对值是_________
（3）若 x 1, y 2 ，且xy>0，x+y= 3或－ 3 。
练习：1. x为何值时，下面各式有意义？ x （1） 2 x （2） x （3） x 1
2.如图，在数轴上表示实数 15的点可能是（C） P Q M N 0 1 2 3 4 A.点P B. 点Q C.点M D.点N
64 的值是
8
64 的平方根是
8
4
64 的立方根是
填空
5 （1） 25 的算术平方根是______;
(2)若 x =3,则
2
3 x 的值是_____;
(3) a 的平方根是 3 ,则
(4)
a
81 =_____;
8 7 82 _____, ( 7) 2 ______ 。
对于 a2 的值得讨论
例题
(1)π的整数部分为3，则它 的小数部分是 ；
(2) 5的整数部分是多少?小数部 分是多少?
6、在 3 ， 2 8 ， 0.3333 ，
3
2 1 3 ， ， 3.14 ， 1 ，8 ， 中， 2 整数是： 有理数是： 无理数是： 实数是：
填空
1 3 的倒数是 3 （ 1）
你知道算术平方根、平方根、立方根的 区别吗？
平方根
立方根
3
a的取值
性 质
正数 0 负数
a a≥
0 没有 0,1
≠
0
a a≥ 0
0 没有 0
a
a 是任何数
0 负数（一个） 0,1,-1
正数（一个） 互为相反数（两个） 正数（一个）
是其本 身
填一填，更深入了解！
8是
64
的平方根
64的平方根是 ±8
非负数a的算术平方根是非负数， 即 a≥0 。 一般地，如果 ，那么 x 叫 a 的立方根 x a
3
数a的立方根用符号 3
a 表示。
一个正数有一个正的立方根；一个负数有一个负的立方根，零的立方根是零。
求一个数的立方根（三次方根）的运算，叫做开立 方，开立方与立方互为逆运算。
区别
算术平方根 表示方法
a a
2
a , ( a 0) 0, ( a 0) a , ( a 0)
1.无理数有几个？ 2.无理数都是用根号表示的数吗？
3.无理数都是开方开不尽的数吗？
4.用根号表示的数都是无理数吗？ 注意： 1.无理数的个数是无限多个. 2.无理数不都是用根号表示的. 3.用根号形式表示的数不都是无理数.
绝对值是
(2)
3
。
；
；
- 8 的相反数是 2 ； 倒数是
； 倒数是
绝对值是 2 . (3) 49 的相反数是
绝对值是 .
2. 169的平方根是_____ 3. -0.216的立方根是_____ 4. 64的立方根的算术平 方根是______
5.下列说法正确的是： （1）无限小数是无理数 （2）有理数都是有限小数 （3）一个数的立方根不一定是 无理数 （4）任何实数都有唯一的立方根 （5）只有正实数才有算术平方根 （6）任何数的平方根有两 个，它们互为相反数 （7）不带根号的数都是有理数
（3） ( 3) 2 3 2 （4） ( 11) 11 （5） ( 7) 7
3 3
错题集
• （1）求 3 64 的绝对值; • （2）已知一个数的平方根 是 2，求这个数及它的另 外一个平方根.
例：比较下列各组里两个数的大小.
（1）1.7 和
3
（2） 6和 7