2020年6月2020届北京市中国人民大学附属中学2017级高三6月统一模拟考试文科综合历史试卷参考答案
北京人大附中2020届高三上学期期末考试数学(文)仿真(B)卷及答案.doc

2017-2018学年上学期高三期末考试仿真测试卷文科数学(B)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2017·榆树一中]设全集,,则图中阴影部分表示的集合是()A.{1,3,5} B.{1,5,6} C.{6,9} D.{1,5}2.[2017·台州中学]已知复,则复数的共轭复数()A.B.C. D.3.[2017·遵义四中]已知焦点在轴上的双曲线的渐近线方程为,则该双曲线的离心率为()A.B.C.或D.2或4.[2017·耀华实验中学]已知空间几何体的三视图如图所示,则该几何体的体积是()A.B.C.4 D.5.[2017·西城13中]已知函数,(其中,)的部分图象,如图所示,那么的解析式为()A.B.C.D.6.[2017·辽宁实验中学]在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关.”则下列说法错误的是()A.此人第二天走了九十六里路B.此人第一天走的路程比后五天走的路程多六里C.此人第三天走的路程占全程的D.此人后三天共走了42里路7.[2017·漯河高级中学]已知,满足约束条件,则的最大值是()A.3 B.5 C.6 D.78.[2017·惠阳高级中学]已知,,则的夹角为()A.B.C.D.9.[2017·德化一中]已知定义在上的偶函数满足,且当时,,则函数的零点个数是()A.0 B.2 C.4 D.610.[2017·咸宁联考]在锐角中,角,,对应的边分别是,,,向量,,且,则的取值范围是()A.B.C.D.11.[2017·华师附中]若直线与曲线有公共点,则的取值范围是()A.B.C.D.12.[2017·乾安县七中]在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是( )A .小方B .小张C .小周D .小马第Ⅱ卷二、填空题:本大题共4小题,每小题5分. 13.[2017·合肥八中]函数在上的单调情况是_______________.14.[2017·南开中学]如图是某算法的程序框图,则程序运行后输出的结果是__________.15.[2017·山东实验中学]已知函数,若,且,则的最小值为_____________.16.[2017·昌平一中]如图,在四面体中,点,,分别在棱,,上,且平面平面,为内一点,记三棱锥的体积为,设,对于函数,则下列结论正确的是__________.①当时,函数取到最大值;②函数在上是减函数;③函数的图像关于直线对称;④不存在,使得(其中为四面体的体积).三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题,考生根据要求作答.(一)必考题:60分,每个试题12分.17.[2017·济南外国语学校]各项均为正数的等比数列,前项和为,且满足,.(1)求数列的通项公式;(2)若,求数列的前项和.18.[2017·临川二中]据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.(1)若销售金额(单位:万元)不低于平均值的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.19.[2017·长春模拟]已知三棱锥中,是等腰直角三角形,且,,平面,.(1)求证:平面平面;(2)若为中点,求点到平面的距离.20.[2017·钦州港开发区中学]已知椭圆的中心在原点,焦点在轴,焦距为,且长轴长是短轴长的倍.(1)求椭圆的标准方程;(2)设,过椭圆左焦点的直线交于、两点,若对满足条件的任意直线,不等式()恒成立,求的最小值.21.[2017·合肥八中]已知二次函数的最小值为,且关于的不等式的解集为.(1)求函数的解析式;(2)求函数的零点个数.(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做第一题计分)22.[2017·西安中学]已知直线的参数方程为(,为参数),曲线的极坐标方程为.(1)将曲线的极坐标方程化为直坐标方程,并说明曲线的形状;(2)若直线经过点,求直线被曲线截得的线段的长.23.[2017·临川一中]已知,,函数的最小值为4.(1)求的值;(2)求的最小值.2017-2018学年上学期高三年级期末考试仿真测试卷文科数学(B)答案第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】D【解析】∵,,∴,∴图中阴影部分表示的集合是,故选D.2.【答案】C【解析】,所以复数的共轭复数,故选C.3.【答案】A【解析】因为焦点在轴上的双曲线的渐近线方程为,所以,,,,,故选A.4.【答案】B【解析】几何体为四棱锥,高为2,底面为正方形面积为,,选B.5.【答案】A【解析】周期,∴,,∵,,∴.故选A.6.【答案】C【解析】由题意可知,每天走的路程里数构成以为公比的等比数列,由求得首项,再由等比数列的通项公式求第二天的,第三天的,后三天的路程,即可得到答案.7.【答案】C【解析】绘制不等式组表达的平面区域如图所示,则目标函数,结合目标函数的几何意义可知目标函数在点处取得最大值:.本题选择C选项.8.【答案】C【解析】由,得,∴,又,∴,即,∵两向量夹角的范围为,∴与的夹角为.故选:C.9.【答案】D【解析】由题意,偶函数的周期为2,作出函数的图象与函数的图象,如图所示,观察图象可知,两个函数的交点个数为6个,所以函数的零点个数是6.10.【答案】B【解析】,,,,,因为是锐角三角形,所以,,,,,由正弦定理,可得:,,,.本题选择B选项.11.【答案】D【解析】将曲线的方程化简为,即表示以为圆心,以2为半径的一个半圆,如图所示:由圆心到直线的距离等于半径2,可得,∴或,结合图像可得,故选D.12.【答案】A【解析】重新整理:篮球:小林,小马;球:小林,小张;羽毛球:小林,小李;足球:小方,小张;排球:小方,小李;跆拳道:小方,小周;棒球:小马,小李;击剑:小周,小张乒乓球:小马;自行车:小周由于小周的自行车与小马的乒乓球没有共同兴趣爱好者,所以小周两边一事实上是跆拳道与击剑的,小马两边只能是棒球与篮球的.即小马与小林一定相邻,所以1号位是小林,2号位一定是小马,3号位就是棒球的小李.小周与小张及小方一定相邻,所以小周坐5号位.从3号位角度,4号位只能是排球和羽毛球(小林,不可能),所以是排球小方.6号位小张.选A.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.【答案】单调递增【解析】在上有,所以在单调递增,故答案为单调递增.14.【答案】【解析】当,时,,则;当,时,,则;当,时,,则;当,时,,此时运算程序结束,输出,应填答案.15.【答案】9【解析】画出了函数图象,,故得到和是关于轴对称的,;.等号成立的条件为.故答案为9.16.【答案】①②④【解析】令,,则,,所以,,,则在单调递增,单调递减,,所以①正确;②正确;③错误;④正确.即正确的是①②④.三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题,考生根据要求作答.(一)必考题:60分,每个试题12分.17.【答案】(1);(2).【解析】(1)设等比数列的公比为,由得,解得或,∵数列为正项数列,∴,代入,得,∴.(2),此时,∴.18.【答案】(1)推断该地区110家微商中有55家优秀;(2).【解析】(1)6家微商一周的销售金额分别为8,14,17,23,26,35,故销售金额的平均值为.由题意知优秀微商有3家,故优秀的概率为,由此可推断该地区110家微商中有55家优秀.(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,有15种,设“恰有1家是优秀微商”为事件,则事件包含的基本事件个数为9种,所以.即恰有1家是优秀微商的概率为.19.【答案】(1)见解析;(2).【解析】(1)证明:因为平面,平面,所以,又因为,,所以平面,平面,所以平面平面.(2)由已知可得,取中点为,连结,由于,所以为等腰三角形,从而,,由(1)知平面,所以到平面的距离为1,,令到平面的距离为,有,解得.20.【答案】(1);(2).【解析】(1)依题意,,,解得,,∴椭圆的标准方程为.(2)设,,则,当直线垂直于轴时,,且,此时,,所以;当直线不垂直于轴时,设直线,由,整理得,所以,,所以,要使不等式()恒成立,只需,即的最小值为.21.【答案】(1);(2)1个.【解析】(1)∵是二次函数,且关于的不等式的解集为,∴,且.∴,.故函数的解析式为.(2)∵,∴,令,得,.当变化时,,的取值变化情况如下:当时,,,又因为在上单调递增,因而在上只有1个零点,故在上仅有1个零点.(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做第一题计分)22.【答案】(1)详见解析;(2)8.【解析】(1)由可得,即,∴曲线表示的是焦点为,准线为的抛物线.(2)将代入,得,∴,∵,∴,∴直线的参数方程为(为参数).将直线的参数方程代入得,由直线参数方程的几何意义可知,.23.【答案】(1);(2)最小值为.【解析】(1)因为,所以,当且仅当时等号成立,又,,所以,所以的最小值为,所以.(2)由(1)知,,所以,故当,时,的最小值为.。
北京市中国人民大学附属中学2020届高三6月统一练习(三模)考试物理试题(无答案)

A. t=0.15 s 时,质点 Q 的加速度达到正向最大 B. t=0.15 s 时,质点 P 的运动方向沿 y 轴正方向 C. 从 t=0.10 s 到 t=0.25 s,该波沿 x 轴正方向传播了 6 m D. 从 t=0.10 s 到 t=0.25 s,质点 P 通过的路程为 30 cm
2. 下列说法错误的是: A.雨后的彩虹是光的衍射现象引起的 B.肥皂膜在阳光的照射下呈现彩色是光的干涉现象 C. 交通信号灯选用红灯的一个重要原因是因为红光更容易穿透云雾烟尘 D.液晶显示应用了光的偏振
3.下列有关原子结构和原子核的认识,其中正确的是: A.γ 射 线 是 高 速 运 动 的 电 子 流 B.氢原子辐射光子后,其绕核运动的电子动能增大 C.太阳辐射能量的主要来源是太阳中发生的重核裂变 D. ᤸ礨ᘣBi的半衰期是 5 天,100 克 ᤸ礨ᘣBi 经过 10 天后还剩下 50 克
第 2 页,共 12 页
人大附中 2019-2020 学年度高三物理 6 月质量检测题
7. 磁流体发电的原理如图所示。将一束速度为 v 的等离子体(含有大量正、负带电粒子) 垂直于磁场方向喷入磁感应强度为 B 的匀强磁场中,在相距为 d、宽为 a、长为 b 的两平行 金属板间便产生电压。如果把上、下板和电阻 R 连接,上、下板就是一个直流电源的两极。 稳定时两板间等离子体有电阻。忽略边缘效应,下列判断正确的是: A.上板为负极 B.上、下两极板间的电压 U=Bvd C.等离子体浓度越高,电动势越大 D.该发电机不需要外界提供能量
等于地面给木楔的摩擦力大小
北京人大附中2020高三5月模拟数学理试题
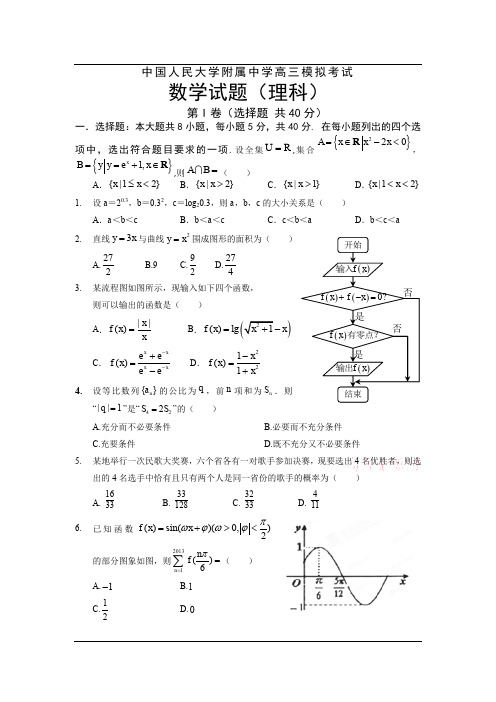
中国人民大学附属中学高三模拟考试数学试题(理科)第I 卷(选择题 共40分)一.选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项.设全集U R =,集合{}220A x x x =∈-<R ,{}1,x B y y e x ==+∈R,则AB =( ) A .{|12}x x ≤<B .{|2}x x >C .{|1}x x >D .{|12}x x << 1. 设a =20.3,b =0.32,c =log 20.3,则a ,b ,c 的大小关系是( )A .a <b <cB .b <a <cC .c <b <aD .b <c <a 2. 直线3y x =与曲线2y x =围成图形的面积为( )A.272B.9C.92 D.2743. 某流程图如图所示,现输入如下四个函数, 则可以输出的函数是( )A .||()x f x x= B.)()lgf x x =C .()x x x x e e f x e e --+=-D .221()1x f x x -=+ 4. 设等比数列{}n a 的公比为q ,前n 项和为n S .则“||1q =”是“422S S =”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分又不必要条件5. 某地举行一次民歌大奖赛,六个省各有一对歌手参加决赛,现要选出4名优胜者,则选出的4名选手中恰有且只有两个人是同一省份的歌手的概率为( ) A. 1633B. 33128C. 3233D. 4116. 已知函数()sin()(0,)2f x x πωϕωϕ=+><的部分图象如图,则20131()6n n f π==∑( ) A.1- B.1 C.12D.07. 如图所示,正方体ABCD A B C D ''''-的棱长为1, ,E F 分别是棱AA ',CC '的中点,过直线,E F 的平面分别与棱BB '、DD '交于,M N ,设 B M x =,[0,1]x ∈,给出以下四个命题:①平面MENF ⊥平面BDD B ''; ②当且仅当x =12时,四边形MENF 的面积最小; ③四边形MENF 周长()L f x =,[0,1]x ∈是单调函数; ④四棱锥C MENF '-的体积()V h x =为常函数;以上命题中假.命题..的序号为( ) A .①④ B .②C .③D .③④第Ⅱ卷(非选择题 共110分)二.填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.8. 如图,在复平面内,复数1z ,2z 对应的向量分别是OA ,OB , 则复数12z z 对应的点位于第________象限。
2020届北京市中国人民大学附属中学2017级高三下学期三模考试理科综合化学试卷及解析

2020届北京市中国人民大学附属中学2017级高三下学期三模考试理科综合化学试卷★祝考试顺利★(解析版)可能用到的相对原子质量:H-1 O-16 Na-23 K-39 Cl-35.5 Ge-73第 I 卷(选择题部分共 42 分)选择题(每小题只有1个正确选项符合题意,每小题 3 分,共 42 分)1.2020年5月1日北京市在全市范围内开展施行垃圾分类,下列垃圾分类不正确是()A.鱼骨、菜叶B.消毒剂及其包装物C.破损的易拉罐D.破碎玻璃厨余垃圾有害垃圾可回收垃圾其他垃圾A. AB. BC. CD. D【答案】D【解析】【详解】A.厨余垃圾是指居民日常生活及食品加工中产生的垃圾,鱼骨和菜叶属于厨余垃圾,A 正确;B.有害垃圾是指对人体健康或者自然环境造成直接或潜在危害的废弃物,如废药品及其包装物,故消毒剂及其包装物属于有害垃圾,B正确;C. 可回收物是指适宜回收利用和资源化利用的生活废弃物,破损的易拉罐为金属铝或铁制品,为可回收垃圾,C正确;D.其他垃圾指危害较小,但无再次利用价值,如建筑垃圾类,生活垃圾类等,破碎玻璃属于可回收垃圾,D错误;答案选D。
2.下列对应化学用语的表示不正确...的是A. 次氯酸的电子式:B. 丁烷的球棍模型:C. 乙烯的结构简式:CH2=CH2D. 原子核内有 8 个中子的碳原子:146C【答案】A【详解】A.次氯酸为共价化合物,分子中存在1个H-O键和1个O-Cl键,次氯酸的结构式为H-O-Cl,其电子式为,故A错误;B.用小球和小棍表示的模型为球棍模型,正丁烷中C原子呈锯齿形,球棍模型为,故B 正确;C.乙烯分子中含有1个碳碳双键,结构简式为:CH2=CH2,故C正确;D.质量数=质子数+中子数,原子核内有8个中子的碳原子的质量数为6+8=14,表示为146C,故D 正确;答案为A。
3.下列说法不正确...的是A. 植物油氢化过程中发生了加成反应B. 苯和甲苯都能发生取代反应C. 氯乙烯和乙醛都能用来合成高分子化合物D. 变质的油脂有难闻的特殊气味,是由于油脂发生了水解反应【答案】D【详解】A.植物油氢化过程是植物油中不饱和碳碳键与氢气发生了加成反应,A正确;B.苯和甲苯都属于芳香烃,在一定条件下能发生取代反应,B正确;C.氯乙烯含有不饱和的碳碳双键,在一定条件下能够发生加聚反应;乙醛含有醛基,在一定条件下能够发生缩聚反应,因此二者都能用来合成高分子化合物,C正确;D.变质的油脂有难闻的特殊气味,是由于油脂中的碳碳双键被氧化产生过氧化物,过氧化物分解产生一些有特殊气味的低分子醛、酮或羧酸,与水解反应无关,D错误;。
2020年6月27日中国人民大学附属中学2020届高三6月统一练习(三模)语文答案

绝密★启用前中国人民大学附属中学2020届高三毕业班下学期6月统一练习(三模)语文试题参考答案2020年6月27日 1.D 2.B 3.A 4.B 5.(6 分)①材料一认为,虽然大多数病毒对人类无害甚至有益,但部分病毒会给人类带来巨大的灾难。
这主要是人类自身造成的,与人类的发展以及对自然的破坏密切相关。
材料二认为,病毒与人类协同进化,紧密相连。
病毒推动了人类进化,没有病毒就没有人类。
②要加强对病毒的研究,客观全面地认识和对待病毒。
一方面,面对病毒带来的危害, 人类要采取必要的措施,注重预防和早期控制,切断病毒传播的途径,也要自省,不滥杀野生动物,保护自然生态环境,从源头上防止病毒危害。
另一方面,要认识到并非所有病毒都对人类有害,与对人类无害甚至有益的病毒和谐共处。
【评分参考】①3分,②3分。
意思对即可。
6.C7.B8.C9.将下面语句译为现代汉语。
(4 分)①孔子当初生于周朝,和今人相比谁距离尧舜更远呢 2 分②像孔子这样圣明又勤奋,却不探讨尧舜之前的事,难道是做不到吗 2 分10.(6 分)答案示例:①张秀才治学的问题是:遵循三皇太古时期的学说,舍近求远,追求高深玄奥的言论,脱离现实。
②作者首先指出君子治学的目的是践行“道”,这种“道”应是易知可法的,对“道”的阐述应是易明可行的;接着用孔子删《书》的例子说明君子所追寻的“道”并非越久远越好,太久远后世就难以理解和效法了;然后以二《典》和孟子的言论为例,说明“道”体现在贴近现实的人与事中。
【评分参考】①2 分,②4 分。
意思对即可。
【附:文言文参考译文】欧阳修叩首禀告秀才足下:(我)前几天离开后,又拿之前(您)赠送的十几篇(谈论)古今的杂文,多次阅读它们,(发现您的)言论十分高深并且志向非常远大。
(我)揣摩您的用意,难道不是忧虑时俗,(因而)深入研究古代学说、阐明圣贤之道,想要改变现今(的状况),(把)它恢复到古代(的样子),整治现今的混乱繁杂的现象吗?这之后(我)更加了解到您是好学、有远大志向的人啊。
2020届北京市人大附中2017级高三一模考试英语试卷及解析

2020届北京市人大附中2017级高三一模考试英语试卷★祝考试顺利★第一部分:知识运用(共两节,45 分)第一节语法填空(共 10 小题;每小题 1.5 分,共 15 分)A阅读下列短文,根据短文内容填空,在未给提示词的空白处仅填写 1 个适当的单词,在给出提示词的空白处用括号内所给词的正确形式填空。
Eventually, I decided to follow her and ___1___ happened truly amazed me. She was taking the food to the refugee camp, ___2___ she distributed it to children. I asked around and found out that my mum was very well known in the area. The kids were very ___3___ (friend) with her and even looked up to her as if she were their own mothers. Then it hit me – why would she not want to tell me about what she ___4___ (do) ?【答案】1. what2. where3. friendly4. had done/was doing/had been doing【解析】这是一篇记叙文。
文章讲述了作者跟踪母亲并得知了母亲帮助难民的事。
【1题详解】考查主语从句。
句意:最终我决定跟踪她,她做的事情确实使我震惊。
主语从句中缺少主语,故填what。
【2题详解】考查定语从句。
句意:她把食物带到了难民营,在那里把食物分发给了孩子们。
先行词the refugee camp在定语从句中作地点状语,故填where。
【3题详解】考查形容词。
【KS5U解析】北京市中国人民大学附属中学2020届高三6月统一练习地理试题 Word版含解析
11.下图是我国某城市1995年和2015年人口密度空间分布统计图。读图,1995-2015年,该城市( )
A. 出现明显的逆城市化现象B. 郊区交通改善,市区环境变差
2020年6月21日,我国迎来十年一遇的天象奇观——日环食。下图展示的是此次日环食带在世界范围穿过的地区。读图,完成下面小题。
14. 图中( )
A. 甲地树木稀疏,草原广布B. 乙地近海海域,寒暖流交汇
C. 丙地板块交界,地震多发D. 丁地河网密布,含沙量较大
15. 该日,日环食带沿线地区( )
A. 西侧比东侧先看到日出B. 日出东南,日落西南
【点睛】主要考查考生获取和解读地理信息、描述和解释地理事物的能力,考查的核心素养是区域认知和综合思维。
每年春季,伊犁河谷花海盛开,但这些鲜花花期非常短,这些春季典型花生长在干旱区,早春生长发育,短短的2个月时间里完成生活周期,随后干枯死亡,图中曲线表达了海拔高度与花期的关系。据此,完成下面小题。
9.图中( )
【点睛】考查城市化,主要考查考生获取和解读地理信息、描述和解释地理事物的能力,考查的核心素养是区域认知和综合思维。
2020年我国将实现全面建成小康社会的奋斗目标,打赢扶贫攻坚战。西起青藏高原东缘,东至华北平原西南部,跨秦岭、大巴山的秦巴山区是扶贫攻坚主战场之一。据此完成下面小题。
12. 秦巴山区( )
图a为马达加斯加岛年降水量分布图(单位:毫米),图b为MN沿线地质剖面示意图。读图,完成下面小题。
3. 图a所示岛屿( )
A. 西侧河流水能更加丰富B. 沿岸洋流降温减湿
人大附中2020年高三 6 月份三模数学(含答案)
Q = 3 ⎪ 5 ⎪ 人大附中2020年高三 6 月份三模数学(含答案)命题人:侯立伟 唐庚 王鼎审题人:于金华2020 年 06 月 27 日本试卷共 5 页,150 分。
考试时长 120 分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效.第一部分(选择题共 40 分)一、选择题共 10 小题,每小题 4 分,共 40 分.在每小题列出的四个选项中,选出符合题目 要求的一项.1.集合 P = {3, log 2 a }, Q = {a , b } ,若P Q = {0},则 P ( )A. {0, 3}2.若复数 z =B. {0, 2,3},则 z = ()C. {0,1,3}D. {0,1, 2,3}A. 12B. 322-1C. 1D. 23. 已知a = ⎛ 1 ⎫5 , b = ⎛ 2 ⎫ 3, c = log ⎝ ⎭ ⎝ ⎭2 ,则()3 5 A. a < b < cB. c < b < aC. b < c < aD. c < a < b4. 已知函数 f (x ) 的图象沿 x 轴向左平移 2 个单位后与函数 y = 2x 的图象关于 x 轴对称,若f (x 0 ) = -1 ,则 x 0 = ()A. -2B. 2 C . -log 2 3D .l og 2 35. 为了解某年级 400 名女生五十米短跑情况,从该年级中随机抽取 8 名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为 9.4 秒)的人数为( )7 8 8 6 1 8 91 5 7 8A.150B.250C.200D.5021+ 3i34 π 6.“ ϕ =- ”是“函数 f ( x ) = sin(2x + 6 π)(x ∈ R ) 与函数 g ( x ) = cos(2x +ϕ)(x ∈ R ) 为同一 3函数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.某四棱锥的三视图如图所示,则该四棱锥的体积是 ()A .6B .12C .24D .36侧视图俯视图a 8. 等比数列{a }中 a =1,且 4a ,2a ,a 成等差数列,则 n(n ∈ N * ) 的最小值为( )n 1 1 2 316 4 1 A.B .C .2592D . 19. 如图,四个棱长为 1 的正方体排成一个正四棱柱,AB 是一条侧棱, P i (i = 1,2, ⋯ ,8) 是上底面上其余的八个点,则 集合{y y = AB ⋅ AP i, i = 1, 2, 3,8} 中的元素个数 ()A. 1B. 2C. 4D. 810. 某校高一年级研究性学习小组利用激光多普勒测速仪实地测量 复兴号高铁在某时刻的速度,其工作原理是:激光器发出的光平均 分成两束射出,在被测物体表面汇聚,探测器接收反射光.当被测物 体横向速度为零时,反射光与探测光频率相同.当横向速度不为零时,反射光相对探测光会发生频移 f p= 2v sin ϕ ,其中v 为测速仪测得被 λ测物体的横向速度,λ 为激光波长,ϕ 为两束探测光线夹角的一半, 如图.若激光测速仪安装在距离高铁 1 m 处,发出的激光波长为 1600nm (1nm = 10-9 m ),测得某时刻频移为8.0 ⨯109(1/h),则该时刻高铁的速度v 约等于正视图 3ny A.320 km/h B.330 km/h C.340 km/h D.350 km/h第二部分(非选择题共 110 分)二、填空题共 5 小题,每小题 5 分,共 25 分.11. 抛物线 y = x 2的焦点到准线的距离是12. 二项式(x2 + 1)5 的展开式中含 x 4 的项的系数是 (用数字作答).x13. 已知关于x 的不等式ax 2 - 2x + 3a < 0 在(0, 2]上有解,则实数a 的取值范围为14. 在平面直角坐标系中,以双曲线 x a 2 2- = 1, (a > 0, b > 0) 的右焦点为圆心,以实半轴ab2为半径的圆与其渐近线相交,则双曲线的离心率的取值范围是15. 在一个不透明的口袋中装有大小、形状完全相同的 9 个小球,将它们分别编号为 1,2,3,…,9,甲、乙、丙三人从口袋中依次各抽出 3 个小球.甲说:我抽到了 8 号和 9 号小球; 乙说:我抽到了 8 号和 9 号小球;丙说:我抽到了 2 号小球,没有抽到 8 号小球.已知甲、乙、丙三人抽到的 3 个小球的编号之和都相等,且甲、乙、丙三人都只说对了一半. 给出下列四各结论:①甲抽到的 3 个小球的编号之和一定为 15; ②乙有可能抽到了 2 号小球; ③丙有可能抽到了 8 号小球; ④3 号,5 号和 7 号小球一定被同一个人抽到. 其中,所有正确结论的序号是.注:全部选对得 5 分,不选或有错选得 0 分, 其他得 3 分.三、解答题共 6 小题,共 85 分.解答应写出文字说明、演算步骤或证明过程. 16.(本小题满分 14 分)在△ABC 中, a = 3 , b = 2 求c 的值.,.从① ∠B = 2∠A , ② sin B = sin 2A ,③ S∆ABC= 3 15 ,这三个条件中任选一个,补充在 2 上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.6 2F EA D 1n i x如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD .四边形ADEF 为正方形,四边形ABCD 为梯形,且AD//BC ,∠BAD = 90︒,AB =AD = 1,BC = 3.(Ⅰ)求证:AF⊥CD;(I I)求直线BF 与平面CDE 所成角的正弦值.C18.(本小题满分14 分)国家环境标准制定的空气质量指数(简称AQI)与空气质量等级对应关系如下表:下表是由天气网获得的全国东西部各6 个城市在某一个月内测到的数据的平均值:(Ⅰ) 从表中东部城市中任取一个,空气质量为良的概率是多少?(Ⅱ)环保部门从空气质量“优”和“轻度污染”的两类城市随机选取3 个城市组织专家进行调研,记选到空气质量“轻度污染”的城市个数为ξ,求ξ的分布列和数学期望.(I I I)设东部城市的AQI 数值的方差为S 2 ,如果将合肥纳入东部城市,则纳入后AQI 数值的方差为S 2 ,判断S 2 和S 2 的大小.(只需写出结论)2 1 2附:方差计算公式S 2=1∑n(x-)2i=1.E : + 已知函数 f (x ) =2x - m (其中m 为常数).ex(I ) 若 m = 0 且直线 y = kx 与曲线 y =f (x ) 相切,求实数 k 的值;(I I ) 若 y = f (x ) 在[1, 2] 上的最大值为 2,求m 的值.e220.(本小题满分 14 分)x 2 y 2椭圆 2 2 = 1(a >b >0) 的离心率是 ,过点 P (0,1)做斜率为 k 的直线 l ,椭 a b 3圆 E 与直线 l 交于 A ,B 两点,当直线 l 垂直于 y 轴时 AB = 3 3 .(I ) 求椭圆E 的方程;(II ) 当 k 变化时,在 x 轴上是否存在点 M (m ,0),使得△AMB 是以 AB 为底的等腰三角形,若存在求出 m 的取值范围,若不存在说明理由.21. (本小题满分 14 分)在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点) A (n ) : A 1 , A 2 , A 3 , , A n 与 B (n ) :B 1 , B 2 , B 3 , , B n ,其中n ≥ 3 ,若同时满足:①两点列的起点和终点分别相同;②线段A i A i +1 ⊥B i B i +1 ,其中i = 1, 2, 3, , n -1, 则称 A (n ) 与 B (n ) 互为正交点列.(Ⅰ)试判断 A (3) : A 1 (0, 2), A 2 (3, 0), A 3 (5, 2) 与 B (3) :B 1 (0, 2), B 2 (2, 5), B 3 (5, 2) 是否互为正交点列,并说明理由;(Ⅱ)求证: A (4) : A 1 (0, 0), A 2 (3,1), A 3 (6, 0), A 4 (9,1) 不存在正交点列 B (4) ;(Ⅲ)是否存在无正交点列 B (5) 的有序整数点列 A (5) ?并证明你的结论.522 5 36 参考答案和评分标准2020.6.27题号 1 2 3 4 5 6 7 8 9 10 答案CCDBBABDAA二、填空题(本大题共 5 小题,每小题 5 分,共 25 分.请把结果填在答题纸中.) 题 号 1112131415答案1 210(-∞, 3 )3(1,2)①②④注:15 题给出的结论中,有多个符合题目要求。
北京市中国人民大学附属中学2020届高三6月模拟(三模)英语试题(解析版)
北京市中国人民大学附属中学2020届高三6月模拟(三模)英语试题第一部分:知识运用(共两节,45分)第一节语法填空(共10小题;每小题1.5分,共15分)A阅读下列短文,根据短文内容填空,在未给提示词的空白处仅填写1个适当的单词,在给出提示词的空白处用括号内所给词的正确形式填空。
A video went viral online that showed a man saving a 2-year-old girl who was stuck in the burglar bars of her apartment in Nanning.On Sunday, the toddler, who was home alone, climbed to the balcony of her home on thefifth floor and became___1___ (trap) in the burglar bars. Xu Hongwei, a former member of the armed police, climbed up the building's balconies ___2___(reach) the girl and held her up with hands to keep her from falling for nearly half an hour. He ___3___comfort) her by saying, "I am with you. Come on, climb down the balcony." The girl was finally saved ___4___ the help of other neighbors.『答案』1. trapped 2. to reach 3. comforted 4. with『解析』这是一篇记叙文。
2020届北京市中国人民大学附属中学高三6月统一练习(三模)考试数学试题(解析版)
2020届北京市中国人民大学附属中学高三6月统一练习(三模)考试数学试题一、单选题1.集合{}23,log P a =,{},Q a b =,若{}0P Q ⋂=,则P Q ⋃= A .{}0,3 B .{}0,2,3C .{}0,1,3D .{}0,1,2,3【答案】C 【详解】{0}P Q ⋂=,2log 0a ∴=,且0b =,解得1,0a b ==,则{3,0}P =,{1,0}Q =,{0,1,3}P Q ∴⋃=.故选:C .【考点】1.集合的运算;2.对数的计算. 2.若复数z =z =( )A .12BC .1D .2【答案】C【分析】利用复数的除法运算化简复数z ,再利用复数的模长公式可求得z .【详解】21121z====+, 因此,1z ==. 故选:C.【点睛】本题考查复数模长的计算,同时也考查了复数的除法运算,考查计算能力,属于基础题.3.已知2513a ⎛⎫= ⎪⎝⎭,1325b -⎛⎫= ⎪⎝⎭,32log 5c =,则( ) A .a b c << B .c b a <<C .b c a <<D .c a b <<【答案】D【分析】分别根据指数函数、对数函数的单调性分析函数值的范围即可.【详解】函数13xy ⎛⎫= ⎪⎝⎭是单调递减函数,所以25110133a ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭,函数52xy ⎛⎫= ⎪⎝⎭是单调递增函数,所以11332551522b -⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭=>⎭⎝, 函数3log y x =是单调递增函数,所以332log log 105c =<=, 即c a b <<. 故选:D.【点睛】本题主要考查了根据指数函数、对数函数的单调性比较大小的问题,属于基础题.4.已知函数()f x 的图象沿x 轴向左平移2个单位后与函数2x y =的图象关于x 轴对称,若()01f x =-,则0x =( ) A .-2 B .2C .2log 3-D .2log 3【答案】B【分析】由题意可得与函数2xy =的图象关于x 轴对称的函数,可得:2x y =-,再向右平移2个单位可得()22x f x -=-,再由()01f x =-即可得解.【详解】先求与函数2xy =的图象关于x 轴对称的函数, 可得:2x y =-,再向右平移2个单位可得()22x f x -=-,所以()02021x f x -=-=-,可得:02x =, 故选:B.【点睛】本题考查了函数的对称和平移,考查了指数的计算,解题方法是反向移动,属于基础题.5.为了解某年级400名女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的人数为( )A .150B .250C .200D .50【答案】B【分析】结合古典概型公式求出成绩合格的概率,再由频数=总数⨯频率即可求解 【详解】由茎叶图可知,成绩在9.4秒以内的都为合格,即合格率为58P =,故估计该年级女生五十米跑成绩及格的人数为54002508⨯=, 故选:B【点睛】本题考查概率及频数的求解,属于基础题 6.“6πϕ=-”是“函数()sin 2()3f x x x R π⎛⎫=+∈ ⎪⎝⎭与函数()cos(2)()g x x x R ϕ=+∈为同一函数”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】A【分析】利用诱导公式,结合充分条件与必要条件的定义,论证充分性与必要性是否成立即可.【详解】若6πϕ=-,则()cos 2sin 2sin 26623g x x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫=-=-+=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,即函数()sin 2()3f x x x R π⎛⎫=+∈ ⎪⎝⎭与函数()cos(2)()g x x x R ϕ=+∈为同一函数,充分性成立;若函数()sin 2()3f x x x R π⎛⎫=+∈ ⎪⎝⎭与函数()cos(2)()g x x x R ϕ=+∈为同一函数,ϕ的值可以为116π,即两个函数数为同一函数不能推出6πϕ=-,必要性不成立,所以,“6πϕ=-”是“函数()sin 2()3f x x x R π⎛⎫=+∈ ⎪⎝⎭与函数()cos(2)()g x x x R ϕ=+∈为同一函数”的充分而不必要条件,故选:A.【点睛】本题主要考查诱导公式的应用,以及充分条件与必要条件的定义,属于基础题. 7.某四棱锥的三视图如图所示,则该四棱锥的体积是( )A .6B .12C .24D .36【答案】B【分析】由三视图可得原图,结合原图,利用四棱锥的体积公式即可得解.【详解】原图如图所示, 可得1334=123V =⨯⨯⨯, 故选:B.【点睛】本题考查了三视图,考查了利用三视图画直观图,同时考查了锥体的体积公式,属于基础题.8.等比数列{}n a 中11a =,且14a ,22a ,3a 成等差数列,则()*na n N n∈的最小值为( ) A .1625B .49C .12D .1【答案】D【分析】首先设等比数列{}n a 的公比为(0)q q ≠,根据14a ,22a ,3a 成等差数列,列出等量关系式,求得2q,比较()*na n N n∈相邻两项的大小,求得其最小值. 【详解】在等比数列{}n a 中,设公比(0)q q ≠, 当11a =时,有14a ,22a ,3a 成等差数列,所以21344a a a =+,即244q q =+,解得2q ,所以12n na ,所以12n n a n n-=, 12111n n a n n a n n++=≥+,当且仅当1n =时取等号, 所以当1n =或2n =时,()*n a n N n∈取得最小值1,故选:D.【点睛】该题考查的是有关数列的问题,涉及到的知识点有等比数列的通项公式,三个数成等差数列的条件,求数列的最小项,属于简单题目.9.如图,四个棱长为1的正方体排成一个正四棱柱,AB 是一条侧棱,(1,2,,8)i P i =⋅⋅⋅是上底面上其余的八个点,则集合{},1238i y y AB AP i =⋅=⋅⋅⋅、、、、中的元素个数( )A .1B .2C .4D .8【答案】A【分析】本题首先可根据图像得出i i AP AB BP =+,然后将i AB AP ⋅转化为2i AB A P B B +⋅,最后根据棱长为1以及i AB BP 即可得出结果.【详解】由图像可知,i i AP AB BP =+,则()2i i i AB BP AB AP AB B AB A P B ⋅==+⋅+, 因为棱长为1,i ABBP ,所以0i AB BP ⋅=,2101i i AB AP AB AB BP ⋅=+=+=⋅,故集合{},1238i yy AB AP i =⋅=⋅⋅⋅、、、、中的元素个数为1, 故选:A .【点睛】本题考查向量数量积的求解问题,关键是能够利用平面向量线性运算将所求向量数量积转化为已知模长的向量和有垂直关系向量的数量积的运算问题,考查了转化与化归的思想,考查集合中元素的性质,是中档题.10.某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度,其工作原理是:激光器发出的光平均分成两束射出,在被测物体表面汇聚,探测器接收反射光.当被测物体横向速度为零时,反射光与探测光频率相同.当横向速度不为零时,反射光相对探测光会发生频移2sin p v f ϕλ=,其中为测速仪测得被测物体的横向速度,λ为激光波长,ϕ为两束探测光线夹角的一半,如图.若激光测速仪安装在距离高铁1m 处,发出的激光波长为()91600nm lnm 10m -=,测得某时刻频移为98.010(1/h)⨯,则该时刻高铁的速度v 约等于( )A .320km /hB .330km /hC .340km /hD .350km /h【答案】A【分析】先计算sin ϕ,再根据所给公式计算v 即可. 【详解】332sin 1.00041(2010)ϕ--==+⨯故91.00048.010v⨯=,即81600 1.0004故v 320/km h ≈.故选:A【点睛】本题主要考查三角函数的计算和应用,意在考查学生对这些知识的理解掌握水平.二、填空题 11.抛物线2y x 的焦点到准线的距离是___________.【答案】12【分析】由抛物线的解析式求出p ,即可求解 【详解】由2y x 变形得2x y =,故抛物线焦点在y 的正半轴,21p =,12p =,故抛物线2y x 的焦点到准线的距离是12p =故答案为:12【点睛】本题考查由抛物线解析式求解基本量,属于基础题12.251()x x+的展开式中,4x 的系数为 .(用数字作答)【答案】10. 【解析】解:因为由二项式定理的通项公式可知103425510342=10r r C x r r x C -∴-=∴=∴的系数为13.已知关于x 的不等式2230ax x a -+<在(]0,2上有解,则实数a 的取值范围为___________.【答案】,3⎛-∞ ⎝⎭【分析】由(]0,2x ∈,2230ax x a -+<,可得:223x a x <+,求出函数223xy x =+的最大值即可.【详解】由(]0,2x ∈,2230ax x a -+<, 可得:223xa x <+, 223xy x =+,当0x =时,0y =,当0x ≠时,22233x y x x x==≤++,当且仅当x =所以a ,故答案为:,3⎛⎫-∞ ⎪ ⎪⎝⎭.【点睛】本题考查了存在性问题,考查了参变分离求参数范围,同时考查了利用基本不等式求最值,属于基础题.14.在平面直角坐标系中,以双曲线22221x y a b-=,(0,0)a b >>的右焦点为圆心,以实半轴a 为半径的圆与其渐近线相交,则双曲线的离心率的取值范围是___________.【答案】【分析】根据圆与直线相交,得到圆心到直线的距离小于半径,求得结果.【详解】根据题意有圆222()a c y x +=-与双曲线22221x y a b-=的渐近线相交,则有圆心(,0)c 到直线0bx ay -=的距离d b a ==<,所以c e a === 因为b a <,所以01ba<<,所以e =,故答案为:.【点睛】该题考查的是有关双曲线的问题,涉及到的知识点有双曲线的离心率的范围的求解,直线与圆相交的特征,属于简单题目.15.在一个不透明的口袋中装有大小、形状完全相同的9个小球,将它们分别编号为1,2,3,,9,甲、乙、丙三人从口袋中依次各抽出3个小球.甲说:我抽到了8号和9号小球;乙说:我抽到了8号和9号小球;丙说:我抽到了2号小球,没有抽到8号小球.已知甲、乙、丙三人抽到的3个小球的编号之和都相等,且甲、乙、丙三人都只说对了一半.给出下列四各结论:①甲抽到的3个小球的编号之和一定为15;②乙有可能抽到了2号小球;③丙有可能抽到了8号小球;④3号,5号和7号小球一定被同一个人抽到.其中,所有正确结论的序号是__________. 【答案】①②④【分析】所有编号之和为9(19)129452⨯++++==,由甲、乙、丙三人每人抽到的3个小球的编号之和为15,在此条件下进行分析判断,即可得解. 【详解】编号为1,2,3,,9的小球所有编号之和为9(19)129452⨯++++==, 由甲、乙、丙三人抽到的3个小球的编号之和都相等, 则每人抽到的3个小球编号之和为15,故①正确, 依题意,由甲和乙的表述可知,甲和乙一人抽到了编号为8的小球,一人抽到了编号为9的小球, 则丙所述没有抽到8号小球是正确的,故乙没有抽到2号小球, 若甲抽到了编号为9的小球,乙抽到了编号为8的小球, 设甲抽到的另外两个小球的编号分别为12,a a , 乙抽到的另外两个小球的编号分别为12,b b , 则12126,7a a b b +=+=,所以12,a a 的取值只有1和5,2和4两种情况,当甲抽到的编号为1和5的小球时,乙只能抽到编号为3和4的小球, 此时丙只能抽到编号为2,6,7,与条件矛盾, 所以甲抽到编号为2与4的小球, 则乙抽到编号为1和6的小球, 所以甲抽到编号为2,4,9的小球, 乙抽到编号为1,6,8的小球, 丙则抽到编号为3,5,7的小球同理,也可以是甲抽到编号为1,6,8的小球, 乙抽到编号为2,4,9的小球, 而丙则抽到编号为3,5,7的小球, 故②正确,③错误,④正确, 故答案为:①②④【点睛】本题考查了命题的真假和逻辑关系,考查了逻辑推理能力和思维判断能力,考查了分类讨论思想,属于较难题.三、解答题16.在ABC 中,3a =,b =_________.求c 的值.从①2B A ∠=∠,②sin sin 2B A =,③2ABC S =△,这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.【答案】选①:5;选②:5或3【分析】如果选①:利用正弦定理求出cos 3A =,再求出sin C ,利用正弦定理得解;如果选②:先求出cos 3A =,再利用余弦定理求出c ;如果选③:先求出cos C =.【详解】如果选①:因为3a =,b =2B A ∠=∠,所以在ABC 中,由正弦定理得3sin A =.所以2sin cos sin A A A =故cos A =.(0,)A π∈,所以sin 3A ==.又因为2B A ∠=∠,所以21cos 2cos 13B A =-=.所以sin 3B ==. 在ABC 中,sin sin()C A B =+sin cos cos sin A B A B =+9=.所以sin 5sin a Cc A==.如果选②:因为3a =,26b =,sin sin 2B A =,所以sin 2sin cos B A A =, 由正弦定理得:2cos b a A =.故6cos 3A =, 由余弦定理可得:269242263c c =+-⋅⋅, 28150c c -+=,解得5c =或3.如果选③:3152ABC S =△,则3151sin 22ABC S ab C ==△,则10sin 4C =,所以6cos C =±. 当6cos C =时,22262cos 924232615c a b ab C =+-=+-⨯⨯⋅=,15c =;当6cos C =-时,22262cos 924232651c a b ab C =+-=++⨯⨯⋅=, 所以51c =或15.【点睛】本题主要考查正弦定理余弦定理解三角形,考查三角形面积公式的应用,意在考查学生对这些知识的理解掌握水平.17.如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD .四边形ADEF 为正方形,四边形ABCD 为梯形,且//AD BC ,90BAD ∠=︒,1AB AD ==,3BC =.(1)求证:AF CD ⊥;(2)求直线BF 与平面CDE 所成角的正弦值.【答案】(1)证明见详解;(2)105【分析】(1)由AF AD ⊥,平面ADEF ⊥平面ABCD ,利用面面垂直的性质定理可得AF ⊥平面ABCD ,再利用线面垂直的性质定理即可证出.(2)取BC 上的点G ,使得1BG =,证明//GE BF 且GE BF =,过G 作GH CD ⊥于H ,则GH ⊥平面CDE ,连接EH ,则GEH ∠为直线BF 与平面CDE 所成角,求解三角形即可得出答案. 【详解】(1)证明:四边形ADEF 为正方形,∴AF AD ⊥,平面ADEF ⊥平面ABCD ,且平面ADEF平面ABCD AD =,∴AF ⊥平面ABCD ,则AF CD ⊥.(2)取BC 上的点G ,使得1BG =, 则//BG AD 且BG AD =,∴//BG EF 且BG EF =,则四边形BGEF 为平行四边形, 则//GE BF 且GE BF =, 由1AB AF ==,90BAF ∠=︒, 可得2GE BF ==,过G 作GH CD ⊥于H ,则GH ⊥平面CDE ,连接EH , 则GEH ∠为直线BF 与平面CDE 所成角,在Rt DGC △中,求得5GH =, 105sin 52GH GEH GE ∴∠===∴直线BF 与平面CDE 10【点睛】本题考查了面面垂直的性质定理、线面垂直的性质定理、线面角,考查了逻辑推理能力,属于基础题.18.国家环境标准制定的空气质量指数(简称AQI )与空气质量等级对应关系如下表:下表是由天气网获得的全国东西部各6个城市在某一个月内测到的数据的平均值:(1)从表中东部城市中任取一个,空气质量为良的概率是多少?(2)环保部门从空气质量“优”和“轻度污染”的两类城市随杋选取3个城市组织专家进行调研,记选到空气质量“轻度污染”的城市个数为ξ,求ξ的分布列和数学期望. (3)设东部城市的AQI 数值的方差为21S ,如果将合肥纳入东部城市,则纳入后AQI 数值的方差为22S ,判断21S 和22S 的大小.(只需写出结论)附:方差计算公式()2211n i i S x x n ==-∑.【答案】(1)13;(2)分布列见解析,()2E ξ=;(3)2212S S >. 【分析】(1)利用古典概型的概率计算公式即可求解.(2)空气质量“优”和“轻度污染”的两类城市的个数,利用组合数以及古典概型的概率计算公式即可列出分布列,由分布列即可求出期望. (3)利用方差的意义以及计算公式即可判断. 【详解】(1)东部城市共6个,空气质量为良有2个,东部城市中任取一个,空气质量为良的概率121613C p C ==.(2)空气质量“优”的城市有2个,“轻度污染”的城市有4个, 根据题意ξ的所有可能取值为1,2,3,()124236115C C p C ξ===,()214236325C C p C ξ===, ()304236135C C p C ξ===, ξ∴的分布列为:所以()1232555E ξ=⨯+⨯+⨯=. (3)如果将合肥纳入东部城市,可得2212S S >【点睛】本题考查了离散型随机变量的分布列、数学期望、方差,考查了基本知识的掌握情况,属于基础题. 19.已知函数2()xx mf x e -=(其中m 为常数). (1)若0m =且直线y kx =与曲线()y f x =相切,求实数k 的值; (2)若()y f x =在[]1,2上的最大值为22e,求m 的值. 【答案】(1)2;(2)2.【分析】(1)代入0m =,得到()f x ,求出导函数,设出切点坐标可得切线方程,与已知切线比较可得答案;(2)求出导函数,讨论导函数的正负情况,根据()f x 在()1,2的单调性求出最大值等于22e,从而求出m . 【详解】(1)0m =时,()222222()()x x x x x x e xe xf x f x e e e --'=⇒==, 设切点为0002,x x x e ⎛⎫ ⎪⎝⎭,则切线方程为()00000222x x x x y x x e e --=- ()0,0点代入,()00000222x x x x x e e --=-化简解得0(0)02k x f '⇒===. (2)22()xx m f x e -++'=,①当24m +≥即2m ≥时,()0f x '>在()1,2上恒成立,故()f x 在()1,2单调递增,()f x 在[]1,2的最大值为2242(2)m f e e-==,故2m =,满足2m ≥; ②当22m +≤即0m ≤时,()0f x '<在()1,2上恒成立,故()f x 在()1,2单调递减,()f x 在[]1,2的最大值为222(1)m f e e-==,故22m e =-,不满足0m ≤,舍去;③当224m <+<即02m <<时,由22()0x x m f x e-++'==得22m x +=, 22m x +<时()0f x '>,22m x +>时()0f x '<, 即()f x 在21,2m +⎡⎫⎪⎢⎣⎭上单调递增,在2,22m +⎛⎤⎥⎝⎦上单调递减,故()f x 的最大值为 22222222m m m m mf e e ++++-⎛⎫== ⎪⎝⎭,即22222m e e +=,所以2m =,不满足02m <<,舍去,综上所述, 2m =.【点睛】本题考查了导数的切线方程,考查了利用导数的单调性求得最值从而得到m 的问题.20.椭圆2222:1(0)x y E a b a b +=>>过点()0,1P 作斜率为k 的直线l ,椭圆E 与直线l 交于A ,B 两点,当直线l 垂直于y轴时,||AB =. (1)求椭圆E 的方程;(2)当k 变化时,在x 轴上是否存在点(),0M m ,使得AMB 是以AB 为底的等腰三角形,若存在,求出m 的取值范围,若不存在说明理由.【答案】(1)22194x y +=;(2)存在,55,1212⎡⎤-⎢⎥⎣⎦. 【分析】(1)由椭圆的离心率可得2249b a =,再代入点⎫⎪⎪⎝⎭即可得解; (2)联立方程组,结合韦达定理可得AB 的中点2294,4949kC k k -⎛⎫ ⎪++⎝⎭,由直线方程转化条件为2549km k =-+,结合基本不等式即可得解.【详解】(1c a ==2249b a =, 故椭圆的方程为2222149x y a a +=,由已知得椭圆过点,12⎛⎫ ⎪ ⎪⎝⎭,所以22279144a a +=,解得29a =, 所以椭圆E 的方程为22194x y +=;(2)由题意得直线l 的方程为1y kx =+, 设()11,A x y ,()22,B x y ,AB 的中点()00,C x y ,由221194y kx x y =+⎧⎪⎨+=⎪⎩,消去y 整理得()224918270k x kx ++-=,>0∆,则1221849k x x k +=-+,1222749x x k =-+, 所以12029249x x k x k +-==+,∴0024149y kx k=+=+, 所以点C 的坐标为2294,4949kC k k -⎛⎫⎪++⎝⎭,假设在x 轴上存在点(,0)M m ,使得AMB 是以AB 为底的等腰三角形, 则点(,0)M m 为线段AB 的垂直平分线与x 轴的交点. ①当0k ≠时,则过点C 且与l 垂直的直线方程224194949k y x k k k ⎛⎫-=-+ ⎪++⎝⎭,令0y =,则2554499k x m k k k==-=-++, 若k 0<,则4912k k --≥=,当且仅当23k =-时,等号成立,所以5504129k k<-≤+,所以5012m <≤; 若0k >,则4912k k +≥=,当且仅当23k =时,等号成立,所以5504129k k<≤+,5401295k k+--≤<,所以5012m -≤<; ②当0k =时,则有0m =.所以存在点M 满足条件,且m 的取值范围是55,1212⎡⎤-⎢⎥⎣⎦. 【点睛】本题考查了椭圆方程的求解及直线与椭圆的综合应用,考查了运算求解能力与转化化归思想,属于中档题.21.在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)123():,,,,n A n A A A A ⋅⋅⋅与123():,,,,n B n B B B B ⋅⋅⋅,其中3n ≥,若同时满足:①两点列的起点和终点分别相同;②线段11i i i i A A B B ++⊥,其中1,2,3,,1i n =⋅⋅⋅-,则称()A m 与()B m 互为正交点列.(1)试判断123(3):(0,2), (3,0), (5,2)A A A A 与123(3):(0,2),(2,5),(5,2)B B B B 是否互为正交点列,并说明理由.(2)求证:1234(4):(0,0), (3,1), (6,0), (9,1)A A A A A 不存在正交点列(4)B ; (3)是否存在无正交点列()5B 的有序整数点列()5A ?并证明你的结论.【答案】(1)互为正交点列,答案见解析;(2)证明见解析;(3)存在,证明见解析. 【分析】(1)根据定义判断即可;(2)点列1B ,2B ,3B ,4B 是点列1A ,2A ,3A ,4A 的正交点列,进而根据正交点列的定义,得到假设不成立,进而说明()4A :1(0,0)A ,2(3,1)A ,3(6,0)A ,4(9,1)A 不存在正交点列()4B ;(3)有序整点列1B ,2B ,3B ,4B ,5B 是点列1A ,2A ,3A ,4A ,5A 的正交点列,利用正交点列的定义,构造方程组,进而根据方程组有解得答案.【详解】解:(1)有序整点列1(0,2)A ,2(3,0)A ,3(5,2)A 与1(0,2)B ,2(2,5)B ,3(5,2)B 互为正交点列. 理由如下:由题设可知12(3,2)A A =-,23(2,2)A A =,12(2,3)B B =,23(3,3)B B =-, 因为12120A AB B ⋅=,23230A A B B ⋅=,所以1212A A B B ⊥,2323A A B B ⊥.所以整点列1(0,2)A ,2(3,0)A ,3(5,2)A 与1(0,2)B ,2(2,5)B ,3(5,2)B 互为正交点列.(2)证明:由题意可得12(3,1)A A =,23(3,1)A A =-,34(3,1)A A =, 设点列1B ,2B ,3B ,4B 是点列1A ,2A ,3A ,4A 的正交点列,则可设121(1,3)B B λ=-,232(1,3)B B λ=,343(1,3)B B λ=-,123,,λλλ∈Z , 因为1A 与1B ,4A 与4B 相同,所以有12312393331λλλλλλ-+-=⎧⎨++=⎩①②因为123,,λλλ∈Z 方程②不成立,所以有序整点列1(0,0)A ,2(3,1)A ,3(6,0)A ,4(9,1)A 不存在正交点列. (3)存在无正交点列的整点列()5A .当5n =时,设()1,i i i i A A a b +=,,i i a b Z ∈,其中a ,b 是一对互质整数,1,2,3,4i =, 若有序整点列1B ,2B ,3B ,4B ,5B 是点列1A ,2A ,3A ,4A ,5A 的正交点列, 则()1,i i i i i B B b a λ+=-,1,2,3,4i =,由441i 111i i i i i A AB B ++===∑∑,得11441144i i i i i i i i i i b a a b λλ====⎧∑-=∑⎪⎨⎪∑=∑⎩①②取1(0,0)A ,3i a =,1,2,3,4i =,12b =,21b =-,31b =,41b =-, 由于1B ,2B ,3B ,4B ,5B 是整点列,所以有Z i λ∈,1,2,3,4i =. 等式②中左边是3的倍数,右边等于1,等式不成立, 所以存在无正交点列的整点列()5A .【点睛】本题考查的知识点是向量垂直的充要条件,存在性问题,反证法,难度较大,运算量也比较大,属于难题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年6月2020届中国人民大学附属中学2017级高三6月统一模拟
考试
文科综合历史参考答案
1-5 ABAAD 6-10 BCCDB 11-15 DBDCA
16. (1)王充所生活汉朝儒家思想已经取得正统地位;(1分)汉代儒学宣扬“君权神授”和“天人感应”的理论;(2分)谶纬迷信流行,认为天象和人事之间有一种神秘的对应关系。
(1分)
(2)王充的思想:王充反对天人感应和谶纬神学,认为天只是自然的存在和运行,与人事无关。
(1分)否定人有“先知之见”,认为人是通过感官和学习获得知识。
(1分)反对神鬼迷信的说法,否认鬼神的存在。
(2分)..
评价:王充是唯物主义思想家。
体现出独立思考和敢于斗争的精神。
(2分)
17. 唐朝是疆域辽阔的统一多民族国家,经济和文化都居世界领先地位。
(2分)
曲辕犁是唐朝农具的重要发明和进步,安装了犁评,可以调节犁耕深度;从“胡人执犁俑”可以看出曲辕犁轻巧便捷,便于操作携带,能适应各种土壤和不同田块的耕作要求;当时已经传播到了边疆少数民族地区。
(4分)
曲辕犁促进了中国以农耕为主的社会经济的发展,促进了中国古代的民族交融。
(2分) 18. 资本主义国家(宗主国)构成了资本主义世界体系的核心。
资本主义国家抢占殖民地,划分势力范围,对广大的亚非拉国家和地区进行殖民统治和殖民掠夺。
(3分)
殖民掠夺促进资本主义国家的资本原始积累和工业化,加剧了广大被殖民地区的贫困和落后。
(3分)……….
工业革命后,西方殖民国家又将这些被地区作为原料产地和工业品市场。
资本主义世界市场建立起来。
(3分)
资本主义国家、资本主义世界殖民体系、资本主义世界市场一起构成了资本主义世界体系。
(3分)……..
19. (1)特点:反对加征关税实行贸易保护,反对官府与民争利,反对凭借特权进行经济垄断;主张工商业的自由经营。
(4分)…….
影响:有利于工商业摆脱封建政府的压迫,有利于民族资本主义的发展,有利引进国外先进的技术和经济制度。
(3分)。
