第2章 SPC与控制图
SPC培训教材(第二版)

统计预测
检验+SPC
全面质量管理 20世纪60年代以来
系统保证
SPC、TQM 6Sigma…
在品质管理发展过程中,SPC 是品质保障的重要工具!
6
客户及标准体系对SPC应用要求
客户要求
-全球产业链之中,供应商必须采用SPC控制其制程; -要求供应商提供过程数据和过程能力;
体系标准要求
-ISO9000、TS16949、QS-9000认证的关键部分; -减少过程不稳定,提高产品质量;
过程品质改进需要
-解决品质顽症,促使工作流的改进; -适应新的生产节拍;
7
工厂SPC应用现状分析
行业内企业普遍面临的问题
管理水平和人员素质跟不上企业发展的要求,工艺和质量的管 控水平不足,影响企业生产高端产品的能力。
外部市场的竞争以及客户对质量提出了更高的要求。 劳动力、生产资源成本不断攀升,降低生产和质量成本成为企
「ISO9000」要求为客戶提供合格的产品,只有稳定而一贯的「过程」与 「系统」,才能保证长期做出合格的产品。然而,如何检核此一贯「过程」 与「系统」仍然稳定的存在?这必须仰赖SPC来发挥功能。
5
质量管理与SPC的关系
质量检验 19世纪末—20世纪30年代
人来保证
事后把关
统计质量控制 20世纪40-50年代
---改变操作 如:培训操作人员、变换输入材料等; ---改变设计 如:设备、沟通方式和相互关系、过程整体设计等; 对输出采取措施:探测并纠正不符合规范的产品,而没有处理过程中根本问 题,可能会持续的对产品进行100%挑选、返工等,直到过程改善了。
2
课程大纲
• 第1章 持续改进和统计过程控制 • 第2章 控制图
SPC与常规控制图
成功案例:青岛海尔集团冰箱
海尔集团冰箱中二事业部,是海尔冰箱重要生产基地之一, 年产100多万台冰箱,远销国内外。冰箱生产主要有钣金、 吸附、发泡、总装等工序,配备来自德国、日本和意大利 等世界最先进的生产设备;已经成功应用SAP ERP系统 和SBU系统,使产品在配货和发货、以及产品生产跟踪上 完全实现了自动化。公司在质量管理方面,经常邀请国内 外专家做交流和培训,引进六西格玛管理,在发泡、总装 等重点工序手工来做统计过程控制SPC。由于受到数据采 集、监控、分析手段的影响,不能很好的体现SPC实时监 控的特点和达到预防目的。特别是发泡工序配备国际最先 进的高端设备,很多重要的工艺质量数据已经能够通过控 制器察看,实现单台设备用规格线报警,但是无法把这些 数据实时通过网络采集起来,工程师对后端生产销售反馈 的质量问题,只能查看记录本的数据,无法进行快速详尽 的质量追溯,查找当时的生产工艺和质量反馈状况,不便 查询质量问题的本源。
有效的利用SPC系统的预警控制功能进行科学的预 防控制,并逐渐形成规范的质量预防控制体系。
质量废品比应用系统前减少47%, 过程参数大大优化,产出率大大提高,改善生产效率
34
操作员发现,如果把控制图中下午1:00~2: 30间的点删除的话,那么上午10:00这个失 控点将不再是失控点,换句话说,上午10: 00这个失控点是由下午1:00~2:30这组失 控点带来的假信号。
35
3、控制图的使用和改进 经过修正的控制图投入使用后通常要
继续改进,以保证和提高控制质量的能 力和水平。如此继续下去,可以清楚看 到控制图的不断改进。这时,如果认为 基本目的达到,就不必再做控制图的每 月修正,只做定期抽样检验判断工序状 态的保持情况就可以了
将子组23的数据从数据组中删除了,子组 16的数据仍然保留,因为没有找到和删除这 个特殊变异源。
管理学统计过程控制SPC与控制图PPT学习教案

控制图原理的第二种解释: 偶波与异波
偶然因素引起偶然波动,简称偶波 异常因素引起异常波动,简称异波
最小波动下(异波已经消除,只剩偶波), 应用统计学原理设计出相应的控制界线,于 异波
休哈特控制图的实质就是区分偶然因素和异 常因素这两类因素
第36页/共52页
P图上点子超出下控制界线
好现象,如果没有以下几种情况 -质量检验人员缺乏经验而漏检 -检验仪表有问题 数据不真实
第37页/共52页
点子距离中心线的真正距离
设过程P=0.2。Pi=0.24,ni=250;pi+1=0.28,
ni+1=50。
第38页/共52页
np((不合格品数)控 制图
管理学统计过程控制SPC与控制图
会计学
1
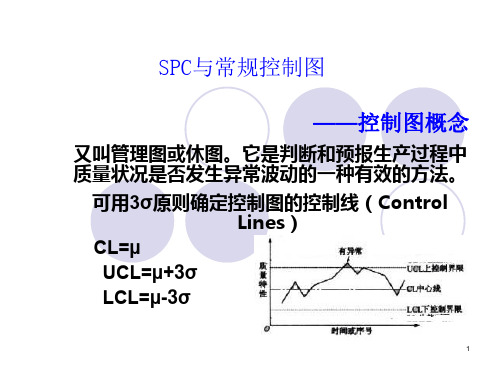
控制图
对质量特性值进行测定记录评 估和监察过程是否处于控制状 态的一种用统计方法设计的图
第1页/共52页
控制图原理的第一种解释: 假设检验
第2页/共52页
第3页/共52页
第4页/共52页
在控制图上描点实质上就是进行统计假设检验, 即检验假设(已知方差): H0:u=u0 H1:u=u1 控制图的上下控制界线即为接收域与拒绝域的 分界线。
对产品的质量有99.73%的把握 生产最经济 过程的变异最小
第9页/共52页
两类错误和3σ方式
虚发警报错 误
造成寻找 并不存在 的异因的 错误的损 失
3σ方式:
漏发警报错
第10页/共52页
误
控制图的分类
分析用控制图
统计稳态? 技术稳态?
控制用控制图
保持生产过程在确定的状态
第11页/共52页
LCLR
spc控制图原理

第二章 控制图原理一控制图的重要性贯彻预防原则是依靠推行SPC和SPCD来实现的而居QC七个工具核心地位的控制图是 SPC和SPCD的重要工具1984年日本名古屋工业大学调查了115家日本各行各业的中小型工厂结果发现平均每家工厂使用137张控制图这个数字对于我们推行SPC和SPCD是有一定的参考意义的可以说工厂中使用控制图的张数在某种意义上反映了管理现代化的程度二什么是控制图控制图是对过程质量加以测定记录从而进行控制管理的一种用科学方法设计的图图上有中心线(CL)上控制界限(UCL)和下控制界限(LCL)并有按时间顺序抽取的样本统计量数值的描点序列参见控制图示例图三控制图原理的第一种解释模具车间有部车床车制直径为10mm的机螺丝为了了解机螺丝的质量从车制好的机螺丝中抽出100个测量并记录其直径数据如表所示机螺丝直径数据(mm)10.210.42 10.30 10.36 10.094 9.94 10.00 9.99 9.85 9.9410.21 9.79 9.70 10.04 9.98 9.81 10.13 10.21 9.84 9.55 10.01 10.36 9.88 9.22 10.01 9.85 9.61 10.03 10.41 10.12 10.15 9.76 10.57 9.76 10.15 10.11 10.03 10.15 10.21 10.059.73 9.82 9.82 10.06 10.42 10.24 10.60 9.58 10.06 9.9810.12 9.97 10.30 10.12 10.14 10.17 10.00 10.09 10.11 9.709.49 9.97 10.18 9.99 9.89 9.83 9.55 9.87 10.19 10.3910.27 10.18 10.01 9.77 9.58 10.33 10.15 9.91 9.67 10.10 10.09 10.33 10.06 9.53 9.95 10.39 10.16 9.73 10.15 9.75 9.79 9.94 10.09 9.97 9.91 9.64 9.88 10.02 9.91 9.54为找出这些数据的统计规律将它们分组统计作直方图如机螺丝直径直方图所示图中的直与比方高度该组的频数成正机螺丝直径直方图 直方图趋近光滑曲线将各组的频数用数据总和N=100除就得到各组的频率它表示机螺丝直径属于各组的可能性大小显然各组频率之和为1若以直方面积来表示该组的频率则所有直方面积总和也为 分布曲线 正态分布曲线1这时直方的高=直方面积/组距=频率/组距=频数/(N ×组距)因此标取为频率或频率/组距各直方的高都与频数成正比故机螺丝直径直方图所示无论纵坐的直方图仍可用只要再作一条频率纵轴和一条直方面积表示频率的纵轴见直方图趋近光滑曲线图如果数据越多分组越密则机螺丝直径直方图的直方图也越趋近一条光滑曲线如直方图趋近光滑曲线图所示在极限情况下得到的光滑曲线即为分布曲线它反映了产品质量的统计规律如分布曲线图所示在质量特性值为连续值时最常见的典型分布为正态分布例如机螺丝直径直方图中机螺丝直径的分布就是如此它的特点是中间高两头低左右对称并延伸至无限正态分布可两个参数即均值用和标准差来决定正态分布有一个结论对质量管理很有用即无论均值和标准差取何值产品质量特性值落在3σ之间的概率为99.73于是落在µ±3σ之外的概率为100%一99.73%=0.27%而超过一侧即大于µ-3σ或小于µ+31‰σ的概率为0.27%/2=0.135%≈如正态分布曲线图这个结论十分重要美国休哈特就根据这事实提出控制图一了控制图的演变过程控制图的演变图首先把正态分布曲线图按顺时针方向转90°成下图控制图的演变a参见图由于上下的数值大小不合常规故再把控制图的演变图上下翻转180°而成下图控制图的演变b图这样就得到一张控制图具体说是单值( χ)控制图现在结合机螺丝的例子来说明控制图的原理设已知机螺丝直径的标准差为0.26mm现从上表的数据算得样本均值x =10.10mm于是有)(00.10)(78.1026.031033mm x mm x =≈=×+=≈+µσσµ)(22.926.01033mm x =×−=−≈−σσµ3+参见x 控制图称µ+3σ为上控制界记为UCL 称µ为中心线记为CL 称µ-3σ为LCL 这三者统称为控制线规定中心线用实线绘制上下控制界用虚线绘为了控制螺丝的质量每隔1小时随机抽取一个车好的螺丝测量其直径将结果描点并用直线段将点子连结以便于观察点子的变化趋势由图可看出前三个上控制界记为制在X 控制图中点子都在控制界内但第四个点子超出上控制界为了醒目把它用小圆圈圈起来表示这个机螺丝的直径过分粗了应引起注意现在对这第四个点子应作何判断根据正态分布的结论在生产正常的条件下点子超出上控制界的概率只有1‰左右可能性非常小可以认为它实际上不发生若发生则认为生产中存在异常而从x 控制图也可看出若生产异常例如由于车刀磨损机螺丝直径将逐渐变粗x 增大分布曲线将上移这时分布曲线超出上控制界那部分面积 (用阴影区表示)可能达到千分之几十几百比1‰大得多于是认为点子出界就判断异常用数学语言来说即根据小概率事件原理小概率事件实际上不发生若发生则判断异常在控制图上描点实质上就是进行统计假设检验即检验假设(已知σ=0.26mm)H拒绝:=10.00:H 110.00而控制图的上下控制界即为接受域与拒绝域的分界限点子落在上下界限之间表明可接受H点子落在上下界限之外表明应H两类偶因是始终存在的对质量的响微影小但难以除去四控制图原理的第二种解释换个角度再来研究控制图的原理根据来源的不同质量因素可以分成4M1E 五个方面但从对质量的影响大小来看质量因素可分成偶然因素(简称偶因)与异常因素(简称异因)例如机床开动时的轻微振动等异因则有时存在对质量影响大但不难除去例如车刀磨损固定机床的螺母松动等偶因引起质量的偶然波动(简称偶波)异因引起质量的异常波动(简称异波)偶波是不可避免的但对质量的影响微小故可把它看作背景噪声而听之任之异波则不然它对质量的影响大且采取措施不难消除故在过程中异波及造成异波的异因是我们注意的对象一旦发生就应该尽快找出采取措施加以消除并纳入标准化保证它不再出现 偶波与异波都是产品质量的波动如何能发现异波的到来呢经验与理论分析表明当生产过程中只存在偶波时产品质量将形成某种典型分布例如在车制螺丝的例子中形成正态分布如果除去偶波外还有异波则产品质量的分布必将偏离原来的典型分布因此根据典型分布是否偏离就能判断异波即异因是否发生而典型分布的偏离可由控制图检出在上述车制螺丝的例子中由于发生了车刀磨损的异因螺丝直径的分布偏离了原来的正态分布而向上移动于是点子超出上控制界的概率大为增加从而点子频频出界表明存在异波控制图上的控制界限就是区分偶波与异波的科学界限根据上述可以说休哈特控制图的实质是区分偶然因素与异常因素两类因素五控制图是如何贯彻预防原则的控制图是如何贯彻预防原则的呢这可以由以下两点看出:1.应用控制图对生产过程不断监控当异常因素刚一露出苗头甚至在未造成不合品之前就能及时被发现例如在控制图重点子形成倾向图中点子有逐渐上升的趋势可以在这种趋势造成不合格品之前就采取措施加以消除起到预防的作用格所以在现场 2.更多的情况是控制图显示异常表明异因已经发生这时一定要贯彻下列20个 字:“查出异因采取措施保证消除不再出现纳入标准”如果不贯彻这20个字控制图就形同虚设不如不搞每贯彻一次这20个字(即经过一次这样的循环)就消除一个异因使它永不再出现从而起到预防的作用由于异因只有有限多个故过经有限次循环(参见达到稳态的循环图)后 最终可以达到这样一种状态:在过程中只存在偶因而不存在异因这种状态称为统计控制状态或稳定状态简称稳态稳态是生产过程追求的目标因为在稳态下生产质量有完的把握质量特性值有99.73%落在上下控制界限之间的范围内(一般合格品率还要高于99.73%);其次在稳态下生产不合格品最少一道工序处于稳态称为稳定工序道道工序都处于稳态称为全稳生产线SPC 就是通过全稳生产线达到全过程预防的对全因而生产也是最经济的所述虽然质量变异不能完全消灭但控制图是使质量变异成为最小的有效工具综上。
SPC(2-控制图)

计数值:通常是指不用仪器即可测出的数据。计件如 ON
不合格品数, 大片外观不良数,服从二项分布;计点 如电池激光焊接的气密性, 短路数等, 服从泊松分布. OFF
格数目,如:布匹上的疵点、铸件上砂眼数、电子设备焊接不良 称为“不合格
数、每页印刷错误数等,样品的大小保持不变时可以应用c图, 数”。2.左列
培训师:卢子俊 当样品的大小变化时则应换算为平均每单位的不合格数后再使用
u控制图。
两图可由通用 不合格数cT图 代替
控制图的分类(按数据种类分)
• 計量值管制图 (Control Charts for Variables)
培训师:卢子俊
控制图的应用
• 建立适用于实施的环境 • 定义过程 • 确定待管理的特性,考虑到
– 客户的需求 – 当前及潜在的问题区域 – 特性间的相互关系 • 确定测量系统 • 使不必要的变差最小.
培训师:卢子俊
控制图的应用
步骤一、选择需控制的产品质量特征值 ◆所控制的产品质量特征值为计量值 ◆所控制的产品质量特征为关键质量特征 ◆若关键质量特征不可测量,采用其它代用质量
– 平均值与全距控制图(X-R Chart) – 平均值标准差控制图(X-σChart)
– 中位数与全距控制图(X-R ~Chart)
– 个别值与移动全距控制图(X-MR Chart)
• 计数值控制图 (Control Charts for Attribute)
– 不合格品率控制图(P Chart) – 不合格品数控制图(Pn Chart) – 不合格数控制图(C Chart) – 单位不合格数控制图(U Chart)
SPC-02控制图

TTM Technologies, Inc. Confidential
21
怎么
选?
三、 Control Chart的选择
计量值
n≧2
n大小
__
~
X
X
中心线
n>10
n大小
n≦10 (一般为2~5)
资料性质 n=1
不良数
计数值
不良/缺点
缺点数
固定
n固定?
不固定 固定
n固定?
不固定
__ X-S图
__ X-R图
绘直方图 是否满足规格 控制用控制图
检讨5M1E 提升流程能力
18
依数据性质分类
1)计量型控制图:是指控制图所取样的数据均来自实际测量而得
1、平均值与极差之控制图(X-R
2、平均值与标准差之控制图(X-S
Chart)
Chart) ~
3、中位值与极差之控制图(X-R Chart4)、个别值与移动极差控制图(X-MR
3、Hale Waihona Puke 量型流程能力4、计数型流程能力
5、6 σ水平值与Cpk、DPMO
6 、流程能力的影响因素
.
TTM Technologies, Inc. Confidential
2
1、专心听讲(请手机 “收声”) 2、积极思维(杜绝“鱼眼”现象)
课 堂 纪 律
3、互动学习(积极投入,但请避免“多动症”)。
4、些许自由(允许小磕睡、短时外出,但须保持安静)。
Chart)
TTM Technologies, Inc. Confidential
19
2)计数型控制图:是指控制图所依据之数据系经由计数方法而得
SPC控制图2篇
SPC控制图第一篇:SPC控制图1. 介绍SPC控制图(Statistical Process Control)是一种质量管理工具,用于监控和管理过程中的变异性。
它基于统计原理,通过收集和分析过程数据,可以帮助我们实时判断过程是否处于控制状态,并及时采取措施进行调整和修正,以保证产品或服务的稳定性和可靠性。
2. SPC控制图的基本原理SPC控制图有两个基本原则:稳定性和可预测性。
稳定性是指过程在一个可控制的范围内运行,没有特殊原因的变异性;可预测性是指过程的性能可以通过数据进行预测和估计,而不需要依赖特殊原因的出现。
3. SPC控制图的类型常用的SPC控制图有以下几种类型:(1)X-Bar和R控制图:用于监控连续性数据的平均值和范围。
(2)X-Bar和S控制图:与X-Bar和R控制图类似,但用标准差代替范围。
(3)P控制图:用于监控离散型数据的不良率或缺陷率。
(4)C控制图:用于监控离散型数据的计数。
4. SPC控制图的使用步骤(1)收集数据:根据所监控的过程特性,选择合适的采样方法和样本大小,收集数据。
(2)构建控制图:根据采集到的数据,计算样本平均值、范围、标准差、不良率等统计指标,绘制控制图。
(3)判断过程状态:分析控制图上的数据点和规则,判断过程是否处于控制状态。
(4)监控过程:定期收集和更新数据,绘制新的控制图,进行持续监控和分析。
5. SPC控制图的应用范围SPC控制图可以应用于各行各业的生产过程和服务过程中,如制造业的生产线、医疗行业的手术过程、金融行业的交易过程等。
通过使用SPC控制图,可以及时发现潜在问题,并采取纠正措施,提升过程的稳定性和可靠性。
6. SPC控制图的优势与挑战(1)优势:- 实时监控:SPC控制图可以提供实时的过程数据,帮助管理者及时判断过程状态。
- 判断能力:通过分析控制图上的数据点和规则,可以判断过程是正常变异还是有特殊原因的变异。
- 效益显著:SPC控制图可以帮助企业降低不良率、提高产品质量,并节约成本。
SPC与常规控制图培训课件
SPC与常规控制图培训课件1. 介绍SPC(Statistical Process Control,统计过程控制)是一种常用的质量管理工具,通过收集和分析过程数据来监控和控制生产过程中的变异性。
常规控制图是SPC的重要组成部分,用于识别过程是否处于控制状态。
本课件将介绍SPC与常规控制图的基本概念、使用方法和应用实例。
2. SPC的基本原理SPC的基本原理是通过收集过程数据并运用统计方法分析这些数据,从而判断过程是否处于控制状态。
SPC的主要目标是降低过程的变异性,确保产品的质量稳定。
3. 常见的常规控制图3.1 控制图的基本结构控制图通常由中心线、上限线和下限线组成。
中心线代表过程的平均值,上限线和下限线代表了过程的可接受变异范围。
3.2 均值控制图均值控制图用于监控过程的平均值是否处于控制状态。
常用的均值控制图包括平均值图、移动平均图和指数加权移动平均图。
3.3 范围控制图范围控制图用于监控过程的变异性是否处于控制状态。
常用的范围控制图包括范围图和标准差图。
3.4 异常值控制图异常值控制图用于检测过程中的异常值。
常见的异常值控制图包括箱线图和帕累托图。
4. 常用的统计方法4.1 均值与标准差均值和标准差是用来描述数据集中趋势和分布的统计指标。
均值代表数据的中心位置,标准差代表数据的离散程度。
4.2 相关性分析相关性分析用于确定两个变量之间的关系强度和方向。
常用的相关性分析方法包括皮尔逊相关系数和斯皮尔曼相关系数。
4.3 回归分析回归分析用于确定两个变量之间的函数关系。
常用的回归分析方法包括线性回归和多项式回归。
5. SPC的应用实例5.1 制造业中的SPC应用在制造业中,SPC被广泛应用于监控生产过程中的变异性,降低次品率和提高产品质量。
通过使用常规控制图,制造商可以及时发现并纠正生产过程中的异常情况。
5.2 服务业中的SPC应用在服务业中,SPC可以用于监控服务过程中的变异性,提高服务质量和满意度。
质量管理-spc控制图培训课件
74.008 74.011 74.002 74.009 74.015 74.014 73.005 73.988 74.004 73.995 73.990
73.996 74.007 73.984 74.007 73.996 74.007 74.000 73.997 74.003 74.003 74.009 74.014 74.010 74.013
准则5:连续3点中有2点在同侧B区以外
UCL A
B C CL C
B LCL A
准则6:连续5点中有4点在同侧C区以外
UCL A
B C CL C
B LCL A
准则7:连续15个点在C区内
准则8:连续8个点都不在C区内
UCL A
B C CL C
B LCL A
UCL A
B C CL C
B LCL A
常规控制图分析和应用
②解决方法是:根据两种错误所造成的总损失最小来确定最优间距 ,经验证明休哈特所提出的3σ方式较好。
注:80年代,出现了经济质量控制EQC学派(学术带头人:德国 乌尔茨堡大学冯·考拉尼教授)以使两种错误所造成的总损失最 小为出发点来设计控制图与抽样方案。
七、3σ方式
3σ方式的公式: UCL=μ+3σ CL=μ LCL=μ-3σ
u 控制图 c 控制图
选择合适的控制图
是
计量型数据吗?
否
性质上是否均匀
或不能按子组取样?
是
否
子组容量≥ 9?
否 是
关心的是 不合格品率吗?
是
否
样本容量
是否恒定?
是
否
np或p图 p图
关心的是 单位零件缺陷数吗?
是
样本容量 是否恒定?
模块2 SPC概述与计量型控制图
建 立 控 制 限
8. 使用最终确定的控制限,应用于现场程控制;
过 程 控 制
选择拟使用控制图进行控制的质量特性 • 顾客/组织的需求
长度、重量、含量、压力。。。。。。
• 想要改进\重点控制的区域、过程
某条生产线、某个操作,某个产品的生产
• 特性之间的相互关系
如果特性之间有明确的因果关系,则选择作为原因的那个变量进行控制
统计过程控制的原理 • 假定为了控制螺丝的质量,每隔一个小时随机抽取1个车好的 螺丝,测量其直径,将结果描点画图如下(共取了4个螺丝):
直 径
3σ 3σ
均值
为什么会出现 超出的现象呢? 可能的原因: A:过程正常,点出限 的概率为1‰左右;
B:车刀磨损,点出限 的概率是1‰的几十倍 甚至是几百倍。 您更相信那种原因?
建 立 控 制 限
8. 使用最终确定的控制限,应用于现场程控制;
过 程 控 制
选用合适的控制图种类 • 若每个子组只能取一个产品,则选择I-MR图(单值移动极差图)
• 若每个子组能够取多个产品,且现场使用处计算方便,则选择
X-S图(均值标准差图) • 若每个子组能够取多个产品,但现场使用处计算不方便,则选 择X-R图(均值极差图)
目标值
预测
如果过程仅存在普
通原因(稳定的过程)
引起过程波动(变差)的主要原因 • 普通原因和特殊原因 • 特殊原因:
– 间歇性的起作用 – 难以预测何时发生
– 数量众多
– 一般可以确切描述和衡量
??? ???
如果过程仅存在特 殊原因(不稳定的过程)
在这个大楼的拐角处有一个打字社,有一个文员负责打字,如 果这个文员连续打字8小时,我们每小时都检查一次,我们会发
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011-1-3
中国人民大学六西格玛质量管理研究中心
24
利用上面的控制图做20天的控制(控制数据 利用上面的控制图做 天的控制(控制数据.xls) 天的控制 )
2011-1-3
中国人民大学六西格玛质量管理研究中心
25
例2.1
x 1 , . . . , x 5 的 X b a r 控制图
5 4 3 2 样本均值 1 0
x 1 , . . . , x 5 的 X b a r 控制图
5 4 3 2 样本均值 1 0 -1 -2
5 1
UCL=4.395
_ _ X =0.544
-3 -4 1 3 5 7 9 11 13 样本 15 17
1
LCL=-3.307 19 21 23 25
2011-1-3
中国人民大学六西格玛质量管理研究中心
• 能发现异常原因,便于解决问题
不仅用于控制,也是过程改进的基础
2011-1-3
中国人民大学六西格玛质量管理研究中心
5
2.3 预 防 原 则 的 实 施
2011-1-3
中国人民大学六西格玛质量管理研究中心
6
2011-1-3
中国人民大学六西格玛质量管理研究中心
7
2.4 如 何 选 择 控 制 变 量
本 章 目 标
• 了解SPC概念 • 树立过程控制的预防观念 • 明确使用控制图的重要意义 • 学会正确绘制控制图
2011-1-3
中国人民大学六西格玛质量管理研究中心
2
2.1 SPC 的 发 展(1)
• 21世纪是质量的世纪 • 贯彻预防原则是现代质量管 理的核心 • 用科学的措施与方法保证预 防原则的实现 • 降低质量成本
2011-1-3
中国人民大学六西格玛质量管理研究中心
20
利用上面的控制图做控制, 录入原先的22组数据之后 利用上面的控制图做控制,将2,5,3,-2,1录入原先的 组数据之后 , , , , 录入原先的
2011-1-3
中国人民大学六西格玛质量管理研究中心
21
2011-1-3
中国人民大学六西格玛质量管理研究中心
16
2011-1-3
中国人民大学六西格玛质量管理人民大学六西格玛质量管理研究中心
18
用打铃数据T=30(每次与标准时间相差不超过 秒) 每次与标准时间相差不超过15秒 用打铃数据 每次与标准时间相差不超过 每天抽查5次 连续记录 连续记录25天 每天抽查 次,连续记录 天
22
2011-1-3
中国人民大学六西格玛质量管理研究中心
23
x 1 , . . . , x 5 的 X b a r 控制图
5 4 3 2 样本均值 1 0 -1 -2 -3 -4 1 3 5 7 9 11 13 样本 15 17 19 21 23 LCL=-3.254 _ _ X =0.691 UCL=4.636
控制限和公差限相同,容易理解和运用; 用不同的颜色表示不同的过程状态, 直观、活泼 适用于小批量生产,灵活有效
2011-1-3
中国人民大学六西格玛质量管理研究中心
27
2.9 预 先 控 制 图 (2)
TU PU M PL TL
异常区 警戒区 安全区 安全区 警戒区 异常区
中国人民大学六西格玛质量管理研究中心
UCL
A B C
x
CL
CL
C
C
x
B LCL A
x
B LCL A
2011-1-3
中国人民大学六西格玛质量管理研究中心
11
2.6 诊 断 准 则 (2)
准则5: 3个点中有2点在A区中连成一串
UCL
A B C
准则6: 5点中有4点在B区中连成一串
UCL
A B C
x
x
CL
x
CL
C
C
B LCL A
x
B LCL A
关键的少数原则
控制输入变量为主原则
选择容易测定的变量原则
2011-1-3
中国人民大学六西格玛质量管理研究中心
8
2.5 控 制 图 原 理 与 结 构(1)
• 假定质量特性值服从正态分布
控制图是根据正态分布的“3σ”原理绘制
•用统计技术判定过程是否发生异常变异 用统计技术判定过程是否发生异常变异
2011-1-3
28
2011-1-3
2.9 预 先 控 制 图 (3)
日期 零件号 红色区
16.60
8月1日 1 2 3 4 5
8月2日
黄色区
16.55
绿色区
16.50 16.45 16.40
16.52
16.50 16.49 16.48
16.55
绿色区 黄色区 红色区
2011-1-3
中国人民大学六西格玛质量管理研究中心
7 7 7
UCL=4.636
_ _ X =0.691
-1 -2 -3 -4 1 5 9 13 17 21 样本 25 29 33 37 41 LCL=-3.254
2011-1-3
中国人民大学六西格玛质量管理研究中心
26
2.9 预 先 控 制 图 (1)
• 预先控制图的优点:
不需要事先抽取样本计算控制限
过程受控 (判稳) 过程失控 (判异)
2011-1-3
实际过程稳定 实际过程异常 控制图使用正确, 漏发警报 , 继续保持控制 与控制图灵敏度有关 误发警报 , 控制图使用正确, 出现的可能性很小 及时寻找质量原因
中国人民大学六西格玛质量管理研究中心
13
2.7 过 程 受 控 与 过 程 稳 定(2)
控制图有哪些作用和特点? 如何选择控制变量? 控制图由哪些要素构成? 控制图诊断准则有几条,分别是什么? 绘制好的控制图是否可以直接用于实际控制?
2011-1-3
中国人民大学六西格玛质量管理研究中心
31
收集数据 绘 制 分 析 否 用 是否 是 图 否 段 阶 是 否 是 是 是否 否 否
2011-1-3
控 制
是否
是
14
2.8 用Minitab软件制作控制图(1) 软件制作控制图( ) 软件制作控制图
2011-1-3
中国人民大学六西格玛质量管理研究中心
15
2011-1-3
中国人民大学六西格玛质量管理研究中心
第2章 SPC与控制图
2.1 SPC的发展 2.2 控制图的作用和特点 2.3 预防原则的实施 2.4 选择控制变量 2.5 控制图的原理和结构 2.6 诊断准则 2.7 过程受控与过程稳定 2.8 用Minitab软件制作控制图 小组讨论与练习
2011-1-3
中国人民大学六西格玛质量管理研究中心
1
x
准则7:在C区中15个点于中心上下侧 连成一串
UCL
A B C
准则8:8个点在中心线两侧排成一串, 但无一在C区中
UCL
A B C
CL
C
x
x
CL
C
B LCL A
B LCL A
2011-1-3
中国人民大学六西格玛质量管理研究中心
12
2.7 过 程 受 控 与 过 程 稳 定(1)
• • • • 过程受控:控制图没有判异 过程失控:控制图判异 过程稳定:没有异常因素出现 过程异常:出现了异常因素
2011-1-3
J.M.Juran
中国人民大学六西格玛质量管理研究中心
3
2.1 SPC 的 发 展(2)
• 质量控制的发展阶段
统计质量 传统管理 管理阶段 阶段 阶段, 阶段 阶段, (QC阶段, (SQC阶段, 阶段 Statistical Quality Quality Control) ) Control) )
中国人民大学六西格玛质量管理研究中心
9
2.5 控 制 图 原 理 与 结 构(2)
• 以样本统计量均值为控制中心线 • 以中心线±3σ为控制图的上下控制限 • 以抽样的时间顺序为控制图横轴坐标 • 以质量特性值单位为控制图纵轴坐标
样本 单位
3σ 3σ
UCL CL LCL
控制图结构
2011-1-3
样本
10
中国人民大学六西格玛质量管理研究中心
2.6 诊 断 准 则 (1)
准则1: 一个点在A区之外(判 异唯一准则) x
UCL
A B C
准则2:连续9个点在C区同一侧
UCL
A B C
x
CL
C
CL
C
B LCL A
B LCL A
x 准则3:6个点递增或递减排成一串
UCL
A B C
准则4:14个点排成一串,上下交替
19
去掉第6、第19、 第17个异常组 后的控制图
x 1 , . . . , x 5 的 X b a r 控制图
5 4 3 2 样本均值 1 0 -1 -2 -3 -4 1 3 5 7 9 11 13 样本 15 17 19 21 LCL=-3.254 _ _ X =0.691 UCL=4.636
29
2.9 预先控制图(4)
• 预控图误发警报的概率与过程能力有关 • 过程能力高误发警报概率就偏小 • 非正态质量特性误发警报的概率增大 • 过程存在偏移时误发警报的概率增大 • 过程能力高时应该减小控制限和警戒限
2011-1-3
中国人民大学六西格玛质量管理研究中心
30
小组讨论与练习
• 思考题:
1900 1930
迈向 全面质量 六西格玛 管理阶段 (TQM阶段, 质量管理 阶段, 阶段 Total 阶段 Quality Management)
