二次回归正交组合设计及其统计分析
元二次回归正交组合设计(上)

结合专业领域知识,将元二次回归正交 组合设计应用于实际问题中,不断积累 实践经验和提升解决问题的能力。
深入了解试验设计原理和方法,如析因 设计、裂区设计、重复测量设计等,以 提高试验设计的效率和准确性。
感谢观看
THANKS
试验方案设计与优化
设计试验方案
根据正交表和因子水平,设计试验方案,包括试验条件、试验步骤和试验数据处理方法等 。
优化试验方案
通过比较不同试验方案的优劣,选择最优方案进行实施。同时,可以根据实际情况对试验 方案进行调整和优化,以提高试验效率和准确性。
注意事项
在进行正交组合设计时,需要注意选择合适的正交表、确定因子水平和编码方式、设计合 理的试验方案,并进行充分的试验前准备和数据处理工作,以确保试验结果的准确性和可 靠性。
率。
预测性
能够建立数学模型,对未知区 域进行预测,为优化提供方向
。
灵活性
可以处理多个因素,每个因素 可以取多个水平,适用于复杂
系统。
直观性
通过图形展示,可以直观地看 出各因素对响应的影响趋势。
缺点分析
模型假设
处理非线性关系的能力有限
元二次回归模型假设响应与因素之间的关 系是二次的,如果实际关系偏离这一假设 ,模型预测可能不准确。
对于高度非线性的系统,元二次回归模型 可能无法提供准确的预测。
对异常值敏感
计算复杂性
如果数据中存在异常值,可能会对模型的 拟合和预测产生较大影响。
对于大量数据和复杂模型,计算可能会变 得复杂和耗时。
适用范围及注意事项
适用范围:适用于需要通过试验来优化响应,且因素水 平不太多、试验成本较高的场合。特别适用于那些对模 型精度要求不高,但需要快速得到优化方向的场合。 1. 在使用元二次回归正交组合设计时,应确保试验数据 满足模型的假设条件。
二次回归正交旋转组合设计优化21~42日龄肉仔鸡胆碱和蛋氨酸需要量

汤建平
( 中国农 业科学院饲 料研究所 , 家禽 营养与饲料 研究室, 北京 10008 1)
要: 本试验以低胆碱 � 低蛋氨酸饲粮为基础饲粮, 通过两因子二次回归正交旋转组合设计, 对 21 42 日龄肉仔鸡胆碱和蛋氨酸需要量进行研究� 试验选用 21 日龄爱拔益加( A A ) 肉仔鸡 摘 48 0 只 , 9 12 组为 中心组 , 随机分为 12 个组 , 其中 1 8 组为试验组 , 每组 4 个重复 , 每个重复 10 只鸡, 公母各占 1/ 2� 分别以胆碱和蛋 氨酸为自变量, 以反映 肉仔鸡生长性能 和屠宰性能的 各项指标为因变量 拟合回 归方 程, 估计 21 42 日 龄肉 仔鸡 胆碱和 蛋氨 酸的 需要 量� 试验期 21 d� 结果表明 : 胆碱和蛋氨酸水平对 21 42 日龄肉仔鸡的平均日采食量 � 料重比 � 腹脂率和肝 kg 时 , 脂率有显著影响( P < 0.05) � 当胆碱水平在 8 60 1 120 m g / 肉仔鸡平均日采食量随着蛋 氨酸水平的增加而升高, 蛋氨酸水平增至 0.40% 后, 继续增 加对平均日采食量的改善作用不明 0.42% , kg 时 , 显 ; 蛋氨酸水平在 0.35% 胆碱水平在 8 6 0 1 120 m g / 肉仔鸡的料重比达到最 0.47 % 时 , 低值 ; 蛋氨酸水平在 0.30% 随着胆碱水平的增加肉仔鸡腹脂率呈下降趋势 ; 当蛋氨 酸水平在0.30% 0.40% , 胆碱水平在 1 000 1 400 m g / kg 时, 肉仔鸡肝脂率随着胆碱水平的 增加和蛋氨酸水平的降低呈下降趋势 � � 在本试验条件下, 当 胆碱水平为 99 0 1 030 m g / kg , 蛋 0.40% � 0. 43% , ; 1 7 8 0 氨酸 水 平 为 时 肉 仔 鸡 可 达到 最 佳 生 长性 能 当胆 碱 水 平 为 1 8 8 0 mg / kg , 蛋氨酸水平为 0.37 % 中图分类号 : S8 31 0.38 % 时 , 肉仔鸡可达到最佳屠宰性能 � 关键词: 胆碱 ; 蛋氨酸 ; 肉仔鸡; 二次回归正交旋转组合设计 ; 响应面 文献标识码 : A 文章编号 : 1006 267 X ( 2012) 06 1019 11 数都是围绕胆碱与其他营养物质的 相互关系进行 的
二次回归正交试验
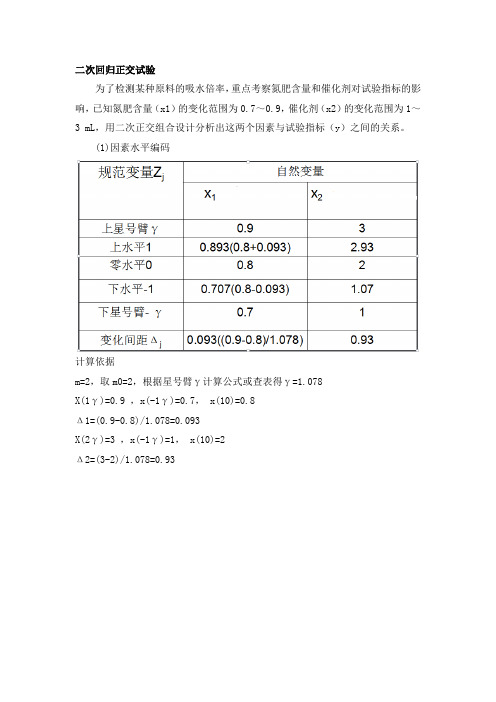
二次回归正交试验为了检测某种原料的吸水倍率,重点考察氮肥含量和催化剂对试验指标的影响,已知氮肥含量(x1)的变化范围为0.7~0.9,催化剂(x2)的变化范围为1~3 mL,用二次正交组合设计分析出这两个因素与试验指标(y)之间的关系。
(1)因素水平编码计算依据m=2,取m0=2,根据星号臂γ计算公式或查表得γ=1.078X(1γ)=0.9 ,x(-1γ)=0.7, x(10)=0.8Δ1=(0.9-0.8)/1.078=0.093X(2γ)=3 ,x(-1γ)=1, x(10)=2Δ2=(3-2)/1.078=0.93(2)试验方案(3)回归方程的建立借助excel分析如下:①回归方程显著性检验:F=186.5564,,,12.4)74(95.0=F因此回归方程非常显著。
'74.41'37.2375.656.2609.952.468y 212121z z z z z z ----+= ②偏回归系数的显著性检验9.496.113305.113806.113308.47058.14583.1822.44615.5528.4705701.274.41)(8.1458701.224.23)(3.182475.6)(2.4461324.656.265.552324.609.95.113801046852206303)(12211122122122222222112111122121212122212222221121122121=-=-==++++=++++==⨯===⨯===⨯===⨯===⨯===-=-=∑∑∑∑∑∑∑=======R T e R ni in i i ni ni i n i in i i n i iT SS SS SS SS SS SS SS SS SS z b SS zb SS z z b SS z b SS z b SS y n y SS 方差分析:dfT=n-1=10-1=9 df1=df2=df12=df1’=df2’=1dfR=df1+df2+df12+df1’+df2’=1+1+1+1+1=5dfe=dfT-dfR=9-5=4MS1=522.5/1=522.5 MS2=SS2/df2=4461.2/1=4461.2 MS12=SS12/df12=182.3MS1’=SS1’/df1’=1458.8MS2’=SS2’/df1’=4705.8MSR=SSR/dfR=11330.6/5=2266.1MSe=SSe/dfe=49.9/4=12.5F1=MS1/MSe=522.5/12.5=41.8F2=MS2/MSe=4461.2/12.5=356.9F12=MS12/MSe=182.3/12.5=14.6F1’=MS1’/MSe=1458.8/12.5=116.7F2’=MS2’/MSe=4705.8/12.5=376.5FR=MSR/MSe=2266.1/12.5=181.3F0.01(1,4)=21.20 F0.05(1,4)=7.71 F0.01(5,4)=15.52 F0.05(5,4)=6.26失拟性检验本例零水平试验次数m0=2,可进行失拟性检验5.45.521220521225)509512(21)259081262144()(12201020101=-=+-+=-=∑∑==m i i m i ie y m y SSSSLf=SSe-SSe1=49.9-4.5=45.4 dfe1=m0-1=2-1=1 dfLf=dfe-dfe1=4-1=359.53)1,3(37.31/5.43/5.45/1/1,01====F df SSe df SS FLf e LfLf检验结果表明,失拟不显著,回归模型与实际情况拟合很好。
二次回归正交大概原理

二次回归正交大概原理
二次回归正交法是一种多元统计分析方法,用于处理多个自变量之间可能存在共线性的情况。
该方法通过对原始自变量进行正交变换,将其转化为一组相互正交的新自变量,从而消除了自变量之间的相关性。
具体实现过程如下:
1. 确定需要进行正交变换的自变量集合。
2. 对每一个自变量进行中心化处理,即将每个自变量减去其均值,使得每个自变量的均值为0。
3. 计算出每两个自变量之间的相关系数矩阵。
4. 利用相关系数矩阵进行特征值分解,得到特征值和特征向量。
5. 将特征值按大小排序,选择前r个较大的特征值所对应的特征向量,构成一个r维的正交基。
6. 将原始自变量与选取的特征向量相乘,得到正交后的自变量。
通过正交变换,可以将原始自变量转化为一组相互正交的新自变量,
消除了它们之间的相关性。
这样可以提高模型的稳定性和可解释性,并降低共线性带来的影响。
需要注意的是,正交变换并不改变因变量与自变量之间的关系,只是对自变量进行了重新编码。
因此,在建立回归模型时,可以使用正交后的自变量进行分析,而不会受到原始自变量之间相关性的干扰。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明
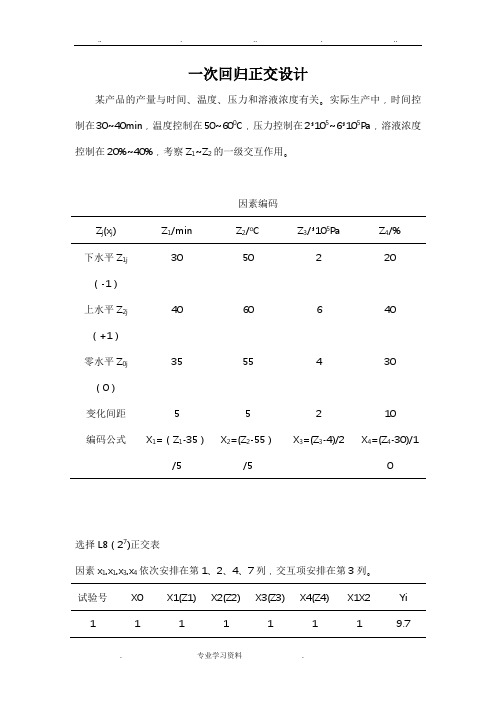
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中,时间控制在30~40min,温度控制在50~600C,压力控制在2*105~6*105Pa,溶液浓度控制在20%~40%,考察Z1~Z2的一级交互作用。
因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j(-1)30 50 2 20上水平Z2j(+1)40 60 6 40零水平Z0j(0)35 55 4 30变化间距 5 5 2 10编码公式X1=(Z1-35)/5 X2=(Z2-55)/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8(27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列,交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验:1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉,不必再重新进行回归分析。
4、高级实验设计—回归的旋转设计(Regressional Rotary Design)

x
i,j =1,2„P;
待定参数
以上为 P 元二次回归旋转设计的旋转性条件。
此外,为了使旋转设计成为可能,还必须使信
息矩阵 A 不退化,为此,必须有不等式:
4 p 2 2 P 2
上式为 P 元二次回归的非退化条件。 已证明,只要使 N 个试验点不在同一个球面上, 就能满足非退化条件。或者说只要使 N 个试验点至少 分布于两个半径不等的球面上,就有可能获得旋转设
P 2 2 ˆ D y P 2 4 PN
4 1 2 P 1 4 P 1 4 1 2 2 4 P 2 4 4
(4.11) 由式(4.11)经研究表明,只有采用恰当的方法 确定 4 ,才能满足通用性的要求。如何确定 4 ?对 4 有什么要求呢?总的来说,它必须使上式中 i处的
ˆ 的 二次旋转组合设计具有同一球面预测值 y
方差相等的优点,但回归统计数的计算较繁琐,
若使它获得正交性就能简化计算手续。
在二次旋转组合计划中,一次项和交互项的 回归系数 bj ,bij 仍保持正交,但 b0 与 bjj 之间,
以及 bii 与 bjj 之间都存在相关,即不具正交性,
它们之间的相关矩分别为:
计方案。
为了获得 P 元二次旋转设计方案,就要求既要
满足非退化条件式,又要满足旋转性条件式。
如何才能满足这两方面的条件呢?这主要借助
于组合设计来实现,因为组合设计中 N 个试验点:
N mc m m0
分布在三个半径不相等的球面上:
mc 个点分布在半径为 P 的球面上; c m 个点分布在半径为 的球面上; m0 个点分布在半径为 0 0 的球面上;
二次正交回归试验设计

二次正交回归试验设计二次正交回归试验设计,这个名字听起来挺复杂对吧?感觉像是数学课上的一堆公式堆积在一起,听得人一头雾水。
别急,咱们慢慢聊,搞清楚这玩意儿到底是个啥。
简单来说,二次正交回归试验设计就是一种聪明的实验方法,用来找出那些对结果有最大影响的因素。
你想呀,咱们做实验不就是想知道:到底什么东西能帮我们搞出最好的结果?这就像你做饭,想知道是盐多点好,还是油多点好。
然后,你一开始根本不知道哪个因素最重要,所以你就得试试看,试了几次后,你就能总结出哪几个东西一变,结果就差得远,哪几个因素是关键。
好啦,接下来咱们说说正交回归的“正交”俩字。
它其实很简单,就是把几个因素按特定的组合方式安排,让实验的结果能最有效地帮助你找出最佳的操作方式。
就像打麻将,四个玩家各有不同的牌,正交设计就像把这些牌按特定规则摆开,保证每个人的牌都有机会碰到关键的“胡牌点”,从而找到最合适的做法。
你可能会问:为什么不直接搞个试验,把所有可能的组合都做一遍?那样不就得了嘛!但问题来了,如果你尝试所有的组合,得花多少钱啊!时间也得浪费,精力也得花费。
比如,你要搞个烤面包的实验,试试不同的温度、时间、酵母量,这得试多少次?估计都能烤出一整车的面包来。
正交回归的聪明之处就在于它帮你减少了不必要的试验次数,给你最有效的提示,告诉你哪个因素最关键,哪个因素影响不大,直接省事儿。
那具体咋做呢?我们先选几个可能的影响因素,然后通过一定的设计方式安排它们的组合。
比如说,你在研究做面包时,可能考虑的因素就有面粉的种类、发酵的时间、温度和湿度等等。
然后你就按照正交设计的规律,安排这些因素的组合,反复试几次,你就能得出一个最佳方案,不至于迷失在海量的数据中。
说到这里,大家是不是觉得挺神奇的?对!正交回归就是这么有趣,简洁高效地帮你减少试验次数,节省时间、金钱和脑细胞。
不过,有人可能会说了:“这不就是实验吗?试试、改改,然后结果出来了呗。
”但它更像是一个聪明的助手,总能在你试探的过程中,给你一些深刻的见解。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明

一次回归正交设计、二次回归正交设计、二次回归旋转设计说
明
一次回归正交设计是一种广泛应用于实验设计中的设计方式,该设计最基本的特点是每一个自变量只考虑一次。
这种设计方法可以通过排列组合的方式得到各种不同的设计方案,使得实验者可以通过设计来达到用最少的实验次数获取尽可能多的信息的目的。
一次回归正交设计在实验设计中被广泛使用,尤其在化学制药、工业生产等领域得到了广泛运用。
二次回归正交设计是一种基于一次回归正交设计的设计方式,这种设计方式可以进一步增加实验信息的获取。
在二次回归正交设计中,依然按照一次正交设计的方式来设计实验,但是在每个单独的自变量上,提高对其的测量次数,使得对这些自变量的测量更加准确。
同时,在某些需要深入探究的因素上,可以通过将这些因素的实验次数进一步提高,来获取相关信息。
二次回归旋转设计是一种在二次回归正交设计的基础上发展而来的设计方式。
在二次回归旋转设计中,实验者可以通过旋转矩阵来达到实验变量间的协方差为0的目的。
这样可以在保证基本信息获取的同时,增加获取高阶信息的可能性。
旋转设计特别适合于需要同时考虑多个变量的实验设计,可以使各个变量之间更加独立,减少不必要的干扰。
总的来说,在实验设计领域中,三种设计方法各自有着各自的优势。
对于需要更精准的信息获取的实验,应该选择更高阶的设计方法,在更基础的实验中则可以选择更为简单的设计方法。
另外,在选择设计方法的过程中,还应该根据实验具体情况灵活选择,使得实验设计更加科学合理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次回归正交组合设计及其统计分析
一、组合设计
(一)组合设计的概念
组合设计:在自变量(因素,也称因子)空间中选择几种类型的点,组合成的试验计划。
(P.31)由于组合设计可选择多种类型的点,而且有些类型的点的数目(试验处理数)又可适当调节,因此组合设计在调节试验处理数N(从而在调节剩余自由度)方面,要比全面试验灵活得多。
(二)组合设计的组成
二次回归正交组合设计试验方案由三种类型的点组成,即:
式中:N为处理组合数;为二水平析因点,(p为因素个数);为轴点,;为中心区(或原点)。
①二水平析因点():这些点的每一个坐标(自变量)都各自分别只取1或-1;这些试验点的数目记为。
当这些点组成二水平全面试验时,。
而若这些点是根据正交表配制的二水平部分实施(1/2或1/4等)的试验点时,。
调节了这个,就相应地调节了剩余自由度。
②轴点():这些点都在坐标轴上,且与坐标原点(中心点)的距离都为。
也就是说,这些点只有一个坐标(自变量)取或,而其余坐标都取零。
这些点在坐标图上通常用星号标出,故又称星号点。
其中称为轴臂或星号臂,是待定参数,可根据下述正交性或旋转性要求而确定。
这些点的数目显然为2P,记为。
③原点():又称中心点,即各自变量都取零水平的点,该试验点可作1次,也可重复多次,其次数记为。
调节,显然也能相应地调节剩余自由度。
(三)试验点(处理)的分布情况
1、P=2(二因素)的分布情况
(1)处理组合数:若=1,处理组合数为9,即
(2)处理组合表2.2.1。
(P.32)
(3)处理组合分布图2.2.1。
(P.31)
二因素(X1、X2)二次回归组合设计的结构矩阵如表2.2.2。
(P.32)
2、P=3(三因素)的分布情况
(1)处理组合数:若=1,处理组合数为15,即
(2)处理组合表:P=3(X1、X2、X3)二次回归正交组合设计,由15个试验点组成。
如表2.2.3所示。
(P.33)
(3)处理组合分布图2.2.2。
(P.32)
三因素(X1、X2、X3)二次回归组合设计的结构矩阵如表2.2.4。
(P.33)
(四)组合设计的优点
1、试验处理数少。
2、保持一定剩余自由度,以便进行显著性检验。
(五)组合设计正交性的实现
1、组合设计的正交性:部分保持正交,部分失去正交。
保持正交部分:
失去正交部分:平方项
2、正交的实现
(1)选取适当的轴臂:可用下式计算:
为了设计方便,将由上式计算出不同P及的值列于表2.2.5。
(P.34-35)
(2)对平方项进行中心化变换:为了获得正交性,将平方项进行中心化变换,中心化变换值以表示:
这样变换后的项之间正交和之间正交:
例:
①P=2,=1,查值表2.2.5,得=1,,则中心化变换为:
的中心化变换为:
的中心化变换为:
于是得中心化变换后的二元二次回归正交组合设计的结构矩阵列于表2.2.6。
(P.35)
②P=3,=1,查值表2.2.5,得=1.215,,则中心化变换为:
类似地可得出三元二次回归正交组合设计的结构矩阵列于表2.2.7。
(P.35-36)
三、二次回归正交组合设计示例
[例2.2] 某玉米氮肥、磷肥、钾肥配比试验,试进行二次回归正交组合设计,并对试验结果进行统计分析。
(P.38)
(一)设计试验处理方案
1、拟定每个因素的上下水平
以该因素零水平施肥量为最佳施肥量为依据来确定上下水平。
上水平:高于最佳施肥量,比零水平高1/3~1/2左右。
下水平:低于零水平,可采用较少的施肥量或不施肥。
本例氮、磷、钾肥上下水平列于表2.2.9。
(P.38)
2、计算零水平:
3、计算变化间距
把上水平和零水平之差以参数除之称为因素的变化间距,以表示。
定义式为:
式中:值是为了使试验计划获得正交性的一个待定参数。
其值可从表2.2.5。
(P.34)查出。
本例:P=3,=1,则=1.215,则计算为:
4、对每个因素各水平取值进行编码变换
所谓编码就是对因素水平的取值作如下的线性变换:
这样,就建立了各因素与取值的一一对应关系,得到如表2.2.8的因素水平编码表(P.36):
本例每个因素为5个水平,即+ ,+1,0,-1,- ,氮肥各水平编码值相应施肥量计算为:N:
P2O5:
K2O:
将算出的氮、磷、钾各水平编码值相应的施肥量列于表2.2.10。
(P.39)
5、拟定试验处理方案
根据本例(三元二次回归正交组合设计)的要求,选用表2.2.7(P.35),将自变量各编
码值相应肥料施用量填入表2.2.7的X1、X2、X3编码值中,即设计成试验处理组合方案列于表2.2.11。
(P.39)
(二)试验结果的统计分析
试验结果列于表2.2.12。
(P.39-40)
1、建立三元二次多项式回归方程
如果研究P个因素,采用二次回归正交组合设计具有N个处理,其试验结果以表示,则二次回归的数学模型为:
为了消除平方项与常数项间的相关性,对平方项进行中心化变换,则数学模型变为:
用样本估计时:
当P=3时,三元二次回归方程为:
要建立二次回归方程,必须计算出回归统计数。
由于二次回归的正交组合设计的结构矩阵具有正交性,因而它的信息矩阵A为:
于是二次回归方程的回归统计数,则
本例:
(1)列表计算回归统计数:根据试验结果列表计算各回归统计数于表2.2.12。
(P.39-40)
计算表的计算方法为:
①计算:
②计算:
③计算:
④计算:
(2)建立三元二次多项式回归方程:
表中由下式计算:
于是玉米氮、磷、钾肥试验三元二次多项式回归方和为:(P.40)
2、回归关系的显著性检验(F检验)
(1)第一次F检验
①计算平方和
②计算自由度
③列出F检验表2.1.13。
(P.40)
④推断:经F检验显示,总回归达0.25显著,说明氮肥、磷肥、钾肥与玉米产量之间存在基本显著的回归关系。
其中一次项X1达显著,X2达0.25显著,互作项X1X3、X2X3以及平方项X3²均不显著(F值均小于1)。
由于试验计划具有正交性,消除了回归系数之间的相关性,故可以直接把它们从回归方程中除去,将平方和及自由度并入剩余项,而互作项X1X2和平方项X1²、X2²的F值大于1,接近0.25显著,故可保留在回归方程中,进行第二次方差分析。
(2)第二次F检验
①计算平方和
②计算自由度
③列出F检验表2.1.14。
(P.41)
④推断:第二次F检验显示,总回归达显著,说明X1(氮)、X2(磷)与玉米产量之间存在显著的回归关系。
其中一次项X1达极显著,X2达显著,互作项X1X2以及平方项X1²、X2²达0.25显著。
说明该试验结果宜用二元二次多项式表达。
3、配置二元二次多项式回归方程
(1)计算
(2)建立二元二次多项式回归方程
三、多项式回归方程的应用
(一)计算最佳施肥量及产量预报
1、计算最佳施肥量
(1)求y对Xi的一阶偏导数:对二元二次多项式回归方程
求y对Xi的一阶偏导数。
①求y对的一阶偏导数:
②求y对的一阶偏导数:
(2)求常数项:最佳施肥方案是边际产值等于边际成本时的施肥量,它受边际产值、产品价格、肥料价格的制约。
因此,有以下关系式:
式(2.2.13)中,和是氮、磷的边际产值,为氮(N)和磷(P2O5)的价格,均为 3.00元/kg,为产品玉米的价格,为0.80元/kg,于是可建立如下方程组:
(3)建立联立方程组:经整理得如下联立方程组:
解此方程组得:,将这些水平编码值换算成施肥量:
相当于尿素,相当于过磷酸钙。
在这一施肥量下可获得玉米产量。
2、确定最高产量施肥方案
同样对所建立的回归方程求y对Xi的一阶偏导数,当最高产量时,于是可建立如下方程组:
解此方程组得:,将这些水平编码值换算成施肥量:
相当于尿素,相当于过磷酸钙。
在这一施肥量下可获得玉米产量。
