电力系统暂态分析(第四章习题答案)
暂态分析部分习题答案
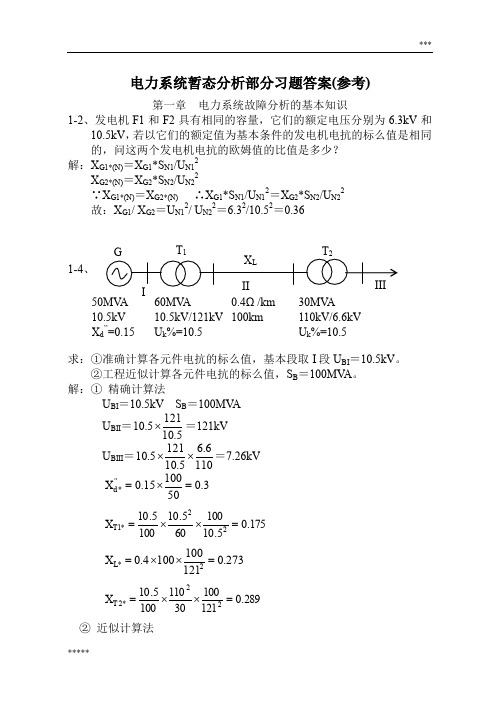
电力系统暂态分析部分习题答案(参考)第一章 电力系统故障分析的基本知识1-2、发电机F1和F2具有相同的容量,它们的额定电压分别为6.3kV 和10.5kV ,若以它们的额定值为基本条件的发电机电抗的标么值是相同的,问这两个发电机电抗的欧姆值的比值是多少? 解:X G1*(N)=X G1*S N1/U N12 X G2*(N)=X G2*S N2/U N22∵X G1*(N)=X G2*(N) ∴X G1*S N1/U N12=X G2*S N2/U N22 故:X G1/ X G2=U N12/ U N22=6.32/10.52=0.361-4、求:①准确计算各元件电抗的标么值,基本段取I 段U BI =10.5kV 。
②工程近似计算各元件电抗的标么值,S B =100MV A 。
解:① 精确计算法U BI =10.5kV S B =100MV AU BII =5.101215.10⨯=121kVU BIII =1106.65.101215.10⨯⨯=7.26kV 3.05010015.0''*=⨯=d X 175.05.10100605.101005.1022*1=⨯⨯=T X 273.01211001004.02*=⨯⨯=L X 289.0121100301101005.1022*2=⨯⨯=T X ② 近似计算法50MV A 10.5kV X d ’’=0.15 60MV A 10.5kV/121kV U k %=10.5 0.4Ω/km 100km 30MV A 110kV/6.6kV U k %=10.5U B =U av S B =100MV A3.05010015.0''*=⨯=d X 175.0601001005.10*1=⨯=T X302.01151001004.02*=⨯⨯=L X 35.0301001005.10*2=⨯=T X1-5、某一线路上安装一台Xk%=5的电抗器,其额定电流为150A ,额定电压为6kV ,若另一台额定电流为300A 、额定电压为10kV 的电抗器来代替它,并要求保持线路的电抗欧姆值不变,问这台电抗器的电抗百分数值应是多少? 解:∵2221113100%3100%N N R N N R R I UX I U X X ⨯=⨯=∴61503001065%%122112=⨯⨯=⨯⨯=N N N N R R I I U U X X1-12、(1) 若短路前空载,计算短路电流的周期分量及短路电流最大有效值; (2) 若A 相非周期分量电流的初值为零及最大时,计算相应的B 、C 相非周期分量电流的初始值;(3) 若短路前变压器满负荷运行,功率因数为0.9(低压侧),计算最大非周期分量电流的初始值,并与空载时短路比较。
电力系统暂态分析(第二、四章习题答案)资料

第2章作业参考答案2-1 为何要对同步发电机的基本电压方程组及磁链方程组进行派克变换?答:由于同步发电机的定子、转子之间存在相对运动,定转子各个绕组的磁路会发生周期性的变化,故其电感系数(自感和互感)或为1倍或为2倍转子角θ的周期函数(θ本身是时间的三角周期函数),故磁链电压方程是一组变系数的微分方程,求解非常困难。
因此,通过对同步发电机基本的电压及磁链方程组进行派克变换,可把变系数微分方程变换为常系数微分方程。
2-2 无阻尼绕组同步发电机突然三相短路时,定子和转子电流中出现了哪些分量?其中哪些部分是衰减的?各按什么时间常数衰减?试用磁链守恒原理说明它们是如何产生的?答:无阻尼绕组同步发电机突然三相短路时,定子电流中出现的分量包含:a)基频交流分量(含强制分量和自由分量),基频自由分量的衰减时间常数为T d’。
b)直流分量(自由分量),其衰减时间常数为T a。
c)倍频交流分量(若d、q磁阻相等,无此量),其衰减时间常数为T a。
转子电流中出现的分量包含:a)直流分量(含强制分量和自由分量),自由分量的衰减时间常数为T d’。
b)基频分量(自由分量),其衰减时间常数为T a。
产生原因简要说明:1)三相短路瞬间,由于定子回路阻抗减小,定子电流突然增大,电枢反应使得转子f绕组中磁链突然增大,f绕组为保持磁链守恒,将增加一个自由直流分量,并在定子回路中感应基频交流,最后定子基频分量与转子直流分量达到相对平衡(其中的自由分量要衰减为0).2)同样,定子绕组为保持磁链守恒,将产生一脉动直流分量(脉动是由于d、q不对称),该脉动直流可分解为恒定直流以及倍频交流,并在转子中感应出基频交流分量。
这些量均为自由分量,最后衰减为0。
2-3 有阻尼绕组同步发电机突然三相短路时,定子和转子电流中出现了哪些分量?其中哪些部分是衰减的?各按什么时间常数衰减?答:有阻尼绕组同步发电机突然三相短路时,定子电流和转子电流中出现的分量与无阻尼绕组的情况相同。
电力系统暂态分析第四章作业参考答案

第四章 作业参考答案1、电力系统发生短路故障时,系统中出现零序电流的条件是什么? 答:因为)(31)0(c b a I I I I ++=,所以电力系统发生短路故障时,系统中出现零序电流的条件有两个:一是短路发生在中性点直接接地系统;二是短路类型为不对接地短路故障。
2、具有架空地线(避雷线)的输电线路,架空地线的导电性能与输电线路正序电抗(负序电抗)和零序电抗之间的关系如何?为什么?答:输电线路正序电抗(负序电抗)与架空地线的导电性能无关;零序电抗架空地线的导电性能有关,架空地线的导电性能越强,其零序阻抗越小。
因为输电线路流过正序电流(或负序电流)时,架空地线中无电流流过,对每相导线的磁链没有影响,也就是说对输电线路通过正序电流(负序电流)时的电感系数(电抗)没有影响;而在输电线路流过零序电流时,架空地线中流过的电流为三相总电流在架空地线与大地等效导线之间的分流,架空地线中的电流与输电线路中的电流方向相反,对输电线路起去磁作用,因此具有架空电线的输电线路其零序阻抗比无架空地线时要小,架空地线导电性能越强,与大地等效导线分流时分得的电流越大,去磁作用越强,输电线路的零序电抗越小。
3、架空输电线路正序电抗、负序电抗、零序电抗三者之间的关系是什么?为什么? 答:架空输电线路正序电抗、负序电抗、零序电抗三者之间的关系是 )0()2()1(x x x <=; 因为架空输电线路任何一相的磁链都是由本相电流产生的自感磁链和其它两相电流产生的互感磁链组成,正序和负序情况下,其它两相所产生的互感磁链对自感磁链起去磁作用,零序情况下互感磁链对自感磁链起助磁作用,所以输电线路的正序电抗与负序电抗相等,而小于零序电抗。
4、为什么电动机的零序阻抗总可以视为无限大?答:因为电力元件的某序阻抗等于在该元件端点施加的该序电压和由它产生的流过元件端点的该序电流的比值。
电动机三相绕组采用三角形接线和中性点不接地的星形接线方式,当在其端点施加零序电压时,在端口产生的零序电流为零,根据序阻抗的定义其零序阻抗为无限大。
电力系统暂态分析电力系统(第三版)习题解答

电力系统暂态分析(第三版) 李光琦 习题解答第一章 电力系统分析基础知识1-2-1 对例1-2,取kV 1102=B U ,MVA S B 30=,用准确和近似计算法计算参数标幺值。
解:①准确计算法:选取第二段为基本段,取kV 1102=B U ,MVA S B 30=,则其余两段的电压基准值分别为:9.5kV kV 1101215.10211=⨯==B B U k U kV 6.66.6110110223===k U U B B 电流基准值:kA U S I B B B 8.15.9330311=⨯==kA U S I B B B 16.0110330322=⨯==各元件的电抗标幺值分别为:发电机:32.05.930305.1026.0221=⨯⨯=*x 变压器1T :222121300.1050.12111031.5x *=⨯⨯= 输电线路:079.011030804.023=⨯⨯=*x 变压器2T :21.01103015110105.02224=⨯⨯=*x 电抗器:4.03.062.26.6605.05=⨯⨯=*x 电缆线路:14.06.6305.208.026=⨯⨯=*x 电源电动势标幺值:16.15.911==*E ②近似算法:取MVA S B 30=,各段电压电流基准值分别为:kV U B 5.101=,kA I B 65.15.103301=⨯=kV U B 1152=,kA I B 15.01153301=⨯=kV U B 3.63=,kA I B 75.23.63301=⨯=各元件电抗标幺值:发电机:26.05.1030305.1026.0221=⨯⨯=*x 变压器1T :11.05.3130115121105.0222=⨯⨯=*x 输电线路:073.011530804.023=⨯⨯=*x 变压器2T :21.01530115115105.0224=⨯⨯=*x 电抗器:44.03.075.23.6605.05=⨯⨯=*x 电缆线路:151.03.6305.208.026=⨯⨯=*x电源电动势标幺值:05.15.1011==*E1-3-1 在例1-4中,若6.3kV 母线的三相电压为: )cos(3.62αω+⨯=t U s a)120cos(3.62ο-+⨯=αωt U s a)120cos(3.62ο++⨯=αωt U s a在空载情况下f 点突然三相短路,设突然三相短路时ο30=α。
电力系统暂态分析第四版课后答案方万良

电力系统暂态分析第四版课后答案方万良电力系统暂态分析(暂态过程)是以电力系统为研究对象,对其进行科学的分析、预测,并通过分析得出其所需的信息,从而为规划决策提供参考。
电力系统暂态分析中,有一个重要的组成部分就是变功率系统。
该系统具有一定的数学模型、时间同步特性以及电气化条件(高压或低压)等,能够为电力系统结构优化提供参考。
该部分内容主要包括变功率系统的数学模型与时间同步特性、变功率系统与输电通道间速度场、变电所内各种保护等几个方面。
一、变功率系统的数学模型与时间同步特性变功率系统在电力系统暂态分析中,主要起到变流器的作用,其时间同步特性是其暂态分析的重要参数之一。
变流器、滤波器与变压器等主要元件组成了变功率系统理论上的各个部分的数学模型。
例如,在电力系统中,变流器等主要元件是由电磁铁来工作的。
此外,变功率系统中所产生的电压与电流也会直接影响到电力系统电网中变流器、滤波器所受负载对电压电流的承受能力。
通过数学模型分析得出结论,在不同情况下,变功率系统具有不一样的时间同步特性。
通常,这些时间同步特性可分为:主电源不能超过最大瞬时输出电压、功率因数偏高或无功补偿电压、以及电流为零等四种类型。
二、变功率系统与输电通道间速度场在电力系统暂态分析中,电网中的各个系统是相互联系、相互制约的,它们之间的速度场可以看作是一种相互联系的网络,也可以看作是一种相互制约的系统。
如果网络中节点数量相匹配,则电力系统各节点之间是处于静止状态,速度场中的各点也处于静止状态。
当电力系统发生事故时,首先要分析事故原因,然后对事故进行建模分析和计算得出结论。
三、变电所内各种保护在电力系统暂态分析中,对变电所内各种保护的研究,是根据电力系统现有发展情况,通过理论分析得到的结果和试验结果,并将理论设计值与实际情况进行比较而进行设计。
对于电力系统暂态分析而言,保护方法主要有隔离法、电压法、断路器脱扣法和断路器跳闸法。
对于一般电网和高压电网而言,可以通过以下方法来保护电力网线路:在电压、电流正常时,对其进行保护;在发生故障时,对其进行保护;在电网发生事故时,对其进行保护;在运行正常时,对其进行保护;在故障时恢复正常时,对其进行保护。
电力系统暂态分析参考答案

电力系统暂态分析参考答案电力系统暂态分析参考答案电力系统暂态分析是电力工程中重要的一部分,它主要研究电力系统在突发故障或者其他异常情况下的动态响应过程。
通过对电力系统暂态分析的研究,可以有效地评估电力系统的稳定性和可靠性,并为系统的设计和运行提供参考。
暂态分析的基本原理是基于电力系统的动态方程和电力设备的特性方程,通过求解这些方程来分析电力系统的暂态响应。
在暂态分析中,常见的故障包括短路故障、断路器故障等。
这些故障会导致电力系统中的电流、电压等参数发生突变,进而影响系统的稳定性和可靠性。
在进行暂态分析时,首先需要建立电力系统的数学模型。
这个模型包括电力系统的拓扑结构、电力设备的参数、负荷特性等。
通过建立准确的数学模型,可以更准确地预测电力系统的暂态响应。
接下来,需要对电力系统的故障进行模拟。
通过模拟故障,可以得到故障时刻电力系统中各个节点的电流、电压等参数。
这些参数是进行暂态分析的基础。
在得到故障时刻的参数后,可以利用数值计算方法求解电力系统的动态方程和设备的特性方程。
常见的数值计算方法包括龙格-库塔法、改进的欧拉法等。
这些方法可以有效地求解电力系统的动态响应。
通过求解动态方程和特性方程,可以得到电力系统的暂态响应。
这个响应包括电流、电压的变化曲线等。
通过观察暂态响应,可以评估电力系统的稳定性和可靠性,并进行相应的优化设计。
除了数值计算方法,还可以利用仿真软件进行暂态分析。
常见的仿真软件包括PSCAD、EMTP等。
这些软件可以通过建立电力系统的模型,模拟电力系统的暂态响应。
通过仿真软件,可以更直观地观察电力系统的暂态响应,并进行相应的优化设计。
电力系统暂态分析在电力工程中具有重要的应用价值。
它可以帮助工程师评估电力系统的稳定性和可靠性,指导电力系统的设计和运行。
同时,电力系统暂态分析也是电力系统保护和控制的基础,可以帮助工程师设计和优化电力系统的保护装置和控制策略。
总之,电力系统暂态分析是电力工程中重要的一部分。
电力系统暂态分析的课件以及习题答案全集

电⼒系统暂态分析的课件以及习题答案全集1-2发电机G 1和G 2具有相同的容量,他们的额定电压分别为 6.3 kV 和 10.5 kV 。
若以其额定条件为基准的发电机电抗标⼳值相等,这两台发电机电抗的欧姆数的⽐值是多少?解: S G1=S G2 U G1=6.3kV U G2=10.5kV x G1*=x G2*2111*1G G G G U S x x = 2222*2G G G G U S x x = 36.05.103.622222122212121====G G G G G G G G U U U U S S x x 1-3如图所⽰的电⼒⽹,图中已标明各元件的参数。
要求:⑴准确计算各元件电抗的标⼳值(采⽤变压器实际变⽐),基本级为I 段,U BI =10.5 kV 。
⑵近似计算各元件电抗的标⼳值(采⽤变压器平均额定变⽐)。
S B 取 100 MV A 。
100kmIIIX ”d=0.1510.5/121 kV 50MVA III 10.5kV 110/6.6kV U k %=10.50.4Ω/km U k %=10.5解:(1)S B =100 MV AU BI =10.5 kV U BII =121kVkV U BIII26.76.6110121=?=3.05.105.105010015.02222""*=??==BI N N Bd d U U S S x x 175.05.105.10601001005.10100%2222*1=??==BI N N B k T U U S S u x2732.01211001004.0221*=??==BII B L U S l x x2892.0121110301001005.10100%2222*2=??==BII N N B k T U U S S u x(2) S B =100 MV A U B = U av3.05010015.0""*=?==N B dd S S x x175.0601001005.10100%*1=?==N B k T S S u x 3024.01151001004.0221*=??==av B L U S l x x35.0301001005.10100%*2=?==N B k T S S u x1-4已知⽹络接线如图,图中已标明各元件的参数。
电力系统暂态分析(第四章习题答案)

za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
1) 当 za = zb = zc 时 , 非 对 角 元 素 Z1 = za 1 + a2 +
a = Z2 = 0,则三序分量可以解藕。
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流:
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
3 12)
负序电流:
I2
=
E2 j2
=
(−
1 12
+
3 12)
−
3 j(12
−
3 12)
零序电压标幺值:
10
U(0) = 220/
= 0.0797 3
按等值电路可求得各側电流:
0.0787 I1 = −0.12+(−0.014)//0.244) = 0.748
0.244 I2 = I1 × ( − 0.014 + 0.244) = 0.794
I3 = I1 − I2 = −0.0455 电流有名值:
障时的正序、负序、零序等效电路; 解:正序: 负序:
零序:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
120 = 0.772kA
3 × 121 120 = 0.315kA
3 × 220
In = 3 × (I1 − I2) = 1.043kA
b)中性点经电抗器接地时:
按等值电路可求得各側电流:
0.143 I1 = I2 = 0.124+0.044 = 0.851
电流有名值: I1 = 0.851 × I2 = 0.851 ×
120
I1 = 0.748 ×
= 0.235kA 3 × 121
120
I2 = 0.794 ×
= 0.454kA 3 × 220
−0.0455 120
I3∆ =
×
= 0.166kA
3
3 × 11
中性点电流为: In = 3 × I1 − I2 = −0.656kA
b)经电抗器接地,各侧的等值漏抗为:
220 120 x′I = 0.12 + 3 × 12.5 × 1 − 121 × 2202 = 0.044
(220 − 121) × 220 120
x′II = −0.014 + 3 × 12.5 ×
1212
× 2202 = 0.124
220 120 x′III = 0.244 + 3 × 12.5 × 121 × 2202 = 0.413
j2Ia − j2Ib = 2
Ec − Ea = j2Ic − j2Ia ⇒ j2Ic − j2Ia = j − 1
Ia + Ib + Ic = 0
Ia + Ib + Ic = 0
11 Ia = − 6 − j 2
⇒
11 Ia = − 6 + j 2
1 Ic = 3
中性点电压为:
1 Un = −Ea + j2Ia = −j 3 计算结果一致。
中性点电流为:
120 = 0.487kA
3 × 121 120 = 0.268kA
3 × 220
In = 3 × (I1 − I2) = 0.658A 中性点电压为:
Un = 12.5 × In = 8.227kV
2)如中压侧接地,高压側加零序电压 10kV
a)各侧的等值漏抗为:
xI = 0.12 xII = −0.014 xIII = 0.244
4-5 教材 P118 习题 4-2-1 解: 方法一:因三相电路结构对称,故用对称分量法求解。 ①电压源电压分解为三序分量
E1 1 1 a a2 Ea 1 1 a a2 1
E2 E0
=3
1 1
a2 1
a 1
Eb Ec
=3
1 1
a2 1
a 1
−1 j
1 1 − a + ja2
=3
1 − a2 + ja j
平行线无接地通路,没有零序电流,可不考虑。 2) 故障点发生的线路与不接地自耦变连接时,两条平
行线均有接地通路出现零序电流,要考虑互感作用。 参照 P105 公式(4-37)画出等值电路。 零序网络图:略
4-8 如图所示的三个习题在 k 点发生不对称短路故障 时,试画出它们的零序等效网络(不用化简),并写 出零序电抗 x0 的表达式。(设 xm0 )
120
I2 = 0.434 ×
= 0.248kA 3 × 121
0.131 120
I3∆ =
×
= 0.475kA
3 3 × 11
中性点电流为:
In = 3 × I1 − I2 = −0.212kA 中性点电压为:
Un = 12.5 × In = −2.651kV
4-4 变压器的零序等效电路取决于哪些因数?架空线 路的三序参数相比较,何者更大?为何? 答:变压器的零序漏抗与正序、负序漏抗相等,而零 序激磁电抗与变压器的铁心结构密切相关。零序等效 电路与外电路的连接有关,与变压器三相绕组连接形 式及中性点是否接地有关。架空线路是静止元件,它 的正序电抗等于负序电抗。由于三相架空线路中,各 相零序电流大小相等、相位相同,各相间互感磁通相 互加强,故零序电抗要大于正序电抗。
零序电流:无通路,
I0 = 0
此时中性点电压为:
Un
= −E0
= −j 1
3
③合并序电流得到相电流
11
Ia
1
Ib = a2
Ic
a
1
a a2
1 1 1
I1
I2 0
=
I1 + I2 a2I1 + aI2 aI1 + a2I2
==
−6−j2 11
−6+j2 1
3
方法二:直接列回路方程求解。
Ea − Eb = j2Ia − j2Ib
障时的正序、负序、零序等效电路; 解:正序: 负序:
零序:
第 4 章作业参考答案
4-1 教材 P118 习题 4-1-2
解:对电压方程进行对称分量变换:
∆UP = ZIP ⇒ T∆Us = ZTIs ⇒ ∆Us = (T−1ZT)Is
则:
T−1ZT
=
1 3
1 1 1
a a2
1
a2 a 1
za 0
0
0
zb 0
0 0 zc
1 a2
a
1
a a2
1 1 1
1 =3
同理按等值电路可求得各側电流:
0.0787 I1 = 0.044+(0.124//0.413) = 0.565
0.413 I2 = I1 × (0.124 + 0.413) = 0.434
I3 = IBiblioteka − I2 = 0.131 电流有名值:
120
I1 = 0.565 ×
= 0.178kA 3 × 220
解:对应于三个网络的零序等效网络如下所示。
(1)图 a 中,在 k 点短路时,由于外接负载 L 不 接地,零序电流不能流通。且零序电压加在变压器 T2 的 Y 侧,零序电流也无法流通。零序电抗 x0 。 (2)图 b 中,在 k 点短路时,因为 xm0 ,所以, 零 序 等 效 电 路 如 图 7 - 10 所 示 。 零 序 电 抗 x 0 xT1(0) xL1(0) 。 (3)图 c 中,在 k 点短路时,因为 xm0 所以零 序电流在短路点右侧没有通路。零序电抗 x 0 xT1(0) xL1(0) 。 4-9 如图所示电力系统, 试作出 k 点发生单相接地故
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流:
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
3 12)
负序电流:
I2
=
E2 j2
=
(−
1 12
+
3 12)
−
3 j(12
−
3 12)
4-3 教材 P118 习题 4-5-1 解:
解:参照例题 p99[4-2]的计算过程和结果: 1) 当 III 侧绕组开路后
a)中性点直接接地
按等值电路可求得各側电流:
0.143 I1 = I2 = −0.014+0.12 = 1.349
电流有名值: I1 = 1.349 × I2 = 1.349 ×
2) 当za ≠ zb ≠ zc时,非对角元素Z1 ≠ 0, Z2 ≠ 0,则三
序分量不能解藕,即不是三序独立的电压降方程。
4-2 教材 P118 习题 4-1-1 答: 1)当该三相设备三相接法为Y 或∆时,三相电流 中的零序电流为零;2)如零序电流为零,零序电压一 般不为零。只有当Ua + Ub + Uc = 0时,零序电压才为 零。
零序电压标幺值:
10
U(0) = 220/
= 0.0797 3
按等值电路可求得各側电流:
0.0787 I1 = −0.12+(−0.014)//0.244) = 0.748
0.244 I2 = I1 × ( − 0.014 + 0.244) = 0.794
I3 = I1 − I2 = −0.0455 电流有名值:
⇒
∆U
0
=
II(0)
1 3
lzI(0)
−
(13lzI−II 0 zII (0)
)2
⇒
z(0)
=
1 3
lzI(0)
−
(13lzI−II 0 zII (0)
)2
该等值零序阻抗表达式与单回线路带架空地线十分类
似。注意故障一回的右边 2/3 部分线路无零序(无通 路)。
等值零序网络图:略
4-7 教材 P118 习题 4-7-1 解: 1) 故障点发生的线路与接地自耦变连接时,另外一条
4-6 教材 P118 习题 4-6-1 解:平行双回线路中某回线路停运接地,相当于单回 线路带接地线的情形,可参照教材上 P107 上的内容推 导其等值电路如下:
∆U 0
0
=
=
1 3
lzI(0)II(0)
−
zI−II (0) III (0)
zII (0) III (0)
−
1 3
lzI−II (0) II(0)
za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
