Abaqus有限元作业
悬臂梁—有限元ABAQUS线性静力学分析实例

线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS中,该类问题通常采用静态通用(Static,General)分析步或静态线性摄动(Static,Linear perturbation)分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I、C3D8I)的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1所示,求梁受载后的Mises应力、位移分布。
ν材料性质:弹性模量3=E=,泊松比3.02e均布载荷:F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法,用户可以任选一种。
(1)在Windows操作系统中单击“开始”--“程序”--ABAQUS 6.10 --ABAQUS/CAE。
(2)在操作系统的DOS窗口中输入命令:abaqus cae。
启动ABAQUS/CAE后,在出现的Start Section(开始任务)对话框中选择Create Model Database。
1.3 创建部件在ABAQUS/CAE顶部的环境栏中,可以看到模块列表:Module:Part,这表示当前处在Part(部件)模块,在这个模块中可以定义模型各部分的几何形体。
基于ABAQUS的砌体结构有限元模拟方法

一、引言
在我国,砌体结构房屋在中小城市、乡镇和农村地区大量存在。由于砌体结构材料自身的抗剪强度较 低,延性差,因此在地震中震害严重。传统的构造柱圈梁技术,可有效保证结构的整体效应,但砌体结构 的数值模拟研究较为困难,本文将基于ABAQUS有限元软件对砌体结构进行模拟,并探讨其方法和效果。
二、有限元分析方法
而且二维Beam单元中不能采用con饿Ic
钒筋采用三结点二次三维桁颦单元T3D2。
Damage
P Lasticity奉构f混凝土损伤鞘性模型模拟效果较好1.摹于
以上原因,本文采用实体单元模拟,对于模型中的混凝土和砌体部分,模型采用线性减缩积分单元C3DSR, abaqus加钢筋的办亍去有几种:I、采用reb盘rlayer的办法,在part里面画一个面,然后在prope对里面 定义一个surface为rebarlayer,然后在interaction中embed巾把钢筋层embed到混糍土实体中上。2、采用
工业建筑2011增刊
1353
第f一届仝国现代结构T程学术目讨会
总体来说.分离模型可以模拟砌块与砂浆之问的作用和砌体破坏机理.适用于模拟小型试验砌体的破 坏行为,但¨算越^,建模繁琐:整体连续体模型适于分析人规模的墙体.但对于详细的应力分析和理衅 砌体多样的失散机理却显得不足。采用哪种模型一般应视分析f1的而定…。本文分析的模型为砌体整体结构. 分析模型较大.是对整体结构进行模拟.主要是考虑结构的宏观反应,宜选取整体式有限元模型进行计算, 建模町更快捷,计算量更小。 (二)单元选择厦建模方法 对于结构的模拟,有两种思路,一种是采用粱单兀模拟构造梓,壳单元模拟堵体及愤制空心楼板,一 种足聚用实体单元模拟柱和墙及楼板,鉴于当用第种方式模拟时,科!和墙,墙和楼板的连接小描处理,
Abaqus扩展有限元(XFEM)例子(裂缝发展)

Abaqus扩展有限元(XFEM)例子(裂缝发展)part模块中的操作:1. 生成一个新的part,取名为plate,本part选取3D deformable solid extrusion类型(如图1)2.通过Rectangle工具画出一长3,高6的矩形。
考虑使用工具栏add-dimension和edit dimension来画出精确长度的模型。
强烈建议此矩形的左上角坐标为(0,3),右下角坐标为(3,-3)(如图2)3. 完成后拉伸此矩形,深度为1.(如图3)4. 生成一个新的part,取名为crack,本part选取3D deformable shell extrusion类型(如图4)5.生成一条线,此线的左端点坐标为(0,0.08),右端点坐标为(1.5,0.08)6 . 完成后拉伸此线,深度为1.(如图6)7.保存此模型为XFEMtutor(如图7),以后经常保存模型,不再累述。
8. 在part Plate中分别创建4个集合,分别为:all,bottom,top和fixZ,各部分的内容如图8~11所示Material模块中的操作:1 创建材料elsa,其弹性参数为E=210GPa,泊松比为0.3(如图12)2 最大主应力失效准则作为损伤起始的判据,最大主应力为84.4MPa(如图13)3.损伤演化选取基于能量的、线性软化的、混合模式的指数损伤演化规律,有关参数为G1C= G2C= G3C=42200N/m,a=1.(如图14)4.创建一个Solid Homogeneous 的section,名为solid(如图15),此section与材料elsa相联(如图16),并将此s ection赋给plate part(也就是集合all)(如图17)3.赋予材料取向,分别如图18~21所示。
三、划分网格:网格控制为:Hex型structured(如图22),单元类型为C3D8R(如图23)设置plate各边的网格种子为8,26,36(如图24),各边种子的个数不能改变(如图25)四、装配模块:选中plate和crack两个part,分别生成2个实体(如图26),生成一个参考点,参考点的坐标为(1.5,-3,0)(如图27,28)。
ABAQUS混凝土框架有限元计算分析
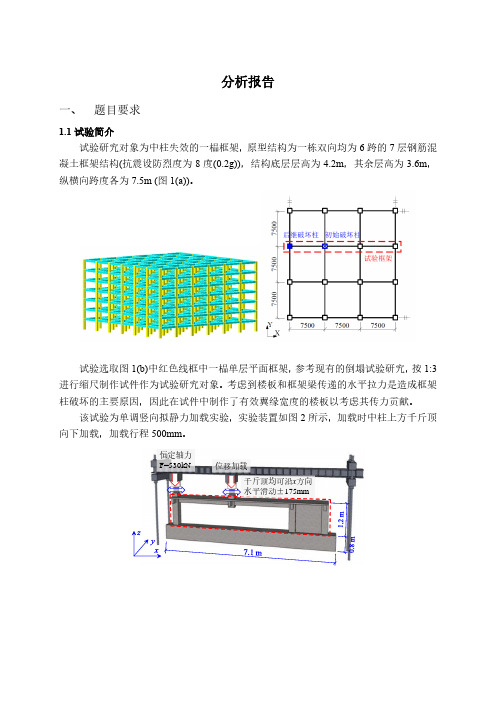
“悬链线”,继续维持该梁一定的承载力。 2.4 加载点荷载-位移曲线
通过计算分析得到的结果,绘制加载点的荷载-位移曲线如下图所示:
荷载/KN
加载点力-位移曲线
120 100
80 60
40
20
0 0
100
200
300
400
500
600
位移/mm
图 2.13 加载点力-位移曲线 通过加载点力-位移曲线可以看到,当位移超过 80mm 后该结构的承载力有所下 降,但下降幅度不大,在 240mm 后荷载保持稳定,值里可以看到梁内塑性铰形成的 “悬链线”机制发挥出来抗倒塌的作用。但是之后还有些许上升,可能是因为计算模 型对于下降段的模拟不够准确所致。
D6
394
519
220
0.3
D10
419
617
219
0.3
D12
625
685
钢筋应力-应变曲线如下图所示:
171
0.3
stress
钢筋应力-应变关系曲线
700
600
500
400
Φ6 300
Φ10 200
Φ12
100
0
0
0.001 0.002 0.003 0.004 0.005 0.006
strain
σ = (1 − ������������)������������������
1 − ������������[1.2 − 0.2 ������5]
������������
=
{1
−
������������(������
������������ − 1)1.7
+
应用固体力学有限元Abaqus算例分析

问题描述:(1)计算出两种工况下的解析解; (2)用有限元软件解决以下问题:探究单元数量对计算结果的影响; 探究边界条件的影响。
工况(a ),令u (L )=0改变到u (L )=±0.02m 工况(b ),令σ(L )=P 改变到σ(L )=P ±0.1P (1)两种工况下的解析解推导过程及结果如下看成是平面应力问题来解决,只有板边上受有平行于板面并且不沿厚度变化的面力,同时,体力也平行于板面并且不沿厚度变化,板很薄,外力又不沿厚度变化应力沿着板的厚度又是连续分布的,所以,可以认为在整个薄板的所有各点都有z 0,0,0zx zy σττ=== (1) 同时,根据剪应力互等定理0,0xz yz ττ== (2)由平衡微分方程,可以知道0;0yxx y xyX x yY y xτσστ∂∂++=∂∂∂∂++=∂∂ (3)几何方程,,x y xy u v v ux y x yεεγ∂∂∂∂===+∂∂∂∂ (4) 物理方程如下:1()1()2(1)x x y y y x xy xyE EEεσμσεσμσμγτ=-=-+= (5)由此可以得到22()1()1()2(1)x y xy E u vx y E v uy x E v ux yσμμσμμτμ∂∂=+-∂∂∂∂=+-∂∂∂∂=+-∂∂ (6)代入平衡微分方程 得到22222222222211()012211()0122E u u vX x y x y E v v uY y x x yμμμμμμ∂-∂+∂+++=-∂∂∂∂∂-∂+∂+++=-∂∂∂∂ (7)0;X Y g ρ==因此根据以上式子可以得到 22200()()01E d v y g dy ρμ=+=- (8)对(8)式积分,得到22()0(1)()2u x g v y y Ay BE μρ=-=++ (9)第1种情况:物体在全部边界上的位移分量是已知的,因此边界条件为位移边界条件在边界上,我们有0;()s y u u v v v y ==== (10)(0)0,()0v v L == (11)得到参数:2(1)0;2gLB A E μρ-==(12)22()(1)()()2()2y g v y Ly y E L g y ρμσρ-=-=- (13)将数据代入式(13)得到22274()(1)()()=(y-y ) 1.691021()()7.6441022y g v y Ly y mE L g y y Paρμσρ--=-⨯⨯=-=-⨯⨯ (14)第2种情况:物体在全部边界上的部分位移分量和应力分量是已知的,因此边界条件为混合边界条件(0)0;()y v L p σ== (15)210;()B A p gL Eμρ-==+⨯ (16)所以有221()[()]2()()y v y p gL y E y p g L y μρσρ-=+-=+- (17)将数据代入(17)可以得到22772541()[()]=8.5110 2.06102()()107.64410(1)y v y p gL y g y y E y p g L y y μρρσρ---=+-⨯-⨯=+-=+⨯- (18)(2)计算中采用Abaqus有限元商业计算软件来模拟题目中的工况材料参数见下表名称数量材料密度ρ7800kg/m3物体长度L 1m物体宽度W 0.1m弹性模量E 2.1*1011重力加速度g 9.8泊松比0.3载荷P 0.1MPa计算单元类型为S4R,单元数量为250工况(a)计算参数设置及结果如下由计算结果可知,最大应力在固定端处取得,最大值为3.798*104Pa由解析解22274()(1)()()=(y-y) 1.691021()()7.6441022ygv y Ly y mELg y y Paρμσρ--=-⨯⨯=-=-⨯⨯得到的固定端点处最大应力为3.822*104Pa;在中间位置位移最大为4.533*10-8m 应力误差为4443.82210-3.79810=100%=0.62%3.82210η⨯⨯⨯⨯位移误差为8884.53310-4.22510=100%=7.28%4.22510η---⨯⨯⨯⨯工况(b )计算参数设置及结果如下由计算结果可知,最大应力在固定端处取得,最大值为1.791*105Pa 由解析解22772541()[()]=8.51102.06102()()107.64410(1)y v y p gL y g y y E y p g L y y μρρσρ---=+-⨯-⨯=+-=+⨯- 得到的固定端点处最大应力为1.7644*105Pa ;自由端最大位移为6.45*10-7m应力误差为5551.79110-1.764410=100%=1.5%1.764410η⨯⨯⨯⨯ 位移误差为7776.57210-6.4510=100%=1.89%6.4510η---⨯⨯⨯⨯通过有限元计算,可以得到和解析解很接近的结果,通过误差分析表明,有限元计算此类平面应力问题可以很好地满足计算精度的要求。
abaqus有限元动力学标准算例

abaqus有限元动力学标准算例
在ABAQUS中,有许多标准的有限元动力学算例可以参考。
以下是一些常见的有限元动力学标准算例:
1. 车辆碰撞:模拟两辆车发生碰撞的情况,可以研究对车辆结构和乘员的影响。
2. 地震分析:模拟建筑物或结构在地震中的响应,了解结构的动力性能。
3. 风力荷载:模拟大型建筑物或桥梁在风力荷载下的响应,评估结构的稳定性和安全性。
4. 冲击分析:模拟物体撞击结构的过程,研究结构的破坏行为。
5. 振动模态分析:计算结构的固有频率和模态形态,用于确定结构设计的合理性。
6. 爆炸分析:模拟炸药爆炸引起的冲击波和结构的响应。
以上只是一些常见的有限元动力学标准算例,根据具体需求和研究对象,还可以设计其他类型的动力学算例。
在ABAQUS
软件中,可以根据具体的算例需求选择相应的分析模块和设置参数。
ABAQUS 有限元分析大作业 凹槽成型实例
有限元分析大作业-凹槽成型一:前处理-利用ABAQUS/CAE创建模型。
1、定义并创建四个部件如下图:图1:可变形毛坯Blank图2:刚性冲头Punch图3:刚性夹具Holder2、定义材料及截面特性图5:分别根据提供的数据定义Elastic和Plastic两个材料特性图6:创建均匀实体截面提交给材料Steel并赋予Blank此截面属性图7:建立一个局部数据坐标系(在随着毛坯运动的共旋坐标系下显示应力和应变的值): 2、装配部件图8:装配图(根据相互关系进行装配)3、创建几何集合创建6个几何集合:每个刚性体参考点各一个,毛坯对称面一个,毛坯中面的每段各一个。
图9:创建六个几何集合4、定义分析步和输出要求图10:创建分析步1 Establish contact 1图11:创建分析步2,Remove right constraint图12:创建分析步3 Holder force图13:创建分析步4 Establish contact 2图14:创建分析步5 Move punch图15:编辑场输出图16:编辑历史输出5、监控自由度的值图17:定义RefPunch的监控自由度6、定义接触相互作用图18:首先在Interaction模块中定义以上5个表面图19:定义一个无摩擦接触相互作用属性图20:再定义一个有摩擦相互作用属性,摩擦系数取为0.1 最后定义三个表面间的相互作用:图21:定义三个表面之间的相互作用(具体见下面三个图)图22:定义Die-Blank 相互作用 图23:定义Holder-Blank 相互作用图24:定义Punch-Blank 相互作用7、各分析步的边界条件首先在STEP1总添加每个初始边界条件:图25:Center、MidLeft、MidRight边界条件图26:RefDie、RefHolder、RefPunch边界条件图27:分析步1边界条件图28:Step2边界条件图29:Step3边界条件图30:Step4边界条件图31:Step5边界条件图:32集中力与负压力施加8、划分网格和定义作业图33:首先在毛坯上下与左右表面分别撒种图34:选择单元类型图35:划分网格二:求解1、创建作业图36:创建作业2、提交求解并监视求解过程图:37:求解完成图:38监视点U2向位移图三:后处理1、成型过程图39:开始图40:开始变形图41:变形扩大图42:最后成型结果2、绘制塑性应变等值线图3、绘制冲头上的反作用力4、绘制接触压力等值线图图45:接触压力等值线图。
abaqus作业题

作业题1.假设砂井地基中砂井为正方形布置,间距为2m ,长度为8m ,砂井半径为m w 1.0=γ,渗透系数为s m k w /102-=。
地基土厚度m L 8=,土地渗透系数s m k h /108-=。
弹性模量KPa E 410=,不考虑土体的水平方向的变形,取泊松比0.0=ν。
地基土底面不排水,顶面完全透水,土体及砂井表面作用有瞬时施加的荷载KPa P 200=。
在有限元数值分析中,取砂井中的一个单元体进行计算,即长,宽,高,分别为2m,2m,8m ,图形如下图1-1所示;模型底部固定三个方向的约束,不排水;四周仅能容许竖向位移,同样不透水,表面位移自由,且是自由排水面。
载荷瞬时施加,然后根据土体表面的竖向位移求的各个时刻土层的固结度。
1-1模型示意图步骤:1.模型的建立(1)建立部件Part模块中,执行[part]/[create]命令通过Extrusion方法建立一个2mx2mx8m的三维变形体,然后通过执行[Tools]/[partion]命令,在弹出的Creation Partition 对话框中将Type选项设置为Face,将Method 选为sketch,将顶面的砂井画出来,再次执[Tools]/[partion]命令,此时在Creation Partition 对话框将type选项设为Cell,对应的Method 选为Extrude/Sweep edges方法,将砂井的空间形状独立出来。
执行[tools]/[set]/[create]命令,分别建立土体(soil)和砂井(sandwell)的集合。
(2)设置材料及截面特性在property模块中,分别建立soil和sand well的材料,并为问题描述的数据设置相应的参数,执行[section]/[creat]命令,分别设置名称为soil和sand well的section,并执行[Assign]/[section]命令赋予相应的区域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《有限元分析及应用》课程
不同板宽的孔边应力集中问题
XX(XXX 1122000000)
摘要:本文通过Abaqus有限元模拟软件对有限板宽的孔边应力集中问题进行分析,分析由圆孔引起的应力集中问题。
并结合分析过程研究网格划分、网格尺度的大小对圆孔应力集中的影响。
1.问题提出
无限板宽孔边应力集中问题,弹性力学解析解中在空边上有σθ分布:
σθ(θ=90o)=q0(1+R02/2r2+3R04/2r4) ;
σθ(θ=90o,r=R0)=3q0; σθ(θ=90o,r=2R0)=1.22q0;
σθ(θ=90o,r=3R0)=1.07q0;
由以上数据可知当逐渐远离孔边的时候,应力逐渐下降,逐渐接近于q0
2.模型建立
○1定义描述板宽与孔径的相对尺度的特征参数ξ,ξ=B/R0
○2定义应力集中系数k,k=σmax/q0
○3在Abaqus中建立模型,根据对称选取1/4模型进行有限元的分析,圆
为变量,模型边长为50cm,施加在模型右侧的应力孔的中心位于原点,半径R
为100N/cm2,板的弹性模量E=210000N/cm2。
○4当圆孔半径取为5cm时,单元选择为CPS6单元(6节点二次平面应力三角形单元)
A.当设置每边单元数为10时,构件的网格划分、云纹图如下:
主要应力集中区域如下:
B.当设置每边单元数为15时,构件的网格划分、云纹图如下:
主要应力集中区域如下:
C.当设置每边单元数为20时,构件的网格划分、云纹图如下:
主要应力集中区域如下:
○5当圆孔半径取为3cm时,单元选择为CPS6单元(6节点二次平面应力三角形
单元)
A. 当设置每边单元数为10时,构件的网格划分、云纹图如下:
主要应力集中区域如下:
B.当设置每边单元数为15时,构件的网格划分、云纹图如下:主要应力集中区域如下:
C.当设置每边单元数为20时,构件的网格划分、云纹图如下:
主要应力集中区域如下:
3.数据分析
○1由Abaqus有限元软件模拟得到应力集中系数K与相对尺度ξ的关系如下:
10 15 20
ξR 单元数
K
100/5 5 K5 2.896 2.914 3.007 100/3 3 K3 2.295 2.594 2.667
○2通过上述云纹图可以清楚看到,在圆孔附近的应力变化,平板的大部分应力集中在
100Mps左右,在圆孔附近应力急剧增长在300Mpa左右,出现了明显的应力集中。
○3通过上述两种模拟计算可知,在圆孔减小后,应力集中的现象更加明显
4.结论
1.应力集中主要发生在与外力方向相垂直的方向,即本文中圆孔的上下两边附近。
随着圆孔半径的减小,应力集中现象更加明显。
2.在有限元分析过程中,网格划分、网格尺寸的大小对数值的精度有影响。
