高等电磁理论第三章答案3
高等电磁场理论习题解答(作业)
第一章基本电磁理论1-1 利用Fourier 变换, 由时域形式的Maxwell方程导出其频域形式。
（作1-2—1-3）解：付氏变换和付氏逆变换分别为：麦氏方程：对第一个方程进行付氏变换：（时谐电磁场）同理可得：上面四式即为麦式方程的频域形式。
1-2 设各向异性介质的介电常数为当外加电场强度为(1) ；(2) ；(3) ；(4) ；(5)求出产生的电通密度。
（作1-6）解：将E分别代入，得：1-3 设各向异性介质的介电常数为试求：(1) 当外加电场强度时，产生的电通密度D；(2) 若要求产生的电通密度，需要的外加电场强度E。
（作1-7—1-8）解：即：.附：又所以1-6 已知理想导电体表面上某点的电磁场为试求该点表面电荷及电流密度。
解：由已知条件，理想导体表面某点：(1-6-1)(1-6-2)知该点处的法向单位矢量为： (1-6-3)理想导体表面上的电磁场满足边界条件：(1-6-4)(1-6-5)将(1-6-2)、(1-6-3)式代入(1-6-4)式，得该点处的表面电流密度为：(1-6-6)将(1-6-1)、(1-6-3)式代入(1-6-5)式，得该点处的表面电荷密度为：(1-6-7)1-9 若非均匀的各向同性介质的介电常数为, 试证无源区中的时谐电场强度满足下列方程:（作1-9）证明：非均匀各向同性介质中（无源区）的时谐电磁场满足(1-9-1)(1-9-2)对(1-9-2)式两边取旋度，并利用(1-9-1)得又所以 (1-9-3)又在非均匀各向同性介质中即 (1-9-4)将(1-9-4)代入(1-9-3)，得即第2章平面电磁波2-1 导出非均匀的各向同性线性媒质中，正弦电磁场应该满足的波动方程及亥姆霍兹方程。
解：非均匀各向同性线性媒质中，正弦电磁场满足的Maxwell方程组为(2-1-1)(2-1-2)(2-1-3)(2-1-4)对(2-1-2)式两边取旋度，并应用(2-1-1)得即对(2-1-1)式两边取旋度，并应用(2-1-2)得所以非均匀各向同性媒质中，正弦电磁场满足的波动方程为 (2-1-5)(2-1-6)由(2-1-4)式得即 (2-1-7)由(2-1-3)式得即 (2-1-8)利用矢量关系式，并将(2-1-7)(2-1-8)式代入，得电磁场满足的亥姆霍兹方程为(2-1-9)(2-1-10)均匀介质中，无源区中2-4 推导式（2-2-8）。
高等电磁场理论课后习题答案
由于是远场,
e 1 e 2 e 3 e 4 e e 1 e 2 e 3 e 4 e
2
I ka sin jkr jk r1 jk r2 E E 1 E 2 E 3 E 4 e e jk r3 e jk r4 e e 4r 1 H e k E
2.7
解：
H j E E j H E k 2 E 0 H 0 E 0
比如 E e z e 2.11
jkz
(1)
2 E ( E) ( E) k 2 E 2 E k 2 E 0 (2)
代入公式，可得，
I ka sin1 jkr1 H e e x cos 1 cos 1 e y cos 1 sin 1 e z sin 1 4r1
2
I ka sin 2 jkr2 e e x cos 2 cos 2 e y cos 2 sin 2 e z sin 2 4r2
推导1 1 1 R ˆ 4 lim 2 dV lim dS lim 3 4 R 2 R V 0 R 0 R 0 R R R V S 1 1 又知道 2 在R 0处值为零，符合 (r r ')函数的定义。 4 R 推导2 点电荷q (r r ')产生的电场强度为 q 1 4 0 R 4 R q (r r ') 1 E 2 4 (r r ') 0 R E q
所以有
H 2 E1 H1 E2 E1 J 2 E2 J1 H 2 M1 H1 M 2
电磁场与电磁波（第4版）第3章部分习题参考解答
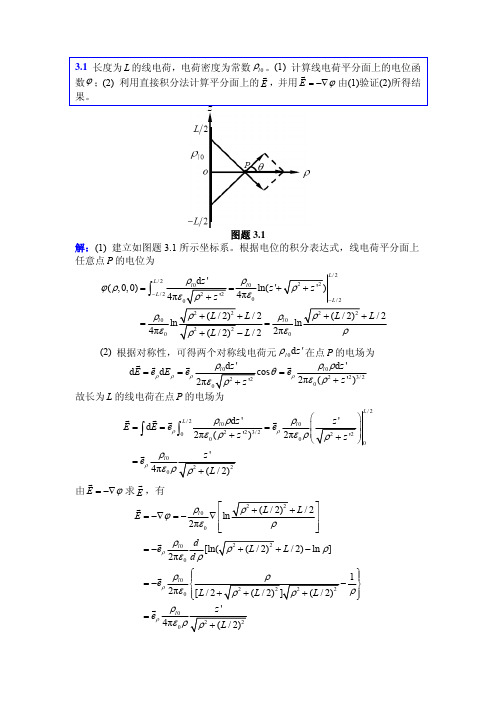
ε − ε 0 3 cos θ a E0 2 r ε + 2ε 0
(r ≥ a)
ϕ =0
ρ ( x)
ϕ = U0
0
d
图题 3.7
x
解：两导体板之间的电位满足泊松方程 ∇ 2ϕ = −
ρ d 2ϕ 1 ρ0 x ，故得 2 = − dx ε0 d ε0
解此方程，得
ϕ =−
ρ0 x3 + Ax + B 6ε 0 d
ρ 2 + ( L / 2) 2 + L / 2 ρl 0 ρ 2 + ( L / 2) 2 + L / 2 ρl 0 = ln ln ρ 4πε 0 ρ 2 + ( L / 2) 2 − L / 2 2πε 0
(2) 根据对称性，可得两个对称线电荷元 ρ l 0 dz ′ 在点 P 的电场为 G G ρl 0dz ' ρ l 0 ρ dz ' G G dE = eρ dEρ = eρ cos θ = eρ 2πε 0 ( ρ 2 + z '2 )3/ 2 2πε 0 ρ 2 + z '2 故长为 L 的线电荷在点 P 的电场为
G G G L/2 E = ∫ dE = eρ ∫
0
ρl 0 ρ dz ' z' G ρl 0 ⎛ e = ⎜ ρ 2 2 3/ 2 2 2 2πε 0 ( ρ + z ' ) 2πε 0 ρ ⎜ ⎝ ρ + z'
z'
2
⎞ ⎟ ⎟ ⎠0
L/2
G = eρ
ρl 0 4πε 0 ρ
ρ + ( L / 2) 2
3.8 试证明：同轴线单位长度的静电储能 We =
电磁场与电磁波第四版第三章部分答案
电磁场与电磁波第四版第三章部分答案电磁场与电磁波第三章3.7无限大导体平板分别置于x =0和x =d 处，板间充满电荷，其体电荷密度为ρ=ρ0x d,极板间的电位分别为0和U 0，如图所示，求两级板之间的电位和电场强度。
解：由泊松定理得d 2φdx 2=?1ε0ρ0xd解得φ=?ρ0x 36ε0d+x +B在x =0处，φ=0，故B =0 在x =d 处，φ=U 0，故U 0=?ρ0x 36ε0d+d故=U 0d+ρ0d 6ε0φ=?ρ0x 36ε0d+(U 0d+ρ0d 6ε0)xE =??φ=?e x ?φ?x=e x [ρ0x 22ε0d?(U 0d+ρ0d 6ε0)]3.8证明：同轴线单位长度的静电储能W e =q l 22C。
式中q l 为单位长度上的电荷量，C 为单位长度上的电容。
解：由高斯定理可知：E (ρ)=q l 2περ故内外导体间的电压为U =∫Edρ=∫q l 2περbb dρ=q l 2πεln b则电容为C =q l U=2πεlnbW e =12∫εE 2dV =12∫εb (q l 2περ)22πρdρ=12q l 22πεln b =q l22C3.9有一半径为,带电量q 的导体球，其球心位于介电常数分别为ε1和ε2的两种介质的分界面上，该分界面为无限大平面。
试求：（1）导体球的电容；（2）总的静电常量。
解：根据边界条件则E 1t =E 2t ,故有E 1=E 2=E ,由于D 1=ε1E 1,D 2=ε2E 2,所以D 1≠D 2，由高斯定理可得D 1S 1+D 2S 2=q即2πr 2ε1E +2πr 2ε2E =qE =q212 导体球的电位为φ( )=∫Edr =∞q2π(ε1+ε2)∫1r ∞dr =q 2π(ε1+ε2)电容为C =q φ( )=2π(ε1+ε2)(2)总的静能量为W e =12qφ( )=q 24π(ε1+ε2)3.13在一块厚度为d 的导电板上，由两个半径分别为r 1和r 2的圆弧和夹角为α的两半径割出的一块扇形体，如图所示。
电磁场理论(柯亨玉)答案第三章静态电磁场.pdf
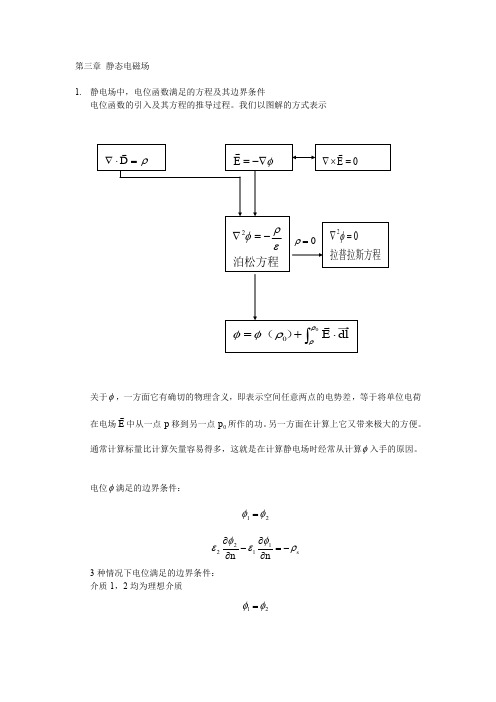
由B A
得： Az Ay 0 y z
Ax Az 0 z x
Ay x
Ax y
B0
可得一解为： Az Ay 0
还可得另一解为： Ax Az 0
还存在其它解。 两者之差的旋度：
Ax B0 y Ay B0 x
eˆx eˆy eˆz
( Ayeˆy Axeˆx ) (B0 xeˆy B0 yeˆx )
磁失势的引入及方程的推导过程我们以图解的方式表示其中引入的条件是无传导电流的单连通区域如电流是环形分布的磁标势适合的区域只能是挖去环形电流所围成的壳形之后剩下的区域
第三章 静态电磁场
1. 静电场中，电位函数满足的方程及其边界条件 电位函数的引入及其方程的推导过程。我们以图解的方式表示
D
E
x
0 y z
B0 y B0 x 0
3-10. 证明：设线圈中的电流分别为 I1, I 2
线圈 1 对线圈 2 的作用力为
f12
0 4
I
2
dl2
(I1
dl1r12 )
L1 L2
r132
0 I1I2
dl2
(dl1r12 )
4
L1 L2
r132
0 I1I 2
[(dl2 r12 )dl1 (dl1 dl2 )r12 ]
设介质被抽出的一段长为 x ， C 便等于无介质部分的电容 C1 与有介质部分的电容
C2 的迭加，即
C
C1
C2
2 0 x ln(b a)
2 (L x) ln(b a)
2 [L ln(b a)
(
0
)x]
则 W V2 C 2
V2 2
2 [L ( ln(b a)
电磁学试题库电磁学第三章试题(含答案)
一、填 空 题1、电介质的极化分为 ，和 。
答案内容：位移极化，取向极化。
2、如图，有一均匀极化的介质球，半径为R ，极化强度为P ，则极化电荷在球心处产生的场强是 。
答案内容：3ε-P ；3、0C C r ε=成立的条件是 。
答案内容：介质为均匀介质；4、通常电介质的极化分为两类，其中无极分子的极化称为 有极分子的极化称为 。
答案内容：位移极化；取向极化；5、如图所示，水平放置的平行电容器，极板长为L ，二极板间距为d ，电容器两极板间加有电压，据板右端L 处放置一个荧光屏S 。
有一个质量为m ，电量为q 的粒子，从电容器左端的中央以速度0v 水平射入电场，粒子穿过电容器后（两板间距离d 的大小能满足粒子穿过电容器），要求以水平速度打在荧光屏S 上，则加在电容器两极板间电压的大小应为 。
答案内容：2mgd/q ；6、如图所示，平行板电容器的极板面积为S ，间距为d ，对此电容器充电之后，拆去电源，再插入相对介电常数为r ε，厚度为/2d 的均匀电介质板，设为插入介质前，两极板间的电场为0E ，插入介质后，介质内外的电场分别为1E 和2E ，则：10/__________E E =，20/__________E E = 。
答案内容： 1/r ε；1.7、有一平板电容器，用电池将其充电，这时电容器中储存能量为W 0，在不断开电池的情况下，将相对介电常数为r ε的电介质充满整个电容器，这时电容器内存储能量W= W 。
答案内容：r ε ；PzR8、在平行板电容器之间放入一电介质板，如图所示，则电容器电容将为 ，设未放介质时电容为C 0 。
答案内容：021r rC εε+ ；单选择题 11、如果电容器两极间的电势差保持不变，这个电容器在电介质存在时所储存的自由电荷与没有电介质（即真空）时所储存的电荷相比：（ ）(A)增多； （B ）减少； （C ）相同； （D ）不能比较。
答案内容：A ；2、内外半径为21R R 和的驻极体球壳被均匀极化，极化强度为PP ；的方向平行于球壳直径，壳内空腔中任一点的电场强度是： ( C )（A ）3ε=P E ； (B)0=E；(C)3ε-=P E；(D)32ε=P E 。
电磁学答案第3章
电磁学答案第3章第三章 静电场的电介质3.2.1 偶极矩为p →=q l →的电偶极子，处于场强为E 的外电场中，p →与E →的夹角为θ。
（1） 若是均匀的，θ为什么值时，电偶极子达到平衡？（2）如果E 是不均匀的，电偶极子能否达到平衡？ 解： （1）偶极子受的力：F + =F _=qE因而F →+=-F →_∴偶极子受合力为零。
偶极子受的力矩T =p ⨯E即 T=qEsin θ当 T=0时，偶极子达到平衡，∴ pEsin θ=0p →≠0 E →≠0 ∴θ=0 , πθ=0这种平衡是稳定平衡。
θ=π是不稳定平衡。
（2） 当E →不是均匀电场时，偶极子除受力矩外还将受一个 力（作用在两个点电荷的电场力的合力）。
所以不能达到平衡。
3.2.2 两电偶极子1p→和2p →在同一直线上，所以它们之间距r比它们自己的线度大的很多。
证明：它们的相互作用力的大小为F=402123rp p πε，力的方向是：1p→与2p→同方向时互相吸引，反方向时互相排斥。
证： 已知当r >>l 时，偶极子在其延长线上一点的场强：E →=302rpπε→当 1p →与2p →同方向时，如图2p →所受的力的大小：+→F =E →q=r lr q p ∧+3201)2(2πε-→F = -E→q=r lr q p ∧--3201)2(2πε∴F→= +→F +-→F =r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =r l r l l r q p ∧⎥⎦⎤⎢⎣⎡---⋅3222322201)2()2(2262πε略去 422l 及 832l 等高级小量。
F→=-r r qlp ∧402146πε= -r r pp ∧402123πε当 1p →与2p →反方向时（如图），同理： F→= r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =012πεq p ⨯r lr l l r ∧-+32223222)4()2(23略去高级小量得：F→=r rP P ∧402123πε3.2.3 一电偶极子处在外电场中，其电偶极矩为 ，其所在处的电场强度为 。
电磁学第三章课后习题答案
电磁学第三章课后习题答案电磁学第三章课后习题答案电磁学是物理学中的重要分支，研究电荷和电流之间相互作用的规律。
在电磁学的学习过程中，习题是巩固知识和提高能力的重要途径。
本文将为大家提供电磁学第三章的课后习题答案，希望能对大家的学习有所帮助。
1. 一个导线的长度为l，电流为I，如图所示。
求导线两端的电势差。
答案：根据欧姆定律，电势差等于电流乘以电阻。
而导线的电阻可以通过电阻率乘以长度除以横截面积来计算。
所以，导线两端的电势差为V = I × (ρl/A)。
2. 一个导线的电阻为R，电流为I，如图所示。
求导线两端的电势差。
答案：根据欧姆定律，电势差等于电流乘以电阻。
所以，导线两端的电势差为V = I × R。
3. 一个导线的电阻为R，电流为I，导线的长度为l，电阻率为ρ，横截面积为A。
求导线两端的电势差。
答案：根据欧姆定律，电势差等于电流乘以电阻。
而导线的电阻可以通过电阻率乘以长度除以横截面积来计算。
所以，导线两端的电势差为V = I × R = I × (ρl/A)。
4. 在一个电路中，有一个电阻为R1的电阻器和一个电阻为R2的电阻器连接在一起，电流为I。
求两个电阻器上的电势差。
答案：根据欧姆定律，电势差等于电流乘以电阻。
所以，第一个电阻器上的电势差为V1 = I × R1，第二个电阻器上的电势差为V2 = I × R2。
5. 在一个电路中，有一个电阻为R1的电阻器和一个电阻为R2的电阻器连接在一起，电阻器之间的电势差为V。
求电流的大小。
答案：根据欧姆定律，电势差等于电流乘以电阻。
所以，V = I × (R1 + R2)。
解方程可得电流的大小为I = V / (R1 + R2)。
6. 一个电路中有两个电阻器，电阻分别为R1和R2，电流为I。
求电路中的总电阻。
答案：电路中的总电阻可以通过电阻器的并联和串联来计算。
如果电阻器是串联的，总电阻等于各个电阻器的电阻之和，即R = R1 + R2。
电磁场与电磁波 第三章答案
x x x 2 ( y h) 2 x 2 ( y h) 2 e x ( y h) ( y h) x 2 ( y h) 2 x 2 ( y h) 2 e y
电场能量密度为
h 2 ( x 4 y 4 h 4 2x 2 h 2 2x 2 y 2 2 y 2 h 2 ) 1 w r E2 l 2 2 r [ x 2 ( y h ) 2 ] 2 [ x 2 ( y h) 2 ] 2
电磁场与电磁波第三章习题及参考答案
第3章习题3-1 半径为的薄圆盘上电荷面密度为s ρ，绕其圆弧轴线以角频率旋转形成电流，求电流面密度。
解：圆盘以角频率旋转，圆盘上半径为r 处的速度为r ω，因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中，每立方米体积中大约有28105.8⨯个自由电子。
如果铜线的横截面为210cm ，电流为A 1500。
计算 1） 电流密度；2） 电子的平均漂移速度； 解：1）电流密度m A S I J /105.11010150064⨯=⨯==- 2) 电子的平均漂移速度 v J ρ=，3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m J v /101.11036.1105.14106-⨯=⨯⨯==ρ 3-3 一宽度为cm 30传输带上电荷均匀分布，以速度s m /20匀速运动，形成的电流，对应的电流强度为A μ50，计算传输带上的电荷面密度。
解：电流面密度为m A L I J S /7.1663.050μ===因为 v J S S ρ= 所以 2/33.8207.166m C v J S S μρ=== 3-4 如果ρ是运动电荷密度，U是运动电荷的平均运动速度，证明：0=∂∂+∇⋅+⋅∇tU U ρρρ证：如果ρ是运动电荷密度，U是运动电荷的平均运动速度，则电流密度为U J ρ=代入电荷守恒定律tJ ∂∂-=⋅∇ρ得0=∂∂+∇⋅+⋅∇t U U ρρρ3-5 由m S /1012.17⨯=σ的铁制作的圆锥台，高为m 2，两端面的半径分别为cm 10和cm 12。
求两端面之间的电阻。
解：用两种方法（1）如题图3.5所示⎰⎰==2122)(tan zz lz dzS dl R ασπσ)11()(tan 1212z z -=ασπ 01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α，m r z 1201.0/12.0tan /22===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R （2）设流过的电流为I ，电流密度为2rI S I J π==电场强度为 2r IJ E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上，媒质1的参数为2,/10011==r m S εσ，电流密度的大小为2/50m A ，方向和界面法向的夹角为030；媒质2的参数为4,/1022==r m S εσ。
高等电磁场理论第三章课后作业
第三章3-2 在Coulomb 规范条件下，矢量位和标量位满足微分方程： （1） （2）可得：又由电荷守恒定律可知：0t J ρ∂∂∇∙+=(r)J j ωρ∴∇∙=-所以， （3）将（3）带入（1）可得：即证明之 3-4 （1）电流元产生的电磁场求解电Hertz 位满足其中(r)(r)e J P j ω=s=I J dS∙⎰又所以可得：电Hertz 位与场量之间的关系为：2(r)j (r)(r)(r)(r)e e e e eH E ωεωμε=∇⨯∏=∇∇∙∏+∏22()()()j ()k μωμε∇+=-∇ΦA r A r J r +r ()()ρε∇Φ=-2r r ()()4V dV ρπε''Φ='-⎰r r |r r |1()()j 4V dV ωπε'∇⋅'Φ=-'-⎰J r r |r r |22()()()()4Vk dV μμπ'∇⋅'∇+=--∇'-⎰J r A r A r J r |r r |e 2e2e()()()k ε∇+=-P r Πr Πr e j ||j ||e j ()11()4||j 4||j 4k k krzz Vl e Ie Il dV dz er επωεπωεπ''-----''==≈''--⎰⎰r r r r P r Πr e e r r r r代入可得： 其中cos e sin z r e e θθ-θ=（2）磁流元产生的电磁场求解 由对偶原理可得：3-13 y11,εμZ22,εμ如图所示，由边界条件 1212(E )0(H H )Sn E n J⨯-=⨯-=e e j j 2j 221()j ()j j 4sin j 1cos sin 44z kr kr krr Il r Il e e k Il e r r kr k r θφωεωεωεπθθθππ---⎛⎫=∇⨯=∇⨯ ⎪⎝⎭⎛⎫⎛⎫=∇⨯-=+ ⎪ ⎪⎝⎭⎝⎭H r Πr e e e e e e33j j 22332233()()j cos j 1sin 1j 1j j 24kr krr k Il k Il e e k r k r kr k r k r θωεθθπωεπωε--∇⨯=⎛⎫⎛⎫=-+--++ ⎪ ⎪⎝⎭⎝⎭H r E r e e m mmj m j j 2m j 221()j ()j j 4sin j 1cos sin 44kr z kr kr krr I l e r I l e e k I l er r kr k r θφωμωμωμπθθθππ----⎛⎫=-∇⨯=-∇⨯ ⎪⎝⎭⎛⎫⎛⎫=-∇⨯-=-+ ⎪ ⎪⎝⎭⎝⎭E r Πr e e e e m m33j j 22332233()()j cos j1sin 1j 1j j 24m m kr kr rk I l k I l e e k rk r kr k rk r θωμθθπωμπωμ--∇⨯=-⎛⎫⎛⎫=-+--++ ⎪ ⎪⎝⎭⎝⎭E r H r e e又因为(y)z J e I =δ所以可知磁场H 方向为x 方向，电场E 方向为z 方向。
大学电磁场课后答案第三章
ε1 ε 2 − ) σ1 σ 2 ε1 ε 2 ≠ σ1 σ 2
因此，分界面上存在自由电荷的条件是
3-8
在导体中有恒定电流而其周围媒质的电导率为零时，试证明导体表面电通量密度的法 向分量 Dn = σ ， 但矢量关系 D = e n σ 不成 立( 式中 e n 是导体表面向 外的法 线单位矢 量)。
W = ∑ σϕi ∫
i =1 n
n
Si
n ∂ϕ ∂ϕ − dS dS = ∑ σϕi ∫ S i ∂n ∂n ' i =1 n n Jn ' dS = ∑ ϕi J ' dS ϕi I i = ∑ ∫ Si n ∂n i =1 i =1
= ∑ σϕi ∫
i =1
Si
故命题得证。 3-10 有一非均匀导电媒质板，厚度为 d ，其两侧面为良导体电极，下板表面与坐标 z = 0 重 ρ − ρ R2 1 合， 介质的电阻率为 ρ R = = ρ R1 + R1 z， 介电常数为 ε 0 ， 而其中有 J = e z J 0 的 γ d 均匀电流。试求：1) 介质中的自由电荷密度。2) 两极板间的电位差。3) 面积为 A 的 一块介质板中的功率损耗。
u v
R铁＝
单位长度的水柱电阻为
ρ铁 S铁
＝
8.7 × 10 −8 π (0.025 2 − 0.02 2 ) ρ水 S水
R水＝
＝
0.01 π 0.02 2
当水管中的电流为 20A 时，水柱和铁管中的电流之比为
I水 I铁
又根据题意
＝
R铁 R水
＝1.5 × 10 −5
(1)
I 水＋I 铁＝20 A
所以将(1)、(2)联立求解，可得管壁和水中的电流强度
电磁场与电磁波(第三版)课后答案第3章
第三章习题解答3.1 真空中半径为a 的一个球面，球的两极点处分别设置点电荷q 和q -，试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。
解 由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e22322232()[]2d 4()()aq a arr r a r a ππ--=++⎰ 221201)0.293()aqa q q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型，其球体内均匀分布有总电荷量为Ze -的电子云，在球心有一正电荷Ze （Z 是原子序数，e 是质子电荷量），通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ，试证明之。
解 位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为 333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为32234344r r ar Ze rr r ρπππ==-D e e 故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中，体密度为30C m ρ, 两圆柱面半径分别为a 和b ，轴线相距为c )(a b c -<，如题3.3图()a 所示。
求空间各部分的电场。
解 由于两圆柱面间的电荷不是轴对称分布，不能直接用高斯定律求解。
但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布，这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布，而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布，如题3.3图()b 所示。
电磁场与电磁波(第四版)课后答案_第三章习题
习题三答案及解析
B选项
$( - frac{1}{2} + frac{3}{2}i)( frac{1}{2} + frac{3}{2}i)$ 可以
化简为 $-i$。
C选项
$( - frac{1}{2} - frac{3}{2}i)( frac{1}{2} + frac{3}{2}i)$ 可以
化简为 $-i$。
D选项
$frac{-2i}{-2i + 1}$ 可以 化简为 $-i$。
习题三答案及解析
答案
A. $-frac{1}{4}$
习题三答案及解析
B. $-i$
1
C. $-i$
2
D. $-i$
3
习题三答案及解析
01
解析
02
此题考查复数的乘法运算，根据复数乘法的定义和性质，可以得出答案。
03
A选项：$( - frac{1}{2} + frac{3}{2}i)( - frac{1}{2} - frac{3}{2}i)$ 可以化简为 $-frac{1}{4}$。
• 下一章将介绍电磁场与电磁波的基本原理和概念，包括电场、 磁场、电磁感应等。同时，还将介绍电磁波的传播方式和在不 同介质中的传播特性，以及电磁波的应用和影响。
THANKS
感谢观看
D选项
$100e^{- frac{pi i}{2}}$ 可以化简 为 $100(cosfrac{3pi}{2} + isinfrac{3pi}{2})$，与题目中的形 式一致。
习题二答案及解析
答案
A. $-frac{1}{2}$
习题二答案及解析
B. $-i$ C. $-i$ D. $-i$
《电磁场与电磁波》课后习题解答(第三章)
【习题 3.1】
解：设导线沿 ez 方向，电流密度均匀分布 则
J ez
4
I d
2
ez
4
2 (10 )
3
2
cos(2 50t ) ez
8
106 cos(2 50t（ ) A
m2
）
导线内的电场
E
J
ez
8 106 cos 2 50t ez 4.39 102 cos 2 50t (V / m) 7 5.8 10
J s n H er H ez 395.1cos(4 108 t ) A / m
（3） r 20mm, z 25mm 处的表面电荷密度
7 2 s n D 0 r er E 0. 7 8 1 0 sin ( 48 t1 0 C ) m /
B 1.328 6 107 0 sin 6 107 t cos zex t
1.328 6 107 4 107 sin 6 107 t cos zex 100sin 6 107 t cos zex
所以有
E
B t
ex
又因为
ey y 0
ex 1 1 E ( D) [ ( z 6 107 t )ex ] 2.5 0 2.5 0 x Ex (e y Ex E 1 ez x ) ey 4.52 1010 ey z y 2.5 0
ey y 0
ez z 0
12
= 4 81 8.854 10
i 6.28 109 E = i 4.5 i 4 E
6
电磁学第三章习题答案
第三章3.1 解：因螺绕环内的磁感应强度I n B 0μ=，所以副线圈中的感应电动势为VdtdI S dtd Sdtd 30103.1nN B N N --⨯===Φ=με副副副感应电流为A103.6RI 4-⨯==ε3.2 解：（1）设线圈发现→n 与→B 的夹角为零度时作为计时的起点，则t 时刻线圈中的感应电动势为tNBS dt t B d dt d ωωωεsin )cos S (-N-N==Φ=由此可以看出，当2t πω=或23t πω=时，即线圈法线与地磁场→B 的夹角为2π或23π时，感应电动势的值最大，此时ωεNBS m=（2）97N==ωεBS m 匝3.3 解：因距直导线为r 处的ri πμ2B 0=，所以（1）穿过回路ABCD 的磁通量t I a b l ldr riS d B basωπμπμsin ln 22000⎪⎭⎫⎝⎛==⋅=Φ⎰⎰⎰→→（2）回路ABCD 中的感应电动势 tI ab l dtωπωμεcos )(ln2d 00-=Φ-=3-5解：设t=0时，线圈与直导线处于同一平面内。
t 时刻俯视线圈与导线的相对位置如图3-19所示。
此时，线圈的有效面积是宽为AB 长为2a 的与长直导线共面的矩形面积。
穿过此有效面积的磁通量t t ab b a t ab b a b Ia tt ωωωπωμsin cos 21cos 21d )(d ε222220⎪⎭⎫⎝⎛-++++=Φ-=3-10解：设l 正方向如图3-23所示，则ac 段产生的感应电动势Vbc vB l d B l d B cbba30109.160cos 0)()(-→→→→→→⨯=+=⋅⨯+⋅⨯=⎰⎰ννε故感应电动势的方向为c a →，即c 点的电位高。
所以 V3oc 109.1U -⨯-=3-13解：（1）a,b 间的感应电动势22222121)(NBRR N B R B ldl B l d B d RLbaππωωυεε=⋅⋅===⋅⨯==⎰⎰⎰→→→（2）因ε的方向从轮心指向边缘，故在外电路上，I 的方向为b 指向a 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 稳恒电流场的边值问题3-1 在电导率为σ的均匀半空间表面布以相距2L 的电极A 和B ，并分别以I +和I -向媒质中供电。
试根据电场的叠加原理，求出A 和B 两个点电流源在表面上M 点形成的电位。
解：易知点电流源A 在介质中任意一点产生的电位为2A I RΦπσ=，同理可得点电流源B 在介质中任意一点产生的电位为2B IRΦπσ=-，则叠加后介质中任意一点的总电位为22A BI IR R Φπσπσ=-对于表面上一点M （设其坐标为(0)x ,）而言，||A R x L =+，||B R x L =-，则有22||||2||2||2||I I I x L x L x L x L x L Φπσπσπσ--+=-=+--3-2 当地表水平、地下为均匀各向同性岩石时，在地层表面布以相距2L 的电极A 和B ，并分别以电流强度I +和I -向地下供电，在地下建立稳定电流场。
试解答如下问题：（1）求A 和B 连线中垂线上h 处电流密度h j 的表达式；（2）计算并绘图说明深度为h 处的电流密度h j 随AB 的变化规律；（3）确定使h j 为最大时，供电电极距AB 与h 的关系式。
解：（1）易知点电流源A 在介质中任意一点产生的电位为2A IRΦπσ=，则31()()()=22A I I E R RσσΦσπσπ==⋅-∇=⋅-⋅∇Rj 同理可得点电流源B 在介质中任意一点产生的电流密度为32B I Rπ=-Rj ，叠加后得介质中任意一点的电流密度为3322A BA BI I R R ππ=-R R j 在A 、B 连线的中垂线上，A B R =R ，A B =2L ρ-R R e ，则有3322222()I I L L R L h ρρππ=⋅=⋅+j e e （2）（3）设3222()()f L L L h -=⋅+，对其求导可得35'2222222()()3()f L L h L L h --=+-+令其等于0，得22230L h L +-=，解得L = 故h j 为最大时电极距AB 与h 的关系为22AB L ===3-3 在习题3-2中，电极距AB 时，均匀各向同性半空间中h 深度处的电流密度最大。
如果在h 深度以下存在高阻或低阻岩层，在这种层状介质空间中，为保持h 深度电流密度不变，AB 将如何变化？为什么？3-4 如习题3-4图所示，在三层均匀地层表面布以相距为2L 的电极A 和B ，并分别以I + 和I -向地层媒质中供电。
试求出在地表M 点和N 点之间形成的电位差MN Φ，并讨论（1）MN Φ与1Z 和2Z 的关系；（2）MN Φ与1σ和2σ的关系。
Z Z Z 习题3-4图解：由题意知131u Au s =-，其中12A PP = 对矩阵1P 有12112212P P σσσ+==，12121212zP e λσσσ-=，12122112z P e λσσσ--= 对矩阵2P 有23112222P P σσσ+==，22231222z P e λσσσ-=，22232122zP e λσσσ--= 则由12A PP =计算后可得122()23231112()()()()=4z z e A λσσσσσσσσσσ-+++--1212 212223231212()()()()=4z z e e A λλσσσσσσσσσσ+-+-+1212 122223232112()()()()=4z z e e A λλσσσσσσσσσσ---+++-1212 212()23232212()()()()=4z z e A λσσσσσσσσσσ---+++1212设12112k σσσσ-=+，23223k σσσσ-=+，则有 1212122212112()2212121z z z z z z k e k e B A k k e k e k eλλλλλ-----+==+-- 则点电源在地表任意一点的电位为01010110(,0)[()2()][12()]22I I J d A J d A J d Φρλρλλρλρλρλπσπσρ∞∞∞=+=+⎰⎰⎰所以M 点的电位为10101010[12()[()]]2()[12()[()]]2()m A BM M M M M M IL L A J L L d L L I L L A J L L d L L ΦΦΦλλπσλλπσ∞∞=+=+++-++---⎰⎰同理可得N 点电位为10101010[12()[()]]2()[12()[()]]2()N N N N N N N I L L A J L L d L L IL L A J L L d L L Φλλπσλλπσ∞∞=+++-++---⎰⎰所以M 点和N 点之间形成的电位差MN M N ΦΦΦ=- （1） （2）3-5 （1）设在均匀各向同性无限大导电岩石中有一半径为a 的球形矿体，围岩电导率为1σ（电阻率为1ρ），球体电导率为2σ（电阻率为2ρ），导电岩石中流着均匀电流场，其电流密度为0J ，如习题3-5(a)图所示。
求稳恒时的电位分布与电流分布。
（2）由于地面电法勘探的供电和测量均在地面进行,如习题3-5(b)图所示，球心距地面距离为0h 。
求地下空间电流分布及地面电位分布。
(a)全空间均匀电流场中的导电球体 (b)半空间均匀电流场中的导电球体习题3-5图解：（a ）有球体存在时，球内球外电位有两部分电位（正常电位和异常电位）叠加而成。
这里将叠加后得电位称为一次场电位，而将异常部分称为一次场异常电位，并表示为(2)(2)101a U U U =+(1)(1)101a U U U =+其中0U 为均匀电流场的电位，(2)1a U 为球内一次场的异常电位，(1)1a U 为球外一次场的异常电位。
取球心电位为零，可以写出均匀电流场的正常电位解为001cos U j r ρθ=-。
易知球内外的电位具有轴对称性即与ϕ无关，于是满足以下形式的拉普拉斯方程21()(sin )0sin u Ur r r θθθθ∂∂∂∂+=∂∂∂∂ 采用分离变量法求解，并结合球内球外电位有限的条件可得得其通解形式为(2)10(,)(cos )n an n n Ur A r P θθ∞==∑(1)(1)10(,)(cos )n an n n U r B r P θθ∞-+==∑于是球内与球外一次电位的一般解为(2)1010cos (cos )n n n n U j r A r P ρθθ∞==-+∑(1)(1)1010cos (cos )n n n n Uj r B r P ρθθ∞-+==-+∑根据球体与围岩的分界面上电位连续的边界条件可得(1)010001000cos (cos )cos (cos )nn n n n n n n j r A r P j r B r P ρθθρθθ∞∞-+==-+=-+∑∑根据球体与围岩的分界面上电流密度法线分量的连续性边界条件可得00(1)(2)111211||r r r r U U r r ρρ==∂∂-=-∂∂ 即(2)(1)10010011221111cos (1)(cos )cos (cos )n n n n n n n n j n B rP j nA rP ρθθρθθρρρρ∞∞-+-==--+=-+∑∑联立以上二式解得21101212A j ρρρρρ-=-+3211010212B j r ρρρρρ-=-+0(1)n n A B n ==≠所以球内与球外的一次电位表达式为：(2)2110121[1]cos 2U j r ρρρθρρ-=-++(1)302110121[1()]cos 2r U j r rρρρθρρ-=-++由公式()A E σσΦ==⋅-∇j 即可求得空间的电流分布。
(b)地面的影响可以用一个镜像球体代替，如球心深度相对球体半径较大，即球体埋藏较深时可以忽略球体与地面以上镜像的相互作用。
这时采用将球外(1)1U 表达式的异常部分加倍的方法可以求得地下一次电位的一级近似解答。
302110121[12()]cos 2r U j r rρρρθρρ-=-++ （1）由公式()A E σσΦ==⋅-∇j 即可求得地下空间的电流分布。
若以球心在地面投影点o 为原点，z 轴垂直向下。
地面观察点坐标为(0)M x y ，， ，球心坐标为0(0 0 )h ，，，于是r =cos θ=代入式（1）中即可得到地面的电位分布。
3-6 球面偶电层产生的电流场。
如习题3-6图所示，有一半径为a ，电导率为2σ的均匀球形矿体，位于电导率为1σ的无限均匀媒质中。
设矿体处于氧化与还原的环境之中，因而在球面上产生一偶电层，其电位跃变为0cos ΦΦθ∆=∆其中0Φ∆为球面电位的最大跃变值，θ为极轴Oz 和球心至观测点P 的矢径之间的夹角。
求此球面偶电层在球内外所产生的电位分布。
习题3-6图解：用分离变量法求解。
设球外电势为1Φ，球内电势为2Φ，因1Φ和2Φ均满足拉普拉斯方程，且具有轴对称性，故1Φ和2Φ仅为θ、r 的函数，与方位角ϕ无关，其通解为1()(cos )n nn n n n B A r P r Φθ∞+==+∑ 定解过程如下：∞→r 时，10Φ→，故1Φ中无nr 项，即110(cos )nnn n B P rΦθ∞+==∑ 0→r 时，2Φ有限，故2Φ中无)1(+-n r项，即20(cos )nnn n A rP Φθ∞==∑球面两侧电势跃变120()cos r a u u ΦΦ∆∆θ=-==，则有θθcos )(cos )(001u P a A a B n n n n n n ∆=-∑∞=+球面两侧n J 连续，即 2121r ar arrΦΦγγ==∂∂=∂∂，则有∑∑∞=+∞=-+-=02112)(cos )1()(cos n n n n n n n n P aB n P anA θγθγ比较以上两式两端的)(cos θn P 系数，当1=n 时，得到0121u a A aB ∆=-， 311122aB A γγ-=联立求解以上两式，得a u A 0121122∆+-=γγγ， 0212212u a B ∆+=γγγ 当1≠n 时，0==n n B A 。
将所求出的各系数代入通解，得221021()cos 2au rγΦ∆θγγ=+120212()cos 2ru aγΦ∆θγγ=-+3-7 球形矿体在点电源中的场如习题3-7图所示，在电导率为2σ的无限大均匀媒质中有一半径为a 、电导率为1σ的均匀球形矿体，在距球心为d 的A 点处有一点电流源，其电流强度为I ，并取A 在oz 轴上。
（1）求球内和球外的电位分布；（2）设球形矿体和点电源均在地表下，求地表下的电位分布。