高三高考模拟试题

合集下载

2024届山东省高三新高考实战模拟全真演练物理试题(三)

2024届山东省高三新高考实战模拟全真演练物理试题（三）一、单选题：本题共7小题，每小题4分，共28分 (共7题)第(1)题下列说法正确的是（）A．电磁波在真空中以光速c传播B．在空气中传播的声波是横波C．声波只能在空气中传播D．光需要介质才能传播第(2)题如图所示，一高考倒计时牌通过一根轻绳悬挂在定滑轮上。

挂上后发现倒计时牌是倾斜的，已知∠AOB=90°，计时牌的重力大小为G。

不计一切摩擦，则平衡时绳OB中的张力大小为（）A．B．C．D．G第(3)题图甲为利用光电管研究光电效应的电路图，其中光电管阴极K的材料是钾，钾的逸出功为。

图乙为实验中用某一频率的光照射光电管时，测量得到的光电管伏安特性曲线，当电压为时，光电流恰好为零。

已知普朗克常量为h，光电子的电荷量为e。

下列说法正确的是（）A．该实验的入射光频率为B．该实验的光电子获得的最大初动能为C．光电管两极间的正向电压越大，光电流越大D．当入射光的频率小于时，仍可以发生光电效应第(4)题某汽车无线充电站的无线充电设备充电效率约为80%，一辆新能源汽车最大充电容量为，从0到100km/h的加速时间为7s。

当汽车电池容量低于最大容量20%，要求进入充电站进行充电。

下列说法正确的是（）A．充电过程能量不守恒B．从电池容量20%到充满电，需要消耗电能C．电机正常工作时的电流等于输入电压与电动机电阻的比值D．保持最大功率恒定不变加速时，汽车的加速度减小第(5)题下列实验中用到了模拟实验方法的是（）A．①②③④全都是B．只有②③④C．只有③④D．只有④第(6)题某种风力发电机的原理如图所示。

发电机的线圈固定，磁体在叶片驱动下绕线圈对称轴匀速转动的角速度为ω。

已知磁体间的磁场近似为匀强磁场，磁感应强度的大小为B，线圈的匝数为N、面积为S。

下列说法正确的是（）A．线圈中感应电动势的有效值B．1s内线圈中感应电流的方向改变次C．当线圈处在图中所示的位置时，线圈中的感应电动势达到最大值D．以图中线圈所处位置开始计时，线圈中感应电动势的瞬时值表达式为第(7)题如图所示，质量为2m的物块甲和质量为m的小球乙静止于固定光滑斜面上，二者间用平行于斜面的轻质弹簧相连，甲用细线拴在挡板上。

河北省石家庄市2024届高三下学期高考模拟预测数学试题【含答案】

2024年河北省石家庄市高考数学模拟试卷附解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．集合{}2024180,Z A k k αα︒==-︒+⋅∈∣中的最大负角α为（）A ．2024-︒B ．224-︒C ．44-︒D ．24-︒2．已知()41i 1iz +=-，则z 的虚部为（）A ．2iB ．2i-C ．2-D ．23．已知平面内的向量a 在向量b 上的投影向量为12b，且1a b == ，则2a b - 的值为（）AB ．1C ．34D ．324．设正项等比数列{}n a 的前n 项和为n S ，11a =，且3a -，2a ，4a 成等差数列，则2024S 与2024a 的关系是（）A ．2024202421S a =-B ．2024202421S a =+C ．2024202443S a =-D ．2024202441S a =+5．已知变量x 和y 的统计数据如表：x 12345y66788根据上表可得回归直线方程0.6y x a =+，据此可以预测当8x =时，y =（）A ．8.5B ．9C ．9.5D ．106．现将四名语文教师，三名心理教师，两名数学教师分配到三所不同学校，每个学校三人，要求每个学校既有心理教师又有语文教师，则不同的安排种数为（）A ．216B ．432C ．864D ．10807．已知椭圆221222:1(0),,x y C a b F F a b+=>>为左､右焦点，P 为椭圆上一点，1260F PF ∠=，直线:l y x t =-+经过点P .若点2F 关于l 的对称点在线段1F P 的延长线上，则C 的离心率是（）A ．13B ．22C ．12D ．238．已知函数()xf x x =，()0,x ∈+∞，则下列命题不正确的是（）A ．()f x 有且只有一个极值点B ．()f x 在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增C ．存在实数()0,a ∈+∞，使得()1ef a =D ．()f x 有最小值1e1e二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9．下列说法中，正确的是（）A ．一组数据10，11，11，12，13，14，16，18，20，22的第40百分位数为12B ．两组样本数据1x ，2x ，3x ，4x 和1y ，2y ，3y ，4y 的方差分别为21s ，22s ，若已知10i i x y +=（1,2,3,4i =），则2212s s =C ．已知随机变量X 服从正态分布()2,N μσ，若()()261P X P X ≥-+≥=，则2μ=D ．已知一系列样本点(),i i x y （1,2,3,i =⋅⋅⋅）的回归方程为ˆˆ3y x a =+，若样本点(),3m 与()2,n 的残差（残差＝实际值i y －模型预测值ˆy）相等，则310m n +=10．若关于x 的不等式22e 2ln x x ax x x -+-≥在()0+∞，上恒成立，则实数a 的值可以是（）A ．1eB ．12C ．e 3D ．211．已知定义在实数集R 上的函数()f x ，其导函数为()f x '，且满足()()()f x y f x f y xy +=++，()()110,12f f '==，则（）A ．()f x 的图像关于点()1,0成中心对称B ．()322f '=C ．()202410122023f =⨯D ．20241()10122024k f k ='=⨯∑三、填空题：本题共3小题，每小题5分，共15分.12．已知集合{}{}22230,0,M x x x N x x ax x =--<=-<∈Z ，若集合M N ⋂恰有两个元素，则实数a 的取值范围是.13．已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点，过2F 与双曲线的一条渐近线平行的直线交双曲线于点P ，若213PF PF =，则双曲线的离心率为.14．如图，在梯形ABCD 中，190,22ABC BAD AB BC AD ∠=∠====，将BAC 沿直线AC 翻折至1B AC △的位置，13AM MB =，当三棱锥1B ACD -的体积最大时，过点M 的平面截三棱锥1B ACD -的外接球所得的截面面积的最小值是.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15．已知函数()e e axf x x b =--在0x =处的切线为x 轴．(1)求,a b 的值；(2)求()f x 的单调区间．16．如图，三棱锥A BCD -中，,,,AD CD AD CD ADB BDC E ∠∠⊥==为线段AC 的中点.(1)证明：平面BED ⊥平面ACD ；(2)设3,2,0AB BD BF FD EF BD ===⋅=，求直线CF 与平面ABC 所成角的正弦值.17．有无穷多个首项均为1的等差数列，记第()*N n n ∈个等差数列的第()N,2m m m ∈≥项为()m a n ，公差为()0n n d d >.(1)若()()22212a a -=，求21d d -的值；(2)若m 为给定的值，且对任意n 有()()12m m a n a n +=，证明：存在实数,λμ，满足1λμ+=，10012d d d λμ=+；(3)若{}n d 为等比数列，证明：()()()()()1122mm m m m a a n n a a a n +⎡⎤⎣⎦+++≤ .18．设椭圆E ：22221x y a b +=()0a b >>经过点()2,1P -，且离心率e =:3m x =垂直x 轴交x 轴于T ，过T 的直线l 1交椭圆E 于()11,A x y ，()22,B x y 两点，连接PA ，PB ，PT ．(1)求椭圆E 的方程；(2)设直线PA ，PB 的斜率分别为1k ，2k ．（ⅰ）求12k k +的值；（ⅱ）如图：过P 作x 轴的垂线l ，过A 作PT 的平行线分别交PB ，l 于M ，N ，求||||MN MA 的值．19．在函数极限的运算过程中，洛必达法则是解决未定式00型或∞∞型极限的一种重要方法，其含义为：若函数()f x 和()g x 满足下列条件：①()lim 0x a f x →=且()lim 0x a g x →=（或()lim x a f x →=∞，()lim x ag x →=∞）；②在点a 的附近区域内两者都可导，且()0g x '≠；③()()lim x af x Ag x →'='（A 可为实数，也可为±∞），则()()()()limlimx ax af x f x Ag x g x →→'=='．(1)用洛必达法则求0limsin x xx→；(2)函数()()232112!3!21!n x x x f x x n -=+++++- （2n ≥，*n ∈N ），判断并说明()f x 的零点个数；(3)已知()()2cos g x g x x =⋅，()01g =，ππ,22x ⎛⎫∈- ⎪⎝⎭，求()g x 的解析式．参考公式：()()lim lim x a x af x f x →→=，()()lim lim x a x a kf x k f x →→=．1．C【分析】利用任意角的定义与集合A 所表示的角即可得解.【详解】因为04420211481︒=-︒-⨯︒-，所以集合{}2024180,Z A k k αα︒==-︒+⋅∈∣中的最大负角α为44-︒.故选：C.2．D【分析】利用复数的乘方运算和四则运算法则求出复数z ，继而得z 的虚部.【详解】由()42221i [(1i)](2i)4(1i)2(1i)22i 1i 1i 1i (1i)(1i)z ++-+=====-+=------+，则22i z =-+，z 的虚部为2.故选：D.3．A【分析】先根据条件，确定向量的夹角，再根据向量数量积的性质求模.【详解】因为2·1·2a b b b b = ⇒2·12a b b= ，又1a b == ，所以·12·a b a b =⇒1cos ,2a b = ⇒,60a b =︒ .所以：()2222a b a b-=-= 2214·41411432a ab b -+=-⨯⨯⨯+=，所以2a b -= 故选：A 4．A【分析】先利用等比数列的通项公式列方程求公比，然后求出2024S 和2024a 观察它们之间的关系即可.【详解】设正项等比数列{}n a 的公比为q ，0q >因为3a -，2a ，4a 成等差数列，所以2342a a a =-+，所以232q q q =-+，解得2q =，所以()20241202420241211a q S q-==--，20232023202412a a q==，则2024202421S a =-.故选：A.5．D【分析】根据给定的数表，求出样本的中心点，进而求出a 即可得解.【详解】依题意，1234535x ++++==，6678875y ++++==，即样本的中心点为(3,7)，于是70.63a =⨯+，解得 5.2a =，即0.6 5.2y x =+，当8x =时，预测0.68 5.210y =⨯+=.故选：D 6．B【分析】根据给定条件，利用分步乘法计数原理，结合分组分配列式计算得解.【详解】求不同的安排种数需要分成3步，把3名心理教师分配到三所学校，有33A 种方法，再把4名语文教师按2:1:1分成3组，并分配到三所学校，有2343C A 种方法，最后把2名数学教师分配到只有1名语文教师的两所学校，有22A 种方法，由分步乘法计数原理得不同的安排种数为32323432A C A A 432⋅⋅=.故选：B 7．B【分析】根据题意，得到点M 与点2F 关于PH 对称，从而2120F PM ∠=，在12PF F △中，利用正弦定理得到121212sin15sin105sin PF PF F F F PF +=+∠ ，结合sin 60sin15sin105c e a ==+，即可求解.【详解】由直线:l y x t =-+，且点2F 关于l 的对称点在线段1F P 的延长线上，如图所示，可得点M 与点2F 关于PH 对称，且1260F PF ∠=,故在2PF M 中，则2120F PM ∠= ,故230PF M ∠=又PH 的倾斜角为135 ，则245HF M ∠=，故在12PF F △中，有1260F PF ∠= ，21105PF F ∠=，1215PF F ∠= ，又由1212211212sin sin sin PF PF F F PF F PF F F PF ==∠∠∠，可得121212sin15sin105sin PF PF F F F PF +=+∠，即1222sin15sin105sin a cF PF =+∠ ，又因为1sin15sin(4530)22224=-⨯-⨯=，1sin105sin(6045)2=++ ，所以sin 602sin15sin1052c e a ===+.故选：B.8．C【分析】由条件可得函数ln z x x =可以看作为函数ln z y =与函数x y x =的复合函数，然后求导判断其单调性与极值，即可得到结果.【详解】由x y x =得ln ln y x x =，令ln z x x =，则函数ln z x x =可以看作为函数ln z y =与函数x y x =的复合函数，因为ln z y =为增函数，所以ln z x x =与x y x =单调性、图象变换等基本一致，ln 1z x '=+，由0z '=得1ex =，列表如下：x10,e ⎛⎫ ⎪⎝⎭1e 1,e ∞⎛⎫+ ⎪⎝⎭z '－＋z1e-由表知，ln z x x =在10,e ⎛⎫ ⎪⎝⎭上单调递减，在1,e ∞⎛⎫+ ⎪⎝⎭上单调递增，在1ex =时，取得极小值（最小值）1e -，所以()xf x x =在1,e ∞⎛⎫+ ⎪⎝⎭上单调递增，即B 正确；在1e x =时，取得唯一极值（极小值，也是最小值）1e 1e e->，即A 、D 都正确，C 错误.故选：C 9．BC【分析】A 选项，根据百分位数的运算公式得到答案；B 选项，利用平均数定义得到10y x =-，根据方差的计算公式得到()()()()2222123422214s x x x x x x x xs -++-++-++-+==；C 选项，由正态分布的对称性得到C 正确；D 选项，由题意得到()()ˆˆ336m an a -+=-+，得到D 错误.【详解】A 选项，0010404⨯=，故从小到大从第4个和第5个数的平均数作为第40百分位数，即121312.52+=，A 错误；B 选项，12344x x x x x +++=，12344y y y y y +++=，因为10i i x y +=，（1,2,3,4i =），故123410101010104x x x x y x -+-+-+-==-，故()()()()22221423124s x x x x x x x x-+-+--=+，()()()()2222123422*********s y x y x y x y x-++-++-++-+=()()()()2222123410101010101010104x x x x x x x x --++--++--++--+=()()()()222212344x x x x x x x x-++-++-++-+=，故2212s s =，B 正确；C 选项，因为()2,X N μσ ，()()261P X P X ≥-+≥=，2,6X X =-=关于x μ=对称，所以2622μ-+==，C 正确；D 选项，由题意得()()ˆˆ336m an a -+=-+，整理得39m n +=，D 错误.故选：BC 10．AB【分析】根据题意分12a ≤和12a >两种情况讨论，当12a ≤时，有222ln e e 12ln 1ln e 1ln x x x x ax x x x x x x x----+-++-+=+-+≥，通过求导，判断函数的单调性，确定函数的最值得出2ln e 1ln 0x x x x --+-+≥结论验证；当12a >时，令()2ln u x x x =--，求导判断出函数存在零点设为0x ，即可判断020000e 12ln (12)0x ax x a x x -+-+=-<，最后综合得出a 的取值范围.【详解】依题意，2e 12ln 0x ax x x -+-+≥在()0+∞，上恒成立，当12a ≤时，222ln e e 12ln 1ln e 1ln x x x x ax x x x x x x x----+-++-+=+-+≥，令2ln t x x =--，则()e 1t h t t =--，()e 1t h t '=-，故当t (,0)∈-∞时，()0h t '<，当(0,)t ∈+∞时，()0h t '>，故()(0)0h t h >=，故2ln e 1ln 0x x x x --+-+≥，则不等式成立；当12a >时，令()2ln u x x x =--，因为(1)10u =-<，(4)22ln 20u =->，故()x μ在()1,4内必有零点，设为0x ，则002ln x x -=，则020ex x -=，故020000e 12ln (12)0x ax x a x x -+-+=-<，不合题意，舍去；综上所述，12a ≤.故选：AB.【点睛】恒成立问题求参数注意分类讨论；适当的构造函数通过函数的最值分析参数的取值.11．BCD【分析】对A 、B ，利用赋值法进行计算即可得；对C 、D ，利用赋值法后结合数列的性质进行相应的累加及等差数列公式法求和即可得.【详解】对A ：令0x y ==，则有()()()0000f f f =++，即()00f =，令1x y ==，则有()()()2111f f f =++，又()10f =，故()21f =，()f x 不关于()1,0对称，故A 错误；对于B ，令1y =，则有()()()()11f x f x f x f x x +=++=+，两边同时求导，得()()11f x f x +='+'，令1x =，则有()()13211122f f =+=+=''，故B 正确；对C ：令1y =，则有()()()11f x f x f x +=++，即()()1f x f x x +-=，则()()()()()()()2024202420232023202211f f f f f f f =-+-+-+ ()2023120232023202210101220232+⨯=++++==⨯ ，故C 正确；对D ：令1y =，则有()()()11f x f x f x +=++，即()()1f x f x x +=+，则()()11f x f x +='+'，即()()11f x f x +-'='，又()112f '=，故()11122f k k k -'=+=-，则()20241112024202422101220242k f k =⎛⎫+-⨯ ⎪⎝⎭==⨯'∑，故D 正确.故选：BCD.【点睛】关键点点睛：本题C 、D 选项关键在于利用赋值法，结合数列的性质进行相应的累加及等差数列公式法求和.12．(2,)+∞【分析】解二次不等式化简集合M ，再利用二次不等式解的形式与交集的结果即可得解.【详解】因为{}2230{13}M x x x xx =--<=-<<∣，{}20,{()0,}N x x ax x x x x a x =-<∈=-<∈Z Z ∣，又集合M N ⋂恰有两个元素，所以M N ⋂恰有两个元素1和2，所以2a >.故答案为：(2,)+∞.13【分析】设过2F 与双曲线的一条渐近线by x a=平行的直线交双曲线于点P ，运用双曲线的定义和条件可得1||3PF a =，2||PF a =，12||2F F c =，再由渐近线的斜率和余弦定理，结合离心率公式，计算即可得到所求值．【详解】解：设过2F 与双曲线的一条渐近线b y x a=平行的直线交双曲线于点P ，由双曲线的定义可得12||||2PF PF a -=，由12||3||PF PF =，可得1||3PF a =，2||PF a =，12||2F F c =，由12tan b F F P a ∠=可得12cos a F F P c ∠=，在三角形12PF F 中，由余弦定理可得：222121221212||||||2||||cos PF PF F F PF F F F F P =+-∠ ，即有2229422aa a c a c c=+- ，化简可得，223c a =，则双曲线的离心率==c e a【点睛】本题考查双曲线的离心率的求法，注意运用双曲线的渐近线方程和定义法，以及余弦定理，考查化简整理的运算能力，属于中档题．14．3π4【分析】当三棱锥1B ACD -的体积最大时，此时1B 到底面ACD 的距离最大，即此时平面1⊥B AC 平面ACD ，取AC 的中点E ，AD 的中点O ，O 是三棱锥1B ACD -的外接球球心，当且仅当过点M 的平面与OM 垂直时，截外接球的截面面积最小，此时，截面的圆心就是点M ，从而求解.【详解】当三棱锥1B ACD -的体积最大时，由于底面ACD 的面积是定值，所以此时1B 到底面ACD 的距离最大，平面1⊥B AC 平面ACD ，且平面1B AC 平面ACD AC =，取AC 的中点E ，则1B E AC ⊥，故1B E ⊥平面ACD ，取AD 的中点O，则OE =1B E =1π2B EO ∠=，则12OB =，又∵2OA OD OC ===，故O 是三棱锥1B ACD -的外接球球心，且该外接球的半径2R =；显然，当且仅当过点M 的平面与OM 垂直时，截外接球的截面面积最小，此时，截面的圆心就是点M ，记其半径为r ，则222R OM r ==+；由于AC CD ⊥，CD ⊂平面ACD ，所以CD ⊥平面1B AC ，而1AB ⊂平面1B AC ，则1CD AB ⊥，则1π2AB D ∠=，在1B AD 中，12,4B A AD ==，故1π3B AD ∠=；又13AM MB = ，故12AM =，又2OA =，故由余弦定理有211π13422cos 4234OM =+-⨯⨯⨯=，∴22234r R OM =-=，故所求面积为3π4.故答案为：3π4【点睛】关键点点睛：取AD 的中点O ，由12OA OD OC OB ====，确定点O O 是三棱锥1B ACD -的外接球球心.15．(1)e a =，1b =(2)单调递减区间为(),0∞-，单调递增区间为()0,∞+【分析】（1）求出函数的导函数，依题意可得()00f =且()00f '=，即可得到方程组，解得即可；（2）求出函数的导函数()f x '，再利用导数说明()f x '的单调性，即可求出()f x 的单调区间.【详解】（1）因为()e e ax f x x b =--，所以()e e ax f x a '=-，依题意()00f =且()00f '=，所以00e 0e e 0b a ⎧-=⎨-=⎩，解得e 1a b =⎧⎨=⎩.（2）由（1）可得()e e e 1x f x x =--函数的定义域为R ，又()()e 1e e e e e 1x xf x +'=-=-，令()()e 1e e xg x f x +'==-，则()e 2e0x g x +'=>，所以()g x （()f x '）在定义域R 上单调递增，又()00f '=，所以当0x <时()0f x '<，当0x >时()0f x ¢>，所以()f x 的单调递减区间为(),0∞-，单调递增区间为()0,∞+.16．(1)证明见解析(2)15【分析】（1）根据等腰三角形的三线合一及全等三角形的性质，利用线面垂直的判定定理及面面垂直的判定定理即可求解；（2）利用线面垂直的判定定理及性质定理，建立空间直角坐标系，求出相关点的坐标，分别求出直线CF 的方向向量与平面ABC 的法向量，利用向量的夹角公式，结合向量的夹角与线面角的关系即可求解.【详解】（1）因为DA DC =，E 为线段AC 的中点，所以DE AC⊥因为DA DC =，DB DB =，ADB CDB ∠=∠，所以ADB CDB ≌，故AB CB =．又E 为线段AC 的中点，所以BE AC ⊥．又DE BE E ⋂=，,DE BE ⊂平面BED .所以AC ⊥平面BED又AC ⊂平面ACD ，所以平面BED ⊥平面ACD ．（2）取DA 的中点G ，连接EG ，BG ，因为EG 为中位线，所以//EG CD ，又AD CD ⊥，所以AD EG ⊥．因为AB BD =，G 为DA 的中点，所以AD BG ⊥．又⋂=EG BG G ，,EG BG ⊂平面BEG ，所以AD ⊥平面BEG ，BE ⊂平面BEG ，所以AD BE ⊥，因为BA BC =，E 为AC 的中点，所以AC BE ⊥，又AC AD A = ，,AC AD ⊂平面ACD ，所以BE ⊥平面ACD ．以E 为坐标原点，分别以EA 、EB 、ED 所在的直线为x 、y 、z 轴，建立空间直角坐标系E xyz -，如图所示设(),0,0A a ，(),0,0B b ，则()0,0,0E ，()0,0,D a ，()0,,0B b ，20,,33b a F ⎛⎫ ⎪⎝⎭．20,,33b a EF ⎛⎫= ⎪⎝⎭，()0,,BD b a =- ，由22222||92033AB a b b a EF BD ⎧=+=⎪⎨⋅=-+=⎪⎩，解得a b ⎧⎪⎨=⎪⎩．所以,33CF ⎫=⎪⎪⎭.又平面ABC 的法向量()0,0,1n = ．设直线CF 与平面ABC 所成角为θ，则232153sin cos ,15CF n CF n CF nθ⋅===⋅ ,所以直线CF 与平面ABC.17．(1)212d d -=；(2)证明见解析(3)证明见解析【分析】（1）代入等差数列的通项公式，即可求解；（2）根据已知条件，代入等差数列的通项公式，得到数列{}n d 的递推公式，再通过构造得到数列{}n d 的通项公式，并根据（1）的结果，证明等式；（3）根据题意，结合等差数列和等比数列的综合应用，首先证明()()()()11m m m m a n i a i a n a +-+≤+，再利用求和，即可证明.【详解】（1）由题意得()()()2221212111a a d d d d -=+-+=-，又()()22212a a -=，所以212d d -=；（2）证明：因为()()12m m a n a n +=，所以()()111211n n m d m d ++-=+-⎡⎤⎣⎦，即1121n n d d m +=+-，所以111211n n d d m m +⎛⎫+=+ ⎪--⎝⎭，因此99100111211d d m m ⎛⎫+=+ ⎪--⎝⎭，所以99100111211d d m m ⎛⎫=+- ⎪--⎝⎭，又21121d d m =+-，即21121d d m =--，因此()()()()99999910012121122222221d d d d d d d d =+---=-+-，所以存在实数999922,21λμ=-=-，满足100121,d d d λμλμ+==+；（3）证明：因为{}n d 为等比数列，所以11n n d d q -=，其中q 为{}n d 的公比，于是()()1111n m a n m d q -=+-，当1i n ≤≤时，()()()()11m m m m a n i a i a n a +-+-+⎡⎤⎣⎦()()11111n i i n m d q q q ---=-+--()()()11111n i i m d q q --=----，因为0,0,10q n i i >-≥-≥，因此()()1110m i i q q ----≥，又()110m d --<，所以()()()()11m m m m a n i a i a n a +-+≤+，因此()()()()111nm m m m m a n i a i n a n a =+-+≤+⎡⎤⎡⎤⎣⎦⎣⎦∑，即()()()()()2121m m m m m a a a n n a n a +++≤+⎡⎤⎡⎤⎣⎦⎣⎦ ，所以()()()()()1122mm m m n a a n n a a a n +⎡⎤⎣⎦+++≤ .【点睛】关键点点睛：本题的关键是利用题意，并能正确表示()m a n 和公差为n d .18．(1)22163x y +=(2)（i ）2；（ii ）1【分析】（1）根据条件，列出关于,,a b c 的方程组，利用待定系数法，即可求解；（2）（ⅰ）首先设直线1l 的方程，并联立椭圆方程，转化为关于斜率的一元二次方程，利用韦达定理，即可求解；（ⅱ）首先设直线,PA PB 的倾斜角分别为,αβ,根据正弦定理利用角表示边长MN ，AN ，再求比值，利用（ⅰ）的结论，即可求解.【详解】（1）由题意知2222241122a b c a a b c ⎧+=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得ab c ==所以椭圆E 的方程为22163x y +=；（2）（ⅰ）易知()3,0T ，1PT k =，11112y k x +=-，22212y k x +=-，设直线1l 的方程为()()211m x n y -++=，由直线1l 过()3,0T 知1m n +=，联立方程()()22163210x y m x n y ⎧+=⎪⎨⎪-++=⎩得()()()()()()()2224144211420n y n m x y m x -++--+++-=，变形得：()()211244414022y y n n m m x x ++⎛⎫-+-++= ⎪--⎝⎭，即()1244144842424242n n n m n k k n n n ----+====---；（ⅱ）设直线,PA PB 的倾斜角分别为,αβ,则1tan k α=，2tan k β=，5π4NMP β∠=-，π2MPN β∠=-,π4PAN α∠=-，π2APN α∠=-，在PMN 中，πsin sin πsin 2sin 4PN PNMN MPN NMP ββ⎛⎫=∠=- ⎪∠⎛⎫⎝⎭- ⎪⎝⎭，在PAN △中，πsin sin πsin 2sin 4PN PN AN APN PAN αα⎛⎫=∠=- ⎪∠⎛⎫⎝⎭- ⎪⎝⎭，所以()ππsin sin cos sin cos tan 1242ππtan 1sin sin 422MN AN βαβαααββα⎛⎫⎛⎫-⋅--- ⎪ ⎪-⎝⎭⎝⎭===--⎛⎫⎛⎫-⋅- ⎪ ⎪⎝⎭⎝⎭由122k k +=知，tan tan 2αβ+=，即tan 11tan 1αβ-=--，故1MNAN =..【点睛】关键点点睛：本题第一问的转化比较巧妙，转化为关于斜率的方程，利用韦达定理即可求解，第二问巧妙设倾斜角，利用三角函数表示MN AN 的值.19．(1)1(2)仅在(),0x ∈-∞时存在1个零点，理由见解析(3)()()()sin ,π,00,π,1,0.x x g x x x ⎧∈-⋃⎪=⎨⎪=⎩【分析】（1）利用洛必达法则求解即可；（2）构造函数()e x f x ，结合()e xf x 的单调性求解即可；（3）利用累乘法求出()2n g x x g ⎛⎫ ⎪⎝⎭的表达式，然后结合()01g =，利用洛必达法则求极限即可.【详解】（1）001lim lim 1sin cos x x x x x →→==（2）()()2321123!21!n x x x f x x n -=+++++- ，()()232212!3!22!n x x x f x x n -'=+++++- ，所以()()()2121!n x f x f x n -'-=--，()()()()21e e e 21!n x x xf x f x f x x n -⎡⎤'-='=-⎢⎥-⎣⎦．当0x >时，()0e x f x ⎡⎤'<⎢⎥⎣⎦，函数()e x f x 在()0,∞+上单调递减，当0x <时，()0e x f x ⎡⎤'>⎢⎥⎣⎦，函数()e x f x 在(),0∞-上单调递增，()lime xx f x →-∞=-∞，()01f =，当0x >时，()0e x f x >，所以仅在(),0x ∈-∞时存在1个零点．（3）()()2cos g x x g x =，所以()cos 22g x x x g =⎛⎫ ⎪⎝⎭，2cos 44x g x x g ⎛⎫ ⎪⎝⎭=⎛⎫ ⎪⎝⎭，…，12cos 22n n n x g x x g -⎛⎫ ⎪⎝⎭=⎛⎫ ⎪⎝⎭将各式相乘得()cos cos cos 2422n n g x x x x x g =⋅⋅⋅⎛⎫ ⎪⎝⎭ cos cos cos sin 1sin 24222sin sin 22n n n n nx x xxx x x ⋅⋅⋅⋅=⋅ ，两侧同时运算极限，所以()1sin sin 22lim lim lim sin sin 222n n n n n n n n x x g x x x x x x g →+∞→+∞→+∞⋅==⋅⎛⎫ ⎪⎝⎭，即()()sin 2lim 0sin 2n n n x g x x xg x →+∞=，令2nx t =，原式可化为()()0sin lim 0sin t g x x t g x t →=，又()01g =，由（1）得0lim1sin t t t →=，故()()sin 0x g x x x=≠，由题意函数()g x 的定义域为()π,π-，综上，()()()sin ,π,00,π,1,0.x x g x x x ⎧∈-⋃⎪=⎨⎪=⎩【点睛】方法点睛：本题考查新定义，注意理解新定义，结合洛必达法则的适用条件，构造函数()2n g x x g ⎛⎫ ⎪⎝⎭，从而利用洛必达法则求极限.。

浙江省宁波市 2023—2024学年高三第一学期高考模拟考试语文试题(含答案)

浙江省宁波市2023—2024学年高三第一学期高考模拟考试语文试题一、现代文阅读(35 分)(一)现代文阅读I (本题共5小题，35 分)阅读下面的文字，完成1~5 题。

对于中国动画电影而言，民族风格既是起点，也是高峰，同时还是整个行业的一大执念，各个时期价动画电影的标准都离不开民族风格这一标尺。

尤其是21 世纪之交，面对好莱坞“狼来了”的生死冲击中国动画电影在《宝莲灯》之后就陷入了长期的低迷。

直到《西游记之大圣归来》《哪吒之魔童降世》之前，中国动画电影甚至没有一部可以达到这一基本考核标准的作品。

对于出品方追光动画而言，在《长安三万里》之前也创作了《白蛇: 缘起》《新神榜:杨》等作品，历经了三个发展阶段。

在其小切口实践创意表达、技术实现等第一阶段，《小门神》《阿唐奇遇》《猫与桃花源》等相对中小成本影片，就呈现出了非常清晰的将中华优秀传统文化与现代价值融会贯通的尝试，并且在现代动画技术上完成了多维度的经验积累。

在完成创意表达、技术实现等初步积累进入到第二阶段之后，《白蛇: 缘起》《新神榜:哪重生》等影片呈现出了“重工业化”的样貌，除了动画视效上接近世界主流动画电影的水平，在类型上也非常大胆地尝试了赛博朋克、蒸汽朋克和废土朋克等20 世纪70 年代以来北美的通俗流行文化类型。

这种整体性“突进”的尝试，在中国动画电影史上还是首次。

所以在经过第二阶段类型、风格等“极限”式探索之后，到了第三阶段，《白蛇2:青蛇劫起》《新神榜: 杨》等影片尽管作为各自系列影片前作的延续，但在题材和类型上都已经呈现出相对“回撤”的艺术上的均衡性，更注重整体的协调度和完成度，特别是《新神榜: 杨》在动画的视觉特效上又默默将行业标尺提升到了新的高度。

《白蛇》系列、《新神榜》系列，不仅有着稳定的票房表现，在很多国家和地区都有着不错的口碑，并且登陆奈飞等知名流媒体平台。

据此，我们再回看《长安三万里》，其意义就不仅仅是合家欢、全年龄向等所能简单概括的。

新高考八省联考2025届高三模拟考试语文试题2(解析版)

新高考八省联考2025届高三模拟考试语文试题2一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，19分）阅读下面的文字，完成1~5小题。

材料一：文学主题与历史主题、时代主题紧密相连。

中华民族伟大复兴是当今中国的时代主题，也是新时代文学的主题。

心系民族复兴伟业，热忱描绘新时代新征程的恢宏气象，是当代作家的使命所在。

以脱贫攻坚为例，中国共产党团结带领中国人民打赢脱贫攻坚战，在中华大地上全面建成了小康社会，历史性地解决了绝对贫困问题，摆脱贫困的广袤乡土正朝着乡村振兴的目标迈进。

相应地，在文学界涌现出赵德发《经山海》、陈毅达《海边春秋》、王松《暖夏》、季栋梁《西海固笔记》等以脱贫攻坚为主题的优秀作品。

这些作品虽然题材各异，形式风格不同，但从中我们能看到因地制宜的脱贫实践，看到扶贫干部、乡村群众、创业青年、支教老师等人物故事，感受到苦干实干的奋斗精神。

与此相似，生态文明建设、中华优秀传统文化创造性转化创新性发展、构建人类命运共同体等新命题，也拓宽着我们的思想视野，给文学创作提供前所未有的广阔空间。

作家们瞄准这些命题，以文学的方式记录时代步伐，描绘发展画卷。

新时代文学主题更加鲜明，源于当代作家更加强烈的历史主动精神和更加自觉地深入生活、扎根人民，同时也离不开作家在文学创作上的锤炼打磨。

“登高使人心旷，临流使人意远。

”越来越多的作家意识到，只有深刻把握民族复兴的时代主题，以文学的方式感国运之变化、立时代之潮头、发时代之先声，不断锤炼文学深入时代、表现时代的能力水平，新时代文学才能真正做到与时代同频共振。

深刻把握民族复兴的时代主题，是当代作家贯穿创作始终的功课。

这不仅意味着作家要带着历史视野穿透现实，认识时代主题的独特性与丰富性，书写时代主题所带来的重大社会变革以及蕴含其中的中国精神；还意味着要对文学手法进行探索打磨，更独到地切入主题，更艺术性地呈现主题，将主题高度真正转化成艺术高度。

我们的现实生活中传统、现代因素相互交织，农业文明、工业文明、信息文明彼此并存，既不同于以往的历史，也不同于经典作家已有的文学叙述。

2024届辽宁省名校联盟高三高考模拟卷四英语试题及答案

辽宁省名校联盟2024年高考模拟卷（信息卷）英语（四）第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题纸上。

第一节（共5小题；每小题1. 5分，满分7. 5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. ￡19. 15.B. ￡9. 18.C. ￡9. 15.答案是C。

1. What’s the woman doing?A. Hanging out with Bob.B. Visiting her aunt.C. Doing some shopping.2. What does the man advise the woman to do?A. See a doctor.B. Take some medicine.C. Have a good rest.3. What will the man do next?A. Look after the baby.B. Help in the kitchen.C. Clean up the mess.4. Where will the woman pick up the man?A. From the city museum.B. From a bus stop.C. From the man’s home.5. How much will the man pay for the tickets?A. 600 yuan.B. 750 yuan.C. 900 yuan.第二节（共15小题；每小题1. 5分，满分22. 5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项。

2024届浙江省宁波市高三上学期高考模拟考试全真演练物理试题

2024届浙江省宁波市高三上学期高考模拟考试全真演练物理试题一、单项选择题（本题包含8小题，每小题4分，共32分。

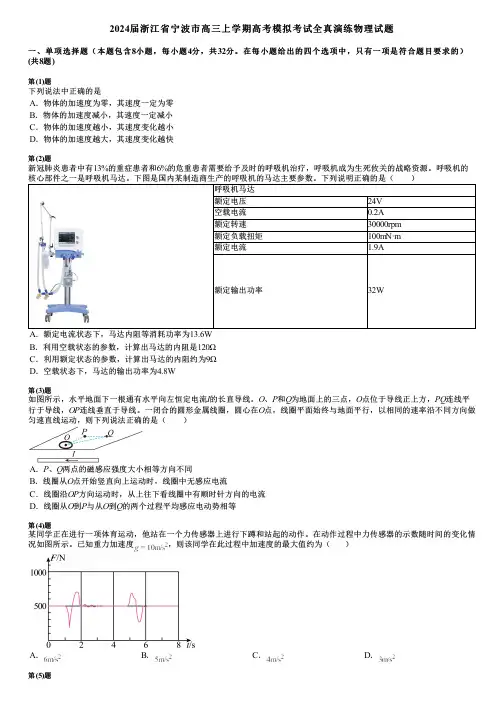
在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题下列说法中正确的是A．物体的加速度为零，其速度一定为零B．物体的加速度减小，其速度一定减小C．物体的加速度越小，其速度变化越小D．物体的加速度越大，其速度变化越快第(2)题新冠肺炎患者中有13%的重症患者和6%的危重患者需要给予及时的呼吸机治疗，呼吸机成为生死攸关的战略资源。

呼吸机的核心部件之一是呼吸机马达。

下图是国内某制造商生产的呼吸机的马达主要参数。

下列说明正确的是（）呼吸机马达额定电压24V空载电流0.2A额定转速30000rpm额定负载扭矩100mN·m额定电流 1.9A额定输出功率32WA．额定电流状态下，马达内阻等消耗功率为13.6WB．利用空载状态的参数，计算出马达的内阻是120ΩC．利用额定状态的参数，计算出马达的内阻约为9ΩD．空载状态下，马达的输出功率为4.8W第(3)题如图所示，水平地面下一根通有水平向左恒定电流I的长直导线。

O、P和Q为地面上的三点，O点位于导线正上方，PQ连线平行于导线，OP连线垂直于导线。

一闭合的圆形金属线圈，圆心在O点，线圈平面始终与地面平行，以相同的速率沿不同方向做匀速直线运动，则下列说法正确的是（）A．P、Q两点的磁感应强度大小相等方向不同B．线圈从O点开始竖直向上运动时，线圈中无感应电流C．线圈沿OP方向运动时，从上往下看线圈中有顺时针方向的电流D．线圈从O到P与从O到Q的两个过程平均感应电动势相等第(4)题某同学正在进行一项体育运动，他站在一个力传感器上进行下蹲和站起的动作。

在动作过程中力传感器的示数随时间的变化情况如图所示。

已知重力加速度，则该同学在此过程中加速度的最大值约为（）A．B．C．D．第(5)题如图所示，一半径为的玻璃半球，点是半球的球心，虚线表示光轴（过球心与半球底面垂直的直线）。

2023届浙江省宁波市高三上学期高考模拟考试全真演练物理试题

2023届浙江省宁波市高三上学期高考模拟考试全真演练物理试题一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题用轻弹簧竖直悬挂质量为m的物体，静止时弹簧伸长量为L。

现用该弹簧沿斜面方向拉住质里为2m的物体，系统静止时弹簧伸长量也为L。

斜面倾角为30°，如图所示．则物体所受摩擦力（）A．等于零B ．大小为，方向沿斜面向下C．大小为，方向沿斜面向上D．大小为mg，方向沿斜面向上第(2)题如图，用长为的轻绳悬挂一质量为M的沙箱，沙箱静止．一质量为m的弹丸以速度水平射入沙箱并留在其中，随后与沙箱共同摆动一小角度．不计空气阻力．对子弹射向沙箱到与其共同摆过一小角度的过程( )A．若保持m、v、不变，M变大，则系统损失的机械能变小B．若保持M、v、不变，m变大，则系统损失的机械能变小C．若保持M、m、不变，v变大，则系统损失的机械能变大D．若保持M、m、v不变，变大，则系统损失的机械能变大第(3)题2020年12月3日，嫦娥五号上升器在月球表面从着陆器上返回，如图所示。

已知携带月壤样本的上升器重量高达，开始一段时间内的加速度大小为，月球表面的重力加速度大小为，上升器发动机向下喷出气体的速度为，不计由于喷出气体上升器质量的变化，则每秒喷出气体的质量为（）A．B．C．D．第(4)题在某介质中位于坐标原点的波源在时刻起振，形成一列沿x轴正方向传播的简谐横波，如图所示为时刻的波形图，已知波恰好传到处。

下列说法正确的是（）A．处质点的首次起振方向沿y轴正方向B．波的传播速度为20m/sC．再经过0.1s，处质点会运动到处D．内质点H通过的路程为5cm第(5)题如图所示，足够长的水平传送带以的速率顺时针匀速运行，时，在最左端轻放一个小滑块，时，传送带突然制动停下，已知滑块与传送带之间的动摩擦因数为，取，下列关于滑块相对地面运动的图像正确的是（）A．B．C．D．第(6)题茫茫宇宙中存在大量的宇宙射线，对宇航员构成了很大威胁。

2024届陕西省宝鸡市高三上学期高考模拟检测(一)语文试题及答案

2024年宝鸡市高考模拟检测（一）语文注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（36分)（一）论述类文本阅读（本题共3小题，9分)阅读下面的文字，完成1～3题。

对科学而言，存在一种已经建立的框架，使得任何科学家都可以证明别人是错误的，而且能确保所有人都能够知道这一点。

因此我觉得似乎是社会的混乱和人类的缺陷帮助了科学事业的存在与发展。

科学家有时也会犯错误，他们常会犯选择性观察的错误，因为他们有时过分主观，倾向于记住那些成功的经历而忽视了另外一些情况。

但是，在很多情况下，这些错误往往蕴含着正确的部分，或是能够激励其他人去发现真正正确的东西。

弗雷德·霍伊尔是当代最杰出的天文物理学家之一，他在恒星演化、宇宙学及其他许多问题上做出了不可磨灭的贡献。

与此同时，他也提出了不少错误的古怪观点，以致观察人员与实验人员觉得必须去验证。

尽管这些验证胜败交错，但几乎在每个问题上这些努力都将相应领域的研究向前大大推进了。

例如，他曾提出流感病毒和艾滋病病毒来源于彗星，认为星际灰尘颗粒是些细菌。

在论证或反驳其观点的过程中，研究人员获得了丰富的和有意义的新知识，尽管最终没有找到任何证据证明这些特别的见解。

列出一些科学家犯错误的例子对科学家不无益处，揭去科学神秘的面纱将有助于启迪年轻的科学家。

在历史上，即使是像牛顿、达尔文、爱因斯坦这样伟大的科学家也曾犯过严重的错误。

幸运的是，正因为科学事业是一种集体的事业，所以任何个人的影响和作用都不能超过集体。

因此，即使那些最有才华的科学家犯了错误，这些错误也能被其他远不如他们的科学家发现并弥补。

不同的科学家有着不同的思考习惯，有一些可能更谨慎一些。

山东省潍坊市2024届高三下学期4月高考模拟考试(二模)英语试题(含答案)

潍坊市高考模拟考试英语2024.4注意事项:1.答题前，考生务必将自己的姓名、座号、考号填写在答题卡和试卷指定位置上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

第一部分阅读(共两节,满分50分)第一节(共15小题;每小题2.5分，满分37.5分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项。

AThe backpack you take can make or break your trip when you go traveling. Here are the four best travel backpacks on the market.Amazon Basics 70LIt's much cheaper than many travel bags on the market and does not sacrifice any of the practical uses or space that comes with more expensive bags. The bag may not be as luxury as some of the more high-end bags, but its simple style lets you focus on the main thing you need to focus on when traveling: the moment.Eurohike Nepal 65LThe Eurohike Backpack is a great choice because of how adaptable it is. Besides having a great amount of storage, it comes with an internal security pocket. It weighs just 1.38kg as opposed to other backpacks, which can weigh up to nearly 2kg. If you're going to go hiking when you travel, then it is perfect.Mountain Warehouse Tor 65LFirst , its brand is one of the most trusted in the industry ,so quality is guaranteed. Second, the backpack's adjustable back allows you to change how the bag fits according to your needs. Available inboth blue and green, this is a great choice if you want a bag that you can depend on.Osprey Europe Farpoint 70LOsprey is one of the best brands for backpacks. Its frame(框架)suspension, which can be adjusted to different needs, allows you to travel more comfortably. Whether you're visiting Switzerland in a thick, wool coat or the south of France in shorts and a T-shirt, the bag will match your look. This bag does say it is marketed for men, but, of course , it can be unisex.1. What is the selling point of the Amazon Basics?A. Its luxury style.B.Its fashionable design.C. Its huge space for use.D. Its good value for money.2. What do Mountain Warehouse Tor 65L and Osprey Europe Farpoint 70L have in common?A. They are rich in color.B. They have the same capacity.C. They can be adjusted as needed.D. They are targeted for male customers.3. Which will you choose if anti-theft function is a concern?A. Amazon Basics 70L. B .Eurohike Nepal 65L.C. Mountain Warehouse Tor 65L,D. Osprey Europe Farpoint 70L.BAt just seven years old, Angelina Tsuboi discovered her passion for innovation. It all began with a simple game she programmed in her Los Angeles public school's Grade 2class. Today ,at18,the Grade 12 student's initial curiosity has evolved into a deep-seated desire to use technology to decode(解码)real-world problems.In 2021, she co-developed Megaphone, one of her first apps, to tackle unanswered post- class questions and poor communication about events and announcements. Her problem-solving ability kept building from there.When she took online CPR classes at the start of the pandemic, she figured it couldn't be just her who was struggling with the steps. So she created an app called CPR Buddy―a winner in the 2022 Apple Swift Challenge―which guides users through CPR using vibrations(震动) to regulate breath. After winning theaward, Angelina presented her work to Apple CEO Tim Cook, a highlight in her young career, but one she didn't lose her cool over. “There's no point putting people on a pedestal (神坛),”she says.The next year, Angelina built an app called Lilac, designed to assist nonEnglish-speaking single parents with resources for housing, job opportunities and translation support. She was inspired by her own experiences as a child of a single mother who immigrated to the US.When Angelina decided to pursue pilot training at the age of 16, she was struck by how difficult it was to find financial support, which encouraged her to create yet another app, Pilot Fast Track, which helps those longing to be pilots find scholarships for flight training.Looking to the future, besides applying to colleges with great labs, Angelina is exploring the field of aerospace cybersecurity and mechatronics―combining computer science, electrical engineering and mechanical engineering.“There's not enough optimism in the world," she says. “I have also been in situations in my life where I've lost a lot of hope. But in the end, it is a mindset, and there are ways in any situation you're in to make it somewhat better."4.What is Angelina's pursuit?A. To design games for kids.B. To stimulate teen's curiosity.C. To address problems through technology.D. To find innovative approaches to digital challenges.5.What can we learn about Angelina from Paragraph 3?A. She couldn't breathe regularly.B. She was inspired by celebrities.C. She replaced CPR with an app.D. She was humble about her success.6.What was the primary goal of developing Pilot Fast Track?A. To direct pilots' career paths.B. To help to-be pilots find funds.C. To pair future pilots with airlines.D. To evaluate pilot training schools.7. What might be the best title?A. Breaking the codeB. Bearing growing painsC. Facing life as it isD. Following role modelsCSome people today might be early risers because of DNA they take after Neanderthals tens of thousands of years ago, suggests new research.When early humans migrated from Africa to Eurasia roughly 70,000 years ago, some of them mated with Neanderthals, who had already adapted to the colder, darker climates of the north. The ripple(涟漪) effects of that intermating still exist today: Modern humans of non- African ancestry(血统)have between 1 and 4 percent Neanderthal DNA. Some of that DNA relates to sleep more specifically, the internal body clock known as the circadian rhythm.For the new study, researchers compared DNA from today's humans and DNA from Neanderthal fossils(化石).In both groups, they found some of the same genetic variants involved with the circadian rhythm. And they found that modern humans who carry these variants also reported being early risers.For Neanderthals, being “morning people” might not have been the real benefit of carrying these genes. Instead, scientists suggest, Neanderthals’ DNA gave them faster, more flexible internal body clocks, which allowed them to adjust more easily to annual changes in daylight. This connection makes sense in the context of human history. When early humans moved north out of Africa, they would have experienced variable daylight hours--shorter days in the winter and longer days in the summer-for the first time. The Neanderthals' circadian rhythm genes likely helped early humans' offspring(后代)adapt to this new environment.Notably ,the findings do not prove that Neanderthal genes are responsible for the sleep habits of all early risers. Lots of different factors beyond genetics can contribute , including social and environmental influences. The study also only included DNA from a database called the U.K. Biobank-so the findings may not necessarily apply to all modern humans. Next, the research team hopes to study other genetic databases to see if the same link holds true for people of other ancestries. If the findings do apply more broadly , they may one day be useful for improving sleep in the modern world, where circadian rhythms are disturbed by night shifts and glowing smartphones.8.What does the new research focus on?A. DNA's dramatic changes.B. Genes’ influence on early risers.C. Neanderthals’ sleeping patterns.D. Ancestors’ environmental adaptability.9.What is paragraph 2 intended to show concerning the new research?A. Historical context.B. Additional proof.C. Sample analysis.D. Studying process.10. What is the real benefit of carrying Neanderthal's DNA for modern humans?A .Getting up earlier. B. Having healthier daily routines.C. Being more flexible in their work.D. Possessing a better circadian rhythm.11. What can be inferred about the findings from the last paragraph?A. They get proof from other studies.B. They are confirmed by early risers.C. They suggest potential applications.D. They reveal factors in sleeping disorders.DI had to say something after reading The Anxious Generation. It is going to sell well , because Jonathan Haidt is telling a scary story about children's development many parents are led to believe. However, the book's repeated suggestion that digital technologies are rewiring our children's brains and causing the epidemic (流行病)of mental illness is unsupported by science. Worse , the rude proposal that social media is to blame might distract (分心)us from effectively responding to the real causes of the current mental-health crisis in young people.Researchers have searched for the effects suggested by Haidt. Our efforts have produced a mix of no, small and mixed associations. Most data are correlative. When associations over time are found, they suggest not that social-media use predicts or causes depression, but that young people who already have mental-health problems use such platforms more often or in different ways from their healthy peers.We are not alone here. Several analyses and systematic reviews centralize on the same message. An analysis done in 72 countries shows no consistent or measurable associations between well-being and social media globally. Moreover, studies from some authorities finds no evidence of intense changes associated with digital-technology use.As a psychologist studying children's and adolescents’ mental health, I appreciate parents’frustration(沮丧)and desire for simple answers. As a parent of adolescents, I would also like to identify a simple source for the pain this generation is reporting. There are, however, no simple answers. The beginning and development of mental disorders are driven by a complex set of genetic and environmental factors.More young people are talking openly about their mental-health struggles than ever before. But insufficient services are available to address their needs. In the United States, there is, on average, one school psychologist for every 1,119 students. We have a generation in crisis and in desperate need of the best of what science and evidence-based solutions can offer. Unfortunately, our time is being spent telling stories that are unsupported by research and that do little to support young people who need, and deserve, more.12.What is presented in The Anxious Generation?A. Scary stories affect children's brains.B. Parents are responsible for children's health.C. Teen's mental illness results from screen time.D. The epidemic of mental illness is unavoidable.13.What does “the same message ”underlined in paragraph 3 refer to?A. Many countries do research in mental health.B. Well-being and social media are closely related.C. The young are trapped in the mental-health crisis,D. Social media don't necessarily cause mental illness.14. What is implied in the last paragraph?A. Effective actions need to be taken.B. Positive stories should be shared.C. Financial support needs to be provided.D. Broader research should be done.15.What is the author's purpose in writing the text?A. To suggest ways to help those in need.B. To encourage parents to brave the crisis.C. To recommend a newly-published book.D. To give a voice to children's mental issues.第二节(共5小题;每小题2.5分,满分12.5分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。

2024届山东省高三下学期高考模拟物理试题

2024届山东省高三下学期高考模拟物理试题一、单项选择题：本题共8小题，每小题3分，共24分，在每小题给出的答案中，只有一个符合题目要求。

(共8题)第(1)题如图所示，间距为L=1m的足够长光滑平行金属导轨间存在垂直于导轨平面向里的匀强磁场，磁感应强度大小为B=1T。

导轨左侧有两个开关S1、S2，S1与一个电容C=1F的电容器串联，S2与一个阻值R=2Ω的定值电阻串联。

一质量为m=1kg电阻不计的导体棒垂直导轨放置，闭合开关S1断开S2，导体棒在恒力F的作用下由静止开始运动，t=2s时导体棒速度v0=4m/s，此时断开开关S1、闭合S2，并撒去F。

下列说法正确的是（）A．恒力F的大小为2NB．t=2s时，电容器极板所带电荷量为2CC．t=2s至导体棒停下的过程中，电阻R上的电流方向为b→aD．从0时刻起至导体棒最终停下，导体棒运动的总位移为12m第(2)题如图所示，在xOy坐标系中一质量为m的小球绕原点O做顺时针方向圆周运动，半径为R。

一束平行光沿x轴正方向照射小球，在处放置一垂直于x轴的足够大屏幕，观察到影子在y轴方向上的运动满足。

则（）A．影子做简谐运动，周期为B．小球做匀速圆周运动的向心力为C．，小球坐标是D．，小球速度沿y轴正方向第(3)题“舞龙贺新春”巡游活动中，“龙”上下摆动形成的波可看做沿x轴正方向传播的简谐波，某时刻的波形图如图所示，A、B、C、D为波形上的四点，下列说法正确的是（）A．此刻B、C振动的方向相反B．B、C平衡位置间的距离为波长的一半C．A、B能同时回到平衡位置D．D的振动比B滞后半个周期第(4)题一质点以某一速度沿直线做匀速运动，从时刻开始做匀减速运动，到时刻速度减为零，然后又做反向的匀加速运动，减速阶段和加速阶段的加速度大小相等。

在下列质点的位移x与时间t的关系图像中（其中A图像为抛物线的一部分，D图像为圆的一部分），可能正确的图像是（）A．B．C．D．第(5)题如图所示，固定的点电荷正下方有一足够大的接地金属板，在金属板的上表面外侧和内侧各取一点A、B，可认为A、B两点到点电荷的距离均为d，静电力常量为，关于此静电感应现象判断正确的是（）A．金属板的下表面一定带正电B．金属板上感应电荷在B点场强大小等于0C．金属板上感应电荷在B点场强大小等于D．A点场强大小等于第(6)题如图，用校准的两个电压表和分别测量串联电路中电阻R两端a、b的电压，两表的示数分别为和，由此可知，下列判断中正确的是（）A．a、b两点间的实际电压可能为B．a、b两点间的实际电压可能为C．电压表的内阻小于电压表的内阻D．电压表和电压表的内阻大小无法比较第(7)题如图所示，甲图是光电管中光电流与电压关系图像，乙图是放射性元素氡的质量和初始时质量比值与时间之间的关系图像，丙图是原子核的比结合能与质量数之间的关系图像，丁图是c、d两种金属遏止电压与入射光频率之间的关系图像，下列判断正确的是（）A．甲图，a光的光子能量小于b光的光子能量B．乙图，每过3.8天反应堆的质量就减少一半C．丙图，核子平均质量比核子平均质量小约D．丁图，用a光照射c、d金属，若c能发生光电效应，则d也一定可以第(8)题如图甲所示，饮水桶上装有压水器，可简化为图乙所示的模型。

2024届海南省高三上学期高考全真模拟卷物理试题(二)

2024届海南省高三上学期高考全真模拟卷物理试题（二）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图所示，一物块静置于水平地面上A点。

当用水平方向的力F拉物块时，物块由A运动到B点所用时间为t；当力F改为与水平方向成60°斜向上拉物块时，物块由A运动到B所用时间仍为t。

则物块与地面之间的动摩擦因数为（）A．B．C．D．第(2)题单镜头反光相机俗称单反，它用一块放置在镜头与感光部件之间的透明平面镜把来自镜头的图像投射到对焦屏上。

对焦屏上的图像通过五棱镜的反射进入人眼中。

图为单反照相机取景器的示意图，ABCDE为五棱镜的一个截面，。

一细束单色光线垂直AB射入，分别在CD和EA上发生反射，且两次反射的入射角相等，最后光线垂直BC射出。

若两次反射都为全反射，则该五棱镜折射率可能是下列那个数值（已知sin22.5°≈0.4）（）A．1.5B．2.0C．2.4D．2.8第(3)题如题图1所示，平面内，轴上和处分别固定A、B两点电荷，一等势面恰好沿轴，区域的部分等势面分布如题图2 所示。

一带正电的点电荷仅在电场力作用下由点运动到点，下列说法正确的是（）A．A、B两点电荷电性相同，电势B．A、B两点电荷电性相同，电势C．A、B两点电荷电性不同，电势D．A、B两点电荷电性不同，电势第(4)题2016年9月25日，被誉为“中国天眼”的500米口径球面射电望远镜（FAST）在贵州落成并启用，已取得一系列重大科学成果，发现脉冲星数百颗。

脉冲星是旋转的中子星，每自转一周，就向地球发射一次电磁脉冲信号。

若观测到某个中子星发射电磁脉冲信号的周期为T，中子星可视为半径为R的匀质球体，已知万有引力常量为G。

由以上物理量可以求出（）A．中子星密度的上限（最大可能值）B．中子星的第一宇宙速度C．中子星赤道表面的重力加速度D．中子星赤道上的物体随中子星转动的向心加速度第(5)题关于下列光学现象，说法正确的是（）A．蓝光比红光的波长短，所以在真空中蓝光的传播速度更大些B．在同种均匀介质中，蓝光比红光折射率小，所以蓝光传播速度大C．在同一条件下，若蓝光能发生全反射则红光也一定能发生全反射D．在同一双缝干涉实验装置中，蓝光条纹间距比红光条纹间距窄第(6)题如图，物体随气球以大小为1m/s的速度从地面匀速上升．若5s末细绳断裂，g取10m/s2，则物体能在空中继续运动（）A．6.1sB．1.2sC．1.1sD．1.0s第(7)题在光滑水平面上有一表面光滑的斜面，质量为M、高度为h、倾角为θ，一质量为m的物块（视为质点）从斜面底端以一定的初速度沿斜面向上运动，如图所示。

2024届山东省高三下学期高考模拟全真演练物理试题

2024届山东省高三下学期高考模拟全真演练物理试题一、单项选择题：本题共8小题，每小题3分，共24分，在每小题给出的答案中，只有一个符合题目要求。

(共8题)第(1)题一个静止的质点，在0~4s时间内受到力F的作用，力的方向始终在同一直线上，力F随时间t的变化如图所示，则质点在（）A．第2s末速度改变方向B．第2s末位移改变方向C．第4s末回到原出发点D．第4s末运动速度为零第(2)题一质量为的物体在水平拉力的作用下，由静止开始在水平地面上沿x轴运动，以出发点为x轴零点，物体的动能与物体坐标x的关系如图所示。

物体与水平地面间的动摩擦因数为0.4，重力加速度大小取。

下列说法正确的是（）A．在时，拉力的大小为2NB．在时，拉力的功率为12WC．从运动到的过程中，物体克服摩擦力做的功为8JD．从运动到的过程中，拉力的冲量大小为第(3)题某节能储能输电网络如图所示，发电机的输出电压U1= 250V，输出功率500kW。

降压变压器的匝数比n3：n4= 50：1，输电线总电阻R= 62.5Ω。

其余线路电阻不计，用户端电压U4= 220V，功率88kW，所有变压器均为理想变压器。

下列说法正确的是（）A．发电机的输出电流为368A B．输电线上损失的功率为4.8kWC．输送给储能站的功率为408kW D．升压变压器的匝数比n1：n2= 1：44第(4)题如图所示，在平面直角坐标系中，有方向平行于坐标平面的匀强电场，其中坐标原点O处的电势为0V，点A处的电势为6V，点B处的电势为3V，则电场强度的大小为（）A．B．C．D．第(5)题如图所示，有一条宽度为800m的小河自西向东流淌，水流速度为v0，各点到较近河岸的距离为，与之间的关系为（均采用国际单位）。

让小船船头垂直河岸由南向北渡河，小船相对于河水的速度恒为下列说法正确的选项是（）A．小船在水中做类平抛运动B．小船到达北岸时位移大小为C．小船刚到达北岸时，相对于河岸的速度大小为5m/sD．小船在行驶过程中，水流一直对小船做正功第(6)题下列说法正确的是（）A．研究“天问一号”调整姿态，利用相机拍摄火星表面地貌时，“天问一号”可视为质点B．国产大飞机C919商业首飞，航行时间约2h，航程约1100km，其中“2h”指的是时刻C．“中国天眼”探测到的引力波，传播速度为光速，若频率为，则其波长比可见光长D．全球最大实验性核聚变反应堆开始运行，核反应方程为第(7)题1885年，瑞士科学家巴尔末对当时已知的氢原子在可见光区的4条谱线（记作、、和）作了分析，发现这些谱线的波长满足一个简单的公式，称为巴尔末公式。

海南省海口市2023届高三高考模拟考试语文试题及参考答案

海南省海口市2023届高三高考模拟考试语文试题及参考答案一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1-5题。

陕西文学，激励几代人在中国文坛上，陕西文学占据重要地位，柳青、路遥、陈忠实、贾平凹、陈彦等“文学陕军”深耕三秦大地，写出了《创业史》《平凡的世界》《白鹿原》《秦腔》《主角》等重要文学作品。

他们塑造的梁生宝、孙少平、白嘉轩等人物形象深入人心，引发万千读者共鸣。

“文学陕军”，何以如此耀眼？“90后”读者小禾今年春节再次捧起《平凡的世界》。

这是她第4遍阅读这部小说，每看一次，便感动一次。

“我们都是平凡的人，尽管生活如此艰难，也不应该忘记最初的梦想。

”小禾说。

第三届茅盾文学奖获奖作品《平凡的世界》，首次出版于1986年，至今已加印超过200次，销量超过2000万册。

如今打开热门购书网站的排行榜，《平凡的世界》仍在好评榜上占有一席之地。

在网络社交平台上，不同年龄、不同地域的读者彼此分享阅读感悟。

长期研究陕西文学的文学评论家邢小利说，陕西文化底蕴深厚，新中国成立后，陕西相继出现了“十七年文学”“文学陕军东征”“文学陕军再出发”等文学发展高潮。

特别是20世纪90年代，陈忠实、贾平凹、高建群、京夫、程海5位陕西作家的长篇小说同时在北京出版，文学评论界一度将之称为“陕军东征”。

陕西文学也为世界推开了一扇了解中国的窗口。

早在1954年，柳青的小说《铜墙铁壁》就被翻译成英文出版。

1964年，英译本和日译本《创业史》出版。

2021年，《平凡的世界》马来文版出版发行。

此前，这部作品已被翻译成塞尔维亚语、阿拉伯语、土耳其语、日语、越南语等多个语种。

目前，柳青、杜鹏程、路遥、陈忠实、贾平凹、高建群、陈彦、叶广芩、红柯、吴克敬等10多位陕西作家的作品已在海外出版发行。

细细品读《创业史》《平凡的世界》《白鹿原》《秦腔》《主角》等作品不难发现，现实主义、乡土气息、史诗品格、家国情怀的文学特质一脉相承，折射出陕西作家的文学风骨。

浙江省宁波市2024届高三上学期高考模拟考试数学试题

一、单选题二、多选题1. 关于的不等式的解集为，则的最大值是（）A．B．C．D．2. 在中，点D 是线段AB 上靠近B 的四等分点，点E 是线段CD 上靠近D的三等分点，则（）A．B．C．D．3. 在△中，，E是上一点．若，则（）A．B．C．D．4. 若f （x ）=x 3，f′（x 0）=3，则x 0的值是（）.A ．1B ．﹣1C ．±1D ．35. 函数是定义在上的偶函数，且当时，.若对任意的，均有，则实数的最大值是（）A．B．C ．0D．6.在空间直角坐标系中，正四面体的顶点、分别在轴，轴上移动．若该正四面体的棱长是，则的取值范围是( )．A．B．C．D．7. 若干年前，某老师刚退休的月退休金为4000元，月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元，则目前该老师的月退休金为（）A ．5000元B ．5500元C ．6000元D ．6500元8. 已知函数的定义域为R ，对任意实数x ，y 都有，当时，，且，则关于x 的不等式的解集为（）A．B．C．D．9. 已知抛物线的焦点为，，是抛物线上两点，则下列结论正确的是（）A．点的坐标为B ．若直线过点，则C ．若，则的最小值为D ．若，则线段的中点到轴的距离为10. 数学中有各式各样富含诗意的曲线，螺旋线就是其中比较特别的一类．螺旋线这个名词源于希腊文，它的原意是“旋卷”或“缠卷”．小明浙江省宁波市2024届高三上学期高考模拟考试数学试题浙江省宁波市2024届高三上学期高考模拟考试数学试题三、填空题四、解答题对螺旋线有着浓厚的兴趣，连接嵌套的各个正方形的顶点就得到了近似于螺旋线的美丽图案，其具体作法是：在边长为1的正方形中，作它的内接正方形，且使得；再作正方形的内接正方形，且使得；与之类似，依次进行，就形成了阴影部分的图案，如图所示．设第个正方形的边长为（其中第1个正方形的边长为，第2个正方形的边长为，…），第个直角三角形（阴影部分）的面积为（其中第1个直角三角形的面积为，第2个直角三角形的面积为，…），则（）A ．数列是公比为的等比数列B．C ．数列是公比为的等比数列D ．数列的前项和11. 中国传统文化中很多内容体现了数学的“对称美”.如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分体现了相互转化､对称统一的形式美､和谐美.定义：图象能够将圆的周长和面积同时等分成两部分的函数称为圆的一个“太极函数”.给出下列命题，其中正确的命题为（）A ．对于任意一个圆，其“太极函数”有无数个B．函数可以是某个圆的“太极函数”C．正弦函数可以同时是无数个圆的“太极函数”D ．函数是“太极函数”的充要条件为函数的图象是中心对称图形12. 已知直线与函数的图象相交，A ，B ，C是从左到右的三个相邻交点，设，，则下列结论正确的是（）．A．将的图象向右平移个单位长度后关于原点对称B．若，则C ．若在上无最值，则的最大值为D．13.函数的最小正周期为________14. __________．15.记为数列的前项和，若，则______．16.如图，直三棱柱中，，，，D 为上的点，二面角的余弦值为.（1）求证：；（2）求点A到平面的距离.17. 已知函数.(1)求的最小值；(2)记为的导函数，设函数有且只有一个零点，求的取值范围.18. 已知函数.(1)若，求实数a的值；(2)已知且，求证：.19. 如图，在四棱锥中，平面，点E为的中点，连．(1)求证：平面；(2)求点D到平面的距离．20. 设函数.（1）求函数的单调区间；（2）若函数有唯一的零点，求实数的值；（3）讨论函数的零点个数.21. 如图，四边形为正方形，，，为锐角三角形，，分别是边，的中点，直线与平面所成的角为.（1）求证：平面；（2）求二面角的余弦值.。

2024届宁夏吴忠市高三下学期高考模拟联考试卷(二)理科综合试题-高中物理核心考点

2024届宁夏吴忠市高三下学期高考模拟联考试卷（二）理科综合试题-高中物理核心考点一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题某游乐场有一项游戏。

游戏规则是几个人轮流用同一个弹簧弹出一颗“炮弹”，“炮弹”水平击打静止在水平桌面上的同一辆小车，使小车运动距离最远者获胜。

已知某次比赛使用小车的质量为0.5kg ，游戏中每次弹射前弹簧的压缩量相同，有多种质量的“炮弹”可供选择。

“炮弹”击中小车后留在小车上（作用时间忽略不计），小车运动时所受阻力与车对地面的压力成正比。

请你给予指导，要想获胜，理论上应选取“炮弹”的质量为（）A ．0.25kgB ．0.5kgC ．1kgD ．2kg第(2)题我国古代人民掌握了卓越的航海技术，曾有“郑和七下西洋”的壮举。

帆船要逆风行驶时要调整帆面的朝向，使船沿“之”字形航线逆风而行。

风吹到帆面，产生的风力垂直于帆面，由于船沿垂直于船身的阻力非常大，风力垂直于航身的分量不会引起船侧向的运动，在风力的作用下，船便会沿平行于船身方向运动。

在下列各图中，风向如图所示，船沿虚线的路线逆风而行，则各图中帆面的方位正确的是（）A ．B ．C ．D ．第(3)题如图甲所示，斜面上气缸和活塞内封闭了一定质量的理想气体，一根平行于斜面的轻绳一端连接活塞，另一端固定，系统处于平衡状态。

开始气体摄氏温度为t ，通过气缸内电热丝缓慢升高气体温度，升温过程封闭气体的图像如图乙所示，已知斜面倾角为30°，重力加速度为g ，大气压强为，气缸和活塞均绝热且不漏气，气缸（含电热丝）质量为M 、活塞面积为S 、质量为m ，所有接触面均光滑。

则（）A ．封闭气体压强恒为B ．在此过程中，封闭气体增加的内能等于吸收热量C ．封闭气体的体积为2V 时，其摄氏温度为2tD．剪断轻绳瞬间，气缸的加速度大小为第(4)题下列现象中，揭示了光的波动性的是（）A ．光电效应B ．黑体辐射C ．光的偏振D ．康普顿效应第(5)题如图所示，空间有一匀强磁场，一直金属棒与磁感应强度方向垂直，当它以速度v沿与棒和磁感应强度都垂直的方向运动时，棒两端的感应电动势大小ε，将此棒弯成两段长度相等且相互垂直的折弯，置于磁感应强度相垂直的平面内，当它沿两段折线夹角平分线的方向以速度v运动时，棒两端的感应电动势大小为，则等于（）A．1/2B．C．1D．第(6)题如图所示，两根细木条搭成顶角为的人字形装置竖直放置在水平桌面上，细木条的左右两端连接一根细铜丝在两根细木条的中间施加一竖直向下的力，此时铜丝受到的拉力为（）A．B．C．D．第(7)题从地面竖直向上抛出一物体，物体在运动过程中除受到重力外，还受到一大小不变、方向始终与运动方向相反的外力作用．距地面高度h在3m以内时，物体上升、下落过程中动能E k随h的变化如图所示．重力加速度取10m/s2．该物体的质量为A．2kg B．1.5kg C．1kg D．0.5kg第(8)题如图所示，一正方形线圈通过电刷与自耦变压器相连，线圈平面与水平向右，磁感应强度为的匀强磁场平行。

高三英语高考模拟冲刺练习题40题答案解析版

高三英语高考模拟冲刺练习题40题答案解析版1.He was so angry at all that she was doing that he walked out without saying a word. This is________ he was so angry.A.whenB.whyC.thatD.how答案解析：B。

本题考查表语从句。

“This is why...”表示“这就是……的原因”。

A 选项“when”表示时间；C 选项“that”在表语从句中不充当成分；D 选项“how”表示方式。

根据句意，此处表示他生气的原因。

2.The place_________ he works is in the city center.A.thatB.whichC.whereD.when答案解析：C。

本题考查定语从句。

先行词是“the place”，在从句中作地点状语，所以用关系副词“where”。

A、B 选项在定语从句中作主语或宾语；D 选项表示时间。

3.__________ he will come or not is still a question.A.WhetherB.IfC.ThatD.What答案解析：A。

本题考查主语从句。

“whether...or not”是固定搭配，表示“是否”。

if 不能引导主语从句放在句首；that 在主语从句中不充当成分，无实际意义；what 在主语从句中充当主语、宾语等成分。

4.I'll never forget the days________ we spent together.A.thatB.whenC.whereD.on which答案解析：A。