2013年我国城镇居民人均消费的SPSS统计分析
基于SPSS软件分析城市居民的消费结构
基于SPSS软件分析城市居民的消费结构消费结构指一国在一定时期内用于生活消费的各种消费资料的比例关系，以及各种消费方式、消费形式、居民各阶层、各地区消费水平之间的比例关系的总和。
利用spss软件将31个省聚成五类，对五类城市居民在各个领域的消费支出情况进行分析，发现我国城市居民消费结构大致是以食品、家庭设备及用品、医疗保健为主体。
然而要想提高和改变人民的生活水平，还应加强文教娱乐消费，使消费结构变得合理化、科学化。
标签：消费结构；spss软件；因子分析；聚类分析1数据的因子分析从中国统计年鉴找出2013年全国各省人均城镇居民消费支出的具体数据，然后利用spss分析数据，求出KMO，结果如表1。
Bartlett的df值为28，P值文教娱乐>食品>家庭设备及用品>居住>其它；第二个因子主要反映衣着和医疗保障方面的差异情况。
最后得出31个省的综合因子得分F：F=0.56545×F1+0.27147×F2算出的各省各因子及综合因子的得分和排名，具体见表7。
表7中，因子得分情况的正负表示该城市与平均水平的相对位置。
中有9个F1为正的城市，这9个城市的经济发展水平较发达，其中上海、广东、北京具有较高的消费水平，同时这三个城市也是经济较发达的城市，这说明城市的经济发展水平较高时，居民的消费理念也较高，而一些经济滞后的省份，像黑龙江、西藏、新疆等，消费水平较低。
由此得出居民在食品、交通通信、文教娱乐、居住、生活用品及服务、其他6各方面与经济发展水平密切相关。
F2的排名中北京、天津分为位于第1和第4，但是上海、广东位于第14和26，所以衣着和医疗保健与经济发展有一定的关系，但这两个指标还与其它因素紧密相关。
仅有10个F值为正数的省，这表明各个省的城市居民的消费水平发展差异较大、不均衡。
其中，北京、上海、广东等地区的城市居民消费水平较高，青海、江西、贵州等地的消费水平较低。
城镇居民消费结构SPSS统计分析
应用多元统计论文题目基于SPSS分析方法的城镇居民消费结构研究院系年级专业姓名基于SPSS分析方法的城镇居民消费结构研究摘要：2012年11月8日将召开中国共产党的十八大，至2013年3月两会召开和政府换届，这段时间将成为市场演化的重要时间窗口；而在这一时期，我国的宏观经济形势也将会产生相应的变化。
近年来，我国经济发展速度加快，居民收入稳定增加，在国家出台的一系列政策后，居民消费支出也开始增长，消费结构显著变化。
本文通过数据的SPSS分析对我国城镇居民消费出现的趋势特点进行了总结。
关键词：城镇居民消费描述分析整体拟合分析方差分析回归分析一、我国城镇居民消费现状近些年来，我国的国民经济状况突飞猛进的发展，人民的物质生活水平也日益的提高，并且得到了很大的改善。
但是，由于我国各地区各地域的资源、技术、科教水平等基础条件的不同，造成各地区各地域的生产力发展水平有很大差异，因此，各地区各地域的经济发展和城镇居民消费性支出的结构、水平是不相同的。
而众所周知，消费是拉动经济增长的主要动力之一，因此消费情况如何对经济发展、人民生活水平有直接的影响。
随着国家政策的不断改革，我国国民经济呈现出高速发展的势头，人民生活水平不断提高。
这不仅体现为目前我国城镇居民的人均收入普遍地有所提高，也在城镇居民的家庭消费性支出结构的变化上有所体现。
二、我国居民消费结构的分析我国居民消费结构有以下几个特点：第一,食品消费支出比重随收入增加呈现出明显的下降趋势,这与恩格尔定律的表述一致。
但最低收入户与最高收入恩格尔系数相差太过悬殊,城镇最低收入户刚刚解决了温饱问题,而最高收入户的生活水平按照恩格尔系数的评价标准早已达到了富裕型,甚至接近最富裕型；第二,衣着消费支出比重随收入增加缓慢上升,到高收入户又有所下降,但各收入组支出比重相差不大。
衣着支出比重没有更多的递增且最高收入户的支出比重有所下降,这些都符合恩格尔定律关于衣着消费的引申。
随着收入的增加,衣着支出比重呈现先上升后下降的走势；第三,家庭设备用品及服务、交通通讯、娱乐教育文化服务和杂项商品与服务的支出比重呈逐组上升趋势,说明居民的生活水平随收入的增加而不断提高和改善；第四,医疗保健支出比重随收入水平提高呈现一种两端高、中间低的走势；第五,居住支出比重基本上呈先上升后下降的趋势,这与我国居民消费能级不断提升,住宅商品正在越来越成为城镇居民关注的热点是相吻合的,同时与恩格尔定律的引申也是一致的。
用spss分析我国各省城镇居民消费水平差异.doc
用sps分析我国各省城镇居民消费水平差异分析文章结构1研究背景及意义 (1)2研究方法 (1)3数据来源与数据处理 (2)4.实证分析 (3)4.1因子分析 (3)4.2聚类分析 (7)5结论 (11)1研究背景及意义我国地域广阔，各省份的经济发展很不平衡，各省之间的居民消费水平差距较大。
经济快速发展的同时我国居民收入稳步增加，各省居民的消费支出也强劲增长，消费结构发生了巨大变化。
为了正确引导消费，进一步改善消费结构，提高我国城市居民的消费水平和生活的质量，有必要对全国各省居民消费结构之间的异同进行考察并做比较研究，以期发现经济水平和城市居民的消费水平之间的关系2研究方法本文运用多元统计分析中的主成分分析方法和聚类分析方法，将描述各省份城镇居民全年现金消费支出的八个指标压缩成两个综合指标（称为主成分），这两个主成分保留了原始八个指标的绝大部分信息，在指标压缩的同时能够最大限度地反映出各省份城镇居民消费水平差异。
在综合因子基础上进行层次聚类分析，根据消费差异将全国31个省分为四类。
因子分析模型是根据变量间的相关性大小，把变量分组，利用同组内的变量之间相关性较高而不同组的变量之间相关性较低，每组变量代表一个基本结构，这个基本结构称为公共因子。
因子分析的出发点是用较少的相互独立的因子变量来代替原来变量的大部分信息，可以通过下面的数学模型来表示：X1 = a 11F1+ a 12F2+…+ a 1m Fm+a 1 £1，X2 = a 21F1 + a 222+…+ a 2m Fm+ a 2 £2，Xp = a p1F1 + a p2F2+…+ a pm Fm+ a p £p，其中：x1, x2,x3,…，xp为p个原有变量，是均值为零、标准差为1的标准化变量；F1, F2, F3,…，Fm为m个因子变量，m小于p,表示成矩阵形式为X = AF + a £ ,其中：F=（F1, F2,…，Fm）为因子变量或公共因子；£ =（£ 1, £ 2,…，£ p）为特殊因子；F与£均为不可观测的随机变量• A = （a ij）p X m为因子载荷矩阵，a j称为第j个因子对第i个变量的载荷系数•在模型中，特殊因子起着残差的作用，被定义为彼此不相关且与公因子也不相关。
我国城镇居民人均消费支出的统计分析论文
我国城镇居民人均消费支出的统计分析论文我国城镇居民人均消费支出的统计分析论文本文采用2013年我国31个省、市、自治区的城镇居民人均消费支出数据，先通过聚类分析方法寻找不同地区城镇居民的消费结构的相似点和差异点;再利用主成分分析方法研究各省城镇居民消费结构水平，得出其经济发展状况;最后利用因子分析方法，根据因子得分对各省城镇居民消费支出进行排序和分类。
城镇居民消费支出聚类分析主成分分析因子分析一、引言近年来，随着我国经济的快速发展，居民消费结构也发生了巨大变化，人们开始根据自身的需求选择多种多样的商品，而且人们在实现物质需求满足的同时，还在不断追求精神需求的满足。
同时，社会产品在经济发展的过程中越来越丰富，居民消费的选择空间也越来越大。
在居民全部消费支出的八项指标(食品、衣着、居住、家庭设备、交通通讯、文教娱乐、医疗保健、其他)中，反应基本生存需要的食品、衣着等项所占的比重大幅度下降，而体现发展与享受需求的住房、交通等项支出的比重则迅速上升，说明人民的生活质量进一步提高。
由于我国各地区的经济发展不平衡，加之各地人口、资源、政策等方面也存在差异，导致各地区居民的消费结构存在着明显差异。
合理的消费结构有利于国民经济的快速发展，而滞后的消费结构则会阻碍经济的健康发展。
因此，消费结构的合理化问题在国民经济中处于至关重要的地位。
所以，为了进一步改善消费结构，引导正确的消费观念，提高我国城镇居民的消费水平，有必要对我国各地区城镇居民消费结构之间的差异进行比较，从宏观上把握各地区城镇居民的消费现状和消费水平的差异，为提高我国总体消费水平、改善消费结构提供决策依据。
本文利用SPSS软件通过聚类分析、主成分分析、因子分析三种统计方法对2013年我国各省城镇居民消费结构作分析。
二、聚类分析聚类分析是将样品或变量进行分类的多元统计学分析方法。
其功能是建立一种分类方法，将一批样品或者变量，按照他们在性质上的亲疏、相似程度进行分析。
我国城镇居民人均消费的SPSS统计分析报告
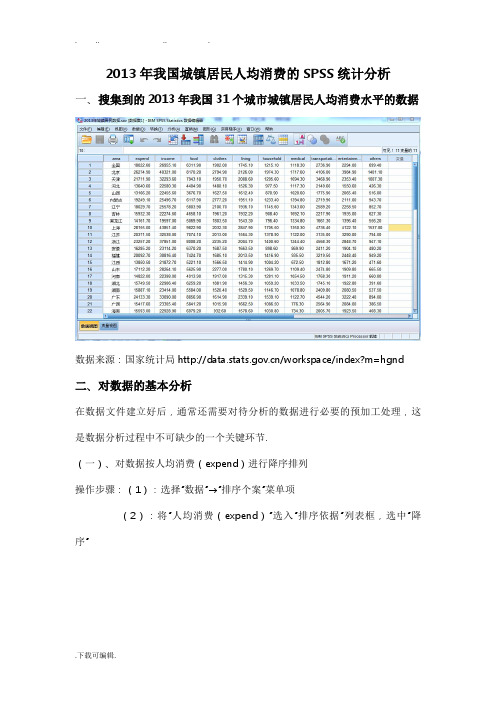
2013年我国城镇居民人均消费的SPSS统计分析一、搜集到的2013年我国31个城市城镇居民人均消费水平的数据数据来源：国家统计局/workspace/index?m=hgnd 二、对数据的基本分析在数据文件建立好后，通常还需要对待分析的数据进行必要的预加工处理，这是数据分析过程中不可缺少的一个关键环节.（一）、对数据按人均消费（expend）进行降序排列操作步骤：（1）：选择“数据”→“排序个案”菜单项（2）：将“人均消费（expend）”选入“排序依据”列表框，选中“降序”（3）：点击“确认”按钮，生成如下降序排列的数据集由数据的降序排列可以看出，全国只有上海、北京、广东等九个城市的城镇人均消费在全国城镇人均消费水平以上.（二）、作出人均收入和人均消费的直方图操作步骤：（1）：选择“图形”，打开“图表构建程序”菜单项（2）：从“库”中选择“直方图”将其拉入“图表预览使用数据实例”（3）：将变量“地区”设置为x轴，将“人均收入”和“人均消费”设置为y轴（4）：点击“确认”按钮，即生成如下直方图通过一个复合条形图，可以很明确的发现我国城镇居民生活水平存在很大的地区差异，地区发展很不平衡，从图中的生活消费支出和人均收入来看，北京，上海，浙江这些省市城镇居民消费水平最高，人均收入也是最高的，各省市的城镇居民消费水平差异较大，大多数省份城镇居民人均消费集中在15000元左右.（三）、对数据按照人均消费作出直方图，以统计我国农村人均消费的水平1、首先对数据分组，分组数目的确定.lg n，计算得组数为6.按照Sturges提出的经验公式来确定组数K,K=1+2lg2、确定组距组距=（最大值-最小值）/组数=（28155.00-12231.90）/6=2653.85，可近似取值为3000.00元.操作步骤：（1）：选择“转换”→“可视离散化”菜单项，将“人均消费”选入“要离散的变量”列表框中，单击“继续”按钮进入主对话框.（2）：单击“生成分割点”按钮，设定分割点数量为6，宽度为3000.00，可见系统会自动会填充第一个分割点的位置为12231.90，单击“应用”返回到主对话框.（3）：此时可以看到下部数值标签网格里的“值”列已被自动填充，单击“生成标签”按钮，是标签列也得到自动填充.（4）：将离散的变量名设定为expendNew.（5）：单击“确定”按钮.3、频数分析操作步骤：（1）：选择“分析”→“描述统计”→“频率”，打开频率对话框.（2）：选定“expendNew”，点击“图表”，选择“条形图”点击继续.（3）：点击“确认”，生成如下三张表.Statistics人均消费(已离散化)N Valid 32Missing 0Mean 3.13Median 3.00Std. Deviation 1.314Minimum 1Maximum 7Percentiles 25 2.0050 3.0075 3.75人均消费(已离散化)Frequency Percent Valid Percent Cumulative Percent Valid <= 12231.90 1 3.1 3.1 3.110 31.3 31.3 34.412231.91 -15231.9015231.91 -13 40.6 40.6 75.018231.903 9.4 9.4 84.418231.91 -21231.903 9.4 9.4 93.821231.91 -24231.9024231.91 -1 3.1 3.1 96.927231.9027231.91+ 1 3.1 3.1 100.0 Total 32 100.0 100.0由上图的频数分析可以看出，我国2013年城镇居民人均消费支出集中在第二组和第三组，大约占到百分之七十.由于在表格中不存在缺失值，因此频数分布表中的百分比和有效百分比相同.从此次分析中可以看出，我国城镇家庭居民人均消费的总体水平比较集中，大约在12000元--18000元之间，还有少数省市的消费水平处在中等阶段，而有上海、北京、浙江等一些经济较发达的地区的城镇家庭居民人均消费达到了21000元以上.三、对数据的回归分析（一）、作出人均收入与消费支出散点图，以观察他们的线性关系如何操作步骤：（1）：选择“图形”，打开“图表构建程序”菜单项（2）：从“库”中选择“散点图”将其拖入“图表预览使用数据实例”（3）：将“人均收入”选定为x轴，将“人均消费”选定为y轴（4）：点击“确认”生成如下散点图由散点图可以看出，人均消费Y和人均收入X大概呈一元线性关系，因此可以建立一元线性模型进行回归分析.（二）假设回归模型为Y=a+b X,其中，Y表示城镇人均消费支出，为被解释变量，X表示人均收入，为解释变量，b为回归系数.操作步骤：（1）选择“分析”→“回归”→“线性”菜单项，打开“线性回归”对话框.（2）将“人均消费”选入“因变量”列表框，将“人均收入”选入“自变量”列表框.（3）单击“确定”按钮.得到如下（1）、（2）、（3）、（4）四张表格，依次分析如下：表（1）：移入/移出的变量Variables Entered/Removed bModel VariablesEnteredVariablesRemoved Method1 人均收入a. EnterVariables Entered/Removed bModel VariablesEnteredVariablesRemoved Method1 人均收入a. Entera. All requested variables entered.b. Dependent Variable: 人均消费从上表可以看出，放入模型的变量只有一个即“人均收入”，选择变量的方法为强行进入法，也就是说将所有的自变量都放入模型中，模型的因变量为“人均消费”.表（2）：模型汇总Model SummaryModel R R Square Adjusted RSquareStd. Error of theEstimate1 .960a.922 .920 1106.90715a. Predictors: (Constant), 人均收入上表是对模型的简单汇总，其实就是对回归方程拟合情况的描述，通过这张表可以知道相关系数R=0.960，决定系数2R=0.922，调整决定系数2R=0.920,和回归系数的标准误=31106.90715.由于决定系数接近于1，说明模型的拟合程度较好.表（3）：方差分析表ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression 4.353E8 1 4.353E8 355.256 .000aResidual 36757303.474 30 1225243.449Total 4.720E8 31a. Predictors: (Constant), 人均收入b. Dependent Variable: 人均消费F=355.256，P=0.000<0.05,表明回归方程高度显著，即农民人均收入对消费有高度影响.表（4）：系数Coefficients aModel Unstandardized CoefficientsStandardizedCoefficientst Sig.B Std. Error Beta1 (Constant) 1897.504 835.983 2.270 .031人均收入.599 .032 .960 18.848 .000 a. Dependent Variable: 人均消费由上表知a=1897.504，b=0.599，由此可以得出以下回归方程：人均消费Y=1897.504+0.599人均收入X上述回归方程给出了如下信息：2013年中国城镇居民人均可支配收入增加1元，人均消费支出增加0.599元.四、单样本的T检验（一）：由频数分析可知，分组后，全国31个省市的城镇家庭居民平均每人生活消费支出合计，大约有23个城市都集中在第一组，数额主要12231.91——18231.90元之间，其中在15231.91 - 18231.90之间的占到了百分之四十，因此可推断，全国农村家庭居民平均每人生活消费支出的平均数应该在15000--20000元之间，假设为18000元，由于该问题涉及的是单个总体，且要进行总体均值检验，同时农村家庭居民平均每人消费的总体可近似认为服从正态分布，因此，应采用单样本t检验来分析推断全国农村家庭居民人均消费的平均值是否为18000元.分析结果如下：（二）：操作步骤：1、选择“分析”→“比较均值”→“单样本天t检验”菜单项，打开“单样本t检验”对话框如下图所示：2、单击“确定”按钮.生成如下两张图表：表（1）：One-Sample StatisticsN Mean Std. Deviation Std. Error Mean人均消费32 17216.6031 3902.16064 689.81106表（2）：One-Sample TestTest Value = 18000t df Sig. (2-tailed)MeanDifference95% Confidence Interval of theDifferenceLower Upper人均消费-1.136 31 0.265 -783.39688 -2190.2758 623.4821 由表（1）可知样本均值为17216.6031，低于基准线18000.00，标准差3902.16064，均值标准差689.81106.由表（2）为单样本t检验的分析结果，第一行注明了用于比较的假设总体均数为18000，下面从左到右依次为t值、自由度、p值、两均数的差值、差值.根据上面的检测结果t=-1.136，p=0.256，由于p>0.05，所以不能拒绝原假设，可以认为人均消费水平在18000元.同时，可知全国城镇居民2013年人均消费在95％的置信水平下的置信区间为：（15809.7242,18623.4821）.五、非参数检验——多配比样本分参数检验数据中我国城镇家庭居民人均消费包括食品、衣着、居住、家庭设备、交通及通讯、文教娱乐、医疗保健、和其他8个指标，为了比较清楚的了解这8项指标对我国城镇居民人均消费总体的影响，以及其大概的消费动向，可以利用多配比样本的非参数检验Friedman 检验对各个指标进行检验.（一）：操作步骤：（1）选择“分析”→“非参数检验”→“旧对话框”→“k个相关样本”菜单项，打开如下对话框：（2）：单击“确定”按钮，得到如下两张表格：表（1）：RanksMean Rank食物消费8.00衣物消费 5.09居住消费 4.50家居设备 2.66交通通讯 6.38医疗保健 2.34文教娱乐 5.88其它 1.16表（2）：Test Statistics aN 32Chi-Square 198.604df 7Asymp. Sig. .000a. Friedman Test（二）、结果分析检验结果中的p值小于给定水平0.05，故拒绝原假设，认为八个指标对我国城镇居民人均消费的影响是有显著差异的.由表（1）知食物消费对人均消费的影响最大，其次是交通通讯和衣物消费，而影响最小的是其它.六、因子分析在研究我国城镇居民的消费情况时收集了食物、衣物、居住等八个影响居民消费情况的因素，以期对问题能够有比较全面、完整的把握和认识.由于数据过多，在实际建模时，这些变量未必能真正发挥预期的作用，会给统计分析带来许多问题，可以表现在：计算量的问题和变量间的相关性问题.为了解决这些问题，最简单和最直接的解决方案是削减变量个数，但这又必然会导致信息丢失和信息不完整等问题的产生.为此，人们希望探索一种更有效的解决方法，它既能大大减少参与数据建模的变量个数，同时也不会造成信息的大量丢失.因子分析正是解决这种问题的方法.（一）操作步骤（1）、选择菜单“分析”→“降维”→“因子分析”，出现因子分析对话框；（2）、把参与因子分析的样本选到变量对话框中，如下图：（3）单击“确定”按钮，得到如下11张图：图（1）原有变量的相关系数矩阵：Correlation Matrix食物消费衣物消费居住消费家居设备医疗保健交通通讯文教娱乐其它Correlatio n 食物消费1.000 .288 .656 .744 .295 .787 .782 .732衣物消费.288 1.000 .337 .517 .694 .368 .374 .634居住消费.656 .337 1.000 .676 .505 .849 .750 .771家居设备.744 .517 .676 1.000 .441 .830 .853 .767医疗保健.295 .694 .505 .441 1.000 .479 .414 .600交通通讯.787 .368 .849 .830 .479 1.000 .860 .782文教娱乐.782 .374 .750 .853 .414 .860 1.000 .831 其它.732 .634 .771 .767 .600 .782 .831 1.000从上图可以看到，大部分的相关系数都较高，各变量呈较强的线性关系，能够从中提取公共因子，适合进行因子分析.图（2）巴特利特球度检验和KMO检验KMO and Bartlett's TestKaiser-Meyer-Olkin Measure of Sampling Adequacy. .833Bartlett's Test of Sphericity Approx. Chi-Square 233.009df 28Sig. .000由上图知，巴特利特球度检验统计量的观测值为233.009，相应的概率p为0.如果给出的显著性水平为0.05，由于概率p小于显著性水平，应拒绝零假设，认为相关系数矩阵与单位阵有显著地差异.同时，KMO值为0.833，根据Kaiser 给出了KMO度量标准可知原有变量适合进行因子分析.图（3）因子分析的初始解CommunalitiesInitial Extraction食物消费 1.000 .798衣物消费 1.000 .862居住消费 1.000 .750家居设备 1.000 .812医疗保健 1.000 .821交通通讯 1.000 .897文教娱乐 1.000 .885其它 1.000 .872Extraction Method: PrincipalComponent Analysis.由上图第二列可知，所有变量的共同度均较高，各个变量的信息丢失较少.因此，本次因子提取的总体效果较理想.图（4）因子解释原有变量总方差的情况：Total Variance ExplainedComponent Initial Eigenvalues Extraction Sums of SquaredLoadingsRotation Sums of SquaredLoadingsTotal% ofVarianceCumulative % Total% ofVarianceCumulative % Total% ofVarianceCumulative %1 5.504 68.794 68.794 5.504 68.794 68.794 4.524 56.545 56.5452 1.192 14.898 83.692 1.192 14.898 83.692 2.172 27.147 83.6923 .473 5.910 89.6024 .258 3.222 92.8245 .237 2.961 95.7856 .178 2.227 98.0127 .091 1.136 99.1478 .068 .853 100.000Extraction Method: Principal Component Analysis.上图◎第一组数据项描述了初始因子解的情况.可以看到，第一个因子解的特征根值为 5.504，解释原有八个变量总方差的68.794％，累计方差贡献率为68.794％.其余数据含义类似.在初始解中由于提取了八个因子，因此原有变量的总方差均被解释掉.◎第二组数据项描述了因子解的情况.可以看到，由于指定提取两个因子，两个因子共解释了原有变量总方差的83.692％.总体上，原有变量的信息丢失较少，因子分析效果较理想.◎第三组数据项描述了最终因子解的情况.可见，因子旋转后，累计方差比没有改变，也就是没有影响原有变量的共同度，但却重新分配了各个因子解释原有变量的方差，改变了各因子的方差贡献，使得因子更容易解释.图（5）因子的碎石图：上图横坐标为因子数目，纵坐标为特征根.可以看到，第一个因子的特征根值很高，对原有变量的贡献最大；第3个以后的因子特征根都较小，对解释原有变量的贡献很小，已经成为可被忽略的“高山脚下的碎石”，因此提取两个因子是合适的.图（6）因子载荷矩阵：Component Matrix aComponent1 2其它.929 .097交通通讯.921 -.222文教娱乐.909 -.241家居设备.895 -.103居住消费.854 -.143食物消费.822 -.350衣物消费.599 .710医疗保健.635 .646a. 2 components extracted.上图因子载荷矩阵是因子分析的核心内容.根据该表可以写出本案例的因子分析模型：其它=0.9291f +0.0972f 交通通讯=0.9211f -0.2222f 文教娱乐=0.9091f -0.2412f 家居设备=0.8951f -0.1032f 居住消费=0.8541f -0.1432f 食物消费=0.8221f -0.3502f 衣物消费=0.5991f +0.7102f 医疗保健=0.6351f +0.6462f 由上表知，八个变量在第一个因子上的载荷都很高，意味着他们与第一个因子的相关度高，第一个因子很重要. 图（7）旋转后的因子载荷矩阵：Rotated Component Matrix aComponent 1 2交通通讯 .915 .244 文教娱乐 .914 .222 食物消费 .889 .084 家居设备 .836 .336 居住消费 .819 .281 其它 .770 .528 衣物消费 .188 .909 医疗保健 .250.871a. Rotationconvergedin3 iterations.由上图知，交通通讯、文教娱乐、食物消费、家居设备、居住消费、其它在第一个因子上有较高的载荷，第一个因子主要解释了这几个变量；衣物消费、医疗保健在第二个因子上的载荷较高，第二个因子主要解释了这几个变量.图（8）因子旋转中的正交矩阵Component Transformation MatrixComponent 1 21 .879 .4772 -.477 .879图（9）因子协方差矩阵：Component Score Covariance MatrixComponent 1 21 1.000 .0002 .000 1.000从上表可以看出，两因子没有线性相关性，实现了因子分析的设计目标.图（10）旋转后的因子载荷图：由上图可以直观的看出，衣物消费和食物消费比较靠近两个因子坐标轴，表明如果分别用第一个因子刻画食物消费，用第二个因子刻画衣物消费，信息丢失较少，效果较好.图（11）因子得分系数矩阵：Component Score CoefficientMatrixComponent1 2食物消费.271 -.187衣物消费-.188 .576居住消费.194 -.032家居设备.184 .001医疗保健-.157 .532交通通讯.236 -.084文教娱乐.241 -.099其它.110 .152根据上表可以得到以下因子得分函数：F=0.271食物消费-0.188衣物消费+0.194居住消费+0.184家居设备-0.157医1疗设备+0.236交通通讯+0.241文教娱乐+0.110其它F=-0.187食物消费+0.576衣物消费-0.032居住消费+0.001家居设备+0.532 2医疗设备-0.084交通通讯-0.099文教娱乐+0.152其它可见计算两个因子得分变量的变量值时，食物消费和衣物消费的权重较高，但方向恰好相反，这与因子的实际含义是相吻合的.七、实验心得本科的时候有概率统计和数理分析的基础，但是从来没有接触过应用统计分析的东西，SPSS也只是听说过，从来没有学过.一直以为这一块儿会比较难，这学期最初学的时候，因为没有认真看教材，课下也没有认真搜集相关资料，所以学起来有些吃力，总感觉听起来一头雾水.老师说最后的考核是通过提交学习报告，然后我从图书馆里借了些教材查了些资料，发现很多问题都弄清楚了.结合软件和书上的例子，实战一下，发现SPSS的功能相当强大.这门课要学习完了，整个学习的过程是充满曲折和挑战的，我见证了自己从一无所知到困惑迷茫再到略懂再到会用的过程.甚至学完之后有些问题还没有彻底搞清楚，自己接下来还会不断的探索的.SPSS是个很神奇的工具，结合AMOS和EXCEL更是如虎添翼，相信学习了SPSS在以后的论文和数据分析中很有用.这门课给我的感觉是看起来很难，但是实际学起来就好很多，因为当我结合具体实例和软件的时候，很多抽象的问题就豁然开朗了.但是想给老师一个建议，这门课需要很强的统计和概率论的基础，要不然就会很难听懂或者听得半懂.然后这门课的很多方法的相关资料都是用在医疗卫生、自然科学领域的，在管理中的应用的资料不怎么多.老师希望我们上课的时候结合在管理中的应用来学习，但是资料有限，希望老师在这个方面多给学生一些引导.。
居民消费水平研究SPSS
课程论文我国居民消费水平研究分析班级：09经51学号：姓名：***2012年 11 月摘要：居民消费水平是指一个国家一定时期内人们在消费过程中对物质和文化生活需要的满足程度。
要刺激消费、扩大内需，必须找出影响我国居民消费水平的关键因素，才能对症下药。
本文结合居民消费水平的影响因素和居民消费水平的历史及现状列出了五个相关因素（国内生产总值GDP、城镇和农村居民可支配收入、人口自然增长率以及居民消费价格指数），运用SPSS 17.0软件进行三个方面的分析：描述性分析、因子分析、回归分析。
本案例的研究目地是分析我国居民消费水平的影响因素，为更好的提高居民消费水平提供科学的依据。
关键字：居民消费水平 SPSS分析扩大内需刺激消费引言居民消费水平是按国民收入或国内生产总值的使用总量中用于居民消费的总额除以年平均人口计算的，它反映一个国家或一个地区居民的一般消费水平。
居民消费水平是GDP 中一个重要组成部分，是拉动经济增长的三驾马车之一，一直是经济学家关注的焦点和研究的热门领域。
在改革开放以来，居民消费水平提高的较快，消费结构也有了很大的改善，因此对其进行分析有较强的经济意义。
分析目地、分析思路与数据选取本案例的研究目地是分析我国居民消费水平的影响因素，为更好的提高居民消费水平提供科学的依据。
分析思路主要如下，首先利用描述性分析对居民消费水平、国内生产总值GDP、城镇和农村居民可支配收入、人口自然增长率以及居民消费价格指数进行基础性的描述，以便对我国居民消费水平和其主要影响因素有一个直观的印象，然后利用因子分析提取对我国居民消费水平影响较为显著的因素，分析我国居民消费水平的影响的因素，最后利用回归分析方法确定这些因素对我国居民消费水平的影响方向和强弱。
在现实生活中，影响消费的因素很多，例如收入水平、商品价格水平、利率水平、收入分配状况、消费者偏好、家庭财产状况、消费信贷状况、消费者年龄构成、制度、风俗习惯等等。
我国城镇居民消费结构的SPSS分析
我国城镇居民消费结构的SPSS分析11级国贸（1）班张子昂学号：1104111027摘要:近年来，我国城镇居民的整体消费水平逐渐提高，但各地区间的消费结构仍存在较大差别。
本文对我国2009 年城镇居民消费结构进行实证分析,简述数据选取、实证方法的变革与演进等，系统分析消费结构的特点及产生原因，为国家制定消费政策及后续研究提供相应参考性意见。
关键词：消费结构；相关分析；因子分析；政策建议1 前言随着我国经济的快速发展,城镇居民的收入不断增加，在国家连续出台住房、教育、医疗等各项改革措施和实施“刺激消费、扩大内需、拉动经济增长”经济政策的影响下，我国各地区城镇居民的消费支出呈现出强劲增长的势头，消费结构发生了巨大的变化，结构不合理的现象也得到了一定程度的调整。
但是，由于各地区的经济发展不平衡及原有经济基础的差异，各地区的消费结构仍存在着明显差别。
为了进一步改善消费结构，正确引导消费，提高我国城市居民的消费水平和生活质量，有必要考察我国各地区城镇居民的消费结构之间的异同并进行比较研究，以期发现特点和规律，从宏观上把握各地区城镇居民的消费现状和不同地区消费水平的差异，为提高我国各地区消费水平和谐增长提供决策依据。
正确把握城镇居民消费结构,了解消费需求变动的规律,不仅在理论分析中有重要的地位,而且对于提高城镇居民的消费质量和档次有着重要的现实意义。
2 数据分析这些指标基本上可以从中国统计年鉴上取得，且反应了城镇经济发展情况和居民消费水平，其原始数据如表1、表2 。
表1 平均每人消费性支出 (元)从图中可以看出，平均可支配性收入是呈现逐步上升趋势的，从1990年的150.16元上升到2009年的17174.65元。
在平均每人消费支出中，也和可支配性收入呈现正相关的关系，随着可支配性收入的稳步增加，平均每人消费性支出（元），从1990年的1278.89元，1995年3537.57元，2000年4998.00元，2008年11242.8元，2009年12264.55元。
SPSS统计分析案例(我国城镇居民消费结构及趋势的统计分析)
SPSS统计分析案例专业：经济学姓名：000 学号：00000000一、我国城镇居民现状近年来,我国宏观经济形势发生了重大变化,经济发展速度加快,居民收入稳定增加,在国家连续出台住房、教育、医疗等各项改革措施和实施“刺激消费、扩大内需、拉动经济增长”经济政策的影响下,全国居民的消费支出也强劲增长,消费结构发生了显著变化,消费结构不合理现象得到了一定程度的改善。
本文通过相关数据分析总结出了我国城镇居民消费呈现富裕型、娱乐教育文化服务类消费攀升的趋势特点。
二、我国居民消费结构的横向分析第一,食品消费支出比重随收入增加呈现出明显的下降趋势,这与恩格尔定律的表述一致。
但最低收入户与最高收入恩格尔系数相差太过悬殊,城镇最低收入户刚刚解决了温饱问题,而最高收入户的生活水平按照恩格尔系数的评价标准早已达到了富裕型,甚至接近最富裕型。
第二,衣着消费支出比重随收入增加缓慢上升,到高收入户又有所下降,但各收入组支出比重相差不大。
衣着支出比重没有更多的递增且最高收入户的支出比重有所下降,这些都符合恩格尔定律关于衣着消费的引申。
随着收入的增加,衣着支出比重呈现先上升后下降的走势。
事实上,在当前的价格水平和服装业的发展水平下,城镇居民的穿着是有一定限度的,而且居民对衣着的需求也不是无限膨胀的,即使收入水平继续提高,也不需要将更大的比例用于购买服饰用品了。
第三,家庭设备用品及服务、交通通讯、娱乐教育文化服务和杂项商品与服务的支出比重呈逐组上升趋势,说明居民的生活水平随收入的增加而不断提高和改善。
第四,医疗保健支出比重随收入水平提高呈现一种两端高、中间低的走势。
这是因为医疗保健支出作为生活必须支出,不论页脚内容1居民生活水平高低,都要将一定比例的收入用于维持自身健康,而且由于医疗制度改革,加重了个人负担的同时,也减小了旧制度可能造成的不同行业、不同体制下居民医疗保健支出的差别,因而不同收入等级的居民在医疗保健支出比重上差别不大。
我国居民人均消费结构研究 基于SPSS软件分析
引言
引言
消费结构是指人们在一定时期内对各类商品和服务的消费支出比例。随着经 济的发展和人民生活水平的提高，我国居民消费结构发生了显著变化。这种变化 对于人们生活质量的提高和经济社会的发展具有重要影响。本次演示通过利用 SPSS软件，对我国居民人均消费结构的演变进行分析，以揭示其内在规律和特点。
文献综述
结论
结论
本次演示基于SPSS软件分析，揭示了2006年至2016年间我国居民人均消费结 构的变化趋势。总体来看，消费结构在不断优化，但同时也存在一些问题，如食 品类支出占比下降、不同地区和收入层次居民消费结构差异等。政策制定者应这 些问题，进一步优化消费结构，促进经济社会可持续发展。
参考内容
摘要
我国居民人均消费结构研究 基于SPSS软件分析
01 摘要
03 文献综述
目录
02 引言 04 研究方法
目录
05 结果与讨论
07 参考内容
06 结论
摘要
摘要
本次演示利用SPSS软件，对2006年至2016年间我国居民人均消费结构的变化 进行了深入研究。研究发现，这一时期内居民消费结构发生了显著变化，呈现出 不同商品和服务消费项目的增长趋势。本次演示旨在揭示消费结构变化对人们生 活的影响，为政策制定者提供有价值的参考依据。
文献综述
已有研究表明，我国居民人均消费结构在不同时期表现出不同的特点。早期 研究主要采用定性描述和简单统计方法，分析了不同收入水平对消费结构的影响。 随着数据的丰富和研究方法的改进，学者们开始运用多元统计分析、模型拟合等 方法，对消费结构问题进行深入研究。然而，大多数研究集中在国家或地区层面， 针对我国居民人均消费结构的变化研究尚不充分。
结果与讨论
SPSS统计分析案例(我国城镇居民
SPSS统计分析案例一、我国城镇居民现状近年来,我国宏观经济形势发生了重大变化,经济发展速度加快,居民收入稳定增加,在国家连续出台住房、教育、医疗等各项改革措施和实施“刺激消费、扩大内需、拉动经济增长”经济政策的影响下,全国居民的消费支出也强劲增长,消费结构发生了显著变化,消费结构不合理现象得到了一定程度的改善。
本文通过相关数据分析总结出了我国城镇居民消费呈现富裕型、娱乐教育文化服务类消费攀升的趋势特点。
二、我国居民消费结构的横向分析第一,食品消费支出比重随收入增加呈现出明显的下降趋势,这与恩格尔定律的表述一致。
但最低收入户与最高收入恩格尔系数相差太过悬殊,城镇最低收入户刚刚解决了温饱问题,而最高收入户的生活水平按照恩格尔系数的评价标准早已达到了富裕型,甚至接近最富裕型。
第二,衣着消费支出比重随收入增加缓慢上升,到高收入户又有所下降,但各收入组支出比重相差不大。
衣着支出比重没有更多的递增且最高收入户的支出比重有所下降,这些都符合恩格尔定律关于衣着消费的引申。
随着收入的增加,衣着支出比重呈现先上升后下降的走势。
事实上,在当前的价格水平和服装业的发展水平下,城镇居民的穿着是有一定限度的,而且居民对衣着的需求也不是无限膨胀的,即使收入水平继续提高,也不需要将更大的比例用于购买服饰用品了。
第三,家庭设备用品及服务、交通通讯、娱乐教育文化服务和杂项商品与服务的支出比重呈逐组上升趋势,说明居民的生活水平随收入的增加而不断提高和改善。
第四,医疗保健支出比重随收入水平提高呈现一种两端高、中间低的走势。
这是因为医疗保健支出作为生活必须支出,不论居民生活水平高低,都要将一定比例的收入用于维持自身健康,而且由于医疗制度改革,加重了个人负担的同时,也减小了旧制度可能造成的不同行业、不同体制下居民医疗保健支出的差别,因而不同收入等级的居民在医疗保健支出比重上差别不大。
第五,居住支出比重基本上呈先上升后下降的趋势,这与我国居民消费能级不断提升,住宅商品正在越来越成为城镇居民关注的热点是相吻合的,同时与恩格尔定律的引申也是一致的。
我国城镇居民人均消费支出的统计分析
我国城镇居民人均消费支出的统计分析作者：脱颖来源：《商情》2016年第14期本文采用2013年我国31个省、市、自治区的城镇居民人均消费支出数据，先通过聚类分析方法寻找不同地区城镇居民的消费结构的相似点和差异点；再利用主成分分析方法研究各省城镇居民消费结构水平，得出其经济发展状况；最后利用因子分析方法，根据因子得分对各省城镇居民消费支出进行排序和分类。
城镇居民消费支出聚类分析主成分分析因子分析一、引言近年来，随着我国经济的快速发展，居民消费结构也发生了巨大变化，人们开始根据自身的需求选择多种多样的商品，而且人们在实现物质需求满足的同时，还在不断追求精神需求的满足。
同时，社会产品在经济发展的过程中越来越丰富，居民消费的选择空间也越来越大。
在居民全部消费支出的八项指标（食品、衣着、居住、家庭设备、交通通讯、文教娱乐、医疗保健、其他）中，反应基本生存需要的食品、衣着等项所占的比重大幅度下降，而体现发展与享受需求的住房、交通等项支出的比重则迅速上升，说明人民的生活质量进一步提高。
由于我国各地区的经济发展不平衡，加之各地人口、资源、政策等方面也存在差异，导致各地区居民的消费结构存在着明显差异。
合理的消费结构有利于国民经济的快速发展，而滞后的消费结构则会阻碍经济的健康发展。
因此，消费结构的合理化问题在国民经济中处于至关重要的地位。
所以，为了进一步改善消费结构，引导正确的消费观念，提高我国城镇居民的消费水平，有必要对我国各地区城镇居民消费结构之间的差异进行比较，从宏观上把握各地区城镇居民的消费现状和消费水平的差异，为提高我国总体消费水平、改善消费结构提供决策依据。
本文利用SPSS软件通过聚类分析、主成分分析、因子分析三种统计方法对2013年我国各省城镇居民消费结构作分析。
二、聚类分析聚类分析是将样品或变量进行分类的多元统计分析方法。
其功能是建立一种分类方法，将一批样品或者变量，按照他们在性质上的亲疏、相似程度进行分析。
居民消费价格指数的SPSS分析
居民消费价格指数的SPSS分析摘要：居民消费价格指数（CPI）是我国物价指数体系中极其重要的一个指数，主要反映消费者支付商品和劳务的价格变化情况，也是一种度量通货膨胀水平的工具，以百分比变化为表达形式。
SPSS（Statistical Product and Service Solutions），是世界上最早的统计分析软件, 广泛应用于通讯、医疗、银行、证券、保险、制造、商业、市场研究、科研教育等多个领域和行业，是世界上应用最广泛的专业统计软件。
我国改革开放以来，社会经济的各个方面发生了巨大的变化，居民消费价格指数的变动也显示出自身的特点，对其过程有SPSS软件进行分析，有利于我们认识它与社会经济发展相联系的变动规律。
关键词：居民消费价格指数（CPI）；SPSS；价格变动指数；时间序列；指数平滑法在市场经济条件下，居民消费价格指数（Consumer Price Index，简称CPI），已经成为一个政府管理者和居民共同关注的重要指标。
分析改革开放以来的居民消费价格指数变动，对该指标所表现出的与社会经济发展密切相连的规律性是个很好的总结。
一、原始数据及预处理二、SPSS指数平滑法分析过程（一）绘序列图Sequence Plot由上图可看出：1、1978-1989年改革开放初期，我国居民消费价格指数的变动比较激烈。
20世纪80年代，居民消费价格指数在105%以上的年份达到6个；1988、1989年达到高峰，居民消费价格上涨幅度达到18.8%和18%，这是改革开放以后第一个居民消费价格指数峰顶。
这一时期居民消费价格指数最高的1988年与最低的1978年之间，其差值为18.1个百分点。
2、1990-1999年20世纪90年代，居民消费价格指数在105%以上的年份有5个；1993、1994、1995年达到高峰，居民消费价格上涨幅度达到14..7%、24.1%、17.1%；这是改革开放以后第二个居民消费价格指数峰顶，其幅度比上一个大。
SPSS统计分析报告案例(我国城镇居民消费结构及趋势地统计分析报告)
合用标准文案SPSS统计解析案例专业：经济学姓名： 000学号： 00000000一、我国城镇居民现状近来几年来 , 我国宏观经济形势发生了重要变化 , 经济睁开速度加快 , 居民收入牢固增加 , 在国家连续出台住所、教育、医疗等各项改革措施和推行“刺激花销、扩大内需、拉动经济增加〞经济政策的影响下 , 全国居民的花销支出也激烈增加 , 花销结构发生了明显变化 , 花销结构不合理现象获取了必然程度的改进。
本文经过相关数据解析总结出了我国城镇居民花销表现丰饶型、娱乐教育文化效劳类花销爬升的趋势特点。
二、我国居民花销结构的横向解析第一 , 食品花销支出比重随收入增加表现出明显的下降趋势, 这与恩格尔定律的表述一致。
但最低收入户与最高收入恩格尔系数相差过分悬殊, 城镇最低收入户方才解决了饱暖问题,而最高收入户的生活水平依照恩格尔系数的议论标准早已到达了丰饶型, 甚至凑近最丰饶型。
第二 , 穿着花销支出比重随收入增加缓慢上升, 到高收入户又有所下降, 但各收入组支出比重相差不大。
穿着支出比重没有更多的递加且最高收入户的支出比重有所下降, 这些都符合恩格尔定律关于穿着花销的引申。
随着收入的增加, 穿着支出比重表现先上升后下降的走势。
事实上 , 在当前的价格水平和服饰业的睁开水平下, 城镇居民的穿着是有必然限度的, 而且居民对穿着的需求也不是无量膨胀的, 即使收入水平连续提升, 也不需要将更大的比率用于购置服饰用品了。
第三, 家庭设备用品及效劳、交通通讯、娱乐教育文化效劳和杂项商品与效劳的支出比重呈逐组上升趋势, 说明居民的生活水平随收入的增加而不断提升和改进。
第四 , 医疗保健支出比重随收入水平提升表现一种两端高、中间低的走势。
这是由于医疗保健支出作为生活必定支出, 无论居民生活水平上下, 都要将必然比率的收入用于保持自己健康, 而且由于医疗制度改革 , 加重了个人负担的同时 , 也减小了旧制度可能造成的不同样行业、不同样系统下居民医疗保健支出的差异, 所以不同样收入等级的居民在医疗保健支出比重上差异不大。
SPSS论文-各地区城镇居民家庭人均消费性支出分析
SPSS论文题目：各地区城镇居民家庭人均消费性支出分析摘要：我国各地区的经济发展水平存在着较大的差异。
本文运用SPSS软件分析方法对我国各地区城镇居民消费性支出进行分析研究,研究表明:各地区城镇居民消费性支出的差异主要是由两方面引起的,首先是地区的经济发展水平,我国东部、中部和西部地区的消费水平存着较大差异;其次是由地区气候因素引起的消费倾向,我国南北地区明显有别。
关键字：SPSS，消费支出，分析数据：我国地域辽阔,各地区的经济发展很不平衡,各地区城镇间的消费性支出存在着较大的差异,而且由于多种因素的影响,这种差异呈现加速扩大的态势。
如何客观、准确、有效地分析这些差异,具有重要的理论和实践意义。
消费性支出的指标有许多,如果直接从诸多指标来分析各地区的差异,那未分析的结果很可能将是繁杂和不得要领的,很难给出直观有效的结论。
如果仅用消费性总支出这个指标,则显得太粗糙,丢失的有用信息太多,不能较充分地反映各地区的消费差异。
那么,如何能使得所作的分析研究即不繁杂又不损失太多的信息呢?这正是本文所要解决的问题。
居民消费支出：是指城乡居民个人和家庭用于生活消费以及集体用于个人消费的全部支出。
包括购买商品支出以及享受文化服务和生活服务等非商品支出。
对于农村居民来说，还包括用于生活消费的自给性产品支出。
集体用于个人的消费指集体向个人提供的物品和劳务的支出；不包括各种非消费性的支出。
其形式是通过居民平均每人全年消费支出指标来综合反映城乡居民生活消费水平。
消费支出特点明显：食品价格上涨使恩格尔系数有所回升；居住支出快速增长；家庭设备消费较快增长；汽车消费热点突出；义务教育负担减轻；衣着和医疗保健支出低速增长。
Descriptive Statistics此表描述了所统计的数据。
Statistics上述数据为用SPSS软件所作出的均值、方差、标准、峰度、偏度差等等数据，还有运用SPSS软件的回归分析、单一样本T检验所得到的数据和曲线图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2013年我国城镇居民人均消费的SPSS统计分析一、搜集到的2013年我国31个城市城镇居民人均消费水平的数据数据来源：国家统计局/workspace/index?m=hgnd 二、对数据的基本分析在数据文件建立好后，通常还需要对待分析的数据进行必要的预加工处理，这是数据分析过程中不可缺少的一个关键环节。
（一）、对数据按人均消费（expend）进行降序排列操作步骤：（1）：选择“数据”→“排序个案”菜单项（2）：将“人均消费（expend）”选入“排序依据”列表框，选中“降序”（3）：点击“确认”按钮，生成如下降序排列的数据集由数据的降序排列可以看出，全国只有上海、北京、广东等九个城市的城镇人均消费在全国城镇人均消费水平以上。
（二）、作出人均收入和人均消费的直方图操作步骤：（1）：选择“图形”，打开“图表构建程序”菜单项（2）：从“库”中选择“直方图”将其拉入“图表预览使用数据实例”（3）：将变量“地区”设置为x轴，将“人均收入”和“人均消费”设置为y轴（4）：点击“确认”按钮，即生成如下直方图通过一个复合条形图，可以很明确的发现我国城镇居民生活水平存在很大的地区差异，地区发展很不平衡，从图中的生活消费支出和人均收入来看，北京，上海，浙江这些省市城镇居民消费水平最高，人均收入也是最高的，各省市的城镇居民消费水平差异较大，大多数省份城镇居民人均消费集中在15000元左右。
（三）、对数据按照人均消费作出直方图，以统计我国农村人均消费的水平 1、首先对数据分组，分组数目的确定。
按照Sturges 提出的经验公式来确定组数K,K=1+2lg lg n，计算得组数为6. 2、确定组距组距=（最大值-最小值）/组数=（28155.00-12231.90）/6=2653.85，可近似取值为3000.00元。
操作步骤：（1）：选择“转换”→“可视离散化”菜单项，将“人均消费”选入“要离散的变量”列表框中，单击“继续”按钮进入主对话框。
（2）：单击“生成分割点”按钮，设定分割点数量为6，宽度为3000.00，可见系统会自动会填充第一个分割点的位置为12231.90，单击“应用”返回到主对话框。
（3）：此时可以看到下部数值标签网格里的“值”列已被自动填充，单击“生成标签”按钮，是标签列也得到自动填充。
（4）：将离散的变量名设定为expendNew 。
（5）：单击“确定”按钮。
3、频数分析操作步骤：（1）：选择“分析”→“描述统计”→“频率”，打开频率对话框。
（2）：选定“expendNew ”，点击“图表”，选择“条形图”点击继续。
（3）：点击“确认”，生成如下三张表。
Statistics人均消费(已离散化)N Valid 32Missing 0 Mean 3.13Median 3.00Std. Deviation 1.314Minimum 1Maximum 7Percentiles 25 2.0050 3.0075 3.75人均消费(已离散化)Frequency Percent Valid Percent Cumulative Percent Valid <= 12231.90 1 3.1 3.1 3.1 12231.91 - 15231.90 10 31.3 31.3 34.4 15231.91 - 18231.90 13 40.6 40.6 75.0 18231.91 - 21231.90 3 9.4 9.4 84.4 21231.91 - 24231.90 3 9.4 9.4 93.8 24231.91 - 27231.90 1 3.1 3.1 96.9 27231.91+ 1 3.1 3.1 100.0 Total 32 100.0 100.0由上图的频数分析可以看出，我国2013年城镇居民人均消费支出集中在第二组和第三组，大约占到百分之七十。
由于在表格中不存在缺失值，因此频数分布表中的百分比和有效百分比相同。
从此次分析中可以看出，我国城镇家庭居民人均消费的总体水平比较集中，大约在12000元--18000元之间，还有少数省市的消费水平处在中等阶段，而有上海、北京、浙江等一些经济较发达的地区的城镇家庭居民人均消费达到了21000元以上。
三、对数据的回归分析（一）、作出人均收入与消费支出散点图，以观察他们的线性关系如何操作步骤：（1）：选择“图形”，打开“图表构建程序”菜单项（2）：从“库”中选择“散点图”将其拖入“图表预览使用数据实例”（3）：将“人均收入”选定为x轴，将“人均消费”选定为y轴（4）：点击“确认”生成如下散点图由散点图可以看出，人均消费Y和人均收入X大概呈一元线性关系，因此可以建立一元线性模型进行回归分析。
（二）假设回归模型为Y=a+b X,其中，Y表示城镇人均消费支出，为被解释变量，X表示人均收入，为解释变量，b为回归系数。
操作步骤：（1）选择“分析”→“回归”→“线性”菜单项，打开“线性回归”对话框。
（2）将“人均消费”选入“因变量”列表框，将“人均收入”选入“自变量”列表框。
（3）单击“确定”按钮。
得到如下（1）、（2）、（3）、（4）四张表格，依次分析如下：表（1）：移入/移出的变量Variables Entered/Removed bModel Variables Entered VariablesRemoved Method1 人均收入a. Entera. All requested variables entered.b. Dependent Variable: 人均消费从上表可以看出，放入模型的变量只有一个即“人均收入”，选择变量的方法为强行进入法，也就是说将所有的自变量都放入模型中，模型的因变量为“人均消费”。
表（2）：模型汇总上表是对模型的简单汇总，其实就是对回归方程拟合情况的描述，通过这张表可以知道相关系数R=0.960，决定系数2R=0.922，调整决定系数2R=0.920,和回归系数的标准误=31106.90715。
由于决定系数接近于1，说明模型的拟合程度较好。
表（3）：方差分析表F=355.256，P=0.000<0.05,表明回归方程高度显著，即农民人均收入对消费有高度影响。
表（4）：系数人均消费Y=1897.504+0.599人均收入X上述回归方程给出了如下信息：2013年中国城镇居民人均可支配收入增加1元，人均消费支出增加0.599元。
四、单样本的T检验（一）：由频数分析可知，分组后，全国31个省市的城镇家庭居民平均每人生活消费支出合计，大约有23个城市都集中在第一组，数额主要12231.91——18231.90元之间，其中在15231.91 - 18231.90之间的占到了百分之四十，因此可推断，全国农村家庭居民平均每人生活消费支出的平均数应该在15000--20000元之间，假设为18000元，由于该问题涉及的是单个总体，且要进行总体均值检验，同时农村家庭居民平均每人消费的总体可近似认为服从正态分布，因此，应采用单样本t检验来分析推断全国农村家庭居民人均消费的平均值是否为18000元。
分析结果如下：（二）：操作步骤：1、选择“分析”→“比较均值”→“单样本天t检验”菜单项，打开“单样本t检验”对话框如下图所示：2、单击“确定”按钮。
生成如下两张图表：表（1）：One-Sample StatisticsN Mean Std. Deviation Std. Error Mean人均消费32 17216.6031 3902.16064 689.81106One-Sample TestTest Value = 18000t df Sig. (2-tailed) Mean Difference 95% Confidence Interval of theDifferenceLower Upper人均消费-1.136 31 0.265 -783.39688 -2190.2758 623.4821由表（1）可知样本均值为17216.6031，低于基准线18000.00，标准差3902.16064，均值标准差689.81106。
由表（2）为单样本t检验的分析结果，第一行注明了用于比较的假设总体均数为18000，下面从左到右依次为t值、自由度、p值、两均数的差值、差值。
根据上面的检测结果t=-1.136，p=0.256，由于p>0.05，所以不能拒绝原假设，可以认为人均消费水平在18000元。
同时，可知全国城镇居民2013年人均消费在95％的置信水平下的置信区间为：（15809.7242,18623.4821）。
五、非参数检验——多配比样本分参数检验数据中我国城镇家庭居民人均消费包括食品、衣着、居住、家庭设备、交通及通讯、文教娱乐、医疗保健、和其他8个指标，为了比较清楚的了解这8项指标对我国城镇居民人均消费总体的影响，以及其大概的消费动向，可以利用多配比样本的非参数检验Friedman 检验对各个指标进行检验。
（一）：操作步骤：（1）选择“分析”→“非参数检验”→“旧对话框”→“k个相关样本”菜单项，打开如下对话框：（2）：单击“确定”按钮，得到如下两张表格：表（1）：RanksMean Rank食物消费8.00衣物消费 5.09居住消费 4.50家居设备 2.66交通通讯 6.38医疗保健 2.34文教娱乐 5.88其它 1.16表（2）：Test Statistics aN 32Chi-Square 198.604df 7Asymp. Sig. .000a. Friedman Test（二）、结果分析检验结果中的p值小于给定水平0.05，故拒绝原假设，认为八个指标对我国城镇居民人均消费的影响是有显著差异的。
由表（1）知食物消费对人均消费的影响最大，其次是交通通讯和衣物消费，而影响最小的是其它。
六、因子分析在研究我国城镇居民的消费情况时收集了食物、衣物、居住等八个影响居民消费情况的因素，以期对问题能够有比较全面、完整的把握和认识。
由于数据过多，在实际建模时，这些变量未必能真正发挥预期的作用，会给统计分析带来许多问题，可以表现在：计算量的问题和变量间的相关性问题。
为了解决这些问题，最简单和最直接的解决方案是削减变量个数，但这又必然会导致信息丢失和信息不完整等问题的产生。
为此，人们希望探索一种更有效的解决方法，它既能大大减少参与数据建模的变量个数，同时也不会造成信息的大量丢失。
因子分析正是解决这种问题的方法。
（一）操作步骤（1）、选择菜单“分析”→“降维”→“因子分析”，出现因子分析对话框；（2）、把参与因子分析的样本选到变量对话框中，如下图：（3）单击“确定”按钮，得到如下11张图：图（1）原有变量的相关系数矩阵：Correlation Matrix食物消费衣物消费居住消费家居设备医疗保健交通通讯文教娱乐其它Correlatio n 食物消费1.000 .288 .656 .744 .295 .787 .782 .732衣物消费.288 1.000 .337 .517 .694 .368 .374 .634居住消费.656 .337 1.000 .676 .505 .849 .750 .771家居设备.744 .517 .676 1.000 .441 .830 .853 .767医疗保健.295 .694 .505 .441 1.000 .479 .414 .600交通通讯.787 .368 .849 .830 .479 1.000 .860 .782文教娱乐.782 .374 .750 .853 .414 .860 1.000 .831 其它.732 .634 .771 .767 .600 .782 .831 1.000从上图可以看到，大部分的相关系数都较高，各变量呈较强的线性关系，能够从中提取公共因子，适合进行因子分析。