缓和曲线上任意点坐标计算程序

合集下载

缓和曲线坐标计算

缓和曲线坐标计算
缓和曲线坐标计算公式:
5222 S=L-(L)/(90×R×K) B= L×180/(6×R×K×π) Q=W，B? ?? X=U，S×CosQ Y=V，S×SinQ ? ?
其中:L为缓和曲线起点至计算桩号的弧长，R为缓和曲线后接圆曲线的半径，K为缓曲线总长，W为缓和曲线起点的切线方位角，U为缓和曲线起点的X坐标，V 为缓和曲线起点的Y坐标。

左转角半径为负，右转角为正。

圆曲线坐标计算公式:
22 B=K×90/(R×π)+L×180/(R×π) Q=K/2-(K×K)/(240×R) ??
2P=K/(24×R) M=R×SinB+Q N= R×(1- CosB)+P ???
-1 2 2E=tan (N/M) F=?(M+N ) T=W+E
X=U+F×CosT ? ???Y=V+F×SinT ?: 开根号 ?
K为缓和曲线总长，R为圆曲线半径，L为圆曲线起点至计算点的弧长，W 为缓和曲线起点的切线方位角，U为缓和曲线起点的坐标，V为缓和曲线起点的坐标.
左转角半径为负，右转角为正。

相关文档：
更多相关文档请访问：。

道路缓和曲线任意点坐标及方位角的计算方法

求点与 ZH 点的距离, ΑZH - P 表示直线 ZH - P 的坐
标方位角 1
要求得 P 点的坐标, 关键是要正确求得 D ZH - P 和 ΑZH - P 1 依据 (7) 可以求得 D ZH - P 1
对于 ΑZH - P 有 ΑZH - P = ΑZH - r + 360°成立, 其中 ΑZH 为路线走向方向或 ZH 点切线方向的坐标方位
参考文献:
[ 1 ] 何景华 1 公路勘测[M ]1 北京: 人民交通出版社, 19981 [ 2 ] 刘延伯 1 工程测量[M ]1 北京: 冶金工业出版社, 19841
T 2= 20. 13 m
466 824. 034 Η= 11°29′37″
简要计算如下:
中点的里程为 K0+ 313. 755 m , 终点的里程为
K0 + 343. 84 m , 起点切线的走向方位角 ΑZH =
54°14′51″, 对于点 K0+ 313. 755 处, l= 30. 085 m
点号起点 (直缓点) 切交点 (JD )
表 1 部分设计数据
Ta b le 1 P a rt de s ign da te
里程桩号 K0+ 283. 67 K0+ 323. 87
xm 3 081 965. 940 3 081 989. 428
ym
切线长和夹角
T 1= 40. 20 m 466 791. 410
A bs tra c t: O n the d ifficu lties in com pu tation and setting of coo rd ination in dem u lcen t cu rre, a new com putation m ethod of the coo rdination of any po in t in dem ulcen t curve of viatical figuration is p ropo sed. B ased on the theo ry of coo rdination com putation, the calculating fo rm ulas is derived. It is useful in the setting of dem ulcen t curve in h igh class h ighw ay’ s adert.

铁路缓和曲线坐标计算方法 (0517)

一、曲线的一般组成厦深铁路12标正线线形设计为直线+缓和曲线+圆曲线+缓和曲线+直线。

从小里程至大里程依次为ZH （直缓点）、HY （缓圆点）、YH （圆缓点）、HZ （缓直点）如下图所示：二、方位角的概念从标准方向的正北端起,顺时针方向到直线的水平角称为该直线的方位角。

方位角的取值范围为0°～360°，如下图A 即为直线L 的方位角。

TT三、某点坐标的计算已知A 点坐标为（491548，2505452），B 点距离A 点L=125m ，直线AB 的方位角为235°，计算B 点坐标。

计算方法：Y=491548+125×SIN235=491445.606X=2505452+125×COS235=2505380.303四、曲线上任一点的坐标及切线方位角计算1 直线段上任一点的坐标及方位角直线上的坐标计算比较简单，只需要求出该点所在直线的方位角以及线路中的里程即可求得例1，求DK495+520处左中线的坐标及方位角由设计院所给的曲线要素表可知该点位于JD57 JD58的直线上，查曲线要素表JD57,JD58的坐标分别为（488809.902，2504127.029），（485660.627，2504491.226）。

通过坐标反算直线JD57 JD58的方位角：TTA=atg((485660.627-488809.902)/( 2504491.226-25 04127.029))=276.59665°注意：A的取值可根据下述条件确定ΔY>0,ΔX>0,第一象限0-90°ΔY>0,ΔX<0,第二象限90°-180°ΔY<0,ΔX<0,第三象限180°-270°ΔY<0,ΔX>0,第四象限270°-360°查曲线表，JD58切线长T= 690.303m，JD58坐标（Y58,X58）=（485660.627，2504491.226）,ZH点里程为DK496+093.885。

圆曲线、缓和曲线计算方法

● 圆曲线方法一：sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二：11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三：180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角，A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段：先由JD1以及JD2的坐标算出JD1到JD2的方位角，即直线段方位角A ，故可算出HZ 、ZH 坐标及其直线段各点坐标。

2、缓和曲线：以HZ 、ZH 为起点，缓和曲线上任意一点离HZ 、ZH 距离为l ，利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标，利用arctan y x算出该点相对起点的方位角B ，再根据线路走向及直线段方位角可算出该点的方位角C （顺时针加，逆时针减），用可求出该点相对起点的距离D ，最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。

（00(,)x y 为缓和曲线起点的坐标）3、圆曲线：用上述方法求出圆曲线两端点HY 、YH 坐标，算出HY 到YH 的方位角F ，以及两点间的距离E ，用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ，根据线路走向求出起点到圆心的方位角H （H=F+/-G ），00(,)x y 圆曲线为起点坐标，根据00cos sin x x R H y y R H=+⎧⎨=+⎩，求出圆心坐标。

缓和曲线计算方法

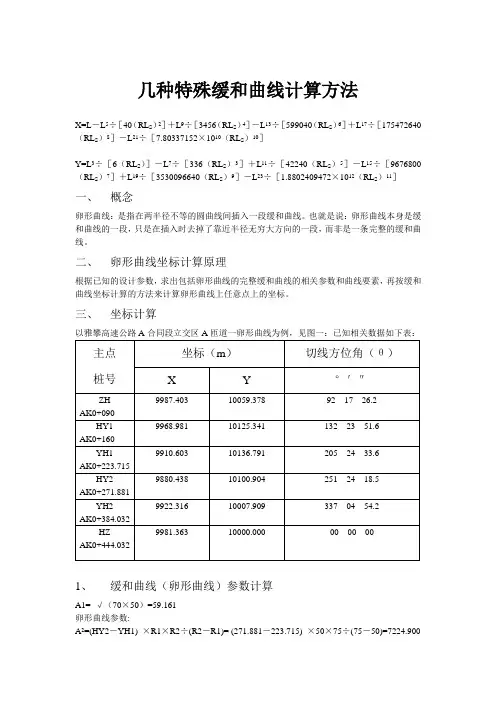
几种特殊缓和曲线计算方法X=L－L5÷［40（RL S）2］＋L9÷［3456（RL S）4］－L13÷［599040（RL S）6］＋L17÷［175472640（RL S）8］－L21÷［7.80337152×1010（RL S）10］Y=L3÷［6（RL S）］－L7÷［336（RL S）3］＋L11÷［42240（RL S）5］－L15÷［9676800（RL S）7］＋L19÷［3530096640（RL S）9］－L23÷［1.8802409472×1012（RL S）11］一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅攀高速公路A合同段立交区A匝道一卵形曲线为例，见图一：已知相关数据如下表：1、缓和曲线（卵形曲线）参数计算A1= √（70×50）=59.161卵形曲线参数:A2=(HY2－YH1) ×R1×R2÷(R2－R1)= (271.881－223.715) ×50×75÷(75－50)=7224.900A2=√（7224.900）=84.999A3=√（60×75）=67.0822、卵形曲线所在缓和曲线要素计算卵形曲线长度L F由已知条件知：L F=HY2－YH1=271.881－223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度L S，由此找出HZ｀点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）L M=L S（YH1至HZ｀的弧长）=A2÷R1=7224.9÷50=144.498∴HZ｀桩号=YH1+L M=223.715+144.498=368.213L E=HY2至HZ｀的弧长=A2÷R2=7224.9÷75=96.332或L E=L M－L F=144.498－48.166=96.332卵形曲线长度L F=L M－L E=144.498－96.332=48.166（校核）HY2=HZ｀－L E=368.213－96.332=271.881（校核）以上说明计算正确3．HZ｀点坐标计算（见图2）㈠用缓和曲线切线支距公式计算，缓和曲线切线支距通式：Xn=［（－1）n+1×L4n－3］÷［（2n-2）！×22n－2×（4n－3）×（RL S）2n－2］Yn=［（－1）n+1×L4n－1］÷［（2n-1）！×22n－1×（4n－1）×（RL S）2n－1］公式中符号含义：N——项数序号（1、2、3、……n）！——阶乘R——圆曲线半径LS——缓和曲线长度㈡现取公式前6项计算（项数越多精度越高，可根据工程精度需求取项数），带入公式后计算如下：X=L－L5÷［40（RL S）2］＋L9÷［3456（RL S）4］－L13÷［599040（RL S）6］＋L17÷［175472640（RL S）8］－L21÷［7.80337152×1010（RL S）10］Y=L3÷［6（RL S）］－L7÷［336（RL S）3］＋L11÷［42240（RL S）5］－L15÷［9676800（RL S）7］＋L19÷［3530096640（RL S）9］－L23÷［1.8802409472×1012（RL S）11］公式中L为计算点至ZH ｀或HZ｀的弧长HZ｀：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ｀－YH1=368.213-223.715=144.498将L=LS带入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2＋Y2）=131.5301偏角a1=arctg（Y÷X）=27°5′0.2″偏角计算用反正切公式，不要用其他公式。

缓和曲线坐标计算

二、公式推导1 、实例数据河北省沿海高速公路一缓和曲线（如图）： AB 段为缓和曲线段， A 为 ZH 点， B 为 HY 点， R B=800m ； A 点里程为 NK0+080 ，切线方位角为θA=100 ° 00 ′ 24.1 ″，坐标为X A=4355189.493,Y A=476976.267 ； B 点里程为 NK0+158.125 ，切线方位角为θB=102 ° 48 ′ 15.6 ″，坐标为 X B=4355174.669 ，Y B=477052.964 ，推求此曲线段内任意点坐标。

2 、公式推导及实例计算方法一：弦线偏角法1 ）公式推导由坐标增量的计算方法我们不难理解，求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。

所以我们可以利用 ZH 点，只要知道待求点距 ZH 点的距离（弦长 S ）和此弦与 ZH 点切线方位角的夹角（转角 a ），即可求出该点坐标。

根据回旋线方程 C=RL ，用 B 点数据推导出回旋线参数：C=RL S=800*78.125=62500 （ L S为 B 点至 ZH 点的距离）设待求点距 ZH 点距离为 L因回旋线上任意点的偏角β0=L2/2RL S, 且转角 a=β0/3 ，可得该点转角 a 。

（曲线左转时 a 代负值）。

根据缓和曲线上的弧弦关系 S=L-L5/90R2L S2，可以求出待求点至 ZH 点的弦长。

然后我们利用坐标增量计算公式可以推导出缓和曲线任意点坐标计算公式：X=X A+S*cos （θA+a ） =4355189.493+ （ L-L5/90R2L S2） *cos （θA+L 2/6RLS）Y=Y A+S*sin （θA+a ） =476976.267+ （ L-L5/90R2L S2） * sin （θA+L 2/6RLS）式中θA=100 ° 0 ′ 24.1 ″2 ）实例计算现在我们利用此公式计算桩号为 NK0+140 的坐标第一步，求出 L=140-80=60 米第二步，求出 a=180L2/6 π RL S=0 ° 33 ′ 00.14 ″第三步，求出 S=L-L5/90R2L S2=60-605/ （ 90*8002*78.1252） =59.998 第四步：将 a ， S 值代入缓和曲线计算公式，可求出桩号为 NK0+160 点的坐标为：X=4355178.501 ， Y=477035.249 。

缓和曲线上各点的计算方法

/dabaoyou668/blog/item/a20d48d978b94fcd8c102954.ht ml一、缓和曲线上的点坐标计算2011年02月23日星期三 18:45一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数。

道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

高速公路上的一些曲线坐标,高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

坐标、高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

缓和曲线逐点坐标计算

为提高计算结果的准确性，提高工作效率和减轻计算的工作量，在实际应用中可以配合电子计算器使用，以下是 CASIO4800P 计算器计算缓和曲线的公式：
Lbl 0:{EG}:A “ X0 ” ：B “ Y0 ” ：C “ C0 ” ：D “ 1/R1 ” ：E “ 1/R2 ” ：F “ DK1 ” ：G “ DK2 ”
第二步，求出 a=180L2/6 π RLS=0 ° 33 ′ 00.14 ″
第三步，求出 S=L-L5/90R2LS2=60-605/ （ 90*8002*78.1252 ） =59.998
第四步：将 a ， S 值代入缓和曲线计算公式，可求出桩号为 NK0+160 点的坐标为：
2 、公式推导及实例计算
方法一：弦线偏角法
1 ）公式推导
由坐标增量的计算方法我们不难理解，求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。所以我们可以利用 ZH 点，只要知道待求点距 ZH 点的距离（弦长 S ）和此弦与 ZH 点切线方位角的夹角（转角 a ），即可求出该点坐标。
二、公式推导
1 、实例数据
河北省沿海高速公路一缓和曲线（如图）： AB 段为缓和曲线段， A 为 ZH 点， B 为 HY 点， RB=800m ； A 点里程为 NK0+080 ，切线方位角为 θA=100 ° 00 ′ 24.1 ″，坐标为 XA=4355189.493,YA=476976.267 ； B 点里程为 NK0+158.125 ，切线方位角为 θB=102 ° 48 ′ 15.6 ″，坐标为 XB=4355174.669 ， YB=477052.964 ，推求此曲线段内任意点坐标。
Y=476976.267+ （ L-L5/40R2LS2 ） sinθA + （ L3/6RLS ） cosθA 。

缓和曲线坐标计算公式

缓和曲线坐标计算公式你说的坐标应该是在整条公路上的坐标不是支距法算出来的坐标吧支距法现在都不怎么用了给你个偏角法的计算公式吧ZH至i点的偏角A=30xL的平方除以派除以R 除以LsZH至i点的弦长C=L（ZH至i点的长）-L的5次方除以90 除以R的平方除以Ls的平方具体是这样的：建立以ZH或（HZ）为原点，过ZH的切线及半径分别X轴与Y轴的坐标系统后，就可以用曲线上各点在这个坐标系统中的x，y测设曲线。

坐标计算如下：缓和曲线：xi=li- li^5／40R^2li^2yi=li／6Rl0-li^7／336R^3li^3圆曲线：xi=R×sinαi+myi=R(1-cosαi)+pα=180°∕πR（li- l0）+β0li是曲线上与测设点距ZH点的弧长，l0缓和曲线长度，m，p，β0是缓和曲线参数缓和曲线计算偏角公式L2（平方）/（2RLs）L:缓和曲线上任一点到ZH点距离R：圆半径Ls：缓和曲线长当L=Ls时，公式就是L/(2R)卵形曲线坐标计算方法简介：在高速公路立交平面线型中，现越来越多采用卵形曲线这一线型形式，而卵形曲线坐标的计算在现有相关书籍中却又很少提到，这就为施工中的坐标计算及放样增加了较大难度，为解决此难道，我在实践中通过对缓和曲线坐标的计算加以分析并结合理论知识，总结出了卵形曲线坐标的计算方法和技巧。

关键字：卵形曲线坐标计算一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：主点桩号坐标（m）切线方位角（θ）X Y ° ’ ”ZHAK0+090 9987.403 10059.378 92 17 26.2HY1AK0+160 9968.981 10125.341 132 23 51.6YH1AK0+223.715 9910.603 10136.791 205 24 33.6HY2AK0+271.881 9880.438 10100.904 251 24 18.5YH2AK0+384.032 9922.316 10007.909 337 04 54.2HZAK0+444.032 9981.363 10000.000 0 00 001、缓和曲线（卵形曲线）参数计算A1= =59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2= =84.999A3= =67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ“点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ“的弧长）=A2÷R1=7224.900÷50=144.498∴HZ“桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ“的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ“-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ“点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH“或HZ“的弧长HZ“：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ“-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

缓和曲线)计算公式

高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式发布时间:2009-06-06 16:58:25高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

缓和曲线圆曲线坐标计算

二、圆曲线要素计算
1、圆曲线要素 R —— 半径 —— 转向角 T —— 切线长
L —— 曲线长
Eo —— 外矢距
q —— 切曲差
R、、T、L、Eo、q 称为圆曲线要素。
2、计算公式
为测量得到，R 为设计值。
T R tg
L R

2

180
Eo R (
1 cos
X YZ1 X JD1 T1 cos αJD1 JD 2 YYZ1 YJD1 T1 sin αJD1 JD 2
通用公式：
X ZYi X JD i Ti cos αi 1,i YZYi YJD i Ti sin αi 1,i
X
JD2
X YZi X JD i Ti cos αi ,i 1 YYZi YJD i Ti sin αi ,i 1

2
1)
q 2T L
三、主点里程计算
1、基本知识里程：由线路起点算起，沿线路中线到该中线桩的距离。

表示方法：DK26＋284.56。
“+”号前为公里数，即26km，“+”后为米数，即 284.56m。 CK —— 表示初测导线的里程。 DK —— 表示定测中线的里程。
Ｋ —— 表示竣工后的连续里程。
YZ2 终点
Y
O
X ZY1 X JD1 T1 cos α起 JD1 YZY1 YJD1 T1 sin α起 JD1
X ZY2 X JD 2 T2 cos αJD1 JD 2 YZY2 YJD 2 T2 sin αJD1 JD 2 X YZ2 X JD 2 T2 cos αJD 2 JD 3 YYZ2 YJD 2 T2 sin αJD 2 JD 3

缓和曲线测设方法及步骤

缓和曲线测设方法及步骤
缓和曲线是指连接两个不同半径的曲线段时所采用的过渡曲线，用于平稳地过渡车辆行驶
方向的改变。

缓和曲线测设方法及步骤如下：
1. 准备工作：确定需要设计缓和曲线的两个曲线段的半径和关键数据，如切线长度等。

2. 计算缓和曲线参数：根据设计要求，计算缓和曲线的切线长、切线倾角和缓和曲线长度等参数。

3. 确定标定点：在缓和曲线上选择若干个标定点，一般包括起始点、终止点、中间点和过渡点等。

4. 进行野外测量：在确定的标定点上进行野外测量，包括测量标定点的坐标和地面高程等。

5. 数据处理：将野外测量的数据进行处理，计算出缓和曲线中的各个点的坐标和地面高程。

6. 绘制缓和曲线：根据计算得到的缓和曲线参数和测量的数据，利用工程绘图软件或绘图工具，绘制出缓和曲线图。

7. 检查和修正：通过对绘制的缓和曲线图进行检查和修正，保证缓和曲线的平滑和连续性。

8. 缓和曲线设计报告：根据设计要求，编写缓和曲线设计报告，包括设计计算数据和绘制的缓
和曲线图等。

以上是缓和曲线测设的一般方法和步骤，具体操作过程可能会因具体情况而有所不同。

缓和曲线的坐标公式及推导

缓和曲线的坐标公式及推导第一章缓和曲线的坐标公式如图1-1所示,其坐标系是以缓和曲线起点ZH 为原点O，以切线为x轴，以过原点的曲线半径为y轴。

若原点O至P点的缓和曲线长度为，过P点切线与x轴的交角为β（即半径由∞变至的中心角）。

若P有微小变化至P′时，则增长，（x,y）增长（）,则有以下关系，图 1-1得，（2-1）由公式(常数)得知，故有则将上式代入（1-1）式中，得（2-3）上式即为缓和曲线上任一点直角坐标（x,y）的计算公式。

缓和曲线上任一点P的切线与x轴的交角，称为缓和曲线螺旋角，或称缓和曲线角。

其计算可由前面公式得（弧度）（2-4）若将代入（2-4）及（2-3）式中，则有以下结果：（2-5）上式即为缓和曲线终点HZ（ZH）的坐标及螺旋角的计算公式。

第二章圆曲线要素及计算公式如图2-1所示，两相邻直线偏角（线路转向角）为，选定其图 2-1连接曲线圆曲线的半径为R，这样，圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来，我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ 和曲中点QZ为圆曲线三主要点。

我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差（切线长和曲线长之差）D为曲线6要素。

只要知道了曲线6要素，便可于实地测放出圆曲线。

现将圆曲线的元素列下：：转向角（实地测出）R：曲率半径（设计给出）T：切线长（计算得出）L：曲线长（计算得出）D：切曲差（计算得出）偏角是在线路祥测时测放出的，圆曲线半径R是在设计中根据线路的等级以及现场地形条件等因素选定的，其余要素可根据以下公式计算：第三章偏角法测设介绍偏角法是一种极坐标标定点位的方法，它是用偏角和弦长来测设圆曲线细部。

如图3-1所示，1，2…，，…，n为设计之详测点，邻点间距均为c，弦长c所对应的圆心角为。

当放样至详测点时，可在ZY点置镜，后视JD方向，拨出偏角,再自-1点量距C和拨出的视线方向交会，即得出点。