构件承载力计算
受压构件的承载力计算

受压构件的承载力计算一、梁柱的承载力计算方法对于受压构件,在弹性范围内,可以采用弹性承载力计算方法。
弹性承载力计算方法是根据梁柱的理论,主要应用弹性力学原理和应变能平衡条件进行计算。
在弹性承载力计算之外,受压梁柱的承载力还受到稳定性要求的限制。
稳定性要求主要包括屈曲的要求和稳定的要求。
稳定性承载力计算方法就是根据稳定性要求来计算的。
二、承载力计算的基本原理和方法1.构件的截面形态与材料的力学性能有关。
几何形态方面,可以通过截面形心深度、截面形态系数和截面面积等参数来描述。
力学性能方面,主要包括材料的抗压强度、屈服强度和弹性模量等参数。
2.构件的边界条件与受力特性有关。
边界条件主要包括自由端的约束、内力的约束和约束条件等。
边界条件对构件的承载力有着直接的影响,需要进行准确的分析和计算。
3.构件的荷载和荷载组合也是影响承载力计算的重要因素。
荷载包括静力荷载和动力荷载,荷载组合则是不同荷载的叠加组合。
需要根据具体情况来确定荷载和荷载组合,并进行相应的计算。
假设一个矩形柱的尺寸为300mm×400mm,材料抗压强度为250MPa,弹性模量为200 GPa。
根据以上参数,可以进行如下步骤的承载力计算。
1.计算截面形态参数:矩形柱的形心深度h=400/2=200mm形态系数α=(h/t)f/π^2=2.692.弹性承载力计算:根据梁柱的理论,弹性承载力可通过以下公式计算:Pcr=(π^2*E*I)/(kl)^2其中,E为弹性模量,I为惯性矩,kl为有效长度系数。
惯性矩I=1/12*b*h^3=1/12*300*400^3=32,000,000mm^4有效长度系数kl可根据梁柱的边界条件和约束情况进行计算。
假设矩形柱两端均固定,则kl=0.5代入以上参数,可以得到弹性承载力Pcr=200,000N=200kN。
3.稳定性承载力计算:稳定性承载力计算主要包括屈曲的要求和稳定的要求。
对于矩形柱,屈曲要求可通过欧拉公式计算,稳定的要求可通过查表确定。
无筋砌体受压构件承载力计算公式中

无筋砌体受压构件承载力计算公式中
无筋砌体受压构件是一种常见的建筑材料。
在进行承载力计算时,需要使用相应的公式。
下面将介绍无筋砌体受压构件承载力计算公式及其相关解释。
首先,无筋砌体受压构件的承载力可以用以下公式表示:
N = 0.45f_m * A
其中,N表示无筋砌体受压构件的承载力,f_m表示砌体的抗压强度,A表示砌体截面的有效面积。
需要注意的是,砌体的抗压强度是指砌体在受压状态下能承受的最大应力,通常使用试验数据进行评估。
砌体截面的有效面积是指砌体截面中,不考虑中空部分的实际有效面积。
此外,根据公式可以发现,无筋砌体受压构件的承载力与砌体抗压强度和砌体截面的有效面积有关。
因此,在进行承载力计算时,需要准确测量砌体的抗压强度和截面的有效面积。
最后,需要注意的是,该公式适用于无筋砌体受压构件在受压状态下的承载力计算。
对于其他类型的构件如受弯构件,其承载力的计算需要使用相应的公式。
总之,无筋砌体受压构件承载力计算公式是一个重要的结构工程计算公式,建筑工程师需要熟练掌握,以确保建筑结构的安全性和稳定性。
矩形截面偏心受压构件正截面的承载力计算

矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 (一)大偏心受压构件正截面受压承载力计算(1)计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件,可以得到下面两个基本计算公式:s y s y c A f A f bx f N -+=''1α (7-23)()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α (7-24)式中: N —轴向力设计值;α1 —混凝土强度调整系数;e —轴向力作用点至受拉钢筋A S 合力点之间的距离;a he e i -+=2η (7-25) a i e e e +=0 (7-26)η—考虑二阶弯矩影响的轴向力偏心距增大系数,按式(7-22)计算;e i —初始偏心距;e 0 —轴向力对截面重心的偏心距,e 0 =M/N ;e a —附加偏心距,其值取偏心方向截面尺寸的1/30和20㎜中的较大者; x —受压区计算高度。
(2)适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度,要求b x x ≤ (7-27)式中 x b — 界限破坏时,受压区计算高度,o b b h x ξ= ,ξb 的计算见与受弯构件相同。
2) 为了保证构件破坏时,受压钢筋应力能达到屈服强度,和双筋受弯构件相同,要求满足:'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。
(二)小偏心受压构件正截面受压承载力计算(1)计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 (7-29)⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α (7-30) ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα (7-31)式中 x — 受压区计算高度,当x >h ,在计算时,取x =h ;σs — 钢筋As 的应力值,可根据截面应变保持平面的假定计算,亦可近似取:y b s f 11βξβξσ--=(7-32)要求满足:y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度,0h x b b ξ=;b ξξ、 — 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ;'e e 、′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) (2)对于小偏心受压构件当bh f N c >时,除按上述式(7-30)和式(7-31)或式(7-32)计算外,还应满足下列条件:()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 '0h — 钢筋's A 合力点至离纵向较远一侧边缘的距离,即s a h h -='0。
混凝土理论6-构件承载力计算
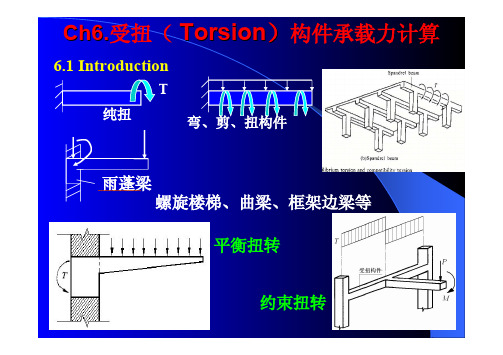
Tco=0.35ftWt, Vco=0.7ftbho
1.5Vc/Vco
Code suggests: when Tc/Tco 0.5,Vc/Vco=1 when Vc/Vco0.5,Tc/Tco=1
1.0 A
1.5- t 0.5 t
BG 1/4 circular C
D 0.5 1.0
1.5Tc/Tco
On line BC: let Tc/Tco=t (1) (2)/(1): Then Vc/Vco=1.5- t (2)
t
1.5
1
0.5
VWt Tbh0
t— 剪扭构件混凝土强度降低系数
0.5 t1.0
剪扭构件受剪承载力计算公式:
V
0.7(1.5 t )
ftbh0
f yv
Asv s
h0
受扭承载力计算公式
T 0.35t ftWt 1.2
f yv
Ast1 Acor s
6.4.3 弯剪扭组合构件承载力计算
P114
1.The calculating principle:
1).按弯矩设计值M进行受弯构件正截面承载力 设计,确定受弯纵筋;
2).按剪扭构件计算受扭箍筋、受剪箍筋,以及 受扭纵筋;
3). 分别叠加纵筋和箍筋.
(c)开裂扭矩计算图
define : Wt
b2 6
3h b
max ft
Tcr ftWt
Wt 受扭构件截面 塑性抵抗矩
* BUT: P92 • 混凝土既非理想弹性材料也非理想塑性材料, 在全截
面达到ft前已开裂; • 因此, In Chinese Code中,纯扭构件开裂扭矩:
Tcr 0.7 ftW t
4钢筋混凝土受压构件承载力计算

4钢筋混凝土受压构件承载力计算钢筋混凝土受压构件的承载力计算是建筑结构设计中非常重要的一个步骤。
本文将围绕钢筋混凝土受压构件的承载力计算进行详细介绍。
首先,我们需要了解一些与承载力计算相关的基本概念。
1.构件尺寸和几何性质:构件的尺寸和几何性质,如截面面积、高度、宽度等,是计算承载力的基础。
这些参数可以通过结构设计的过程或者实际测量获得。
2.受力分析:在进行承载力计算之前,我们需要对受力分析进行准确的估计。
受力分析包括水平力、垂直力、弯矩和剪力等。
3.材料性能:钢筋混凝土由钢筋和混凝土组成,每种材料都具有其特定的力学性能。
钢筋的弹性模量、屈服强度和抗压强度是承载力计算的关键参数。
混凝土的抗压强度也是一个重要的参数。
计算步骤如下:1.根据结构设计图,确定所需计算的受压构件的几何尺寸。
通常情况下,我们可以使用截面面积来计算构件的承载力。
2.判定构件的计算长度。
构件的计算长度取决于构件的支撑条件和构件的几何形状。
常见的计算长度包括等于构件高度的长度、2倍构件高度的长度和4倍构件高度的长度等。
$$R_c = \phi \cdot A_c \cdot f_{cd}$$其中,$R_c$为构件的抗压承载力(kN),$\phi$为构件的抗压承载力系数(通常为0.65),$A_c$为构件的截面面积(m²),$f_{cd}$为混凝土的抗压强度(MPa)。
4.计算钢筋的抗拉强度。
根据人民共和国行业标准GB1499.2-2024《钢筋机械连接的技术规定》,钢筋的抗拉强度可以通过以下公式计算:$$R_s = A_s \cdot f_{yd}$$其中,$R_s$为钢筋的抗拉承载力(kN),$A_s$为钢筋的截面面积(m²),$f_{yd}$为钢筋的屈服强度(MPa)。
5.比较构件的抗压强度和钢筋的抗拉强度。
如果构件的抗压强度大于钢筋的抗拉强度,则构件的承载力为钢筋的抗拉强度;如果构件的抗压强度小于钢筋的抗拉强度,则构件的承载力为构件的抗压强度。
受扭构件承载力计算

(1)腹板
(6-8)
(2)受压翼缘
(6-9)
(3)受拉翼缘
(6-10)
上一页 下一页 返回
第一节纯扭构件承载力计算
四、箱形截面纯扭构件承载力计算
箱形截面纯扭构件承载力按下式计算:
(6-11) (6-12)
(6-13)
上一页 返回
第二节弯剪扭构件承载力计算
一、弯剪扭构件截面限制条件 (1)在弯矩、剪力和扭矩共同作用下,对hw/b毛6的矩形、T形、I形截面和 hw/tw ≤ 6的箱形截面构件(图6-2 ),其截面应符合下列条件: (6-14) (6-15)
试验表明,对于钢筋混凝土矩形截面受扭构件,其破坏形态与配置 钢筋的数量多少有关,可以分为三类: (1)少筋破坏。 (2)适筋破坏。 (3)超筋破坏。
上一页 下一页 返回
第一节纯扭构件承载力计算
二、矩形截面纯扭构件承载力计算
矩形截面纯扭构件承载力按下式计算:
(6-2) (6-3)
三、T形和I形截面纯扭构件承载力计算
(3)在轴向压力、弯矩、剪力和扭矩共同作用下的钢筋混凝土矩形截面框架 柱,其纵向钢筋截面面积应分别按偏心受压构件的正截面受压承载力和 剪扭构件的受扭承载力计算确定,并应配置在相应的位置;箍筋截面面积 应分别按剪扭构件的受剪承载力和受扭承载力计算确定,并应配置在相 应的位置。
上一页 下一页 返回
第二节弯剪扭构件承载力计算
上一页 返回
图6-1工程中常见的受扭构件
返回
图6-2受扭构件截面
返回
图6-2受扭构件截面
返回
表6-2受扭构件纵筋的构浩要求
返回
(6-4) (6-5) (6-6)
上一页 下一页 返回
第一节纯扭构件承载力计算
钢筋混凝土受压构件承载力计算

钢筋混凝土受压构件承载力计算首先,我们需要了解一些基本的概念和符号。
在计算中,常用的符号有:-$f_c$:混凝土的抗压强度;-$f_s$:钢筋的抗拉强度;-$A_c$:构件的混凝土截面面积;-$A_s$:构件的受拉钢筋截面面积;-$N_d$:构件所受到的设计轴向力;-$M_d$:构件所受到的设计弯矩;-$h$:构件的高度;-$b$:构件的宽度;-$d$:构件的有效高度。
接下来,我们将介绍两种常用的承载力计算方法:受压钢筋混凝土柱的承载力计算和板梁的承载力计算。
受压钢筋混凝土柱的承载力可以通过弯矩轴心法进行计算。
承载力的计算可以分为以下几个步骤:-第一步,计算混凝土在压力作用下的承载力。
可以使用以下公式:$$N_c = \gamma_c f_c A_c$$-第二步,计算钢筋的抗拉强度。
根据构件的横截面形状和受力状态,可以计算钢筋的受拉面积。
-第三步,计算钢筋的受压承载力。
可以使用以下公式:$$N_s = \eta \gamma_s f_s A_s$$其中,$\eta$为钢筋受压构件的局部稳定系数,$\gamma_s$为钢筋的材料抗拉强度。
-第四步,计算构件的总承载力。
可以使用以下公式:$$N=N_c+N_s$$板梁的承载力计算可以分为以下几个步骤:-第一步,计算构件的混凝土承载力。
可以使用以下公式:$$N_c = \gamma_c f_c A_c$$-第二步,计算构件的钢筋承载力,可以使用以下公式:$$N_s = \gamma_s f_s A_s$$-第三步,计算板梁的破坏模式,根据不同的破坏模式选择合适的计算方法。
-第四步,计算构件的总承载力。
可以使用以下公式:$$N=N_c+N_s$$总结:钢筋混凝土受压构件承载力的计算方法主要有弯矩轴心法和板梁承载力计算法。
在计算过程中需要明确构件的几何形状、材料强度以及荷载的大小等因素,并按照一定的计算步骤进行计算。
在实际设计过程中,还需要考虑其他因素如构件的构造形式、构造材料的可靠性等,以确保构件的安全性和经济性。
结构构件的承载力计算

。 (3)确定临界应力的大小,是解决压杆稳定问题的关键。
工程力学与建筑结构
计算临界应力的公式为
1)细长杆( P )使用欧拉公式:
cr
2E 2
2)中长杆( P )使用经验公式: a b2
3)柔度:柔度是压杆长度、支撑情况、截面形状和尺寸等
因素的综合值。
l i
i I A
λ是稳定计算中的重要几何参数,有关压杆稳定计算
应先计算出 。
4)稳定性计算
ቤተ መጻሕፍቲ ባይዱ
工程中常采用折减系数法,稳定条件为
F [ ]
A
工程力学与建筑结构
工程力学与建筑结构
2. 内力及其分析计算方法 (1)内力 因外力作用而引起的杆件内部相互作用力。 (2)截面法 内力分析计算的基本方法,基本依据是平衡条
件,其解法有三个步骤:截开、代替、平衡。 3. 几种基本变形的内力和内力图 (1)内力表示一个具体截面上内力的大小和方向。 (2)内力图表示内力沿着杆件轴线的变化规律。 (3)应力是单位面积上的内力及其计算公式和强度条件。
工程力学与建筑结构
工程力学与建筑结构
结构构件的承载力计算
本章以构件的承载能力和构件变形的基本形式为前提 ,讨论了杆件的轴向拉伸(压缩)、剪切、弯曲三种基本 变形的内力、应力和强度条件的分析计算方法和压杆稳定 的概念及其实用计算。
1. 构件的承载能力 强度 构件在荷载作用下抵抗破坏的能力。 刚度 构件在荷载作用下抵抗变形的能力。 稳定性 构件在荷载作用下保持原有平稳状态的能力。
工程力学与建筑结构
4. 强度计算的步骤 (1)分析外力 画受力图,求约束反力。 (2)画内力图 确定危险截面及其内力。 (3)利用强度条件解决三类问题的计算:1)杆件的强度核
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
截面面积A=370 ×490=0.1813m2<0.3m2, 强度修正系数ra=0.7+A=0.8713, 砌体强度设计值raf=0.8713×1.5=1.3N/mm2。 2)确定长边承载力影响系数
(1)确定偏心距e 偏心距e=73.5mm,
混合结构设计
一、轴心受压: β≤3时为短柱
短柱: N fA
长柱:
N 0 fA
N:轴向力设计值;
0:轴心受压的纵向弯曲系数;
f:考虑调整系数后砌体抗压强度设计值。
混合结构设计
0
cri A
fm A
cri
fm
2EI
cri
AH02
Et
d d
fm
fm (1
) fm
砖砌体: 0 460 2
β:砌体受压构件的高厚比
矩形截面 T形截面
H0 h
H0 hT
混合结构设计
H0 h
H0 hT
γβ:不同砌体材料的高厚比修正系数 对烧结普通砖、烧结多孔砖、灌孔混凝土砌块砌体γβ=1.0; 对混凝土及轻骨料混凝土砌块砌体γβ=1.1; 对蒸压灰砂砖、蒸压粉煤灰砖、细料石、半细料石砌体γβ=1.2; 对粗料石、毛石砌体γβ=1.5。
3)验算长边承载力 Nu= fA=0.51x1.3x181300=120kN>=120kN,满足承载力要
求.
4)验算短边承载力 按照轴心受压计算, 偏心距e=0,计算长度Ho=5.88m,h=370mm, β= γβ Ho/ h= 1.0×5.880/0.37=16, =0.72 , Nu=0.72×1.3×181300=170kN>120kN,满足承载力要求.
N 0 fA
2.轴向力的偏心距应符合下列限值要求,即 e≤0.6y
式中y为截面重心至轴向力所在偏心方向截面受压边缘 的距离。(该规定的目的是:截面受拉边不产生过大的 裂缝)
例题1:截面尺寸为370×490mm的砖柱,烧结普通砖的强度等 级为MU10,混合砂浆强度等级为M5,柱高5.88mm,两端为不动 铰支座。柱顶承受作用在截面长边方向的竖向压力设计值 N=120KN,偏心距e=73.5mm,施工质量为B级;请验算该柱的 受压承载力。
矩形截面y=h/2=245mm,e=73.5<0.6y=147mm,可行
(2)计算高厚比β 高厚比β=γβHo/h, 计算长度Ho=5.88m,h=490mm,烧结普通砖γβ=1.0 ,
β= γβ Ho/ h=1.0x5.880/0.49=12。
(3)确定承载力影响系数 查表或通过公式计算, =0.51.
2000 240120 490 380(240 190)
y1
666200
207mm
y2 620 207 413mm
截面惯性矩:I 174.4 108mm4
回转半径: i I 162 mm ,
A
截面折算厚度:hT 3.5i 566 mm ,
(2)确定偏心距e e=M/N=38400000/320000=120mm, y=0.413mm,e=120<0.6y,可行。
例2 某带壁柱的窗间墙,截面尺寸如图,壁柱高5.4m,
计算高度为6.8m,用MU10粘土砖及M2.5混合砂浆砌筑。 控制截面内力为N=320kN,M=38.4kNm,弯矩方向是翼 缘受拉,施工质量为B级,验算该墙体的承载力。
解: 1)确定砌体强度f
MU10烧结普通砖, M2.5混合砂浆,查表, f=1.3N/mm2, 截面面积A=2000×240+380×490=0.666200m2 >0.3m2,强度修正系数ra=1.0, 砌体强度设计值raf=1.0x1.3=1.3N/mm2。 2)确定承载力影响系数 (1)计算截面折算厚度hT A=0.666200m2, 截面重心位置(y1为翼缘外皮到中心线的距离):
系数
β≤3; e=0: φ≤1
β>3; e=0: φ=φ0
β≤3; e>0: φ=φ1
:查表
β>3; e>0: φ=φ
三、受压承载力计算时应注意的几个问题 1.对于矩形截面构件,当轴向力偏心方向的截面边长 大于另一方向的边长时, 除按偏心受压构件计算外, 还应对较小边b方向,按轴心受压进行验算,即还应 满足:1ຫໍສະໝຸດ 11 ( e )2
i
1
1
1 12(
e
)2
h
混合结构设计
e 二、偏心受压:
1、偏心受压长柱:
N fA
1
e+ei
1 ( e ei )2
i
:高厚比β和轴向力的偏心距e对受压构
件承载力的影响系数
1 1 ( ei )2
0
i
ei i
1 1
0
混合结构设计
受压构件计算:
N fA
:高厚比β和轴向力的偏心距e对受压构件承载力的影响
例3 由混凝土小型空心砌块砌筑独立柱截面尺寸为400×600mm,
砌块的强度等级MU10,混合砂浆强度等级Mb5,柱高3.6M,两端 为不动铰支座。柱顶承受轴向压力标准值Nk=225KN(其中永久荷 载180KN,已包括柱自重),施工质量为B级,试验算柱的承载力。 解:要点:
(3)计算高厚比β 计算长度Ho=6.8m,hT=566mm, 烧结普通砖γβ=1.0 , β= γβ Ho/ hT =1.0x6.8/0.566=12。
(4)确定承载力影响系数 e/hT=120/566=0.212, β=12, 查表得: =0.38,
3)承载力验算 Nu= fA=0.38× 1.3 ×666200 =329KN>320KN, 满足承载力要求。
fm
(1
cri
fm
)(
i H
0
)2
1
0
1 1
1
1
混合结构设计
1 460 2
f
m
(
i H
0
)2
矩形截面: i h 12
0
1 1 1
1
H0
h
1 370
fm
1
2
0
1
1 1
2
1
1
2
370 fm
混合结构设计
η:与砂浆强度等级有关的系数
砂浆强 度等级
≥M5
M2.5
η
0.0015 0.002
0 0.009
混合结构设计
e
二、偏心受压:
1、偏心受压短柱:
N Ne y f
AI
实验表明:砌体结构的承载力高于上式计算出的数值。
1、弹塑性,压应力分布丰满。 2、开裂,使偏心距减小。 3、实际受压的砌体,呈现局部受压性质。
混合结构设计
e
N 1 fA
1 :轴向力的偏心距e对受压构件承载力的影响系数
矩形截面:
