第28章锐角三角函数形
第28章-锐角三角函数-全章教案

====Word 行业资料分享--可编辑版本--双击可删====
一、在 Rt△ABC 中,∠C =90°: B
a 对边
c 斜边
视,对学习基 A 的对边与斜边的比;
础 较 弱 的 学 求 sinB 就是要确定∠B
生 及 时 给 予 的对边与斜边的比.
指点.
教师引导学
生作知识总
结,不断扩充
培养学生概括的能
学 生 的 知 识 力,使知识形成体系,
结构,学习新 并渗透数学思想方法。
的解题方法.
Cb
A
五、体验 收获
即
sin
A
A的对边 斜边
a c
.
同样 sinB= B的对边 斜边
b c
当∠A=300 时,sinA=? 当∠A=450 时,sinA=? 当∠A=600 时,sinA=?
也随之确
定”.但是怎
样证明这个
C
A C1
A!
命题呢?学
生这时的思
经过学生的实验和证明,得出:
维很活跃.对
于这个问题,
在 Rt△ABC 中,∠C=90°,我们把锐
部分学生可
角 A 的对边与斜边的比叫做∠A 的正弦
能能解决
(sine),记作:sinA,
它.因此教师
此时应让学
B
生展开讨论,
独立完成.
a 对边
长 50m,那么斜坡与水平面所成角的度数是多少
呢?
二、探究 1.请每一位同学拿出自己的三角板,分别测量并 教 师 提 出 问 在培养学生动手能力的
====Word 行业资料分享--可编辑版本--双击可删====
说理
三、感悟 深化
第二十八章 锐角三角函数(单元总结)-2021学年九年级数学下册(人教版)(解析版)
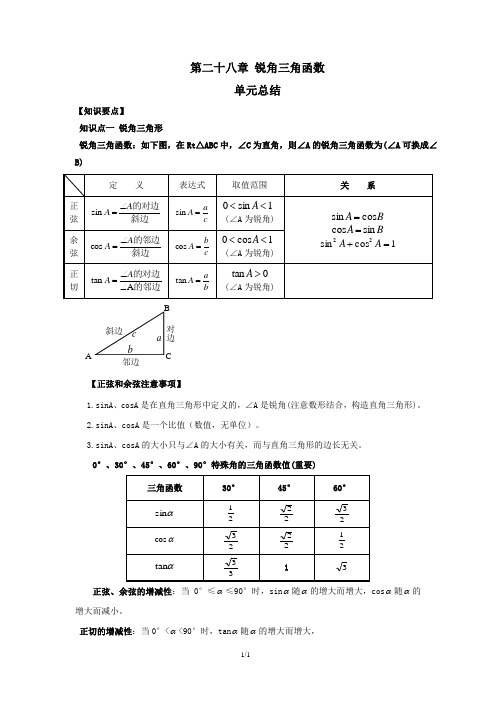
第二十八章 锐角三角函数单元总结【知识要点】 知识点一 锐角三角形锐角三角函数:如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)【正弦和余弦注意事项】1.sinA 、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA 、cosA 是一个比值(数值,无单位)。
3.sinA 、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,对边邻边C知识点二 解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形. 直角三角形五元素之间的关系: 1. 勾股定理()2. ∠A+∠B=90°3. sin A==4. cos A= =5.tan A= =【考查题型】考查题型一 正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为( )A .43B .34C .35D .45【答案】D 【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,∴AC =222234=+=+AC AD CD =5. ∴4sin 5CD BAC AC ∠==. 故选D . 【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C =∠,10AB =,8AC =,则sin A 等于( )A .35B .45C .34D .43【答案】A 【解析】分析:先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 详解:在Rt △ABC 中,∵AB=10、AC=8, ∴2222=108=6AB AC --,∴sinA=63105BC AB ==. 故选:A .点睛:本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt△ABC中,∠C=90°,sin A=45,AC=6cm,则BC的长度为()A.6cm B.7cm C.8cm D.9cm 【答案】C【详解】已知sinA=45BCAB=,设BC=4x,AB=5x,又因AC2+BC2=AB2,即62+(4x)2=(5x)2,解得:x=2或x=﹣2(舍),所以BC=4x=8cm,故答案选C.考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A 5B25C5D.23【答案】B【详解】由格点可得∠ABC所在的直角三角形的两条直角边为2,4,222425+=∴cos∠25525=.故选B .变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠=,AB 6=,1cosA 3=,则AC 等于( ) A .18 B .2C .12D .118【答案】B 【分析】根据三角函数的定义,在直角三角形ABC 中,cosA =ACAB,即可求得AC 的长. 【详解】解:∵在△ABC 中,∠C =90°,∴cosA =ACAB , ∵cosA =13,AB =6,∴AC =123AB =,故答案选:B . 【点睛】本题考查了解直角三角形中三角函数的应用,解题的关键是要熟练掌握直角三角形中边角之间的关系.变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M (5,2),那么cosα的值是( )A 5B .23C 25D 5【答案】D 【分析】如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.【详解】解:如图,作MH⊥x轴于H.∵M(5,2),∴OH=5,MH=2,∴OM=22(5)2+=3,∴cosα=5 OHOM=,故选:D.【点睛】本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.12B.1 C3D3【答案】B【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【详解】 如图,连接BC ,由网格可得AB=BC=5,AC=10,即AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为( ).A .2B .3C .2D .1【答案】A 【解析】分析:本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解. 解析:如图,作DE ⊥AB 于E .∵tan ∠DBA==,∴BE=5DE .∵△ABC 为等腰直角三角形,∴∠A=45°,∴AE=DE .∴BE=5AE ,又∵AC=6,∴AB=6,∴AE+BE=AE+5AE=6,∴AE=,∴在等腰直角△ADE中,由勾股定理,得AD=,AE=2.故选A.变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若2tan5BAC∠=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m 【答案】A【分析】根据BC的长度和tan BAC∠的值计算出AC的长度即可解答.【详解】解:因为2tan5BCBACAC=∠=,又BC=30,所以,3025AC=,解得:AC=75m,所以,故选A.【点睛】本题考查了正切三角函数,熟练掌握是解题的关键.考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A.(32,12) B.(-32,-12)C.(312) D.(-123【答案】B 【详解】∵点(-sin60°,cos60°)即为点(312),∴点(-sin60°,cos60°)关于y 3,12).变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A.cos40°=sin50°B.tan15°•tan75°=1C.sin225°+cos225°=1 D.sin60°=2sin30°【答案】D【详解】试题分析:选项A,sin40°=sin(90°﹣50°)=cos50°,式子正确;选项Btan15°•tan75°=tan15°•cot15°=1,式子正确;选项C,sin225°+cos225°=1正确;选项D,sin60°=3,sin30°=12,则sin60°=2sin30°错误.故答案选D.变式4-2.(2018·河北唐山市·九年级期末)如果△ABC中,sin A=cos B=22,则下列最确切的结论是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C【解析】因为sin A=cos B 2,所以∠A=∠B=45°,所以△ABC是等腰直角三角形. 故选C.考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt△ABC中,∠C =90°,sinA=45,则cosB的值等于( )A.35B.45C.34D5【答案】B 【解析】在Rt△ABC中,∠C=90°,∠A+∠B=90°,则cos B=sin A=45.故选B.点睛:本题考查了互余两角三角函数的关系.在直角三角形中,互为余角的两角的互余函数变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA= 12,那么sinA 的值是( )A .2B .2C .3D .12【答案】B 【分析】利用同角三角函数间的基本关系求出sinA 的值即可. 【详解】:∵Rt △ABC 中,cosA=12 ,∴ =2, 故选B . 【点睛】本题考查了同角三角函数的关系,以及特殊角的三角函数值,熟练掌握同角三角函数的关系是解题的关键.变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠=,如果4cosA 5=,那么tanA 的值是( ) A .35B .53C .34D .43【答案】C 【分析】本题可以利用锐角三角函数的定义求解. 【详解】解:∵在Rt △ABC 中,∠C=90°,∴cosA=b c ,tanA=ab ,a 2+b 2=c 2. ∵cosA=45,设b=4x ,则c=5x ,a=3x .∴tanA=a b =3344x x =. 故选C.【点睛】利用锐角三角函数的定义,通过设参数的方法求三角函数值.考查题型六 解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα【答案】B【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题;【详解】在Rt △ABC 中,AB=AC sin α, 在Rt △ACD 中,AD=AC sin β, ∴AB :AD=AC sin α:AC sin β=sin sin βα, 故选B .【点睛】 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题. 变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为( )A .10B .15C .6D .10 【答案】D【分析】过点A 作AD BC ⊥,垂足为D ,在Rt ACD ∆中可求出AD ,CD 的长,在Rt ABD ∆中,利用勾股定理可求出AB 的长,再利用正弦的定义可求出sinB 的值.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ACD ∆中,1CD CA cosC ⋅==,2215AD AD CD ∴=-=;在Rt ABD ∆中,315BD CB CD AD =﹣=,=,22BD AD 26AB ∴=+=,AD 10sin AB B ∴==. 故选:D .【点睛】考查了解直角三角形以及勾股定理,通过解直角三角形及勾股定理,求出AD ,AB 的长是解题的关键.变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为( )A.11米B.(36﹣153)米C.153米D.(36﹣103)米【答案】D【分析】分析题意可得:过点A作AE⊥BD,交BD于点E;可构造Rt△ABE,利用已知条件可求BE;而乙楼高AC=ED=BD﹣BE.【详解】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=103(米),∴AC=ED=BD﹣BE=(36﹣103)(米).∴甲楼高为(36﹣103)米.故选D.【点睛】此题主要考查三角函数的应用,解题的关键是熟知特殊角的三角函数值.考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,2≈1.4)【答案】云梯需要继续上升的高度BC 约为9米.【分析】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,在Rt ABD ∆中,求得AD 的长;在Rt ACD ∆中,求得CD 的长,根据BC=CD-BD 即可求得BC 的长.【详解】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,∵CN EF ⊥ ,∴90AMN MND ADN ∠=∠=∠=︒,∴四边形AMND 为矩形.∴ 2.5DN AM ==米.∴10.5 2.58BD BN DN =-=-=(米),由题意可知,45BAD ∠=︒,65CAD ∠=︒,∵AD BC ⊥,∴90ADB ∠=︒,在Rt ABD ∆中,tan BD BAD AD ∠=, ∴88tan tan45BD AD BAD ===∠︒(米). 在Rt ACD ∆中,tan CD CAD AD∠=, ∴tan 8tan658 2.116.8CD AD CAD =⋅∠=︒≈⨯=(米).∴16.888.89BC CD BD =-≈-=≈(米).答:云梯需要继续上升的高度BC 约为9米.【点睛】本题考查解直角三角形﹣仰角俯角问题,添加辅助线,构造直角三角形,建立直角三角形模型是解决问题的关键.变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC 的高度,从距离楼底C 处603米的点D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1:3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).【答案】153+【分析】如图作BN ⊥CD 于N ,BM ⊥AC 于M ,先在RT △BDN 中求出线段BN ,在RT △ABM 中求出AM ,再证明四边形CMBN 是矩形,得CM=BN 即可解决问题.【详解】如图作BN ⊥CD 于N ,BM ⊥AC 于M .在RT △BDN 中,BD=30,BN :ND=13,∴BN=15,DN=153,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=603153453-=,在RT△ABM中,tan∠ABM=43 AMBM=,∴AM=603,∴AC=AM+CM=15603+.【点睛】构造适当的直角三角形,并应用锐角的三角函数,正确理解坡比的概念.变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)【答案】高、低杠间的水平距离CH 的长为151cm .【解析】分析:利用锐角三角函数,在Rt △ACE 和Rt △DBF 中,分别求出AE 、BF 的长.计算出EF .通过矩形CEFH 得到CH 的长.详解:在Rt △ACE 中,∵tan ∠CAE=CE AE, ∴AE=()15515521tan tan82.47.5CE cm CAE =≈≈∠︒ 在Rt △DBF 中,∵tan ∠DBF=DF BF, ∴BF=()23423440tan tan80.3 5.85DF cm DBF =≈=∠︒. ∵EF=EA+AB+BF≈21+90+40=151(cm )∵CE ⊥EF ,CH ⊥DF ,DF ⊥EF∴四边形CEFH 是矩形,∴CH=EF=151(cm ).答:高、低杠间的水平距离CH 的长为151cm .点睛:本题考查了锐角三角函数解直角三角形.题目难度不大,注意精确度.。
28.1锐角三角函数

感悟新知
知3-练
例 7 (1)已知α=45°,求2sin2α-2 2 sinα·tanα+tan2α;
(2)计算
1 4
tan2
45+
sin
1 2 30
-3 cos2
30-
sin cos
45 45
.
解题秘方:用“代入法”求值.
感悟新知
解:(1)原式 2 sin-tan 2
2
(4)sin2A 表示sin A·sin A=(sin A)2,不能写成sin A2;cos2A 表示cos A·cos A=(cos A)2,不能写成cos A2;tan2A 表示 tan A·tan A=(tan A)2,不能写成tan A2.
感悟新知
特别提醒
知1-讲
1. 正弦、余弦、正切都是一个比值,是没有单位的数
AB 3k 3k
AB 3k 3
tan B AD 2 2k 2 2. BD k
感悟新知
知1-练
3-1. 将一副三角尺(Rt△ ABC 与Rt△BDC)按如图所示的方 式摆放在一起,连接AD, 试求∠ ADB 的正切值.
感悟新知
解:过点 A 作 AM⊥DB,交 DB 的延长线于点 M. 知1-练
3
sin A-sin B的值.
知2-练
,求
解:∵sinA+sinB=43,∴(sinA+sinB)2=196.
∴sin2A+sin2B+2sinA·sinB=196.
∵∠A+∠B=180°-∠C=90°,∴sinB=cosA,
感悟新知
∴sin2A+cos2A+2sinA·sinB=196, ∴1+2sinA·sinB=196,∴2sinA·sinB=79, ∴sin2A+sin2B-2sinA·sinB=1-79=29, ∴(sinA-sinB)2=29,∴sinA-sinB=± 32.
第28章+锐角三角函数知识点总结及思维导图+2023—2024学年人教版数学九年级下册

第28章锐角三角函数【思维导图】28.1锐角三角函数【知识点】1.Rt△ABC中,∠C=90°.(1)∠A的对边与斜边比,叫做∠A的正弦,记为sinA,即sinA=∠A的对边斜边=aa(2)∠A的邻边与斜边比,叫做∠A的余弦,记为cosA,即cosA=∠A的邻边斜边=aa(3)∠A的对边与邻边比,叫做∠A的正切,记为tanA,即tanA=∠A的对边∠A的邻边=aa∠A的正弦、余弦、正切统称为∠A的锐角三角函数.提示:sin A 不是sin与A的乘积,而是一个整体,cosA和tanA同理;锐角三角函数的三种表示方法:sin A,sin 56°,sin∠DEF.2.一个锐角的三角函数值是一个比值,它与三角形的大小无关,它没有单位.在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的锐角三角函数值为定值.锐角三角函数锐角α30°45°60°sin α12√22√32cos α√32√2212tan α√331√3(1)正弦值、正切值随角度的增大而增大,余弦值随角度的增大而减小.(2)sin α=cos(90°-α)cos α=sin(90°-α)tan α·tan(90°-α)=1(3)锐角A 的正弦、余弦的取值范围分别为:0<sin A<1,0<cos A<1, (4)cos 2A+sin 2A=1 sin 2A+sin 2(90°-α)=1(5)tan A=sin A cos A4.锐角三角函数值是个常数值,它只与角的度数有关,将来离开了直角三角形也存在.5.若α=45°,则sin α=cos α; 若α<45°,则sin α<cos α; 若α>45°,则sin α>cos α;28.2解直角三角形及其应用 28.2.1 解直角三角形【知识点】1.在直角三角形中,由已知元素求出其余未知元素的过程就是解直角三角形.2.在直角三角形中,三边之间的关系是a 2+b 2=c 2(勾股定理); 两锐角之间的关系是∠A+∠B=90° 边角之间的关系有sinA=∠A 的对边斜边,cosA=∠A 的邻边斜边,tanA=∠A 的对边∠A 的邻边3.在直角三角形的六个元素中,除直角外的五个元素只要知道其中的两个元素,就可以求出其余三个元素,其中至少有一个是边.4.在Rt △ABC 中,∠C=90°,若已知∠A=α,AB=c ,较简便的方法是用正弦求出BC ,用余弦求出AC ,也可用勾股定理求出AC ,根据直角三角形的两锐角互余求出∠B.单元练习一、选择题1.已知∠α为锐角,且sin a=12,则∠α=( )A.30°B.45°C.60°D.90°2.sin 60°的相反数是( )A.-12B.−√33C.−√32D.−√223.如图,在∠ABC中,∠B=90°,BC=2AB,则cosA的值为( )A.52B.12C.255D.554.如图,在4×5 的正方形网格中,每个小正方形的边长都是1,∠ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB 的值为( )A.3√55B.√175C. 35D. 455.在∠ABC中,∠A,∠B均为锐角,且|2sin A-1|与(cos a-√22)2互为相反数,则∠C的度数是( )A.45°B.75°C.105°D.120°6.如图,在∠ABC中,∠C=90°,AB=15,sinB=35,则AC的长为( )A.3 B.9 C.4 D.127.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪的高A D为1.5米,则铁塔的高BC为( )A.(1.5+150tanα)米a.(1.5+150tan a)米C.(1.5+150sinα)米a.(1.5+150sin a)米8.在Rt∠ABC 中,∠C=90°,AB=2BC,则cos A 的值为 ( ) A.√32 B .12 C .√33 D .√229.如图,在∠ABC 中,CA =CB =4,cosC =14 ,则sinB 的值为( )A.102 B .153 C .64 D .10410.如图,电线杆CD 的高度为h ,两根拉线 AC 与BC 相互垂直,∠CAB=α,则拉线 BC 的长度为(点 A,D,B 在同一条直线上)( ) a .asin a a .acos a a .atan a D. h·cosα11.定义一种运算:cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β.例如:当α=60°,β=45°时,cos(60°-45°)=12×√22+√32×√22=√2+√64,则cos 75°的值为 ( )A.√6+√24 B .√6-√24C.√6-√22 D .√6+√2212.如图,由边长为1的小正方形构成的网格中,点A ,B ,C 都在格点上,以AB 为直径的圆经过点C ,D ,则cos∠ADC 的值为( )A .21313B .31313C .23D .53 二、填空题,则cos B=_______.13.在∠ABC中, aa=90°,tan a=√3314.已知α为锐角,当无意义时,cos α的值是_______.√3tan a-115.如图,在Rt∠ABC中,∠ACB=90°,CD∠AB,垂足为D,若AC= 5 ,BC =2,则sin∠ACD的值为_________.16.某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了_______米.17.如图,已知正方形ABCD和正方形BEFG,点G在AD上,GF与CD交于点,正方形ABCD的边长为8,则BH的长为_______.H,tan∠ABG=1218.如图,在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是_________.三、解答题19.图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50 cm,∠AB C=47°.(1)求车位锁的底盒BC的长;(2)若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位? (参考数据:aaa47°≈0.73,aaa47°≈0.68,aaa47°≈1.07)20.某景区为给游客提供更好的游览体验,拟在如图∠所示的景区内修建观光索道.其设计示意图如图∠所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC,BC长为50 m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A、B两处的水平距离AE为576 m,DF∠AF,垂足为点F.(图∠中所有点都在同一平面内,点A、E、F 在同一水平线上)(1)求索道AB的长(结果精确到1 m);(2)求AF的长(结果精确到1 m).(参考数据:sin 15°≈0.25,cos 15°≈0.96,tan 15°≈0.26,√2≈1.41)21.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上,求菜园与果园之间的距离.(结果保留整数.参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)。
人教版九年级数学下第28章28.1《锐角三角函数》优秀教学案例

四、教学评价
1.评价学生的知识掌握程度:通过课堂提问、作业批改等方式,了解学生对锐角三角函数知识的掌握情况;
2.评价学生的实践操作能力:通过实际问题解决,评价学生运用锐角三角函数解决实际问题的能力;
3.评价学生的合作交流能力:通过小组讨论、互动交流等方式,评价学生在团队合作中的表现;
3.讲练结合:在课堂中及时进行练习,巩固所学知识,提高学生的实际操作能力;
4.反馈调整:根据学生的学习情况,及时调整教学方法,以提高教学效果。
五、教学过程
1.创设情境,引入新课:通过生活实例,引导学生思考并引入锐角三角函数的概念;
2.自主探究,小组合作:让学生在小组内讨论交流,共同探究锐角三角函数的定义及应用;
(三)情感态度与价值观
1.培养学生对数学学科的兴趣和热爱,激发学生学习数学的内在动力;
2.培养学生合作交流的意识,提高学生团队协作的能力;
3.让学生感受数学与生活的紧密联系,培养学生的应用意识;
4.通过对本节课的学习,使学生树立正确的数学学习观念,相信自己通过努力可以掌握并运用好数学知识。
三、教学重难点
4.评价学生的情感态度与价值观:通过观察学生的学习态度、课堂表现等,评价学生对数学学科的兴趣和热爱。
五、教学拓展
1.利用多媒体技术,展示锐角三角函数在实际生活中的应用,激发学生的学习兴趣;
2.推荐相关的数学读物和网站,让学生课后进行拓展学习,提高学生的数学素养;
3.结合学校或社区的活动,让学生运用所学知识解决实际问题,提高学生的实践能力。
六、教学反思
在教学过程中,教师应不断反思自己的教学方法、教学内容等方面,以确保教学的质量和效果。同时,关注学生的学习反馈,根据学生的需求调整教学策略,以提高教学效果。通过不断的反思和调整,使教学更加符合学生的实际情况,提高学生的数学素养。
第二十八章“锐角三角函数”简介 (1)

本章“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
本章包括锐角三角函数的概念(主要是正弦、余弦和正切的概念),以及利用锐角三角函数解直角三角形等内容。
锐角三角函数为解直角三角形提供了有效的工具,解直角三角形在实际当中有着广泛的应用,这也为锐角三角函数提供了与实际联系的机会。
研究锐角三角函数的直接基础是相似三角形的一些结论,解直角三角形主要依赖锐角三角函数和勾股定理等内容,因此相似三角形和勾股定理等是学习本章的直接基础。
本章重点是锐角三角函数的概念和直角三角形的解法。
锐角三角函数的概念既是本章的难点,也是学习本章的关键。
难点在于,锐角三角函数的概念反映了角度与数值之间对应的函数关系,这种角与数之间的对应关系,以及用含有几个字母的符号sinA、cosA、tanA表示函数等,学生过去没有接触过,因此对学生来讲有一定的难度。
至于关键,因为只有正确掌握了锐角三角函数的概念,才能真正理解直角三角形中边、角之间的关系,从而才能利用这些关系解直角三角形。
本章内容与已学“相似三角形”“勾股定理”等内容联系紧密,并为高中数学中三角函数等知识的学习作好准备。
本章教学时间约需12课时,具体分配如下(仅供参考):28.1 锐角三角函数约6课时28.2 解直角三角形约4课时数学活动小结约2课时一、教科书内容与课程学习目标(一)本章知识结构框图本章知识的展开顺序(二)教科书内容本章内容分为两节,第一节主要学习正弦、余弦和正切等锐角三角函数的概念,第二节主要研究直角三角形中的边角关系和解直角三角形的内容。
人教版九年级下册数学第28章 锐角三角函数 利用解直角三角形解含方位角、坡角(坡度)的应用
感悟新知
知1-练
1. 如图,海中有一个小岛A,它周围8nmile内有暗礁. 渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏
东60°方向上,航行12nmile到达D点,这时测得小 岛A在北偏东30° 方向上.如果渔船不改 变航线继续向东航行, 有没有触礁的危险?
感悟新知
解:如图,过点A作AC⊥直线BD,垂足为点C.
C.200D3.300
3
感悟新知
知识点 2 用解直角三角形解坡角问题
探究
B
一、如图是某一大坝的横断面:
坡面AB的垂直高度与 水平宽度AE的长度之 比是α的什么三角函数?
Aα
E
知2-练
C
D
tan
BE 坡面AB与水平面的夹角叫做坡角.
AE
感悟新知
坡度的定义:
知2-练
坡面的垂直高度与水平宽度之比
B
叫做坡度,记作i.
感悟新知
例1 如图, 一艘海轮位于灯塔P的北 偏东65°方向,距离灯塔 80nmile的A处,它沿正南方向 航行一段时间后,到达位于灯
塔P的南偏东34°方向上的B处. 这时,B处距离灯塔P有多远 (结果取整数)?
北 65°
P 34°
知1-练
A
C
B
感悟新知
解:如图,在Rt△APC中, PC=PA•cos(90°-65°) =80×cos25° ≈72. 505. 在Rt△BPC中,∠B=34°,
第二十八章锐角三角函数
28.2解直角三角形及其应用
第6课时利用解直角三 角形解含方位角、坡角 (坡度)的应用
学习目标
1 课时讲解 用解直角三角形解方位角问题
用解直角三角形解坡角(或坡度) 问题
28章 锐角三角函数专题 解直角三角形实际应用的基本模型初中数学模型
(2)“母子”型 模型 已知三角形中的两角(∠1 和∠2)及其中一边, 模型分 在三角形外边作高 BC,构造两个直角三角形求 析 解,以高 BC 为桥梁是解题的关键
3.(成都中考)越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极 落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面 的高度.如图,已知测倾器的高度为 1.6 米,在测点 A 处安置测倾器,测得点 M 的 仰角∠MBC=33°,在与点 A 相距 3.5 米的测点 D 处安置测倾器,测得点 M 的仰角 ∠MEC=45°(点 A,D 与 N 在一条直线上),求电池板离地面的高度 MN 的长.(结 果精确到 1 米,参考数据:sin 33°≈0.54,cos 33°≈0.84,tan 33°≈0.65)
ME x+25 5 公楼 AB 的高度约为 20 米
(2)一般梯形模型 模型
模型 过较短的底 AD 作梯形的两条高 AE 和 DF,构造一个长方 分析 形和两个直角三角形,分别解两个直角三角形再加减求解
7.某轮滑特色学校准备建立一个如图①的轮滑技巧设施,从侧面看如图②,横 截面为梯形,高 1 米,AD 长为 2 米,坡道 AB 的坡度为 1∶1.5,DC 的坡度为 1∶2.
+40 3 .∴小山 BC 的高度为(10+40 3 )米
模型二:四边形模型 (1)直角梯形模型
模型
模型 过较短的底 AB 作直角梯形的高 BE,构造一个矩形和一
分析
个直角三角形,先解直角三角形再加减求解
6.如图,某办公楼 AB 的后面有一建筑物 CD,当光线与地面的夹角是 22°时, 办公楼在建筑物的墙上留下高 2 米的影子 CE,而当光线与地面夹角是 45°时,办公 楼顶 A 在地面上的影子 F 与墙角 C 有 25 米的距离(点 B,F,C 在一条直线上).求办 公楼 AB 的高度.(参考数据:sin 22°≈25 ,cos 22°≈1156 ,tan 22°≈25 )
人教版九年级数学下册第28章 锐角三角函数:余弦函数和正切函数
5. sin70°,cos70°,tan70°的大小关系是 A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70° C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
∴ cos A AC = 4,tan B AC = 4 .
AB 5
BC 3
随堂即练
如图,在 Rt△ABC 中,∠C = 90°,AC = 8,
tanA= 3 , 求sinA,cosB 的值.
4
B
解:∵ tan A BC 3,
AC 4
∴ BC 3 AC 3 8 6, C
8
A
4
4
∴ AB AC 2BC2 82 62 10,
RJ九(下) 教学课件
第二十八章 锐角三角函数
28.1 锐角三角函数
第2课时 余弦函数和正切函数
学习目标
1. 认识并理解余弦、正切的概念进而得到锐角三角函 数的概念. (重点)
2. 能灵活运用锐角三角函数进行相关运算.(重点、难 点)
新课引入
如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定 时,∠A的对边与斜边的比就随之确定.
随堂即练
( )D
解析:根据锐角三角函数的概念,知 sin70°< 1,cos70°<1,tan70°>1. 又∵cos70°=sin20°, 正弦值随着角的增大而增大,∴sin70°>cos70°= sin20°.
随堂即练
6. 如图,在 Rt△ABC 中,∠C = 90°,cosA = , 15 17
A
C
cos A AC = 8 = 4,tan A BC = 6 = 3 .
锐角三角形精品讲解三份
第28章:锐角三角函数一、基础知识1.定义:如图在△ABC中,∠C为直角,我们把锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA;sinA=a sinAc=把锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA;cosb Ac =把锐角∠A的对边与邻边的比叫做∠A的正切,记作tanA 。
tana Ab =把锐角∠A的邻边与对边的比叫做∠A的余切,记作cosA。
cosb Aa =2、三角函数值锐角三角函数的大小比较:在︒<<︒900A时,随着A的增大,正弦值越来越大,而余弦值越来越小.即:Asin是增函数,Acos减函数。
○1锐角三角函数值都是正数。
○2当角度在0-90度间变化时:正弦、正切值随着角度的增大而增大;余弦、余切随着角度的增大而减小。
3、同角、互余角的三角函数关系:1、同角三角函数关系:1cossin22=+AA.sintancos∂∂=∂;coscotsin∂∂=∂;tan cot1∂∙∂=2、互余锐角的三角函数关系:)90cos(cossin ABA-︒==,)90sin(sincos ABA-︒==。
解直角三角形:由直角三角形中除直角以外的两个已知元素(其中至少有一条边),求出所有未知元素的过程,叫做解直角三角形。
二、精典例题第一部分:锐角三角函数的运算一、直角三角形中锐角的正弦、余弦的概念与表达式: 例1:如图所示,则()()()()====E E D D cos ,sin ,cos ,sin 。
[考点透视]本例主要是考查锐角三角函数的概念例2:在ABC ∆Rt 中,如果各边长度都扩大4倍,则锐角A 的正弦值和余弦值()(A )都没有变化 (B )都扩大4倍 (C )都缩小4倍 (D )不能确定[考点透视]本例主要是考查锐角三角函数的定义和性质,通过计算可以知道正弦值和余弦值,只与直角三角形中锐角的大小有关。
例3:已知:A ∠为锐角,并且5sin 12A =,则A cos 的值为 . [考点透视]本例主要是考查锐角三角函数的定义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十八章 锐角三角函数
(时间:100分钟 分数100分)
班级: 姓名: 得分:
一、选择题(每题给出四个答案,其中只有一个答案是正确的,将正确答案的代码填在后面括号中,每小题3分,共30分.)
1. 如图,CD 是ABC Rt △斜边上的高,43AC BC ==,,则
cos BCD ∠的值是( ) A.35 B.34 C.43 D.45
2. Rt △ABC 中,∠C =90°,若BC =4,,32sin =
A 则AC 的长为( ) A .6
B .52
C .53
D .132
3.以直角坐标系的原点O 为圆心,以1为半径作圆.若点P 是该圆上第一象限内的一点,且OP 与x 轴正方向组成的角为α,则点P 的坐标为 ( )
A .(cosα,1)
B . (1,sinα)
C .(sinα,cosα)
D .(cosα,sinα)
4. 李红同学遇到了这样一道题:3tan(α+20°)=1,你猜想锐角α的度数应是( )
A.40°
B.30°
C.20°
D.10°
5. 在△ABC 中,若tanA=1,sinB=2
2,你认为最确切的判断是( ) A.△ABC 是等腰三角形 B.△ABC 是等腰直角三角形
C.△ABC 是直角三角形
D.△ABC 是一般锐角三角形
6.如图,坡角为30°的斜坡上两树间的水平距离AC 为2m ,则两树间的坡面距离AB 为( )
A .4m B
C .m 3
D .
7. 若某人沿倾斜角为α 的斜坡前进100m ,则他上升的最大高度是( )
A .m sin 100α
B .100sin α m
C .m cos 100β
D .100cos β m
8.如果α是锐角,且Sin α=5
4,那∠COS(90°-α)= ( ) A .54 B .43 C .53 D .5
1
9.如图,一电线杆AB 高为10米,当太阳光线与地面的夹角为60°时,其影长AC 约为取1.732,结果保留3个有效数字)( )
A. 5.00米.
B. 8.66米
C. 17. 3米
D. 5.77米
10. 如图,四边形ABCD 中,∠A=135°,∠B=∠D=90°,BC=23,AD=2,则四边形ABCD 的面积是( ) A.42 B.43 C.4 D.6
二、填空题(每小题3分,计18分)
11. 在△ABC 中,∠C =90°,∠ABC =60°,若D 是AC 边中点,则tan ∠DBC 的值为______.
12.直角三角形ABC 的面积为24cm 2,直角边AB 为6cm ,∠A 是锐角,则sin A = .
13.如图,小亮在操场上距离旗杆AB 的C 处,用测角仪测得旗杆顶端A 的仰角为300,已知BC =9米,测角仪的高CD 为1.2米,那么旗杆AB 的高为 _米(结果保留根号).
14. 在Rt △ABC 中,∠C =90°,a =10,若△ABC 的面积为33
50,则∠A =______度. 15. 如下图,表示甲、乙两山坡的情况, _____坡更陡.(填“甲”“乙”)
16. 如图,我校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为30 ,90BCA ∠=
,台阶的高BC 为2米,那么请你帮忙算一算需要
米长的地毯恰好能铺好台阶.(结果精确
到0.1m 1.414= 1.732=) 三、解答题(本大题有7个小题,共52分.)
17.(本题满分8分) (1)计算:(1) 6tan 2 30°-3sin 60°-2sin 45°
(2)
50
cos 40sin 60cos 45tan 30cos 330sin 145tan 41222-+-+
18. (本题满分8分) △ABC 中,∠C =90°.
(1)已知:c = 83,∠A =60°,求∠B 、a 、b .
(2) 已知:a =36, ∠A =30°,求∠B 、b 、c.
19. (本题满分5分)如图,在Rt △ABC 中,∠C=90°,AC=8,∠A 的平分线AD=3
316,求∠B 的度数及边BC 、AB 的长.
20. (本题满分6分)已知:如图,在距旗杆25m 的A 处,用测角仪测得旗杆顶点C 的仰角为30°,已知测角仪AB 的高为1.5m ,求旗杆CD 的高(精确到0.1m).
21.(本题满分7分)某民航飞机在太平洋某海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A 处以每小时8海里的速度向正东方向划行,在A 处测得黑匣子B 在北偏东60°的方向,划行半小时后到达C 处,测得黑匣子B 在北偏东30 °的方向,在潜水员继续向东划行多少小时,距离黑匣子B 最近,并求最近距离.
22. (本题满分8分)已知:如图,直线y =-x +12分别交x 轴、y 轴于A 、B 点,将△AOB 折叠,使A 点恰好落在OB 的中点C 处,折痕为DE .
(1)求AE 的长及sin ∠BEC 的值; (2)求△CDE 的面积.
23. (本题满分10分)某大草原上有一条笔直的公路,在紧靠公路40千米的A 、B 两地分别有甲、乙两个医疗队,如图所示,在A 地北偏东45°,B 地的北偏西60°方向上有一牧民区C 地,一天,甲接到牧民区C 地的求救电话,立刻设计了两种方案:
方案1:从A 地沿公路到牧民区C 地最近的D 处,再开车穿越草地沿DC 方向搭配牧民区. 方案2:从A 地直接开车穿越草原到牧民区C 地,已知汽车在公路上行驶的速度是在草地上行驶的速度的3倍.
(1)求牧民区C 地到公路的最短距离CD ;
(2)你认为甲医疗队设计的两种救助方案,哪一种比较合理,并说明理由。
(结果精确到0.1千米,参考数据41.1273.13==,)。
