数学_2014年甘肃省高考数学一模试卷(文科)(含答案)
数学_2014年甘肃省武威市凉州区高考数学一模试卷(文科)(含答案)

2014年甘肃省武威市凉州区高考数学一模试卷(文科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知全集U =R ,集合M ={x|2x >1},集合N ={x|log 2x >1},则下列结论中成立的是( )A M ∩N =MB M ∪N =NC M ∩(∁U N)=⌀D (∁U M)∩N =⌀ 2. 已知i 为虚数单位,则z =1+i i在复平面内对应的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限3. 已知命题p:∃x ∈R ,x −2>lgx ,命题q:∀x ∈R ,x 2>0,则( )A 命题p ∨q 是假命题B 命题p ∧q 是真命题C 命题p ∧(¬q)是真命题D 命题p ∨(¬q)是假命题 4. 已知sinα+3cosα3cosα−sinα=5,则sin 2α−sinαcosα的值是( )A 25B −25C −2D 25. 某几何体的三视图如图所示,则它的体积是( )A 8−2π3B 8−π3C 8−2πD 2π3 6. 执行如图的程序框图,输出的S 等于( )A 34 B 45 C 56 D 677. 函数y =log a (x +3)−1(a >0, a ≠1)的图象恒过定点A ,若点A 在直线mx +ny +1=0上,其中mn >0,则1m +2n 的最小值为( )A 6B 8C 10D 128. 已知等比数列{a n }的公比q =2,且2a 4,a 6,48成等差数列,则{a n }的前8项和为( )A 127B 255C 511D 10239. 已知f(x)=14x 2+sin(π2+x),f ′(x)为f(x)的导函数,则f ′(x)的图象是( )A B C D10. 设函数f(x)=cosωx(ω>0),将y =f(x)的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ) A 13 B 3 C 6 D 911. 点P 在双曲线:x 2a 2−y 2b 2=1(a >0, b >0)上,F 1,F 2是这条双曲线的两个焦点,∠F 1PF 2=90∘,且△F 1PF 2的三条边长成等差数列,则此双曲线的离心率是( ) A 2 B 3 C 4 D 512. 定义方程f(x)=f′(x)的实数根x 0叫做函数f(x)的“新驻点”,若函数g(x)=2x ,ℎ(x)=lnx ,φ(x)=x 3(x ≠0)的“新驻点”分别为a ,b ,c ,则a ,b ,c 的大小关系为( ) A a >b >c B c >b >a C a >c >b D b >a >c二、填空题(本大题共4小题,每小题5分,共20分,把答案填写在横线上).13. 若圆C 的半径为1,圆心在第一象限,且与直线4x −3y =0和x 轴都相切,则该圆的标准方程是________.14. 若向量a →,b →满足|a →|=1,|b →|=√2,且a →⊥(a →+b →),则a →与b →的夹角为________. 15. 若函数y =log 3x 的图象上存在点(x, y),满足约束条件{x +y −4≤02x −y +1≥0y ≥m ,则实数m 的最大值为________.16. 在△ABC 中,已知a ,b ,c 分别为角A ,B ,C 所对的边,S 为△ABC 的面积.若向量p →=(4, a 2+b 2−c 2),q →=(√3,S)满足p → // q →,则∠C =________.三、解答题(解答应写出文字说明,证明过程或演算步骤.共70分)17. 等差数列{a n }是递增数列,前n 项和为S n ,且a 1,a 3,a 9成等比数列,S 5=a 52. (1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =n 2+n +1⋅,求数列{b n }的前n 项的和.18. 为了了解湖南各景点在大众中的熟知度,随机对15∼65岁的人群抽样了n 人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.第5组[55, 65]3y(Ⅰ)分别求出a,b,x,y的值;(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.19. 如图,正三棱柱ABC−A1B1C1中,D是BC的中点,AA1=AB=a.(1)求证:AD⊥B1D;(2)求证:A1C // 平面AB1D;(3)求点A1到平面AB1D的距离.20. 已知椭圆C的中心在坐标原点,短轴长为4,且有一个焦点与抛物线y2=4√5x的焦点重合.(1)求椭圆C的方程.(2)已知经过定点M(2, 0)且斜率不为0的直线l交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得PM始终平分∠APB?若存在求出P点坐标,若不存在请说明理由.21. 已知函数f(x)=(ax−2)e x在x=1处取得极值.(1)求a的值;(2)求函数f(x)在[m, m+1]上的最小值;(3)求证:对任意x1,x2∈[0, 2],都有|f(x1)−f(x2)|≤e.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.【选修4-1:几何证明选讲】22. 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.(1)求证:直线AB是⊙O的切线;(2)若tan∠CED =12,⊙O 的半径为3,求OA 的长.【选修4-4:极坐标系与参数方程】23. 在平面直角坐标系xoy 中,已知曲线C 的参数方程为{x =2cosαy =sinα(α为参数).以直角坐标系原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为ρcos(θ−π4)=2√2(1)求直线l 的直角坐标方程;(2)点P 为曲线C 上的动点,求点P 到直线l 距离的最大值.【选修4-5:不等式选讲】24. 已知函数f(x)=|2x −1|+|2x +a|,g(x)=x +3. (1)当a =−2时,求不等式f(x)<g(x)的解集;(2)设a >−1,且当x ∈[−a2,12)时,f(x)≤g(x),求a 的取值范围.2014年甘肃省武威市凉州区高考数学一模试卷(文科)答案1. D2. D3. C4. A5. A6. B7. B8. B9. A 10. C 11. D 12. B13. (x −2)2+(y −1)2=1 14. 3π4 15. 116. π317. 解:(1)设{a n }的公差为d ,(d >0) ∵ a 1,a 3,a 9成等比数列, ∴ (a 1+2d)2=a 1(a 1+8d), 整理,得d 2=a 1d ,∵ d ≠0,∴ a 1=d ,①∵ S 5=a 52,∴ 5a 1+5×42⋅d =(a 1+4d)2,②由①②,得:a 1=35,d =35, ∴ a n =35+(n −1)×35=35n .(2)b n =n 2+n +1⋅=n 2+n+135n⋅35(n+1)=259⋅n 2+n+1n(n+1)=259(1+1n−1n+1),∴ b 1+b 2+...+b n =259[n +(1−12)+(12−13)+⋯+(1n −1n +1)] =259(n +1−1n +1) =259⋅n 2+2n n+1.18. 正确的人数共有54人,∴ 利用分层抽样在54人中抽取6人,每组分别抽取的人数为:第2组:1854×6=2人;第3组:2754×6=3人;第4组:954×6=1人 (Ⅲ)设第2组2人为:A 1,A 2;第3组3人为:B 1,B 2,B 3;第4组1人为:C 1.则从6人中随机抽取2人的所有可能的结果为:(A 1, A 2),(A 1, B 1),(A 1, B 2),(A 1, B 3),(A 1, C 1),(A 2, B 1),(A 2, B 2),(A 2, B 3),(A 2, C 1),(B 1, B 2),(B 1, B 3),(B 1, C 1),(B 2, B 3),(B 2, C 1),(B 3, C 1)共15个基本事件,其中恰好没有第3组人共3个基本事件,∴ 所抽取的人中恰好没有第3组人的概率是:P =315=1519. 解:(1)证明:∵ ABC−A1B1C1是正三棱锥,∴ BB1⊥平面ABC,∴ BB1⊥AD,在正△ABC中,∵ D是BC的中点,∴ AD⊥BD.BB1∩BD=B,∴ AD⊥平面BB1D,∴ AD⊥B1D.(2)连接DE.AA1=AB,四边形A1ABB1是正方向,∴ E是A1B的中点,又D是BC的中点,∴ DE // A1C,∵ DE⊂平面AB1D,A1C⊄平面AB1D,∴ A1C // 平面AB1D.(3)V A1−AB1D =V B1−A1AD,所以13⋅12⋅√32a⋅√52a⋅d=13⋅12⋅√32a⋅a⋅a2,解得d=√55a.20. 解:(1)设椭圆的标准方程为x2a2+y2b2=1(a>b>0),焦距为2c.由抛物线y2=4√5x方程得焦点(√5,0),∴ c=√5.又短轴长为4,∴ 2b=4,解得b=2.∴ a2=b2+c2=9.∴ 椭圆C的方程为x29+y24=1.(2)假设在x轴上存在一个定点P(t, 0)(t≠2)使得PM始终平分∠APB.设直线l的方程为my=x−2,A(x1, y1),B(x2, y2).联立{my=x−2x29+y24=1,化为(9+4m2)y2+16my−20=0,则y1+y2=−16m9+4m2,y1y2=−209+4m2.(∗)∵ PM平分∠APB,∴ |PA||PB|=|AM||BM|,∴ √(x1−t)2+y12√(x2−t)+y2=|y1||y2|,化为(x1−t)2(x2−t)2=y12y22,把x1=my1+2,x2=my2+2代入上式得(2−t)(y1−y2)[2my1y2+(2−t)(y1+y2)]= 0,∵ 2−t≠0,y1−y2≠0,∴ 2my1y2+(2−t)(y1+y2)=0.把(∗)代入上式得−40m9+4m2+−16(2−t)m9+4m2=0,化为m(9−2t)=0,由于对于任意实数上式都成立,∴ t=92.因此存在点P(92,0)满足PM 始终平分∠APB .21. 解:(1)f′(x)=ae x +(ax −2)e x =(ax +a −2)e x , 由已知得f′(1)=0,即(2a −2)e =0, 解得:a =1,验证知,当a =1时,在x =1处函数f(x)=(x −2)e x 取得极小值,所以a =1; (2)f(x)=(x −2)e x ,f′(x)=e x +(x −2)e x =(x −1)e x .所以函数f(x)在(−∞, 1)上递减,在(1, +∞)上递增. 当m ≥1时,f(x)在[m, m +1]上单调递增, f min (x)=f(m)=(m −2)e m . 当0<m <1时,m <1<m +1,f(x)在[m, 1]上单调递减,在[1, m +1]上单调递增,f min (x)=f(1)=−e . 当m ≤0时,m +1≤1,f(x)在[m, m +1]单调递减,f min (x)=f(m +1)=(m −1)e m+1. 综上,f(x)在[m, m +1]上的最小值f min (x)={(m −2)e m ,m ≥1−e,0<m <1(m −1)e m+1,m ≤0 (3)由(1)知f(x)=(x −2)e x ,f′(x)=e x +(x −2)e x =(x −1)e x . 令f′(x)=0得x =1,因为f(0)=−2,f(1)=−e ,f(2)=0, 所以f max (x)=0,f min (x)=−e ,所以,对任意x 1,x 2∈[0, 2],都有|f(x 1)−f(x 2)|≤f max (x)−f min (x)=e , 22. 如图,连接OC , ∵ OA =OB ,CA =CB , ∴ OC ⊥AB .∴ AB 是⊙O 的切线;∵ BC 是圆O 切线,且BE 是圆O 割线, ∴ BC 2=BD ⋅BE ,∵ tan∠CED =12,∴ CDEC =12. ∵ △BCD ∽△BEC ,∴ BDBC =CDEC =12,设BD =x ,BC =2x .又BC 2=BD ⋅BE ,∴ (2x)2=x ⋅(x +6),解得x 1=0,x 2=2,∵ BD =x >0,∴ BD =2,∴ OA =OB =BD +OD =3+2=5..23. 解:(1)∵ 直线l的极坐标方程为ρcos(θ−π4)=2√2,即ρcosθ+ρsinθ=4,化为直角坐标方程为x+y−4=0.(2)设点P(2cosα, sinα),点P到直线l距离d=√2=√5sin(α+β)−4|√2,其中,sinβ=√5,cosβ=√5.故当sin(α+β)=−1时,d取得最大值为√5+4√2=√102+2√2.24. 解:(1)当a=−2时,求不等式f(x)<g(x)化为|2x−1|+|2x−2|−x−3<0.设函数y=|2x−1|+|2x−2|−x−3,则y={−5x,x<12,−x−2,12≤x≤1,3x−6,x>1,它的图象如图所示:结合图象可得,y<0的解集为(0, 2),故原不等式的解集为(0, 2).(2)设a>−1,且当x∈[−a2,12)时,f(x)=1+a,不等式化为1+a≤x+3,故x≥a−2对x∈[−a2,12)都成立.故−a2≥a−2,解得a≤43.故a的取值范围为(−1, 43].。
2014年全国统一高考数学试卷(文科)(大纲版)(含答案及解析)

2014年全国统一高考数学试卷(文科)(大纲版)一、选择题(本大题共12小题,每小题5分)1.(5分)设集合M={1,2,4,6,8},N={1,2,3,5,6,7},则M∩N中元素的个数为()A.2B.3C.5D.72.(5分)已知角α的终边经过点(﹣4,3),则cosα=()A.B.C.﹣D.﹣3.(5分)不等式组的解集为()A.{x|﹣2<x<﹣1}B.{x|﹣1<x<0}C.{x|0<x<1}D.{x|x>1}4.(5分)已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为()A.B.C.D.5.(5分)函数y=ln(+1)(x>﹣1)的反函数是()A.y=(1﹣e x)3(x>﹣1)B.y=(e x﹣1)3(x>﹣1)C.y=(1﹣e x)3(x∈R)D.y=(e x﹣1)3(x∈R)6.(5分)已知,为单位向量,其夹角为60°,则(2﹣)•=()A.﹣1B.0C.1D.27.(5分)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种8.(5分)设等比数列{a n}的前n项和为S n.若S2=3,S4=15,则S6=()A.31B.32C.63D.649.(5分)已知椭圆C:+=1(a>b>0)的左、右焦点为F1、F2,离心率为,过F2的直线l交C于A、B两点,若△AF1B的周长为4,则C的方程为()A.+=1B.+y2=1C.+=1D.+=110.(5分)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A.B.16πC.9πD.11.(5分)双曲线C:﹣=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为,则C的焦距等于()A.2B.2C.4D.412.(5分)奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=()A.﹣2B.﹣1C.0D.1二、填空题(本大题共4小题,每小题5分)13.(5分)(x﹣2)6的展开式中x3的系数是.(用数字作答)14.(5分)函数y=cos2x+2sinx的最大值是.15.(5分)设x,y满足约束条件,则z=x+4y的最大值为.16.(5分)直线l1和l2是圆x2+y2=2的两条切线,若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于.三、解答题17.(10分)数列{a n}满足a1=1,a2=2,a n+2=2a n+1﹣a n+2.(Ⅰ)设b n=a n+1﹣a n,证明{b n}是等差数列;(Ⅱ)求{a n}的通项公式.18.(12分)△ABC的内角A、B、C的对边分别为a、b、c,已知3acosC=2ccosA,tanA=,求B.19.(12分)如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影D在AC 上,∠ACB=90°,BC=1,AC=CC1=2.(Ⅰ)证明:AC1⊥A1B;(Ⅱ)设直线AA1与平面BCC1B1的距离为,求二面角A1﹣AB﹣C的大小.20.(12分)设每个工作日甲,乙,丙,丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立.(Ⅰ)求同一工作日至少3人需使用设备的概率;(Ⅱ)实验室计划购买k台设备供甲,乙,丙,丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.21.(12分)函数f(x)=ax3+3x2+3x(a≠0).(Ⅰ)讨论f(x)的单调性;(Ⅱ)若f(x)在区间(1,2)是增函数,求a的取值范围.22.(12分)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|=|PQ|.(Ⅰ)求C的方程;(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.2014年全国统一高考数学试卷(文科)(大纲版)参考答案与试题解析一、选择题(本大题共12小题,每小题5分)1.(5分)设集合M={1,2,4,6,8},N={1,2,3,5,6,7},则M∩N中元素的个数为()A.2B.3C.5D.7【考点】1A:集合中元素个数的最值;1E:交集及其运算.【专题】5J:集合.【分析】根据M与N,找出两集合的交集,找出交集中的元素即可.【解答】解:∵M={1,2,4,6,8},N={1,2,3,5,6,7},∴M∩N={1,2,6},即M∩N中元素的个数为3.故选:B.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.(5分)已知角α的终边经过点(﹣4,3),则cosα=()A.B.C.﹣D.﹣【考点】G9:任意角的三角函数的定义.【专题】56:三角函数的求值.【分析】由条件直接利用任意角的三角函数的定义求得cosα的值.【解答】解:∵角α的终边经过点(﹣4,3),∴x=﹣4,y=3,r==5.∴cosα===﹣,故选:D.【点评】本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,属于基础题.3.(5分)不等式组的解集为()A.{x|﹣2<x<﹣1}B.{x|﹣1<x<0}C.{x|0<x<1}D.{x|x>1}【考点】7E:其他不等式的解法.【专题】59:不等式的解法及应用.【分析】解一元二次不等式、绝对值不等式,分别求出不等式组中每个不等式的解集,再取交集,即得所求.【解答】解:由不等式组可得,解得0<x<1,故选:C.【点评】本题主要考查一元二次不等式、绝对值不等式的解法,属于基础题.4.(5分)已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为()A.B.C.D.【考点】LM:异面直线及其所成的角.【专题】5G:空间角.【分析】由E为AB的中点,可取AD中点F,连接EF,则∠CEF为异面直线CE 与BD所成角,设出正四面体的棱长,求出△CEF的三边长,然后利用余弦定理求解异面直线CE与BD所成角的余弦值.【解答】解:如图,取AD中点F,连接EF,CF,∵E为AB的中点,∴EF∥DB,则∠CEF为异面直线BD与CE所成的角,∵ABCD为正四面体,E,F分别为AB,AD的中点,∴CE=CF.设正四面体的棱长为2a,则EF=a,CE=CF=.在△CEF中,由余弦定理得:=.故选:B.【点评】本题考查异面直线及其所成的角,关键是找角,考查了余弦定理的应用,是中档题.5.(5分)函数y=ln(+1)(x>﹣1)的反函数是()A.y=(1﹣e x)3(x>﹣1)B.y=(e x﹣1)3(x>﹣1)C.y=(1﹣e x)3(x∈R)D.y=(e x﹣1)3(x∈R)【考点】4R:反函数.【专题】51:函数的性质及应用.【分析】由已知式子解出x,然后互换x、y的位置即可得到反函数.【解答】解:∵y=ln(+1),∴+1=e y,即=e y﹣1,∴x=(e y﹣1)3,∴所求反函数为y=(e x﹣1)3,故选:D.【点评】本题考查反函数解析式的求解,属基础题.6.(5分)已知,为单位向量,其夹角为60°,则(2﹣)•=()A.﹣1B.0C.1D.2【考点】9O:平面向量数量积的性质及其运算.【专题】5A:平面向量及应用.【分析】由条件利用两个向量的数量积的定义,求得、的值,可得(2﹣)•的值.【解答】解:由题意可得,=1×1×cos60°=,=1,∴(2﹣)•=2﹣=0,故选:B.【点评】本题主要考查两个向量的数量积的定义,属于基础题.7.(5分)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种【考点】D9:排列、组合及简单计数问题.【专题】5O:排列组合.【分析】根据题意,分2步分析,先从6名男医生中选2人,再从5名女医生中选出1人,由组合数公式依次求出每一步的情况数目,由分步计数原理计算可得答案.【解答】解:根据题意,先从6名男医生中选2人,有C62=15种选法,再从5名女医生中选出1人,有C51=5种选法,则不同的选法共有15×5=75种;故选:C.【点评】本题考查分步计数原理的应用,注意区分排列、组合的不同.8.(5分)设等比数列{a n}的前n项和为S n.若S2=3,S4=15,则S6=()A.31B.32C.63D.64【考点】89:等比数列的前n项和.【专题】54:等差数列与等比数列.【分析】由等比数列的性质可得S2,S4﹣S2,S6﹣S4成等比数列,代入数据计算可得.【解答】解:S2=a1+a2,S4﹣S2=a3+a4=(a1+a2)q2,S6﹣S4=a5+a6=(a1+a2)q4,所以S2,S4﹣S2,S6﹣S4成等比数列,即3,12,S6﹣15成等比数列,可得122=3(S6﹣15),解得S6=63故选:C.【点评】本题考查等比数列的性质,得出S2,S4﹣S2,S6﹣S4成等比数列是解决问题的关键,属基础题.9.(5分)已知椭圆C:+=1(a>b>0)的左、右焦点为F1、F2,离心率为,过F2的直线l交C于A、B两点,若△AF1B的周长为4,则C的方程为()A.+=1B.+y2=1C.+=1D.+=1【考点】K4:椭圆的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】利用△AF1B的周长为4,求出a=,根据离心率为,可得c=1,求出b,即可得出椭圆的方程.【解答】解:∵△AF1B的周长为4,∵△AF1B的周长=|AF1|+|AF2|+|BF1|+|BF2|=2a+2a=4a,∴4a=4,∴a=,∵离心率为,∴,c=1,∴b==,∴椭圆C的方程为+=1.故选:A.【点评】本题考查椭圆的定义与方程,考查椭圆的几何性质,考查学生的计算能力,属于基础题.10.(5分)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A.B.16πC.9πD.【考点】LG:球的体积和表面积;LR:球内接多面体.【专题】11:计算题;5F:空间位置关系与距离.【分析】正四棱锥P﹣ABCD的外接球的球心在它的高PO1上,记为O,求出PO1,OO1,解出球的半径,求出球的表面积.【解答】解:设球的半径为R,则∵棱锥的高为4,底面边长为2,∴R2=(4﹣R)2+()2,∴R=,∴球的表面积为4π•()2=.故选:A.【点评】本题考查球的表面积,球的内接几何体问题,考查计算能力,是基础题.11.(5分)双曲线C:﹣=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为,则C的焦距等于()A.2B.2C.4D.4【考点】KC:双曲线的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】根据双曲线的离心率以及焦点到直线的距离公式,建立方程组即可得到结论.【解答】解:∵:﹣=1(a>0,b>0)的离心率为2,∴e=,双曲线的渐近线方程为y=,不妨取y=,即bx﹣ay=0,则c=2a,b=,∵焦点F(c,0)到渐近线bx﹣ay=0的距离为,∴d=,即,解得c=2,则焦距为2c=4,故选:C.【点评】本题主要考查是双曲线的基本运算,利用双曲线的离心率以及焦点到直线的距离公式,建立方程组是解决本题的关键,比较基础.12.(5分)奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=()A.﹣2B.﹣1C.0D.1【考点】3K:函数奇偶性的性质与判断.【专题】51:函数的性质及应用.【分析】根据函数的奇偶性的性质,得到f(x+8)=f(x),即可得到结论.【解答】解:∵f(x+2)为偶函数,f(x)是奇函数,∴设g(x)=f(x+2),则g(﹣x)=g(x),即f(﹣x+2)=f(x+2),∵f(x)是奇函数,∴f(﹣x+2)=f(x+2)=﹣f(x﹣2),即f(x+4)=﹣f(x),f(x+8)=f(x+4+4)=﹣f(x+4)=f(x),则f(8)=f(0)=0,f(9)=f(1)=1,∴f(8)+f(9)=0+1=1,故选:D.【点评】本题主要考查函数值的计算,利用函数奇偶性的性质,得到函数的对称轴是解决本题的关键.二、填空题(本大题共4小题,每小题5分)13.(5分)(x﹣2)6的展开式中x3的系数是﹣160.(用数字作答)【考点】DA:二项式定理.【专题】11:计算题.【分析】根据题意,由二项式定理可得(x﹣2)6的展开式的通项,令x的系数为3,可得r=3,将r=3代入通项,计算可得T4=﹣160x3,即可得答案.【解答】解:根据题意,(x﹣2)6的展开式的通项为T r=C6r x6﹣r(﹣2)r=(﹣1)+1r•2r•C6r x6﹣r,令6﹣r=3可得r=3,此时T4=(﹣1)3•23•C63x3=﹣160x3,即x3的系数是﹣160;故答案为﹣160.【点评】本题考查二项式定理的应用,关键要得到(x﹣2)6的展开式的通项.14.(5分)函数y=cos2x+2sinx的最大值是.【考点】HW:三角函数的最值.【专题】11:计算题.【分析】利用二倍角公式对函数化简可得y=cos2x+2sinx=1﹣2sin2x+2sinx=,结合﹣1≤sinx≤1及二次函数的性质可求函数有最大值【解答】解:∵y=cos2x+2sinx=1﹣2sin2x+2sinx=又∵﹣1≤sinx≤1当sinx=时,函数有最大值故答案为:【点评】本题主要考查了利用二倍角度公式对三角函数进行化简,二次函数在闭区间上的最值的求解,解题中要注意﹣1≤sinx≤1的条件.15.(5分)设x,y满足约束条件,则z=x+4y的最大值为5.【考点】7C:简单线性规划.【专题】31:数形结合.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,由图得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.【解答】解:由约束条件作出可行域如图,联立,解得C(1,1).化目标函数z=x+4y为直线方程的斜截式,得.由图可知,当直线过C点时,直线在y轴上的截距最大,z最大.此时z max=1+4×1=5.故答案为:5.【点评】本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.16.(5分)直线l1和l2是圆x2+y2=2的两条切线,若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于.【考点】IV:两直线的夹角与到角问题.【专题】5B:直线与圆.【分析】设l1与l2的夹角为2θ,由于l1与l2的交点A(1,3)在圆的外部,由直角三角形中的边角关系求得sinθ=的值,可得cosθ、tanθ 的值,再根据tan2θ=,计算求得结果.【解答】解:设l1与l2的夹角为2θ,由于l1与l2的交点A(1,3)在圆的外部,且点A与圆心O之间的距离为OA==,圆的半径为r=,∴sinθ==,∴cosθ=,tanθ==,∴tan2θ===,故答案为:.【点评】本题主要考查直线和圆相切的性质,直角三角形中的变角关系,同角三角函数的基本关系、二倍角的正切公式的应用,属于中档题.三、解答题17.(10分)数列{a n}满足a1=1,a2=2,a n+2=2a n+1﹣a n+2.(Ⅰ)设b n=a n+1﹣a n,证明{b n}是等差数列;(Ⅱ)求{a n}的通项公式.【考点】83:等差数列的性质;84:等差数列的通项公式;8H:数列递推式.【专题】54:等差数列与等比数列.【分析】(Ⅰ)将a n=2a n+1﹣a n+2变形为:a n+2﹣a n+1=a n+1﹣a n+2,再由条件得+2b n+1=b n+2,根据条件求出b1,由等差数列的定义证明{b n}是等差数列;(Ⅱ)由(Ⅰ)和等差数列的通项公式求出b n,代入b n=a n+1﹣a n并令n从1开始取值,依次得(n﹣1)个式子,然后相加,利用等差数列的前n项和公式求出{a n}的通项公式a n.=2a n+1﹣a n+2得,【解答】解:(Ⅰ)由a n+2a n+2﹣a n+1=a n+1﹣a n+2,由b n=a n+1﹣a n得,b n+1=b n+2,即b n﹣b n=2,+1又b1=a2﹣a1=1,所以{b n}是首项为1,公差为2的等差数列.(Ⅱ)由(Ⅰ)得,b n=1+2(n﹣1)=2n﹣1,由b n=a n+1﹣a n得,a n+1﹣a n=2n﹣1,则a2﹣a1=1,a3﹣a2=3,a4﹣a3=5,…,a n﹣a n﹣1=2(n﹣1)﹣1,所以,a n﹣a1=1+3+5+…+2(n﹣1)﹣1==(n﹣1)2,又a1=1,所以{a n}的通项公式a n=(n﹣1)2+1=n2﹣2n+2.【点评】本题考查了等差数列的定义、通项公式、前n项和公式,及累加法求数列的通项公式和转化思想,属于中档题.18.(12分)△ABC的内角A、B、C的对边分别为a、b、c,已知3acosC=2ccosA,tanA=,求B.【考点】GL:三角函数中的恒等变换应用;HP:正弦定理.【专题】58:解三角形.【分析】由3acosC=2ccosA,利用正弦定理可得3sinAcosC=2sinCcosA,再利用同角的三角函数基本关系式可得tanC,利用tanB=tan[π﹣(A+C)]=﹣tan(A+C)即可得出.【解答】解:∵3acosC=2ccosA,由正弦定理可得3sinAcosC=2sinCcosA,∴3tanA=2tanC,∵tanA=,∴2tanC=3×=1,解得tanC=.∴tanB=tan[π﹣(A+C)]=﹣tan(A+C)=﹣=﹣=﹣1,∵B∈(0,π),∴B=【点评】本题考查了正弦定理、同角的三角函数基本关系式、两角和差的正切公式、诱导公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.19.(12分)如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影D在AC 上,∠ACB=90°,BC=1,AC=CC1=2.(Ⅰ)证明:AC1⊥A1B;(Ⅱ)设直线AA1与平面BCC1B1的距离为,求二面角A1﹣AB﹣C的大小.【考点】LW:直线与平面垂直;MJ:二面角的平面角及求法.【专题】5F:空间位置关系与距离.【分析】(Ⅰ)由已知数据结合线面垂直的判定和性质可得;(Ⅱ)作辅助线可证∠A1FD为二面角A1﹣AB﹣C的平面角,解三角形由反三角函数可得.【解答】解:(Ⅰ)∵A1D⊥平面ABC,A1D⊂平面AA1C1C,∴平面AA1C1C⊥平面ABC,又BC⊥AC∴BC⊥平面AA1C1C,连结A1C,由侧面AA1C1C为菱形可得AC1⊥A1C,又AC1⊥BC,A1C∩BC=C,∴AC1⊥平面A1BC,AB1⊂平面A1BC,∴AC1⊥A1B;(Ⅱ)∵BC⊥平面AA1C1C,BC⊂平面BCC1B1,∴平面AA1C1C⊥平面BCC1B1,作A1E⊥CC1,E为垂足,可得A1E⊥平面BCC1B1,又直线AA1∥平面BCC1B1,∴A1E为直线AA1与平面BCC1B1的距离,即A1E=,∵A1C为∠ACC1的平分线,∴A1D=A1E=,作DF⊥AB,F为垂足,连结A1F,又可得AB⊥A1D,A1F∩A1D=A1,∴AB⊥平面A1DF,∵A1F⊂平面A1DF∴A1F⊥AB,∴∠A1FD为二面角A1﹣AB﹣C的平面角,由AD==1可知D为AC中点,∴DF==,∴tan∠A1FD==,∴二面角A1﹣AB﹣C的大小为arctan【点评】本题考查二面角的求解,作出并证明二面角的平面角是解决问题的关键,属中档题.20.(12分)设每个工作日甲,乙,丙,丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立.(Ⅰ)求同一工作日至少3人需使用设备的概率;(Ⅱ)实验室计划购买k台设备供甲,乙,丙,丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.【考点】C8:相互独立事件和相互独立事件的概率乘法公式.【专题】5I:概率与统计.【分析】(Ⅰ)把4个人都需使用设备的概率、4个人中有3个人使用设备的概率相加,即得所求.(Ⅱ)由(Ⅰ)可得若k=2,不满足条件.若k=3,求得“同一工作日需使用设备的人数大于3”的概率为0.06<0.1,满足条件,从而得出结论.【解答】解:(Ⅰ)由题意可得“同一工作日至少3人需使用设备”的概率为0.6×0.5×0.5×0.4+(1﹣0.6)×0.5×0.5×0.4+0.6×(1﹣0.5)×0.5×0.4+0.6×0.5×(1﹣0.5)×0.4+0.6×0.5×0.5×(1﹣0.4)=0.31.(Ⅱ)由(Ⅰ)可得若k=2,则“同一工作日需使用设备的人数大于2”的概率为0.31>0.1,不满足条件.若k=3,则“同一工作日需使用设备的人数大于3”的概率为0.6×0.5×0.5×0.4=0.06<0.1,满足条件.故k的最小值为3.【点评】本题主要考查相互独立事件的概率乘法公式,体现了分类讨论的数学思想,属于中档题.21.(12分)函数f(x)=ax3+3x2+3x(a≠0).(Ⅰ)讨论f(x)的单调性;(Ⅱ)若f(x)在区间(1,2)是增函数,求a的取值范围.【考点】6B:利用导数研究函数的单调性;6D:利用导数研究函数的极值.【专题】53:导数的综合应用.【分析】(Ⅰ)求出函数的导数,通过导数为0,利用二次函数的根,通过a的范围讨论f(x)的单调性;(Ⅱ)当a>0,x>0时,f(x)在区间(1,2)是增函数,当a<0时,f(x)在区间(1,2)是增函数,推出f′(1)≥0且f′(2)≥0,即可求a的取值范围.【解答】解:(Ⅰ)函数f(x)=ax3+3x2+3x,∴f′(x)=3ax2+6x+3,令f′(x)=0,即3ax2+6x+3=0,则△=36(1﹣a),①若a≥1时,则△≤0,f′(x)≥0,∴f(x)在R上是增函数;②因为a≠0,∴a≤1且a≠0时,△>0,f′(x)=0方程有两个根,x1=,x2=,当0<a<1时,则当x∈(﹣∞,x2)或(x1,+∞)时,f′(x)>0,故函数在(﹣∞,x2)或(x1,+∞)是增函数;在(x2,x1)是减函数;当a<0时,则当x∈(﹣∞,x1)或(x2,+∞),f′(x)<0,故函数在(﹣∞,x1)或(x2,+∞)是减函数;在(x1,x2)是增函数;(Ⅱ)当a>0,x>0时,f′(x)=3ax2+6x+3>0 故a>0时,f(x)在区间(1,2)是增函数,当a<0时,f(x)在区间(1,2)是增函数,当且仅当:f′(1)≥0且f′(2)≥0,解得﹣,a的取值范围[)∪(0,+∞).【点评】本题考查函数的导数的应用,判断函数的单调性以及已知单调性求解函数中的变量的范围,考查分类讨论思想的应用.22.(12分)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|=|PQ|.(Ⅰ)求C的方程;(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.【考点】KH:直线与圆锥曲线的综合.【专题】5E:圆锥曲线中的最值与范围问题.【分析】(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C的方程,求得x0=,根据|QF|=|PQ|求得p的值,可得C的方程.(Ⅱ)设l的方程为x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN 四点共圆等价于|AE|=|BE|=|MN|,由此求得m的值,可得直线l的方程.【解答】解:(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C:y2=2px (p>0),可得x0=,∵点P(0,4),∴|PQ|=.又|QF|=x0+=+,|QF|=|PQ|,∴+=×,求得p=2,或p=﹣2(舍去).故C的方程为y2=4x.(Ⅱ)由题意可得,直线l和坐标轴不垂直,y2=4x的焦点F(1,0),设l的方程为x=my+1(m≠0),代入抛物线方程可得y2﹣4my﹣4=0,显然判别式△=16m2+16>0,y1+y2=4m,y1•y2=﹣4.∴AB的中点坐标为D(2m2+1,2m),弦长|AB|=|y1﹣y2|==4(m2+1).又直线l′的斜率为﹣m,∴直线l′的方程为x=﹣y+2m2+3.过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,把线l′的方程代入抛物线方程可得y2+y﹣4(2m2+3)=0,∴y3+y4=,y3•y4=﹣4(2m2+3).故线段MN的中点E的坐标为(+2m2+3,),∴|MN|=|y3﹣y4|=,∵MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|=|MN|,∴+DE2=MN2,∴4(m2+1)2 ++=×,化简可得m2﹣1=0,∴m=±1,∴直线l的方程为x﹣y﹣1=0,或x+y﹣1=0.【点评】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理、弦长公式的应用,体现了转化的数学思想,属于难题.。
2014年甘肃省张掖市高台一中高考数学一模试卷(文科)

2014年甘肃省张掖市高台一中高考数学一模试卷(文科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共12小题,共60.0分)1.已知集合A={x||2x+1|>3},集合,则A∩(∁R B)=()A.(1,2)B.(1,2]C.(1,+∞)D.[1,2]【答案】B【解析】解:由A中的不等式变形得:2x+1>3或2x+1<-3,解得:x>1或x<-2,∴A=(-∞,-2)∪(1,+∞),由B中y=,得到≥0,即>或<,解得:x>2或x≤-1,∴B=(-∞,-1]∪(2,+∞),∵全集为R,∴∁R B=(-1,2],则A∩(∁R B)=(1,2].故选:B.求出A中不等式的解集确定出A,求出B中函数的定义域确定出B,根据全集R求出B 的补集,找出A与B补集的交集即可.此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.若复数z满足(3-4i)z=|4+3i|,则z的虚部为()A.-4B.C.4D.【答案】D【解析】解:∵复数z满足(3-4i)z=|4+3i|,∴z====+i,故z的虚部等于,故选:D.由题意可得z==,再利用两个复数代数形式的乘除法法则化简为+i,由此可得z的虚部.本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,属于基础题.3.若=2,=1,且与的夹角为60°,当取得最小值时,实数x的值为()A.2B.-2C.1D.-1【答案】C【解析】解:∵=2,=1,且与的夹角为60°,∴=2×1×cos60°=1.∵===,故当x=1时,取得最小值为,故选:C.由题意可得=1,再根据==,可得当取得最小值时,实数x的值.本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题.4.直线xsinα+y+2=0的倾斜角的取值范围是()A.[0,π)B.[0,]∪[,π)C.[0,]D.[0,]∪(,π)【答案】B【解析】解:直线xsinα+y+2=0的斜率为k=-sinα,∵-1≤sinα≤1,∴-1≤k≤1∴倾斜角的取值范围是[0,]∪[π,π)故选B由直线的方程可确定直线的斜率,可得其范围,进而可求倾斜角的取值范围.本题考查直线的斜率与倾斜角的关系,属基础题.5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为()A. B. C. D.【答案】C【解析】解:三视图复原的几何体,下部是放倒的四棱柱,底面是直角梯形,边长分别为:3,2,1,;高为:1;上部是正方体,也可以看作是三个正方体和半个正方体的组合体,所以几何体的体积为:3×13+=,故选C.三视图复原的几何体,下部是放倒的四棱柱,上部是正方体,根据三视图的数据,求出几何体的表面积.本题是基础题,考查几何体的三视图的视图能力,计算能力,空间想象能力,转化思想的应用.6.已知△ABC的面积为2,在△ABC所在的平面内有两点P、Q,满足,=2,则△APQ的面积为()A. B. C.1 D.2【答案】B【解析】解:由题意可知,P为AC的中点,=2,可知Q为AB的一个三等分点,如图:因为S△ABC==2.所以S△APQ===.故选B.画出△ABC,通过足,=2,标出满足题意的P、Q位置,利用三角形的面积公式求解即可.本题考查向量在几何中的应用,三角形的面积的求法,考查转化思想与计算能力.7.执行如图所示的程序框图(其中[x]表示不超过x的最大整数),则输出的S值为()A.7B.6C.5D.4【答案】A【解析】解:由程序框图得:第一次运行n=0,S=0;第二次运行n=1,S=1;第三次运行n=2,S=1+1=2;第四次运行n=3,S=2+1=3;第五次运行n=4,S=3+2=5;第六次运行n=5,S=5+2=7;满足n>4结束运行,输出S=7.故选A.由程序框图依次计算第一、第二…的运行结果,直到满足条件n>4时,输出S,即为所求.本题考查了直到型循环结构的程序框图,解答的关键是读懂程序框图.8.函数 , , > ,若方程f (x )=x +a 恰有两个不等的实根,则a 的取值范围为( )A.(-∞,0)B.[0,1)C.(-∞,1)D.[0,+∞) 【答案】 C【解析】解:由函数, , >,可得f (x )的图象和函数y =x +a 有两个不同的交点, 如图所示:故有a <1, 故选C .由题意可得f (x )的图象和函数y =x +a 有两个不同的交点,结合图象,求出a 的取值范围.本题考查根的存在性及根的个数判断,以及函数与方程的思想、数形结合的数学思想,解答关键是运用数形结合的思想,属于中档题.9.过双曲线> , > 的左焦点F 作圆x 2+y 2=a 2的两条切线,切点分别为A 、B ,双曲线左顶点为M ,若∠AMB=120°,则该双曲线的离心率为( )A. B. C.3 D.2 【答案】 D【解析】解:依题意,作图如下:∵OA ⊥FA ,∠AMO=60°,OM=OA , ∴△AMO 为等边三角形, ∴OA=OM=a ,在直角三角形OAF 中,OF=c ,∴该双曲线的离心率e = = ==2, 故选:D .依题意,作出图形,易求该双曲线的离心率e = ==2,从而得到答案. 本题考查双曲线的简单性质,考查作图能力与解三角形的能力,属于中档题.10.设S n 是等差数列{a n }的前n 项和,若,则=( )A.1B.-1C.2D.【答案】 A【解析】解:由题意可得====1故选A由等差数列的求和公式和性质可得=,代入已知可得.本题考查等差数列的求和公式,涉及等差数列的性质,属基础题.11.在直角三角形ABC中,∠ACB=90°,AC=BC=2,点P是斜边AB上的一个三等分点,则•+•=()A. B.2 C. D.4【答案】D【解析】解:如图所示:==,∴•+•=()+()===4,故选D.不妨作出图象,由向量加法法则得=,代入式子利用数量积运算可求.本题考查平面向量数量积运算、向量加法的三角形法则,属基础题.12.设F为抛物线y2=16x的焦点,A,B,C为该抛物线上三点,若,则的值为()A.36B.24C.16D.12【答案】B【解析】解:由题意可得F(4,0),是抛物线的焦点,也是三角形ABC的重心,故故=4,∴x A+x B+x C=12.再由抛物线的定义可得:=x A+4+x B+4+x C+4=12+12=24,故选B.由题意可得F(4,0),是三角形ABC的重心,故=4,再由抛物线的定义可得=x A+4+x B+4+x C+4=24.本题考查三角形的重心坐标公式,抛物线的定义、标准方程,以及简单性质的应用,求得x A+x B+x C=12,是解题的关键.二、填空题(本大题共4小题,共20.0分)13.已知α∈(,π),且sinα=,则tanα的值为______ .【答案】-【解析】解:∵α∈(,π),且sinα=,∴cosα=-=-,则tanα==-.故答案为:-由α的范围以及sinα的值,利用同角三角函数间的基本关系求出cosα的值,即可确定出tanα的值.此题考查了同角三角函数间的基本关系,熟练掌握基本关系是解本题的关键.14.已知a>b>0,ab=1,则的最小值为______ .【答案】【解析】解:∵a>b>0,ab=1∴a-b>0∴=当且仅当a-b=时取等号故答案为本题是基本不等式问题,可以利用a>b>0得到a-b>0(正数),再利用条件ab为定值将a2+b2转化为(a-b)2与ab,化简后,运用基本不等式解决问题.本题主要考查了基本不等式的应用和转化化归的数学思想,注意不等式成立的条件(一正二定三相等)15.已知等比数列{a n}的第5项是二项式展开式的常数项,则a3a7= ______ .【答案】【解析】解:二项式展开式的通项公式为T r+1=•••x-r=••.令6-3r=0,r=2,故展开式的常数项为T3=•=.由题意可得,等比数列{a n}的第5项为展开式的常数项,即a5=,∴a3a7==,故答案为.在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项,即得a5的值.再根据等比数列的性质求得a3a7的值.本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数.等比数列的性质应用,属于中档题16.已知函数f(x)=lnx+2x,若f(x2-4)<2,则实数x的取值范围______ .【答案】(-,-2)∪(2,)【解析】解:解法一:∵函数f(x)=lnx+2x,∴f(x2-4)=ln(x2-4)+,∴不等式即ln(x2-4)+<2.令t=x2-4>0,不等式即lnt+2t<2①.令h(t)=lnt+2t,显然函数h(t)在(0,+∞)上是增函数,且h(1)=2,∴由不等式①可得t<1,即x2-4<1,即x2<5.由><解得-<x<-2,或2<x<,故答案为:(-,-2)∪(2,).解法二:由于函数f(x)=lnx+2x,∴f(1)=2,再根据函数f(x)=lnx+2x在定义域(0,+∞)上式增函数,∴由f(x2-4)<2可得x2-4<1,求得-<x<-2,或2<x<,故答案为:(-,-2)∪(2,).解法一:不等式即ln(x2-4)+<2,令t=x2-4>0,不等式即lnt+2t<2①.令h (t)=lnt+2t,由函数h(t)的单调性可得x2-4<1,从而求得x的范围.解法二:根据函数f(x)=lnx+2x在定义域(0,+∞)上是增函数,f(1)=2,由不等式可得x2-4<1,从而求得x的范围.本题主要考查函数的单调性的应用,体现了转化的数学思想,属于基础题.三、解答题(本大题共8小题,共94.0分)17.设函数f(x)=2cos2x+2sinx•cosx+m(m,x∈R).(1)求f(x)的最小正周期;(2)当x∈[0,]时,求实数m的值,使函数f(x)的值域恰为,,并求此时f(x)在R上的对称中心.【答案】解:(1)∵f(x)=2cos2x+2sinxcosx+m=1+cos2x+sin2x+m=2sin(2x+)+m+1,∴函数f(x)的最小正周期T=π.(2)∵0≤x≤,∴≤2x+≤,∴-≤sin(2x+)≤1,∴m≤f(x)≤m+3,又≤f(x)≤,∴m=,令2x+=kπ(k∈Z),解得x=-(k∈Z),∴函数f(x)在R上的对称中心为(-,)(k∈Z).【解析】(1)利用二倍角的正弦与余弦及辅助角公式可求得f(x)=2sin(2x+)+m+1,从而可求其最小正周期;(2)利用正弦函数的单调性可求得0≤x≤时,m≤f(x)≤m+3,利用使函数f(x)的值域为[,]可求得m的值,从而可求f(x)在R上的对称中心.本题考查:两角和与差的正弦函数,着重考查二倍角的正弦与余弦及辅助角公式,考查正弦函数的单调性、周期性与对称性,属于中档题.18.如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.(1)求证:DE∥平面PBC;(2)求证:AB⊥PE;(3)求二面角A-PB-E的大小.【答案】解:(Ⅰ)∵D、E分别为AB、AC中点,∴DE∥BC.∵DE⊄平面PBC,BC⊂平面PBC,∴DE∥平面PBC.…(4分)(Ⅱ)连接PD,∵PA=PB,D为AB中点,∴PD⊥AB.….(5分)∵DE∥BC,BC⊥AB,∴DE⊥AB…(6分)又∵PD∩DE=D,PD,DE⊂平面PDE∴AB⊥平面PDE…(8分)∵PE⊂平面PDE,∴AB⊥PE…(9分)(Ⅲ)∵AB⊥平面PDE,DE⊥AB…(10分)如图,以D为原点建立空间直角坐标系,由PA=PB=AB=2,BC=3,则B(1,0,0),P(0,0,),E(0,,0),∴=(1,0,),=(0,,).设平面PBE的法向量,,,∴令得,,…(11分)∵DE⊥平面PAB,∴平面PAB的法向量为,,.…(12分)设二面角的A-PB-E大小为θ,由图知,<,>,所以θ=60°,即二面角的A-PB-E大小为60°…(14分)【解析】(Ⅰ)由三角形中位线定理可得DE∥BC,进而由线面平行的判定定理得到DE∥平面PBC(II)连接PD,由等腰三角形三线合一,可得PD⊥AB,由DE∥BC,BC⊥AB可得DE⊥AB,进而由线面垂直的判定定理得到AB⊥平面PDE,再由线面垂直的性质得到AB⊥PE;(Ⅲ)以D为原点建立空间直角坐标系,分别求出平面PBE的法向量和平面PAB的法向量,代入向量夹角公式,可得二面角A-PB-E的大小.本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定,熟练掌握空间直线与平面位置关系的判定,性质是解答(I)和(II)的关键,而(III)的关键是建立空间坐标系,将空间角问题转化为向量夹角问题.19.为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出12人组成男子篮球队代表所在区参赛,队员来源人数如下表:(Ⅰ)求这两名队员来自同一学校的概率;(Ⅱ)设选出的两名队员中来自学校甲的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.【答案】解:(I)“从这12名队员中随机选出两名,两人来自于同一学校”记作事件A,则.…(6分)(II)ξ的所有可能取值为0,1,2…(7分)则,,∴ξ的分布列为:…(10分)∴…(13分)【解析】(I)“从这12名队员中随机选出两名,两人来自于同一学校”记作事件A,根据题设条件,利用排列组合知识能求出这两名队员来自同一学校的概率.(II)ξ的所有可能取值为0,1,2,分别求出其相对应的概率,由此能求出随机变量ξ的分布列及数学期望Eξ.本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.20.已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1(-,0)、F2(,0),椭圆上的点P满足∠PF1F2=90°,且△PF1F2的面积为S=.(1)求椭圆C的方程;(2)设椭圆C的左、右顶点分别为A、B,过点Q(1,0)的动直线l与椭圆C相交于M、N两点,直线AN与直线x=4的交点为R,证明:点R总在直线BM上.【答案】解:(Ⅰ)由题意知:,…(1分)∵椭圆上的点P满足∠PF1F2=90°,且,∴.∴,.∴2a=|PF1|+|PF2|=4,a=2…(2分)又∵,∴…(3分)∴椭圆C的方程为.…(4分)(Ⅱ)由题意知A(-2,0)、B(2,0),(1)当直线l与x轴垂直时,,、,,则AN的方程是:,BM的方程是:,直线AN与直线x=4的交点为,,∴点R在直线BM上.…(6分)(2)当直线l不与x轴垂直时,设直线l的方程为y=k(x-1),M(x1,y1)、N(x2,y2),R(4,y0)由得(1+4k2)x2-8k2x+4k2-4=0∴,…(7分),,,,A,N,R共线,∴…(8分)又,,,,需证明B,M,R共线,需证明2y1-y0(x1-2)=0,只需证明若k=0,显然成立,若k≠0,即证明(x1-1)(x2+2)-3(x2-1)(x1-2)=0∵(x1-1)(x2+2)-3(x2-1)(x1-2)=-2x1x2+5(x1+x2)-8=成立,…(11分)∴B,M,R共线,即点R总在直线BM上.…(12分)【解析】(Ⅰ)通过椭圆的截距以及三角形的面积求出a,b,即可得到椭圆C的方程;(Ⅱ)求出A、B坐标通过(1)当直线l与x轴垂直时,求出AN的方程,BM的方程,然后求出直线AN与直线x=4的交点,判断交点R在直线BM上;(2)当直线l不与x 轴垂直时,设直线l的方程为y=k(x-1),M(x1,y1)、N(x2,y2),R(4,y0)利用直线与椭圆方程联立结合韦达定理,利用分析法证明A,N,R共线,即点R总在直线BM上即可.本题考查椭圆的定义及其性质,椭圆方程的求法,直线与椭圆的位置关系,直线方程以及韦达定理的应用.难度比较大,解题需要一定的运算能力以及分析问题解决问题的能力.21.已知函数,<,>,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.(Ⅰ)指出函数f(x)的单调区间;(Ⅱ)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2-x1的最小值;(Ⅲ)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.【答案】解:(I)当x<0时,f(x)=(x+1)2+a,∴f(x)在(-∞,-1)上单调递减,在[-1,0)上单调递增;当x>0时,f(x)=lnx,在(0,+∞)单调递增.(II)∵x1<x2<0,∴f(x)=x2+2x+a,∴f′(x)=2x+2,∴函数f(x)在点A,B处的切线的斜率分别为f′(x1),f′(x2),∵函数f(x)的图象在点A,B处的切线互相垂直,∴′′,∴(2x1+2)(2x2+2)=-1.∴2x1+2<0,2x2+2>0,∴=1,当且仅当-(2x1+2)=2x2+2=1,即,时等号成立.∴函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2-x1的最小值为1.(III)当x1<x2<0或0<x1<x2时,∵′′,故不成立,∴x1<0<x2.当x1<0时,函数f(x)在点A(x1,f(x1)),处的切线方程为,即.当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为,即.函数f(x)的图象在点A,B处的切线重合的充要条件是①,由①及x1<0<x2可得-1<x1<0,由① 得=.∵函数,y=-ln(2x1+2)在区间(-1,0)上单调递减,∴a(x1)=在(-1,0)上单调递减,且x1→-1时,ln(2x1+2)→-∞,即-ln(2x1+2)→+∞,也即a(x1)→+∞.x1→0,a(x1)→-1-ln2.∴a的取值范围是(-1-ln2,+∞).【解析】(I)利用二次函数的单调性和对数函数的单调性即可得出;(II)利用导数的几何意义即可得到切线的斜率,因为切线互相垂直,可得′′,即(2x1+2)(2x2+2)=-1.可得,再利用基本不等式的性质即可得出;(III)当x1<x2<0或0<x1<x2时,∵′′,故不成立,∴x1<0<x2.分别写出切线的方程,根据两条直线重合的充要条件即可得出,再利用导数即可得出..本题主要考查了基本函数的性质、利用导数研究函数的单调性、导数的几何意义、基本不等式的性质、直线的位置关系等基础知识,考查了推理论证能力、运算能力、创新意识,考查了函数与方程、分类与整合、转化与化归等思想方法.22.如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点P,CE=BE,点E在BC上.求证:PE是⊙O的切线.【答案】解:连接BP,OP,∵AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点P,CE=BE,点E在BC上,∴∠APB=90°,∠ABC=90°,∠BAC=∠PBC,∴∠BPC=180°-∠PBC-∠C=180°-∠BAC-∠C=∠ABC=90°,∴PE=BE=CE,∵OB=OP,∴∠OPE=90°,∴PE是⊙O的切线.【解析】连接BP,OP,由题设条件导出∠BPC=180°-∠PBC-∠C=180°-∠BAC-∠C=∠ABC=90°,故PE=BE=CE,再由OB=OP,能够证明PE是⊙O的切线.本题考查了平行线的性质、等腰三角形的性质、三角形的中位线定理、切线的判定、圆周角定理等知识点的运用,能综合运用这些性质进行推理是解此题的关键,注意证切线的方法:知道过圆上一点,连接圆心和该点证垂直.23.选修4--4;坐标系与参数方程已知动点P,Q都在曲线C:为参数上,对应参数分别为β=α与β=2α(0<α<2π),M为PQ的中点.(Ⅰ)求M的轨迹的参数方程(Ⅱ)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.【答案】解:(I)根据题意有:P(2cosα,2sinα),Q(2cos2α,2sin2α),∵M为PQ的中点,故M(cosα+cos2α,sin2α+sinα),∴求M的轨迹的参数方程为:(α为参数,0<α<2π).(II)M到坐标原点的距离d==(0<α<2π).当α=π时,d=0,故M的轨迹过坐标原点.【解析】(I)根据题意写出P,Q两点的坐标:P(2cosα,2sinα),Q(2cos2α,2sin2α),再利用中点坐标公式得PQ的中点M的坐标,从而得出M的轨迹的参数方程;(II)利用两点间的距离公式得到M到坐标原点的距离d==,再验证当α=π时,d=0,故M的轨迹过坐标原点.本题主要考查把参数方程化为普通方程的方法,两点间的距离公式的应用,轨迹方程,属于基础题.24.已知a∈R,设关于x的不等式|2x-a|+|x+3|≥2x+4的解集为A.(Ⅰ)若a=1,求A;(Ⅱ)若A=R,求a的取值范围.【答案】解:(I)若a=1,则|2x-1|+|x+3|≥2x+4当x≤-3时,原不等式可化为-3x-2≥2x+4,可得x≤-3当-3<x≤时,原不等式可化为4-x≥2x+4,可得3x≤0当x>时,原不等式可化为3x+2≥2x+4,可得x≥2综上,A={x|x≤0,或x≥2};(II)当x≤-2时,|2x-a|+|x+3|≥0≥2x+4成立当x>-2时,|2x-a|+|x+3|=|2x-a|+x+3≥2x+4∴x≥a+1或x≤∴a+1≤-2或a+1≤∴a≤-2综上,a的取值范围为a≤-2.【解析】(I)利用绝对值的几何意义,化去绝对值,解不等式,可得结论;(II)当x≤-2时,|2x-a|+|x+3|≥0≥2x+4成立,当x>-2时,|2x-a|+|x+3|=|2x-a|+x+3≥2x+4,从而可求a的取值范围.本题考查绝对值不等式,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.。
2014年高考文科数学全国卷1(含详细答案)
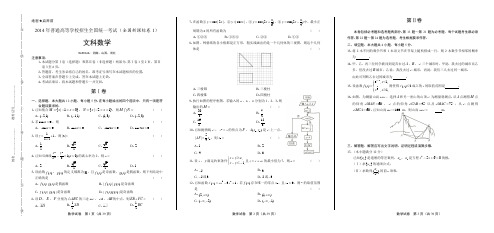
数学试卷 第1页(共39页) 数学试卷 第2页(共39页) 数学试卷 第3页(共39页)绝密★启用前2014年普通高等学校招生全国统一考试(全国新课标卷1)文科数学使用地区:河南、山西、河北注意事项:1.本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页.2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|13}M x x =-<<,{|21}N x x =-<<,则M N = ( ) A .(2,1)- B .(1,1)- C .(1,3) D .(2,3)-2.若tan 0α>,则( )A . sin 0α>B .cos 0α>C . sin20α>D .cos20α> 3.设1i 1iz =++,则|z |=( )A .12B .22 C .32D .24.已知双曲线2221(0)3x y a a -=>的离心率为2,则a = ( )A .2B .62C .52D .1 5.设函数()f x ,()g x 的定义域都为R ,且()f x 是奇函数,()g x 是偶函数,则下列结论中正确的是( )A .()f x ()g x 是偶函数B .|()|f x ()g x 是奇函数C .()f x |()|g x 是奇函数D .|()()|f x g x 是奇函数6.设D ,E ,F 分别为ABC △的三边BC ,CA ,AB 的中点,则EB FC += ( )A .ADB .12AD C .BCD .12BC 7.在函数①cos |2|y x =,②|cos |y x =,③πcos(2)6y x =+,④πtan(2)4y x =-中,最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③8.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )A .三棱锥B .三棱柱C .四棱锥D .四棱柱 9.执行如图的程序框图,若输入的a ,b ,k 分别为1,2,3.则输出的M =( )A .203B .72C .165D .15810.已知抛物线C :2y x =的焦点为F ,00(,)A x y 是C 上一点,05||4AF x =,则0x = ( )A .1B .2C .4D .811.设x ,y 满足约束条件,1,x y a x y +⎧⎨--⎩≥≤且z x ay =+的最小值为7,则a =( )A .5-B .3C .5-或3D .5或3-12.已知函数32()31f x ax x =-+,若()f x 存在唯一的零点0x ,且00x >,则a 的取值范围是( )A .(2,)+∞B .(1,)+∞C .(,2)-∞-D .(,1)-∞-第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为 .14.甲、乙、丙三位同学被问到是否去过A ,B ,C 三个城市时,甲说:我去过的城市比乙多,但没去过B 城市;乙说:我没去过C 城市;丙说:我们三人去过同一城市. 由此可判断乙去过的城市为 .15.设函数113e ,1,(),1,x x f x x x -⎧⎪=⎨⎪⎩<≥则使得()2f x ≤成立的x 的取值范围是 .16.如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角60MAN ∠=,C 点的仰角45CAB ∠=以及75MAC ∠=;从C 点测得60MCA ∠=.已知山高100BC = m ,则山高MN = m .三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知{}n a 是递增的等差数列,2a ,4a 是方程2560x x -+=的根. (Ⅰ)求{}n a 的通项公式; (Ⅱ)求数列{}2nn a 的前n 项和.姓名________________ 准考证号_____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第4页(共39页) 数学试卷 第5页(共39页) 数学试卷 第6页(共39页)18.(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结(Ⅰ)在答题卡上作出这些数据的频率分布直方图:(Ⅱ)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?19.(本小题满分12分)如图,三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1B C 的中点为O ,且AO ⊥平面11BB C C .(Ⅰ)证明:1B C AB ⊥;(Ⅱ)若1AC AB ⊥,160CBB ∠=,1BC =,求三棱柱111ABC A B C -的高.20.(本小题满分12分)已知点(2,2)P ,圆C :2280x y y +-=,过点P 的动直线l 与圆C 交于A ,B 两点,线段AB 的中点为M ,O 为坐标原点. (Ⅰ)求M 的轨迹方程;(Ⅱ)当||||OP OM =时,求l 的方程及POM △的面积.21.(本小题满分12分)设函数21()ln (1)2a f x a x x bx a -=+-≠,曲线()y f x =在点(1,(1))f 处的切线斜率为0.(Ⅰ)求b ;(Ⅱ)若存在01x ≥,使得0()1af x a <-,求a 的取值范围.请考生在第22、23、24三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.(本小题满分10分)选修4—1:几何证明选讲如图,四边形ABCD 是O 的内接四边形,AB 的延长线与DC 的延长线交于点E ,且CB CE =.(Ⅰ)证明:D E ∠=∠;(Ⅱ)设AD 不是O 的直径,AD 的中点为M ,且MB MC =,证明:ADE △为等边三角形.23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C :22149x y +=,直线l :2,22,x t y t =+⎧⎨=-⎩(t 为参数). (Ⅰ)写出曲线C 的参数方程,直线l 的普通方程;(Ⅱ)过曲线C上任意一点P 作与l 夹角为30的直线,交l 于点A ,求||PA 的最大值与最小值.24.(本小题满分10分)选修4—5:不等式选讲若0a >,0b >,且11a b+=(Ⅰ)求33a b +的最小值;(Ⅱ)是否存在a ,b ,使得236a b +=?并说明理由.3 / 132014年普通高等学校招生全国统一考试(全国新课标卷1)文科数学答案解析第Ⅰ卷一、选择题 1.【答案】B【解析】根据集合的运算法则可得:{|11}MN x x =-<<,即选B .【提示】集合的运算用数轴或者Venn 图可直接计算。
2014年全国高考数学卷文科卷1试题及答案解析-精选.pdf

( II )估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间 的中点值作代表) ; ( III )根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指 标值不低于 95 的产品至少要占全部产品的 80%”的规定?
20.已知点 P ( 2,2) ,圆 C : x2 y2 8y 0 ,过点 P 的动直线 l 与圆 C 交于 A, B 两点,线段 AB 的中点为 M , O 为坐标原点 .
23.已知曲线
x2 C:
y2
x2t
1,直线 l :
( t 为参数)
49
y 2 2t
写出曲线 C 的参数方程,直线 l 的普通方程;
过曲线 C 上任意一点 P 作与 l 夹角为 30°的直线,交 l 于点 A ,求 PA 的最大
值与最小值 .
22.如图,四边形 ABCD 是 交于点 E ,且 CB CE .
(1) 求 M 的轨迹方程; (2) 当 OP OM 时,求 l 的方程及 POM 的面积
试卷第 3 页,总 4 页
21.设函数 f x a ln x
处的切线斜率为 0
1a2 x
2
bx a
1 ,曲线 y
f x 在点 1,f 1
求 b; 若存在 x0 1, 使得 f x0
a
,求 a 的取值范围。
a1
试卷第 4 页,总 4 页
1. B 【解析】
参考答案
试题分析:根据集合的运算法则可得: M N x | 1 x 1 ,即选 B.
[115 ,且12A5O)
8
平面 BB1C1C .
( I )在答题卡上作出这些数据的频率分布直方图:
A1B1C1 中,侧面 BB1C1C 为菱形, B1C 的中点为 O ,
2014甘肃高考文科数学真题及答案

2014甘肃高考文科数学真题及答案注意事项1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号,写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A=﹛-2,0,2﹜,B=﹛x ∣2x -x -20=﹜,则A B ⋂=( ) A . ∅ B.{}2 C.{}0 D.{}2- 2.131ii+=-( ) A. 12i + B. 12i -+ C. 1-2i D. 1-2i -3. 函数()f x 在0x=x 处导数存在,若()0p f 0x '=:,0:q x x =是()f x 的极值点,则( ) A.p 是q 的充分必要条件B.p 是q 的充分条件,但不是q 的必要条件C.p 是q 的必要条件,但不是 q 的充分条件D.p 既不是q 的充分条件,也不是q 的必要条件 4. 设向量a ,b 满足|a+b|=10,|a-b|=6,则a b =( )A. 1B. 2C. 3D. 55. 等差数列{}n a 的公差为2,若2a ,4a ,8a 成等比数列,则{}n a 的前n 项和n s =( ) A. ()1n n + B. ()1n n - C.()12n n + D.()12n n -6. 如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.137. 正三棱柱111ABC A B C-的底面边长为2,侧棱长为3,D为BC终点,则三棱锥111A AB C-的体积为( )A.3B.32C.1D.328. 执行右面的程序框图,如果如果输入的x,t均为2,则输出的S=( )A.4B.5C.6D.79. 设x,y满足的约束条件1010330x yx yx y+-≥⎧⎪--≤⎨⎪-+≥⎩,则2z x y=+的最大值为( )A. 8B. 7C. 2D. 110. 设F 为抛物线2:y =3x C 的焦点,过F 且倾斜角为°30的直线交于C 于,A B 两点,则AB =11.若函数()ln f x kx x =-在区间(1,+∞)单调递增,则k 的取值范围是( ) A.(],2-∞- B.(],1-∞- C.[)2,+∞ D. [)1,+∞12.设点0(x ,1)M ,若在圆22:x y =1O +上存在点N ,使得°45OMN ∠=,则0x 的取值范围是A. []1,1-B.1122⎡⎤-⎢⎥⎣⎦, C.⎡⎣ D. 22⎡-⎢⎣⎦,第Ⅱ卷本卷包括必考题和选考题两部分。
甘肃省兰州一中2014年高考冲刺模拟考试(一)数学(文)试题

甘肃省兰州一中2014年高考冲刺模拟考试(一)数学(文)试题第Ⅰ 卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}2|3100M x R x x =∈--<,{|||2}N x Z x =∈<,则M N 为 ( )A .)2,2(-B .)2,1(C .{-1,0,1}D .}2,1,0,1,2{--2.若复数3()1x iz x R i+=∈-是实数,则x 的值为( ) A .3-B .3C .0D .33.角α的终边经过点A ()a ,且点A 在抛物线214y x =-的准线上,则sin α=( ) A .12- B .12C. D4.已知变量x ,y 满足125,31x y x y z x y x -≤⎧⎪+≤=+⎨⎪≥⎩则的最大值为 ( )A .5B .6C .7D .85.如图是一个几何体的三视图,则此三视图所描述几何体的表面积为 ( ) A .π)3412(+ B .20πC .π)3420(+D .28π 6.给出如下四个命题:①若“p ∨q ”为真命题,则p 、q 均为真命题; ②“若,221a b a b >>-则”的否命题为“若a b ≤,则221a b -≤”;③“2,1x x x ∀∈+R ≥”的否定是“2000,1x x x ∃∈+R ≤”;④“0x >”是“12x x+≥”的充要条件.其中不正确的命题是( )A .①②B .②③C .①③D .③④7.双曲线12222=-by a x 的离心率为3,则它的渐近线方程是( )A .x y 2±=B .x y 22±=C .x y 2±=D .x y21±=8. 函数()()sin 0,2f x A x A πωϕϕ⎛⎫=+>< ⎪⎝⎭其中的图象如图所示,为了得到()sin 3g x x =的图象,只需将()f x 的图象( )A .向右平移4π个单位 B .向左平移4π个单位 C .向右平移12π个单位D .向左平移12π个单位9.数列{}n a 的前n 项和21n s n n =++;(1)n n n b a =-(n ∈N*);则数列{}n b 的前50项和为 ( )A .49B .50C .99D .10010.在区间[],ππ-内随机取两个数分别为,a b ,则使得函数()2222f x x ax b π=+-+有零点的概率为( )A .18π-B .14π-C .12π-D .314π-11. 设函数()f x 的定义域为R ,(),0111,103xx x f x x R x ≤≤⎧⎪=∈⎨⎛⎫--<<⎪⎪⎝⎭⎩,且对任意的都有()()11f x f x +=-,若在区间[]()()1,5g x f x mx m -=--上函数,恰有6个不同零点,则实数m 的取值范围是( ) A .11,46⎛⎤⎥⎝⎦B .11,34⎛⎤ ⎥⎝⎦C .10,5⎛⎤ ⎥⎝⎦D .10,6⎛⎤ ⎥⎝⎦12.已知函数()f x 是定义在R 上的可导函数,其导函数记为()f x ',若对于任意实数x ,有()()f x f x '>,且()1y f x =-为奇函数,则不等式()x f x e <的解集为( ) A .(,0)-∞B .(0,)+∞C .4(,)e -∞D .4(,)e +∞第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分. 13.已知某一段公路限速60公里/小时,现抽取200辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这200辆汽车中在该路段没有超速的有 辆.14. 执行如图所示的程序框图,若输入10,n S ==则输出的___15. 若,αβ为两个不同的平面,m 、n 为不同直线,下列推理:①若,,,m n m n αβαβ⊥⊥⊥⊥则直线; ②若直线//m n m α⊥平面,直线直线, n α⊥则直线平面;③若直线m//n ,,m n αβ⊥⊂, αβ⊥则平面平面; ④若平面//m αββ⊥平面,直线平面,,n m α⊂⊥则直线直线n ;其中正确说法的序号是________.16. 设双曲线()222210,0x y a b a b-=>>的右焦点为F ,过点F 作与x 轴垂直的直线l 交两渐近线于A 、B 两点,且与双曲线在第一象限的交点为P ,设O 为坐标原点,若()3,,16OP OA OB R λμλμλμ=+∈=,则该双曲线的离心率为________. 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分12分)设函数22()cos()2cos ,32xf x x x π=++∈R .(1)求()f x 的值域;(2)记△ABC 的内角A ,B ,C 的对边长分别为a ,b ,c,若()1,1,f B b c ===,求a 的值. 18.(本小题满分12分)如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E ,F 分别是AB ,PB 的中点.(I )求证://EF 平面PAD ; (II )求证:EF CD ⊥;(III )设PD=AD=a , 求三棱锥B-EFC 的体积.19.(本小题满分12分)为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:(Ⅰ)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;(Ⅱ)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过5.0的概率. 20.(本小题满分12分)已知函数()f x =x x ax ln 232+-,a 为常数. (I )当a =1时,求()f x 的单调区间;(II )若函数()f x 在区间[1,2]上为单调函数,求a 的取值范围.21. (本小题满分12分) 已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,以原点O 为圆心,椭圆的短半轴长为半径的圆与直线0x y -+=相切..(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线:L y kx m =+与椭圆C 相交于A 、B 两点,且22OA OBb k k a⋅=-,判断△AOB 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.请考生在第22、23两题中任选一题作答。
2014年甘肃省武威市凉州区高考数学一模试卷(文科)

2014年甘肃省武威市凉州区高考数学一模试卷(文科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共12小题,共60.0分)1.已知全集U=R,集合M={x|2x>1},集合N={x|log2x>1},则下列结论中成立的是()A.M∩N=MB.M∪N=NC.M∩(∁U N)=∅D.(∁U M)∩N=∅【答案】D【解析】解:由M中的不等式变形得:2x>1=20,得到x>0,即M=(0,+∞),由N中的不等式变形得:log2x>1=log22,得到x>2,即N=(2,+∞),∴M∩N=(2,+∞)=N,M∪N=(0,+∞)=M,∁U N=(-∞,2],∁U M=(-∞,0],则M∩(∁U N)=(0,2],(∁U M)∩N=∅.故选D求出M与N中不等式的解集,确定出M与N,求出M与N的交集,并集,M与N的补集找出M与N补集的交集,M补集与N的交集,即可做出判断.此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.已知i为虚数单位,则z=在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】解:所以z在复平面内对应的点为(1,-1)位于第四象限故选D将复数的分子、分母同乘以i,利用多项式的乘法分子展开,将i2用-1代替;利用复数对应点的坐标实部为横坐标,虚部为纵坐标,判断出所在的象限.本题考查利用复数的除法法则:分子,分母同乘以分母的共轭复数、考查复数对应点的坐标是以实部为横坐标,虚部为纵坐标.3.已知命题p:∃x∈R,x-2>lgx,命题q:∀x∈R,x2>0,则()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∧(¬q)是真命题D.命题p∨(¬q)是假命题【答案】C【解析】解:由于x=10时,x-2=8,lgx=lg10=1,故命题p为真命题,令x=0,则x2=0,故命题q为假命题,依据复合命题真假性的判断法则,得到命题p∨q是真命题,命题p∧q是假命题,¬q是真命题,进而得到命题p∧(¬q)是真命题,命题p∨(¬q)是真命题.故答案为C.先判断出命题p与q的真假,再由复合命题真假性的判断法则,即可得到正确结论.本题考查复合命题的真假,属于基础题.4.已知,则sin2α-sinαcosα的值是()A. B. C.-2 D.2【答案】A【解析】解:∵,∴,∴tanα=2.∴sin2α-sinαcosα====,故选A.由由已知条件求出tanα值,化简sin2α-sinαcosα=,把tanα值代入运算.本题考查同角三角函数的基本关系的应用,1的代换,把所求的sin2α-sinαcosα变形为是解题的难点.5.某几何体的三视图如图所示,则它的体积是()A. B. C.8-2π D.【答案】A【解析】解:三视图复原的几何体是棱长为:2的正方体,除去一个倒放的圆锥,圆锥的高为:2,底面半径为:1;所以几何体的体积是:8-=故选A.三视图复原的几何体是正方体,除去一个倒放的圆锥,根据三视图的数据,求出几何体的体积.本题是基础题,考查三视图复原几何体的判定,几何体的体积的求法,考查空间想象能力,计算能力,常考题型.6.执行如图的程序框图,输出的S等于()A. B. C. D.【答案】B【解析】解:根据题意,本程序框图为求和运算第1次循环:S=0+n=2第2次循环:S=+n=3…第4次循环:S═++…+n=5此时,n=5输出S=1-=故选B.首先根据程序框图,理解其意义,然后按照程序顺序进行执行循环,当满足跳出循环的条件时输出结果.分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件S═++…+的值.本题考查程序框图,通过对程序框图的认识和理解按照程序框图的顺序进行执行.通过按照循环体的执行,考查运算能力.属于基础题7.函数y=log a(x+3)-1(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则+的最小值为()A.6B.8C.10D.12【答案】B【解析】解:∵x=-2时,y=log a1-1=-1,∴函数y=log a(x+3)-1(a>0,a≠1)的图象恒过定点(-2,-1)即A(-2,-1),∵点A在直线mx+ny+1=0上,∴-2m-n+1=0,即2m+n=1,∵mn>0,∴m>0,n>0,+=+=2+++2≥4+2•=8,当且仅当m=,n=时取等号.故选B.根据对数函数的性质先求出A的坐标,代入直线方程可得m、n的关系,再利用1的代换结合均值不等式求解即可.本题考查了对数函数的性质和均值不等式等知识点,运用了整体代换思想,是高考考查的重点内容.8.已知等比数列{a n}的公比q=2,且2a4,a6,48成等差数列,则{a n}的前8项和为()A.127B.255C.511D.1023【答案】B【解析】解:∵2a4、a6、48成等差数列,∴2a6=2a4+48,∴2a1q5=2a1q3+48,又等比数列{a n}的公比q=2,∴解得,a1=1,∴{a n}的前8项和为故选B.根据且a1,a3,a2成等差数列,列出方程2a6=2a4+48,求出首项a1,再根据等比数列的求和公式,即可得答案.本题主要考查等差数列的定义和性质、等比数列的定义和性质,等比数列的通项公式,以及等比数列的前n项和公式.属于基础题.9.已知f(x)=x2+sin,f′(x)为f(x)的导函数,则f′(x)的图象是()A. B. C. D.【答案】A【解析】解:由f(x)=x2+sin=x2+cosx,∴f′(x)=x-sinx,它是一个奇函数,其图象关于原点对称,故排除B,D.又f″(x)=-cosx,当-<x<时,cosx>,∴f″(x)<0,故函数y=f′(x)在区间(-,)上单调递减,故排除C.故选:A.先化简f(x)=x2+sin=x2+cosx,再求其导数,得出导函数是奇函数,排除B,D.再根据导函数的导函数小于0的x的范围,确定导函数在(-,)上单调递减,从而排除C,即可得出正确答案.本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.10.设函数f(x)=cosωx(ω>0),将y=f(x)的图象向右平移个单位长度后,所得的图象与原图象重合,则ω的最小值等于()A. B.3 C.6 D.9【答案】C【解析】解:f(x)的周期T=,函数图象平移个单位长度后,所得的图象与原图象重合,说明函数平移整数个周期,所以,k∈Z.令k=1,可得ω=6.故选C.函数图象平移个单位长度后,所得的图象与原图象重合,说明函数平移整数个周期,容易得到结果.本题是基础题,考查三角函数的图象的平移,三角函数的周期定义的理解,考查技术能力,常考题型.11.点P在双曲线:(a>0,b>0)上,F1,F2是这条双曲线的两个焦点,∠F1PF2=90°,且△F1PF2的三条边长成等差数列,则此双曲线的离心率是()A.2 B.3 C.4 D.5【答案】D【解析】解:因为△F1PF2的三条边长成等差数列,不妨设|PF2|,|PF1|,|F1F2|成等差数列,分别设为m-d,m,m+d,则由双曲线定义和勾股定理可知:m-(m-d)=2a,m+d=2c,(m-d)2+m2=(m+d)2,解得m=4d=8a,c=,故离心率e===5,故选D.通过|PF2|,|PF1|,|F1F2|成等差数列,分别设为m-d,m,m+d,则由双曲线定义和勾股定理求出m=4d=8a,c=,由此求得离心率的值.本题主要考查等差数列的定义和性质,以及双曲线的简单性质的应用,属于中档题.12.定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=lnx,φ(x)=x3(x≠0)的“新驻点”分别为a,b,c,则a,b,c的大小关系为()A.a>b>cB.c>b>aC.a>c>bD.b>a>c【答案】B【解析】解:由题意方程f(x)=f'(x)的实数根x0叫做函数f(x)的“新驻点”,对于函数g(x)=2x,由于g′(x)=2,故得x=1,即a=1对于函数h(x)=lnx,由于h′(x)=,故得lnx=,令r(x)=lnx-,可知r(1)<0,r(2)>0,故1<b<2对于函数φ(x)=x3,由于φ′(x)=3x2,故得x3=3x2,∵x≠0,∴x=3,故c=3综上c>b>a故选B根据所给的定义,对三个函数所对应的方程进行研究,分别计算求出a,b,c的值或存在的大致范围,再比较出它们的大小,即可选出正确选项本题是一个新定义的题,考查了推理判断的能力,理解定义,分别建立方程解出a,b,c的值或存在范围是解题的关键.二、填空题(本大题共4小题,共20.0分)13.若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是______ .【答案】(x-2)2+(y-1)2=1【解析】解:∵圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,∴半径是1,圆心的纵坐标也是1,设圆心坐标(a,1),则1=,又a>0,∴a=2,∴该圆的标准方程是(x-2)2+(y-1)2=1;故答案为(x-2)2+(y-1)2=1.依据条件确定圆心纵坐标为1,又已知半径是1,通过与直线4x-3y=0相切,圆心到直线的距离等于半径求出圆心横坐标,写出圆的标准方程.本题考查利用圆的切线方程求参数,圆的标准方程求法.14.若向量,满足||=1,||=,且⊥(+),则与的夹角为______ .【答案】【解析】解:∵向量,满足||=1,||=,且⊥(+),设与的夹角为θ,则有=0,即,故有1=-1××cosθ,∴cosθ=-.再由0≤θ≤π,可得θ=,故答案为.设与的夹角为θ,则有=0,化简可得1=-1××cosθ,求出cosθ的值,即可求得θ的值.本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题.15.若函数y=log3x的图象上存在点(x,y),满足约束条件,则实数m的最大值为______ .【答案】1【解析】解:作对数函数y=log3x的图象与约束条件对应的可行域如图,由图可知,函数y=log3x的图象与直线x+y-4=0相交于A(3,1),∴只有当m≤1时,函数y=log3x的图象经过可行域三角形ABC边界及其内部的点,∴实数m的最大值为1.故答案为:1作出函数y=log3x的图象与约束条件对应的可行域,求出函数y=log3x的图象与直线x+y-4=0交点A,数形结合可知当m小于等于A点纵坐标时函数y=log3x的图象上存在点(x,y),满足约束条件,则答案可求.本题考查了简单的线性规划,考查了数形结合的解题思想方法,利用数形结合是解决本题的关键.16.在△ABC中,已知a,b,c分别为角A,B,C所对的边,S为△ABC的面积.若向量=(4,a2+b2-c2),=(,)满足∥,则∠C= ______ .【答案】【解析】解:由∥,得4S=(a2+b2-c2),则S=(a2+b2-c2).由余弦定理得cos C=,所以S=又由三角形的面积公式得S=,所以,所以tan C=.又C∈(0,π),所以C=.故答案为:.通过向量的平行的坐标运算,求出S的表达式,利用余弦定理以及三角形面积,求出C 的正切值,得到C的值即可.本题考查向量的平行,三角形的面积公式以及余弦定理的应用,考查计算能力.三、解答题(本大题共8小题,共90.0分)17.等差数列{a n}是递增数列,前n项和为S n,且a1,a3,a9成等比数列,S5=a52.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若数列{b n}满足b n=,求数列{b n}的前n项的和.【答案】解:(Ⅰ)设{a n}的公差为d,(d>0)∵a1,a3,a9成等比数列,∴(a1+2d)2=a1(a1+8d),整理,得d2=a1d,∵d≠0,∴a1=d,①∵,∴5a1+=(a1+4d)2,②由①②,得:,d=,∴=.(Ⅱ)b n====,∴b1+b2+…+b n===.【解析】(Ⅰ)由已知条件利用等差数列的通项公式、前n项和公式和等比数列性质,求出首项和公差,由此能求出数列{a n}的通项公式.(Ⅱ)由已知条件推导出b n=,由此利用裂项求和法能求出数列{b n}的前n项的和.本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.18.为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.(Ⅰ)分别求出a,b,x,y的值;(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.【答案】解:(Ⅰ)由频率表中第4组数据可知,第4组总人数为,再结合频率分布直方图可知n=,∴a=100×0.01×10×0.5=5,b=100×0.03×10×0.9=27,,;(Ⅱ)因为第2,3,4组回答正确的人数共有54人,∴利用分层抽样在54人中抽取6人,每组分别抽取的人数为:第2组:人;第3组:人;第4组:人(Ⅲ)设第2组2人为:A1,A2;第3组3人为:B1,B2,B3;第4组1人为:C1.则从6人中随机抽取2人的所有可能的结果为:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1)共15个基本事件,其中恰好没有第3组人共3个基本事件,∴所抽取的人中恰好没有第3组人的概率是:.【解析】(I)由频率表中第4组数据可知,第4组的频数为25,再结合频率分布直方图求得n,a,b,x,y的值;(II)因为第2,3,4组回答正确的人数共有54人,抽取比例为,根据抽取比例计算第2,3,4组每组应抽取的人数;(III)列出从6人中随机抽取2人的所有可能的结果,共15基本事件,其中恰好没有第3组人共3个基本事件,利用古典概型概率公式计算.本题考查了频率分布表与频率分布直方图,考查了古典概型的概率计算,解题的关键是读懂频率分布直方图.19.如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=a.(1)求证:AD⊥B1D;(2)求证:A1C∥平面AB1D;(3)求点A1到平面AB1D的距离.【答案】解:(1)证明:∵ABC-A1B1C1是正三棱锥,∴BB1⊥平面ABC,∴BB1⊥AD,在正△ABC中,∵D是BC的中点,∴AD⊥BD.BB1∩BD=B,∴AD⊥平面BB1D,∴AD⊥B1D.(4分)(2)连接DE.AA1=AB,四边形A1ABB1是正方向,∴E是A1B的中点,又D是BC的中点,∴DE∥A1C,∵DE⊂平面AB1D,A1C⊄平面AB1D,∴A1C∥平面AB1D.(8分)(3),所以,解得.(12分)【解析】(1)根据已知条件,证明出AD⊥平面BB1D,再根据线面垂直的性质,即可得到AD⊥B1D;(2)证明DE∥A1C后,根据线面平行的判定定理,即可得到答案;(3)根据等体积法,即,求出棱锥体积,及底面面积,即可求出点A1到平面AB1D的距离本题考查空间垂直关系、平行关系的证明,根据三棱锥的体积求点到平面的距离,这是文科立体几何试题的一般考查方式.20.已知椭圆C的中心在坐标原点,短轴长为4,且有一个焦点与抛物线的焦点重合.(1)求椭圆C的方程.(2)已知经过定点M(2,0)且斜率不为0的直线l交椭圆C于A、B两点,试问在x 轴上是否另存在一个定点P使得PM始终平分∠APB?若存在求出P点坐标,若不存在请说明理由.【答案】解:(1)设椭圆的标准方程为(a>b>0),焦距为2c.由抛物线方程得焦点,,∴c=.又短轴长为4,∴2b=4,解得b=2.∴a2=b2+c2=9.∴椭圆C的方程为.(2)假设在x轴上存在一个定点P(t,0)(t≠2)使得PM始终平分∠APB.设直线l的方程为my=x-2,A(x1,y1),B(x2,y2).联立,化为(9+4m2)y2+16my-20=0,则,.(*)∵PM平分∠APB,∴,∴,化为,把x1=my1+2,x2=my2+2代入上式得(2-t)(y1-y2)[2my1y2+(2-t)(y1+y2)]=0,∵2-t≠0,y1-y2≠0,∴2my1y2+(2-t)(y1+y2)=0.把(*)代入上式得,化为m(9-2t)=0,由于对于任意实数上式都成立,∴t=.因此存在点P,满足PM始终平分∠APB.【解析】(1)设椭圆的标准方程为(a>b>0),焦距为2c.由抛物线方程得焦点,,可得c.又短轴长为4,可得2b=4,解得b.再利用a2=b2+c2即可得到a.(2)假设在x轴上存在一个定点P(t,0)(t≠2)使得PM始终平分∠APB.设直线l 的方程为my=x-2,A(x1,y1),B(x2,y2).与椭圆的方程联立化为(9+5m2)y2+20my-25=0,得到根与系数的关系,由于PM平分∠APB,利用角平分线的性质可得,经过化简求出t的值即可.本题考查了椭圆与抛物线的标准方程及其性质、角平分线的性质、两点间的距离公式、恒成立问题等基础知识与基本技能方法,属于难题.21.已知函数f(x)=(ax-2)e x在x=1处取得极值.(Ⅰ)求a的值;(Ⅱ)求函数f(x)在[m,m+1]上的最小值;(Ⅲ)求证:对任意x1,x2∈[0,2],都有|f(x1)-f(x2)|≤e.【答案】解:(Ⅰ)f′(x)=ae x+(ax-2)e x=(ax+a-2)e x,由已知得f′(1)=0,即(2a-2)e=0,解得:a=1,验证知,当a=1时,在x=1处函数f(x)=(x-2)e x取得极小值,所以a=1;(Ⅱ)f(x)=(x-2)e x,f′(x)=e x+(x-2)e x=(x-1)e x.所以函数f(x)在(-∞,1)上递减,在(1,+∞)上递增.当m≥1时,f(x)在[m,m+1]上单调递增,f min(x)=f(m)=(m-2)e m.当0<m<1时,m<1<m+1,f(x)在[m,1]上单调递减,在[1,m+1]上单调递增,f min(x)=f(1)=-e.当m≤0时,m+1≤1,f(x)在[m,m+1]单调递减,.综上,f(x)在[m,m+1]上的最小值,,<<,(Ⅲ)由(Ⅰ)知f(x)=(x-2)e x,f′(x)=e x+(x-2)e x=(x-1)e x.令f′(x)=0得x=1,因为f(0)=-2,f(1)=-e,f(2)=0,所以f max(x)=0,f min(x)=-e,所以,对任意x1,x2∈[0,2],都有|f(x1)-f(x2)|≤f max(x)-f min(x)=e,【解析】(Ⅰ)求导数f′(x),由题意得f′(1)=0,可得a值,代入检验即可;(Ⅱ)当a=1时可求出f(x)的单调区间及极值点,按极值点在区间[m,m+1]的左侧、内部、右侧三种情况进行即可求得其最小值;(Ⅲ)对任意x1,x2∈[0,2],都有|f(x1)-f(x2)|≤e,等价于|f(x1)-f(x2)|≤f max (x)-f min(x)≤e.问题转化为求函数f(x)的最大值、最小值问题,用导数易求;本题考查利用导数研究函数的单调性、最值,考查分类讨论思想、转化思想,关于恒成立问题往往转化为函数最值问题解决.22.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.(1)求证:直线AB是⊙O的切线;(2)若tan∠CED=,⊙O的半径为3,求OA的长.【答案】解:(1)如图,连接OC,∵OA=OB,CA=CB,∴OC⊥AB.∴AB是⊙O的切线;(2)∵BC是圆O切线,且BE是圆O割线,∴BC2=BD•BE,∵tan∠CED=,∴.∵△BCD∽△BEC,∴,设BD=x,BC=2x.又BC2=BD•BE,∴(2x)2=x•(x+6),解得x1=0,x2=2,∵BD=x>0,∴BD=2,∴OA=OB=BD+OD=3+2=5.(10分).【解析】(1)要想证AB是⊙O的切线,只要连接OC,求证∠ACO=90°即可;(2)先由三角形判定定理可知,△BCD∽△BEC,得BD与BC的比例关系,最后由切割线定理列出方程求出OA的长.本题考查的是切线的判定、相似三角形的判定和性质,以及切割线定理的综合运用,属于基础题.23.在平面直角坐标系xoy中,已知曲线C的参数方程为(α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos (θ-)=2(Ⅰ)求直线l的直角坐标方程;(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.【答案】解:(Ⅰ)∵直线l的极坐标方程为ρcos(θ-)=2,即ρcosθ+ρsinθ=4,化为直角坐标方程为x+y-4=0.(Ⅱ)设点P(2cosα,sinα),点P到直线l距离d==,其中,sinβ=,cosβ=.故当sin(α+β)=-1时,d取得最大值为=+2.【解析】(Ⅰ)根据x=ρcosθ,y=ρsinθ,把直线l的极坐标方程化为直角坐标方程.(Ⅱ)设点P(2cosα,sinα),求得点P到直线l距离d=,可得d的最大值.本题主要考查把极坐标化为直角坐标方程的方法,点到直线的距离公式、两角和差的正弦公式、正弦函数的值域,属于基础题.24.(选修4-5:不等式选讲)已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.(Ⅰ)当a=-2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>-1,且当,时,f(x)≤g(x),求a的取值范围.【答案】解:(Ⅰ)当a=-2时,求不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.设y=|2x-1|+|2x-2|-x-3,则y=,<,,>,它的图象如图所示:结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).(Ⅱ)设a>-1,且当,时,f(x)=1+a,不等式化为1+a≤x+3,故x≥a-2对,都成立.故-≥a-2,解得a≤,故a的取值范围为(-1,].【解析】(Ⅰ)当a=-2时,求不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.设y=|2x-1|+|2x-2|-x-3,画出函数y的图象,数形结合可得结论.(Ⅱ)不等式化即1+a≤x+3,故x≥a-2对,都成立.故-≥a-2,由此解得a的取值范围.本题主要考查绝对值不等式的解法,函数的恒成立问题,函数的单调性的应用,体现了数形结合以及转化的数学思想,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年甘肃省高考数学一模试卷(文科)一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项符合题目要求的.1. 已知集合A ={x ∈Z||x|<5},B ={x|x −2≥0},则A ∩B 等于( )A (2, 5)B [2, 5)C {2, 3, 4}D {3, 4, 5}2. 复数1−i 1+i (i 是虚数单位)化简的结果是( )A 1B −1C iD −i3. 如图是一个几何体的三视图,则该几何体的体积为( )A 3πB 203πC 73πD π 4. 设a =30.5,b =log 53,c =cos3,则( )A c <b <aB c <a <bC a <b <cD b <c <a5. 阅读如图程序框图,输出的结果i 的值为( )A 5B 6C 7D 96. 已知数列{a n }为等差数列,且a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于( )A 40B 42C 43D 457. 已知两条直线m ,n 和平面α,且m 在α内,n 在α外,则“n // α”是“m // n”的( )A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件8. 已知α是第二象限角,且sin(π+α)=−35,则tan2α的值为( ) A 45 B −237 C −247 D −839. 已知点P(x, y)满足线性约束条件{y ≤2x +y ≥1x −y ≤1,点M(3, 1),O 为坐标原点,则OM →⋅OP →的最大值为( )A 12B 11C 3D −110. 已知抛物线方程为y 2=4x ,直线l 的方程为x −y +4=0,在抛物线上有一动点P 到y 轴的距离为d 1,P 到直线l 的距离为d 2,则d 1+d 2的最小值为( )A 5√22+2B 5√22+1C 5√22−2D 5√22−111. 四棱锥P −ABCD 的五个顶点都在一个球面上,且底面ABCD 是边长为1的正方形,PA ⊥ABCD ,PA =√2,则该球的表面积为( )A πB 2πC 3πD 4π12. 定义在R 上的函数f(x)满足f(−x)=f(x),f(x +1)=2f(x)(f(x)≠0),且在区间(2013, 2014)上单调递增,已知α,β是锐角三角形的两个内角,则f(sinα)、f(cosβ)的大小关系是( )A f(sinα)<f(cosβ)B f(sinα)>f(cosβ)C f(sinα)=f(cosβ)D 以上情况均有可能二、填空題:本大题共4小题,每小题5分.13. 在边长为3的正方形ABCD 内任取一点P ,则P 到正方形四边的距离均不小于l 的概率为________.14. 已知函数f(x)={x +1,x <0e x ,x ≥0,则f(f(0)−3)=________. 15. 已知双曲线x 2a 2−y 2b 2=1(a >0,b >0)的一条渐近线经过点(1, 2),则该双曲线的离心率的值为________.16. 已知数列{a n }满足a 1=100,a n+1−a n =2n ,则an n 的最小值________.三、解答题:本大题共5小题,共70分.解答应写出说明文字,证明过程或演算步骤.17. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .cosC =45,c =2bcosA . (1)求证:A =B ;(2)若△ABC 的面积S =152,求c 的值.18. 如图,在四棱锥P −ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC =2,E 是PC 的中点.(1)证明:PA // 平面EDB ;(2)求三梭锥A 一BDP 的体积.19. 2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;(2)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.20. 已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的离心率为√22,其中左焦点F(−2, 0).(1)求椭圆C 的方程;(2)若直线y =x +m 与椭圆C 交于两个不同的两点A ,B ,且线段的中点M 总在圆x 2+y 2=1的内部,求实数m 的取值范围.21. 已知函数f(x)=1x +alnx(a ≠0, a ∈R). (I )若a =1,求函数f(x)在x =1处的切线方程;(II )若在区间(0, e]上至少存在一点x 0,使得f(x 0)<0成立,求实数a 的取值范围.请从22、23、24三个小题中任选一题作答,并用2B 铅笔在答题卡上将所选题目对应的题号方框涂黑.(本小题满分10分)选修4-1:几何证明选讲22. 如图,⊙O 的半径OB 垂直于直径AC ,M 为AO 上一点,BM 的延长线交⊙O 于N ,过N 点的切线交CA 的延长线于P .(Ⅰ)求证:PM 2=PA ⋅PC ;(Ⅱ)若⊙O 的半径为2√3,OA =√3OM ,求MN 的长.选修4-4:坐标系与参数方程23. 已知直线C 的极坐标方程是ρ=4cosθ.以极点为平面直角坐标系的原点,极值为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是:{x =m +t y =t ,(t 是参数).(1)将曲线C 的极坐标方程化为直角坐标方程,直线l 的参数方程化为普通方程;(2)若直线l 与曲线C 相交于A ,B 两点,且|AB|=√14,试求实数m 的值.选修4-5:不等式选讲24. 已知函数f(x)=lg(|x+1|+|x−2|+a).(1)当a=−5时,求函数f(x)的定义域;(2)若函数f(x)的定义域为R,求实数a的取值范围.2014年甘肃省高考数学一模试卷(文科)答案1. C2. D3. C4. A5. C6. B7. B8. C9. B10. D11. D12. A13. 1914. −115. √516. 1917. 解:(1)∵ c=2bcosA,∴ 根据正弦定理得:sinC=2sinB⋅cosA,又sinC=sin[π−(A+B)]=sin(A+B),∴ sinC=sin(A+B)=sinAcosB+cosAsinB=2sinB⋅cosA,整理得:sinAcosB−cosAsinB=sin(A−B)=0,在△ABC中,∵ 0<A<π,0<B<π,∴ −π<A−B<π,则A=B;(2)由(1)A=B,可得a=b,∵ cosC=45,且C为三角形的内角,∴ sinC=√1−cos2C=35,又△ABC的面积S=152,∴ S=12absinC=310ab=152,即ab=a2=25,∴ a=b=5,又cosC=45,由余弦定理得:c2=a2+b2−2abcosC=10,则c=√10.18. 解:(1)证明:连接AC交BD于O,连接OE,∵ ABCD是正方形,∴ O为AC的中点,又E是PC的中点,∴ OE // PA,PA⊄平面BDE,OE⊂平面BDE,∴ PA // 平面BDE;(2)∵ 侧棱PD⊥底面ABCD,∴ PD为三棱锥P−ABD的高,PD=DC=2,∴ V A−BDP=V P−ABD=13×S△ABD×PD=13×12×2×2×2=43.19. 解:(1)设PM2.5的24小时平均浓度在(50, 75]内的三天记为A1,A2,A3,PM2.5的24小时平均浓度在(75, 100)内的两天记为B1,B2.所以5天任取2天的情况有:A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2,A3B1,A3B2共10种.…其中符合条件的有:A1B1,A1B2,A2B1,A2B2,A3B1,A3B2共6种.…所以所求的概率P=610=35.…(2)去年该居民区PM2.5年平均浓度为:12.5×0.25+37.5×0.5+62.5×0.15+87.5×0.1=40(微克/立方米).…因为40>35,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.…20. 解:(1)∵ 椭圆的离心率为√22,其中左焦点F(−2, 0).∴ {ca=√22 c=2a2=b2+c2,∴ a=2√2,b=2,∴ 椭圆C的方程为x28+y24=1;(2)设点A、B的坐标分别为(x1, y1),(x2, y2),线段AB的中点为M(x0, y0),由直线代入椭圆方程消y得,3x2+4mx+2m2−8=0,△=96−8m2>0,∴ −2√3<m<2√3.∴ x0=x1+x22=−2m3,y0=x0+m=m3.∵ 点M(x0, y0)在圆x2+y2=1上的内部,∴ (−2m3)2+(m3)2<1,∴ −3√55<m<3√55.21. 解:(I)∵ f(x)=1x+alnx(a≠0, a∈R).∴ x>0,且f′(x)=−1x2+ax=ax−1x2若a=1,则f′(x)=−1x2+ax=ax−1x2=x−1x2,f′(1)=0,f(1)=1+ln1=1,故函数f(x)在x=1处的切线方程是y=1;(II)∵ f(x)=−1x2+ax=ax−1x2,(a≠0, a∈R).令f′(x)=0,得到x=1a,若在区间[0, e]上存在一点x0,使得f(x0)<0成立,其充要条件是f(x)在区间(0, e]上的最小值小于0即可.(1)当x=1a<0,即a<0时,f′(x)<0对x∈(0, +∞)成立,∴ f(x)在区间[1, e]上单调递减,故f(x)在区间(0, e]上的最小值为f(e)=1e +alne=1e+a,由1e +a<0,得a<−1e.(2)当x=1a>0,即a>0时,①若e≤1a,则f′(x)≤0对x∈(0, e]成立,∴ f(x)在区间(0, e]上单调递减,∴ f(x)在区间(0, e]上的最小值为f(e)=1e +alne=1e+a>0,显然,f(x)在区间(0, e]上的最小值小于0不成立.②若1<1a <e,即a>1e时,则有∴ f(x)在区间[0, e]上的最小值为f(1a )=a+aln1a,由f(1a )=a+aln1a=a(1−lna)<0,得1−lna<0,解得a>e,即a∈(e, +∞).综上,由(1)(2)可知:a∈(−∞, −1e)∪(e, +∞).22. (1)证明:连接ON ,因为PN 切⊙O 于N ,∴ ∠ONP =90∘,∴ ∠ONB +∠BNP =90∘∵ OB =ON ,∴ ∠OBN =∠ONB因为OB ⊥AC 于O ,∴ ∠OBN +∠BMO =90∘,故∠BNP =∠BMO =∠PMN ,PM =PN∴ PM 2=PN 2=PA ⋅PC(2)∵ OM =2,BO =2√3,BM =4∵ BM ⋅MN =CM ⋅MA =(2√3+2)(2√3−2)(2√3−2)=8,∴ MN =223. 解:(1)∵ ρ=4cosθ,∴ ρ2=4ρcosθ,化为直角坐标方程x 2+y 2=4x .由直线l 的参数方程:{x =m +t y =t ,(t 是参数),消去t 可得x −y −m =0.(2)由圆C 的方程(x −2)2+y 2=4可得圆心C(2, 0),半径r =2.∴ 圆心C 到直线l 的距离d =√2=√2. ∵ (|AB|2)2+d 2=r 2,|AB|=√14 ∴ (√142)2+(√2)2=22,化为|m −2|=1,解得m =1或3.24. 解:(1)当a =−5时,要使函数有意义,则|x +1|+|x −2|−5>0,即|x +1|+|x −2|>5,在同一坐标系中作出函数y =|x +1|+|x −2|与y =5的图象如图:则由图象可知不等式的解为x <−2或x >3,即函数f(x)的定义域为{x|x <−2或x >3}.(2)∵ 函数f(x)的定义域为R ,|x +1|+|x −2|+a >0恒成立,即|x +1|+|x −2|>−a 恒成立,由图象可知|x +1|+|x −2|≥3,即−a<3,解得a>−3.。
