第11章_稳恒电流磁场(磁感应强度)

合集下载

11稳恒电流和稳恒磁场习题解答讲解

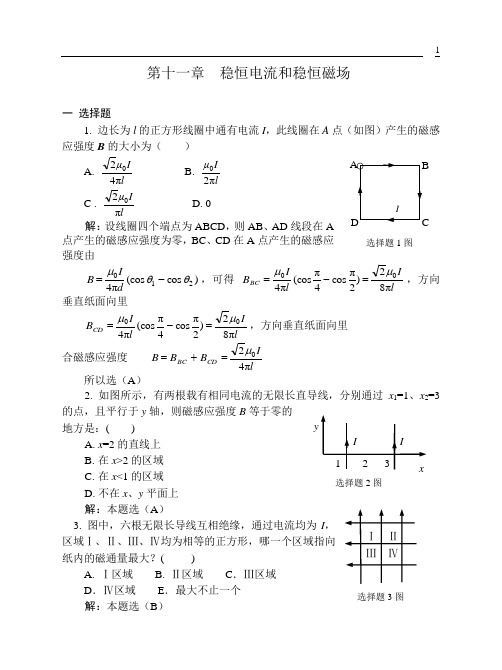
第十一章稳恒电流和稳恒磁场一选择题1. 边长为l 的正方形线圈中通有电流I ，此线圈在A 点（如图）产生的磁感应强度B 的大小为（）A. l I μπ420B. lIμπ20 C .lIμπ20 D. 0 解：设线圈四个端点为ABCD ，则AB 、AD 线段在A 点产生的磁感应强度为零，BC 、CD 在A 点产生的磁感应强度由)cos (cos π4210θθμ-=dIB ，可得 lIl IB BC π82)2πcos 4π(cosπ400μμ=-=，方向垂直纸面向里lI l I B CD π82)2πcos 4π(cos π400μμ=-=，方向垂直纸面向里合磁感应强度 lIB B B CD BC π420μ=+=所以选（A ）2. 如图所示，有两根载有相同电流的无限长直导线，分别通过x 1=1、x 2=3的点，且平行于y 轴，则磁感应强度B 等于零的地方是：( )A. x =2的直线上B. 在x >2的区域C. 在x <1的区域D. 不在x 、y 平面上解：本题选（A ）3. 图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大？( )A. Ⅰ区域B. Ⅱ区域 C ．Ⅲ区域D ．Ⅳ区域E ．最大不止一个解：本题选（B ）选择题2图Ⅰ Ⅱ Ⅲ Ⅳ 选择题3图选择题1图4. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知：（）A. ∮L B ·d l =0，且环路上任意一点B =0B. ∮L B ·d l =0，且环路上任意一点B ≠0C. ∮L B ·d l ≠0，且环路上任意一点B ≠0D. ∮L B ·d l ≠0，且环路上任意一点B =常量解：本题选（B ）5. 无限长直圆柱体，半径为R ，沿轴向均匀流有电流，设圆柱体内（r <R ）的磁感应强度为B i ，圆柱体外（r >R ）的磁感应强度为B e ，则有：（）A. B t 、B e 均与r 成正比B. B i 、B e 均与r 成反比C. B i 与r 成反比，B e 与r 成正比D. B i 与r 成正比，B e 与r 成反比解：导体横截面上的电流密度2πR IJ =，以圆柱体轴线为圆心，半径为r的同心圆作为安培环路，当r <R ，20ππ2r J r B i ⋅=⋅μ，20π2R IrB i μ=r <R ，I r B e ⋅=⋅0π2μ， rIB e π20μ=所以选（D ）6. 有三个质量相同的质点a 、b 、c ，带有等量的正电荷，它们从相同的高度自由下落，在下落过程中带电质点b 、c 分别进入如图所示的匀强电场与匀强磁场中，设它们落到同一水平面的动能分别为E a 、E b 、E c ，则（）A. E a <E b =E cB. E a =E b =E cC. E b >E a =E cD. E b >E c >E a解：由于洛伦兹力不做功，当它们落到同一水平面上时，对a 、c 只有重力做功，则E a =E c ，在此过程中，对b 不仅有重力做功，电场力也要做正功，所以E b >E a =E c所以选（C ）7. 图为四个带电粒子在O 点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片，磁场方向垂直纸面向外，四个粒子的质量相等，电量大小也相等，则其中动能最大的带负电的粒子的轨迹是：( )A. OaB. ObC. Oc D . Od解：根据B F ⨯=v q ，从图示位置出发，带负选择题7图c dba B O• B× × × × × × Ea bc 选择题6图选择题4图电粒子要向下偏转，所以只有Oc 、Od 满足条件，又带电粒子偏转半径Bqm R v=，22k 22qB m E R =∴，质量相同、带电量也相等的粒子，动能大的偏转半径大，所以选Oc 轨迹所以选（C ）8. 如图，一矩形样品，放在一均匀磁场中，当样品中的电流I 沿X 轴正向流过时，实验测得样品A 、A '两侧的电势差V A -V A '>0，设此样品的载流子带负电荷，则磁场方向为：（）A ．沿X 轴正方向B ．沿X 轴负方向C ．沿Z 轴正方向D ．沿Z 轴负方向解：本题选（C ）9. 长直电流I 2与圆形电流I 1共面，并与其一直径相重合如图（但两者间绝缘），设长直电流不动，则圆形电流将：（）A. 绕I 2旋转B. 向左运动C. 向右运动D. 向上运动E. 不动解：圆形电流左半圆和右半圆受到长直电流安培力的方向均向右，所以圆形电流将向右运动所以选（C ）二填空题1. 成直角的无限长直导线，流有电流I =10A ，在直角决定的平面内，距两段导线的距离都是a =20cm 处的磁感应强度B = 。

磁感应强度

元代指南龟指南龟
结束
返回
自南宋至明中叶,中国航海中所用的罗盘, 自南宋至明中叶,中国航海中所用的罗盘, 都是"水罗盘" 所谓水罗盘, 都是"水罗盘".所谓水罗盘,是指磁针浮于水面 , , 没有固定支点的水浮针盘. 没有固定支点的水浮针盘.明初随郑和下西洋的巩珍,在他的《西洋番国志》巩珍,在他的《西洋番国志》自序中曾对这种水罗盘作了记述: 木为盘,书刻干支之字, 罗盘作了记述: "皆□木为盘,书刻干支之字, 浮针于水,指向行舟指向行舟. 浮针于水指向行舟."(1522～1566)
结束
返回
东汉王充在《论衡》中曾有记述: 东汉王充在《论衡》中曾有记述:"司南之投之于地,其柢指南. 杓,投之于地,其柢指南."
司南
结束
返回
司南与地盘
结束
返回
大连出土元代磁州浮针瓷碗
结束
返回
北宋科学家沈括在《梦溪笔谈》中记述梦溪笔谈》另一种磁性指向仪器. 另一种磁性指向仪器. 他写道:"方家以磁石他写道方家以磁石摩针锋,则能指南. 摩针锋则能指南." 则能指南这是一种由经验积累的更为简单的磁化法沈括的指南针结束返回
A的作的用于磁场运动电荷 B B的的作用生磁场产于生产
运动电荷 A
结束
返回
二,磁感应强度运动电荷在磁场中要受到磁力作用, 运动电荷在磁场中要受到磁力作用,实验证明: 验证明: 1.磁力大小和电荷运动方向有关磁力大小和电荷运动方向有关; 磁力大小和电荷运动方向有关 2.当电荷沿某一特定方向运动时磁力为零, 当电荷沿某一特定方向运动时磁力为零, 当电荷沿某一特定方向运动时磁力为零定义磁力为零的方向为磁场的方向( 定义磁力为零的方向为磁场的方向(磁场指向另行规定) 向另行规定). 3.当电荷运动方向和磁场方向垂直时,所当电荷运动方向和磁场方向垂直时, 当电荷运动方向和磁场方向垂直时受磁力最大.并且: 受磁力最大.并且:F m ∝ q v Fm 和 q v 无关它反映了该点磁场无关,它反映了该点磁场而比值 qv 的强弱,为此定义为此定义: 结束返回的强弱为此定义

第十一章稳恒电流的磁场(一)作业解答

一、利用毕奥—萨法尔定律计算磁感应强度毕奥—萨法尔定律：304r rl Id B d⨯=πμ1.有限长载流直导线的磁场)cos (cos 4210ααπμ-=a I B ,无限长载流直导线a IB πμ20=半无限长载流直导线a IB πμ40=,直导线延长线上0=B2. 圆环电流的磁场232220)(2x R IR B +=μ，圆环中心R I B 20μ=，圆弧中心πθμ220∙=R I B电荷转动形成的电流：πωωπ22q q T q I === 【】基础训练1、载流的圆形线圈(半径a 1 )与正方形线圈(边长a 通有相同电流I ．如图若两个线圈的中心O 1 、O 2处的磁感强度大小相同，则半径a 1与边长a 2之比a 1∶a 2为 (A) 1∶1 (B) π2∶1 (C) π2∶4 (D) π2∶8【】基础训练3、有一无限长通电流的扁平铜片，宽度为a ，厚度不计，电流I 在铜片上均匀分布，在铜片外与铜片共面，离铜片右边缘为b 处的P 点的磁感强度B的大小为(A))(20b a I+πμ． (B)b b a aI +πln20μ．(C) b b a b I +πln 20μ． (D) )2(0b a I+πμ．解法：【】自测提高2、通有电流I 的无限长直导线有如图三种形状，则P ，Q ，O 各点磁感强度的大小B P ，B Q ，B O 间的关系为 (A) B P > B Q > B O . (B) B Q > B P > B O ． B Q > B O > B P ． (D) B O > B Q > B P ．解法：根据直线电流的磁场公式和圆弧电流产生磁场公式可得【】自测提高7、边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷．此正方形以角速度ω 绕AC 轴旋转时，在中心O 点产生的磁感强度大小为B 1；此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感应强度的大小为B 2，则B 1与B 2间的关系为 (A) B 1 = B 2． (B) B 1 = 2B 2． (C) B 1 = 21B 2． (D) B 1 = B 2 /4．解法：设正方形边长为a ω 相同，所以每个点电荷随着正方形旋转时形成的等效电流相同，为当正方形绕AC 轴旋转时，一个点电荷在O 旋转产生电流，在O 点产生的总磁感小为O 点产生的磁感应强度的大小为基础训练12、一长直载流导线，沿空间直角坐标Oy 轴放置，电流沿y 正向．在原点O 处取一电流元l Id ，则该电流元在(a ，0，0)点处的磁感强度的大小为，方向为。

第11章-恒定磁场

3、当带电粒子在磁场中垂直于此特定方向运动时受力最大.
Fmax 大小与 q, v 无关
qv
13
11-3
磁场
磁感强度
磁感强度 B的定义：
➢ 方向：若带电粒子在磁场中某点向某方向运动
不受力，且该方向与小磁针在该点指向一致，此特
定方向定义为该点的 B 的方向.
➢ 大小：B F / qv
Fmax
➢ 运动电F荷在q磁v 场B中受力
Idl er r2
真空磁导率 0 4π 107 N A2
P * r
Idl
任意载流导线在点 P 处的磁感强度
磁感强度叠加原理
B
dB
0I dl er
4π r2
15
11-4 毕奥—萨伐尔定律
dB 0 Idl er 毕奥—萨伐尔定律
4π r2
例判断下列各点磁感强度的方向和大小.
1
1、5 点：dB 0
30
11-5 磁通量磁场的高斯定理
二磁通量磁场的高斯定理
磁感线密度：磁场中某点处垂直于 B矢量的单位面积上通过的磁感线数目 N / S
磁场中某点处的磁感线密度等于该点 B矢量的大小
B N S
S B
31
11-5 磁通量磁场的高斯定理
enB B
磁通量：通过某一曲面的磁感线数为通过此曲面的磁通量.
方向有关。
➢ 实验结论
1、带电粒子在磁场中某点P 沿某一特定方向（或其反方向）运动时不受力，此特定方向与小磁针指向一致.
y
F 0
v +* v
P
o
z
x
12
11-3 磁场磁感强度
2、带电粒子在磁场中沿

第十一章电磁学恒定磁场 Ma 2016

0 qnS d lv er dB 4 r2
d B 0 qv er B d N 4 r 2 方向根据右手螺旋法则， B 垂直 v 、正， B 为 v r 的方向；q为负， B 与
q
+
r B
v
q－
q为 r组成的平面。 v r 相反。
μ0 I B (cos θ1 cos θ 2 ) 4πr0
0 π
2
I
无限长载流长直导线的磁场
θ1 θ2
μ0 I B 2πr0
注意用右手螺旋关系判断方向。半无限长载流长直导线的磁场
1
r0
P
θ1 θ2

2 π

μ0 I B 4πr0
I
r0
P
大学物理电磁学
2、载流圆线圈轴线上的磁场真空中，半径为R的载流导线，通有电流I，称圆电流。求其轴线上一点 P的磁感强度的方向和大小
1、5 点： dB 0
7

6 5
Idl
R
×
× 3
3、7点： dB
0 Idl 4 π R2
4
2、4、6、8 点：
dB
0 Idl
4π R
2
sin 45
0
大学物理电磁学
3. 毕—萨定律应用举例
dB 的方向均
沿x 轴负方向
(1) 载流长直导线的磁场
z
dz
解
2

dB
大学物理电磁学
磁现象与电现象有没有联系？
静电场？
静止的电荷运动的电荷
1820年奥斯特：发现电流的磁效应
N

大学物理稳恒电流电流密度

大小：单位时间通过导体某一横截面的电量。方向：正电荷运动的方向。
I dq dt
单位：A
二、电流密度
电流强度对电流的描述比较粗糙：
对于横截面不相等的导体， I 不能反映不同截面处及同一截面不同位置处电流流动的情况。
电流密度矢量—描写空间各点电流大小和方向的物理量。
方向：该点正电荷定向运动的方向。
第11章真空中的稳恒磁场
1、静止电荷周围存在电场，电场对处于其中的电荷施加电场力。 2、当电荷运动时，它周围不仅有电场，还有磁场。 3、磁场对运动电荷施加作用力，对静止电荷毫无影响。
学习提示：
稳恒磁场与静电场的性质完全不同，但在研究方法上有许多类似之处，学习过程中注意与静电场进行对比。
§11-1 稳恒电流电流密度一、电流强度
大小：通过垂直于该点正电荷运动方向的单位面积
上的电流强度。
dS
n
j
j
dI dS
dI
dS cos
单位：A/㎡
三、电流密度和电流强度的关系 (1)通过面元dS的电流强度
dI jds cos
(2)通过电流场中任一面积S的电流强度
四、稳恒电流
定义：电流强度I等于常量，这种
电流叫做稳恒电流。
特点：通过导线中任意两个横截面
1.电流（现象）
电流—带电粒子的定向运动。载流子—电子、质子、离子、空穴。电流形成条件(导体内)： (1)导体内有可以自由运动的电荷； (2)导体内要维持一个电场。 (导体内有电荷运动说明导体内肯定有电场，这和静电平衡时导体内场强为零情况不同。)
2.电流强度
电流的大小强弱，通过电流强度来度量
的电流强度相等
I1 I2

稳恒磁场

安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向：方向：×
v
dl
B
I
设截面积为S,单位体积电子数为设截面积为单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视，线圈是逆时针转动。向上,从上往下俯视，线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图，求圆心O点的 B . 如图，求圆心点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O

大学物理——11-1磁感应强度B

电源电动势的方向：电源内部电势升高的方向；或在电源内部从负极指向正极。
§11.1磁场磁感应强度
一、基本磁现象
永磁体的性质：
（1）具有磁性，能吸引铁、钴、镍等物质。（2）具有磁极，分磁北极N和磁南极S。（3）磁极之间存在相互作用，同性相斥，异性相吸。（4）磁极不能单独存在。
司南勺
在磁极区域，磁性最强。

S

S

载流子：导体中宏观定向运动的带电粒子。
电流强度（I）：单位时间内通过导体任一横截面的电荷。
dq I dt
3
单位：安培 1A 1 C s 1
6
1A 10 mA 10 μ A
恒定电流（直流电）：导体中通过任一截面的电流不随时间变化（I = 恒量）。电流的方向：导体中正电荷的流向。
B
dF
dF
B
θ
Idl
三、安培力
电流元 Idl 置于磁感应强度为 B 的外磁场中时，
电流元所受的力为：安培定律:
dF Idl B
安培定律:
一段电流元Idl在磁场中所受的力dF，其大小与电流元Idl成正比，与电流元所在处的磁感应强度B成正比，与电流元Idl和B的夹角的正弦成正比，即
dS
n
dI 大小： j j 速度方向上的单位矢量 d S d 对任意小面元 d S ， I j d S j d S dS 对任意 dI I j d S j S 曲面S：
d S
P 处正电荷定向移动 j
三、电源和电动势
+
第11章恒定电流的磁场
11.1 磁感应强度 B

大学物理——第11章-恒定电流的磁场

单位：特斯拉（T） 1 T = 1 N· -1· -1 A m 1 特斯拉 ( T ) = 104 高斯( G )
3
★ 洛仑兹力运动的带电粒子，在磁场中受到的作用力称为洛仑兹力。
Fm q B
的方向一致；粒子带正电，F 的指向与矢积 B m 粒子带负电，Fm的指向与矢积 B的方向相反。
L
dB
具体表达式
?
5
★ 毕－萨定律
要解决的问题是：已知任一电流分布其磁感强度的计算
方法：将电流分割成许多电流元 Idl
毕－萨定律：每个电流元在场点的磁感强度为：
0 Idl r ˆ dB 4 πr 2
大小： dB
0 Idl sin
4 πr
2
方向：与 dl r 一致 ˆ
整段电流产生的磁场：
r 相对磁导率
L
B dB
8
试判断下列各点磁感强度的方向和大小？
8
7

6

R
1
1、5 点：
dB 0
0 Idl
4π R 2
Idl

2
3、7 点： dB 2、4、6、8 点：
3 4
5
dB
0 Idl
4π R
sin 450 2
9
★ 直线电流的磁场
29
★ 磁聚焦洛仑兹力
Fm q B （洛仑兹力不做功）
与 B不垂直

//
// cosθ
sin θ
m 2π m R T qB qB
2πm 螺距 d // T cos qB

第11章稳恒磁场

z
D
无限长载流长直导线的磁场无限长载流长直导线的磁场. 载流长直导线的磁场
θ2
v B
B=
4 π r0
（cosθ 1 − cosθ 2 ）
B=
I
o
µ0 I
2 π r0
θ1 → 0 θ2 → π
x
C
θ1
P y
无限长载流长直导线的磁场
B=
µ0I
2πr
I B
I
X
B
电流与磁感应电流与磁感应强度成右螺旋关系半无限长载流长直导线的磁场
=
I
2π R
v B
o
l
R
v v ∫ B ⋅ dl =
l
∫ 2πR
µ0 I
v dl
dl
v v µ0 I ∫l B ⋅ d l = 2 π R ∫l d l v v 设闭合回路 l 为圆形 ∫l B ⋅ dl = µ0 I 回路（成右螺旋）回路（ l 与 I 成右螺旋）
I
o
v B
R
若回路绕向为顺时针时，若回路绕向为顺时针时，则
z
带电粒子在磁场中沿其他方向运动时 F 垂直于 v 与特定直线所组成的平面与特定直线所组成的平面. 当带电粒子在磁场中垂直于此特定直线运动时受力最大. 时受力最大
F = Fmax = F⊥
Fmax ∝ qv
Fmax q , v 无关 qv 大小与
磁感应的定义：磁感应强度 B 的定义：当正电荷垂直于特定直线运动时，受力 Fmax 将 Fmax ×v 方向的方向. 定义为该点的 B 的方向
I I I
I S S N I N
磁通量磁场的高斯定理
v ∆S B

11稳恒电流和稳恒磁场习题解答

1第十一章稳恒电流和稳恒磁场一选择题1. 如图所示，有两根载有相同电流的无限长直导线，分别通过x 1=1、x 2=3的点，且平行于y 轴，则磁感应强度B 等于零的地方是 ( )A. x =2的直线上B. 在x >2的区域C. 在x <1的区域D. 不在x 、y 平面上解：本题选（A ）2. 图中六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大 ( )A. Ⅰ区域B. Ⅱ区域C ．Ⅲ区域D ．Ⅳ区域解：本题选（B ）3. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知（）A. ∮L B ·d l =0，且环路上任意一点B =0B. ∮L B ·d l =0，且环路上任意一点B ≠0C. ∮L B ·d l ≠0，且环路上任意一点B ≠0D. ∮L B ·d l ≠0，且环路上任意一点B =常量解：本题选（B ）4. 无限长直圆柱体，半径为R ，沿轴向均匀流有电流，设圆柱体内（r <R ）的磁感应强度为B i ，圆柱体外（r >R ）的磁感应强度为B e ，则有（）A. B t 、B e 均与r 成正比B. B i 、B e 均与r 成反比C. B i 与r 成反比，B e 与r 成正比D. B i 与r 成正比，B e 与r 成反比解：导体横截面上的电流密度2πRIJ =，以圆柱体轴线为圆心，半径为r 的同心圆作为安培环路，当r <R ，20ππ2r J r B i ⋅=⋅μ，20π2R IrB i μ=r <R ，I r B e ⋅=⋅0π2μ， rIB e π20μ=选择题1图Ⅰ Ⅱ Ⅲ Ⅳ 选择题2图选择题3图2 所以选（D ）5. 有三个质量相同的质点a 、b 、c ，带有等量的正电荷，它们从相同的高度自由下落，在下落过程中带电质点b 、c 分别进入如图所示的匀强电场与匀强磁场中，设它们落到同一水平面的动能分别为E a 、E b 、E c ，则（）A. E a <E b =E cB. E a =E b =E cC. E b >E a =E cD. E b >E c >E a解：由于洛伦兹力不做功，当它们落到同一水平面上时，对a 、c 只有重力做功，则E a =E c ，在此过程中，对b 不仅有重力做功，电场力也要做正功，所以E b >E a =E c所以选（C ） 6. 图为四个带电粒子在O 点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹，磁场方向垂直纸面向外，四个粒子的质量相等，电量大小也相等，则其中动能最大的带负电的粒子的轨迹是 ( )A. OaB. ObC. Oc D . Od解：根据B F ⨯=v q ，从图示位置出发，带负电粒子要向下偏转，所以只有Oc 、Od 满足条件，又带电粒子偏转半径Bq m R v=，22k 22qB m E R =∴，质量相同、带电量也相等的粒子，动能大的偏转半径大，所以选Oc 轨迹所以选（C ）7. 如图，一矩形样品放在一均匀磁场中，当样品中的电流I 沿X 轴正向流过时，实验测得样品A 、A '两侧的电势差V A -V A '>0，设此样品的载流子带负电荷，则磁场方向为（）A ．沿X 轴正方向B ．沿X 轴负方向C ．沿Z 轴正方向D ．沿Z 轴负方向解：本题选（C ）8. 长直电流I 1与圆形电流I 2共面，并与其一直径相重合如图（但两者间绝缘），设长直电流不动，则圆形电流将（）选择题6图 c dba BO • B× × × × × × Ea bc 选择题5图选择题7图3A. 绕I 1旋转B. 向左运动C. 向右运动D. 向上运动解：圆形电流左半圆和右半圆受到长直电流安培力的方向均向右，所以圆形电流将向右运动所以选（C ）二填空题1. 两段不同金属导体电阻率之比为ρ1 : ρ2=1:2，横截面积之比为S 1 : S 2=1:4，将它们串联在一起后两端加上电压U ，则各段导体内电流之比I 1 : I 2 = ，电流密度之比J 1 : J 2 = 。

第十一章恒定电流的磁场(二)作业答案

一、选择题【 C 】1.（基础训练2）三条无限长直导线等距地并排安放，导线Ⅰ、Ⅱ、Ⅲ分别载有1 A ，2 A ，3 A 同方向的电流．由于磁相互作用的结果，导线Ⅰ，Ⅱ，Ⅲ单位长度上分别受力F 1、F 2和F 3，如图所示．则F 1与F 2的比值是：(A) 7/16． (B) 5/8． (C) 7/8． (D) 5/4．【答】设导线Ⅰ、Ⅱ、Ⅲ的电流强度分别为321,,I I I ，产生的磁感应强度分别为321,,B B B ，相邻导线相距为a ，则()()0203011123110301022231227,2224222II F I l B B I l a a a I I F I l B B I l a a aμμμπππμμμπππ⎛⎫=+=+= ⎪⋅⎝⎭⎛⎫=-=-= ⎪⎝⎭式中121231, 1, I 1A, I 2A, I 3A l m l m =====，得 8/7/21=F F .【 D 】2. (基础训练6)两个同心圆线圈，大圆半径为R ，通有电流I 1；小圆半径为r ，通有电流I 2，方向如图．若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场)，当它们处在同一平面内时小线圈所受磁力矩的大小为 (A) Rr I I 22210πμ． (B)Rr I I 22210μ． (C)rR I I 22210πμ． (D) 0．【答】大圆电流在圆心处的磁感应强度为，方向垂直纸面朝内2RI B 101μ=；小圆电流的磁矩为方向垂直纸面朝内，,222r I p m π=所以，小圆电流受到的磁力矩的大小为2211sin 00m m M p B p B =⨯=︒=[ B ]3.（自测提高2）如图所示，一电子以速度v垂直地进入磁感强度为B的均匀磁场中，此电子在磁场中运动轨道所围的面积内的磁通量将(A) 正比于B ，反比于v 2． (B) 反比于B ，正比于v 2． (C)正比于B ，反比于v ． (D) 反比于B ，反比于v ．【答】电子在磁场中做匀速率圆周运动，运动平面的法向平行于磁感应强度方向，因此，磁通量为2R B πΦ=，其中半径R 可由式2v evB m R =求得：mv R eB =，所以222mv m v B eB eB ππ⎛⎫Φ== ⎪⎝⎭.F 1F 2F 31 A2 A3 A ⅠⅡⅢOrR I 1 I 2[ B ]4、（自测提高4）一个动量为p 的电子，沿图示方向入射并能穿过一个宽度为D 、磁感强度为B(方向垂直纸面向外)的均匀磁场区域，则该电子出射方向和入射方向间的夹角为 (A)p eBD 1cos-=α．(B)p eBD 1sin -=α． (C)epBD 1sin -=α． (D) ep BD 1cos -=α．【答】电子在磁场中的轨迹为一段圆弧，如图。

大学物理电磁学第11章恒定磁场

四、毕-萨定律的应用
dB
0 4
Idl r r2
方法：
(1)将电流分解为无数个电流元
(2)由电流元求dB (据毕—萨定律)
(3)对dB积分求B = dB 矢量积分须化作分量积分去做
Bx dBx , By dBy , Bz dBz
例题1 直线电流在P点的磁场
2
解：
任取电流元 I dl
所有磁现象可归纳为：
运动电荷
运动电荷
载流导体
磁场
载流导体
磁体
磁体
磁场的宏观性质：对运动电荷(或电流)有力的作用，磁场有能量
二、磁感应强度
B 1、磁场的描述:磁感应强度
方向：磁针静止时，N极指向即B的正方向
S
N
2、B的大小：
以磁场对载流导线的作用为例
电流元所受到的磁场力
dF Idl sin
l
r
B
3）说明磁场为非保守场称为涡旋场
静电场是保守场、无旋场
二、简证(用特例说明安培环路定理的正确性)
(1)闭合路径L环绕电流
L在垂直于导线的平面内
B 0I 2 r
L
I d
o
B
r
dl
磁感线
(2)闭合路径L不包围电流
B dl1 dl2 L
P
·
I
d
o
dl2
dl1
L2
L1
磁感线
·
Q
三、运用安培环路定理求磁场安培环路定理适用于任何形状恒定电流的载流体
P·
Idl r
B
dB
0 4
Idl r r2
B
dB
0 4
Idl r r2

稳恒磁场11如图11所示两根长直导线互相平行地放置

第十一章稳恒磁场11-1 如图11-1 所示，两根长直导线互相平行地放置，导线中的电流大小相等，均为A I 10=方向相同，求图中M 、N 两点的磁感应强度B 的大小和方向（图中m r 020.00=）。

解：两导线在M 、N 点产生的磁感应强度如图11-1（a ）所示。

在M 点，1B 和2B 大小相等方向相反，由场强叠加原理可知0B B B 21m =-=在N 点，两导线产生的磁感应强度大小为：002122''r IB B πμ==且21''B B ⊥，由场强叠加原理可得T r IB B N 4001100.12'2-⨯===πμ，方向水平向左。

11-2 已知地球北极磁场强度为B 的大小为T 5100.6-⨯。

如果想此地磁场是由地球赤道上一圆电流所激发的，此电流大小为多少？流向如何？解：设所求电流为I ，方向如图所示，因为圆形电流在距轴体上的磁感应强度为：232220)(2x R IR B +=μ对于北极点，R x =于是有：RIR R IR B 24)(20232220μμ=+=赤道上的电流强度为：A RBI 901073.124-⨯==μ11-3 如图11-3所示，有两根导线沿半径方向接触铁环的a 、b 两点，并与很远处的电源图11-1图11-2相接。

求环心O 的磁感应强度。

解：设圆环以acb 弧长1l ，其电流为1I ，而adb 弧长为2l ，电流为2I 。

因这两段弧可形成并联电路所以两端电压相等，于是有：2211R I R I =考虑环的截面积和电阻率是一样的，电阻与弧长成正比，所以上式改写为：2211L I L I =1l 弧：一电流在O 点产生的磁感应强度为：dl RI dB 21014πμ=，方向垂直纸面向里。

整个弧在O 点产生的磁感应强度为：210021011441R I dl R I dB B l πμπμ===⎰⎰，方向垂直纸面向里。

第十一章稳恒磁场

于π)的正弦成正比，即：结论
式的中单K位为有比关例。系数，其值与介质的种dB类和选用
14
在国际单位制中， μ0称为真空磁导率，
K
0
0
4
/ 4P
10r7 Tθ
mId lA
I
1
故有：
dB的方向用右手螺旋法则确定：
右手弯曲的四指由Idl的方
向沿小于180°的θ角转向 r的方向，则伸直拇指的指向就是dB 的方向。
5
一、磁感应强度
为了描述磁场中各点的磁场强弱和方向，引入磁感应强度。用B表示，
定义
B Fm q0v
单位：特斯拉（T）。
比值B是一个与运动电荷的性质无关、仅与该点磁场的性质有关的常量。
B为矢量，其方向用右手螺旋法则确定:
6
特斯拉
右手螺旋法则：
将右手拇指与其余四指垂直，先将四指的指向与 7 Fm方向相同，再使其向的v方向弯曲，这时拇指
大多数生物大分子是抗磁质，少数是顺磁质，极少呈铁磁质
43
三、超导体及其磁学特性
1、超导体超导现象：当物质的温度下降到某一定值时，该物质的电阻完全消失的现象称为超导现象。超导性：物质失去电阻的性质叫超导性。超导体：具有超导性的物质叫超导体。超导体失去电阻的温度称为临界温度Tc，可能成为超导体的物质是：①位于元素周期表中部的金属元素（除一价金属、铁磁质、和抗磁质）②许多化合物或合金。
磁感应线的特点:
I
I
通电螺线管的磁感应线
磁感应线是闭合的曲线，密集的地方磁场较
强，稀疏的地方磁场较弱。
9
1、磁通量
通过某曲面磁感应线的总数称为通过该曲面的磁通量。
用Φ表示。
通过面积元dS的磁通量为：

大学物理第十一章电流与磁场

2）提供非静电力的装置。
A
E
B
Ek
凡电源内部都有非静电力，
U
非静电力使正电荷由负极经电源内部到达正极。
A
UB
引入：非静电场强
Ek
=
单位正电荷所受的非静电力。
Ek E
Fk qEk
2 电动势ε
A非
L qEk
dl
内
qEk
dl
qEk 外
dl
内 qEk
dl
★ 结论：当电荷在闭合电路中运动一周时，只有非静电力做功
右手法则，dB (
Idl
r
)
(11-29)
2. 载流导线的磁场
B
l
0 4
Idl r0
r2
（矢量积分） (11-30)
方向判断练习
• dB
r
Idl
dB
r
Idl
r
Idl
dB
dB
r
Idl
•
二、毕 - 沙定律的应用（重点计算B的方法之一）
1. 一段直电流的磁场
I
讲义 P.324 例 11-1
一磁现象磁场 — 运动电荷周围存在的一种物质。
1. 运动电荷电流
磁场；
2. 磁场可脱离产生它的“源”独立存在于空间；
3. 磁力通过磁场传递，作用于运动电荷或载流导线；
4. 磁场可对载流导线做功，所以具有能量。
演示磁场电流相互作用
I
SN
二、磁感应强度 B
1. 实验结果
z
F
B
F q, v, B, sin
五、欧姆定律 (Ohm’s law)
R是与U 和I 无关的常量。
I U R

第十一章恒定电流的磁场作业磁介质磁介质中的安培环路定理小结

作业11.1、11.211.4、11.8、11.9、11.15、11.1787磁介质90顺磁质B B >（铝、氧、锰等）弱磁质B B >>铁磁质（铁、钴、镍等）强磁性物质B B <抗磁质（铜、铋、氢等）弱磁质抗磁质顺磁质SI SI B L宏观上构成沿介质表面的等效环形电流, 称为表面束缚电流或磁化电流。

B AI 0I cbad.l113五、磁场对载流导线和运动电荷的作用（1）磁场对载流导线的作用力—安培力微分形式积分形式B l I F ⨯=d d Bl I F l⨯=⎰d 其中，是载流导线上的电流元，是所在处的磁感应强度。

l Id l I d B（2）均匀磁场对平面载流线圈的作用合力=∑F 磁力矩B p M m ⨯=式中，是载流线圈的磁矩，，其中N 是线圈匝数，I 是线圈中的电流，S 是线圈的面积，且S 的方向与电流环绕方向满足右螺旋法则。

m p S NI p m=114（3）磁力的功⎰=m1m2m d ΦΦΦI A mm1m2)(ΦI ΦΦI ∆=-=磁力的功等于电流强度I 乘以通过回路磁通量的增量∆Φm 。

（4）磁场对运动电荷的作用Bq F⨯=v 洛仑兹力:116六、磁介质（1）磁介质的分类抗磁质1<r μ顺磁质1>r μ铁磁质1>>r μ（2）磁介质的磁化在外磁场中固有磁矩沿外磁场的取向或感应磁矩的产生使磁介质的表面（或内部）出现束缚电流。