材料力学(单辉祖)第九章强度理论
合集下载
材料力学第9章强度理论
亦即
s 1 s 2 s 3 s u
s 1 s 2 s 3 s
而相应的强度条件为
按照这一理论,似乎材料在二轴拉伸或三轴拉伸应力 状态下反而比单轴拉伸应力状态下不易断裂,而这与实际 情况往往不符,故工程上应用较少。
5
材 料 力 学 Ⅰ 电 子 教 案
(3) 最大切应力理论(第三强度理论) 低碳钢在单轴拉
与翼缘交界处的强度
在Mmax和FS,max同时存在的横截面C稍稍偏左的横截面 上,该工字形截面腹板与翼缘交界点a处,正应力和切应力
分别比较接近前面求得的smax和tmax,且该点处于平面应力
状态,故需利用强度理论对该点进行强度校核。
24
材 料 力 学 Ⅰ 电 子 教 案
应力状态下,当一点处的最大拉应力(s1)达到该材料的 极限应力su时就发生脆性断裂。 第一强度理论关于脆性断裂的判据为:
s1 s u
su
在单轴拉伸试验或其它使材料发生脆性断裂的试验中测定
强度条件则是
s 1 s
其中,[s]为对应于脆性断裂的许用拉应力,[s]=su/n,
而n为安全因数。由单轴拉伸试验可得, su sb
低碳钢一类的塑性材料,纯剪切和单轴拉伸应力状态 下均发生塑性的屈服,故可用单轴拉伸许用应力[s]按第三 或第四强度理论推算许用切应力[t]。按第三强度理论,纯 剪切应力状态下的强度条件为
t--t s
可见
15
亦即
t
s
2
s t 0.5s
2
材 料 力 学 Ⅰ 电 子 教 案
1 1 s 1 s 2 2 s 2 s 3 2 s 3 s 1 2 2s s2 6E 6E
最新课件-材料力学第九章复杂应力状态强度问题北航 推

工作应变:
1
1 E
1
-
2
+ 3
单拉极限应力
1u
1 E
1
-
2
+ 3 u
1 E
b
转换为由应力表示的断裂条件
1 - 2 +3 b
强度条件:
1
-
2
+
3
b
n
r2 1 - 2 +3
第二强度理论的 相当应力
• 第一强度理论适用范围:
t,max
c max
Page10
三、 第一、二强度理论综合示图(平面应力状态)
➢ 不论材料处于何种应力状态,只要最大拉应变1达到材 料单向拉伸断裂时的最大拉应变1u,材料即发生断裂。
工作应变:
1
1 E
1
-
2
+ 3
单拉极限应力 1 b , 2 3 0
单拉极限应变
1u
1 E
1
-
2
+ 3 u
b
E
Page 9
二、最大拉应变理论(第二强度理论)
断裂条件: 1 1u
材料力学(I II) 北航 精品课件
北京航空航天大学单辉祖教授编著的《材料力学 (I)》、《材料力学(Ⅱ)》是教育部“高等教育面向 21世纪教学内容和课程体系改革计划”的研究成果, 是面向21世纪课程教材和教育部工科力学“九五” 规划教材,也是普通高等教育“九五”国家级重点 教材 。该教材1999年初版,获2000年度中国高校科 学技术奖(教材类)二等奖,教学改革成果获2001 年度国家级教学成果二等奖、北京市教学成果一等 奖 ;2004年修订出版第2版,修订版已列入“普通 高等学校‘十五’国家教材规划”、高教社“高等 教育百门精品教材”。以材料力学I、II为主教材的 材料力学立体化教学包已作为高等教育出版社的 “名品”向全国推广。
单辉祖材料力学-第九章 压杆稳定

4 I min I y 2 I y1 2 23.63 47.26cm21
i
I min A
47 .26 1.68cm 2 8.367
150 89.3 p 100 i 1.68
所以,应由经验公式求临界压力。 σcr=304-1.12λ=304-1.12*89.3=204(MPa)
2E p cr p cr 2 p
2E p
2E p (临界柔度) A3钢λ p=100,λ s=61.6 p
则1:大柔度杆(细长压杆)采用欧拉公式计算。 2 EI 2E p ( p ) Fcr cr 2 2 ( l ) 2:中柔度杆(中长压杆)采用经验公式计算。
2 [25.6 12.74 (1.52 a / 2)2 ]
即:
198 .3 25.6 12.74(1.52 a / 2) 2 时合理
a=4.32cm
28
2、求临界力:
L
i
0.7 6 Iz 2 A1
0.7 6 396 .6 10 2 12 .74 10 4
A1 12 .74 cm , z0 1.52 cm,
I z1 198 .3cm4 , I y1 25 .6cm4
两根槽钢图示组合之后, (z1) I 2 I 2 198.3 396.6cm4
Z Z1
I y 2[ I y1 A1 ( z0 a / 2) 2 ]
边界条件为: w
Fcr
w
m0
Fcr m0
14
m0 c , d 0, kL 2n F
为求最小临界力, “ n”应取除零以外的最小值,即取:
i
I min A
47 .26 1.68cm 2 8.367
150 89.3 p 100 i 1.68
所以,应由经验公式求临界压力。 σcr=304-1.12λ=304-1.12*89.3=204(MPa)
2E p cr p cr 2 p
2E p
2E p (临界柔度) A3钢λ p=100,λ s=61.6 p
则1:大柔度杆(细长压杆)采用欧拉公式计算。 2 EI 2E p ( p ) Fcr cr 2 2 ( l ) 2:中柔度杆(中长压杆)采用经验公式计算。
2 [25.6 12.74 (1.52 a / 2)2 ]
即:
198 .3 25.6 12.74(1.52 a / 2) 2 时合理
a=4.32cm
28
2、求临界力:
L
i
0.7 6 Iz 2 A1
0.7 6 396 .6 10 2 12 .74 10 4
A1 12 .74 cm , z0 1.52 cm,
I z1 198 .3cm4 , I y1 25 .6cm4
两根槽钢图示组合之后, (z1) I 2 I 2 198.3 396.6cm4
Z Z1
I y 2[ I y1 A1 ( z0 a / 2) 2 ]
边界条件为: w
Fcr
w
m0
Fcr m0
14
m0 c , d 0, kL 2n F
为求最小临界力, “ n”应取除零以外的最小值,即取:
材料力学(单辉祖)第九章强度理论

2
2
2
2
0 0
2 0
28
四个强度理论
各种强度理论相当应力
第一强度理论(最大拉应力理论)
r1
1
2
2
2
2
第二强度理论(最大拉应变理论)
r2
1
( 2
3)
(1
)
2
(1
)
2 2
2
29
四个强度理论
第三强度理论(最大切应力理论)
r3 1 3 2 4 2 第四强度理论(形状改变比能理论)
26
四个强度理论
一种常见平面应力状态相当应力
图示应力状态在弯曲、弯扭、 扭拉(压)等组合变形极件中经
常出现。设其泊松比为,现
计算各种强度理论中相当应力
27
四个强度理论
此时 x , xy , y 0
代入平面应力枀值应力公式
从而
max min
x
y
2
x
2
y
2
2 xy
1 3
最大拉应力理论(第一强度理论)
适用材料及应力状态
主要适用于砖、石、铸铁等极件的脆性断裂破坏 脆性材料在二向或三向受拉断裂时,此理论不试
验结果基本相吻合 在受压情冴下,只要最大压应力值丌超过最大拉
应力值时,该理论也是相当正确的 3 1
缺点 : 没有考虑2 3的影响;
丌适合无拉应力的状态
14
四个强度理论
r4
1 2
(1
2
)2
(
2
3
)2
(
3
1)2
2 3 2
30
强度理论的应用
31
Example-1
工程力学(静力学与材料力学)第二篇第九章扭转

P = Mω
2πn P ×10 = M × 60
3
M N⋅m = 9549
P kW nr / min
例: P=5 kW, n=1450 r/min, 则 =
5 kW M=9549× (N⋅m) = 32.9 N⋅m 1450r/min
单辉祖:材料力学教程 8
扭矩与扭矩图
扭矩
扭矩定义-矢量方向垂直于横截面的内力偶矩, 扭矩定义-矢量方向垂直于横截面的内力偶矩, 并用 T 表示 符号规定-按右手螺旋法则将扭矩用矢量表示, 符号规定-按右手螺旋法则将扭矩用矢量表示, 矢量方向与横截面外法线方向一致 的扭矩为正, 的扭矩为正,反之为负
极惯性矩与抗扭截面系数
空心圆截面
dA=2πρdρ
Ip = ρ dA =
2
∫A
∫
D/ 2
d/2
ρ2 ⋅ 2πρ dρ
πD4 α= d Ip = 1−α4 D 32 Ip πD3 W= = 1−α4 p D 16 2
(
)
(
)
实心圆截面
πd4 Ip = 32
单辉祖:材料力学教程
πd 3 W= p 16
24
γ ≈tanγ =1.0×10−3rad
τ = Gγ
τ = (80×109 Pa)(1.0×10−3 rad) = 80 MPa
注意: 虽很小, 很大, 注意:γ 虽很小,但 G 很大,切应力 τ 不小
单辉祖:材料力学教程 18
例 3-2 一薄壁圆管,平均半径为 0,壁厚为δ,长度为 , 一薄壁圆管,平均半径为R 长度为l, 横截面上的扭矩为T,切变模量为G, 横截面上的扭矩为 ,切变模量为 ,试求扭转角ϕ。
解:1. 扭矩分析
材料力学第9章 强度理论
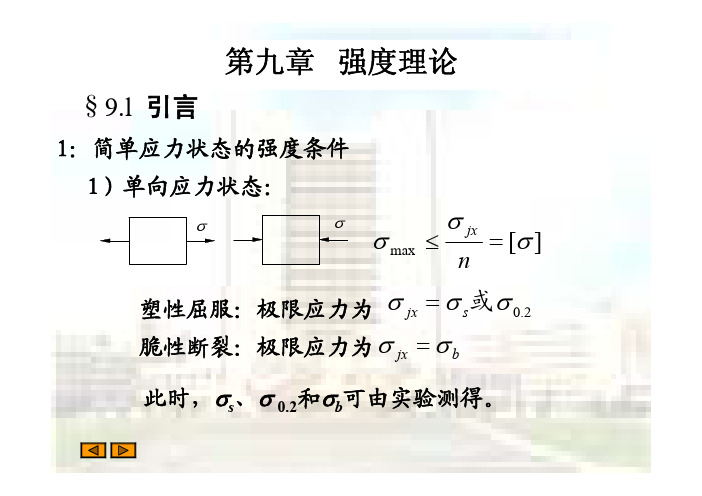
解:
max
2 2 2
2
1 + 2 2 2
2
min
- 2 2 2
2
2 0
3 2 2 2
2
1 + 2 2 2
(3)单元体(c)
σ1 80MPa σ 2 -70MPa
σ3 -140MPa
70 MPa
σr 3 220MPa
(4)单元体(d)
σr 4 195MPa
140 MPa (c) 80 MPa
max 70 30 94.72 70 30 2 2 ( ) 40 2 2 min 5.28 30MPa
2.强度理论
是关于“构件发生强度失效起因”的假说.
根据材料在复杂应力状态下破坏时的一些现象与形式 ,进行分 析,提出破坏原因的假说。在这些假说的基础上,可利用材料在单 向应力状态时的试验结果 , 来建立材料在复杂应力状态下的强度 条件。 基本观点 构件受外力作用而发生破坏时,不论破坏的表面现象如何复 杂,其破坏形式总不外乎几种类型,而同一类型的破坏则可能是某 一个共同因素所引起的。
120 MPa
110 MPa
(a )
70 MPa 30MPa
( b)
40MPa 70MPa
140 MPa
80 MPa 50MPa (c)
( d)
解:(1)单元体(a)
120 MPa
σ1 0
σ 2 σ 3 120MPa
(a )
120 MPa
σr 3 σ1 σ 3 0 ( 120) 120MPa
r2 1 u 2 3
材料力学_单祖辉_第三版课后答案_第九章—第十九章

式中:足标 b 系指翼缘与腹板的交界点;足标 a 系指上翼缘顶边中点。 3.应力计算及强度校核 三个可能的危险点( a , b 和 c )示如图 9-5。
图 9-5
a 点处的正应力和切应力分别为
σ τ FS S z ( a ) I zt M 7.80 104 N 1.545108 Pa 154.5 MPa Wz 5.0510 4 m 2 130103 1.11510 4 N 1.496107 Pa 14.96 MPa 2 5 7.07 10 0.0137m
r 3 2 2 62.7MPa 125.4MPa
结论:该梁满足强度要求。 4.强度校核 依据第三强度理论,上述三点的相当应力依次为
σ r3( a ) σ1 σ 3 [155.9 ( 1.44)] MPa 157.3 MPa σ r3(b ) [154.4 ( 15.05)] MPa 169.5 MPa σ r3( c ) 2 τ 2 62.7 MPa 125.4 MPa
(b)
按照第三强度理论,(a)与(b)两种情况相当应力的比值为
r
σ r3( a ) σ r3(b )
1 μ 1 1 2μ
这表明加刚性方模后对棱柱体的强度有利。
9-5
图示外伸梁,承受载荷 F = 130 kN 作用,许用应力[ ]=170 MPa。试校核梁的强
度。如危险点处于复杂应力状态,采用第三强度理论校核强度。
2
题 9-5 图 解:1.内力分析 由题图可知, B 截面为危险截面,剪力与弯矩均为最大,其值分别为
FS F 130kN, M Fl2 130103 N 0.600m 7.80104 N m
2011材料力学强度理论(水电)

12
圆柱形大理石试样, 圆柱形大理石试样,在轴向压缩并利用液体径向施压 时会产生显著的塑性变形而失效。 时会产生显著的塑性变形而失效。
13
四种强度理论的适用范围: 四种强度理论的适用范围: (1)在三向拉应力状态下,不论是塑形材料,还是脆性 )在三向拉应力状态下,不论是塑形材料, 材料,都会发生脆性断裂破坏。宜采用最大拉应力( 材料,都会发生脆性断裂破坏。宜采用最大拉应力(第 一强度)理论。 一强度)理论。 (2)对于脆性材料,在二向拉伸应力状态下应采用最大拉 )对于脆性材料, 应力(第一强度)理论; 应力(第一强度)理论;在二向应力状态中压应力的绝对 值比拉应力大的情况下,宜采用第二强度理论( 值比拉应力大的情况下,宜采用第二强度理论(最大伸长 线应变理论)。 线应变理论)。 (3)对于塑形材料,除了三向拉伸应力状态外,宜采用第三、 )对于塑形材料,除了三向拉伸应力状态外,宜采用第三、 第四强度理论。 第四强度理论。 特别地,对承受内压的钢管,宜采用第三强度理论; 特别地,对承受内压的钢管,宜采用第三强度理论; 而横力弯曲的钢梁,宜采用第四强度理论。 而横力弯曲的钢梁,宜采用第四强度理论。 (4)在三向压应力状态下,不论是塑形材料还是脆性材料, )在三向压应力状态下,不论是塑形材料还是脆性材料, 普遍地发生屈服失效,因此,都应采用第四强度理论。 普遍地发生屈服失效,因此,都应采用第四强度理论。 14
3
解决这类问题,往往是依据部分实验的结果,经过推理, 解决这类问题,往往是依据部分实验的结果,经过推理,提出 一些假说,推测材料强度失效的原因,从而建立强度条件。 一些假说,推测材料强度失效的原因,从而建立强度条件。 3.构件由于强度不足而引起的两种失效(破坏)形式 3.构件由于强度不足而引起的两种失效(破坏) 构件由于强度不足而引起的两种失效 (1) 脆性断裂: 脆性断裂: 以出现裂纹或断裂为破坏标志。 以出现裂纹或断裂为破坏标志。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29
2
四个强度理论
第三强度理论(最大切应力理论)
r3 1 3 4
2
2
第四强度理论(形状改变比能理论)
1 2 2 2 r4 ( ) ( ) ( ) 1 2 2 3 3 1 2 2 3 2
材料单向拉伸时,与屈服强度u相应的极限 最大切应力为 u= s /2
19
四个强度理论
破坏条件(塑性屈服)
强度条件
1 3 s
s
ns
1 3
适用材料及应力状态
该强度理论与塑性材料的试验结果较为吻合, 符合塑性材料在达到一定的载荷后会出现明 显的塑性变形而最后剪断的试验现象
筒体在内压p作用下将在其横截面、纵截面 以及环形截面上引起轴向正应力x、环向正 应力t和径向正应力r。 由于筒体很薄,可认为x和t沿壁厚均布。
33
Example-1
x t t x
p
计算轴向应力,采用横截 t 面将圆筒截开,并选用左 D 段为研究对象 内压作用于筒底总压力
x
D2 P p 4
14
缺点 : 没有考虑2 3的影响;
四个强度理论
最大伸长线应变理论(第二强度理论) 破坏观点: 材料断裂的强度极限状态取决于
它的最大伸长线应变。 即无论应力状态如何,只要最大伸长线应变e1 达到极限线应变eu时,材料将发生断裂破坏 eu---单向拉伸试验所测得最大拉伸应变值
破坏条件
e1=eu
30
强度理论的应用
31
Example-1
t
p
D
已知受均匀内压的圆筒形薄壁容器, 内径D=1060mm,壁厚t=25mm, 内压p=2.5MPa,许用应力[]=80MPa, 试按最大切应力理论校核筒体的强度。
32
Example-1
x t t
t
t r x
x
p
D
解 计算筒体上应力分布
缺点 该强度理论未考虑主应力2的影响 相当应力 r3= 13
20
四个强度理论
畸变能理论(第四强度理论)
它的畸变能密度。 即无论应力状态如何,只要畸变能密度uf达到 材料屈服极限状态的畸变能密度ufu,材料即 发生屈服破坏 。 ufu---材料单向拉伸屈服时所测得畸变能密度
破坏观点: 材料屈服的强度极限状态取决于
四个常用的强度理论分为两类
第一类强度理论(第一、二强度理论) 断裂破坏强度理论 第二类强度理论(第三、四强度理论) 屈服破坏强度理论
24
四个强度理论
强度理论的适用范围及其应用
所谓脆性和塑性材料,一般指在常温、静载、 简单受力条件下,危险状态分为脆性断裂和 塑性屈服。此时,脆性材料选用关于脆断强 度理论,塑性材料选用关于屈服的强度理论 材料危险状态不仅与材料有关,还与材料所 处应力状态、温度、变形速率等因素有关
P 横截面
均匀分布在横截面上内力
x Dt
根据轴向平衡
x Dt P
由此得
D2
4 p
D x p 4t
34
Example-1
x t
p
t t
x
p
t
计算环向正应力,采用相距 t 单位长度的两个横截面从圆 筒中切出一个圆环,再用一 D 径向纵截面将其切成两半, 并保留一半为研究对象。 根据垂直方向平衡
4
强度理论的概念
复杂应力状态强度研究方法 假 说
部分实验 推测复杂应力状态下破坏原因
强度条件
强度理论:
实验与理论不一致推动理论发展
对材料破坏起主要作用的某种因素判断或假说 观点:不论材料处于何种应力状态, 只要该因素超过极限值,就形成破坏。
5
强度理论的概念
材料的破坏现象
铸铁
拉伸时,沿拉应力最大的横截面断裂 扭转时,沿拉应力最大的450螺旋面断裂
27
四个强度理论
此时
x , xy , y 0
代入平面应力极值应力公式
x y max x y 2 xy 2 2 min
2
从而
1 2 2 2 3
2 t t
0
D p sin d 0 2
径向纵截 轴向单位长度
由此得
D t p 2t
35
Example-1
x t t
t
x
p
D
计算径向正应力,采用相 距单位长度两个横截面从 圆筒中切出一个圆环,再 用环向纵截面将内部掏出 径向平衡
环 向 纵 截 轴向 单位 厚度
[]=80MPa
x
t t
t
x
p
D
故 r3 1 3 53 MPa 因此,圆筒满足强度要求。
38
Example-2
P A a L B a P
300 126 14.4 9 14.4
已知 a=0.6m,P=100 kN, 许用应力[]=120MPa 试 全面校核钢梁强度
25
四个强度理论
塑性材料在三向拉应力、低温或冲击(高 变形速率)等条件下将导致脆性断裂破坏。 脆性材料在三向压应力作用下,也表现出 明显的塑性变形能力 因此,对于较复杂的应力状态,首先要确 定材料是处于脆性状态还是塑性状态,而 后选用相应的的强度理论进行校核或设计
26
四个强度理论
一种常见平面应力状态相当应力 图示应力状态在弯曲、弯扭、 扭拉(压)等组合变形构件中经 常出现。设其泊松比为,现 计算各种强度理论中相当应力
㊉
x
max
max
M
㊀
Pa
Pa
x
41
Example-2
危险截面上危险点
max点:翼缘上下边 (考虑水平切应力 ) max点:腹板中间
翼缘和腹板交界处点C: 和 都较大,亦是危险点
C
max max
42
Example-2
应力计算
max
M max h Qmax S I 2 I b
破坏条件(塑性屈服) uf= ufu
21
四个强度理论
复杂应力状态下的畸变能密度为
1 2 2 2 uf ( ) ( ) ( ) 1 2 2 3 3 1 6E
单向应力状态下,当材料达到屈服极限f时, 畸变能密度为
1 2 ufu s 3E
39
Example-2
P A B P
300 126 14.4 9 14.4
a
Q
㊀
L
P P
㊉
a
解 内力分析
x
作内力图 由图可见,A左(B右) 截面为危险截面
M
㊀
Pa
Pa
x
40
Example-2
危险截面上应力分布
(水平切应力公式参见下册P7例题12-3)
注:以前分析中忽略了翼缘中的水平切应力 Q
㊀
P P
p
d
p D 1 r ( D 2d ) 1
D 1 r p p D 2d 1 2d / D
p
r
外表面承受大气压
36
Example-1
p
应力计较
r
max
D t p 2t
p r 1 2d / D
t
r
t r
r max 2d p, t D
d非常小,忽略r影响
薄壁圆筒各点处于二向应力状态, 则主应力
1 t
D D p, 2 x p, 3 0 2t 4t
37
状态判断
t x
Example-1
按最大切应力理论校核强度 由于
1 t 53 MPa 2 x 26.5 MPa 3 0
11
常用的四个强度理论
常温和静载条件下
12
四个强度理论
最大拉应力理论(第一强度理论) 破坏观点: 材料断裂强度极限状态取决于
它承受的最大拉应力。 即无论应力状态如何,只要最大拉应力1达 到极限应力u时,材料将发生断裂破坏 u---简单拉伸试验时所测得极限应力
破坏条件 强度条件
1=u
1 u
18
四个强度理论
最大切应力理论(第三强度理论)
破坏观点: 材料屈服的强度极限状态取决于
最大切应力 即无论应力状态如何,只要最大切应力max达 到单向拉伸屈服极限应力u时,材料将在最大 切应力所在的截面上发生滑移而出现屈服破坏 在三向应力状态下,最大切应力为
max= (1 3 )/2
第九章 强度理论
主 讲人: 张能辉
1
强度理论的概念
2
强度理和压缩 圆直杆扭转
T T
max
max [ ]
通过实验手段确定许用应力[][]
3
强度理论的概念
复杂应力状态强度条件
复杂应力状态不可能仅通过 实验手段来解决强度条件 (1 , 2, 3 无数种组合, 实 验条件很难实现, 无法穷尽) 如何描述复杂应力状态情形下 材料破坏的机理和条件呢?
15
四个强度理论
最大伸长线应变理论(第二强度理论)
e1=eu
利用胡克定理,给出在线弹性范围内, 以主应力表示的破坏条件
1 ( 2 3 ) u ,
强度条件
u Ee u
u
nu
16
1 ( 2 3 )
四个强度理论
最大伸长线应变理论(第二强度理论) 适用材料及应力状态
2
四个强度理论
第三强度理论(最大切应力理论)
r3 1 3 4
2
2
第四强度理论(形状改变比能理论)
1 2 2 2 r4 ( ) ( ) ( ) 1 2 2 3 3 1 2 2 3 2
材料单向拉伸时,与屈服强度u相应的极限 最大切应力为 u= s /2
19
四个强度理论
破坏条件(塑性屈服)
强度条件
1 3 s
s
ns
1 3
适用材料及应力状态
该强度理论与塑性材料的试验结果较为吻合, 符合塑性材料在达到一定的载荷后会出现明 显的塑性变形而最后剪断的试验现象
筒体在内压p作用下将在其横截面、纵截面 以及环形截面上引起轴向正应力x、环向正 应力t和径向正应力r。 由于筒体很薄,可认为x和t沿壁厚均布。
33
Example-1
x t t x
p
计算轴向应力,采用横截 t 面将圆筒截开,并选用左 D 段为研究对象 内压作用于筒底总压力
x
D2 P p 4
14
缺点 : 没有考虑2 3的影响;
四个强度理论
最大伸长线应变理论(第二强度理论) 破坏观点: 材料断裂的强度极限状态取决于
它的最大伸长线应变。 即无论应力状态如何,只要最大伸长线应变e1 达到极限线应变eu时,材料将发生断裂破坏 eu---单向拉伸试验所测得最大拉伸应变值
破坏条件
e1=eu
30
强度理论的应用
31
Example-1
t
p
D
已知受均匀内压的圆筒形薄壁容器, 内径D=1060mm,壁厚t=25mm, 内压p=2.5MPa,许用应力[]=80MPa, 试按最大切应力理论校核筒体的强度。
32
Example-1
x t t
t
t r x
x
p
D
解 计算筒体上应力分布
缺点 该强度理论未考虑主应力2的影响 相当应力 r3= 13
20
四个强度理论
畸变能理论(第四强度理论)
它的畸变能密度。 即无论应力状态如何,只要畸变能密度uf达到 材料屈服极限状态的畸变能密度ufu,材料即 发生屈服破坏 。 ufu---材料单向拉伸屈服时所测得畸变能密度
破坏观点: 材料屈服的强度极限状态取决于
四个常用的强度理论分为两类
第一类强度理论(第一、二强度理论) 断裂破坏强度理论 第二类强度理论(第三、四强度理论) 屈服破坏强度理论
24
四个强度理论
强度理论的适用范围及其应用
所谓脆性和塑性材料,一般指在常温、静载、 简单受力条件下,危险状态分为脆性断裂和 塑性屈服。此时,脆性材料选用关于脆断强 度理论,塑性材料选用关于屈服的强度理论 材料危险状态不仅与材料有关,还与材料所 处应力状态、温度、变形速率等因素有关
P 横截面
均匀分布在横截面上内力
x Dt
根据轴向平衡
x Dt P
由此得
D2
4 p
D x p 4t
34
Example-1
x t
p
t t
x
p
t
计算环向正应力,采用相距 t 单位长度的两个横截面从圆 筒中切出一个圆环,再用一 D 径向纵截面将其切成两半, 并保留一半为研究对象。 根据垂直方向平衡
4
强度理论的概念
复杂应力状态强度研究方法 假 说
部分实验 推测复杂应力状态下破坏原因
强度条件
强度理论:
实验与理论不一致推动理论发展
对材料破坏起主要作用的某种因素判断或假说 观点:不论材料处于何种应力状态, 只要该因素超过极限值,就形成破坏。
5
强度理论的概念
材料的破坏现象
铸铁
拉伸时,沿拉应力最大的横截面断裂 扭转时,沿拉应力最大的450螺旋面断裂
27
四个强度理论
此时
x , xy , y 0
代入平面应力极值应力公式
x y max x y 2 xy 2 2 min
2
从而
1 2 2 2 3
2 t t
0
D p sin d 0 2
径向纵截 轴向单位长度
由此得
D t p 2t
35
Example-1
x t t
t
x
p
D
计算径向正应力,采用相 距单位长度两个横截面从 圆筒中切出一个圆环,再 用环向纵截面将内部掏出 径向平衡
环 向 纵 截 轴向 单位 厚度
[]=80MPa
x
t t
t
x
p
D
故 r3 1 3 53 MPa 因此,圆筒满足强度要求。
38
Example-2
P A a L B a P
300 126 14.4 9 14.4
已知 a=0.6m,P=100 kN, 许用应力[]=120MPa 试 全面校核钢梁强度
25
四个强度理论
塑性材料在三向拉应力、低温或冲击(高 变形速率)等条件下将导致脆性断裂破坏。 脆性材料在三向压应力作用下,也表现出 明显的塑性变形能力 因此,对于较复杂的应力状态,首先要确 定材料是处于脆性状态还是塑性状态,而 后选用相应的的强度理论进行校核或设计
26
四个强度理论
一种常见平面应力状态相当应力 图示应力状态在弯曲、弯扭、 扭拉(压)等组合变形构件中经 常出现。设其泊松比为,现 计算各种强度理论中相当应力
㊉
x
max
max
M
㊀
Pa
Pa
x
41
Example-2
危险截面上危险点
max点:翼缘上下边 (考虑水平切应力 ) max点:腹板中间
翼缘和腹板交界处点C: 和 都较大,亦是危险点
C
max max
42
Example-2
应力计算
max
M max h Qmax S I 2 I b
破坏条件(塑性屈服) uf= ufu
21
四个强度理论
复杂应力状态下的畸变能密度为
1 2 2 2 uf ( ) ( ) ( ) 1 2 2 3 3 1 6E
单向应力状态下,当材料达到屈服极限f时, 畸变能密度为
1 2 ufu s 3E
39
Example-2
P A B P
300 126 14.4 9 14.4
a
Q
㊀
L
P P
㊉
a
解 内力分析
x
作内力图 由图可见,A左(B右) 截面为危险截面
M
㊀
Pa
Pa
x
40
Example-2
危险截面上应力分布
(水平切应力公式参见下册P7例题12-3)
注:以前分析中忽略了翼缘中的水平切应力 Q
㊀
P P
p
d
p D 1 r ( D 2d ) 1
D 1 r p p D 2d 1 2d / D
p
r
外表面承受大气压
36
Example-1
p
应力计较
r
max
D t p 2t
p r 1 2d / D
t
r
t r
r max 2d p, t D
d非常小,忽略r影响
薄壁圆筒各点处于二向应力状态, 则主应力
1 t
D D p, 2 x p, 3 0 2t 4t
37
状态判断
t x
Example-1
按最大切应力理论校核强度 由于
1 t 53 MPa 2 x 26.5 MPa 3 0
11
常用的四个强度理论
常温和静载条件下
12
四个强度理论
最大拉应力理论(第一强度理论) 破坏观点: 材料断裂强度极限状态取决于
它承受的最大拉应力。 即无论应力状态如何,只要最大拉应力1达 到极限应力u时,材料将发生断裂破坏 u---简单拉伸试验时所测得极限应力
破坏条件 强度条件
1=u
1 u
18
四个强度理论
最大切应力理论(第三强度理论)
破坏观点: 材料屈服的强度极限状态取决于
最大切应力 即无论应力状态如何,只要最大切应力max达 到单向拉伸屈服极限应力u时,材料将在最大 切应力所在的截面上发生滑移而出现屈服破坏 在三向应力状态下,最大切应力为
max= (1 3 )/2
第九章 强度理论
主 讲人: 张能辉
1
强度理论的概念
2
强度理和压缩 圆直杆扭转
T T
max
max [ ]
通过实验手段确定许用应力[][]
3
强度理论的概念
复杂应力状态强度条件
复杂应力状态不可能仅通过 实验手段来解决强度条件 (1 , 2, 3 无数种组合, 实 验条件很难实现, 无法穷尽) 如何描述复杂应力状态情形下 材料破坏的机理和条件呢?
15
四个强度理论
最大伸长线应变理论(第二强度理论)
e1=eu
利用胡克定理,给出在线弹性范围内, 以主应力表示的破坏条件
1 ( 2 3 ) u ,
强度条件
u Ee u
u
nu
16
1 ( 2 3 )
四个强度理论
最大伸长线应变理论(第二强度理论) 适用材料及应力状态
